Thorough subcells diagnosis in a multi-junction solar cell via absolute electroluminescence-efficiency measurements

Abstract

World-wide studies on multi-junction (tandem) solar cells have led to record-breaking improvements in conversion efficiencies year after year. To obtain detailed and proper feedback for solar-cell design and fabrication, it is necessary to establish standard methods for diagnosing subcells in fabricated tandem devices. Here, we propose a potential standard method to quantify the detailed subcell properties of multi-junction solar cells based on absolute measurements of electroluminescence (EL) external quantum efficiency in addition to the conventional solar-cell external-quantum-efficiency measurements. We demonstrate that the absolute-EL-quantum-efficiency measurements provide I–V relations of individual subcells without the need for referencing measured I–V data, which is in stark contrast to previous works. Moreover, our measurements quantify the absolute rates of junction loss, non-radiative loss, radiative loss, and luminescence coupling in the subcells, which constitute the “balance sheets” of tandem solar cells.

Multi-junction (tandem) solar cells play an essential role in achieving the highest conversion efficiencies¹,²,³,⁴,⁵ through the optimal utilization of the broad solar spectrum with several series-connected subcells with sequentially lower bandgap energies and have been widely studied using various materials such as silicon⁶,⁷, germanium⁸, III–V semiconductors⁹,¹⁰, II–VI compounds¹¹ and polymers¹²,¹³,¹⁴. Although multi-junction tandem solar cells have attracted enormous global attention, their practical efficiencies are still far below the theoretical maxima¹⁵,¹⁶,¹⁷,¹⁸, and practical improvements of tandem solar cells still rely mainly on traditional trial-and-error methods, which invoke huge costs in terms of both time and money. Consequently, it is imperative to develop an effective nondestructive method for diagnosing individual subcells in a fabricated tandem solar cell to obtain detailed and proper feedback for cell design¹⁹,²⁰ and fabrication.

An example of such characterizations is the external-quantum-efficiency (EQE) measurement for tandem solar cells with a light-bias method²¹,²²,²³, which evaluates the efficiency of internal current generation in respective subcells. Although it is a widely used characterization method, the unknown contribution of luminescence coupling²³,²⁴,²⁵,²⁶ is an obstacle, and additional investigations on the effects of luminescence coupling²⁴,²⁵ between subcells have been carried out with a technique that use a specific light source to generate photocurrent in a specific subcell while over-illuminating the others with a bias light.

More recently, a smart method for evaluating internal voltages in subcells via electroluminescence (EL) measurements²⁷,²⁸,²⁹ has been developed and used to characterize state-of-the-art tandem cells⁵,²⁷,²⁸,²⁹. This method is based on the very basic reciprocity relation³⁰ between the solar-cell EQE and EL efficiency in light-emitting-diode (LED) operation. In these reports²⁷,²⁸,²⁹, the EL intensity was formulated and measured in an arbitrary unit, and an artificial adjustment (post-renormalization) of the internal subcell voltages to the measured total voltage was necessary. We need caution because such an adjustment leads to erroneous conclusions about the optimal design when additional sources of voltage alterations exist in tunnel junctions, ohmic contacts, and/or series resistance. Hence, a direct experimental evaluation method to characterize subcell internal properties is highly demanded.

Here we propose a direct experimental diagnosis method of individual subcells in a tandem solar cell via quantitative measurements of the absolute EL efficiency y_ext^LED and the formulations of the subcell external-luminescence-quantum efficiency y_ext (see details in Methods). We applied the proposed method to a satellite-use GaInP/GaAs/Ge 3-junction tandem solar cell and verified that the absolute-EL-efficiency measurement provides a simple, reliable, and straightforward diagnosis method without requiring any artificial adjustments. Moreover, this experiment thoroughly disclosed not only the subcell I–V curves and essential photovoltaic parameters but also the detailed tables or graphs of energy losses, such as junction loss, non-radiative loss, radiative loss, luminescence couplings, and thermalization loss in the respective subcells. We obtained useful analysis tables, exactly like balance sheets established in bookkeeping or accounting, to assess and provide intriguing insights into the apparently complicated characteristics of tandem solar cells.

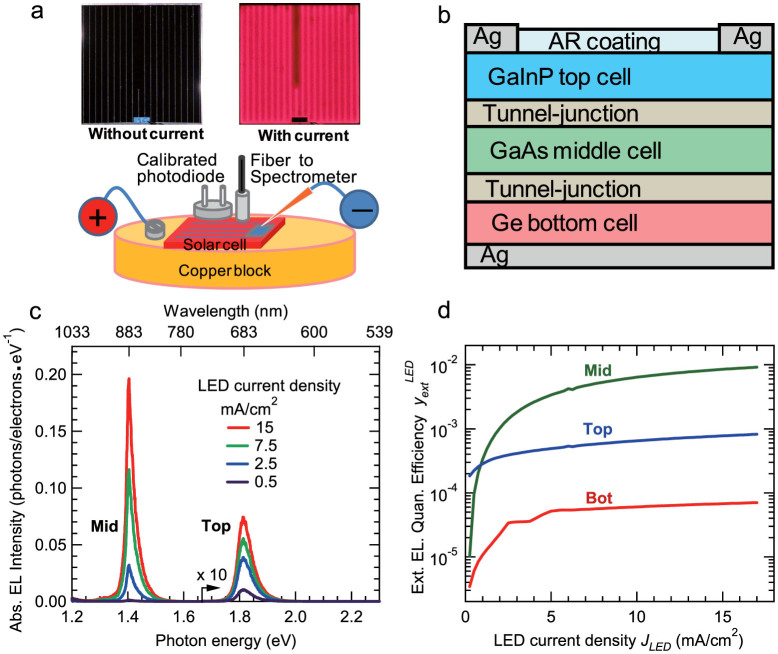
Figure 1a presents a schematic of the solar-cell sample and the EL measurement. The two photographs show the solar cell without and with a forward-bias injection current, where the solar-cell device is operated as a LED for the EL measurement. Figure 1b presents the schematic structure of the tandem GaInP/GaAs/Ge 3-junction solar cell. Figure 1c presents the measured absolute EL spectra (above 1.2 eV) of the solar cell with various injection-current densities. The photon energies (1.40 and 1.81 eV) of the two EL peaks correspond to the bandgap energies of the middle (GaAs) and top (GaInP) subcells. Note that the two peaks have an intensity difference of approximately a factor of 10, and the dependences on the injection current also differ. Figure 1d shows the measured external EL quantum efficiency y_ext^LED = qR_{ext_i →0} /J_LED of the top (i = 1), middle (i = 2), and bottom (i = 3) subcells, plotted on a log scale as functions of the injection current density J_LED, where R_{ext_i→0} is the external radiative emission rate of the subcell. It is demonstrated that y_ext^LED of all the subcells increases gradually with increasing injection-current density, which indicates an increased radiative recombination rate at increased carrier densities in the subcells³¹,³².

Figure 1. Absolute EL measurement of the 3-junction solar cell.

(a). Schematic of the experimental setup for the absolute EL measurement of the solar cell. The top panel presents a photograph of the solar cell without and with injection current (15 mA/cm²). (b). Schematic structure of the GaInP/GaAs/Ge 3-junction solar cell. (c). Absolute EL spectra divided by injection-electron number (abs. EL efficiency) for various injection-current densities of the triple-junction solar cell. (d). The measured external EL quantum efficiencies (ext. EL. quan. efficiency) of the subcells under the operation of an LED (y_ext^LED) as a function of the injection-current density. Note that the y-axis of the EL spectra is the absolute photon number per second divided by the injection carrier number per second, i.e., the y-axis represents the external EL quantum efficiency (y_ext^LED) as a function of the photon energy. Consequently, the y_ext^LED of the subcells (Fig. 1d) can be obtained through the integrations of the EL peaks in the EL spectra.

Based on the carrier-balance equations (1)–(3) (see Methods) and the data in Fig. 1d, we derived the external luminescence quantum efficiency y_ext of the 3 subcells as a function of the solar-cell output current density J under the AM0 1-sun solar-cell operation, where we used subcell photon fluxes corresponding to qR_sun1 = 17.1 mA, qR_sun2 = 17.9 mA, and qR_sun3 = 26.4 mA derived via the solar-cell EQE data presented in Supplementary Information.

Figure 2a plots y_ext for 3 subcells on a log scale as a function of the solar-cell output current density J. The values of J_m (current density of solar cell under maximum-output-power condition) and J_sc (current density of solar cell under short-circuit condition) marked in Fig. 2a are obtained from the measured experimental results as shown in Fig. 2b. The solid curves in Fig. 2b represent the I–V curves of three subcells and their total under equal-subcell-current constraint. The dashed curve represents the I–V curve in the theoretical radiative limit as a reference. The open circles represent the independently measured I–V curve of the solar cell under the AM0 1-sun condition, which agrees very well with the total I–V curve derived via the EL measurement, demonstrating that the present method is reliable and feasible.

Figure 2. External luminescence quantum efficiency under solar-cell operation and I-V curves of the 3-junction solar cell.

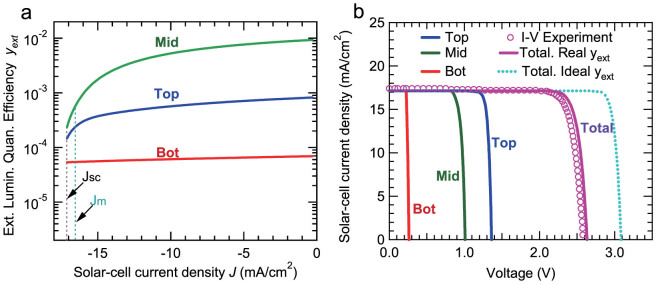
(a) External luminescence quantum efficiencies (ext. lumin. quan. efficiency) of the subcells under solar-cell operation y_ext as a function of the photo-generated current density. (b) The theoretically calculated and experimentally measured I–V curves of the GaInP/GaAs/Ge 3-junction solar cell under the condition of 1-sun AM0. The I–V curve with ideal y_ext (radiative limit) was calculated under the assumption that the subcells are in a condition of the radiative limit (R_nr = 0), and the ideal conversion efficiency of the present tandem solar cell structure with ideal y_ext was calculated to be 35.6%. The values of J_m (current density of solar cell under maximum-output-power condition) and J_sc (current density of solar cell under short-circuit condition) marked in (a) are obtained from the experimental results as shown (b).

Note that the bending of the I–V curves near the maximum-power point (J_m, V_m) is softer than that in the radiative limit, which lowers the filling factor (FF). Because the sum of the subcell I–V curves exhibits almost the same bending as that obtained by the independently measured I–V curve, our analysis revealed that the soft bending in the I–V curves stems from the soft bendings of the y_ext curves near J_m in Fig. 2a. In other words, the soft bending is caused by the lowered luminescence quantum efficiency, or radiative recombination efficiency, at low carrier density and not by series resistance.

We additionally comment that the very small difference between the experimental and predicted I–V curves proves an important point that additional sources of voltage in tunnel junctions, ohmic contacts, or/and series resistance are negligibly small or that the I–V data were not degraded by flaws in the transport properties of the tandem cell thanks to the high quality of the present device. We emphasize that this point cannot be assumed without justification but was experimentally proven via our two independent measurements of the absolute EL efficiency and the I–V curve. Note also that we did not characterize possible non-uniformity of the sample, which may limit the accuracy of the present experiments and should be studied in the future. However, the very small difference between the experimental and predicted I–V curves proves that the effects of such limitations are presently very small.

Table 1 summarizes the essential subcell photovoltaic parameters derived from these I–V curves. The respective contributions of the subcells (top, middle, and bottom) to the open-circuit voltage (1.361 V, 1.010 V, and 0.262 V, respectively), maximum-power voltage (1.230 V, 0.862 V, and 0.226 V, respectively), and conversion efficiency (15.2%, 10.7%, and 2.8%, respectively) were clearly revealed. The short-circuit current, open-circuit voltage, and conversion efficiencies (J_sc^cal = 17.14 mA/cm², V_oc^cal = 2.63 V, and η _sc^cal = 28.7%, respectively) derived through the solar-cell EQE and the EL efficiency show good agreement with the measured results (J_sc^exp = 17.38 mA/cm², V_oc^exp = 2.58 V, and η _sc^exp = 27.4%, respectively) determined via the direct I–V measurement.

Table 1. Major parameters of the GaInP/GaAs/Ge 3-junction solar cell obtained using the present method and experiments under the condition of AM0 1Sun. V_oc__ideal is defined as the open-circuit voltage under the condition of a radiative limit, and ΔV_oc is defined as the difference between V_oc__ideal and V_oc.

Cell	ΔVoc (V)	Voc_ideal (V)	Voc (V)	|Jsc| (mA/cm2)	Vm (V)	|Jm| (mA/cm2)	FF	ηsc
Top	0.12	1.48	1.36	–	1.23	–	0.88	0.152
Middle	0.07	1.08	1.01	–	0.86	–	0.832	0.107
Bottom	0.27	0.53	0.26	–	0.23	–	0.847	0.028
Total	0.46	3.09	2.63	17.14	2.32	16.7	0.859	0.287
I–V Exp.	–	–	2.58	17.38	2.24	16.5	0.826	0.274
Deviation	–	–	0.05	0.24	0.08	0.2	0.033	0.013

Because the present measurements of EL efficiency and solar-cell EQE provide all the terms of emission-loss, luminescence-coupling, and nonradiative-loss processes (R_{ext_i→0}, R_{ext_i→i+1}, and R_{nr_i}) in addition to the I–V curves (Fig. 2b) as well as the essential subcell photovoltaic parameters (Table 1), we finally evaluated in Table 2 all the loss/output rates in the tandem solar cell under AM0 1-sun irradiation under the working condition of maximum output power. We illustrate the portions of the detailed energy losses of the solar cell in Fig. 3.

Table 2. Parameters of the GaInP/GaAs/Ge 3-junction solar cell working at the maximum-output-power condition. All the values are given in ratio.

	Input		Loss
Cell	AM0 1Sun	LC	TH	EM	LC	NR	JN	Power output
Top	0.305	–	0.076	1E-6	2E-05	0.006	0.072	0.152
Middle	0.224	2E-05	0.037	6E-6	7E-05	0.012	0.067	0.107
Bottom	0.207	7E-05	0.072	3E-6	–	0.050	0.057	0.028
TR	0.264	–	–	–	–	–	–	–
Total	1.000	9E-5	0.185	1E-5	9E-5	0.068	0.196	0.287

Figure 3. Schematic diagram of the quantified energy losses during photovoltaic operation of the GaInP/GaAs/Ge 3-junction solar cell, made on the base of the measured external luminescence quantum efficiencies.

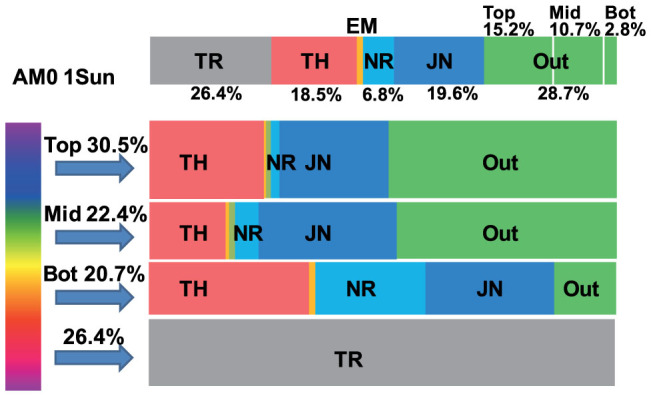
The working condition of the solar cell was 1-sun AM0 with the maximum output power. The input power of sun light is normalized to 100%, and all the values of the parameters are ratio. Out: Output power of the solar cell. TR: transmission loss, TH: thermalization loss, EM: external emission loss, NR: non-radiative recombination loss, JN: junction loss (the energy loss caused by the voltage drop of the carriers from bandgap voltage to internal voltage of the junction). The values of the energy losses are summarized in Table 2.

Table 2 and Fig. 3 analyze the sources of energy gain and loss in the respective subcells. In the top subcell, 30.5% solar energy is absorbed, and 15.2% is converted into electric energy, while the remainder goes into 0.6% nonradiative recombination (NR) loss, 7.6% thermalization (TH) loss and 7.2% junction (JN) loss. In the middle subcell, 22.4% of the solar energy is absorbed, and 10.7% goes to output power, while the remainder goes into 1.2% NR loss, 3.7% TH loss and 6.7% JN loss. In the bottom subcell, 20.7% of the solar energy is absorbed, and only 2.8% goes to output power, while the remainder goes into 5.0% NR loss, 7.2% TH loss and 5.7% JN loss. The solar energy below the bottom-cell bandgap is not absorbed but accounts for a transmission (TR) loss of 26.4%. More detailed balance sheets are provided in Supplementary Information.

The contributions of radiative emission (EM) loss and luminescence coupling (LC) were negligibly small in the maximum-output-power condition, as shown in Table 4 and Fig. S2a in Supplementary Information. In the open-circuit condition, the quantum efficiencies of the top-to-middle LC and the middle-to-bottom LC were 1.0% and 12.0%, respectively, as shown in Table 5 and Fig. S2b in Supplementary Information. These values are important in investigating the problem of artifact signals in EQE measurement with light bias²¹,²²,²³, and also for optimal solar cell design.

Table 3. Calculation formulas of the parameters (in power density) of the solar cell.

Item of energy loss	Calculation formula
EM (Radiative emission)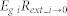
LC (Luminescence coupling)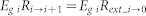
NR (Nonradiative recombination)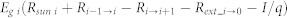
TH (Thermalization loss)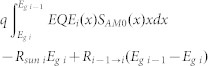
TR (Transmission loss)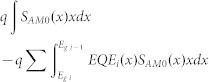
JN (Junction loss)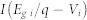

Table 4. Carrier balance sheet for maximum-output-power condition (J = J_m, V = V_m) with 1-sun AM0. The input ratios of all the subcells are normalized to 1.

	Input (Ratio)		Loss (Ratio)
Cell	AM0 1Sun	LC	EM	LC	NR	Output (Ratio)
Top	1.00	–	5E-06	6E-05	0.025	0.975
Middle	1.00	6E-05	3E-05	4E-04	0.067	0.933
Bottom	1.00	3E-04	2E-05	–	0.368	0.632

Table 5. Carrier balance sheet for open-circuit condition (J = 0, V = V_oc) with 1-sun AM0. The input ratios of all the subcells are normalized to 1.

	Input (Ratio)		Loss (Ratio)
Cell	AM0 1Sun	LC	EM	LC	NR	Output (Ratio)
Top	1.00	–	8E-04	0.01	0.989	0
Middle	1.00	0.01	0.009	0.12	0.881	0
Bottom	1.00	0.081	8E-05	–	1.081	0

It is evident from Fig. 3 that the NR and TH losses in the bottom cell are much larger than those in the other cells and that improvements in the design and material quality of the bottom-cell are straightforward approaches to obtain a higher conversion efficiency. The total conversion efficiency in the radiative limit of the present solar cell, where all the R_{nr_i} values are zero, is 35.6%. To reduce the large TH and TR losses, changes in the sub-cell bandgap energies or additional subcells are necessary.

In conclusion, we demonstrated the complete quantification of the subcell I–V curves, the essential photovoltaic parameters, and especially the detailed energy losses caused by all loss mechanism including thermal loss, nonradiative loss, junction loss and radiative emission loss of subcells in multi-junction solar cells based on the absolute EL quantum efficiency measurement. The established method is simple, straightforward, unambiguous, and useful for any type of tandem solar cells. Hence, the proposed method has the potential to become a standard method to thoroughly characterize individual subcell properties, playing an important role in the design and development of high-efficiency tandem solar cells.

Methods

Carrier-balance equations and the measurement principle

Considering that the subcells of a 3-junction tandem solar cell are series-connected and in sequential order of lower bandgap energies E_g1 > E_g2 > E_g3, the carrier-balance equations describing the optoelectronic processes in the tandem solar cell irradiated with sunlight are expressed as

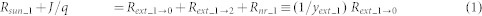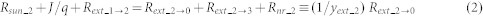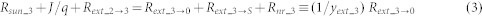Here, 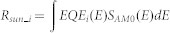is the absorption rate of sunlight, and the subscripts i = 1, 2 and 3 refer to the top, middle and bottom subcells, respectively; J is current density (+ for forward injection current and - for photo-generated current) ; q is electron charge; R_{ext_i→0} is the external radiative emission rate, where the subscript 0 refers to air and the arrows indicate the directions of the radiative emissions. The values of R_{ext_i→0} were experimentally obtained using absolute EL efficiency measurements; R_{nr_i =} (1/y_{ext_i}-1)R_{ext_i→0} - R_{ext_i→i+1(S)} is the nonradiative recombination rate; R_ext is radiative emission rates; R_{ext_i→i+1} = (a_bottom/a_top)n²_i+1 R_{ext_i→0} (n_i+1 < = n_i) or (a_bottom/a_top)n²_i R_{ext_i→0} (n_i+1 > = n_i) is the radiative emission rate from the upper cells to the lower cells (namely, luminescence coupling), where a_bottom and a_top are angle-averaged absorptivities or emissivities on the bottom and top sides, respectively, and can be evaluated from reflectivity measurements, reflectivity calculations via refractive indices, or/and the measurements of EQE_i. When reflectivity for EL is close to zero at upper and lower interfaces of ith layers and n_i < n_i+1, we have an approximate form of R_{ext_i→i+1} = n²_i R_{ext_i→0}; R_{ext_3→S} is a term showing radiative emission from the bottom subcell to a substrate and is set to 0 for the present device. The second equalities in equations (1)–(3) give the definitions of the external luminescence quantum efficiency y_{ext_i}. The first equalities in equations (1)–(3) represent the balance between the carrier generation (left-hand side) and the carrier loss (right-hand side).

In the LED or dark operation, we have R_sun1 = R_sun2 = R_sun3 = 0 and J = J_LED > 0. We measure R_{ext_i→0}, or the external EL quantum efficiency y_ext^LED = qR_{ext_i→0}/J_LED, as functions of the injection current density J_LED. In the solar-cell or light operation, we have R_sun1 > 0, R_sun2 > 0, R_sun3 > 0, and J < 0. The values of R_sun1, R_sun2, and R_sun3 can be calculated from measured data of solar-cell EQE and the solar spectrum.

By measuring absolute data sets of y_ext^LED versus J_LED in the LED operation, we obtain absolute data sets of y_ext versus J under the solar-cell operation via equations (1)–(3).

Prediction of I-V characteristics

According to the reciprocity relation between EL and 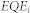of a solar cell³⁰, the external radiative emission rate R_{ext_i→0} can also be given as

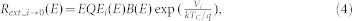where 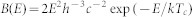is the spectral photon density of a blackbody, 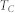is the temperature of the cell (300 K), and 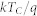is the thermal voltage. R_{ext_i→0} as a function of the current density J are experimentally measured. Therefore, the I-V curves of the subcells can be predicted according to the equation:

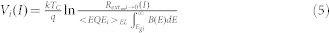Note that the subcell voltage includes a loss contribution²⁰,³⁰ equal to kTlny_{ext_i}, from which we obtain the internal subcell I-V relations and essential photovoltaic parameters such as V_oc, V_m, J_m, FF, and .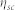

Moreover, if we know the absolute value of R_{ext_i→0}, then we can obtain the absolute values of R_{ext_i→i+1}, as n²_i R_{ext_i→0} for negligible reflectivity for EL at upper and lower interfaces of ith layers and for n_i < n_i+1, and those of R_{nr_i} as the difference between the carrier generation (J_LED/q or R_{sun i} - J/q) and R_{ext_i→0} + R_{ext_i→i+1}. Thus, we can determine the absolute values of all the terms of R_{ext_i→0}, R_{ext_i→i+1}, and R_{nr_i}, from which we may evaluate all the energy-loss/output rates via radiative and non-radiative recombinations, luminescence coupling, junction loss, and output powers. Formulas used for the derivation of the parameters EM, LC, TH, NR, JN, and TR are summarized in Table 3.

Absolute-EL and solar-cell EQE measurements

We used a satellite-use high-efficiency GaInP/GaAs/Ge multi-junction solar cell to verify the proposed method. The size of the solar cell is 2 × 2 cm². The absolute EL powers emitted from the tandem solar cell were measured with calibrated Si and InGaAs photodiodes in the face-to-face geometry as shown in Fig. 1a. The uncertainty in the calibration of the standard Si photodiode was below 1.6%. The results of the measurements were verified using an integrating-sphere total-flux measurement system, arranged in Photometry and Radiometry Division, National Metrology Institute of Japan.

Because the Si photodiode was sensitive to EL signals from the top and middle subcells, we characterized the EL spectra using a spectrometer and corrected the power sensitivity of the Si photodiode. The spectrometer consists of a monochromator and a liquid-nitrogen-cooled silicon charge-coupled device (CCD), which has a spectral response calibrated with a standard white lamp.

The absolute EL powers of the Ge bottom cell were measured with a 1.5-μm long-pass filter and the calibrated InGaAs photodiode.

We estimated the overall uncertainty of 20% in the worst case for the measured absolute EL efficiencies y_ext^LED of the subcell. This uncertainty is negligibly small in the present study, because contributes to an uncertainty within only 8 meV in voltage loss through kTln(y_ext^LED). The uncertainties in the current and voltage measurements were within 0.03%, and an estimated spectral deviation of the AM0 solar simulator was within 10% in the spectral regions of interest.

The solar-cell external quantum efficiency (EQE^sc) of each subcell was measured using the light-bias method via a standard procedure²¹,²², and a standard correction was added for the measurement artifacts²³. The reflectivity of the solar cell was measured with a UV-visible spectrophotometer (JASCO-V570). These measured results are given in Supplementary Information.

Author Contributions

H.A., M.Y., and Y.K. supervised the project. M.I. supplied the sample. S.C., M.Y. and L.Z. performed the characterizations and calibrations. L.Z., S.C., M.Y., H.A., T.M., and C.K. performed the theoretical calculations. S.C. and H.A. analyzed the results and wrote the paper. All the authors joined in the discussion and commented on the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information