Photoresistance Switching of Plasmonic Nanopores

Abstract

Fast and reversible modulation of ion flow through nanosized apertures is important for many nanofluidic applications, including sensing and separation systems. Here, we present the first demonstration of a reversible plasmon-controlled nanofluidic valve. We show that plasmonic nanopores (solid-state nanopores integrated with metal nanocavities) can be used as a fluidic switch upon optical excitation. We systematically investigate the effects of laser illumination of single plasmonic nanopores and experimentally demonstrate photoresistance switching where fluidic transport and ion flow are switched on or off. This is manifested as a large (∼1–2 orders of magnitude) increase in the ionic nanopore resistance and an accompanying current rectification upon illumination at high laser powers (tens of milliwatts). At lower laser powers, the resistance decreases monotonically with increasing power, followed by an abrupt transition to high resistances at a certain threshold power. A similar rapid transition, although at a lower threshold power, is observed when the power is instead swept from high to low power. This hysteretic behavior is found to be dependent on the rate of the power sweep. The photoresistance switching effect is attributed to plasmon-induced formation and growth of nanobubbles that reversibly block the ionic current through the nanopore from one side of the membrane. This explanation is corroborated by finite-element simulations of a nanobubble in the nanopore that show the switching and the rectification.

The manipulation of fluidic transport through nanoscale apertures can benefit many applications,¹ including water desalination,^2,3 molecule/particle separations,⁴⁻⁶ biosensing,⁷⁻¹³ and fuel cells.^14,15 Unlike micro- and macrofluidic devices, which can easily be controlled using pressure changes and mechanical valves, it remains challenging to control the flow in nanochannels, particularly in tiny nanopores. Pressure control is not suitable for nanochannels due to high fluidic resistances, and it is not trivial to implement fluidic valves at the nanoscale. Furthermore, effects from interactions between the liquid and surrounding surfaces, such as electrostatic interactions, van der Waals interactions, hydrogen bonds and hydrophobic interactions, become more pronounced for nanofluidic systems.¹⁶ Control of the flow in nanopores was so far primarily limited to artificial hydrophobic nanopores that were opened or closed by reversible filling the pores with water by applying high transmembrane electric fields.^17,18

Recently, plasmonic gold nanostructures were integrated into nanofluidic devices with the aim to provide new functionalities.^11,19−23 Plasmon excitation (optically induced charge oscillations of the metal electrons) in such gold nanostructures opens up the way to various applications, including biosensing¹¹ and plasmonic trapping.^21,24,25 Furthermore, local heating is a prominent effect in nanoplasmonic systems,^22,26,27 which was, for example, recently used to improve the detection rate of a plasmonic nanopore sensor by thermophoretically attracting molecules to a plasmon-heated nanopore.²³

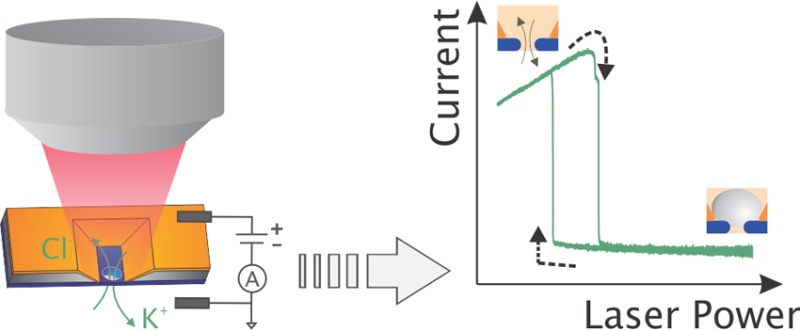
Here, we present the first demonstration of plasmon-induced switching of the ionic transport through a solid-state plasmonic nanopore. We have fabricated a nanofluidic device (see Figure 1), which comprises a solid-state silicon nitride (SiN) nanopore inside a plasmonic gold nanoslit cavity (so-called “pore-in-cavity”). We show that laser illumination can reversibly lead to a huge (≥500%) increase in the pore resistance and simultaneously to a rectified ionic current–voltage characteristic. We elucidate the origin of this intriguing effect and conclude that the most likely scenario involves optical triggering of a nanobubble that blocks the nanopore. Simulations of the current–voltage response with the exclusion of fluidic transport by a nanobubble corroborate the experimental results, including rectification in the high-resistance state. Our plasmonic nanopore acts as an open nanovalve in the initial resting state (without illumination), whereas previously reported nanopore valves were initially in a closed state.^17,18 Moreover, the device operates as a reversible ion rectifier in the high-resistive state, without the need to chemically modify the nanopore surfaces or to alter the buffer properties. The ability to dynamically control fluidic transport through nanopores using plasmon excitation may impact the understanding of optical control of fluidic transport in nanopores systems, which in turn may aid the development of sensor and filter applications.

Figure 1.

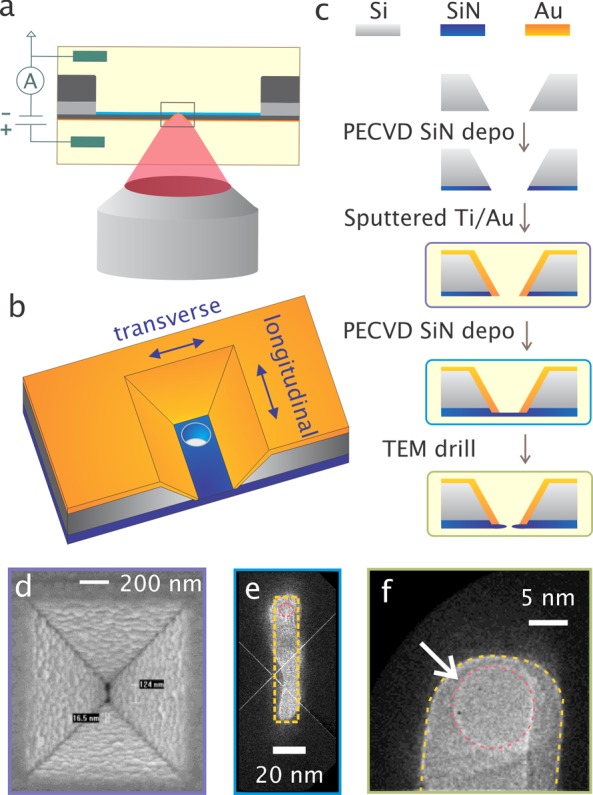
Solid-state nanopore integrated with a plasmonic nanoslit cavity. (a) Schematic representation of the concept. Plasmon-induced effects are measured electrically through changes in the ionic current flowing through the nanopore. (b) Three-dimensional schematic representation of the plasmonic nanopore device, consisting of a plasmonic cavity on top of a nanopore. The figure is not to scale and the membrane may also not be perfectly uniform. The arrows indicate the longitudinal and transverse direction of plasmon excitation. (c) The membrane formation process involves coating the membrane with PECVD silicon nitride, followed by sputtering of Au and an additional layer of PECVD silicon nitride. Finally, a nanopore is drilled using a TEM. (d) SEM images of the plasmonic nanocavity. (e) TEM image of a silicon nitride membrane surrounded by the gold nanocavity. The yellow dashed line indicates the designed boundary of the gold cavity. (f) Zoomed TEM image of the top part of panel (e), showing a typical 10 nm nanopore inside the gold nanocavity (marked by the arrow). The interfaces between the gold and the SiN are delineated by a yellow dashed curve and the nanopore is marked with a red dashed circle overlaid on the image.

Solid-State Nanopore Integrated with a Plasmonic Nanoslit Cavity

We fabricated plasmonic pore-in-cavity devices from 200 mm silicon-on-insulator (SOI) wafers, consisting of 200 μm of bulk Si, 1 μm of buried dioxide layer (BOX), and an additional 700 nm thick top Si layer. Deep-UV lithography and standard process steps were used to fabricate rectangular nanoslits in the top Si layer, with open access through the whole wafer, as described in detail before.²⁸ Figure 1c shows the additional processing steps. First, a 50 nm layer of PECVD SiN was deposited on the backside to reduce the device capacitance. Next, gold was sputtered on top of the silicon membrane to support excitation of surface plasmons. Another 50 nm SiN layer was then deposited from the backside to form a free-standing closed membrane at the bottom of the nanoslit. Finally, a transmission electron microscope (TEM) was used to open a single 10 nm pore in the closed membrane. Figure 1e and 1f show TEM images of a final device with a SiN/Au cavity and a drilled nanopore. For device characterization and experiments, the chip was mounted in a custom-made flow cell such that it separated two buffer compartments. The plasmonic nanopore was then aligned with the focal spot of a laser in our custom-built microscope (see Figure 1a). The ionic current flowing through the pore-in-cavity was measured using a commercial amplifier, as detailed in the Methods section. The electrical potential was applied to the side with the gold cavity, and the other side was connected to ground, which defines the applied bias direction for positive and negative values in the experiments.

Plasmon-Induced Resistance Switching

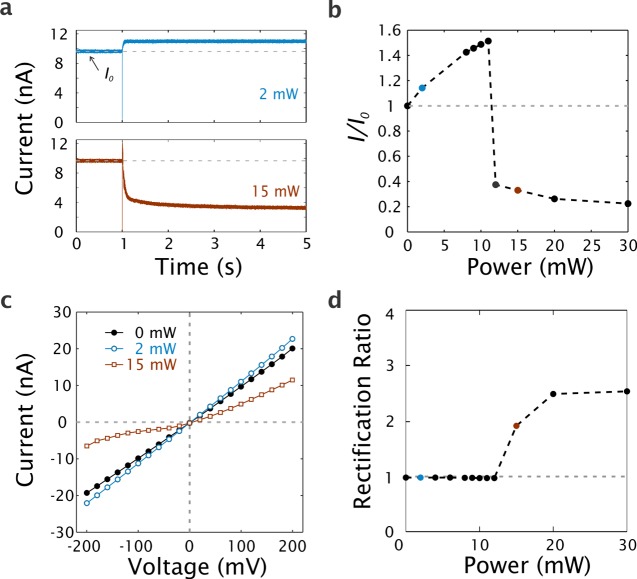
From previous simulations and experiments,^29,30 we know that surface plasmons can be resonantly excited in the plasmonic nanocavities at NIR wavelengths. We therefore use a 785 nm laser, tightly focused through a microscope objective (NA 1.2), to illuminate the plasmonic nanopore chips. Figure 2a shows examples of time traces without and with laser illumination, recorded at −100 mV. Upon switching on the laser excitation, the current response shows opposite behavior for 2 mW and 15 mW laser power. At 2 mW, the steady-state nanopore current increases, whereas it instead decreases strongly at 15 mW laser power. We define the baseline without laser illumination as the open-pore current (I₀) and measure how the nanopore current (I) changes upon light illumination at different powers. The normalized current I/I₀ is presented in Figure 2b. The current increases monotonically with laser power up to around 12 mW. This is attributed to plasmonic heating and the corresponding increase in the buffer conductivity, as reported for other types of plasmonic nanopores.²² Above 12 mW, the current level instead decreases dramatically upon plasmon excitation. In the example of Figure 2, the photoresistance at 30 mW becomes 500% of the original resting pore resistance. This current decrease is reversible: after switching off the laser illumination, the current level returned to its original value. Qualitatively, the results are the same when switching the polarity of the voltage that is used to monitor the ionic current (to +100 mV, see Supporting Information Figure S1). However, the threshold laser power at which excitation results in a current decrease instead of an increase is higher at positive polarity and the magnitude of the current decrease is also slightly lower. This is a first indication of an asymmetry in our system, as discussed further below.

Figure 2.

Ionic currents upon plasmonic excitation. (a) Ionic current versus time for 2 mW and 15 mW illumination turned on at 1 s, recorded at −100 mV. The sign of the current traces is reversed for clarity. The dashed lines indicate the open-pore current level I₀ before light illumination. (b) Normalized current deviation I/I₀ as a function of laser power at −100 mV. Blue and brown points indicate the laser powers of 2 mW and 15 mW, respectively. The dashed line at I/I₀ = 1 divides the figure into a top area of current increase and a bottom area of current decrease. (c) Current–voltage curves at 0 mW (black), 2 mW (blue), and 15 mW (brown). (d) Rectification ratio γ(100 mV) versus laser power. The dashed line of γ(100 mV) = 1 indicates perfect linearity.

The complete current–voltage (I–V) characteristics was investigated for three cases: (1) without laser illumination, (2) for a plasmon-induced current increase at low laser power, and (3) for a plasmon-induced current decrease at higher laser power. I–V curves in the range between −200 mV and +200 mV are presented in Figure 2c. Without laser illumination, the I–V curve (black) is linear and the slope yields a pore resistance of 11.0 MΩ. For a nanopore with a diameter of 10 nm, as determined from TEM images, and using the model by Kowalczyk et al.,³¹ this gives an effective pore length of 9.1 nm. In agreement with previous reports on other solid-state nanopore systems,³¹ the effective thickness is significantly thinner than the deposited SiN (50 nm). We also note that the SiN membrane thickness was not perfectly uniform (as measured by TEM), and we chose the thinnest area to drill our nanopore. The I–V curve is linear also upon illumination with 2 mW laser light, with the pore resistance reduced to 9.1 MΩ. By contrast, at 15 mW illumination, the I–V curve becomes rectified, with a significantly stronger plasmon-induced current decrease at negative voltages. We evaluate the degree of the rectification by defining a rectification ratio

1

In Figure 2d, V_app is set at 100 mV and the rectification is hence, calculated as the ratio between the measured current at +100 mV and −100 mV. The rectification ratio stays around 1 (no rectification) up to around 12 mW, followed by a significant increase to around 2.5 at higher powers. Notably, the power at which γ(100 mV) starts to increase (12 mW) coincides with the power at which the current starts to drop (see Figure 2b).

Rectification in nanopore systems is usually caused by overlapping electric double layers (EDL) in combination with an asymmetric structure, such that the charged nanopore walls partly restrict ions of the same sign from moving through the pore in one direction.^32,33 Although primarily observed at low salt concentrations (more extended EDLs),³⁴ rectification has also been reported at high salt concentrations, for example, for conical nanopores in combination with nanoprecipitation^35,36 or hydrophobic entrances.^17,37 The rectification in the high-resistance state of our device is also likely related to asymmetry. By contrast, SiN nanopores have been shown to behave as Ohmic devices, with a constant conductance throughout the transmembrane voltage range, both with and without laser illumination.³⁸ This behavior is in line with our observations at no or weak laser illumination.

To investigate the dynamic response of the plasmon-induced resistance switching, we recorded the ionic current while continuously sweeping the laser power up and down. The laser power was modulated using a motorized rotatable wave plate and a polarizing beam splitter. It was calibrated in the linear power range between 2.3 mW and 16.2 mW, with a sweep rate from 0.05 mW/s to 5.7 mW/s. Details are described in the Supporting Information Figure S2. Figure 3 presents the ionic current versus laser power during power sweeps (I–P curves). In agreement with the results presented in Figure 2b, the current increased monotonically with increasing laser power for low powers. This is followed by an abrupt transition from high to low current at a certain laser power (P_down), after which the current decreased further for higher powers. When the power is instead swept from high to low power, a similar behavior is observed, with an abrupt transition (at P_up) from low to high current, after which the current follows the initial linear dependence at low powers. Notably, the photoresistance at high power reaches values as high as 2.1 GΩ, which yields an over 150-fold increase over the original resistance of 13.1 MΩ. There is a clear hysteresis in the behavior: P_down is considerably higher than P_up, showing that a higher laser power is required to reach the high-resistance state than to switch it back to the low resistance state.

Figure 3.

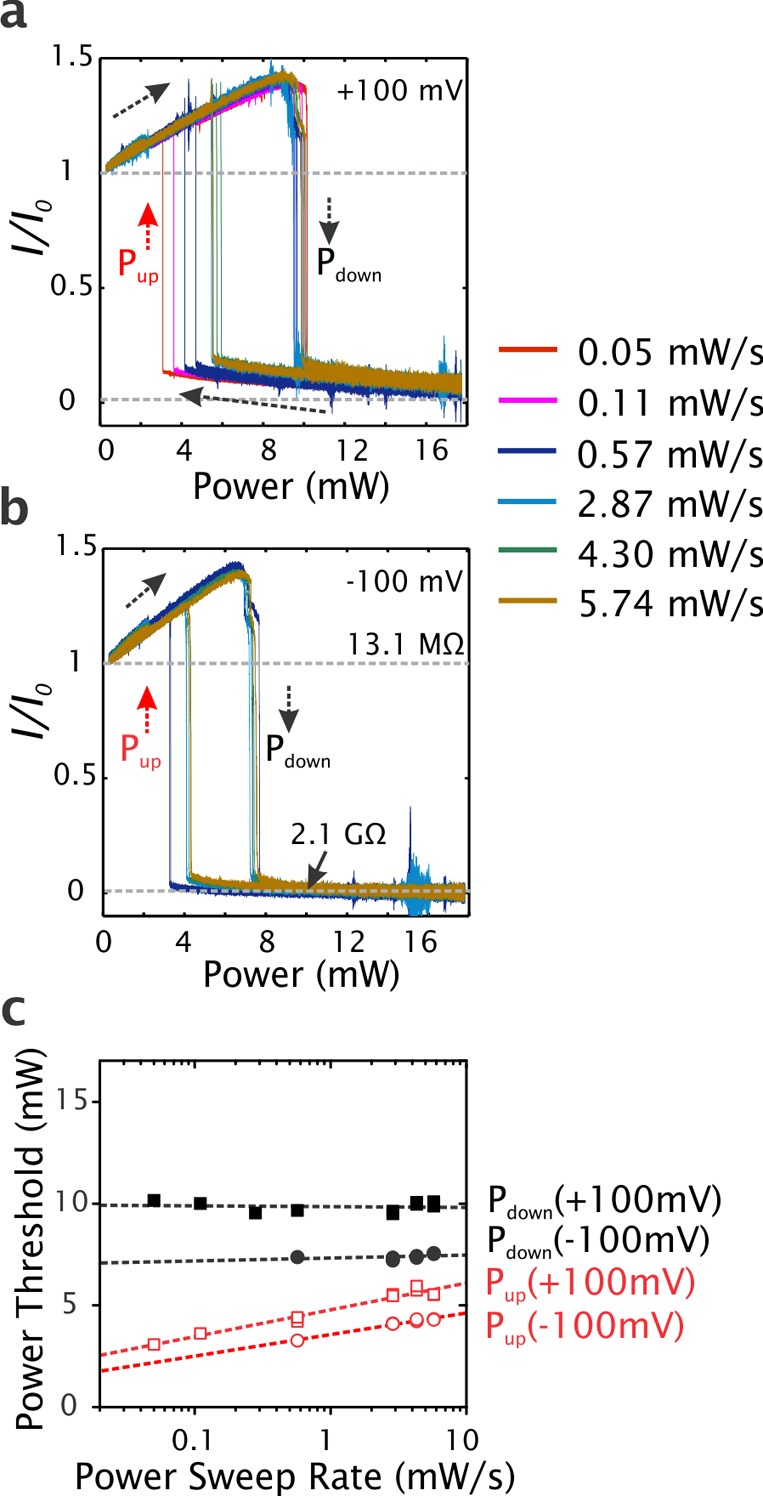
Normalized ionic current at (a) +100 mV and (b) −100 mV during power sweeps at different sweep rates (longitudinal excitation). The gray dashed lines show the photoresistance values of 13.1 MΩ and 2.1 GΩ at the initial resting state and high power state, respectively. (c) Transition thresholds as a function of sweep rate. The thresholds are chosen at I/I₀ = 0.5. Black solid markers correspond to P_down and red hollow markers correspond to P_up.

The hysteresis is quantitatively investigated in Figure 3c, for which the laser powers at I/I₀ = 0.5 define the power thresholds for the transitions. Three clear trends are observed. First, P_up is always lower than P_down, reflecting a similar hysteresis behavior for all sweep rates. Second, while P_down is largely independent of the power sweep rate, P_up increased with increasing sweep rate, thereby narrowing the hysteresis windows for higher sweep rates. Third, the thresholds are found to be dependent on the transmembrane voltage and they are consistently lower for negative bias. For example, P_down shifted from 10 mW at +100 mV to 7 mW at −100 mV (see Figure 3c). The power sweep results for transverse excitation were qualitatively the same as for longitudinal excitation (see Figure S3 in the Supporting Information), although the threshold for the two transitions were shifted to lower laser powers due to the better coupling of light to plasmons in the transverse mode.

Origin of the Photoresistance Switch

In order to understand the origin of the plasmon-induced photoresistance switching, several hypotheses were explored. Various processes are known to affect the ionic current of solid-state nanopores, including changes in the buffer temperature²² or changes in the surface charge of the nanopore walls.³⁸ However, although both surface charge and temperature were recently shown to vary upon laser illumination,^22,23,38 this resulted in monotonic increase in the ionic current upon laser excitation for increasing power. Hence, although such processes are consistent with the initial current increase at low laser powers, they cannot explain the observed abrupt resistance switch and current decrease at higher laser powers. Instead, the photoresistance switch is likely related to blockage of the pore and a corresponding restriction of the ionic flow through the pore at high laser powers. Biomolecules or other nanoparticles that could potentially block a pore were not present in our buffers, as confirmed by dynamic light scattering. Instead, we propose that the photoresistance switch is due to plasmon-induced formation and growth of nanometer-sized gaseous bubble(s)³⁹⁻⁴¹ that block the plasmonic nanopore.

We use several reported methods to evaluate if nanobubble blockage is the most plausible explanation for the high-resistance state of our plasmonic nanopore. First, we note that a strong decrease in the ionic nanopore conductance have been previously correlated with the presence of gaseous nanobubbles.¹⁷ In that study, experiments were repeated at a high concentration of protons (HCl) to verify that the current decrease corresponded to the pore being blocked by bubbles and not by a volume filled with (nonionic) liquid water. The fact that we observe a pronounced photoresistance switching also in 0.1 M HCl (Supporting Information Figure S4) is a strong indication that the high-resistance state is related to vapor that blocks the plasmonic nanopore. Furthermore, the presence of gaseous nanobubbles inside nanopores was also recently correlated with an increase in the nanopore current noise.⁴⁰ This is consistent with our results, as we observe a significant increase in the current noise when the system enters the high-resistance state (Supporting Information Figure S5a). Smeets et al.⁴⁰ also reported that scanning the position of a nanobubble-containing nanopore through a laser focus resulted in a double-peak in the ionic conductance, with a small dip at the focal spot due to nanobubble growth inside the nanopore. Indeed, we sometimes also observed this behavior for our system when scanning at intermediate laser powers close to the switching threshold (Supporting Information Figure S5b). All these experimental results match with and strengthen the proposed bubble hypothesis.

We use finite-element simulations to investigate if nanobubble blockage of the nanopore is consistent with the experimental observations, including the rectification behavior for the low-conductance state. We simulated the I–V response of the plasmonic pore-in-cavity using COMSOL Multiphysics 4.3b (see Methods section). Figure 4a illustrates three possible scenarios: (1) an open 10 nm in diameter pore, (2) the same 10 nm nanopore with a bubble on top of the orifice near the gold cavity, and (3) the same nanopore with a bubble facing away from the gold cavity. We used aqueous 1 M KCl solution as buffer medium. The surface charge density of the SiN wall was configured as −49 mC/m², corresponding to the reported data⁴² for SiN at pH 8.0. The closest distance from the bubble to the nanopore wall was chosen as 0.5 nm in order to have overlap between the electric double layers (EDL) of the pore and the bubble (the EDL thickness is only 0.3 nm at 1 M KCl).⁴³ The simulated results of I–V curves of the three scenarios are shown in Figure 4b. As expected, the open pore (blue curve) gives a linear I–V dependence. Both scenarios with a bubble partially blocking the nanopore (brown full curve and gray dashed curve) result in a significant decrease in the nanopore conductance and nonlinear I–V curves, with opposite rectification behavior. For both bubble scenarios, the preferential current direction is toward the constricted side where the bubble is positioned, as previously also reported for conical nanopores.⁴⁴ The rectification behavior observed experimentally (see Figure 1a) is in agreement with the simulated results for a bubble that blocks the pore from the top of the membrane near the gold cavity (scenario 2). The opposite rectification behavior was never observed experimentally. Hence, the combined experimental and simulated results strongly indicate that the low-conductance state at high laser power illumination is due to a bubble that blocks the pore and that the bubble formation occurs on the side of the plasmonic cavity. The rectification behavior may also be influenced by the dynamic nature of the bubble–nanopore system, as discussed further below.

Figure 4.

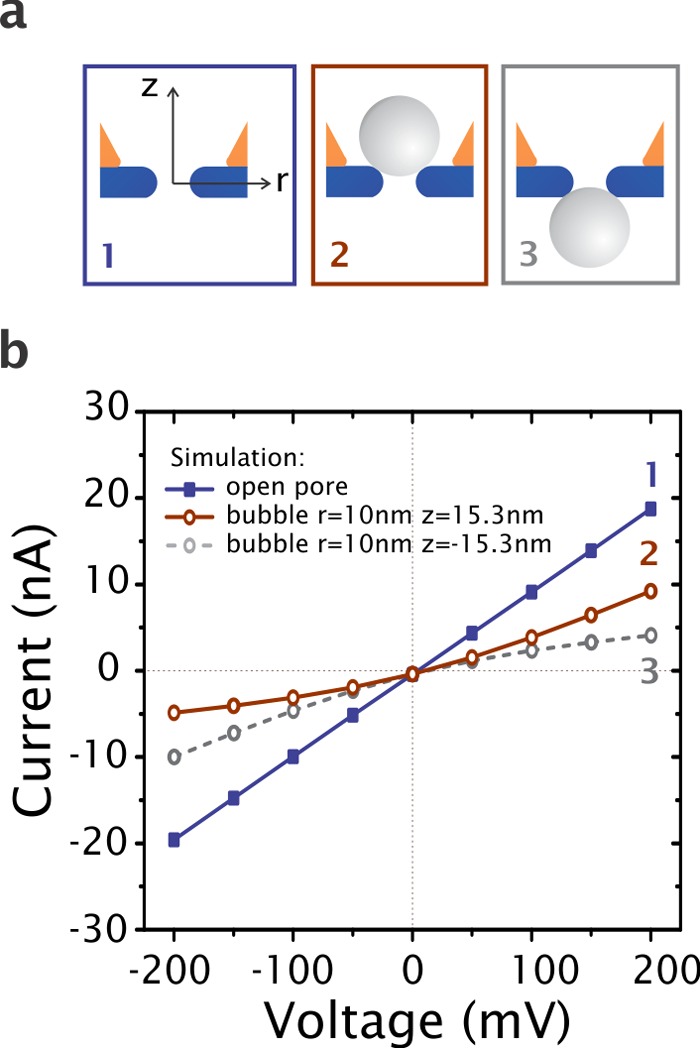
Numerical simulation of current–voltage curves of plasmonic nanopores. (a) Schematics that represents the three different simulations. The blue scenario 1 represents the nanopore without any bubble, whereas the brown scenario 2 has a nanobubble on top. The gray scenario 3 has a bubble at the other side of the pore entrance. (b) Simulated I–V curves of three scenarios in panel a.

Work Flow of the Photoresistance Switch

Figure 5 depicts the proposed workflow of the photoresistance switch. At low powers, the current increases with increasing laser power, which could be primarily attributed to local plasmonic heating and corresponding increase in buffer conductivity.²² Nanobubble(s) may be nucleated in this phase and start to grow in size with increasing laser power, but they do not block the ionic current. Upon a further increase in illumination power, the current exhibits an abrupt drop to a high-resistance state. This switch corresponds to the lumen of the pore becoming blocked by one (or several) bubble(s), located at the interface between the gold cavity and the SiN pore. We typically observe an abrupt drop with multiple steps in the ionic current (see Figure S6 in the Supporting Information), which is likely due to coalescence of multiple bubbles. At even higher powers, the pore lumen is increasingly further blocked by the growing nanobubble. When sweeping back to low power, the abrupt switch to the low resistance state can be attributed to bubble release from the orifice of the pore, which may be accompanied by multiple-step bubble collapse. Potential tiny bubble(s) that remain away from the pore lumen will not significantly affect the ionic current. The recovered current after P_up follows the same slope as before the bubble blockage.

Figure 5.

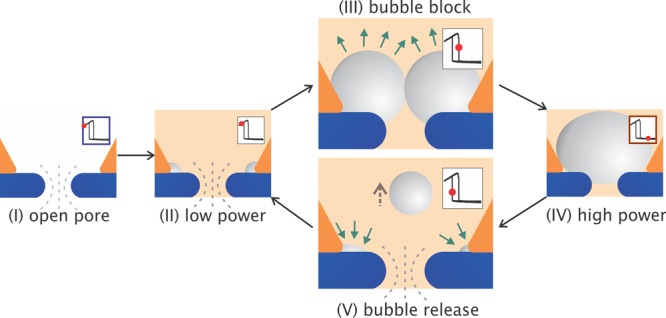
Proposed workflow of the photoresistance switch. (I) Original state without laser illumination, (II) bubble growth at low power, (III) transition to bubble block, (IV) bubble retention at high power, and (V) bubble release that may contain the processes of bubble residues shrink at the interfaces and bubbles escape away from the pore entrance. The insets indicate each scenario as a red spot located in the hysteretic I–P curve.

The hysteresis observed during laser power sweeps (Figure 3) shows that higher powers are required to block the pore with a bubble than to keep the bubble from releasing from the pore when it is already there. This is similar to the hysteresis in the force curves and jump-in/off events that were observed for the interaction between AFM-tips and nanobubbles,⁴⁵ especially on gold surfaces.⁴⁶ This behavior was in good agreement with a capillary force model based on positive forces between the bubble and the AFM tip. We anticipate that the hysteresis in our system is also related to attractive forces between the bubble and the plasmonic pore, which create an energy barrier that needs to be overcome in order to release the bubble from the pore.

The dependence on bias voltage for the transitions for blockade and release may be related to the dynamic nature of the bubble–nanopore system. Previous reports suggested that nanobubbles are negatively charged,⁴⁷ and therefore, they will be pulled toward the pore at negative bias. Negative transmembrane voltage may therefore assist bubble blockage, whereas positive bias does not. This is in agreement with our experimental finding that the transition thresholds for bubble blockage and release shift to higher laser powers for positive bias (see Figure 3c). In this respect, we also note that electrophoretic forces may influence how tightly the bubble blocks the pore in the high-resistance state and, in turn, contribute to the rectification.

Nanobubble Generation

Plasmon-induced Joule heating and the heterogeneity of the gold/silicon nitride interface are likely to play a role in the nanobubble formation. The plasmonic local heating leads to an estimated nanopore temperature of around 50 °C at P_down (using I/I₀ = 1.5 before the switching).²² This temperature, which is expected to be slightly higher at the gold surface, is sufficiently high to facilitate nucleation of surface nanobubbles.⁴⁸ Hence, it is plausible that the formation and growth of gaseous nanobubbles is the result of plasmonic heating. We further note that the abrupt switching occurs at approximately the same temperature (i.e., same I/I₀) regardless of the power sweep rate (see Figure 3), indicating that the process of pore blockage (at P_down) does not require a rapid change in temperature. By contrast, the bubble release (at P_up) occurs at lower temperatures for decreasing sweep rates. This observation indicates that a rapid change in temperature aids the bubble release, possibly due to forces related to changes of the fluidic flow upon rapid temperature variations.

Finally, we use remote plasmon excitation based on a grating structure on the side of the plasmonic cavity^19,29 to confirm that the photoresistance switching indeed is a plasmonic effect and not due to, for example, direct light absorption by the buffer medium. Tightly focusing the laser on the gratings allowed for excitation of surface plasmon polaritons (SPPs) (and, in turn, remote excitation of the plasmonic nanocavity)⁴⁹ without direct illumination of the nanocavity and the nanopore. The results are presented in Supporting Information Figure S7 and unambiguously show a current decrease also by remote plasmon excitation at high (15 mW) laser power.

In conclusion, this paper demonstrates photoresistance switching of a novel plasmonic nanopore based on a solid-state nanopore located within a plasmonic gold nanoslit cavity. We have shown that laser light focused onto such plasmonic nanopore can reversibly cause ∼1–2 orders of magnitude photoresistance switching. On the basis of the combined results from several different types of measurements, we conclude that the most plausible explanation of the high-resistance state is blockage of the nanopore by a bubble. Furthermore, the low-conductance state is accompanied by a rectified I–V response. Finite-element simulations show that this is in agreement with a bubble that blocks the nanopore from the side of the cavity. To the best of our knowledge, this is the first demonstration of a plasmon-controlled fluidic nanovalve. Moreover, the presented device is also a plasmon-assisted ionic rectifier, which remarkably operates at high salt concentration. Whereas previous reports of systems that were based on long channel lengths (>300 nm) and required a few volts as bias voltage for opening the nanopore,^17,18 our plasmonic nanopores provide a membrane thickness as thin as tens of nanometers or less, and the switching can operate at low (±100 mV) bias voltages with the assistance of light, which allows for use in fast solid-state nanopore sensing applications.⁹

There is a growing interest in using bubbles as an active element in nanoscale fluidic devices.^1,50,51 Utilizing nanobubbles for rapid and reversible switching of nanopores can accelerate the development of such novel nanofluidic systems and can also help to gain a better understanding of the mechanism of nanobubble formation. By exploiting the highly sensitive ionic transport through plasmon-modulated nanobubble-pore systems, our devices provide a unique system to probe the still largely unknown nanobubble properties. We believe the results of this work will help to understand the basic principles of plasmon-assisted fluidic nanosystems.

Methods

Device Fabrication

The processing flow of 200 mm wafer scale silicon nanocavity arrays was previously described.²⁸ Briefly, nanocavity structures were defined on 8 in. wafers by DUV lithography and anisotropically etched by TMAH. Then the wafer was temporarily bonded to a carrier wafer and thinned down to 200 μm. A vertical fluidic channel of 70 μm was opened by deep reactive ion etching (DRIE). We diced the wafer to 20 mm × 20 mm pieces, which contains single cavity arrays and then remove the bonding polymer HT10.10 (Brewer Science Inc.) by RCA-1 cleaning. Vapor hydrogen fluoride (HF) etching was performed for 35 min to remove the buried oxide layer. A 50 nm SiN layer was deposited on the backside by plasma enhanced CVD at 250 °C. Then, 10 nm of Ti and 200 nm of Au was sputtered on the top of the cavity. Complete dielectric membranes were formed by depositing additional 50 nm SiN on the backside. After dicing into 3 × 3 mm² chips, the electron beam of a TEM (Philips CM300UT-FEG operated at 200 kV, with a ∼10 nA beam current and an ∼10 nm beam diameter) was used to drill a single 10 nm in diameter pore through the SiN membrane beneath the gold nanocavity.

Experimental Setup

To clean the surface, the chip was rinsed with acetone, isopropanol, and ethanol. Then a 30 s O₂ plasma treatment was performed on each side of the chip to remove any trace of organic materials and to aid the surface wettability. The chip was immediately mounted onto a custom-made optical flow cell with Kwik-Cast (World Precision Instrument). Then the chip was placed between the two flow cell’s independent chambers that were filled with 1 M KCl, 10 mM Tris, and 1 mM EDTA buffer (pH = 8.0). The solutions were previously degassed in a vacuum chamber for 0.5 h. A pair of Ag/AgCl electrodes were inserted into both reservoirs and connected to the headstage of the Axopatch. We used an Axopatch 200B patch clamp amplifier (Molecular Devices Cooperation) at 100 kHz and NI USB-6251 (National instruments) at 500 kHz sampling rate for ionic current recording.

Numerical Calculation

We used three modules in the COMSOL v4.3b environment: electrostatics (AC/DC Module), transport of diluted species (Chemical Species Transport Module) for the calculation of K⁺ ions and Cl^– ions, and laminar flow (Fluidic Flow Module). The resulting ionic current was obtained by integration of the flux density along the boundary of the reservoir. The physical parameters⁴² used in the calculation are relative permittivity ε_r = 80, K⁺ ion mobility μ_K = 7.8 × 10^–8 m²/s·V, Cl^– ion mobility μ_Cl = 7.909 × 10^–8 m²/s·V, diffusion constant of K⁺ ions D_K = 1.957 × 10^–9 m²/s, diffusion constant of Cl^– ions D_Cl = 2.032 × 10^–9 m²/s, fluidic density ρ = 1000 kg/m³, dynamic viscosity μ = 8.91 × 10^–4 Pa·S, and the surface charge density of SiN wall ρ_wall = −49 mC/m². We validated our model by comparing analytical solutions of the Poisson–Nernst–Planck system with our numerical results, as has been described in previous papers.⁵²⁻⁵⁴

Supporting Information Available

Figure S1, normalized current changes at +100 mV; Figure S2, calibration of the motorized power sweeps; Figure S3, power sweep measurement at transverse excitation; Figure S4, high proton concentration measurement; Figure S5, current noise and current profiles; Figure S6, stepwise drop in the ionic currents; Figure S7, remote photoresistance switch on gratings. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Present Address

^⊥ Organic Electronics, Department of Science and Technology, Campus Norrköping, Linköping University, SE-60174 Norrköping, Sweden.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States