The Use of MRI Modeling to Enhance Osteochondral Transfer in Segmental Kienböck’s Disease

Abstract

Kienböck’s disease, defined as avascular necrosis of the lunate, is a relatively rare condition with a poorly understood etiology. Conservative and invasive treatments for Kienböck’s disease exist, including wrist immobilization, surgical joint-leveling procedures, vascularized bone grafting, proximal row carpectomy, and total wrist arthrodesis. Staging Kienböck’s disease using radiography assumes near complete avascularity of the lunate. The staging distinguishes only the “state of collapse” in an ordinal classification scheme and does not allow localization or indicate partial involvement of the lunate, which the image contrast from MRI may provide. In this short communication, we report the treatment of a patient’s Kienböck’s disease by combining MRI with mathematical modeling to optimize the congruency between the curvature of donor and recipient sites of an autologous osteoarticular plug transfer. Follow-up MRI and radiographs at 1 year postoperatively demonstrated gradual graft incorporation and bone healing. The purpose of this study was to describe the feasibility of a novel surgical technique. The results indicate that donor site selection for autologous osteoarticular transfer using a quantitative evaluation of articular surface curvature may be beneficial for optimizing the likelihood for restoring the radius of curvature and thus joint articulation following cartilage repair.

Introduction

Kienböck’s disease, defined as avascular necrosis of the lunate,¹ is a relatively rare condition with a poorly understood etiology. The disease is a relatively rare condition in which the etiology and natural history of this condition are poorly understood and even more poorly documented in the literature. A wide array of treatment recommendations is available, and reported results vary, which may hinder consistent treatment recommendations. Conservative and invasive treatments for Kienböck’s disease include the following: wrist immobilization with a splint during early disease stages,^2,3 surgical joint-leveling procedures to attempt to reduce loading on the joint and to promote revascularization and increased blood flow,⁴ vascularized bone grafting,⁵ proximal row carpectomy, and total wrist arthrodesis.^6,7 Proximal row carpectomy^8,9 and total wrist arthrodesis¹⁰ attempt to alleviate arthritis pain due to carpal collapse; however, these 2 interventions greatly limit range of motion. None of these treatments effectively address the chronic pain, loss of range of motion, and decreased grip strength associated with Kienböck’s disease.^3,11

Staging Kienböck’s disease using radiography assumes near complete avascularity of the lunate. The staging distinguishes only the “state of collapse” in an ordinal classification scheme⁶ and does not allow localization or indicate partial involvement of the lunate, which the image contrast from MRI may provide.

Osteochondral transfer for treatment of Kienböck’s disease may be possible for individuals with segmental or incomplete avascular necrosis of the lunate. Previous investigators have acknowledged the importance of donor site cartilage thickness to aid in minimizing postoperative abnormal stresses and resulting poor function.¹² Selection of donor cartilage with an appropriate thickness may be difficult due to source availability and donor site location relative to the load-bearing region of a joint, which may lead to donor site morbidity. An alternative to matching cartilage thickness is the matching of curvature of the articular surface. Matching the curvature of donor and recipient sites has been shown to maintain preoperative contact stresses for a given loading regimen.¹³

In this short communication, we report the treatment of a patient’s Kienböck’s disease by combining MRI with mathematical modeling to optimize the congruency between the curvature of donor and recipient sites of an autologous osteoarticular plug transfer. The purpose of this study was to describe the feasibility of a novel surgical technique. The results indicate that donor site selection for autologous osteoarticular transfer using a quantitative evaluation of articular surface curvature may be beneficial for optimizing the likelihood for restoring the radius of curvature and thus joint articulation following cartilage repair.

Methods

A 48-year-old, right hand–dominant woman had left wrist pain associated with decreased wrist flexion since September 2009. In November 2009, the patient experienced severe wrist pain after falling on her hand. After acquiring standard radiographs, the woman was diagnosed with Kienböck’s disease, and a proximal row carpectomy was recommended by an initial orthopedic surgeon. The patient sought a second opinion after understanding that the carpectomy would not only reduce pain during activities of daily living but would also limit range of motion.

Upon presentation to our institution, physical examination of the left wrist revealed no focal swelling, dystrophic changes, or evidence of muscular atrophy. The left wrist range of motion was 20° of flexion and 30° of extension; the patient had full, painless range of motion in her right wrist. Grip strength in her left hand was 111.2 N as compared with 333.6 N in her right hand.

MRI of the wrist was performed utilizing a clinical superconducting 3-T imaging unit (Sigma HDx, General Electric Healthcare, Waukesha, WI) and a dedicated wrist coil. Pulse sequencing included a 3-dimensional gradient-recalled sequence with TR/TE of 39/14 milliseconds, field of view of 9 cm, slice thickness of 1 mm with no gap, flip angle of 10°, and band width of ±41.7 kHz. Coronal, sagittal, and axial cartilage–sensitive fast spin echo sequences were obtained with a long TR (4,000-5,500 milliseconds), moderate TE (31-38 milliseconds), field of view of 8 to 9 cm, slice thickness of 2 to 3 mm, acquisition matrix of 512 × 512 (320-352), 2 excitations, a band width of ±14.7 to ±41.7 kHz, and echo train length of 10 to 12. Coronal fast inversion recovery sequence was performed with a TR of 5200 milliseconds, TE of 23 milliseconds, inversion time of 170 milliseconds, field of view of 9 cm, slice thickness of 2.5 mm, matrix of 288 × 192, 2 excitations, band width of ±31.2 kHz, and echo train length of 12.

The examination demonstrated collapse of the proximal pole of the lunate, with subchondral sclerosis and a mild bone marrow edema pattern (Fig. 1). Foci of completely devitalized marrow were noted in the proximal pole with an associated intense synovitis. Moderate partial wear of cartilage was seen over the collapsed lunate with preservation over the radial side of the lunate fossa. The adjacent intrinsic ligaments were intact. A best-fit circle was manually placed on the lunate with its articulation with the distal radius to determine the joint curvature.

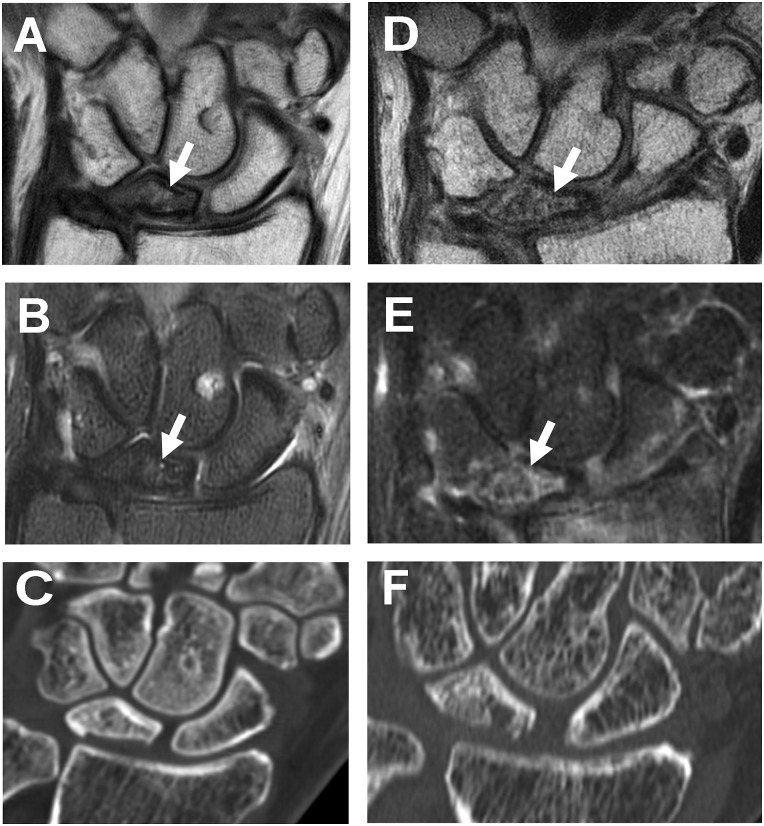
Figure 1.

Preoperative coronal (A) and fat-suppressed (B) fast spin echo images of the wrist demonstrate sclerosis and partial collapse of the lunate (arrows) with hyperintensity in the adjacent cartilage. The computerized tomographic evaluation (C) also demonstrates the degree of subchondral collapse. One-year postoperative sagittal (D) and fat-suppressed (E) fast spin echo images and computerized tomographic evaluation (F) demonstrate partial bony incorporation expected for the time interval.

Computerized tomographic examination was performed utilizing axial acquisition with a slice resolution of 0.8 mm, subsequently reformatted into sagittal and coronal reformations. Concurrent computerized tomography was performed to quantify the extent of subchondral collapse, which measured up to 1 mm.

MRI of the left knee was subsequently acquired to provide a digital template for the planned osteochondral transplantation. A 3-dimensional T1-weighted spoiled gradient echo data set with frequency-selective fat suppression was acquired for cartilage segmentation: TR of 13.6 milliseconds, TE of 3.0 milliseconds, field of view of 16 cm, flip angle of 20°, slice thickness of 1.5 mm, matrix of 512 × 512, receiver bandwidth of ±41.7 kHz, and 1.2 excitations.

The cartilage was segmented from the image data using custom-written semiautomated software (General Eelectric Healthcare), with minimal manual editing performed as needed.¹⁴ A 3-dimensional mesh representation of the segmented lateral condyle image data was constructed and smoothed¹⁵ for curvature calculations.

Curvature calculations were performed on the 3-dimensional surface mesh using a custom-written MATLAB (MathWorks, Natick, MA) program. An outline of the computational method is shown in Figure 2. The 2-Ring neighborhood was determined for each point (Fig. 2A), and a best-fit paraboloid (z(x,y) = Ax² + Bxy + Cy²) was fit to each vertex and the surrounding 2-Ring neighborhood^16,17 (Fig. 2B). The analytical solutions for maximum curvature (κ_max) and minimum curvature (κ_min) were determined from the best-fit paraboloid¹⁸ (Fig. 2C). The principal directions were also calculated. This process is repeated for each vertex on the 3-dimensional surface mesh to generate κ_max and κ_min maps. Regions with large values of κ_min display concavities on a surface, and regions with large values of κ_max display convexities of a surface. The model of a paraboloid was chosen due to the computational efficiency as well as the verified accuracy of the curvature calculation as compared to other numerical methods.^17,19

Figure 2.

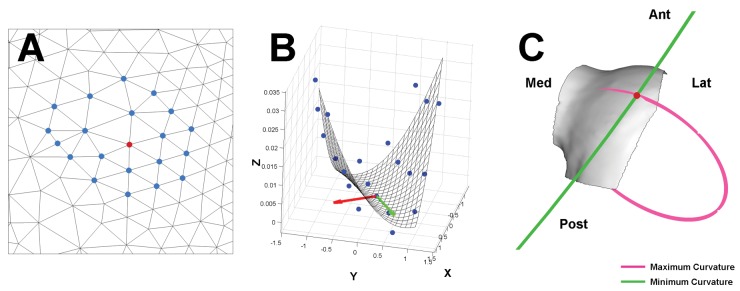
Outline of computational method for curvature calculation. (A) Each mesh vertex (red point) had a 2-Ring neighborhood (blue points) calculated. (B) The coefficients of a best-fit paraboloid through the vertex and 2-Ring neighborhood were used to calculate the maximum and minimum curvatures. The directions of maximum curvature (red arrow) and minimum curvature (green arrow) were also calculated. (C) The direction and magnitude of the maximum curvature and minimum curvature at the vertex are shown by the orientation and radius of the pink and green circles, respectively. The radius of each circle (ρ) is the inverse of the calculated curvature (ρ = 1/κ). At the indicated vertex (red dot), the anterolateral femoral condyle had the maximum curvature in the mediolateral direction and minimum curvature in the anteroposterior direction.

The patient underwent osteochondral transfer from her left femoral condyle to her left lunate. Using a tourniquet to control bleeding, the necrotic area of the lunate, which measured approximately 8 mm × 1 mm × 1 cm, was debrided. After thorough debridement of the avascular necrotic bone, intraoperative fluoroscopy was used to identify and better assess the defect in the lunate. The donor site was filled with a synthetic acellular biphasic copolymer plug (Trufit, Smith and Nephew, Andover, MA).

Using the digital template acquired from the algorithm, an osteochondral plug from the left femoral condyle that closely matched the radius of curvature of the lunate, 12.7 mm from the manual measurement, was harvested during knee arthroscopy (Fig. 3). The location of the plug was assessed from the previously constructed 3-dimensional model of the articular surface, relative to the local anatomy. A 10 blade and rongeur were used to fit the dimensions of the osteochondral plug with those of the lunate. The plug was then impacted into place with an excellent fit (Fig. 4), and a No. 2 FiberWire (Arthrex, Naples, FL) stitch was placed through the scapholunate ligament. Intraoperative fluoroscopy demonstrated an excellent position and reconstitution of the lunate. Internal fixation was performed with a 1-mm drill, drilled antegrade through the lunate to fix the osteochondral plug; a 1.5-mm × 8-mm screw was then compressed across the plug with fixation in the distal aspect of the lunate. Intraoperative fluoroscopy demonstrated the correct position, depth, and placement of the hardware. There was no block in flexion, extension, or radial deviation, and the osteochondral fragment remained stable through a full range of motion. The patient was placed in a sling and discharged with instructions to return for regular follow-up visits.

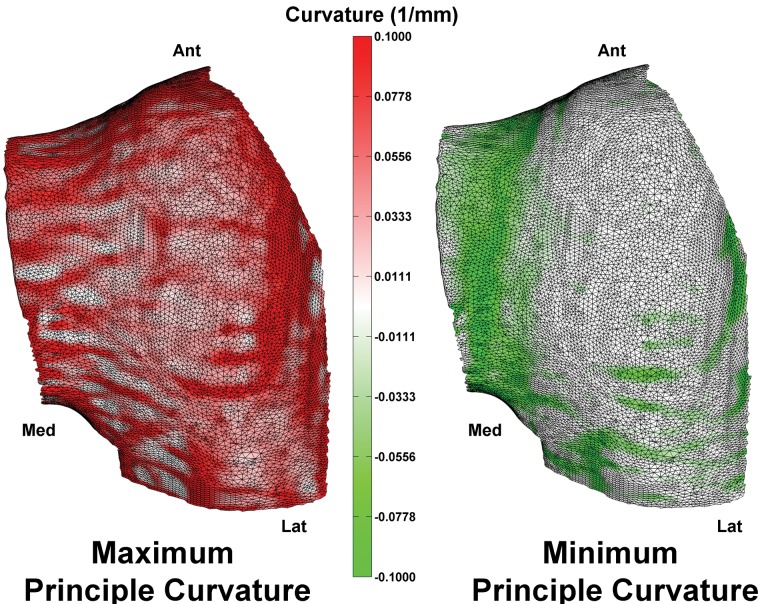
Figure 3.

Maximum (left) and minimum (right) principal curvature maps of the anterior portion of the lateral femoral condyle.

Figure 4.

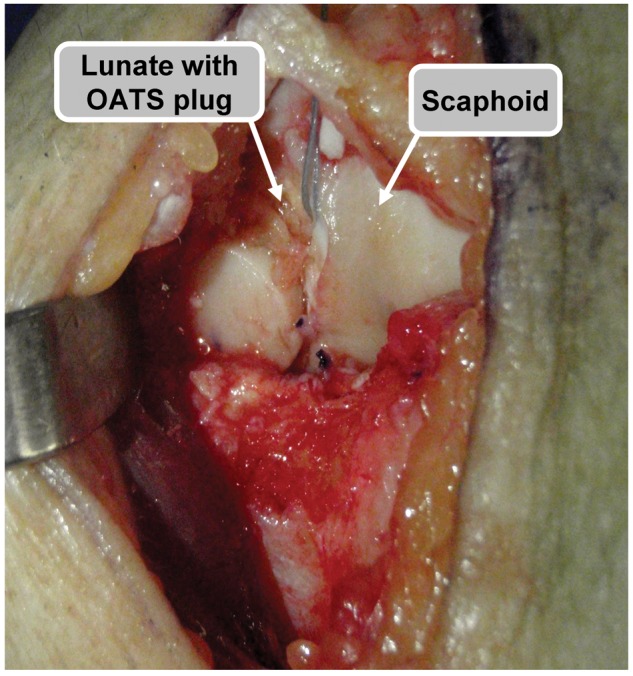
Intraoperative image through a radiocarpal incision demonstrating delivery of the osteochondral plug.

Results

Postoperative radiographs demonstrated that the wrist was in good alignment and the hardware was intact. Follow-up radiographs and physical examinations were performed at 2, 4, 6, 8, and 10 weeks; 3, 4, 7, and 10 months; and 1 year postoperatively.

Discussion

We treated Kienböck’s disease with the aid of a 3-dimensional model of femoral articular surface and calculated the principal curvatures of the surface. This was performed to determine the optimal congruency of the chondral donor and recipient sites. Postoperative results demonstrated gradual graft incorporation and bone healing. Surgical challenges for autologous osteoarticular transfer include restoration of the articular surface as well as the tidemark. Koh et al. have shown in a preclinical model that plugs left elevated or angled result in increased contact pressures, thus presenting potential risk to the cartilage on the opposite side of the joint.¹³ The mesh model created in the knee allowed for objective assessment of the articular surface to ensure more optimal plug alignment, provide reconstitution of joint architecture, and promote biologic incorporation of the plug into the recipient site. We did not seek to evaluate the functional outcome of the surgical procedure in this short report but to introduce the feasibility of this novel surgical planning technique for osteochondral repair.

This case report presents the unique application of MRI and mathematical modeling when applying the autologous osteoarticular transfer procedure to the lunate. These techniques require only an additional limited 3-dimensional model of the knee with minimal scan time beyond the routine examination of the wrist for assessment of marrow viability and the integrity of the articular surfaces. Additional applications would include osteochondral lesions of the distal femur, capitellum, talus, and potentially, over the femoral head. Future studies will refine the image acquisition and 3-dimensional modeling processes for optimal selection of the osteochondral plug based on local tissue morphology.