Abstract
We explored stability of multi-finger cyclical accurate force production action by analysis of responses to small perturbations applied to one of the fingers and inter-cycle analysis of variance. Healthy subjects performed two versions of the cyclical task, with and without an explicit target. The “inverse piano” apparatus was used to lift/lower a finger by 1 cm over 0.5 s; the subjects were always instructed to perform the task as accurate as they could at all times. Deviations in the spaces of finger forces and modes (hypothetical commands to individual fingers) were quantified in directions that did not change total force (motor equivalent) and in directions that changed the total force (non-motor equivalent). Motor equivalent deviations started immediately with the perturbation and increased progressively with time. After a sequence of lifting-lowering perturbations leading to the initial conditions, motor equivalent deviations were dominating. These phenomena were less pronounced for analysis performed with respect to the total moment of force with respect to an axis parallel to the forearm/hand. Analysis of inter-cycle variance showed consistently higher variance in a subspace that did not change the total force as compared to the variance that affected total force. We interpret the results as reflections of task-specific stability of the redundant multi-finger system. Large motor equivalent deviations suggest that reactions of the neuromotor system to a perturbation involve large changes of neural commands that do not affect salient performance variables, even during actions with the purpose to correct those salient variables. Consistency of the analyses of motor equivalence and variance analysis provides additional support for the idea of task-specific stability ensured at a neural level.
Keywords: Motor equivalence, synergy, finger force, perturbation, uncontrolled manifold hypothesis
INTRODUCTION
Stability of human movements is one of their most crucial characteristics for success in changing and unpredictable external conditions. The problem of ensuring action stability is complicated by the fact that movements involve redundant sets of elements at any level of analysis (cf. motor redundancy, Bernstein 1967). Recently, the problem of motor redundancy has been reformulated as motor abundance (Latash 2012). According to this view, the seemingly redundant sets of elemental variables (those produced by elements at a selected level of analysis) are allowed to vary as long as these variations are compatible with low variance (high stability) of a task-specific performance variable (Schöner 1995). The introduction of the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner 1999) was an important step toward analyzing variance to learn about different levels of a motor control hierarchy. According to this hypothesis, a neural controller acts to limit variance at the level of elemental variables to a sub-space (UCM) within which performance variables specific to a task do not vary.
The UCM approach allows overcoming the problem of comparing elemental and performance variables expressed in different units by using a formal model that relates small changes in elemental variables with changes in performance variables, the Jacobian matrix, J (Scholz and Schöner 1999; Latash et al. 2001). The UCM is commonly approximated by the null-space of J. In contrast, the combinations of elemental variables along the orthogonal to the UCM space lead to errors in performance.
In this method, the inter-trial variability of elemental variables is analyzed within the UCM, VUCM (“good variability”), and orthogonal to it, VORT (“bad variability”). If VUCM > VORT, a conclusion is drawn that the performance variable is preferentially stabilized in the action. An extensive number of studies have demonstrated that purposeful movements lead to a structure of the trial-to-trial variability in the space of elemental variables (VUCM > VORT) reflecting a family of goal-equivalent solutions used to solve a particular task (Schöner 1995; Li et al. 1998; Scholz et al. 2000; Latash et al. 2001; Scholz et al. 2002).
One consequence of the motor abundance is the phenomenon of motor equivalence. This notion has been used in the field of movement studies for many years as the ability to accomplish the same task using different effectors (Wing 2000) or with different contributions from a set of effectors (Hughes and Abbs 1976; Kelso et al. 1984; Levin et al. 2003). A conceptual problem with this classical formulation is that in reality, the task level performance is never exactly identical under the different circumstances. Assessing motor equivalence thus requires comparing the amount of change at the task level with the amount of change at the level of elemental variables. Because these two levels have different metrics (e.g., distances in space for the task level, and joint angles at the elemental level), this comparison cannot be made directly. Similarly to the mentioned analysis of variance, the analysis of differences between the trajectories of task-specific performance variables when a motor task is solved under different conditions must be based on a metric at the level of elemental variables. Jacobian J linking the two levels can then be used to quantify components of trajectories that lead to a change in the performance variables and components that do not.
Recently, such an analysis of motor equivalence has been developed within the UCM hypothesis framework (Scholz et al. 2007; Schöner et al. 2008). In that analysis, unexpected movement perturbations were applied, and the deviations of elemental variables in the perturbed trials from the unperturbed movements were projected onto the corresponding UCM space and its orthogonal complement, ORT. Deviations within the UCM space are motor equivalent (ME) components, while deviations within the ORT are non-motor equivalent (nME). For instance, a perturbation that affects the position of the hand in space is expected to induce changes within the ORT subspace in the joint configuration space followed by corrective actions within ORT. Large ME deviations suggest that different joint configurations are used to achieve the same task performance.
Only a few previous experiments have tested the effects of perturbations using the described UCM-based approach (Scholz et al. 2007; Schöner et al. 2008). Motor equivalence was observed at the end of a reaching movement when comparing reaching at different speeds (Scholz et al. 2011). Because differences in movement speed disappear when the movement ends, the remaining difference between joint configurations within the UCM space reflected different solutions to the movement task at different speeds. In a subsequent reaching study, individuals were instructed to insert a pointer into spherical and cylindrical targets. At random trials their elbow joint extension was limited by an elastic band (Mattos et al. 2011, 2013). Most of the deviations in both joint configuration and muscle activation spaces during the perturbation were ME, starting immediately with the perturbation and lasting until the end of the movement. The cited studies analyzed ME and nME components when the perturbation was continuously applied to the moving effector. This made it difficult to decide if the observed reorganization of joint configurations was a consequence of the mechanical effect of the perturbation itself or reflected changes at the level of neural control of those movements.
A problem in assessing motor equivalence is distinguishing between ME components that are reflections of the direct, mechanical, effects of the perturbation and ME components that reflect a reorganization of the multi-degree-of-freedom movement at the neural control level. The main goal of this study was to address this problem by observing (1) how ME components evolve in time while a perturbation is held constant and (2) whether ME components persist after the perturbation is removed. ME components that persist after a perturbation has been removed reflect a change in the neural solution to the degree-of-freedom problem.
We used a cyclic multi-finger accurate force production task and the “inverse piano” device (Martin et al. 2011) that allows applying controlled perturbations in the course of task performance. The perturbation consisted of lifting by 1 cm and keeping elevated the middle fingerpad and then lowering it back to the pre-perturbation position. Each of the two phases led to immediate adjustments of all finger forces (Martin et al. 2011; Wilhelm et al. 2013) as well as to corrective actions that kept task performance accurate. Note that after the lifting-lowering sequence, the external conditions of the task returned to the pre-perturbation ones. The motor equivalence analysis was done at two time scales. The Micro-analysis involved time windows of 50 ms starting from the perturbation onset to 500 ms post-perturbation. This analysis was aimed at distinguishing corrections due to the action of various physiological mechanisms, from peripheral reactions of tissues to action of reflexes and reflex-like responses, and to voluntary corrections. The Macro-analysis explored steady states before, during and after the perturbation. After the perturbation, the observed ME vs. nME structure was hypothesized to reflect primarily changes in neural control. Overall, our main hypothesis was that strong ME components would be observed in all phases of the action reflecting the task-specific stability of the four-finger system with respect to total force. In addition, we used the more traditional UCM-based analysis of the two components of variance computed across cycles, VUCM and VORT. The inequality VUCM > VORT was expected across conditions (Latash et al. 2001; Friedman et al. 2009).
METHODS
Subjects
Eleven healthy adult subjects (8 males, 3 females), averaging 26.27 ± 5.29 years old, mass 69.39 ± 12.85 kg, height 1.72 ± 0.12 m took part of this study. All subjects were self-reported right hand dominant and had no history of any neurological or musculoskeletal disorder that could affect the upper arm. Subjects gave written informed consent as approved by the Office for Research Protection of the Pennsylvania State University.
Equipment
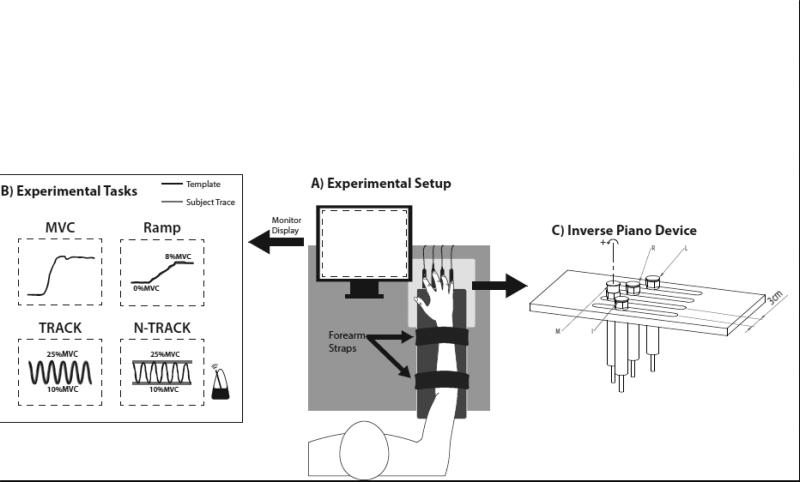
This experiment used the “inverse piano” device details in Martin et al. (2011) that consists of four unidirectional piezoelectric force transducers (208C01; PBC Piezotronics Inc) individually connected to linear actuators (PS01-23x80; LinMot). Each sensor top was covered with sandpaper (300 grit) to increase the friction between the sensor and the fingertips. The sand paper also thermo-insulated the sensors from the body heat. The sensors were mounted within slots in a steel frame (140 × 90 mm), with 3-cm of distance between the centers of the sensors in the mediolateral direction, allowing for adjustments in the anterior-posterior direction as needed. The frame was attached to a wooden board (460 × 175 × 27 mm) to support the subject's arm. The signals from each sensor were sent through a DC-coupled signal conditioner (PCB) to a 16-bit analog-to-digital converter (CA-1000; National Instruments). A Labview-software (National Instruments) was developed to run the experiment, acquire, and record the force signals from individual fingers at 200 Hz, as well as to control the linear actuators through a controller (E-400-AT; LinMot). In addition, the customized Labview program recorded the timings of perturbation onset. See Figure 1 for a schematic representation of the experimental setup.
Figure 1.
A) A schematic of the experimental setup showing the subject's position and the sensor arrangement; B) Illustration of the feedback given to the subject on the monitor display. Signals for the maximum voluntary contraction (MVC), ramp force production, and cyclic force production with (TRACK) and without (N-TRACK) template are illustrated. A metronome paced the N-TRACK task; C) Schematic of force sensors mounted on linear motors. In the illustration, the ring force sensor is lifted. Moment arms with respect to mid-hand were 4.5 cm, 1.5 cm, -1.5 cm, and -4.5 cm for the index (I), middle (M), ring (R), and little (L) fingers, respectively. Counterclockwise rotation (+) around the axis represents pronation moment.
Experimental Procedure
Subject Position
Subjects sat on an adjustable chair in front of the table with their right forearm supported, facing a 19” monitor, placed 0.8 m away from the subject at the eye level. The monitor was used to provide visual feedback for the subjects. The right arm was at 60° of shoulder abduction, 120° of elbow flexion, hand pronated, and the wrist in neutral position. Foam paddings were placed under the subject's forearm and palm for comfort. Once the initial position was adjusted, the subject's forearm was fixed with two Velcro straps to prevent changes in the elbow and shoulder joint angles throughout the trials.
Experimental Tasks
For all tasks, the subjects started each trial by placing all fingers on the top of the sensors and relaxing; the initial forces were set to zero, such that the sensors measured only the active downward forces. Finger pressing tasks using the index (I), middle (M), ring (R), and little (L) fingers were performed as follows.
1) Maximal Voluntary Contraction (MVC) Task
Subjects were instructed to press on the sensors with all four fingers as hard as possible and reach maximal force within 6 s. Verbal encouragement as well as visual feedback on the total force was provided. Two trials, at least 30-s apart, were recorded per subject, and the trial with maximal peak force was selected. The MVC task was used to normalize the Ramp, Tracking and Non-Tracking Tasks (described below).
2) Ramp Task
Subjects placed all the fingers on the sensors and tracked a ramp template with one finger at a time. The visual feedback on the force produced by the instructed finger (master-finger) was provided; however, the other three fingers (slave-fingers) also produced forces due to the phenomenon of enslaving (Zatsiorsky et al. 1998; Danion et al. 2003). The total duration of the ramp task was 8 s, which was divided in 3 parts: a horizontal line corresponding to 0% MVC for 2 s, an oblique line from 0 to 8% of MVC over 6 s, and another horizontal line corresponding to 8% of MVC for 2 s. After a few familiarization trials, two ramp trials were collected for each finger; the order of the fingers was randomized. This task was performed in two conditions: 1) all fingers at the same level; and 2) the middle finger lifted by 1 cm. The Ramp Task was used to estimate the enslaving index among fingers, and to compute finger modes (see later).
3) Tracking (TRACK) and non-tracking (N-TRACK) cyclic force production tasks
We explored two tasks involving and not involving an explicit force trajectory presented on the screen. The no-tracking task was expected to lead to higher nME components across all comparisons as compared to the tracking task. In the TRACK task, subjects were instructed to track a sine-like signal changing between 10 and 25% of each subject's MVC at 0.5 Hz with the cursor representing the current total force. The target was displayed on the monitor as a solid blue line. In the N-TRACK task, two horizontal lines were displayed on the monitor corresponding to 10% and 25% of each individual's MVC. Subjects were instructed to produce smooth force oscillations in-between the targets at 0.8 Hz controlled by audio beeps of a metronome, each beep representing half-cycle. All subjects reported 0.8 Hz to be a comfortable frequency to perform this task. For both tasks, the total trial duration was 22 s. Each trial had two perturbations involving lifting (PTUP) and lowering (PTDN) of the M finger by 1 cm over 0.5 s. This manipulation increased and decreased the M-finger force, respectively. The onset of PTUP varied randomly between 6 and 10 s from the trial initiation, the M-finger remained at the lifted position for 6 s, followed by PTDN. Twenty-four trials were performed, with not less than 30-s interval between trials, and 2-min break after every six trials to avoid fatigue. Additional rest intervals were offered as needed. Subjects had 2-10 familiarization trials before data collection. Accurate total force production was emphasized at all times.
Data Processing
The main outcome variables of this study were those of the motor equivalence and variance analyses described below. The UCM-based methods of analysis of inter-trial variance were used with finger forces and modes as elemental variables. As indicated by previous studies (Li et al. 1998; Latash et al. 2001) in multi-finger tasks, the total moment of force can be stabilized by the co-variation of fingers forces (or modes) without being explicitly instructed by the task. Therefore, the analyses were performed with respect to both total force and moment of force.
Initial Data Processing
The digital signals were converted to force units, and force signals were filtered with a 4th order, zero-lag Butterworth low-pass filter with a cutoff frequency of 5 Hz. The low cutoff frequency was used to eliminate the high-frequency noise caused by the motors during the perturbation. The frequency spectrum analysis showed that most of the power of the data was under 5 Hz. The total force was computed by summing the individual finger forces.
Enslaving Matrix and Finger Modes
Finger forces during the oblique part of the Ramp Task were extracted. Linear regressions of the total force (FTOT) produced by the four fingers against individual finger forces were used to estimate the 4 × 4 enslaving matrix, [E], formed by the regression coefficients (k) for trials performed by each master finger, i = (I, M, R, L):
| (1) |
| (2) |
The diagonal entries of the enslaving matrix represent the fraction of FTOT produced by the master-finger, while the off-diagonal entries represent the fractions of FTOT produced by the slave-fingers. The total amount of enslaving (EN) for each subject was computed as the sum of the off-diagonal entries. The enslaving matrix was used to convert finger force data into finger modes:
| (3) |
where, ƒ is the 4×1 finger forces vector, and m is the 4×1 finger mode vector. We performed further analysis in two spaces, ƒ and m. Note that m are hypothetical variables that, unlike forces, can be manipulated by the central nervous system one at a time (Danion et al. 2003).
Total Moment of Force
The total moment of force, MTOT, produced by the fingers about the longitudinal axis of the forearm/hand was computed as follows:
| (4) |
where di and fi stand for the force and the lever arm for each finger i, respectively (i = I, M, R, and L). As indicated in figure 1, the force sensors were 3-cm apart; hence, dI = 4.5 cm, dM = 1.5 cm, dR = 1.5 cm and dL = -4.5 cm. Pronation and supination directions are represented by positive and negative signs, respectively. The moment estimation assumed no change in the point of application of the force in the medium-lateral direction.
Analysis of Motor Equivalence
Lifting the M finger led to force changes in all fingers, as compared to unperturbed conditions, which were expected to include an increase in the M finger force, a drop in the other finger forces, and an overall increase in FTOT (Martin et al. 2011) Hence, a change in the sharing of FTOT among the four fingers was expected. The motor equivalence analysis tested whether most of the changes in individual finger forces and modes due to the perturbation preserved FTOT produced pre-perturbation (ME) or leads to different values of FTOT (nME). Similar analyses were performed with respect to MTOT produced by the fingers forces/modes.
Individual cycles were identified as intervals between successive points when force derivative reached 5% of its maximal value in that cycle; for the TRACK task the definition of cycles was based on the template used as feedback to the subjects. Only full cycles were included in the analysis. Then, the average forces and modes (x0,AV) produced by the fingers before the onset of PTUP (Pre-Pert) were computed. Therefore, the N-TRACK Pre-Pert cycles were time normalized to the mean number of samples across all cycles and trials for each subject separately. This normalization was not necessary for the TRACK condition given that the number of samples for each cycle was consistent when subjects tracked the sine template. To align x0,AV with the cycles produced at each j trial, x0,AV was time normalized for each cycle of the j trial and reproduced approximately 10 and 16 times to match the number of cycles in the TRACK and N-TRACK conditions, respectively. Then, the deviation vector (Δxj = xj – x0,AV) between the force/mode during the perturbed trials (xj) and the mean Pre-Pert (x0,AV) was obtained for each sample of j trial. To analyze the adjustments during PTDN, the last cycle before the PTDN was used as the Pre-Pert cycle.
The Jacobian (J) matrices reflecting how changes in individual finger forces/modes affect FTOT were defined. For ƒ-based analyses, JF = [1,1,1,1]. For m-based analyses, JM = [1,1,1,1]•[E]. Analysis with respect to MTOT used JMOM = [dI, dM, dR, dL], where dI = 4.5 cm, dM = 1.5 cm, dR = 1.5 cm and dL = -4.5 cm. To estimate ME and nME components Δx was projected onto the null-space (NULL) of the corresponding J and onto the orthogonal to NULL space (ORT). The length of Δx projection in the NULL and ORT spaces reflects the ME and nME deviations in the ƒ (m) space, respectively. For quantitative comparison, the projections onto the ME space were normalized by the square root of three (dimensionality of the NULL space, Mattos et al. 2011). More detail can be found in Appendix 1.
UCM-based Variance Analysis
This analysis investigated whether the trial-to-trial variance in the ƒ (m) pattern led to changes in FTOT (VORT) or kept FTOT unchanged (VUCM). This computation was similar to the ME analysis described above. In this case, however, the trial-to-trial variance of the de-meaned ƒ (m) data for each time sample was projected onto the NULL (VUCM) and ORT spaces (VORT) of the corresponding J during each phase of the analysis. Each variance component was normalized to the number of DOF in each dimension (DOFUCM=3; DOFORT=1). The analysis was also performed for MTOT. Details of this analysis can be found in (Latash et al. 2001).
Definition of Phases of Analysis
We analyzed effects of finger perturbation on the ME and nME components of ƒ and m changes within different time windows immediately following initiation of the perturbation as well as at steady states (Micro and Macro analyses, respectively). To evaluate the Macro adjustments, three phases were defined as follows: Pre-perturbation (Pre-Pert): mean of all the full cycles before the PTUP, During perturbation (During-Pert): mean of all the full cycles performed with the M finger lifted by 1 cm, and Post-Perturbation (Post-Pert): mean of all the full cycles after PTDN when the M finger was lowered to the initial position. To evaluate the micro adjustments, four phases were defined for each perturbation as follows: 1-50 ms post-perturbation (Post-Pert50), 51-100 ms post-perturbation (Post-Pert100), 101-150 ms post-perturbation (Post-Pert150), and 151-500 ms post-perturbation (Post-Pert500). The phases were selected to reflect purely mechanical effects of the perturbation (Post-Pert50), effects that could get contribution from spinal reflexes (Post-Pert100), effects that could include action of long-loop reflexes or preprogrammed reactions (Post-Pert150), and effects of all of the above plus those of voluntary corrections (Post-Pert500) (Prochazka et al. 2000).
Statistical Analysis
All statistical analyses were performed with SPSS (IBM Statistics 2012b). The significance level was set as p<0.05 for all analyses. Paired t-tests were performed to test the differences between the enslaving indices, EN, measured in two finger configurations. The effects of phase in the analysis of both macro and micro adjustments on the forces/modes of individual fingers and total force were tested using one-way ANOVA. Three-way repeated measures ANOVAs were used to test the effects of Projection-Component (Motor Equivalence Analysis: two levels, ME and nME; UCM Analysis: two levels, VUCM and VORT), Phase (Macro Analysis: three levels, Pre-Pert, During Pert, and Post-Pert; Micro Analysis during PTUP and PTDN: five levels, Pre-Pert, Post-Pert50, Post-Pert100, Post-Pert150, and Post-Pert500), and Condition (two levels, TRACK and N-TRACK) computed with respect to FTOT and MTOT. M-Matrix was used for post-hoc pairwise comparisons.
RESULTS
Enslaving Index
Indices of unintentional finger force production (enslaving, EN) were computed over trials when the subjects were instructed to press with one finger only. To confirm that these indices could be used for analysis using finger modes (see Methods), we compared EN indices across finger configurations (with the M finger lifted and not lifted) and also across force increase and force decrease segments of the ramp-trials. Overall, there were no significant differences in the EN indices across the finger configurations and force directions. On average, EN was 0.81 ± 0.31 when all four fingers were at the same level and 0.76 ± 0.29 when the middle finger was lifted by 1 cm.
Force Change Patterns: Macro Analysis
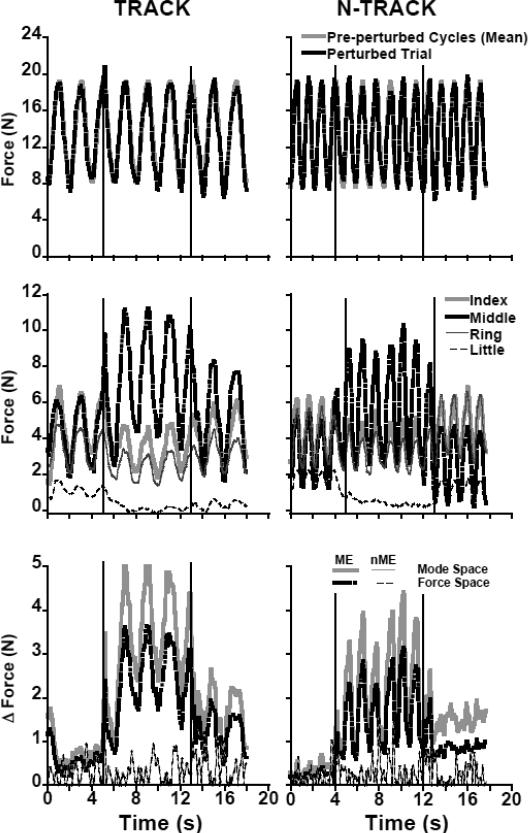
The subjects showed consistent performance of the main task in conditions both with (TRACK) and without (N-TRACK) a target line on the screen. Lifting and lowering the M finger (perturbations) introduced large changes in the individual finger forces, while the changes in the total force (FTOT) time profile were relatively modest. This is illustrated in the top two panels of Figure 2. Relatively minor differences between the perturbed (black dashed line) and non-perturbed (gray, solid line) conditions can be seen in FTOT. For the TRACK task, when the M finger was lifted, FTOT remained unchanged (F1,10 =1.96, p=0.19) and there was a tendency for an increase in FTOT for the N-TRACK task (F1,10 =4.94, p=0.051). For the TRACK task, FTOT showed a tendency to decrease when the M finger was lowered as compared to during-perturbation (F1,10 = 4.21, p=0.067) and pre-perturbation (F1,10 = 6.966, p<0.05). For the N-TRACK task, FTOT also decreased after perturbation compared with the FTOT applied when the M finger was lifted (F1,10 = 6.97, p<0.05), but the pre- and post-perturbation conditions only approached significance. Despite being significant in some comparisons, the decrease in FTOT was below 0.26 N, which represents only 1.9% of the pre-perturbation FTOT.
Figure 2.
Time profiles of a representative subject illustrating changes in total force (upper plots), individual finger forces (middle plots) and the motor equivalence analysis (lower plots) pre-, during-, and post-perturbation during the TRACK (right plots) and N-TRACK (left plots) task. The black vertical lines represent the perturbation onsets for PTUP (middle finger lifted at 1 cm height) and PTDN (middle finger lowered, at 0 cm height).
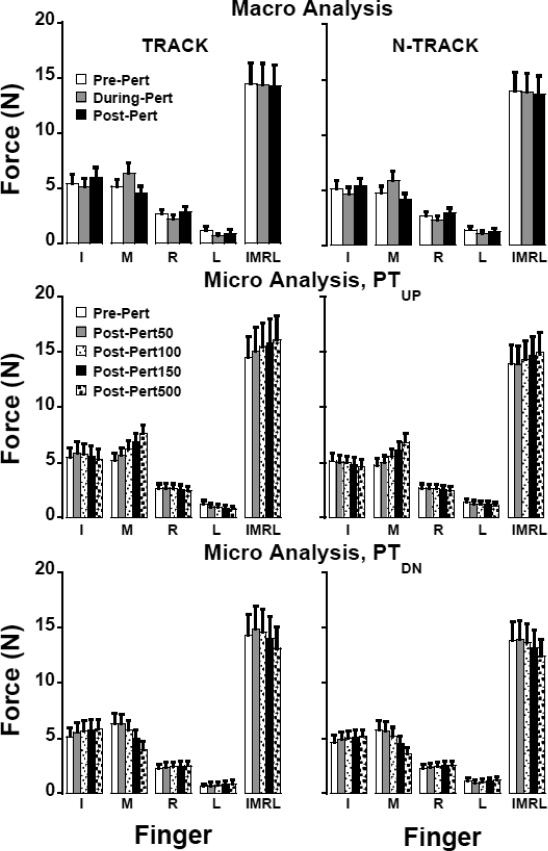
In contrast, individual finger forces showed rather dramatic changes induced by the perturbation in both tasks (the middle panels of Figure 2; for across-subjects comparisons see the top panels of Figure 3). Lifting the M finger led to an increase in its force in both tasks (F1,10 > 5.3, p<0.05) and to a significant decrease in the force of the R and L fingers for the TRACK task, and of the I and R fingers for the N-TRACK task (F1,10 > 5.9, p<0.05); the decrease in the L finger force for the N-TRACK task approached significance (F1,10 = 4.21, p = 0.067). Lowering the M-finger back to the initial position led to a drop in its force (F1,10 > 10.0, p<0.01) and an increase in the forces by the I and R fingers (F1,10 > 7.4, p<0.05) while the change in the L finger force was under the significance level. This was true for both TRACK and N-TRACK tasks. After the M finger was lowered to the initial position, force sharing among the four fingers differed from the pattern seen prior to the perturbation (compare the time intervals before the first vertical dashed line and after the second one).
Figure 3.
Finger force (I: Index, M: Middle, R: Ring, L: Little, IMRL: Total force) during different phases (means ± standard errors are shown): A) general adjustments: pre-, during-, and post-perturbation, B) quick adjustments following PTUP and PTDN: Pre-Pert, Post-Pert50, Post- Pert100, Post-Pert150, Post-Pert500. Left and right plots show the TRACK and N-TRACK conditions, respectively. Pre-perturbation phase for the PTUP condition is the mean pre-perturbed cycles and pre-perturbation phase of PTDN condition is the mean of the last cycle before PTDN.
The overall effect of the lifting-lowering perturbation was a significant increase in the M finger force in the TRACK task (F1,10 = 9.18, p<0.05) but not in the N-TRACK task. There was a significant drop in the R finger force for both tasks (F1,10 > 6.9, p<0.05) while other finger force changes were under the significance level.
Force Change Patterns: Micro Analysis
During the processes of the M finger lifting and lowering, finger forces showed consistent patterns of changes with time. The group average forces after the initiation of the perturbation are illustrated in the middle (for the M finger lifting phase, PTUP) and in the bottom (for the M finger lowering phase, PTDN) panels of Figure 3. There was a gradual increase in the M finger force during PTUP and its decrease during PTDN while the I and R fingers showed opposite trends of force change (effect of Phase, F1.381,18.811 > 6.6; p < 0.05). No significant effects of Phase on the L finger force were observed. Pairwise contrasts showed significant differences between all pairs of phases for the M finger force (p < 0.05) with the exception of Pre-Pert vs. Post-Pert50. For the I and R fingers, almost all force comparisons between phases starting from PostPert50 were significant with a few exceptions.
The forces of the I, R, and L finger showed changes in the opposite direction to the changes in the force of the M finger, while FTOT changed with the M finger force. In particular, both FTOT and M finger force increased when the M finger was lifted. Pairwise comparisons confirmed significant differences across phases (p < 0.05) with a few exceptions such as Pre-Pert vs. Post-Pert50 for both tasks and PRE-pert vs. Post-Pert100 for N-TRACK. FTOT decreased when the M finger was lowered and its force decreased. The following significant pairwise contrasts were found: Pre-Pert vs. Post-Post500 for both tasks F1,10 > 17.0, p<0.01, Pre-Pert vs. Post-Pert100 for N-TRACK F1,10 = 7.1, p<0.05 as well as all comparisons between Post-Pert phases for both tasks: F1,10 > 11.0, p<0.01).
Motor Equivalence Analysis: Macro Analysis
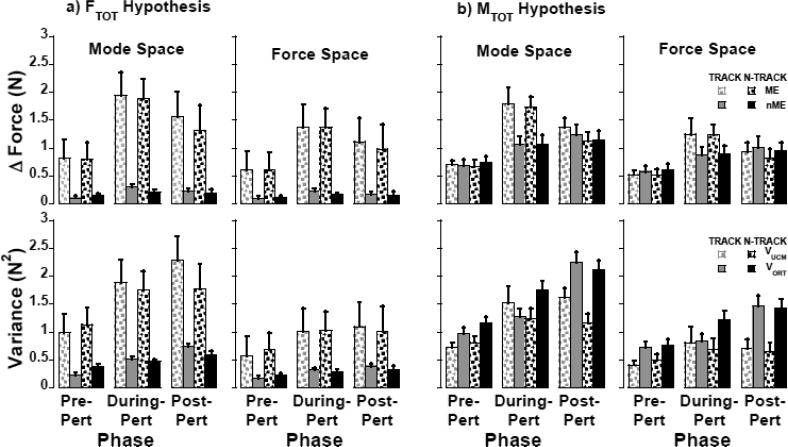
When two components of the finger force/mode (ƒ/m) changes, motor equivalent (ME) and non-motor equivalent (nME), were quantified (see Methods), the ME component showed a dramatic increase during the perturbation (between the two vertical lines in the bottom panels of Figure 2). In fact, the ME component was dominating even during the Pre-Pert cycles reflecting the fact that deviations of finger forces from the average performance were primarily within the sub-space leading to no changes in FTOT (the UCM). These results are illustrated in the top panels of Figure 4A using the averaged across subjects data for the TRACK and N-TRACK tasks, in both m (Figure 4A, left plots) and ƒ spaces (Figure 4A, right plots). It is obvious that in both spaces, both tasks, and all three phases the ME component (dotted bars) was much larger than the nME one (gray and black bars) (F1,10 > 49.0, p<0.0001).
Figure 4.
Motor equivalence (upper plots) and UCM analysis (lower plots) with respect to the to the stabilization of the A) total force (FTOT) and B) total moment of force (MTOT) during phases pre-, during- and post-perturbation for TRACK and N-TRACK tasks. Left and right plots show analyses in the mode and force spaces, respectively. Means ± standard errors are shown.
There were differences in the magnitude of both ME and nME components across the three main phases, Pre-Pert, During-Pert, and Post-Pert (F > 17.0, p<0.001). Both components increased after the M finger was lifted and decreased after the M finger was lowered in both ƒ and m spaces; Post-Pert components were larger than Pre-Pert (pairwise contrasts, p < 0.05). The differences among the three phases were larger for the ME than non-ME component in both ƒ and m spaces (interactions Projection-Component × Phase, F > 17.0, p<0.001; with all pairwise contrasts at p<0.01).
The motor equivalence analysis with respect to MTOT is presented in the upper plots of Figure 4B. The relative magnitude of ME and nME components differed across phases in both ƒ and m spaces (Projection Component × Phase: F > 11.70, p < 0.005). In the pre-perturbed cycles, nME was higher than ME (F1,10 > 22.83, p < 0.001). During perturbation, both ME and nME components increased (F1,10 > 19.0, p < 0.0001) and ME became significantly higher than the nME component, which indicates that most of deviations in the sharing pattern of finger ƒ and m led to no changes in MTOT (F1,10 > 25.0, p < 0.001). Post-perturbation the ME and nME components did not differ in the m space (F1,10 = 0.529, p = 0.484) while nME > ME in the ƒ space (F1,10 = 6.41, p < 0.05). After the perturbation the ME component decreased (F1,10 > 6.90, p < 0.05), while the nME component did not change (F1,10 < 4.1, p > 0.07) for both ƒ and m spaces analyses.
Motor Equivalence Analysis: Micro Analysis
The analysis of the ME and nME components over the time of the M finger lifting and lowering showed a consistent pattern: There was a gradual increase in the ME component over the phases accompanied by a smaller and less consistent increase in the nME component. These findings are illustrated in Figure 5 for both TRACK and N-TRACK tasks (left and right panels of Figure 5) and for the finger lifting (PTUP) and finger lowering (PTDN) phases of the perturbation. The predominance of the ME component (gray bars) is obvious in all the graphs.
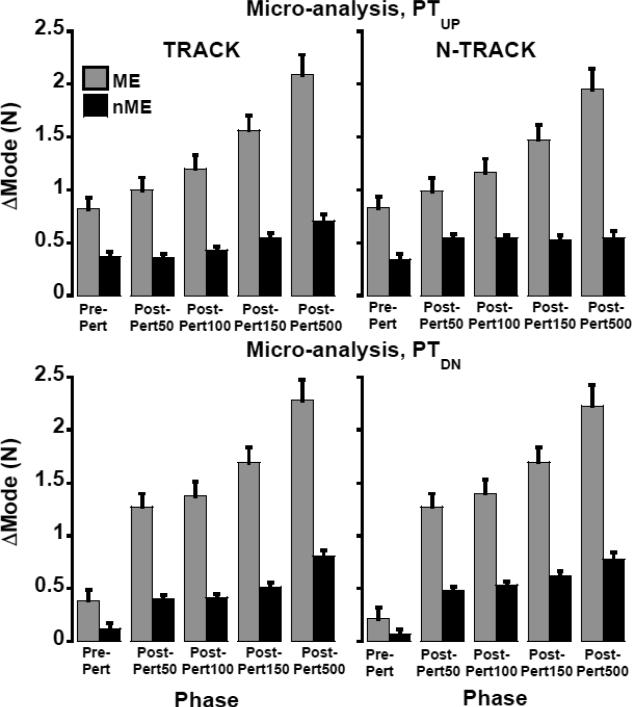
Figure 5.
Motor equivalence analysis during phases pre-, and post-perturbation (Post-Pert50, Post-Pert100, Post-Pert150, Post-Pert500) following PTUP (upper plots) and PTDN (lower plots) for TRACK (left plots) and N-TRACK (right plots) tasks in the mode space. Analysis in the force space (not shown) had similar profiles. Means ± standard errors are shown.
These results were confirmed by the main effects of Projection-Component (F > 35, p < 0.0001) and Phase (F > 78, p < 0.0001) with a significant Projection-Component × Phase interaction (F > 45, p < 0.001). For the PTUP during the TRACK task, all pairwise comparisons between phases were significant with the exception of nME component between the Pre-Pert vs. Post-Pert 50 and vs. Post-Pert 100. During the N-TRACK task, analysis in both ƒ and m spaces showed significance in all pairwise comparisons for the ME component, while only the difference between Pre-Pert and Post-Pert50 was significant for the nME component. The differences between the TRACK and N-TRACK tasks were confirmed by significant Task × Phase (F > 9.0, p < 0.01) and Projection-Component ×Task × Phase (F > 4.1, p < 0.05) interactions. Pairwise comparisons, however, failed to show significant differences in the nME component between Post-Pert50 and Post-Pert100 for the TRACK task. Note that quick adjustments were not tested with respect to the total moment of force because the primary task performance was the total force, and not total moment.
Analysis of the Structure of Variance
Analysis of across-cycle variance performed for each phase of the cycle confirmed that most variance in both ƒ and m spaces was compatible with no changes in FTOT (within the corresponding UCM; effects of Variance-Component, F1,10 > 12.1; p < 0.01). These results are illustrated in the bottom panels of Figure 4 for the TRACK and N-TRACK tasks. The UCM-based analysis revealed that, compared to the Pre-Pert force cycles, the increase in the variance During-Pert and Post-Pert (effect of Phase, F > 4.3, p < 0.05) was primarily within the UCM (Variance-Component × Phase interaction, F > 3.54, p < 0.05).
For the ƒ and m-based analysis, pairwise contrasts confirmed an increase in VUCM from Pre-Pert to During-Pert and Post-Pert (p < 0.05) while there were no differences in VUCM During-Pert and Post-Pert. VORT Post-Pert was higher than During-Pert, and both were significantly larger than VORT in the Pre-Pert steady-state (p < 0.05). There was no main effect of Task and no other significant effects.
For the analysis with respect to MTOT, ANOVA revealed a significant Variance-Component × Phase (F > 6.08, p < 0.05) in both ƒ and m spaces. Overall, the across-trials variance did not stabilize MTOT as illustrated in Figure 4B (lower plots, VORT > VUCM). The main effect of task approached significance for the m analysis (Projection Component × Task: F1.,10=3.614; p = 0.086). The lower-left plot of Figure 4B shows a progressive increase of VORT during- and post-perturbation in the m space (F1,10 > 6.88, p < 0.025). In the ƒ space (right plots Figure 4B), VORT magnitude was not affected by the perturbation (F1,10 = 4.278, p = 0.065), but it increased significantly after the perturbation (F1,10 = 5.28, p < 0.05). In contrast, VUCM in both ƒ and m spaces increased with the perturbation (F1,10 > 6.04, p < 0.05) but did not change after the perturbation (F1,10 < 0.34, p > 0.574).
DISCUSSION
Our main hypothesis formulated in the Introduction has been confirmed in the study. In particular, ME components dominated finger force deviations from the average pre-perturbation performance for the analyses in both spaces of elemental variables (ƒ and m) during all phases of the task. A perturbation led to an increase in the ME component with respect to the pre-perturbation cycles. The Micro-analysis showed that deviations from the mean unperturbed sharing pattern due to the changes in the middle finger position were mostly in the ME space and these responses were partially due to mechanical factors, such as coupling among the fingers and responses of the extrinsic multi-tendon muscles to the perturbation, since ME was observed in the period Post-Pert50, before any mechanical effects mediated by reflex loops could be expected. ME increased substantially along the post-perturbation phases suggesting contributions of local reflexes, pre-programmed and voluntary actions to the motor equivalence. In addition, the UCM-based analysis of variance (Scholz and Schöner 1999) showed that most of the variance of individual finger forces/modes across trials was compatible with unchanged total finger force (was within the UCM computed for the total force; Latash et al. 2001; Scholz et al. 2002). All these results were consistent between the TRACK and N-TRACK conditions.
Mechanisms for motor equivalence
Motor equivalence (ME, deviations of finger forces/modes that did not affect total force) was observed in our experiment immediately following a perturbation and then ME increased in time while the perturbation was kept constant. The non-motor equivalent (nME) component also increased, but to a lesser extent. These results are consistent with those in earlier studies of ME during multi-joint reaching (Mattos et al. 2011, 2013). In contrast to those earlier studies, the perturbation was removed in our experiment. When the perturbation was removed, individuals did not recover their pre-perturbation force/moment sharing patterns. The persistent change from pre- to post-perturbation was large within the UCM, showing ME induced by the transient perturbation and observed under conditions equivalent to the pre-perturbation baseline.
The modulation of finger forces observed as ME within the first 50 ms of the onset of the perturbation may be due to preflexes (Loeb 1999). Preflexes rely on the force-length and force-velocity muscle characteristics that change with muscle activation and hence can be tuned by the central nervous system. Interestingly, the amount of ME increased progressively on a time scale of 100 to 500 ms as shown in Figure 5. This increase likely involved the action of spinal reflexes and long-loop responses as well as voluntary reactions. ME observed shortly after the perturbation also might reflect the structure of the mechanical perturbation itself, e.g., how much of the mechanical effect of the perturbation lied within the UCM and how much lied in the ORT subspace.
The persistent change in the sharing pattern observed after the transient perturbation can be interpreted within the neuronal dynamics model of multi-joint movement by Martin and colleagues (Martin et al. 2009), if the ideas of that model are transferred to the multi-finger task setting of this experiment. According to that model, neural activation variables that generate control signals to muscles converging on each joint are coordinated in such a way that the UCM and ORT subspaces are decoupled. This means that both descending and feedback signals produce two effects, those that do and do not lead to changes in a salient performance variable (FTOT in our study), and these effects do not interfere with each other. The second element of the model is a form of back-coupling similar to the one introduced earlier (Latash et al. 2005), which uses sensory information about the actual joint configuration to produce changes in muscle activation that may affect both UCM and ORT subspaces. Through this back-coupling, the neural control signals respond to sensed changes in each elemental variable leading to larger changes within the UCM, which translate into ME deviations of the system. The fact that ME increases with time is consistent with the gradual updating of the neural commands by the neural dynamics driven by input from the back-coupling.
Task-specific stability and its behavioral consequences
We would like to analyze the main results of our study within a scheme based on a few assumptions (Martin et al. 2009; Latash 2010). First, we accept the main axiom of the equilibrium-point hypothesis (Feldman 1966; Feldman 1986) and its later development as the referent configuration (RC) hypothesis (Feldman 2009) that neural signals associated with the control of a movement can be adequately represented as subthreshold depolarization of neuronal pools leading to the emergence of referent values for salient, task-specific variables (given the external force field) - RCTASK. The differences between referent and actual values of these variables lead to muscle activation via a chain of few-to-many mappings organized into a hierarchy, which leads to RCs at hierarchically lower levels, for example those associated with the control of individual limbs, digits, joints, muscles, etc. All muscle activations contribute to moving actual body configuration towards the RCTASK. If this configuration is not attainable, e.g., due to external or anatomical constraints, a new equilibrium state is reached with non-zero muscle activations.
Second, we assume that the few-to-many (redundant) mappings are organized in a synergic way, that is, variance at the lower (higher-dimensional) level is larger in directions that do not affect the RC at the higher (lower-dimensional) level. This can be achieved via the aforementioned central back-coupling loops and/or feedback loops from peripheral receptors (Latash et al. 2005; Martin et al. 2009). This assumption is readily compatible with the main ideas of the UCM hypothesis.
Stability of performance within this scheme is ensured with respect to task-related, salient variables. In contrast, elemental variables at lower levels of the assumed hierarchy are expected to show relatively large deviations in directions that keep those salient variables unchanged, i.e., within the UCM for those variables. Indeed, several recent experiments have provided evidence for equifinality of task-specific variables under transient perturbations, i.e., their return to pre-perturbation values, while elemental variables showed large deviations from their pre-perturbation values (Wilhelm et al. 2013; Zhou et al. in press). Those studies used changes in external mechanical variables as the means to introduce perturbations. Similar effects, however, may be expected from changes in neural, task-related variables.
A series of recent studies (Mattos et al. 2011, 2013) have shown that an unexpected perturbation during an ongoing movement leads to immediate large deviations within a redundant set of elemental variables (joint rotations and muscle modes, cf. Krishnamoorthy et al. 2003), with a large ME component. This component becomes even larger during movement correction although, obviously, it leads to deviations in the joint configuration and muscle activation spaces that, by definition, have no effect on task-related variables. In other words, most of the corrective action was not correcting anything. This result is hardly compatible with theoretical approaches based on ideas of action optimization (Todorov and Jordan 2002; Diedrichsen et al. 2010). It is, however, a natural consequence of the general theoretical scheme described above. In particular, these results support the aforementioned model of movement control proposed by Martin and colleagues (Martin et al. 2009).
Our main observations in this study generalize the earlier finding to multi-finger action with several important distinctions. First, we studied cyclic tasks that, according to some authors (Hogan and Sternad 2007), have qualitatively different control as compared to discrete tasks studied in the mentioned works by Mattos and her colleagues. Within our scheme, there is no distinction in the control of discrete and cyclic tasks, and our results in the current study of cyclic tasks are qualitatively similar to those in earlier studies of discrete tasks.
Previous experiments suggest that sharing patterns of force in multi-finger pressing tasks are chosen to minimize pronation and supination moments acting on the hand (minimization of secondary moments, Li et al. 1998; Zatsiorsky et al. 1998; Zatsiorsky et al. 2000). During multi-finger accurate cyclic force production, similar to the task used in this experiment, subjects showed stabilization of the total moment of force (MTOT) in a sense VUCM > VORT in the space of finger modes (Latash et al. 2001; Scholz et al. 2002). The authors have suggested that moment stabilization is a default developed during everyday tasks. Our results provide indirect support for the hypothesis on unintended moment stabilization. Indeed, there were large ME components in the deviations of finger forces (and modes) computed with respect to MTOT as the performance variable. However, the relative magnitude of ME deviations in the analysis with respect to MTOT was smaller than for the analysis with respect to FTOT. We also failed to see the signature of MTOT stabilization in the analysis of inter-cycle variance (see Fig. 4): In contrast to the results of this analysis with respect to FTOT (VUCM > VORT), analysis with respect to MTOT showed an opposite inequality (VUCM < VORT). The difference in the current results from those in the cited earlier studies has to be explored in future,
Earlier studies of the ME and nME components in response to perturbations explored unidirectional perturbations that led to a new force field (Mattos et al. 2011, 2013). Our study used transient perturbations, such that at the end of the trial the subjects were performing the task in the same external conditions as prior to the perturbation. Nevertheless, there was a significant increase in the ME component suggesting that effects of perturbations on the two components of motion (ME and nME) are seen even when the system apparently returns to a pre-perturbation state. These results follow naturally the introduced theoretical scheme: Each of the two components of the perturbation (PTUP and PTDN) contributed to ME motion, which was not corrected by the subject, while the nME motion was corrected.
Robustness of the results in the two spaces of elemental variables, finger forces and finger modes (cf. Danion et al. 2003) provides extra validity for the conclusion that stability at any of the lower levels of the hierarchy is structured with respect to task-specific variables with higher stability (lower variance) in directions that lead to changes in those variables (ORT, leading to nME deviations) as compared to directions that do not (UCM, leading to ME deviations).
Motor equivalence and UCM
The analysis of the structure of inter-trial variance within the UCM hypothesis and analysis of the two components, ME and nME, do not have to lead to similar outcomes. The UCM-based analysis of inter-trial variance quantifies deviations of the system from its average across trials behavior (Scholz and Schöner 1999). Assuming that each trial starts from somewhat different initial conditions and is associated with somewhat different changes in external conditions, variance is expected to be larger in directions of low stability (those spanning the UCM) as compared to directions of high stability (ORT). Hence, the signature inequality VUCM > VORT has been used as a proxy of different stability properties in sub-spaces computed with respect to a potentially important performance variable (reviewed in Latash et al. 2007).
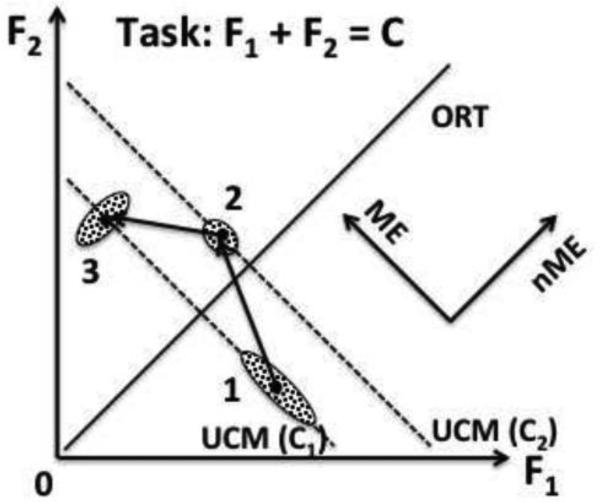
Figure 6 illustrates a task of producing a constant force with two effectors: F1 + F2 = C1. If the CNS organizes stability of (F1 + F2), a cloud of data points elongated along the UCM (the dashed, slanted line) is expected in a series of trials (the cloud 1). Imagine now that an external perturbation changes the total force to C2. Since the two-effector system is less stable along the UCM (shown with the slanted dashed line), in addition to the deviation orthogonal to the UCM leading to a change in the total force (ORT, solid, thick line in Figure 6), a large deviation is expected along the UCM. If the subject in this mental experiment tries to bring the force back to C1, the corrective action may also be expected to lead to a large deviation of the two forces along the UCM. The deviations along the UCM are ME, while orthogonal to the UCM deviations – are nME. In multi-finger pressing tasks, the ME component represents a change in the force sharing pattern leading to the same total force, while changes in the magnitude of total force correspond to the nME component. Relative magnitudes of the ME and nME components are independent of the shape of data point distribution (compare the data clouds 1, 2, and 3), and hence this analysis is complementary to analysis of variance components within the UCM-framework. However, within our theoretical scheme, both of these potentially independent analyses are expected to lead to qualitatively similar results because they both reflect different task-specific stability in different directions within a redundant space of elemental variables. This was indeed the case for the analyses with respect to FTOT.
Figure 6.
An illustration of the idea of motor equivalence. Two effectors are involved in a common task F1 + F2 = C. In the initial steady state (C = C1, cloud of data points 1), inter-trial variance is mostly along the UCM for this task (dashed line). A perturbation changes the output of the system to C2 (cloud of points 2). It is expected to lead to larger deviation along the less stable direction (ME, along the UCM) as compared to more stable direction (nME, along ORT). A correction leads to the same output of the system, C1 (cloud of points 3), again with a large ME deviation along the UCM. Note that the ME vs. nME deviations may be associated with different structure of inter-trial variance as illustrated with the different shapes of the clouds of data points.
The analyses with respect to MTOT, which was not an explicit task-related variable, led to conflicting results. We observed relatively large ME components but no signs of stabilization of MTOT in the across-cycles variance indices. The relatively similar amounts of ME and nME components observed in the analysis with respect to MTOT suggest that the neural controller did not consider MTOT as an important performance variable. Note that stabilization of FTOT and MTOT are in competition. Indeed, stabilization of FTOT requires negative co-variation of forces across cycles, while stabilization of MTOT requires positive co-variation of forces produced by finger pairs acting in opposite direction (IM and RL). Both variables can be stabilized simultaneously as shown in earlier studies (Scholz et al. 2002; Zhang et al. 2008). So, the strong stabilization of FTOT observed on our experiment (VUCM >> VORT) might contribute to the inequality VUCM < VORT observed for MTOT. It is possible that the practice given to the subjects, the instruction emphasizing accurate FTOT production, and the presence of perturbations played a role in the current results being different from those in earlier reports (Latash et al. 2001; Scholz et al. 2002).
We would like to emphasize the consistency of results obtained so far in studies of motor equivalence in different spaces of elemental variables, joint configuration space (Mattos et al. 2011), muscle mode space (Mattos et al. 2013), and finger force/mode spaces (the present study). The results were also consistent across discrete and cyclic tasks and tracking and no-tracking tasks. Overall, they provide so far the most consistent support for the scheme for the neural control of natural movements performed by redundant sets of elements.
Concluding Comments
To summarize the main lesson from this study, consider the following example. Imagine that you press with a finger on the top of a long spring (similar to the one in the pen) placed vertically (cf. Valero-Cuevas et al. 2003). The spring shows relatively high resistance to deformation (high stability) along its axis and relatively low resistance (low stability) orthogonal to its long axis. Even if you try your best to compress the spring slowly and accurately, at some point it will buckle (the so-called Euler's buckling). This buckling action is a consequence of different stability of the spring in different directions. Similarly, in our experiments, as well as in the previous studies (Mattos et al. 2011, 2013), a purposeful action along a desired direction (trying to correct total force) led to large deviations orthogonal to that direction (ME). Those deviations were not part of the movement plan but natural consequences of the physics of the system resulting in its lower stability in directions spanning the UCM and contributing to the ME component.
Acknowledgments
The study was supported by NIH grants NS-035032 and AR-048563. We are grateful to Dr. Yen-Hsun Wu for his help at early stages of this project.
APPENDIX
Variance and motor equivalence analyses
The force data were converted into a mode vector m by using the enslaving matrix E, where f = [fI, fM, fR, fT] (T represents matrix transpose).
| (A1) |
The Jacobian matrix J defining the linear map between changes in finger forces (df) modes (dm) and changes in total force dFTOT was defined:
| (A2) |
| (A3) |
The J matrix defining the changes between the finger force and modes (ƒ/m) and changes in total moment about the longitudinal axis of the forearm/hand with respect to the mid-point of the hand is:
| (A4) |
where the di entries representing the lever arm of fingers, dI = 4.5 cm, dM = 1.5 cm, dR = 1.5 cm and dL = -4.5 cm. The UCM is the null-space of the Jacobian matrix J, spanned by the basis vectors εi, solving:
| (A5) |
For the variance analysis, the mean-free ƒ/m (Δxjk) for a given j trial and k phase (pre-, during- and post-perturbation) was computed:
| (A6) |
where x was either force or mode. The Δx was projected into the null and orthogonal spaces of J as follows:
| (A7) |
| (A8) |
where f∥ is the f parallel component and f⊥ is the orthogonal component, n is the number of elemental variables (ƒ/m), and p is the number of constraints defined by the performance variable There are n–p basis vectors, so that the null space has n–p dimensions.
The variance across trials per degree of freedom along Vucm and orthogonal Vort to the UCM was computed.
| (A9) |
| (A10) |
For the motor equivalence analysis, the force/mode deviation vectors Δxj were computed for each j trial by subtracting the mean pre-perturbed force/mode x0,AV.
| (A11) |
The alignment between x0,AV and the xj, involved temporal normalization of x0,AV for each cycle of j trial. The Δxj was projected along and orthogonal to the UCM according to equations A7 and A8. The motor equivalence (ME) and non-motor equivalence components (nME) were computed as the length of the projection vector in each subspace, respectively, and normalized by the square root of the degrees of freedom of each space:
| (A12) |
| (A13) |
REFERENCES
- Bernstein NA. The co-ordination and regulation of movements. Pergamon Press; Oxford: 1967. [Google Scholar]
- Danion F, Schöner G, Latash ML, Li S, Scholz JP, Zatsiorsky VM. A mode hypothesis for finger interaction during multi-finger force-production tasks. Biol Cybern. 2003;88:91–98. doi: 10.1007/s00422-002-0336-z. [DOI] [PubMed] [Google Scholar]
- Diedrichsen J, Shadmehr R, Ivry RB. The coordination of movement: optimal feedback control and beyond. Trends Cogn Sci. 2010;14:31–39. doi: 10.1016/j.tics.2009.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldman AG. Functional tuning of the nervous system with control of movement or maintenance of a steady posture. II. Controllable parameters of the muscle. Biophysics. 1966;11:565–578. [Google Scholar]
- Feldman AG. Once more on the equilibrium-point hypothesis (λ model) for motor control. J Mot Behav. 1986;18:17–54. doi: 10.1080/00222895.1986.10735369. [DOI] [PubMed] [Google Scholar]
- Feldman AG. Origin and advances of the equilibrium-point hypothesis. Adv Exp Med Biol. 2009;629:637–643. doi: 10.1007/978-0-387-77064-2_34. [DOI] [PubMed] [Google Scholar]
- Friedman J, SKM V, Zatsiorsky VM, Latash ML. The sources of two components of variance: an example of multifinger cyclic force production tasks at different frequencies. Exp Brain Res. 2009;196:263–277. doi: 10.1007/s00221-009-1846-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hogan N, Sternad D. On rhythmic and discrete movements: reflections, definitions and implications for motor control. Exp Brain Res. 2007;181:13–30. doi: 10.1007/s00221-007-0899-y. [DOI] [PubMed] [Google Scholar]
- Hughes OM, Abbs JH. Labial-mandibular coordination in the production of speech: implications for the operation of motor equivalence. Phonetica. 1976;33:199–221. doi: 10.1159/000259722. [DOI] [PubMed] [Google Scholar]
- Kelso JA, Tuller B, Vatikiotis-Bateson E, Fowler CA. Functionally specific articulatory cooperation following jaw perturbations during speech: evidence for coordinative structures. J Exp Psychol: Hum Percept Perform. 1984;10:812–832. doi: 10.1037//0096-1523.10.6.812. [DOI] [PubMed] [Google Scholar]
- Krishnamoorthy V, Latash ML, Scholz JP, Zatsiorsky VM. Muscle synergies during shifts of the center of pressure by standing persons. Exp Brain Res. 2003;152:281–292. doi: 10.1007/s00221-003-1574-6. [DOI] [PubMed] [Google Scholar]
- Latash ML. Motor synergies and the equilibrium-point hypothesis. Motor Control. 2010;14:294–322. doi: 10.1123/mcj.14.3.294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML. The bliss (not the problem) of motor abundance (not redundancy). Exp Brain Res. 2012;217:1–5. doi: 10.1007/s00221-012-3000-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML, Scholz JF, Danion F, Schöner G. Structure of motor variability in marginally redundant multifinger force production tasks. Exp Brain Res. 2001;141:153–165. doi: 10.1007/s002210100861. [DOI] [PubMed] [Google Scholar]
- Latash ML, Shim JK, Smilga AV, Zatsiorsky VM. A central back-coupling hypothesis on the organization of motor synergies: a physical metaphor and a neural model. Biol Cybern. 2005;92:186–191. doi: 10.1007/s00422-005-0548-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levin O, Wenderoth N, Steyvers M, Swinnen SP. Directional invariance during loading-related modulations of muscle activity: evidence for motor equivalence. Exp Brain Res. 2003;148:62–76. doi: 10.1007/s00221-002-1277-4. [DOI] [PubMed] [Google Scholar]
- Li ZM, Latash ML, Zatsiorsky VM. Force sharing among fingers as a model of the redundancy problem. Exp Brain Res. 1998;119:276–286. doi: 10.1007/s002210050343. [DOI] [PubMed] [Google Scholar]
- Loeb GE. What might the brain know about muscles, limbs and spinal circuits? Prog Brain Res. 1999;123:405–409. doi: 10.1016/s0079-6123(08)62875-7. [DOI] [PubMed] [Google Scholar]
- Martin JR, Budgeon MK, Zatsiorsky VM, Latash ML. Stabilization of the total force in multi-finger pressing tasks studied with the ‘inverse piano’ technique. Hum Mov Sci. 2011;30:446–458. doi: 10.1016/j.humov.2010.08.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin V, Scholz JP, Schöner G. Redundancy, self-motion, and motor control. Neural Comput. 2009;21:1371–1414. doi: 10.1162/neco.2008.01-08-698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattos D, Kuhl J, Scholz JP, Latash ML. Motor equivalence (ME) during reaching: is ME observable at the muscle level? Motor Control. 2013;17:145–175. doi: 10.1123/mcj.17.2.145. [DOI] [PubMed] [Google Scholar]
- Mattos DJ, Latash ML, Park E, Kuhl J, Scholz JP. Unpredictable elbow joint perturbation during reaching results in multijoint motor equivalence. J Neurophysiol. 2011;106:1424–1436. doi: 10.1152/jn.00163.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prochazka A, Clarac F, Loeb GE, Rothwell JC, Wolpaw JR. What do reflex and voluntary mean? Modern views on an ancient debate. Exp Brain Res. 2000;130:417–432. doi: 10.1007/s002219900250. [DOI] [PubMed] [Google Scholar]
- Scholz JP, Danion F, Latash ML, Schöner G. Understanding finger coordination through analysis of the structure of force variability. Biol Cybern. 2002;86:29–39. doi: 10.1007/s004220100279. [DOI] [PubMed] [Google Scholar]
- Scholz JP, Dwight-Higgin T, Lynch JE, Tseng YW, Martin V, Schöner G. Motor equivalence and self-motion induced by different movement speeds. Exp Brain Res. 2011;209:319–332. doi: 10.1007/s00221-011-2541-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scholz JP, Schöner G. The uncontrolled manifold concept: identifying control variables for a functional task. Exp Brain Res. 1999;126:289–306. doi: 10.1007/s002210050738. [DOI] [PubMed] [Google Scholar]
- Scholz JP, Schöner G, Hsu WL, Jeka JJ, Horak F, Martin V. Motor equivalent control of the center of mass in response to support surface perturbations. Exp Brain Res. 2007;180:163–179. doi: 10.1007/s00221-006-0848-1. [DOI] [PubMed] [Google Scholar]
- Scholz JP, Schöner G, Latash ML. Identifying the control structure of multijoint coordination during pistol shooting. Exp Brain Res. 2000;135:382–404. doi: 10.1007/s002210000540. [DOI] [PubMed] [Google Scholar]
- Schöner G. Recent developments and problem in human movrement science and their conceptual implications. Ecol Psychol. 1995;7:23. [Google Scholar]
- Schöner G, Martin V, Reimann H, Scholz J. Motor Equivalence and the uncontrolled manifold.. Proceedings 8th International Seminar on Speech Production; Strasbourg, France. 2008. pp. 23–28. [Google Scholar]
- Todorov E, Jordan MI. Optimal feedback control as a theory of motor coordination. Nat Neurosci. 2002;5:1226–1235. doi: 10.1038/nn963. [DOI] [PubMed] [Google Scholar]
- Valero-Cuevas FJ, Smaby N, Venkadesan M, Peterson M, Wright T. The strength-dexterity test as a measure of dynamic pinch performance. J Biomech. 2003;36:265–270. doi: 10.1016/s0021-9290(02)00340-8. [DOI] [PubMed] [Google Scholar]
- Wilhelm L, Zatsiorsky VM, Latash ML. Equifinality and its violations in a redundant system: multifinger accurate force production. J Neurophysiol. 2013;110:1965–1973. doi: 10.1152/jn.00461.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wing AM. Motor control: Mechanisms of motor equivalence in handwriting. Curr Biol. 2000;10:R245–248. doi: 10.1016/s0960-9822(00)00375-4. [DOI] [PubMed] [Google Scholar]
- Zatsiorsky VM, Li ZM, Latash ML. Coordinated force production in multi-finger tasks: finger interaction and neural network modeling. Biol Cybern. 1998;79:139–150. doi: 10.1007/s004220050466. [DOI] [PubMed] [Google Scholar]
- Zatsiorsky VM, Li ZM, Latash ML. Enslaving effects in multi-finger force production. Exp Brain Res. 2000;131:187–195. doi: 10.1007/s002219900261. [DOI] [PubMed] [Google Scholar]
- Zhang W, Scholz JP, Zatsiorsky VM, Latash ML. What do synergies do? Effects of secondary constraints on multidigit synergies in accurate force-production tasks. J Neurophysiol. 2008;99:500–513. doi: 10.1152/jn.01029.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou T, Solnik S, Wu Y-H, Latash ML. Equifinality and its violations in a redundant system: Control with referent configurations in a multi-joint positional task. Motor Control. doi: 10.1123/mc.2013-0105. (in press) [DOI] [PubMed] [Google Scholar]