Pseudo-random Center Placement O-space Imaging for Improved Incoherence Compressed Sensing Parallel MRI

Abstract

Purpose

Nonlinear spatial encoding magnetic (SEM) field strategies such as O-space imaging have previously reported dispersed artifacts during accelerated scans. Compressed sensing (CS) has shown a sparsity-promoting convex program allows image reconstruction from a reduced data set when using the appropriate sampling. The development of a pseudo-random center placement (CP) O-space CS approach optimizes incoherence through SEM field modulation to reconstruct an image with reduced error.

Theory and Methods

The incoherence parameter determines the sparsity levels for which CS is valid and the related transform point spread function measures the maximum interference for a single point. The O-space acquisition is optimized for CS by perturbing the Z² strength within 30% of the nominal value and demonstrated on a human 3T scanner.

Results

Pseudo-random CP O-space imaging is shown to improve incoherence between the sensing and sparse domains. Images indicate pseudo-random CP O-space has reduced mean squared error compared with a typical linear SEM field acquisition method.

Conclusion

Pseudo-random CP O-space imaging, with a nonlinear SEM field designed for CS, is shown to reduce mean squared error of images at high acceleration over linear encoding methods for a 2D slice when using an eight channel circumferential receiver array for parallel imaging.

INTRODUCTION

This work combines two methods, O-space imaging (1,2), a nonlinear spatial encoding magnetic (SEM) field parallel imaging method, and compressed sensing (3), a sampling and reconstruction method, to provide further gains in accelerated MRI. Benefits have been shown when using a total variation norm with linear and nonlinear SEM field imaging (4–6). While compatible, there has been no CS motivated acquisition design using nonlinear SEM field parallel imaging or of the improved incoherence available in O-space imaging.

Parallel imaging methods seek to approximate data using coil sensitivity profile information to collect fewer phase encoding steps, which are typically taken one per repetition time (TR) (7–9). When undersampling is performed with multiple receivers, the sensitivity profiles of the detectors (coils) provide enough spatial information to allow certain amounts of aliasing to be unwrapped. With SENSE (10), de-aliasing performance is evaluated in terms of the amount of noise amplification that occurs in each voxel as a consequence of the unwrapping problem becoming poorly conditioned with undersampling (10,11). Many hardware developments in parallel imaging have focused on building phased array coils with more receiver channels, preamplifiers, and data acquisition boards in order to gain additional spatial localization from the coils (12,13). However, diminishing returns below ultimate limits occur with further increases in detectors, in part because of limits on using geometrical and preamplifier decoupling to eliminate mutual inductance and interference (14–16).

SEM fields, commonly known as gradient fields in the linear case, combine with RF coil profiles to form composite encoding functions (17). For instance, linear imaging gradients create a constant frequency encoding across the image weighted by the coil sensitivity profile (18). Developments in the application of nonlinear SEM fields for parallel imaging have focused on reducing peripheral nerve stimulation (19–21), perfecting local k-space coverage (22,23), signal to noise (SNR) optimization through frame analysis (24), and algebraic determination of arbitrary encoding fields such as Null Space imaging (NSI) (25,26). Local k-space analysis, which plots the k-space from the spatial derivative of encoded phase, k(t) = ∇φ(x, t), provides an intuitive examination of the spatially-varying nature of nonlinear acquisitions albeit without accounting for spatial localization from the receivers (22). Other applications of nonlinear SEM fields include tailoring resolution to a region of interest (27) and spread spectrum conditioning through prephasing for single detector CS (28). For O-space imaging, it was hypothesized that a radially symmetric encoding shape would complement a circumferentially-arranged coil array better than a linear SEM field, reducing the amount of data that must be acquired (1,2). Imaging performance in terms of noise amplification and sum of squared error demonstrates nearly uniform white noise amplification with sampling (1,26).

CS has been shown to be an effective approach that leads to further acceleration by pseudo-randomly undersampling the k-space data and enforcing sparsity in a transform domain during image reconstruction (3,29). More specifically, the CS approach consists of 1) an image that is sparse in a transform domain, 2) a measurement basis incoherent with the sparse domain (reached through a sparsifying transform Ψ), and 3) a reconstruction in the sparse domain that enforces sparsity (3). In CS image reconstruction, convergence to the correct image is guaranteed to an arbitrarily close limit related to the log of the number of measurements. Notably, the measurement basis for a 2D and a 3D acquisition was to pseudo-randomly undersample the phase encoding direction, that is the k_y – direction in 2D, and both k_y & k_z directions in 3D acquisitions (3).

The CS approach has been combined with parallel imaging (5,30–33) in conjunction with a conventional MRI k-space acquisition. It has been demonstrated that some MRI undersampling schemes produce better incoherence than others, i.e. k_y & k_z undersampling outperforms k_y undersampling and radial provides more incoherence vs. Cartesian (3,6). As Liang et. al. noted, SENSE may not be strictly optimal for CS with parallel imaging, and the SENSE undersampling should be kept as low as a factor of two (31). Higher SENSE factors lead to aliasing patterns with poor incoherence, adversely affecting CS reconstruction. They proposed a two-tier CS-SENSE method, which generates intermediate aliased images prior to a Cartesian SENSE reconstruction. No transform point spread function (TPSF) or incoherence parameter analysis was performed to examine the interaction of the SENSE reconstruction with incoherence levels.

O-space imaging imposes a quadratic variation in frequency encoding through the use of a Z² (short-hand for $z^2-\frac{x^2+y^2}{2}$, see Figure 1) SEM field to generate incoherence with the sparse domain. Linear gradients are used to offset the center placement (CP) of the circularly symmetric encoding. Accelerated O-space shows inherent incoherence with both the image domain and sparse domain that enables a straight-forward gradient echo sequence to be used in CS O-space imaging.

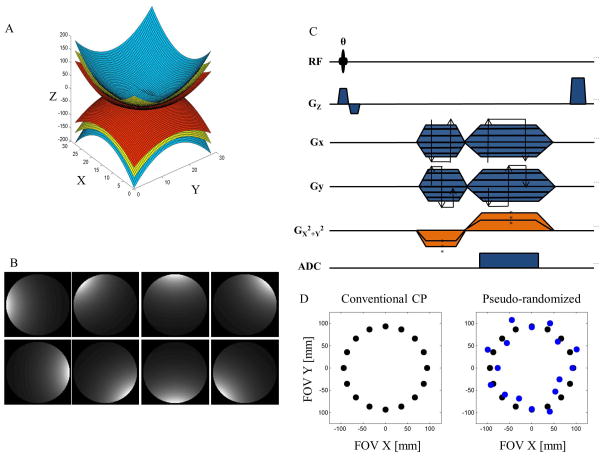
Figure 1.

(A) Gradient shape of the Z² spherical harmonic, short-hand for a circularly symmetric encoding field with spatial variation z²-½(x²+y²). (B) Simulated sensitivities for an eight element circumferential microstrip receiver array. (C) Pulse sequence diagram of the pseudo-random O-space imaging sequence. The sequence is a gradient echo sequence that uses a radial-like progression for the linear strengths and randomizes the Z² strength within 30% of the nominal O-space strength (D) to increase incoherence for a sparsity-promoting reconstruction.

The current work proposes that offsetting CPs by perturbing the Z² strength generates greater incoherence, as measured by off-peak TPSF energy, relative to regular O-space imaging. Residual artifacts are iteratively removed through CS reconstruction. The incoherence of O-space with the sparsity basis is optimized by pseudo-randomization of the CP radius (where each different CP is equivalent in time to each different phase encode step in Cartesian sampling) and performance is confirmed through TPSF, the incoherence parameter, and local k-space analyses. In the sections below, we demonstrate that the improved efficiency of spatial localization associated with O-space may be combined with the benefits of CS at high parallel imaging accelerations to provide further acceleration.

THEORY

Conventional O-space Imaging

With O-space imaging, the Fourier transform of an echo obtained in the presence of the radially-symmetric Z² SEM field yields a projection of the object onto a set of concentric rings. With radial localization provided by the gradient coils, the surface coils provide circumferential spatial localization. In O-space imaging, rather than performing phase encoding, the center of the quadratic SEM field is moved to different locations to obtain projections of the object. The pulse sequence in Figure 1c shows different TRs have different CPs rather than different phase encoding. The different CPs, timing, and readout parameters determine the measurement basis, Φ, also known as the encoding matrix. The measurements, y, are of the form:

$$s_{l,i}\in \{s_{1,1}=<\mathbf{x},{\varphi }_{1,1}>,\dots ,s_{M,L}=<\mathbf{x},{\varphi }_{M,L}>\}$$ Eq. [1]

$${\varphi }_{l,i}={\mathbf{C}}_l·{\mathbf{G}}_i,{\varphi }_{l,i}\in \mathrm{\Phi }$$ Eq. [2]

$${\mathbf{G}}_i=exp(-j2\pi G_{Z2}\frac{1}{2}{(\mathbf{r}-r_p)}^2{t}_i)$$ Eq. [3]

where s_l,i is the measured data, x is the imaged object, C_l is a coil sensitivity profile, r is the radius from the center, M is the total number of measurements, l is the index running to the total number of detectors L, r_p is the p-th center placement, φ_l,i is a composite encoding vector whose set forms the measurement basis (φ_l,i ∈ Φ), G_Z2 is the strength of the Z² SEM field, t_i is the indexed time points for data collection, and G_i is the encoding from the SEM fields. The O-space sequence considered here has one CP per readout (TR). The formalism follows the CS notation from (3), and the familiar signal equation in this notation is:

$$s_{l,i}=\int {\varphi }_{l,i}(\mathbf{r})\mathbf{x}(\mathbf{r})d\mathbf{r}$$ Eq. [4]

where r is a spatial position and the integration is over the FOV.

Optimizing the O-space sampling method

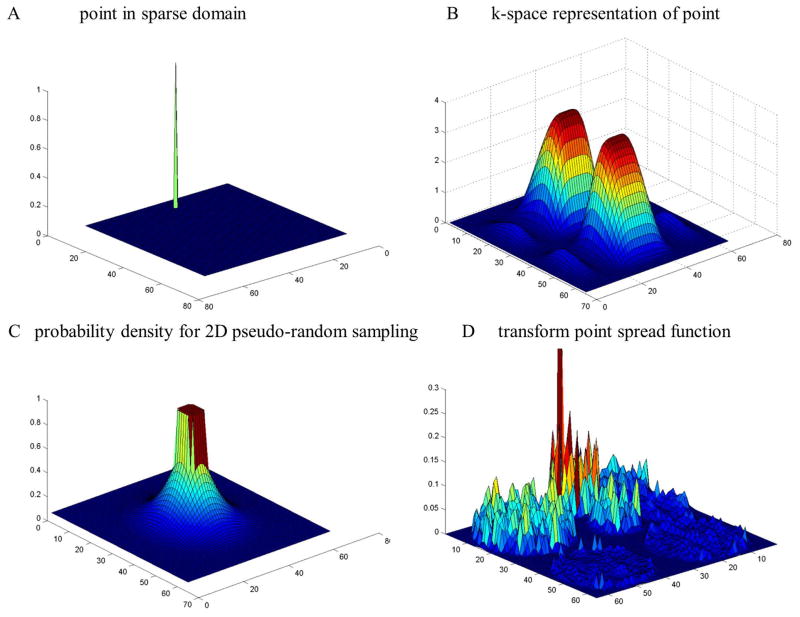
As introduced previously in (3), the sidelobe to peak ratio (SPR) of the TPSF evaluates the extent to which the measurement domain, represented by the encoding matrix, is incoherent with respect to the sparse domain. The formula for the TPSF is TPSF_ij = e_j*ΨΦ⁻¹ΦΨ⁻¹e_i with e_i and e_j as the standard unit bases (3). The SPR measure finds the second highest peak (sidelobe) and divides it by the signal from the original point (peak). SPRs may be simulated for each acquisition and associated encoding matrix. The TPSF is simulated by selecting a point in the sparse domain, e.g. the wavelet domain. The point is then transformed to the measurement basis and the experiment (acquisition process) is simulated. After the experiment, the result is transformed back into the sparse domain. Comprehensively measuring the TPSF SPR values effectively determines whether CS theory guarantees recovery. Namely, one requires the restricted null space property, which similar to the restricted isometry property, is sufficient to guarantee convergence in CS as shown in (34,35). For the restricted null space property to apply, the pairwise incoherence parameter δ must satisfy:

$$\delta =max\left|\frac{\langle {\left(\mathrm{\Phi }{\mathrm{\Psi }}^{-1}\right)}_i,{\left(\mathrm{\Phi }{\mathrm{\Psi }}^{-1}\right)}_j\rangle }{N}\right|\le \frac{1}{3k}\forall i\ne j$$ Eq. [5]

where Ψ is the sparsifying transform, the indices refers to a single column in ΦΨ⁻¹, N is the number of pixels in the image, and the sparsity cardinality k specifies the largest subset of vectors in the sparse domain that will be exactly recovered (29,34,35). The matrix combination ΦΨ⁻¹ contains the salient design parameters in the system and may be known as the design matrix. The significance of the TPSF value is evident as it is equivalent to the argument in eq. 5 multiplied by an additional constant coefficient for a given image. To reduce δ, the undersampling performed during the experiment should generate noise-like and distributed artifacts in the sparse domain (29). Figure 2 illustrates the TPSF for a pseudo-randomly under sampled k-space. Several TPSFs are presented for flat top SEM field methods described in the following section.

Figure 2.

The transform point spread function workflow. A point in the wavelet domain (A) is expressed in the measurement domain, in this case the k-space domain (B). The k-space is pseudo-randomly under sampled with probability density function (C). The subsampled k-space is then transformed into the wavelet domain where the incoherence can be seen as noise-like off-peak energy in the transform point spread function.

For a given system, the TPSF SPR values may be measured for each index i and j which numerically determines the maximum over the image (the incoherence parameter δ). TPSF SPR values at each spatial position to measure the incoherence of a system and effectiveness under a CS framework.

CS reconstruction for O-space

The CS reconstruction used here is an iterative conjugate gradients method published by Lustig et. al. (3), with the measurement basis incorporating nonlinear SEM field parallel imaging. The equation for convex optimization may be written as:

$$\mathbf{x}=argmin\{{\Vert \mathrm{\Phi }\mathbf{x}-\mathbf{s}\Vert }_2+\lambda {\Vert \mathrm{\Psi }\mathbf{x}\Vert }_1\}$$ Eq. [6]

where Φ denotes the measurement basis (sometimes known as the encoding matrix or the sensing basis) with its inverse calculated by the Kaczmarz iterative algebraic reconstruction technique, a pseudo-inverse algorithm that converges to the minimum least squares norm solution (2,36). The first term in the argument imposes data consistency and the 2nd term is the sparsity-promoting ℓ₁ constraint. The sparse domain may be chosen as a variety of orthogonal domains, including Haar and Daubeuchies wavelets of varying order, contourlets, finite differences, or some combination of weighted domains (3).

METHODS

Simulations

O-space images were created using a circumferentially-arranged center placement pattern (2). The imaging plane was a transverse slice set at isocenter. For O-space imaging a set of projections, one per TR, was simulated with each echo arising from a different center placement. All the simulations were implemented in MATLAB® (Natick, MA). Simulated receiver coil sensitivity profiles for a single uniform birdcage, two, and eight element array (Figure 1) were calculated using analytical expressions for circumferentially arranged microstrip RF detectors (37). Undersampling omitted CPs in an interleaved fashion (2,26) similar to the procedure used in undersampling radial spokes for a radial acquisition. To generate a CS acquisition for O-space imaging, CP radii were perturbed from the default radius within 30% of the nominal strength using a uniform random distribution. The nominal Z2 strength was set such that CP = FOV/2. For optimization of the incoherence, twenty trials were evaluated and the strategy was used that yielded the best TPSF SPR value at a uniform grid of twenty points in the transform domain.

Sample TPSFs were created for O-space, NSI, pseudo-randomly undersampled Cartesian k-space sampling, and pseudo-random CP O-space sampling (Figure 3). For the pseudo-random undersampling of k-space in 2D, a Poisson disk undersampling of phase encoding lines was used and the k-space acquisition is shown as an inset of Figure 3b. The sampling pattern enforces a minimum separation between acquired lines of k-space (38). The sparse basis is the Daubechies wavelets with mother and father coefficients of four and two, respectively. The measurement basis is generated from the acquisition method and imaging parameters following Eq. 2. Sample TPSFs are shown for pseudo-random radial encoding and pseudo-random O-space encoding for one versus two detectors at R=8 (Figure 4). The TPSF values for a point are summarized in Table 1 of the supplementary material comparing one versus two detectors for linear and nonlinear imaging. The TPSFs do not capture the spatial dependence of the parallel imaging reconstruction. To elucidate an understanding of spatial dependence, PSFs at two different points, one in the center and one 2/3 of the distance to the edge of the FOV, are shown for O-space and O-space with CS at R=8 (Figure 5). Local k-space plots (Figure 6) were created for O-space and pseudo-random CP O-space to evaluate spatially-dependent resolution effects. The blue lines in the local k-space plots refer to acquired local k-space data (color figures viewable in the electronic version). Local k-space plots were created by evaluating the spatial derivative of the accumulated phase as described in (22).

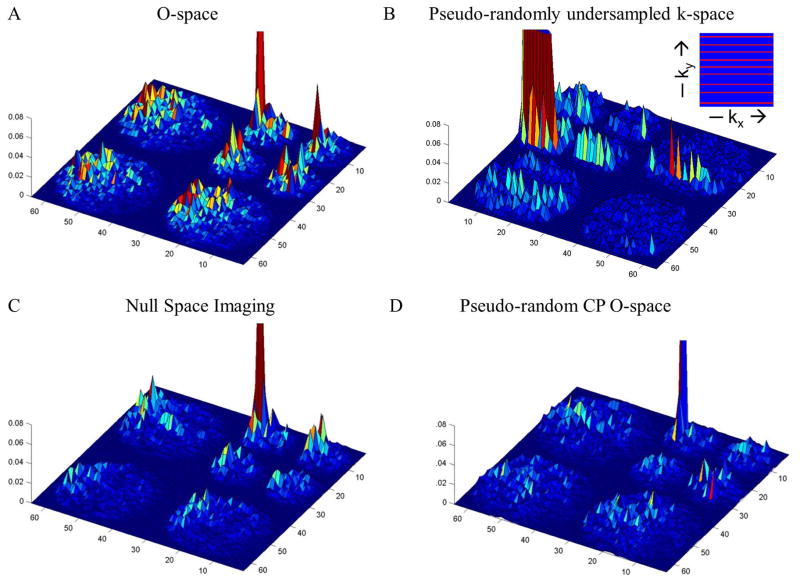
Figure 3.

Sample TPSFs for are shown for an arbitrary point at coordinates (7, 29) in the wavelet domain at reduction factor R=8. The spatially-varying nature of the acquisition is examined in the following figure. The TPSF with highest peak and low noise-like background denotes greatest incoherence and suitability for a sparsity-promoting reconstruction. The inset figure in panel B is the acquired k-space for the Cartesian compressed sensing, namely Poisson disk sampling of phase encoding steps. O-space imaging shows interference patterns that spread more evenly across length scales and orientations. As a result the scale of the incoherence is reduced. O-space with pseudo-random CPs (D) has the greatest incoherence of the methods shown.

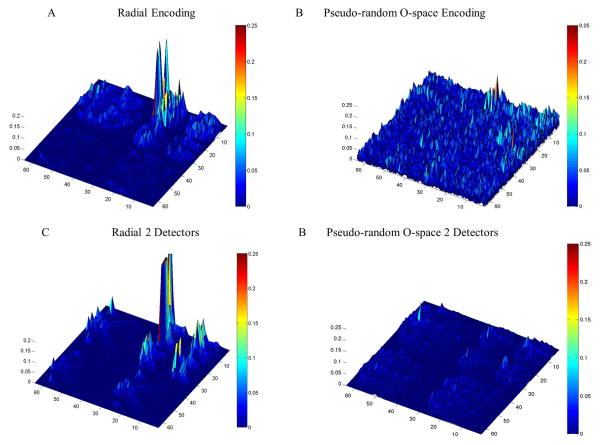
Figure 4.

TSPFs are compared for linear encoding versus O-space nonlinear encoding for CS optimized acquisitions at reduction factor R=8 with the main peak nulled to visualize the off-peak energy clearly. The off peak energy is reduced when moving to multiple detectors, and the effect is pronounced for nonlinear encoding (see Table 1 in the supplementary material for TPSF SPR values).

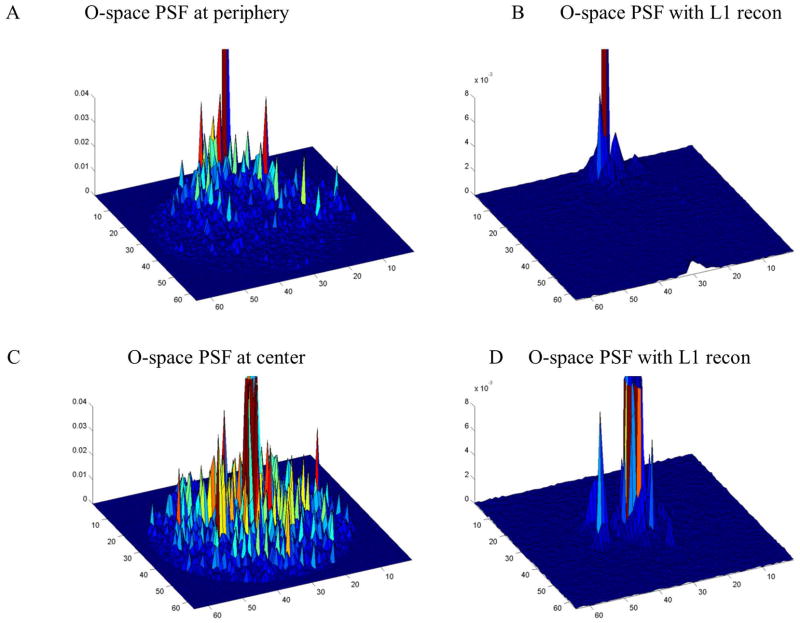
Figure 5.

In the spatial domain, PSF maps for different locations in the FOV for O-space and O-space with sparsity-enforcing reconstruction demonstrate that the sparsity constraint reduces low energy artifacts. However, PSFs, as a single point in the spatial domain, do not provide information on incoherence of the wavelet domain for the entire measurement basis.

Figure 6.

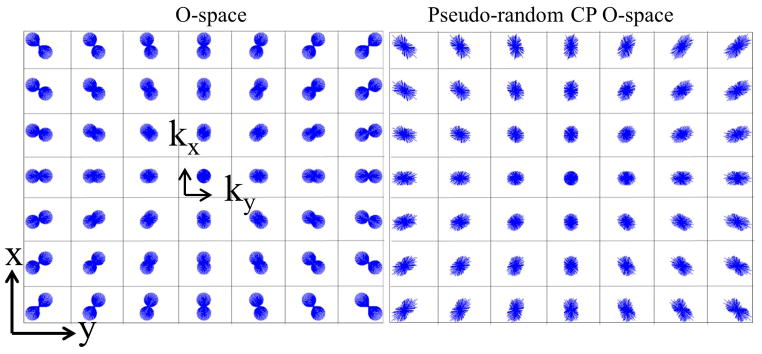
The local k-space illustrates the shape of the sampled k-space for different points throughout the FOV. From the local k-space distribution, we can qualitatively estimate the regularity of the encoding functions and the related incoherence. O-space (A) does not maximize incoherence. (B) Perturbed CP O-space with a 30% pseudo-randomization of the nonlinear Z² gradient generates a more distributed and pseudo-random sampling.

Incoherence parameter maps, where the argument of the incoherence parameter at each point is calculated, were created to visualize the incoherence parameter. Incoherence parameter maps were calculated for O-space, CS SENSE, and pseudo-random CP O-space acquisitions (Figure 7). The CS SENSE encoding was performed according to the methods specified in (31). For the SENSE undersampling, a reduction factor of four was used to uniformly undersample the phase encoding steps and a two-fold pseudo-random undersampling was used for the remaining phase encoding steps. For all cases, an eight channel receive array was used. The matrix sizes for the maps and the simulated images were 64×64 and 256×256 respectively. Simulations of the reconstruction were performed using a numerical brain phantom at R=16 for O-space and pseudo-random CP O-space with and without a sparsity-promoting reconstruction (Figure 8).

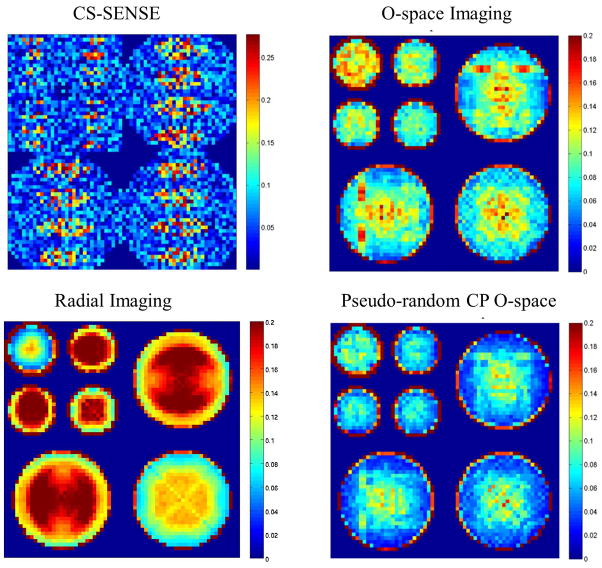
Figure 7.

Transform PSF maps compare the incoherence across CS-SENSE, Radial, O-space, and pseudo-random CP O-space methods by computing the side-lobe-to-peak-ratio (SPR) value at different positions. A lower SPR value (blue) indicates greater incoherence. CS-SENSE shows noise amplification patterns. Radial imaging has greater spatial uniformity, as expected from using linear gradients, at the cost of a higher SPR for some regions. O-space has regions where interference accumulates due to regularity in the frequency encoding scheme. Pseudo-random O-space has the lowest SPR values in the center and overall.

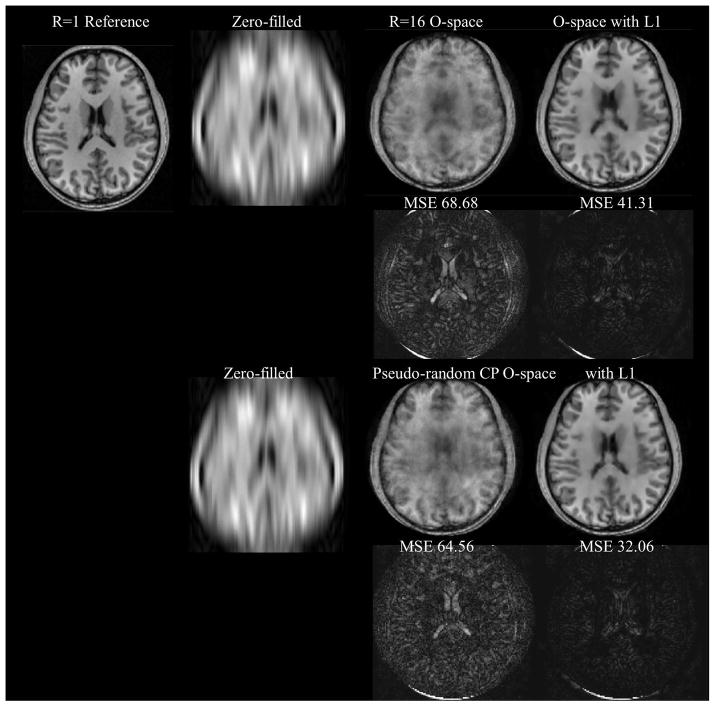
Figure 8.

Simulation results showing the effect of pseudo-randomization of O-space CPs at R=16 which is an acquisition data set of 16×512 and 8 receiver channels. SENSE is not shown as the reconstruction fails due to noise amplification at R=16. Without an ℓ₁ convex reconstruction, the O-space has degradation at high acceleration. With the convex optimization, features are sharper. For the difference images using the ℓ₁ reconstruction, pseudo-random CPs improved on O-space (MSE = 32.06 vs. 41.31 respectively).

Reconstruction

The reconstruction algorithm follows closely the published methods in (2) and (3) for Kaczmarz iterative reconstruction and CS respectively. The modification of CS for O-space imaging used the Kaczmarz algebraic reconstruction algorithm instead of Fourier transform reconstruction (1,2,26,36). For strongly under-relaxed reconstruction, Kaczmarz approaches the minimum norm least squares solution (39). CS implementation was derived from (3) with Kaczmarz enforcing data consistency and allowing nonlinear SEM field image reconstruction. The CS algorithm works best with the addition of a total variation constraint through the use of finite differences (3). The weights used were 0.001 for the wavelet transform penalty and 0.0005 for the total variation constraint. For limiting parameters, the convex optimization ran through 10 iterations, while the Kaczmarz algorithm ran through 7 iterations for simulated data and 5 iterations for the scanner data. The relaxation parameter λ was set to 0.075 for under-relaxed reconstruction. The reconstructions were performed on a 64 bit workstation PC (3.2 GHz Intel® Xeon 5500, 96 GB RAM) or desktop PC (2.4 GHz Intel® Core 2 Quad, 6 GB RAM). Reconstruction times ranged from several minutes for highly accelerated 256×256 O-space algebraic reconstruction to several hours for the convex optimization with algebraic reconstruction. The reconstruction time for a single CG iteration with Fourier reconstruction may take 1–2s on the workstation for a 128×128 image, and a little over a half a minute when using Kaczmarz reconstruction. A Z² field synthesized from polynomical coefficients was used in the simulation and imaging experiment reconstructions.

Imaging Experiments

Imaging experiments were performed on a Siemens MAGNETOM 3.0T Trio scanner (Erlangen, Germany). Two Z² SEM field inserts were provided by Resonance Research, Inc. (Billerica, MA). The first SEM field insert was a 12 cm diameter actively shielded and liquid cooled coil. The coil was rated at 151 A max current and 4.26 Gauss/cm² Z² strength. Amplitude instructions were sent to the insert through transistor-transistor logic (TTL) pulses handled by a gradient controller (40). The second Z² SEM field insert had a diameter of 38 cm. The insert was controlled through a master-slave Siemens integrated workstation and was rated at 625 A max current and 0.94 Gauss/cm². Reference (41) has a full description of this particular SEM field coil design.

Within the small insert, we used an eight-channel microstrip transmit-receive array coil and a birdcage transmit-receive to map coil sensitivities, see (2,37) for a full description. The transmit-receive coil and the insert are tightly nested to maximize the imaging volume in this small radius. No eddy currents were observed during operation. For the large insert, a Siemens birdcage head coil with another nested eight-channel receiver coil was used.

For use in the O-space reconstruction, a field was derived from a polynomial fit to high-resolution phase maps using a point spread function mapping sequence (2,42–45). The Z² field only needs to be mapped once and was used across several months to generate accurate reconstructions (2). Radial sequences were performed using the O-space sequence, but with the strength set to null on the Z² SEM field. The radial sequence was undersampled by uniformly omitting spokes. The linear x, y SEM fields were set to the amplitudes required for a radial sequence, where k_max = √2/(2 res_x), where res_x is one dimension of a voxel. The linear (radial-like) portion of the O-space sequence collects readouts in angular intervals spanning 0 to 2π around k-space. An axial slice at the isocenter of the linear and Z² SEM fields was imaged. For pseudo-random O-space, the Z² strength was randomized according to the optimization procedure detailed earlier. Imaging parameters were TE = 11 ms, TR = 1000 ms, Hz/px = 80, CP = 12.5 cm, FOV = 25 cm, Ns = 256, slice thickness = 3 mm, and flip angle = 25° for the imaging phantom and TE = 9 ms, TR = 750 ms, Hz/px = 130, CP = 4 cm, Ns = 512, slice thickness = 3 mm, and flip angle = 15° for the in vivo images. Images were reconstructed to 128×128 for the contrast phantom (Phantom Laboratory, Greenwich, NY) and 256×256 for the human hand images. The undersampling in Figure 9 corresponds to acquisition data of 32 spokes for the radial image and 32 CPs for the O-space image. For the data in Figure 10, the number of spokes and CPs were 16 and 8 for R=8 and 16 respectively. Both cases used an eight channel receiver array. The Human Investigation Committee granted Institutional Review Board approval to permit the imaging of healthy human volunteers for the smaller coil. Informed consent was obtained. Subjects accessed the scanner bore by manually placing extremities inside the transmit-receive coil with typical scans running several minutes.

Figure 9.

In vivo O-space with fixed CP and radial images through the hand at R=8 (acquisition matrix of 32×256 with eight receiver channels). The sparsity promoting reconstruction does not benefit a radial acquisition to the same magnitude without incoherence optimization (see also Figure 10).

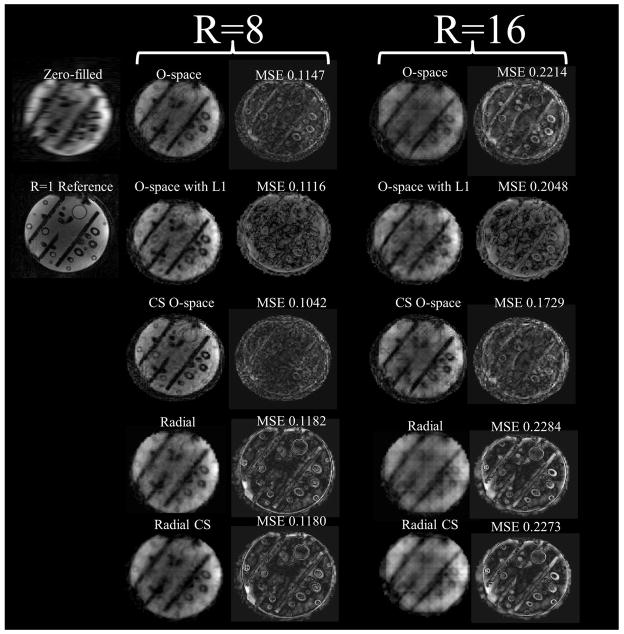
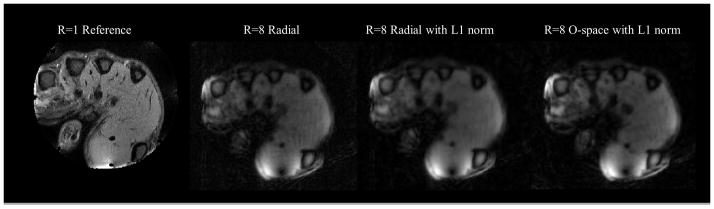
Figure 10.

Images of a contrast phantom at R=8 comparing algebraic reconstruction with a sparsity-promoting algebraic reconstruction for O-space, Radial, and a CP-optimized O-space for CS. Optimization meant an acquisition change of modulating the Z2 SEM field strength per TR and using a sparsity promoting reconstruction. Experiments were performed on a 3T Siemens Trio. SENSE is not shown as the reconstruction is intractable due to noise amplification at R=8. Features are better resolved when using pseudo-random CPs compared to regular CPs.

RESULTS

All images were labeled to reflect the method of acquisition and the undersampling factor. Simulations included pseudo-random variable density sampling Fourier encoding, CS SENSE, NSI, O-space, and O-space with pseudo-random CPs. There was negligible through-slice spin dephasing due to nonlinear SEM fields when at isocenter (46).

Figure 2 shows the TPSF for pseudo-randomly undersampled 2D Fourier encoding used in traditional CS (3). Figure 3 shows the TPSFs with a single, mid-scale point for four different methods: O-space, NSI, pseudo-randomly under sampled k-space in the phase encoding dimension using Poisson disk sampling, and pseudo-random CP O-space. Off-peak energy propagates in the undersampled phase encoding dimension. The O-space and NSI acquisitions show interference patterns that spread across all length scales and orientations. Figure 4 and Table 1 from the supplementary materials show an improvement in the incoherence when moving to multiple detectors with the pseudo-random O-space encoding compared to linear encoding. The argument of the incoherence parameter decreases by 51.6 percent moving from single to double detectors for pseudo-random O-space imaging for the compared point. Figure 5 reveals how CS affects projection imaging reconstructions. Compressed sensing shows a denoising effect as seen in the point reconstructions. Simulation results of O-space nonlinear imaging compared with several other existing acceleration methods including PatLoc and Cartesian SENSE have been previously presented (1). The distributed interference in the nonlinear SEM field TPSFs is manifested in the reduced amplitude for equivalent undersampling as off-peak energy is distributed over more of the transform domain. The O-space and NSI interference is clustered around the same location in the other length scales but decreases away from the original location. Addressing clustered interference, the pseudo-random CP O-space showed more distributed interference at all length scales for this point. The local k-space plot, Figure 6, reveals that pseudo-randomization of the CPs renders k-space coverage more isotropic. The plots show the action of the nonlinear Z² gradient causes radial elongation of the acquired local k-space. The pseudo-randomization of the CPs spreads the coverage of the acquired local k-space data. The sampling at the center of local k-space at the periphery in the FOV has been expanded.

Figure 7 shows the spatial maps with the SPR as the plotted parameter. Radial imaging has the most uniform SPR value across the FOV, which may be predicted from a local k-space analysis. The local k-space of a radial acquisition is constant for each position due to use of purely linear SEM fields. While CS SENSE outperforms the nonlinear SEM field methods at R=4 (with twofold SENSE unwrapping), we corroborate Liang et. al.’s result that SENSE with four-fold unwrapping and an eight element receiver array leads to undesirable patterned noise amplification (31). O-space has a graceful TPSF SPR map which gradually decreases from the center of the length scale. When comparing NSI to O-space, NSI appears to have a sharper center peak in the center of the length scale, but a more rapid falloff in SPR values away from the center. Pseudo-random CP O-space imaging has the lowest incoherence parameter suggesting recovery of a larger set of sparse vectors with an ℓ₁ reconstruction.

The numerical phantom in Figure 8 compares O-space with fixed CPs and O-space with pseudo-random CPs. Figure 9 shows the ℓ₁ reconstruction on an in vivo hand image. Figure 10, showing the comparison between radial, O-space, and their pseudo-random counterparts with a contrast phantom on a 3T scanner, illustrates the removal of artifacts and improvement in MSE with the pseudo-random O-space approach. The images in Figure 10 are grouped with brackets into eight-fold and sixteen-fold reduced TR acquisitions. Mean squared error and difference images against a fully sampled reference are shown to the right of the image. Zero-filled images, where undersampled phase encodes were filled with zeroes and the image reconstructed using the inverse Fourier transform, are shown. Between Figure 8 and Figure 10, it is possible to make several comparisons using the non-optimized O-space acquisitions using ℓ₂ data consistency and adding an ℓ₁ norm constraint respectively (3rd and 4th column of Figure 8, 1st and 2nd row of Figure 10, and 3rd and 4th row of Figure 10 respectively), and O-space acquisitions with pseudo-random CP using a ℓ₂ data consistency and adding an ℓ₁ norm constraint (last column of Figure 8 and 1st and 2nd rows of Figure 10 respectively).

DISCUSSION

We have demonstrated the efficacy of applying the CS approach to nonlinear SEM field projection imaging, specifically O-space imaging. The incoherence of pseudo-random CP O-space was found to be satisfied across length scales in the wavelet domain. As viewed through TPSF studies, O-space imaging permits incoherent measurement for compressed sensing from boxcar waveforms, reducing the acquisition complexity for a single 2D slice in acquiring 2D pseudo-random k-space with linear gradients.

The artifacts that arise from O-space undersampling are more incoherent (less structured) to begin with compared to the regular fold-over artifacts that occur in the phase encoding direction with Cartesian SENSE suggesting that O-space imaging alone represents an excellent basis set for accelerated imaging. Increasing sampling in the readout direction for Cartesian sampling does not address the fold-over artifact problem in the phase encode direction but this may help with nonlinear SEM fields where frequency encoding spans both the x- and y-directions. There is some evidence that nonlinear encoding effectively samples several k-space coefficients for each time point (47). The reduction factor for a separate SENSE step has been previously been recommended to be kept as low as R=2 for Cartesian sampling (31). As evidenced in incoherence parameter maps (Figure 7), noise amplification limits the incoherence normally obtained by pseudo-randomly undersampling the data and the image quality.

Parallel imaging and CS, which are from different theoretical bases, are brought together here. Parallel imaging serves to increase the number of equations leading to an overdetermined system at low accelerations and an ill-conditioned system at high accelerations. CS uses a pseudo-randomized undersampling pattern to create noise-like artifacts in a sparsity domain where incoherent artifacts may be filtered. As shown with the incoherence parameter maps, parallel imaging with linear SEM fields do not necessarily generate incoherent artifacts in the sparse domain. Sparsity in the transform domain however may be optimized with nonlinear SEM fields.

Optimizing O-space incoherence in the sparsity domain proved successful in this analysis. Using a pseudo-randomization CP O-space acquisition improved the incoherence compared to traditional O-space. The perturbed CP radii prevent encoding energy from concentrating in the regular intervals visualized in PSF diagrams from (1). The simulations show that moving from a single detector to two facing detectors decreases δ by 51.6%, corresponding to an increased recovery by a factor 1.94 of vectors in the sparse domain. For further incoherence gains, multi-dimensional encoding (22,25) could possibly be optimized for CS. However, five encoding channels come at increased hardware expense and such optimization is beyond the scope of this study.

Pseudo-randomization of O-space CPs only perturbs the Z² SEM field term and has two effects – changing the distribution in local k-space and compressed sensing incoherence. Gallichan et. al. used prephasing to increase local k-space coverage, which improved O-space resolution uniformity. It should be noted that local k-space predicts increased resolution at the periphery of the image, not increased quality throughout the image, which must be attributed to CS. Furthermore, the reconstructions in figs. 8 and 10 without sparsity-promoting reconstruction confirm that the improvement from improved distribution is confined to the periphery of the image. The effects predicted by a local k-space distribution may be mitigated by localization from parallel receivers, and parallel receiver effects are not considered under the local k-space theory. Preliminary data supports such a conclusion and will be presented in a future study.

The O-space method emphasized here used a straight-forward projection imaging sequence with a single gradient echo per TR. Pulse sequences with an echo train such as Rapid Acquisition with Refocused Echoes (48) and Steady State Free Procession (49) could be adopted under an O-space strategy with reconstruction via convex optimization. Although the results presented here were for the case of a circumferential eight element receive array, the encoding of O-space along 2D rings bring incoherence to any application with multiple receivers.

While reconstruction is currently slow, several factors could bring the reconstruction time more in line with clinically relevant speeds. The use of the Kaczmarz algorithm in the CG iterations adds an order of magnitude to the reconstruction time. Preliminary testing of consumer-grade graphics processing unit accelerated Kaczmarz reconstruction has yielded promising results with at least a ten-fold reduction in reconstruction time. A further improvement would be the incorporation of the ℓ₁ constraint into the Kaczmarz algorithm, which results in a minimal increase in computation time over the usual algorithm (50,51). When evaluating reconstruction tools, the Kaczmarz reconstruction can be compared to conjugate gradients and nonuniform fast Fourier transform (nuFFT). Kaczmarz reconstruction presents few memory requirements and the option of directly using measured encoding functions, both features relevant to experimentalists. For the clinical setting, the nuFFT may perform regularized nonlinear SEM field reconstructions with both speed and accuracy (52). Such an implementation could be envisioned for the work presented here.

The current work evaluated the efficacy of adding compressed sensing methods to nonlinear SEM field strategies. The results indicated improvements in accelerated imaging quality when randomizing CPs in O-space imaging with CS. Future investigations will examine the new degrees of freedom with shaped nonlinear gradient pulses and CS approaches to further reduce image acquisition times in MRI.