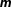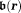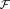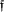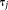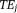Abstract
In MRI, the main magnetic field polarizes the electron cloud of a molecule, generating a chemical shift for observer protons within the molecule and a magnetic susceptibility inhomogeneity field for observer protons outside the molecule. The number of water protons surrounding a molecule for detecting its magnetic susceptibility is vastly greater than the number of protons within the molecule for detecting its chemical shift. However, the study of tissue magnetic susceptibility has been hindered by poor molecular specificities of hitherto used methods based on MRI signal phase and T2* contrast, which depend convolutedly on surrounding susceptibility sources. Deconvolution of the MRI signal phase can determine tissue susceptibility but is challenged by the lack of MRI signal in the background and by the zeroes in the dipole kernel. Recently, physically meaningful regularizations, including the Bayesian approach, have been developed to enable accurate quantitative susceptibility mapping (QSM) for studying iron distribution, metabolic oxygen consumption, blood degradation, calcification, demyelination, and other pathophysiological susceptibility changes, as well as contrast agent biodistribution in MRI. This paper attempts to summarize the basic physical concepts and essential algorithmic steps in QSM, to describe clinical and technical issues under active development, and to provide references, codes, and testing data for readers interested in QSM. Magn Reson Med 73:82–101, 2015. © 2014 The Authors. Magnetic Resonance in Medicine Published by Wiley Periodicals, Inc. on behalf of International Society of Medicine in Resonance. This is an open access article under the terms of the Creative commons Attribution License, which permits use, distribution, and reproduction in any medium, provided the original work is properly cited.
Keywords: QSM, quantitative susceptibility mapping, gradient echo, metabolism, iron, oxygen consumption, ferritin, hemoglobin, hemorrhage, calcification, myelin, contrast agent, quantification, dipole field, dipole kernel, morphology enabled dipole inversion, Bayesian
Introduction
Magnetic susceptibility is one of the following major categories of tissue contrast mechanisms in proton MRI 1: 1) spin thermal relaxation in a voxel of water; 2) water motion, including diffusion, perfusion, flow and tissue deformation; and 3) molecular electron cloud polarization by the main magnetic field . A polarized molecule generates its own magnetic field, which is known as a chemical-shift shielding field for observer protons inside the molecule and as a magnetic-susceptibility inhomogeneity field for observer protons outside the molecule. This field adds phase accumulation and consequently causes intravoxel dephasing or magnitude T2* decay in the commonly available gradient echo (GRE) MRI. Therefore, noninvasive MRI is well suited for investigating the magnetic susceptibility of tissue. The GRE phase is equal to the magnetic field multiplied by the gyromagnetic ratio
. A polarized molecule generates its own magnetic field, which is known as a chemical-shift shielding field for observer protons inside the molecule and as a magnetic-susceptibility inhomogeneity field for observer protons outside the molecule. This field adds phase accumulation and consequently causes intravoxel dephasing or magnitude T2* decay in the commonly available gradient echo (GRE) MRI. Therefore, noninvasive MRI is well suited for investigating the magnetic susceptibility of tissue. The GRE phase is equal to the magnetic field multiplied by the gyromagnetic ratio and the echo time (
and the echo time ( . This phase may be used to further attenuate the signal for enhancing T2* image contrast, which is called susceptibility weighted imaging 2–4. However, the field at an observer location is the sum of contributions from all surrounding magnetic susceptibility sources, with each contribution dependent on the source-observer distance and orientation 5. Consequently, the phase or T2* contrast does not exclusively depict the local tissue magnetic property but is a weighted summation of the magnetic properties of the surrounding tissue, reflecting only the “shadow” of the surrounding susceptibility sources. For example, the phase and T2* contrast of tissues with weak susceptibility may primarily come from nearby air-tissue interfaces, across which there are large susceptibility changes. To uncover local tissue magnetic properties, the field has to be deconvolved, which is referred to as quantitative susceptibility mapping (QSM).
. This phase may be used to further attenuate the signal for enhancing T2* image contrast, which is called susceptibility weighted imaging 2–4. However, the field at an observer location is the sum of contributions from all surrounding magnetic susceptibility sources, with each contribution dependent on the source-observer distance and orientation 5. Consequently, the phase or T2* contrast does not exclusively depict the local tissue magnetic property but is a weighted summation of the magnetic properties of the surrounding tissue, reflecting only the “shadow” of the surrounding susceptibility sources. For example, the phase and T2* contrast of tissues with weak susceptibility may primarily come from nearby air-tissue interfaces, across which there are large susceptibility changes. To uncover local tissue magnetic properties, the field has to be deconvolved, which is referred to as quantitative susceptibility mapping (QSM).
QSM was contemplated at the early days of MRI 6. However, the inversion from field to susceptibility is ill-posed 7,8: There are zeroes in the kernel connecting the susceptibility distribution and the field, and a simple kernel division causes large errors that present as streaking artifacts in the reconstructed susceptibility map 9,10. Regularization or conditioning is necessary to select a unique solution for a given field 10–16. Fortunately, MRI provides plenty of information on tissue anatomical structures. This information can serve as a prior in Bayesian regularization to overcome this ill-posed inverse problem, generating a reasonably accurate susceptibility map 17–20. Various regularizations have since been developed 17,19–30, making QSM a feasible tool for the MRI community.
As indicated by a PubMed search of QSM papers (6 in 2011; 18 in 2012; and 37 in 2013), there is rapidly growing interest in developing techniques for QSM data acquisition and processing, and in developing clinical and scientific applications ranging from iron distribution and metabolic consumption of oxygen to myelin in white matter (WM) tracts (Fig. 1). This review tries to serve these interests by summarizing the basic physical concepts in QSM, outlining the fundamental algorithmic steps in QSM, organizing the available MATLAB (MathWorks, Natick, MA) codes for QSM algorithms, and surveying the clinical and technical QSM issues that are under active development.
Figure 1.
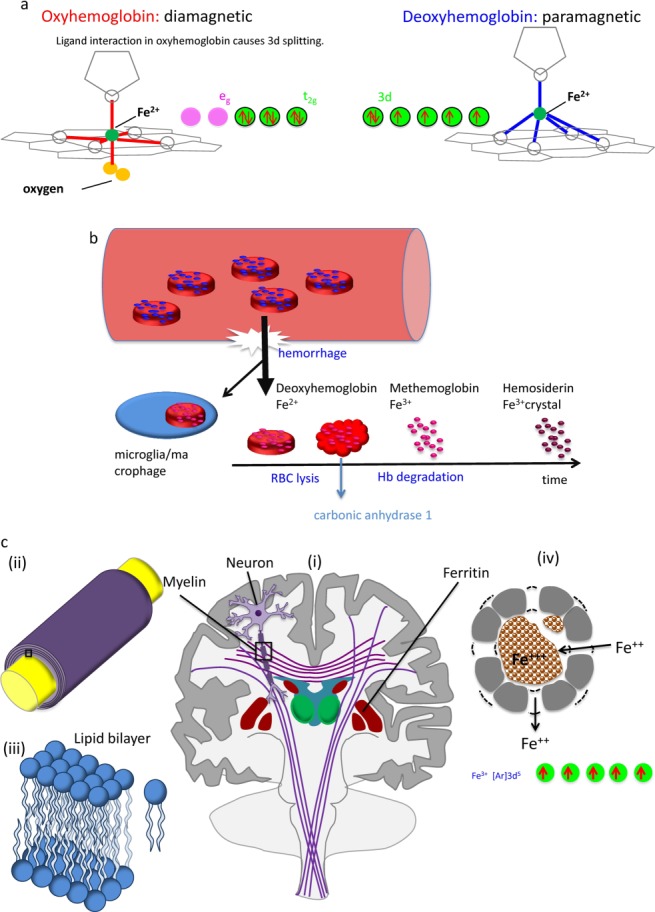
Biomedical magnetic materials. (a) Diamagnetic hemoglobin and paramagnetic deoxyhemoglobin. During metabolic consumption of oxygen in the brain, heart, and kidney, weakly diamagnetic oxyhemoglobin releases O2 and becomes strongly paramagnetic deoxyhemoglobin. Whereas the 3d electron orbits of Fe2+ in deoxyhemoglobin may be approximated as an isolated iron atom with four unpaired electrons (right), the intramolecular interaction between the porphyrin ring and Fe2+ in oxyhemoglobin (ligand interaction) splits the Fe atom’s 3d-orbit into two levels, eg and t2g, with all six electrons paired in the three t2g orbits. (b) Blood degradation in hemorrhage. Following the onset of a hemorrhage, a small fraction of red blood cells (RBCs) may be endocytosed by microglia/macrophages. The majority of RBCs undergo cell lysis and hemoglobin (Hb) degradation from deoxyhemoglobin into methemoglobin (Fe3+) and hemosiderin (possible magnetic domain). Modeled after: Lancet Neurol 2012;11:720–731. (c) Susceptibility sources in the human brain. Major susceptibility sources in (i) the brain include myelin and ferritin. The white matter tracts in the brain consist of myelinated nerve fibers. (ii) Zoomed view of the box in (i) showing axon (yellow) and myelin sheath (purple). Myelin consists of several layers of lipid bilayer. (iii) Zoomed view of the box in (ii) showing a lipid bilayer and an individual lipid. (iv) Ferritin in a cross-section. Ferritin consists of a peptide spherical shell 2-nm thick with a 8-nm diameter cavity. Fe2+ enters through a four-fold symmetric channel, is stored as Fe3+ oxide mineral, and is released as Fe2+ through a three-fold symmetric channel. There are five unpaired 3d electrons in Fe3+, generating strong paramagnetism.
Preparation: Estimating Susceptibility-Generated Field from its Effects on MRI Signal
In the MRI main field , a molecule in tissue gains a magnetic moment
, a molecule in tissue gains a magnetic moment through its electron cloud polarization. Correspondingly, a tissue with volume magnetic susceptibility
through its electron cloud polarization. Correspondingly, a tissue with volume magnetic susceptibility gains magnetization
gains magnetization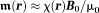 (see TISSUE MAGNETISM in supporting information for a brief summary of the molecular physics). Tissue magnetization generates its own magnetic field that affects MRI signal. Here we review the mathematical relationships that link magnetization, field, and MRI signal, based on which the field can be estimated from the MRI signal.
(see TISSUE MAGNETISM in supporting information for a brief summary of the molecular physics). Tissue magnetization generates its own magnetic field that affects MRI signal. Here we review the mathematical relationships that link magnetization, field, and MRI signal, based on which the field can be estimated from the MRI signal.
Magnetic Dipole Field and Field Observed by a Proton in Tissue
According to Maxwell’s equations in vacuum, a magnetic dipole moment at a source location
at a source location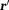 generates a magnetic field
generates a magnetic field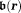 at an observation location
at an observation location 5 (
5 (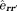 is a unit vector along
is a unit vector along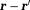 ),
),
| 1 |
Here, the inverse-cube of the distance term characterizes the spatial extent of the dipole field. The delta-function term can be understood from the field of a current loop with a fixed magnetic moment and a radius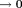 (Fig. 2). In water MRI, the delta-function term is dropped; the probability of the polarized electron cloud penetrating into the space of the observer water protons is negligible. Thus, the field (scaled to
(Fig. 2). In water MRI, the delta-function term is dropped; the probability of the polarized electron cloud penetrating into the space of the observer water protons is negligible. Thus, the field (scaled to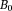 ) observed by a water proton is the sum of contributions from all surrounding susceptibility sources [their distribution defined by magnetization
) observed by a water proton is the sum of contributions from all surrounding susceptibility sources [their distribution defined by magnetization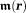 ], excluding that from the proton’s own location:
], excluding that from the proton’s own location:
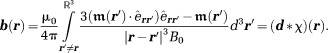 |
2 |
Figure 2.
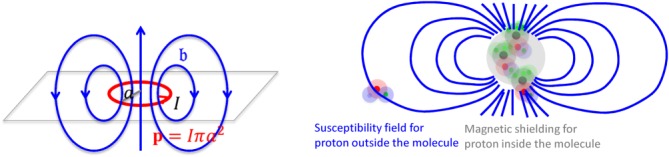
Magnetic fields, chemical shift, and magnetic susceptibility.(Left) The field of a magnetic dipole modeled by a current loop of radius . At the loop center,
. At the loop center,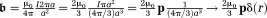 as
as .(Right) The electron cloud of a molecule polarized by
.(Right) The electron cloud of a molecule polarized by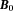 generates magnetic shielding or chemical shift for the observer proton in the molecule and a susceptibility field (in dipole pattern) for the observer proton outside the molecule.
generates magnetic shielding or chemical shift for the observer proton in the molecule and a susceptibility field (in dipole pattern) for the observer proton outside the molecule.
The exclusion of the observer point in the integration of Eq. 2 represents the Cauchy principal value, commonly known as the Lorentz correction. This is conventionally, but unnecessarily, interpreted as subtracting a sphere of magnetization that has a uniform interior field
that has a uniform interior field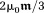 from the sum of the fields of all sources according to Eq. 1 5. In Eq. 2,
from the sum of the fields of all sources according to Eq. 1 5. In Eq. 2,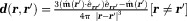 . (Here [expression] – 1 if expression is true and 0 otherwise.)
. (Here [expression] – 1 if expression is true and 0 otherwise.)
Eq. 2 relates the field at to the magnetization distribution over the whole space. This can be expressed in a differential form that relates the field at
to the magnetization distribution over the whole space. This can be expressed in a differential form that relates the field at to the magnetization located at
to the magnetization located at 31:
31:
| 3 |
Eq. 3 can be Fourier transformed into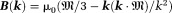 . For notational convenience, we use lower case for
. For notational convenience, we use lower case for -space quantities and upper case for corresponding
-space quantities and upper case for corresponding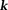 -space quantities (except constant
-space quantities (except constant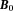 ), the z-component (
), the z-component (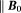 ) of
) of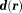 is referred to as the dipole kernel
is referred to as the dipole kernel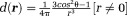 with Fourier transform
with Fourier transform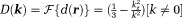 , and the z-component of
, and the z-component of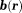 is noted as
is noted as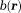 . For scalar susceptibility, Eq. 2 becomes
. For scalar susceptibility, Eq. 2 becomes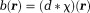 with Fourier transform
with Fourier transform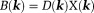 .
.
On the other hand, the electron cloud of a molecule does penetrate into and interact with observer protons within the molecule. Consequently, electron cloud polarization by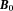 induces a shielding magnetic field
induces a shielding magnetic field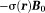 (Fig. 2) 32, or chemical shift (referenced to water), that alters the field experienced by protons within the molecule:
(Fig. 2) 32, or chemical shift (referenced to water), that alters the field experienced by protons within the molecule: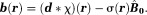 Both the magnetic susceptibility (observed by a large number of water protons outside the molecule) and the chemical shift (observed by protons inside the molecule) reflect the same molecular electron-cloud polarization 33–35.
Both the magnetic susceptibility (observed by a large number of water protons outside the molecule) and the chemical shift (observed by protons inside the molecule) reflect the same molecular electron-cloud polarization 33–35.
Field Effects on MRI Signal
The magnetic field of a polarized molecule may affect the MRI signal magnitude through a chemical exchange between free water and water bound to the molecule (inner sphere relaxation) and through a free water diffusion in the field (outer sphere relaxation) 36. These complicated effects are characterized as relaxation enhancement 37–41. Susceptibility estimation from MRI signal magnitude affected by relaxation is prone to large errors 31. Fortunately, the phase of a water proton spin linearly increases with the field. Using multiple radio frequency (RF) coils, with the th coil element having a complex coil sensitivity function
th coil element having a complex coil sensitivity function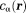 and acquisition noise
and acquisition noise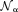 , the k-space signal measured in coil
, the k-space signal measured in coil at time
at time is 1:
is 1:
| 4 |
Here,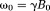 and
and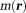 is the proton transverse magnetization [
is the proton transverse magnetization [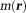 is proportional to proton density and is much smaller than
is proportional to proton density and is much smaller than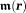 the electronic magnetization]. Typically,
the electronic magnetization]. Typically,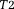 is homogeneous within a voxel and is much longer than the readout duration (
is homogeneous within a voxel and is much longer than the readout duration (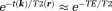 ), and the data sampling gradient
), and the data sampling gradient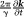 is much larger than
is much larger than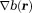 (
(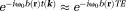 ). Then, the complex image
). Then, the complex image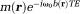 can be reconstructed using the Moore-Penrose pseudo-inverse 1 for both full
can be reconstructed using the Moore-Penrose pseudo-inverse 1 for both full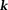 -space sampling 42 and parallel imaging 43. Approximating the voxel sensitivity function 44 as a box function, the signal detected at
-space sampling 42 and parallel imaging 43. Approximating the voxel sensitivity function 44 as a box function, the signal detected at in a voxel centered at
in a voxel centered at with size
with size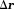 (volume
(volume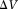 ) is the summation over signals from all proton spins in the voxel,
) is the summation over signals from all proton spins in the voxel,
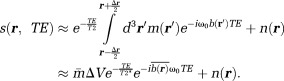 |
5 |
Here, the integration is evaluated by assuming small phase inhomogeneity in a voxel: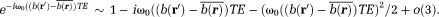 The quantities in Eq. 5 are defined as:
The quantities in Eq. 5 are defined as: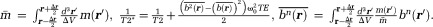
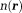 is the noise in the reconstructed image. Common imaging situations involve weak tissue susceptibilities, short TEs (and small echo spacing in multiple echo sampling), and small voxels. Then, the phase of the signal in a voxel is approximately equal to
is the noise in the reconstructed image. Common imaging situations involve weak tissue susceptibilities, short TEs (and small echo spacing in multiple echo sampling), and small voxels. Then, the phase of the signal in a voxel is approximately equal to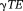 times the proton density-weighted average of the field in the voxel, and the T2* decay rate differs from
times the proton density-weighted average of the field in the voxel, and the T2* decay rate differs from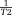 by
by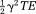 times the proton density-weighted field variance in a voxel. As a result, MRI phase signals allow us to measure the magnetic field generated by tissue susceptibility.
times the proton density-weighted field variance in a voxel. As a result, MRI phase signals allow us to measure the magnetic field generated by tissue susceptibility.
Pulse Sequences Sensitizing Susceptibility
The three-dimensional (3D) GRE sequence is currently the most frequently used to acquire data for QSM. Multiple echoes (number of echoes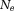 – 1–12 having been reported in literature) can be used with short TE for detecting strong susceptibility and long TEs for weak susceptibilities. The GRE sequence on a typical 3T MRI system may allow a high-resolution acquisition (∼0.5 × 0.5 × 2.0 mm3) with minimal first TE ∼5 msec, uniform TE spacing ∼5 msec, readout bandwidth ∼300 Hz/pixel, last TE ∼45 msec, and TR ∼50 msec (whole brain scan time ∼5–10 min). For imaging regions with very strong susceptibility variations, such as those containing the bone-tissue and air-tissue interfaces, ultra-short 45,46 or zero TE 47 and small TE increments may be used to achieve adequate signal-to-noise ratio (SNR). Flow compensation can be used to account for phases caused by motion 48. Resolution should be as high as possible to minimize averaging effects in Eq. 5. Parallel imaging and spiral sampling trajectories 49,50 can be used to reduce scan time. Susceptibility effects may also be detected with asymmetric spin echo (SE) sequences. It is also possible to measure the magnetic field in a voxel through direct saturation of the water protons at a range of off resonance frequencies and Lorentzian lineshape fitting (water saturation shift referencing) 51, similar to continuous-wave NMR spectroscopy. Whereas GRE sequences generally are faster than SE sequences, there may be applications that benefit from a combination of GRE and SE acquisitions.
– 1–12 having been reported in literature) can be used with short TE for detecting strong susceptibility and long TEs for weak susceptibilities. The GRE sequence on a typical 3T MRI system may allow a high-resolution acquisition (∼0.5 × 0.5 × 2.0 mm3) with minimal first TE ∼5 msec, uniform TE spacing ∼5 msec, readout bandwidth ∼300 Hz/pixel, last TE ∼45 msec, and TR ∼50 msec (whole brain scan time ∼5–10 min). For imaging regions with very strong susceptibility variations, such as those containing the bone-tissue and air-tissue interfaces, ultra-short 45,46 or zero TE 47 and small TE increments may be used to achieve adequate signal-to-noise ratio (SNR). Flow compensation can be used to account for phases caused by motion 48. Resolution should be as high as possible to minimize averaging effects in Eq. 5. Parallel imaging and spiral sampling trajectories 49,50 can be used to reduce scan time. Susceptibility effects may also be detected with asymmetric spin echo (SE) sequences. It is also possible to measure the magnetic field in a voxel through direct saturation of the water protons at a range of off resonance frequencies and Lorentzian lineshape fitting (water saturation shift referencing) 51, similar to continuous-wave NMR spectroscopy. Whereas GRE sequences generally are faster than SE sequences, there may be applications that benefit from a combination of GRE and SE acquisitions.
Digitized Dipole Field: Field and Susceptibility Averaged over a Voxel and Localized at the Voxel Center
The field averaged over a voxel in Eq. 5 requires digitization of Eq. 2. The assumption that the distributions of the observation protons and susceptibility sources are fairly uniform within a voxel (physical smoothness) may allow for digital interpretation of Eq. 2: as the voxel center,
as the voxel center,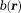 as the field value at
as the field value at , and
, and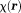 as the average of the susceptibilities in the source voxel positioned at
as the average of the susceptibilities in the source voxel positioned at . This digitization can be analytically derived for spherically shaped voxels: The field’s spherical mean value equals the field value at the sphere center 5; the field outside of a uniformly magnetized sphere is equivalent to the field of a dipole defined by the sphere’s total moment placed at the sphere’s center; and the field inside the sphere is zero (with the Lorentz correction by Eq. 2). The physical smoothness requirement is reasonably valid for high resolution MRI, and sinc-interpolation or zero-padding 44 may be used to reduce the digitization error. Accordingly, Eq. 2 will be used to model the MRI signal with voxels indexed by
. This digitization can be analytically derived for spherically shaped voxels: The field’s spherical mean value equals the field value at the sphere center 5; the field outside of a uniformly magnetized sphere is equivalent to the field of a dipole defined by the sphere’s total moment placed at the sphere’s center; and the field inside the sphere is zero (with the Lorentz correction by Eq. 2). The physical smoothness requirement is reasonably valid for high resolution MRI, and sinc-interpolation or zero-padding 44 may be used to reduce the digitization error. Accordingly, Eq. 2 will be used to model the MRI signal with voxels indexed by .
.
QSM Step 0: Estimate the Total Field from MRI Data
Eq. 5 models the MRI signal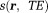 as a product of an exponential factor
as a product of an exponential factor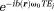 that describes a phase linear in time and a complex amplitude
that describes a phase linear in time and a complex amplitude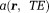 that contains a constant phase and an amplitude decay with time. Then, the total field
that contains a constant phase and an amplitude decay with time. Then, the total field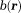 can be estimated from MRI signals at multiple TEs as a nonlinear least-squares problem per voxel 20,21,27:
can be estimated from MRI signals at multiple TEs as a nonlinear least-squares problem per voxel 20,21,27:
| 6 |
In the case of large SNR, Eq. 6 can be approximated as a linear regression of the signal phases at various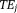 , allowing for a closed form solution 21. In general, Eq. 6 can be solved iteratively and efficiently using a gradient search method, such as the Gauss-Newton 20 or Levenberg-Marquardt method 52, with
, allowing for a closed form solution 21. In general, Eq. 6 can be solved iteratively and efficiently using a gradient search method, such as the Gauss-Newton 20 or Levenberg-Marquardt method 52, with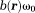 initialized as the linear rate of phase evolution between the first two echoes (
initialized as the linear rate of phase evolution between the first two echoes (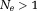 ). Eq. 6 may also be solved rapidly using autoregression 53. Interestingly, although Eq. 5 requires the estimation of complex coil sensitivity from calibration data 42,43, the field can be estimated without full knowledge of complex coil sensitivities from the phase difference at two TEs 54–57 or even at a single echo 58.
). Eq. 6 may also be solved rapidly using autoregression 53. Interestingly, although Eq. 5 requires the estimation of complex coil sensitivity from calibration data 42,43, the field can be estimated without full knowledge of complex coil sensitivities from the phase difference at two TEs 54–57 or even at a single echo 58.
The field estimated from Eq. 6 can contain many artificial jumps from voxel to voxel because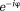 is periodic in
is periodic in and can only define
and can only define up to a period such as
up to a period such as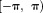 . Consequently,
. Consequently,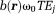 outside
outside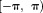 is aliased or wrapped into
is aliased or wrapped into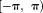 , resulting in abrupt artificial jumps of
, resulting in abrupt artificial jumps of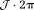 (
(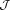 is an integer) in the output phase, which is called the wrapped phase denoted by
is an integer) in the output phase, which is called the wrapped phase denoted by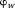 . To estimate
. To estimate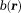 , these phase wraps have to be compensated by adding
, these phase wraps have to be compensated by adding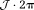 as needed:
as needed:
| 7 |
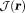 is determined by the physical consideration that the unwrapped phase is spatially continuous. Unfortunately, it is difficult to impose continuity in discrete space because discretization is an undersampled approximation of the continuous space, and noise—ubiquitous in MRI data—causes jumps in regions of low SNR. There are many algorithms to impose continuity or smoothness in phase unwrapping 59, typically via path finding (including noncontinuous path, residual balancing, or branch cut) 60 or global error minimization (least squares) (Fig. 3). Phase can also be unwrapped rapidly by the Fourier spectral solution of the Laplacian of the phase 23,61; however, second order derivatives in the Laplacian may not allow large phase changes to occur in regions with big susceptibility variations, such as near veins 62. Phase unwrapping may be avoided for field data estimated from direct water saturation lineshape 51. A frequently used method is the path-finding type, image-quality-guided region growth 63, which works robustly and rapidly on MRI data using SNR as the image-quality guidance 17,64,65.
is determined by the physical consideration that the unwrapped phase is spatially continuous. Unfortunately, it is difficult to impose continuity in discrete space because discretization is an undersampled approximation of the continuous space, and noise—ubiquitous in MRI data—causes jumps in regions of low SNR. There are many algorithms to impose continuity or smoothness in phase unwrapping 59, typically via path finding (including noncontinuous path, residual balancing, or branch cut) 60 or global error minimization (least squares) (Fig. 3). Phase can also be unwrapped rapidly by the Fourier spectral solution of the Laplacian of the phase 23,61; however, second order derivatives in the Laplacian may not allow large phase changes to occur in regions with big susceptibility variations, such as near veins 62. Phase unwrapping may be avoided for field data estimated from direct water saturation lineshape 51. A frequently used method is the path-finding type, image-quality-guided region growth 63, which works robustly and rapidly on MRI data using SNR as the image-quality guidance 17,64,65.
Figure 3.
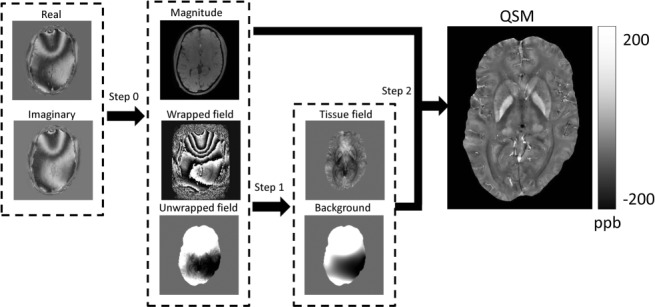
Schematics for quantitative susceptibility mapping. Quantitative susceptibility mapping (QSM) in general consists of three steps. Step 0: Generate magnitude image and field with unwrapping. Step 1: Remove background field and generate tissue field. Step 2: Generate QSM from tissue field and magnitude image.
After phase unwrapping, a few bad points with fields not consistent with Eq. 2 may remain due to turbulent flow or idiopathic causes, and their effects can be reduced using a consistency check during QSM iteration 20. As the phase measurement in MRI is relative to RF carrier frequency, the field can only be determined up to a constant uniform field, which may be removed by background field removal in the next section.
QSM Algorithm: Formulating and Solving the Field-to-Susceptibility Inverse Problem
The goal of QSM is to determine tissue susceptibility from the field (Eq. 6) or the complex MRI signal (Eq. 5) using Eq. 2, which connects the magnetic field and the tissue susceptibility. There are two fundamental challenges that are imbedded in Eq. 2 and Eq. 5, as outlined below, and we describe two QSM steps to address them correspondingly: 1) background field removal and 2) dipole inversion (Fig. 3).
Two Fundamental Challenges in QSM
The first fundamental challenge is the lack of MRI signal in regions with susceptibility sources. MRI signal in Eq. 5 can only be detected in the region with water or the tissue of interest ( ). Magnetic susceptibility sources exist outside
). Magnetic susceptibility sources exist outside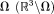 , which is the background. However, there is no MRI signal in the background. If we regard each voxel in MRI as a field detector, then the number of detectors is less than the number of sources, making the field-to-source inverse problem ill-posed. Therefore, this lack of MRI signal in the background forms the first fundamental challenge for QSM. Susceptibility sources in tissue (
, which is the background. However, there is no MRI signal in the background. If we regard each voxel in MRI as a field detector, then the number of detectors is less than the number of sources, making the field-to-source inverse problem ill-posed. Therefore, this lack of MRI signal in the background forms the first fundamental challenge for QSM. Susceptibility sources in tissue ( ) generate the tissue field
) generate the tissue field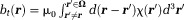
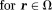 . Background susceptibility sources generate the background field
. Background susceptibility sources generate the background field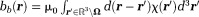 for
for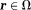 . Together, they form a total field
. Together, they form a total field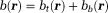 in tissue.
in tissue.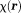 is tissue susceptibility when
is tissue susceptibility when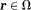 .
.
The second fundamental challenge is the zero cone surface in the dipole kernel in -space or in
-space or in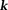 -space:
-space: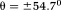 with respect to the main magnetic field (magic angle) (Fig. 4) 14. The dipole kernel in
with respect to the main magnetic field (magic angle) (Fig. 4) 14. The dipole kernel in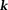 -space is nearly flat (with all derivatives vanishing) at the ends of the cone neighborhood
-space is nearly flat (with all derivatives vanishing) at the ends of the cone neighborhood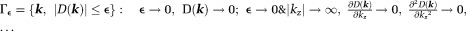 , implying that the standard analysis cannot be used to define
, implying that the standard analysis cannot be used to define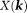 in
in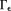 66. Noise in the data would allow many possible susceptibility solutions that differ by an arbitrary amount in
66. Noise in the data would allow many possible susceptibility solutions that differ by an arbitrary amount in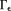 for a given field map
for a given field map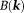 , causing a substantial dipole kernel null space. Therefore, the magnetic field-to-susceptibility inverse problem is ill-posed and lacks a unique solution 21.
, causing a substantial dipole kernel null space. Therefore, the magnetic field-to-susceptibility inverse problem is ill-posed and lacks a unique solution 21.
Figure 4.
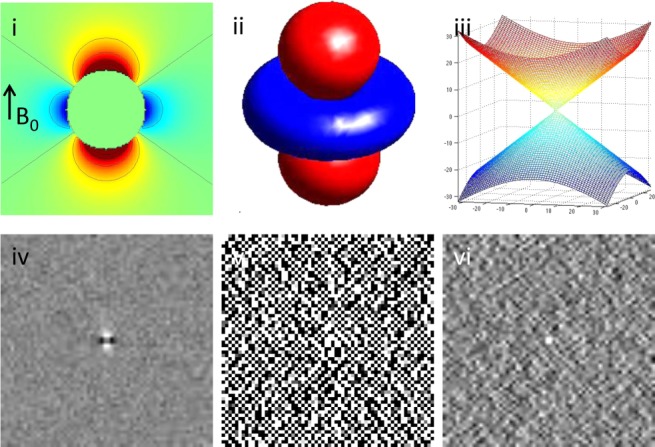
The ill-posedness of the dipole inverse problem. The unit dipole field in sagittal section (i) and its surface rendered contour (ii). (iii) The zero cone surfaces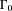 of the dipole kernel in k-space. (iv) Field map derived at signal-to-noise ratio (SNR) – 20 induced by a point source. (v, vi) Susceptibility in image space obtained by truncated k-space division with the threshold
of the dipole kernel in k-space. (iv) Field map derived at signal-to-noise ratio (SNR) – 20 induced by a point source. (v, vi) Susceptibility in image space obtained by truncated k-space division with the threshold – 0 and 0.1. As a consequence of the dipole kernel zero behavior in the cone surface neighborhood
– 0 and 0.1. As a consequence of the dipole kernel zero behavior in the cone surface neighborhood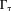 , there is substantial noise propagation from the field measurements into the susceptibility estimate (40), as illustrated in an example of reconstruction by direct division (v and vi). A little noise added in the phase map (peak SNR – 20) leads to a totally corrupted susceptibility image that bears no physical resemblance to the true susceptibility source.
, there is substantial noise propagation from the field measurements into the susceptibility estimate (40), as illustrated in an example of reconstruction by direct division (v and vi). A little noise added in the phase map (peak SNR – 20) leads to a totally corrupted susceptibility image that bears no physical resemblance to the true susceptibility source.
QSM Step 1: Background Field Removal
To address the first QSM challenge of the lack of MRI signal in the background regions with susceptibility sources, prior knowledge is needed. The background field may be regarded as slow varying and can be removed by high-pass filtering (HPF). Unfortunately, HPF erroneously removes the low spatial frequency components of the tissue field and fails to remove the high spatial frequency components of the background field near the tissue border 3,67,68, causing substantial errors in QSM. Better priors on the separation between the background and tissue fields are required for accurate determination of the tissue field, such as approximate orthogonality in the projection onto dipole fields (PDF) method 69 or the harmonic property in the sophisticated harmonic artifact reduction on phase data (SHARP) method 70. These priors are systematically organized in the following as solutions to Maxwell’s Equations (Eq. 3).
By definition, the background field has no source in
has no source in , whereas the local tissue field
, whereas the local tissue field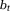 has sources
has sources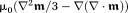 inside
inside (Eq. 3). From electrodynamics 5 or partial differential equation 71, for a finite domain
(Eq. 3). From electrodynamics 5 or partial differential equation 71, for a finite domain , a unique solution to Laplace’s equation Eq. 3 can be obtained according to the values at the boundary
, a unique solution to Laplace’s equation Eq. 3 can be obtained according to the values at the boundary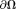 5,72. In MRI, the tissue field is typically weak. At
5,72. In MRI, the tissue field is typically weak. At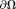 , the background field may be approximated as the total field. This is the Laplacian boundary value (LBV) method (Fig. 5) to estimate background field 73.
, the background field may be approximated as the total field. This is the Laplacian boundary value (LBV) method (Fig. 5) to estimate background field 73.
| 8 |
Figure 5.
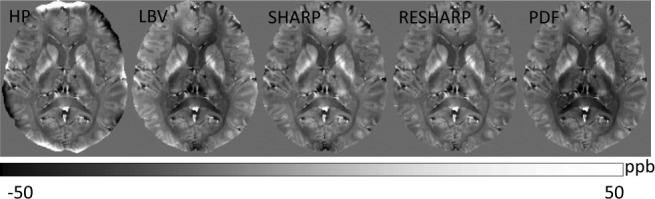
Background field removal using various algorithms. The tissue fields in a healthy volunteer estimated using HPF, LBV, SHARP, RESHARP, and PDF methods, respectively, demonstrate similar tissue patterns but with slight and different accents. HPF, high-pass filtering; LBV, Laplacian boundary value; PDF, projection onto dipole fields; RESHARP, regularization enabled SHARP; SHARP, sophisticated harmonic artifact reduction on phase data.
Eq. 8 can be solved numerically as a system of linear equations by expressing the Laplacian with a difference operator 74: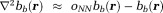 . Here,
. Here, denotes the nearest neighbor average operator. It is advantageous in SNR to express Eq. 8 using the spherical mean value (SMV) operator
denotes the nearest neighbor average operator. It is advantageous in SNR to express Eq. 8 using the spherical mean value (SMV) operator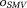 5,70,75:
5,70,75: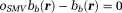 . The system matrix is diagonally dominant (with diagonal elements
. The system matrix is diagonally dominant (with diagonal elements ), and the Jacobian iterative method can be used 74 to give the (n+1)th iteration solution
), and the Jacobian iterative method can be used 74 to give the (n+1)th iteration solution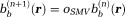 . With an initialization
. With an initialization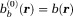 that satisfies the boundary value condition in Eq. 8, the background field can be obtained numerically by repeatedly applying
that satisfies the boundary value condition in Eq. 8, the background field can be obtained numerically by repeatedly applying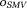 , which is the iterative spherical mean value (iSMV) method 76. However, iSMV is slow to converge. Eq. 8 can be efficiently solved using the full multi-grid solver that first finds the solution on a coarse grid and then successively refines the solution on finer grids 74.
, which is the iterative spherical mean value (iSMV) method 76. However, iSMV is slow to converge. Eq. 8 can be efficiently solved using the full multi-grid solver that first finds the solution on a coarse grid and then successively refines the solution on finer grids 74.
When the boundary condition is not known, a partial differential equation in difference form may be regarded as an ill-posed problem, which can be solved by regularization. One regularization is to impose spectral truncation when evaluating the inverse Laplacian (therefore altering the inverse Laplacian),
| 9 |
Here,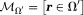 requires
requires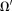 is smaller by a border layer than the available tissue region
is smaller by a border layer than the available tissue region for computing
for computing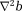 . Eq. 9 can be solved as
. Eq. 9 can be solved as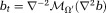 :
: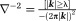 , using truncated singular value decomposition (TSVD) (with a carefully chosen truncation value
, using truncated singular value decomposition (TSVD) (with a carefully chosen truncation value ) in
) in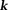 -space, and
-space, and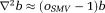 , using
, using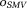 for possible denoising benefit. This is the sophisticated harmonic artifact reduction for phase data (SHARP) 70.
for possible denoising benefit. This is the sophisticated harmonic artifact reduction for phase data (SHARP) 70.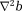 in the border layer
in the border layer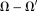 may be recovered using a continuity assumption as in harmonic (background) phase removal using the Laplacian operator [HARPERELLA 62]. Another regularization is the minimal norm of the tissue field (implicitly modifying inverse Laplacian) 62,77:
may be recovered using a continuity assumption as in harmonic (background) phase removal using the Laplacian operator [HARPERELLA 62]. Another regularization is the minimal norm of the tissue field (implicitly modifying inverse Laplacian) 62,77:
| 10 |
Here,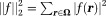 for any field
for any field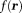 (squared L2 norm). This method is called regularization-enabled SHARP (RESHARP) 77. Eq. 2 can be expressed in a Lagrangian form
(squared L2 norm). This method is called regularization-enabled SHARP (RESHARP) 77. Eq. 2 can be expressed in a Lagrangian form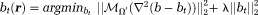 .
.
There is another approach to estimate the background field based on the equivalent source or charge simulation method 78. The background field can be represented by fields of dipoles outside that are approximately orthogonal to the fields of dipoles inside
that are approximately orthogonal to the fields of dipoles inside except near
except near . Then the background field can be estimated by all possible PDFs 17,22,69:
. Then the background field can be estimated by all possible PDFs 17,22,69:
| 11 |
Here, noise-weighting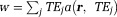 is the phase SNR, which is assumed to be large by linearizing the signal model Eq. 5. Note that
is the phase SNR, which is assumed to be large by linearizing the signal model Eq. 5. Note that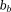 in tissue
in tissue is unique, although
is unique, although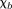 in background
in background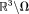 is not. This PDF method may provide a slight advantage in dealing with noise in
is not. This PDF method may provide a slight advantage in dealing with noise in by avoiding the inversion of the Laplacian in Eq. 8 through Eq. 10, and by extending to the nonlinear form, as in Eq. 6 20. However, the orthogonality between fields of dipoles breaks down near the boundary, making PDF prone to over-fitting errors near the border.
by avoiding the inversion of the Laplacian in Eq. 8 through Eq. 10, and by extending to the nonlinear form, as in Eq. 6 20. However, the orthogonality between fields of dipoles breaks down near the boundary, making PDF prone to over-fitting errors near the border.
Because background and tissue fields are approximately orthogonal, the minimal norm of the tissue field in Eq. 10 is similar to the dominance of the background field at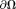 in Eq. 8, making RESHARP similar to LBV. The minimization in Eq. 10 is similar to that in Eq. 11, without noise weighting
in Eq. 8, making RESHARP similar to LBV. The minimization in Eq. 10 is similar to that in Eq. 11, without noise weighting , making RESHARP similar to PDF. Therefore, all four methods (LBV, SHARP, RESHARP, and PDF) based on Maxwell’s equations in Figure 5 provide similar performance, whereas there are very strong values near the tissue boundary in the HPF processed tissue field. The assumption or regularization in any method may contain errors, which propagate through into errors in the final reconstructed tissue susceptibility, a challenge for future research.
, making RESHARP similar to PDF. Therefore, all four methods (LBV, SHARP, RESHARP, and PDF) based on Maxwell’s equations in Figure 5 provide similar performance, whereas there are very strong values near the tissue boundary in the HPF processed tissue field. The assumption or regularization in any method may contain errors, which propagate through into errors in the final reconstructed tissue susceptibility, a challenge for future research.
QSM Step 2: Field-to-Susceptibility Inversion
To address the second fundamental challenge in QSM, the ill-posedness caused by the dipole kernel zeroes, prior knowledge is again needed to uniquely identify the susceptibility component in the dipole kernel null space. For simplicity, we consider the high SNR case for which the phase noise is approximately Gaussian with variance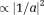 [and we can extend to the general SNR case using the complex signal as in Eq. 6 20]. Then Eq. 5, after background field removal, is reduced to a linear field-to-susceptibility inverse problem (Eq. 2 with noise),
[and we can extend to the general SNR case using the complex signal as in Eq. 6 20]. Then Eq. 5, after background field removal, is reduced to a linear field-to-susceptibility inverse problem (Eq. 2 with noise),
| 12 |
Arbitrary susceptibility values in the dipole zero cone neighborhood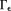 are allowed in Eq. 12. A regularization can be used to specify susceptibility values in
are allowed in Eq. 12. A regularization can be used to specify susceptibility values in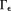 . Alternatively, “missing data” about the susceptibility in one orientation can be recovered by reorienting the subject in a fixed magnet and resampling the MRI signal 14,79. This method is known as the calculation of susceptibility using multiple orientation sampling (COSMOS), which delivers an exact reconstruction by fully sampling the susceptibility 14,22. Unfortunately, acquiring multiple scans of patients in different orientations is not clinically acceptable. We should focus on the regularization approach to QSM using single orientation data.
. Alternatively, “missing data” about the susceptibility in one orientation can be recovered by reorienting the subject in a fixed magnet and resampling the MRI signal 14,79. This method is known as the calculation of susceptibility using multiple orientation sampling (COSMOS), which delivers an exact reconstruction by fully sampling the susceptibility 14,22. Unfortunately, acquiring multiple scans of patients in different orientations is not clinically acceptable. We should focus on the regularization approach to QSM using single orientation data.
Regularizations can be expressed in various mathematical forms including TSVD and assumptions of a smooth, sparse, or piece-wise smooth solution. Consequently, there are too many QSM methods to be characterized by a unifying framework. For the purpose of illustrating concepts, we outline two important classes of QSM methods: 1) the closed-form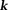 -space approach, exemplified by TSVD based on matrix computation 80, and 2) the Bayesian approach based on optimization 52, also known as the
-space approach, exemplified by TSVD based on matrix computation 80, and 2) the Bayesian approach based on optimization 52, also known as the -space approach. Specific algorithm formulas, codes, and results are summarized in the next section on experimental validation. All of these solutions may suffer from model errors when the mathematical properties are not consistent with the physical reality 7,10,11,17,21,81. Additionally, noise will always propagate into the final solution.
-space approach. Specific algorithm formulas, codes, and results are summarized in the next section on experimental validation. All of these solutions may suffer from model errors when the mathematical properties are not consistent with the physical reality 7,10,11,17,21,81. Additionally, noise will always propagate into the final solution.
Closed-form solutions form a class of noniterative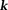 -space methods. One example is TSVD 82:
-space methods. One example is TSVD 82: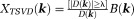 with
with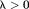 , which is similar to a Tikhonov-regularized minimal norm (MN) solution
, which is similar to a Tikhonov-regularized minimal norm (MN) solution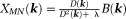 21,22. More commonly used in QSM is a TSVD variant called truncated
21,22. More commonly used in QSM is a TSVD variant called truncated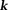 -space division (TKD) 10:
-space division (TKD) 10:
| 13 |
Truncation obviously leads to an underestimation of the susceptibility values in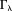 , and consequently produces streaking artifacts along the magic angle in the susceptibility map. This error in the TKD method is
, and consequently produces streaking artifacts along the magic angle in the susceptibility map. This error in the TKD method is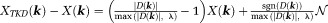 : the first part is the regularization error from points in
: the first part is the regularization error from points in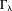 where the kernel has been modified by truncation; the second part is the noise error from all data points in k-space, but interestingly is also dominated by points in and near
where the kernel has been modified by truncation; the second part is the noise error from all data points in k-space, but interestingly is also dominated by points in and near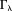 . The underestimation in Eq. 13 may be compensated by a scale factor 26. The streaking in Eq. 13 may be reduced using a high threshold [
. The underestimation in Eq. 13 may be compensated by a scale factor 26. The streaking in Eq. 13 may be reduced using a high threshold [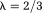 , susceptibility – field convolving with a kernel 26] or using iterative filtering (defined by
, susceptibility – field convolving with a kernel 26] or using iterative filtering (defined by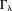 in
in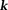 -space) of signals outside high-susceptibility structures in
-space) of signals outside high-susceptibility structures in -space defined by a mask [iterative Susceptibility Weigted Imaging and susceptibility Mapping (iSWIM), 30]. A variant of MN is a Tikhonov-regularized minimal gradient norm [29:
-space defined by a mask [iterative Susceptibility Weigted Imaging and susceptibility Mapping (iSWIM), 30]. A variant of MN is a Tikhonov-regularized minimal gradient norm [29: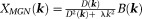 ].
].
Bayesian regularizations form a class of iterative optimization methods. To allow optimal treatment of regularization error 83, prior information is regarded as a probability distribution function (pdf) typically expressed as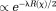 :
: is a tunable regularization parameter and
is a tunable regularization parameter and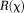 is a functional of the susceptibility map. Noise is also characterized by its pdf. Then, the optimal solution with minimal total error from regularization and noise is the maximum a posteriori (MAP) estimate 84. For Gaussian noise with pdf
is a functional of the susceptibility map. Noise is also characterized by its pdf. Then, the optimal solution with minimal total error from regularization and noise is the maximum a posteriori (MAP) estimate 84. For Gaussian noise with pdf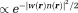 (
( as in Eq. 11) in the estimated field, the posterior probability is
as in Eq. 11) in the estimated field, the posterior probability is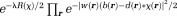 , the maximization of which is the MAP solution:
, the maximization of which is the MAP solution:
| 14 |
The first term in Eq. 14 is the weighted data fidelity term, which contains noise; the second term is the regularization term, which contains the regularization error. The regularization parameter, , may be chosen to provide a minimal total error in a given imaging situation, and is typically chosen such that the regularization error is approximately equal to the expected noise level, a criterion known as the discrepancy principle 85–87.
, may be chosen to provide a minimal total error in a given imaging situation, and is typically chosen such that the regularization error is approximately equal to the expected noise level, a criterion known as the discrepancy principle 85–87.
There are connections between Bayesian optimization and noniterative -space methods. If
-space methods. If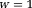 in Eq. 14, then L2 norm-based Tikhonov regularization
in Eq. 14, then L2 norm-based Tikhonov regularization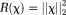 leads to
leads to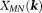 and
and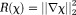 leads to
leads to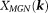 ; both are noniterative
; both are noniterative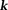 -space methods. Because MRI phase noise requires spatially varying weighting
-space methods. Because MRI phase noise requires spatially varying weighting , noniterative
, noniterative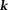 -space methods may suffer from noise errors 88. A wide range of forms for
-space methods may suffer from noise errors 88. A wide range of forms for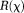 in Eq. 14 have been reported, including piece-wise constant susceptibility 11,89, smooth susceptibility or susceptibility gradient 21, sparse susceptibility gradient or wavelet 21,27,90, and morphological consistency of the susceptibility map 17,19,21,25, some of which are detailed in the next section. We should note the property of the conjugate gradient method that typically is used to minimize the data fidelity term in Eq. 14 as in LSQR: The solution is initialized as zero by default, points outside the zero cone neighborhood
in Eq. 14 have been reported, including piece-wise constant susceptibility 11,89, smooth susceptibility or susceptibility gradient 21, sparse susceptibility gradient or wavelet 21,27,90, and morphological consistency of the susceptibility map 17,19,21,25, some of which are detailed in the next section. We should note the property of the conjugate gradient method that typically is used to minimize the data fidelity term in Eq. 14 as in LSQR: The solution is initialized as zero by default, points outside the zero cone neighborhood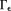 are calculated firstly (and properly) according to Krylov sequence, and later iterations fill structured noise in
are calculated firstly (and properly) according to Krylov sequence, and later iterations fill structured noise in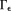 that cause streaking artifacts 16,52,91 (Fig. 6). Use of a small iteration number (n – 5) may be regarded as an implicit regularization for a solution with moderate streaking and zero value at the
that cause streaking artifacts 16,52,91 (Fig. 6). Use of a small iteration number (n – 5) may be regarded as an implicit regularization for a solution with moderate streaking and zero value at the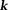 -space center
-space center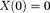 16,88. For a solver of Eq. 14 that includes use of LSQR, such as in the Gauss-Newton method, its final solution may have
16,88. For a solver of Eq. 14 that includes use of LSQR, such as in the Gauss-Newton method, its final solution may have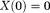 . Eq. 14 may only determine the susceptibility up to a constant [similar to the Neumann boundary value problem for Laplace’s equation 5]. Specific solvers may introduce implicit regularization in their output. A reference to water, such as the cerebrospinal fluid in the ventricles, may be used for consistent display of susceptibility values in QSM.
. Eq. 14 may only determine the susceptibility up to a constant [similar to the Neumann boundary value problem for Laplace’s equation 5]. Specific solvers may introduce implicit regularization in their output. A reference to water, such as the cerebrospinal fluid in the ventricles, may be used for consistent display of susceptibility values in QSM.
Figure 6.

Evolution of susceptibility solutions in conjugate gradient. Susceptibility images in k-space (left column) and r-space after the first, third, fifth, 10th, and 100th iterations using the conjugate gradient solver demonstrate that the none-cone region in k-space converges quickly in the first few iterations; and the later iterations mainly contribute to signal in the cone region that manifests as streaking artifacts in the sagittal view and noise in the axial view in r-space.
Available anatomic information in a specific imaging situation defines a physical prior for morphology-enabled dipole inversion (MEDI) 19,83,92. The edges in the desired susceptibility map are likely to be colocated with edges in known anatomical images, because they reflect the same anatomy. The colocalization of edges may be expressed as the sparsity of susceptibility edges outside the known edge locations using the L0-norm or the more manageable L1-norm 93. This minimizes streaking artifacts common to the dipole kernel nullspace. From Eq. 14, one MEDI implementation to reconstruct QSM can be formulated as 17,19:
| 15 |
Here, is evaluated in Fourier space by
is evaluated in Fourier space by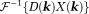 ,
,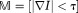 for anatomic image
for anatomic image and threshold
and threshold (
( is chosen such that approximately 30% of voxels are labeled as edges), and
is chosen such that approximately 30% of voxels are labeled as edges), and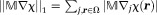 (L1 norm). Because the dipole kernel (Fig. 4), similar to a HPF, preserves susceptibility edges in the tissue field image 5 and accordingly in the T2*-weighted (T2*w) magnitude image, the GRE magnitude 17 and phase images 25 can be used as the anatomic images. The nonlinear Eq. 15 can be solved using the Gauss-Newton method 52 without explicit formation of the memory costly inverse Hessian matrix 19. The data fidelity term in Eq. 15 can be generalized to Gaussian noise in complex data (e.g., Eq. 6) and can be solved using a procedure identical to Eq. 15 20.
(L1 norm). Because the dipole kernel (Fig. 4), similar to a HPF, preserves susceptibility edges in the tissue field image 5 and accordingly in the T2*-weighted (T2*w) magnitude image, the GRE magnitude 17 and phase images 25 can be used as the anatomic images. The nonlinear Eq. 15 can be solved using the Gauss-Newton method 52 without explicit formation of the memory costly inverse Hessian matrix 19. The data fidelity term in Eq. 15 can be generalized to Gaussian noise in complex data (e.g., Eq. 6) and can be solved using a procedure identical to Eq. 15 20.
New priors continue to be proposed; the search for the best prior is ongoing. An optimal prior may be specific to the imaging application. There has been a preliminary attempt to compare several priors 88. Multicenter trials are needed to establish a consensus on application-specific priors, which leads to the topic of the next section.
QSM Source Codes and Experimental Validations
To enable readers to try QSM algorithms on their own, here we organize the available MATLAB (MathWorks) codes for certain QSM algorithms, along with testing data (http://weill.cornell.edu/mri/pages/qsm.html). We tried to consider all the QSM methods that were published before December 1, 2013, classifying similar methods into the same category. We asked the first or corresponding authors to share MATLAB (MathWorks) codes of their methods, proofread our implementations, and comment on results of testing data, and we thank them for their valuable feedback. The page limitation forced us to select one (perhaps the most widely used) of multiple algorithms published by each group, leading to the following seven methods in Table 1: TSVD 22; TKD 10; iSWIM 30; MEDI 19; compressed sensing compensated (CSC) inversion 27; homogeneity-enabled incremental dipole inversion (HEIDI) 25; and total variation using split Bregman (TVSB) 28. The first two methods do not require anatomic prior information. The third method, iSWIM, incorporates an anatomic prior iteratively into the k-space approach. The last four methods are based on the Bayesian approach and are listed in chronologic order. The Bayesian methods all aim to minimize a function consisting of a data fidelity term in the L2 norm (measuring noise power) and a regularization term in the L1 norm or total variation (promoting sparsity). Whereas MEDI and HEIDI attempt to sparsify the edge difference with known anatomical priors, CSC promotes image sparsity in the wavelet domain, and TVSB hugely accelerates reconstruction speed by dropping noise whitening.
Table 1.
Accuracy Assessments via Linear Regression Based on Voxel Values Between Methods and Reference Standards (Truth for Simulated Brain, Prepared Concentration for Gadolinium Phantom and COSMOS for In Vivo Brain) as well as Recon Time for In Vivo Brain Imaging
| Simulated Brain | Gadolinium Phantom | In Vivo Brain | |||||
|---|---|---|---|---|---|---|---|
| Slope | R2 | Slope | R2 | Slope | R2 | Time (sec) | |
| TSVD | 0.83 | 0.83 | 0.76 | 0.99 | 0.80 | 0.45 | 1.7 |
| TKD | 0.91 | 0.89 | 0.82 | 0.99 | 0.88 | 0.34 | 1.8 |
| iSWIM | 0.81 | 0.82 | 0.84 | 0.99 | 0.81 | 0.48 | 14 |
| MEDI | 0.99 | 0.99 | 0.92 | 1.00 | 0.93 | 0.59 | 1008 |
| CSC | 0.63 | 0.65 | 0.87 | 0.99 | 0.79 | 0.60 | 3463(1) |
| HEIDI | 0.82 | 0.90 | 0.82 | 0.99 | 0.80 | 0.55 | 715(2) |
| TVSB | 0.83 | 0.94 | 0.87 | 1.00 | 0.84 | 0.42 | 40 |
All the calculations were performed on a PC equipped with Intel® Core i7–3770k CPU @ 3.5 GHz and 32 GB of memory, except 1 was performed on a personal laptop with Intel Core i5-M2450 CPU @ 2.5 GHz and 8 GB of memory, and 2 was performed on a PC with Intel Core i5–2320 CPU @ 3.00 GHz and 16 GB of memory.
CPU, central processing unit; COSMOS, calculation of susceptibility using multiple orientation sampling; CSC, compressed sensing compensated; GB, gigabytes; GHz, gigahertz; HEIDI, homogeneity-enabled incremental dipole inversion; iSWIM, iterative susceptibility weighted imaging and susceptibility mapping; MEDI, morphology-enabled dipole inversion; PC, personal computer; TKD, truncated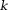 -space division; TSVD, truncated singular value decomposition; TVSB, total variation using split Bregman.
-space division; TSVD, truncated singular value decomposition; TVSB, total variation using split Bregman.
Rigorous experimental validation with a reference standard is required to assess the accuracy of any quantitative technique. This is particularly necessary for a technique involving regularization such as the QSM algorithms in Table 1. We performed three validation experiments: 1) numerical simulation with known truth, 2) MRI data of gadolinium phantom with known susceptibilities, and 3) in vivo brain MRI with susceptibilities assessed by COSMOS 92,94. These validations were imperfect, particularly because COSMOS contains errors from noise, orientation registration, and WM susceptibility anisotropy. However, they can serve as a starting point for readers to experience various QSM methods. Details of the experimental setup are described in Validation data in the supporting information. Although evaluations here are not intended to be conclusive, they allow readers to assess various QSM methods by their qualities (by examining the streaking artifacts), accuracies (by voxel-based linear regression with ground truth or reference), and computing costs (by taking the median running time of 5 consecutive runs).
The numerical simulation (Fig. S1a,b in the supporting information) demonstrated that all methods yielded satisfactory image quality, with minimal streaking in the sagittal view. The phantom experiment (Fig. S2a–c in the supporting information) demonstrated that constraining solutions’ energies at the cone region alone was not sufficient to suppress streaking (TSVD, TKD). The iSWIM method reduced streaking by iterative filtering, and the most significant improvement was observed when spatial constraints were incorporated during dipole inversion (MEDI, CSC, HEIDI, TVSB). The in vivo brain MRI (Fig. 7) demonstrated that all methods successfully generated QSMs. The major structures containing high levels of ferritin (basal ganglia and nuclei in deep gray matter) or deoxyhemoglobin (veins) are shown with high paramagnetic values on QSM, and WM tracts are shown with diamagnetic values on QSM. Rapid streaking signal variations not on COSMOS were observed in TSVD and TKD, likely artifacts originating from veins. The iSWIM method reduced but did not eliminate these artifacts. TVSB overblurred compared to COSMOS; one of the causes may be its lack of noise whitening. MEDI, CSC, and HEIDI yielded QSM images similar to COSMOS.
Figure 7.

Comparison of various quantitative susceptibility mapping reconstruction methods. QSM images are reconstructed using various methods from left to right and then top to bottom: TSVD, TKD, iSWIM, CSC, COSMOS, MEDI, HEIDI, TVSB, and R2* map. Most similar to COSMOS are MEDI, CSC, and HEIDI, with only very subtle differences among them: CSC has less black dots; MEDI has better defined dorsomedial nuclei of thalamus. CSC, compressed sensing compensated; COSMOS, calculation of susceptibility using multiple orientation sampling; HEIDI, homogeneity-enabled incremental dipole inversion; MEDI, morphology-enabled dipole inversion; QSM, quantitative susceptibility mapping; TKD, truncated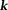 -space division; TSVD, truncated singular value decomposition; TVSB, total variation using split Bregman.
-space division; TSVD, truncated singular value decomposition; TVSB, total variation using split Bregman.
In the accuracy assessment (Table 1), MEDI and TVSB achieved the best slope and coefficient of determination (R2) in both numerical simulation and phantom experiments, presumably because the piece-wise constant nature of the susceptibility distribution matched the assumptions in MEDI and TVSB. In the human brain, although MEDI provided the highest slope, none of the methods provided adequate R2 values. A possible cause may be voxels of WM with susceptibility anisotropy. The reconstruction speed of the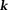 -space methods were much faster than that of the iterative Bayesian methods (Table 1). However, the split Bregman implementation in TVSB showed promise of fast online reconstruction for the Bayesian methods.
-space methods were much faster than that of the iterative Bayesian methods (Table 1). However, the split Bregman implementation in TVSB showed promise of fast online reconstruction for the Bayesian methods.
Clinical Applications Under Development
QSM has become sufficiently accurate for measuring the strong susceptibilities of biomaterials, including iron distribution (ferritin), in the deep brain nuclei and basal ganglia; deoxyhemoglobin in the veins; blood degradation products (hemosiderin in late stage); calcification (hydroxylapatite crystals); and exogenous species such as gadolinium. Clinical applications of QSM are being developed to probe neurodegenerative and inflammatory diseases, to assess hemorrhage, to measure metabolic consumption of oxygen, and to guide and monitor therapy. QSM can also remove blooming artifacts in traditional T2*w imaging 95, providing an accurate definition of the distribution of magnetic biomaterials in MRI. In this brief survey, we focus on neurological applications, although applications outside the brain are also promising 96.
Diamagnetic Biomaterial-Based Applications
QSM can easily differentiate diamagnetic calcification from paramagnetic materials such as hemosiderin 89,97. Both calcification and chronic hemorrhage appear hypointense on GRE magnitude images and may be undetectable on conventional T1- and T2-weighted SE imaging 98,99. GRE phase imaging has long been recognized for its ability to identify diamagnetic calcifications 100,101, but there is no study demonstrating its diagnostic accuracy. As such, CT is widely used for detecting calcifications despite its use of ionizing radiation 102. QSM may replace CT for detecting calcification in neurocysticercosis (Fig. 8) and tumors 103–106. A clinical study demonstrated that QSM is superior to phase imaging and has a very high sensitivity (90%) and specificity (95%) for the detection of intracranial hemorrhage and calcification 97. QSM can also be used to measure the loss of myelin 107, another important diamagnetic biomaterial.
Figure 8.
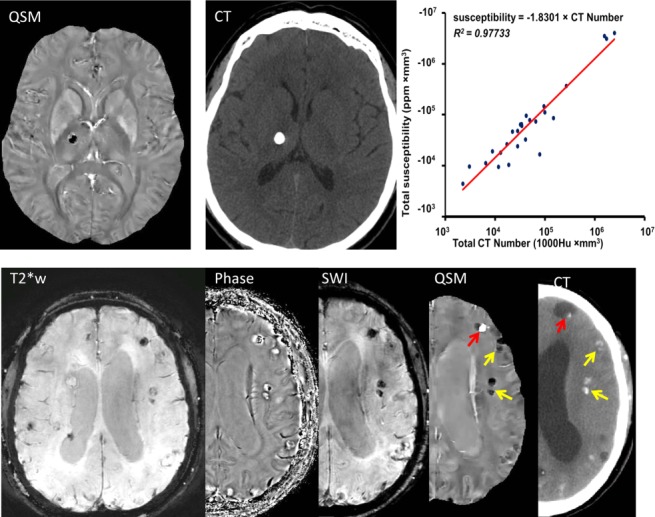
Quantitative susceptibility mapping for measuring diamagnetic biomaterials such as calcifications. Top row: susceptibility of calcification measured on QSM (dark oval in right thalamus) demonstrates very good linear correlation with Hounsfield units measured on CT. Twenty six patients (64 calcifications) were included in the linear regression. Bottom row: Neurocysticercosis in T2* weighted, magnitude, phase, SWI, QSM, and CT images has both calcified and active lesions. Among all MRI images, only QSM shows the active lesion with positive susceptibility (red arrow) and clearly show the calcified lesions with negative susceptibilities (yellow arrows). The CT section is slightly tilted from the orientation of the MRI section, causing a discrepancy in the lesion’s appearances. QSM, quantitative susceptibility mapping; SWI, susceptibility weighted imaging. Source: Chen et al, Radiology 2014;270:496–505.
Paramagnetic Heme Iron (Deoxyhemoglobin, Metahemoglobin, Hemosiderin)-Based Applications
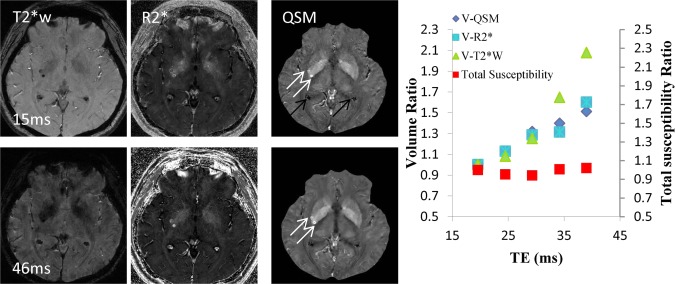
During blood degradation in hemorrhage (Fig. 1b), susceptibility progressively increases from oxyhemoglobin (diamagnetic) to deoxyhemoglobin (paramagnetic with 4 unpaired electrons in Fe2+), methemoglobin (strongly paramagnetic with 5 unpaired electrons in Fe3+), and hemosiderin (super paramagnetic with possible magnetic domain formation or ferromagnetic) 108–111. GRE is more sensitive than CT at detecting intracerebral hemorrhage 112,113. However, the T2* hypointensity in GRE suffers from blooming artifacts that are highly dependent on imaging parameters. Reliably estimating the hematoma volume is critical for managing hemorrhagic stroke patients 114,115, but it is difficult to do on GRE 95. QSM removes these blooming artifacts 17,19,20 and can be used as a universal measurement of microbleeds (Fig. 9) and hematoma volume in GRE MRI 111,116,117.
Figure 9.
Quantitative susceptibility mapping for measuring paramagnetic heme iron. The total susceptibility of a cerebral microbleed measured on QSM is a physical property that is independent of TE, providing a universal measure for cerebral microbleeds burden (10 patients with 40 microbleeds). Left image panel: Microbleed appearance changes with TE (15 msec top row; 46 msec bottom row) drastically in magnitude and moderately in the R2* map but little in QSM (white arrows). Ventricle calcifications have the same sign on T2*w and R2* but opposite sign on QSM (black arrows) as microbleeds. Right graph: When TE was increased from approximately 20 to 40 msec, the measured cerebral microbleed volume increased by mean factors of 1.49 ± 0.86 (standard deviation), 1.64 ± 0.84, and 2.30 ± 1.20, respectively, for QSM, R2*, and T2*w, respectively (P < .01). However, the measured total susceptibility with QSM did not show significant change over TE (P – .31), and the variation was significantly smaller than any of the volume increases (P < .01 for each). QSM, quantitative susceptibility mapping; TE, echo time. Source: Liu et al, Radiology 2012;262:269–278.
Susceptibility values in QSM can be converted to the venous deoxyhemoglobin concentration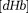 according to deoxyhemoglobin’s molar susceptibility
according to deoxyhemoglobin’s molar susceptibility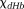 –10765 ppb 48,118–120, allowing quantitative fMRI 117. The tissue metabolic rate of oxygen consumption (
–10765 ppb 48,118–120, allowing quantitative fMRI 117. The tissue metabolic rate of oxygen consumption (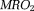 ) is regarded as a fundamental biomarker for assessing viability of aerobic tissue such as those in the brain, heart, and kidney 121. Measurements of regional blood flow
) is regarded as a fundamental biomarker for assessing viability of aerobic tissue such as those in the brain, heart, and kidney 121. Measurements of regional blood flow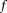 by quantitative perfusion, such as the arterial spin labeling 122 and
by quantitative perfusion, such as the arterial spin labeling 122 and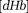 by QSM, can be used to map
by QSM, can be used to map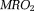 according to oxygen mass conservation 123–126:
according to oxygen mass conservation 123–126: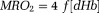 . For tissues with nonheme iron such as ferritin, susceptibility contributions can be corrected using iso-metabolism manipulation 127.
. For tissues with nonheme iron such as ferritin, susceptibility contributions can be corrected using iso-metabolism manipulation 127.
Paramagnetic Nonheme Iron (Ferritin)-Based Applications
Iron overload can generate biologically toxic reactive oxygen species, causing oxidative stress and damaging macromolecules including proteins, lipids, and DNA 128,129. Excessive iron deposition in specific regions of the brain has been observed in many neurodegenerative diseases 130–133, including Parkinson’s disease, Alzheimer’s disease, amyotrophic lateral sclerosis, Huntington’s disease, Friedreich’s ataxia, and multiple sclerosis 134–137. Consider the example of Parkinson’s disease (PD). Several studies demonstrate an increase of iron deposits in the substantia nigra in PD 138–142, perhaps increasing with disease progression 143. The abnormal increase in nigral iron generates reactive oxygen species 131, possibly causing nigrostriatal dopamine neuron degeneration 144,145 and alpha-synuclein aggregation 146,147. MRI R2* (1/T2*) has been used to measure tissue iron content 9,148–153, but R2* in a voxel reflects the field variance within that voxel (see definition after Eq. 5). The latter depends on the background field, surrounding tissue susceptibilities, and imaging parameters including field strength, voxel size, and TE. The MRI phase has also been used to measure brain iron in PD 9,154–159, but phase is a convolution of tissue susceptibility in space (Eq. 2). QSM overcomes the problems of R2* and phase images, enabling reliable iron quantification when there is no other substantial susceptibility contributor 90,132,133,142,160–162. Perhaps for this reason, QSM has been widely used to measure brain susceptibility 94,163.
QSM can improve visualization of the target in deep brain stimulation (DBS), the surgical implementation of stimulating electrodes in the subthalamic nuclei (STN), or the globus pallidus pars interna (GPi) for treating neurological disorders including PD 164–167. The anatomical accuracy of electrode lead placment is critical for a successful surgical outcome 168–176. Intraoperative CT, typically used to guide DBS, has poor contrast for the basal ganglia structures 170,172,177–181. MRI provides better tissue contrast than CT, but the visualization contrast for STN and GPi is still poor in standard T2-weighted imaging, and high field MRI using T2*w imaging has been sought for DBS 182–186. QSM can be used to remove the blurring present in T2*w and improve contrast-to-noise-ratio by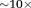 for the visualization of the STN 160,161,187 (Fig. 0).
for the visualization of the STN 160,161,187 (Fig. 0).
Figure 10.
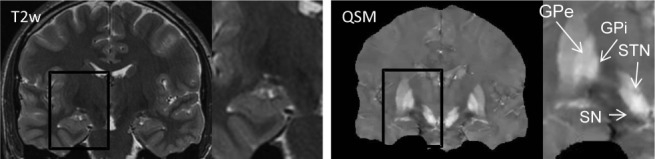
Quantitative susceptibility mapping for visualizing deep brain stimulation targets. Globus pallidus interna (GPi) and subthalamic nucleus (STN), surgical targets for deep brain stimulation, are either invisible or inseparable from surrounding tissues on T2W image (with zoom), but are clearly visualized on deep brain stimulation (QSM) (with zoom). Other basal ganglia structures well-defined on QSM include globus pallidus pars externa (GPe) and substantia nigra (SN). Source: Liu et al, Radiology 2013;269:216–23.
Paramagnetic Contrast Agent Biodistribution Quantification-Based Application
QSM can be applied to measure the biodistribution of highly paramagnetic contrast agents (CA), providing an effective tool for quantifying CA concentration [CA] in MRI 188,189. The quantitative study of the phase change observed in contrast-enhanced MRA 190 was an initial motivation to formulate the field-to-susceptibility inverse problem 31. Absolute determination of [CA] according to T1/T2 enhancement effects requires calibration and is highly susceptible to flip angle errors 191–193. CAs with limited access to water demonstrate the well-known T1/T2 relaxation quench 191,192,194–197; relaxation enhancement requires CA binding with bound water, which, in turn, exchanges chemically with surrounding bulk water (CA↔bound H2O↔bulk H2O) 36,198–200 (see Supporting Figure S4). [CA] has no well-defined relationship with R2*. QSM overcomes these problems of mapping [CA] in T1/T2/T2* imaging and may be useful for determining the biodistribution of targeted CAs in molecular MRI. A high temporal-spatial gadolinium concentration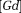 map can be obtained using QSM and fast imaging 201, from which quantitative perfusion map may be generated 50,202 (Fig. 11).
map can be obtained using QSM and fast imaging 201, from which quantitative perfusion map may be generated 50,202 (Fig. 11).
Figure 11.
Quantitative susceptibility mapping for quantifying paramagnetic contrast agents. In an in vivo dynamic gadolinium (Gd) enhancement study of the brain, time-resolved Quantitative susceptibility mapping (QSM) was developed using spiral readout and temporal resolution acceleration with constrained evolution reconstruction (TRACER) complex image reconstruction. The difference image divided Gd molar susceptibility generates time-resolved Gd concentration map. Source: Xu et al, MRM 2014, epub.
Mixed Diamagnetic and Paramagnetic Applications
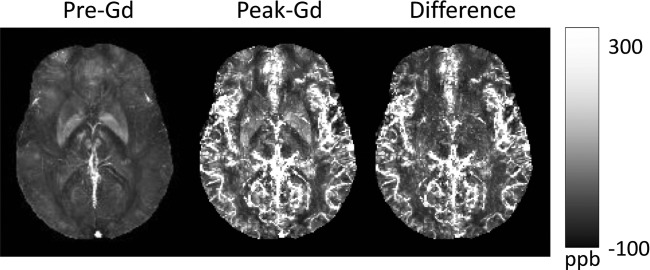
GRE phase images have been used to study iron distribution and demyelination in multiple sclerosis (MS) lesions 203–207. Iron distribution has been reported to be abnormally high in both the basal ganglia and lesions in MS patients 137,203,204,208,209 and may vary with lesion age and inflammatory status 204,210,211. QSM can be used to measure susceptibility changes in both lesions and nonlesion tissues in MS brains 212,213. A recent QSM study of magnetic susceptibilities of MS lesions 214 demonstrates that MS lesion susceptibilities start at the level of normal appearing WM (NAWM) (age – 0y, acute enhancing), quickly increase (within 0.5y) above that of NAWM, remain almost constant for a period (0–4y, intermediately aged and nonenhancing), and then decay gradually back to that of NAWM (> 7y, chronic nonenhancing) (Figs.12 and 13). This MS lesion susceptibility time course is consistent with the no-phase-variation on the 2.5y follow-up of nonenhancing MS lesions seen in another study 215, and with the rapid increase of off-resonance frequency observed in acute enhancing lesions in a third study 216. Investigations are ongoing to connect susceptibility time course and MS cellular activities. QSM may constitute an important new biomarker for the inflammatory and neurodegenerative activities in MS.
Figure 12.
Quantitative susceptibility mapping for quantifying a mixture of paramagnetic and diamagnetic biomaterials. (i) Acute enhancing lesions in a 32-year-old male with RRMS at two time points: initial study (T1w + c1 and QSM1, 1st row) and 3-month follow-up (T1w + c2 and QSM2, 2nd row) (T1w + c – T1-weighted imaging with Gd). Lesions appear in the right frontal WM (white arrows) and in the lcc (black arrows). Both lesions are enhancing (arrows) on T1w + c1 and isointense (white boxes) on QSM1. The lesions changed on follow up to nonenhancing on T1w + c2 and hyperintense on QSM2 (arrows). The right frontal WM matter lesion shrunk between QSM1 and QSM2. The lcc lesion (black arrow) recovered to normal appearing on T2w and T1w (not shown), T1w + c. (ii) Nonenhancing lesions (33y, f, RRMS) on QSM at two time points (2nd row was 6 months later). All QSM lesions at time point 1 were estimated to be 1.2y using prior MRIs. All lesions (arrows) are QSM hyperintense on both time points with similar values. (iii) Chronic nonenhancing lesions (50y f RRMS) on QSM and T2W. Two lesions over 10 years old were detected (white arrows). They appear isointense on both QSM (white boxes, only initial study shown). lcc, left cingulate cortex; QSM, quantitative susceptibility mapping; RRMS, relapsing-remitting multiple sclerosis; WM, white matter. Source: Chen et al, Radiology 2014;271:183–192.
Figure 13.
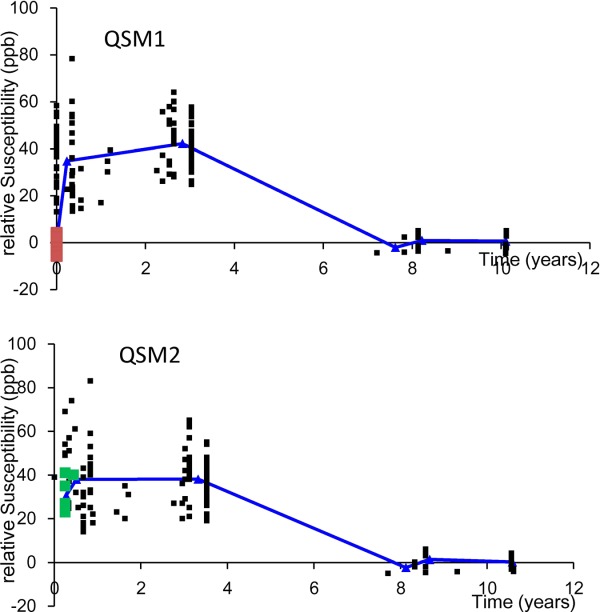
Time course of susceptibilities of multiple sclerosis lesions. The susceptibility time course may provide new insight into pathophysiologic features of MS lesions (23 patients with 162 lesions): Magnetic susceptibility of MS lesion increases rapidly as it changes from enhanced to nonenhanced, attains a high-susceptibility value relative to NAWM during its initial few years (approximately 4 years), and gradually dissipates back to susceptibility similar to that of NAWM as it ages. The graphs depict lesion susceptibility values (relative to NAWM) at various ages in QSM1 performed at a first time point (top) and in QSM2 at a second time point (bottom). Red points in QSM1 denote acute enhancing lesions at lesion age – 0 year; follow-up presented as green points in QSM2 demonstrated a substantial increase in susceptibility. Blue lines represent average susceptibilities of nonenhanced lesions in the age groups of 0 to 2, 2 to 4, 6 to 8, and 8 to 10 years and enhancing lesions. QSM, quantitative susceptibility mapping; MS, relapsing-remitting multiple sclerosis; NAWM, normal appearing white matter. Source: Chen et al, Radiology 2014;271:183–192.
Initial Results in Aorta, Breast, Extremity, and Kidney
QSM applications beyond the brain are also under active development (Fig. 14). The susceptibility values from phase data of the aortic arch during a Gd bolus passage may provide quantitative contrast-enhanced MRA 31 (Supp. Fig. S5). QSM is feasible for applications in other body parts including the breast, extremity, and abdomen (liver and kidney) for studying hemorrhage, metabolic oxygen consumption, mineral distribution, and contrast agent kinetics 96.
Figure 14.
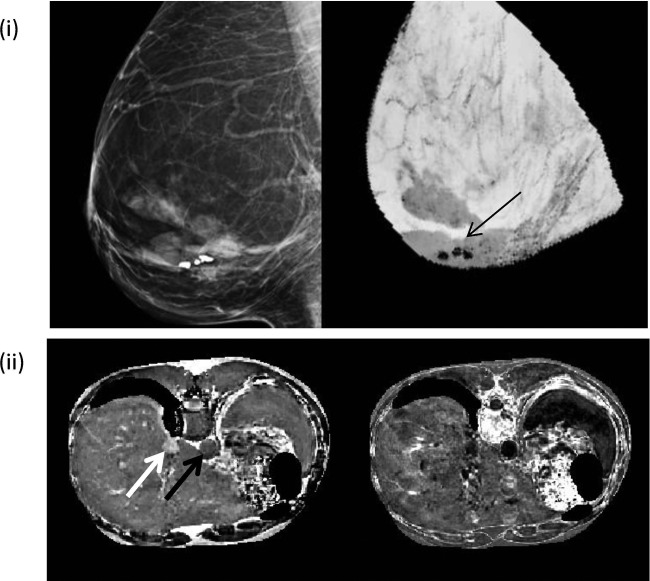
Quantitative susceptibility mapping applications in the breast and liver. (i) Left image is a mammogram and right image is the corresponding QSM (minimal intensity project through the 3D volume) of a breast in a female patient with three calcified nodules (arrow on QSM). Fatty tissues in the breast appear less diamagnetic compared to the gland. (ii) QSM and R2* images of a liver are shown in the left and right, respectively. Hepatic vein and subcutaneous fat (white arrows in left) appear paramagnetic. The susceptibility difference between the hepatic vein (white arrow) and the aortic artery (black arrow) are 0.53 ppm. 3D, three dimensional; QSM, quantitative susceptibility mapping.
QSM of Tissue Complexity: Multiple Species and Microstructures
QSM techniques have started to proliferate, an indication that QSM is a fertile field for innovation. This review so far has focused on modeling a voxel of tissue with a scalar susceptibility. Here we briefly survey investigations to model MRI signal with tissue complexity: multiple species of different chemical shifts, subvoxel structures, and molecular structures.
Nonlinear Phase Behavior of Multiple Spectral Species, Long TE, Large Voxel
The signal model in Eq. 5 may be regarded as a first order (linear temporal phase evolution) approximation, which may be good enough for many brain applications. For imaging other body parts, there may be signal contribution from proton sources other than free water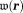 , such as fat
, such as fat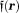 with chemical shift (characterized by a constant frequency offset
with chemical shift (characterized by a constant frequency offset ∼ −3.4 ppm). Eq. [14] can be generalized to account for the chemical shift effects on signal phase 217,218. The spatial smoothness of the tissue magnetic field can be used for fat–water separation 219–221:
∼ −3.4 ppm). Eq. [14] can be generalized to account for the chemical shift effects on signal phase 217,218. The spatial smoothness of the tissue magnetic field can be used for fat–water separation 219–221:
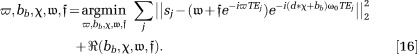 |
16 |
Note that the signal phase from a voxel is now nonlinear in its temporal evolution. Initial results in solving Eq. 16 are very encouraging, promising to extend QSM to body parts with fat (Fig. 14). The approximation in Eq. 5 works very well in most imaging situations but may break down in the presence of unusually strong susceptibility sources, long TEs, large voxels, or a combination of these factors. We may need to include higher-order terms in the evaluation of the exponential and include contributions from the neighboring voxels using an accurate voxel sensitivity function 44,222. These complications lead to a voxel signal phase that varies nonlinearly with TE.
Signal Behavior with Subvoxel Structure
There is growing interest in modeling tissue microstructure using MRI 215,223–231. Subvoxel structures may be characterized as gradients and higher-order spatial derivatives in spin density and magnetic field 232. These violations of the smoothness assumption in digitizing Eq. 2 result in voxel signal phases with nonlinearly temporal evolutions. More useful models may include specific geometries for the underlying tissue microstructure such as solid or hollow cylinders for capillaries, fibers, and other linear microstructure (Supp. Fig. S6), also leading to phase nonlinear in time 225,227,233. Microstructures may be considered as static and observer water as undergoing rapid random motion. The ergodic hypothesis may be assumed: the sum over the observer water path becomes the sum over the ensemble distribution that is proportional to spin density. Then, voxel signal may be modeled as the sum of the contributions from water protons inside magnetic microstructures or compartments ( ) within the voxel. An example compartment is the cylinder or generalized Lorentz model 225. When water exchange among compartments is small, the signal model is a simple extension of Eq. 5,
) within the voxel. An example compartment is the cylinder or generalized Lorentz model 225. When water exchange among compartments is small, the signal model is a simple extension of Eq. 5,
| 17 |
Here, for a given subvoxel compartment model, Maxwell’s Equations can be used to determine the field’s dependence on subvoxel structures ( ) such as their orientations and underlying molecular susceptibility anisotropies 225,227,233. With a sufficient number of measurements, the compartmental susceptibility may be estimated from the MRI signals:
) such as their orientations and underlying molecular susceptibility anisotropies 225,227,233. With a sufficient number of measurements, the compartmental susceptibility may be estimated from the MRI signals:
| 18 |
Susceptibility Tensor
The diamagnetic susceptibilities of anisotropic molecules (Supp. Fig. S6) must be described by recognizing the susceptibility in Eq. 2 as a tensor. If all types of anisotropic molecules are sufficiently smoothly distributed in the space, and the spatial dispersion of phase accruals is sufficiently small in a voxel—as assumed in Eq. 5—then the corresponding digital form of Eq. 2 with tensor susceptibility can be used, forming the foundation for susceptibility tensor imaging (STI) 234. Group symmetry theory suggests that susceptibility anisotropy can only be observed in a voxel if and only if anisotropic molecules are arranged orderly on a macroscopic scale 235,236. The increased number of variables in STI requires acquisitions at many orientations 237, which may be reduced by using prior information obtained from diffusion tensor imaging 235,236. Similar to Eq. 17, subvoxel structures may be incorporated into the MRI signal equation, introducing phase nonlinear in time and other complexities 233. The most interesting biomaterial demonstrating susceptibility anisotropy may be myelin 107,238, and the assessment of myelin integrity using MRI remains an important unmet clinical need.
CONCLUSION
Magnetic susceptibility directly reflects the molecular electron cloud behavior in the main magnetic field. Tissue susceptibility effects can be readily sensitized in MRI, for example using the widely available GRE sequence. Maxwell’s equations and the MRI signal equation can be used to quantitatively model the relationship between MRI signal and tissue susceptibility. Regularization is necessary to obtain a unique solution for determining the tissue susceptibility map from the acquired MRI signal, which is an ill-posed problem due to the lack of MRI signal in the background and the zeroes in the dipole kernel. The current status of QSM is very encouraging. The first order solution of QSM can be robustly obtained using physically meaningful regularizations, including the Bayesian approach. QSM has promising clinical and scientific applications that involve large susceptibility changes by hemoglobin, ferritin, calcification, and contrast agents. The investigations of higher order solutions have also been initiated, including studies of important magnetic anisotropies and tissue microstructures.
Acknowledgments
We thank the members and collaborators of Professor Wang’s lab: Ludovic de Rochefort, Jing Liu, Dong Zhou, Bryan Kressler, Cynthia Wisnieff, Bo Xu, Rebecca Cramer, Mitchell Cooper, Shuai Wang, Shuo Wang, Yan Wen, Alexey Dimov, Jingwei Zhang, Sarah Eskreis-Winkler, Kofi Deh, Pascal Spincemaille, Shixing Chang, Huan Tan, Pottumarthi Prasad, Robert Edelman, Weiwei Chen, Susan Gauthier, Ajay Gupta, Toshinori Hirai, Xuemei Huang, Shingo Kakeda, Brian Kopell, Yukunori Korogi, Christian Langkammer, Min Lou, Thanh Nguyen, David Pitt, Martin Prince, Stefan Ropele, and John Tsiouris.
We also thank the following QSM developers, who have generously contributed to sources codes and experimental validations: Elfar Adalsteinsson, Berkin Bilgic, Richard Bowtell, Jeff Duyn, E. Mark Haacke, Wei Li, Chunlei Liu, Saifeng Liu, Jürgen Reichenbach, Ferdinand Schweser, Karin Shmueli, and Samuel Wharton.
Supporting Information
Additional Supporting Information may be found in the online version of this article.
Supplementary Information.
References
- Wang Y. 2012. . Principles of Magnetic Resonance Imaging: physics concepts, pulse sequences & biomedical applications. Available at: www.createspace.com/4001776. Accessed December 1, 2013.
- de Crespigny AJ, Roberts TP, Kucharcyzk J, Moseley ME. Improved sensitivity to magnetic susceptibility contrast. Magn Reson Med. 1993;30:135–137. doi: 10.1002/mrm.1910300121. [DOI] [PubMed] [Google Scholar]
- Haacke EM, Xu Y, Cheng YC, Reichenbach JR. Susceptibility weighted imaging (SWI) Magn Reson Med. 2004;52:612–618. doi: 10.1002/mrm.20198. [DOI] [PubMed] [Google Scholar]
- Haacke EM, Reichenbach J. Susceptibility weighted imaging in MRI: basic concepts and clinical applications. Hoboken, NJ: Wiley-Blackwell; 2011. [Google Scholar]
- Jackson JD. Classical electrodynamics. 3rd ed. Hoboken, NJ: John Wiley and Son; 1999. pp. 184–188. [Google Scholar]
- Young IR, Khenia S, Thomas DG, Davis CH, Gadian DG, Cox IJ, Ross BD, Bydder GM. Clinical magnetic susceptibility mapping of the brain. J Comput Assist Tomogr. 1987;11:2–6. doi: 10.1097/00004728-198701000-00002. [DOI] [PubMed] [Google Scholar]
- Li L, Leigh JS. Quantifying arbitrary magnetic susceptibility distributions with MR. Magn Reson Med. 2004;51:1077–1082. doi: 10.1002/mrm.20054. [DOI] [PubMed] [Google Scholar]
- Mahdi K, Wlodarczyk W, Lange T, Scholz R, Jordan A, Wust P. Proceedings of the 9th Annual Meeting of ISMRM. Glasgow, Scotland, UK: 2001. Quantitative mapping of magnetic fluid distributions by means of MR susceptometry; p. 797. [Google Scholar]
- Haacke EM, Cheng NY, House MJ, Liu Q, Neelavalli J, Ogg RJ, Khan A, Ayaz M, Kirsch W, Obenaus A. Imaging iron stores in the brain using magnetic resonance imaging. Magn Reson Imaging. 2005;23:1–25. doi: 10.1016/j.mri.2004.10.001. [DOI] [PubMed] [Google Scholar]
- Shmueli K, de Zwart JA, van Gelderen P, Li TQ, Dodd SJ, Duyn JH. Magnetic susceptibility mapping of brain tissue in vivo using MRI phase data. Magn Reson Med. 2009;62:1510–1522. doi: 10.1002/mrm.22135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Rochefort L, Brown R, Prince MR, Wang Y. Quantitative MR susceptibility mapping using piece-wise constant regularized inversion of the magnetic field. Magn Reson Med. 2008;60:1003–1009. doi: 10.1002/mrm.21710. [DOI] [PubMed] [Google Scholar]
- Kressler B, de Rochefort L, Spincemaille P, Liu T, Wang Y. Proceedings of the 16th Annual Meeting of ISMRM, Toronto. Canada: 2008. Estimation of sparse magnetic susceptibility distributions from MRI using non-linear regularization; p. 1514. [Google Scholar]
- Yeo DT, Fessler JA, Kim B. Motion robust magnetic susceptibility and field inhomogeneity estimation using regularized image restoration techniques for fMRI. Med Image Comput Comput Assist Interv. 2008;11:991–998. doi: 10.1007/978-3-540-85988-8_118. [DOI] [PubMed] [Google Scholar]
- Liu T, Spincemaille P, de Rochefort L, Kressler B, Wang Y. Calculation of susceptibility through multiple orientation sampling (COSMOS): a method for conditioning the inverse problem from measured magnetic field map to susceptibility source image in MRI. Magn Reson Med. 2009;61:196–204. doi: 10.1002/mrm.21828. [DOI] [PubMed] [Google Scholar]
- Wang Y, de Rochefort L, Liu T, Kressler B. Magnetic source MRI: a new quantitative imaging of magnetic biomarkers. Conf Proc IEEE Eng Med Biol Soc. 2009;2009:53–56. doi: 10.1109/IEMBS.2009.5335128. [DOI] [PubMed] [Google Scholar]
- Morgan J, Irarrazaval P. Proceedings of the 15th Annual ISMRM Meeting-ESMRMB, Berlin. Germany: 2007. Efficient solving for arbitrary susceptibility distributions using residual difference fields; p. 35. [Google Scholar]
- de Rochefort L, Liu T, Kressler B, Liu J, Spincemaille P, Lebon V, Wu J, Wang Y. Quantitative susceptibility map reconstruction from MR phase data using bayesian regularization: validation and application to brain imaging. Magn Reson Med. 2010;63:194–206. doi: 10.1002/mrm.22187. [DOI] [PubMed] [Google Scholar]
- Kressler B, De Rochefort L, Spincemaille P, Liu T, Wang Y. Proceedings of the 16th Annual Meeting of ISMRM, Toronto. Canada: 2008. Estimation of sparse magnetic susceptibility distributions from MRI using non-linear regularization; p. 1514. [Google Scholar]
- Liu J, Liu T, de Rochefort L, et al. Morphology enabled dipole inversion for quantitative susceptibility mapping using structural consistency between the magnitude image and the susceptibility map. Neuroimage. 2012;59:2560–2568. doi: 10.1016/j.neuroimage.2011.08.082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu T, Wisnieff C, Lou M, Chen W, Spincemaille P, Wang Y. Nonlinear formulation of the magnetic field to source relationship for robust quantitative susceptibility mapping. Magn Reson Med. 2013;69:467–476. doi: 10.1002/mrm.24272. [DOI] [PubMed] [Google Scholar]
- Kressler B, de Rochefort L, Liu T, Spincemaille P, Jiang Q, Wang Y. Nonlinear regularization for per voxel estimation of magnetic susceptibility distributions from MRI field maps. IEEE Trans Med Imaging. 2010;29:273–281. doi: 10.1109/TMI.2009.2023787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wharton S, Schafer A, Bowtell R. Susceptibility mapping in the human brain using threshold-based k-space division. Magn Reson Med. 2010;63:1292–1304. doi: 10.1002/mrm.22334. [DOI] [PubMed] [Google Scholar]
- Li W, Wu B, Liu C. Quantitative susceptibility mapping of human brain reflects spatial variation in tissue composition. Neuroimage. 2011;55:1645–1656. doi: 10.1016/j.neuroimage.2010.11.088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Z, Calhoun V. Computed inverse resonance imaging for magnetic susceptibility map reconstruction. J Comput Assist Tomogr. 2012;36:265–274. doi: 10.1097/RCT.0b013e3182455cab. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schweser F, Sommer K, Deistung A, Reichenbach JR. Quantitative susceptibility mapping for investigating subtle susceptibility variations in the human brain. Neuroimage. 2012;62:2083–2100. doi: 10.1016/j.neuroimage.2012.05.067. [DOI] [PubMed] [Google Scholar]
- Schweser F, Deistung A, Sommer K, Reichenbach JR. Toward online reconstruction of quantitative susceptibility maps: superfast dipole inversion. Magn Reson Med. 2013;69:1582–1594. doi: 10.1002/mrm.24405. [DOI] [PubMed] [Google Scholar]
- Wu B, Li W, Guidon A, Liu C. Whole brain susceptibility mapping using compressed sensing. Magn Reson Med. 2012;67:137–147. doi: 10.1002/mrm.23000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bilgic B, Fan AP, Polimeni JR, Cauley SF, Bianciardi M, Adalsteinsson E, Wald LL, Setsompop K. Fast quantitative susceptibility mapping with L1-regularization and automatic parameter selection. Magn Reson Med. 2014;72:1444–1459. doi: 10.1002/mrm.25029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bilgic B, Chatnuntawech I, Fan AP, Setsompop K, Cauley SF, Wald LL, Adalsteinsson E. Fast image reconstruction with L2-regularization. J Magn Reson Imaging. 2014;40:181–191. doi: 10.1002/jmri.24365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang J, Liu S, Neelavalli J, Cheng YC, Buch S, Haacke EM. Improving susceptibility mapping using a threshold-based K-space/image domain iterative reconstruction approach. Magn Reson Med. 2013;69:1396–1407. doi: 10.1002/mrm.24384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Rochefort L, Nguyen T, Brown R, Spincemaille P, Choi G, Weinsaft J, Prince MR, Wang Y. In vivo quantification of contrast agent concentration using the induced magnetic field for time-resolved arterial input function measurement with MRI. Med Phys. 2008;35:5328–5339. doi: 10.1118/1.3002309. [DOI] [PubMed] [Google Scholar]
- Lamb WE. Internal diamagnetic fields. Phys Rev. 1941;60:817–819. [Google Scholar]
- Ramsey NF. Magnetic shielding of nuclei in molecules. Phys Rev. 1950;78:5. [Google Scholar]
- Schindler M, Kutzelnigg W. Theory of magnetic-susceptibilities and NMR chemical-shifts in terms of localized quantities. III. Application to Hydrocarbons and Other Organic-Molecules. J Am Chem Soc. 1983;105:1360–1370. [Google Scholar]
- Duyn J. MR susceptibility imaging. J Magn Reson. 2013;229:198–207. doi: 10.1016/j.jmr.2012.11.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauffer RB. Paramagnetic metal complexes as water proton relaxation agents for NMR imaging: theory and design. Chem Rev. 1987;87:901–927. [Google Scholar]
- Hahn EL. Spin echoes. Phys Rev. 1950;80:580–594. [Google Scholar]
- Bloembergen N, Morgan LO. Proton relaxation times in paramagetic solutions. effects of electron spin relaxation. J Chem Phys. 1961;34:8. [Google Scholar]
- Solomon I. Relaxation processes in a system of two spins. Phys Rev. 1955;99:559–565. [Google Scholar]
- Yablonskiy DA, Haacke EM. Theory of NMR signal behavior in magnetically inhomogeneous tissues: the static dephasing regime. Magn Reson Med. 1994;32:749–763. doi: 10.1002/mrm.1910320610. [DOI] [PubMed] [Google Scholar]
- Jensen JH, Chandra R, Ramani A, Lu H, Johnson G, Lee SP, Kaczynski K, Helpern JA. Magnetic field correlation imaging. Magn Reson Med. 2006;55:1350–1361. doi: 10.1002/mrm.20907. [DOI] [PubMed] [Google Scholar]
- Roemer PB, Edelstein WA, Hayes CE, Souza SP, Mueller OM. The NMR phased array. Magn Reson Med. 1990;16:192–225. doi: 10.1002/mrm.1910160203. [DOI] [PubMed] [Google Scholar]
- Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med. 1999;42:952–962. [PubMed] [Google Scholar]
- Parker DL, Du YP, Davis WL. The voxel sensitivity function in Fourier transform imaging: applications to magnetic resonance angiography. Magn Reson Med. 1995;33:156–162. doi: 10.1002/mrm.1910330203. [DOI] [PubMed] [Google Scholar]
- Tyler DJ, Robson MD, Henkelman RM, Young IR, Bydder GM. Magnetic resonance imaging with ultrashort TE (UTE) PULSE sequences: technical considerations. J Magn Reson Imaging. 2007;25:279–289. doi: 10.1002/jmri.20851. [DOI] [PubMed] [Google Scholar]
- Robson MD, Gatehouse PD, Bydder M, Bydder GM. Magnetic resonance: an introduction to ultrashort TE (UTE) imaging. J Comput Assist Tomogr. 2003;27:825–846. doi: 10.1097/00004728-200311000-00001. [DOI] [PubMed] [Google Scholar]
- Weiger M, Pruessmann KP, Hennel F. MRI with zero echo time: hard versus sweep pulse excitation. Magn Reson Med. 2011;66:379–389. doi: 10.1002/mrm.22799. [DOI] [PubMed] [Google Scholar]
- Xu B, Liu T, Spincemaille P, Prince M, Wang Y. Flow compensated quantitative susceptibility mapping for venous oxygenation imaging. Magn Reson Med. 2014;72:438–445. doi: 10.1002/mrm.24937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu B, Li W, Avram AV, Gho SM, Liu C. Fast and tissue-optimized mapping of magnetic susceptibility and T2* with multi-echo and multi-shot spirals. Neuroimage. 2012;59:297–305. doi: 10.1016/j.neuroimage.2011.07.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu B, Liu T, Spincemaille P, Thimmappa N, Prince MR, Wang Y. Proceedings of the 21st Annual Meeting of ISMRM, Salt Lake City. Utah, USA: 2013. Dynamic quantitative susceptibility mapping for contrast agent concentration; p. 3847. [Google Scholar]
- Lim IA, Li X, Jones CK, Farrell JA, Vikram DS, van Zijl PC. Quantitative magnetic susceptibility mapping without phase unwrapping using WASSR. Neuroimage. 2014;86:265–279. doi: 10.1016/j.neuroimage.2013.09.072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nocedal J, Wright SJ. Numerical optimization. Vol. 664. New York: Springer; 2006. p. xxii. [Google Scholar]
- Pei M, Nguyen TD, Thimmappa ND, Salustri C, Dong F, Cooper MA, Li J, Prince MR, Wang Y. Algorithm for fast monoexponential fitting based on auto-regression on linear operations (ARLO) of data. Magn Reson Med. 2014 doi: 10.1002/mrm.25137. . doi: 10.1002/mrm.25137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernstein MA, Grgic M, Brosnan TJ, Pelc NJ. Reconstructions of phase contrast, phased array multicoil data. Magn Reson Med. 1994;32:330–334. doi: 10.1002/mrm.1910320308. [DOI] [PubMed] [Google Scholar]
- Thunberg P, Karlsson M, Wigstrom L. Comparison of different methods for combining phase-contrast images obtained with multiple coils. Magn Reson Imaging. 2005;23:795–799. doi: 10.1016/j.mri.2005.06.002. [DOI] [PubMed] [Google Scholar]
- Lu K, Liu TT, Bydder M. Optimal phase difference reconstruction: comparison of two methods. Magn Reson Imaging. 2008;26:142–145. doi: 10.1016/j.mri.2007.04.015. [DOI] [PubMed] [Google Scholar]
- Robinson S, Grabner G, Witoszynskyj S, Trattnig S. Combining phase images from multi-channel RF coils using 3D phase offset maps derived from a dual-echo scan. Magn Reson Med. 2011;65:1638–1648. doi: 10.1002/mrm.22753. [DOI] [PubMed] [Google Scholar]
- Parker DL, Payne A, Todd N, Hadley JR. Phase reconstruction from multiple coil data using a virtual reference coil. Magn Reson Med. 2014;72:563–569. doi: 10.1002/mrm.24932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghiglia DC, Pritt MD. Two-dimensional phase unwrapping : theory, algorithms, and software. Vol. 493. New York: Wiley & Sons; 1998. p. xiv. [Google Scholar]
- Jenkinson M. Fast, automated, N-dimensional phase-unwrapping algorithm. Magn Reson Med. 2003;49:193–197. doi: 10.1002/mrm.10354. [DOI] [PubMed] [Google Scholar]
- Schofield MA, Zhu Y. Fast phase unwrapping algorithm for interferometric applications. Opt Lett. 2003;28:1194–1196. doi: 10.1364/ol.28.001194. [DOI] [PubMed] [Google Scholar]
- Li W, Avram AV, Wu B, Xiao X, Liu C. Integrated Laplacian-based phase unwrapping and background phase removal for quantitative susceptibility mapping. NMR Biomed. 2014;27:219–227. doi: 10.1002/nbm.3056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu W, Cumming I. A region-growing algorithm for InSAR phase unwrapping. IEEE Trans Geosci Remote Sens. 1999;37:11. [Google Scholar]
- Witoszynskyj S, Rauscher A, Reichenbach JR, Barth M. Phase unwrapping of MR images using Phi UN—a fast and robust region growing algorithm. Med Image Anal. 2009;13:257–268. doi: 10.1016/j.media.2008.10.004. [DOI] [PubMed] [Google Scholar]
- Cusack R, Papadakis N. New robust 3-D phase unwrapping algorithms: application to magnetic field mapping and undistorting echoplanar images. Neuroimage. 2002;16:754–764. doi: 10.1006/nimg.2002.1092. [DOI] [PubMed] [Google Scholar]
- Seo JK, Woo EJ, Katscher U, Wang Y. In: Electro-magnetic tissue properties MRI. Ammari H, editor. London, UK: Imperial College Press; 2014. , editor. [Google Scholar]
- Langham MC, Magland JF, Floyd TF, Wehrli FW. Retrospective correction for induced magnetic field inhomogeneity in measurements of large-vessel hemoglobin oxygen saturation by MR susceptometry. Magn Reson Med. 2009;61:626–633. doi: 10.1002/mrm.21499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Yu Y, Li D, Bae KT, Brown JJ, Lin W, Haacke EM. Artery and vein separation using susceptibility-dependent phase in contrast-enhanced MRA. J Magn Reson Imaging. 2000;12:661–670. doi: 10.1002/1522-2586(200011)12:5<661::aid-jmri2>3.0.co;2-l. [DOI] [PubMed] [Google Scholar]
- Liu T, Khalidov I, de Rochefort L, Spincemaille P, Liu J, Tsiouris AJ, Wang Y. A novel background field removal method for MRI using projection onto dipole fields (PDF) NMR Biomed. 2011;24:1129–1136. doi: 10.1002/nbm.1670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schweser F, Deistung A, Lehr BW, Reichenbach JR. Quantitative imaging of intrinsic magnetic tissue properties using MRI signal phase: an approach to in vivo brain iron metabolism? Neuroimage. 2011;54:2789–2807. doi: 10.1016/j.neuroimage.2010.10.070. [DOI] [PubMed] [Google Scholar]
- Evans LC. Partial differential equations. Vol. 749. Providence, RI: American Mathematical Society; 2010. p. xxi. [Google Scholar]
- Courant R, Hilbert D. Methods of mathematical physics. New York: Interscience Publishers; 1989. [Google Scholar]
- Zhou D, Liu T, Spincemaille P, Wang Y. Background field removal by solving the Laplacian boundary value problem. NMR Biomed. 2014;27:312–319. doi: 10.1002/nbm.3064. [DOI] [PubMed] [Google Scholar]
- Press WH. Numerical recipes : the art of scientific computing. 3rd ed. Cambridge, UK; New York: Cambridge University Press; 2007. pp. 636–643. [Google Scholar]
- Li L. Averaging of harmonic physical fields over an annular region enclosing field sources. Am J Phys. 2002;70:1029–1033. doi: 10.1119/1.1491264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wen Y, Zhou D, Liu T, Spincemaille P, Wang Y. An iterative spherical mean value method for background field removal in MRI. Magn Reson Med. 2014;72:1065–1071. doi: 10.1002/mrm.24998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun H, Wilman AH. Background field removal using spherical mean value filtering and Tikhonov regularization. Magn Reson Med. 2014;71:1151–1157. doi: 10.1002/mrm.24765. [DOI] [PubMed] [Google Scholar]
- Zhou P-b. Numerical analysis of electromagnetic fields. Vol. 406. Berlin, Germany; New York: Springer-Verlag; 1993. p. xxi. [Google Scholar]
- Marques JP, Bowtell R. Application of a Fourier-based method for rapid calculation of field inhomogeneity due to spatial variation of magnetic susceptibility. Concept Magn Reson. 2005;25B:65–78. [Google Scholar]
- Golub G, Loan CV. Matrix computations. Baltimore, MD: Johns Hopkins University Press; 1996. [Google Scholar]
- Pruessmann KP, Weiger M, Peter B, Peter B. Advances in sensitivity encoding with arbitrary k-space trajectories. Magn Reson Med. 2001;46:638–651. doi: 10.1002/mrm.1241. [DOI] [PubMed] [Google Scholar]
- Hansen PC. The truncated SVD as a method for regularization. BIT Numer Math. 1987;27:534–553. [Google Scholar]
- Liu T, Xu W, Spincemaille P, Avestimehr AS, Wang Y. Accuracy of the morphology enabled dipole inversion (MEDI) algorithm for quantitative susceptibility mapping in MRI. IEEE Trans Med Imaging. 2012;31:816–824. doi: 10.1109/TMI.2011.2182523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tarantola A. Inverse problem theory and methods for model parameter estimation. Philadelphia, PA: SIAM; 2005. [Google Scholar]
- Bauer F, Lukas MA. Comparingparameter choice methods for regularization of ill-posed problems. Mathematics and Computers in Simulation. 2011;81:1795–1841. [Google Scholar]
- Morozov VA, Nashed MZ. Methods for solving incorrectly posed problems. Vol. 257. New York: Springer-Verlag; 1984. p. xviii. [Google Scholar]
- Engl HW, Hanke M, Neubauer A. Regularization of inverse problems. Dordrecht. The Netherlands: Kluwer; 2000. [Google Scholar]
- Wang S, Liu T, Chen W, Spincemaille P, Wisnieff C, Tsiouris AJ, Zhu W, Pan C, Zhao L, Wang Y. Noise effects in various quantitative susceptibility mapping methods. IEEE Trans Biomed Eng. 2013;60:3441–3448. doi: 10.1109/TBME.2013.2266795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schweser F, Deistung A, Lehr BW, Reichenbach JR. Differentiation between diamagnetic and paramagnetic cerebral lesions based on magnetic susceptibility mapping. Med Phys. 2010;37:5165–5178. doi: 10.1118/1.3481505. [DOI] [PubMed] [Google Scholar]
- Bilgic B, Pfefferbaum A, Rohlfing T, Sullivan EV, Adalsteinsson E. MRI estimates of brain iron concentration in normal aging using quantitative susceptibility mapping. Neuroimage. 2012;59:2625–2635. doi: 10.1016/j.neuroimage.2011.08.077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shewchuk JR. An introduction to the conjugate gradient method without the agonizing pain. Pittsburgh, PA: School of Computer Science, Carnegie Mellon University; 1994. . Available at: http://www.cs.cmu.edu/∼quake-papers/painless-conjugate-gradient.pdf. Accessed December 1, 2013. [Google Scholar]
- Liu T, Liu J, de Rochefort L, Spincemaille P, Khalidov I, Ledoux JR, Wang Y. Morphology enabled dipole inversion (MEDI) from a single-angle acquisition: comparison with COSMOS in human brain imaging. Magn Reson Med. 2011;66:777–783. doi: 10.1002/mrm.22816. [DOI] [PubMed] [Google Scholar]
- Elad M. Sparse and redundant representations: from theory to applications in signal and image processing. New York: Springer; 2010. p. 396. [Google Scholar]
- Wharton S, Bowtell R. Whole-brain susceptibility mapping at high field: a comparison of multiple- and single-orientation methods. Neuroimage. 2010;53:515–525. doi: 10.1016/j.neuroimage.2010.06.070. [DOI] [PubMed] [Google Scholar]
- Li J, Chang S, Liu T, Wang Q, Cui D, Chen X, Jin M, Wang B, Pei M, Wisnieff C, Spincemaille P, Zhang M, Wang Y. Reducing the object orientation dependence of susceptibility effects in gradient echo MRI through quantitative susceptibility mapping. Magn Reson Med. 2012;68:1563–1569. doi: 10.1002/mrm.24135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie L, Sparks MA, Li W, Qi Y, Liu C, Coffman TM, Johnson GA. Quantitative susceptibility mapping of kidney inflammation and fibrosis in type 1 angiotensin receptor-deficient mice. NMR Biomed. 2013;26:1853–1863. doi: 10.1002/nbm.3039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen W, Zhu W, Kovanlikaya I, Kovanlikaya A, Liu T, Wang S, Salustri C, Wang Y. Intracranial calcifications and hemorrhages: characterization with quantitative susceptibility mapping. Radiology. 2014;270:496–505. doi: 10.1148/radiol.13122640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarmiento de la Iglesia MM, Lecumberri Cortes G, Lecumberri Cortes I, Oleaga Zufiria L, Isusi Fontan M, Grande Icaran D. [Intracranial calcifications on MRI] Radiologia. 2006;48:19–26. doi: 10.1016/s0033-8338(06)73125-3. [DOI] [PubMed] [Google Scholar]
- Kozic D, Todorovic-Djilas L, Semnic R, Miucin-Vukadinovic I, Lucic M. MR imaging—an unreliable and potentially misleading diagnostic modality in patients with intracerebral calcium depositions. Case report. Neuro Endocrinol Lett. 2009;30:553–557. [PubMed] [Google Scholar]
- Wu Z, Mittal S, Kish K, Yu Y, Hu J, Haacke EM. Identification of calcification with MRI using susceptibility-weighted imaging: a case study. J Magn Reson Imaging. 2009;29:177–182. doi: 10.1002/jmri.21617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamada N, Imakita S, Sakuma T, Takamiya M. Intracranial calcification on gradient-echo phase image: depiction of diamagnetic susceptibility. Radiology. 1996;198:171–178. doi: 10.1148/radiology.198.1.8539373. [DOI] [PubMed] [Google Scholar]
- Prokop M, Galanski M. Spiral and multislice computed tomography of the body. Vol. 1090. Stuttgart, Germany; New York: Thieme; 2003. p. xii. [Google Scholar]
- Huisman TA. Intracranial hemorrhage: ultrasound, CT and MRI findings. Eur Radiol. 2005;15:434–440. doi: 10.1007/s00330-004-2615-7. [DOI] [PubMed] [Google Scholar]
- Makariou E, Patsalides AD. Intracranial calcifications. Appl Radiol. 2009;38:48–60. [Google Scholar]
- Shental N, Bar-Hillel A, Hertz T, Weinshall D. Computing Gaussian mixture models with EM using side-information. Jerusalem, Israel: Hebrew University of Jerusalem; 2003. [Google Scholar]
- Deistung A, Schweser F, Wiestler B, et al. Quantitative susceptibility mapping differentiates between blood depositions and calcifications in patients with glioblastoma. PloS One. 2013;8:e57924. doi: 10.1371/journal.pone.0057924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu C, Li W, Johnson GA, Wu B. High-field (9.4 T) MRI of brain dysmyelination by quantitative mapping of magnetic susceptibility. Neuroimage. 2011;56:930–938. doi: 10.1016/j.neuroimage.2011.02.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bradley WG., Jr MR appearance of hemorrhage in the brain. Radiology. 1993;189:15–26. doi: 10.1148/radiology.189.1.8372185. [DOI] [PubMed] [Google Scholar]
- Heier LA, Amster JL, Zimmerman RD, Deck MD. Focal recurrent hemorrhage on magnetic resonance at 0.5 Tesla. An aid to the diagnosis of cryptic cerebral vascular malformations. Acta Radiol Suppl. 1986;369:113–115. [PubMed] [Google Scholar]
- Zimmerman RD, Heier LA, Snow RB, Liu DP, Kelly AB, Deck MD. Acute intracranial hemorrhage: intensity changes on sequential MR scans at 0.5 T. AJR Am J Roentgenol. 1988;150:651–661. doi: 10.2214/ajr.150.3.651. [DOI] [PubMed] [Google Scholar]
- Liu T, Surapaneni K, Lou M, Cheng L, Spincemaille P, Wang Y. Cerebral microbleeds: burden assessment by using quantitative susceptibility mapping. Radiology. 2012;262:269–278. doi: 10.1148/radiol.11110251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kidwell CS, Chalela JA, Saver JL, et al. Comparison of MRI and CT for detection of acute intracerebral hemorrhage. JAMA. 2004;292:1823–1830. doi: 10.1001/jama.292.15.1823. [DOI] [PubMed] [Google Scholar]
- Fiebach JB, Schellinger PD, Gass A, et al. Stroke magnetic resonance imaging is accurate in hyperacute intracerebral hemorrhage: a multicenter study on the validity of stroke imaging. Stroke. 2004;35:502–506. doi: 10.1161/01.STR.0000114203.75678.88. [DOI] [PubMed] [Google Scholar]
- Broderick JP, Brott TG, Duldner JE, Tomsick T, Huster G. Volume of intracerebral hemorrhage. A powerful and easy-to-use predictor of 30-day mortality. Stroke. 1993;24:987–993. doi: 10.1161/01.str.24.7.987. [DOI] [PubMed] [Google Scholar]
- Davis SM, Broderick J, Hennerici M, Brun NC, Diringer MN, Mayer SA, Begtrup K, Steiner T. Hematoma growth is a determinant of mortality and poor outcome after intracerebral hemorrhage. Neurology. 2006;66:1175–1181. doi: 10.1212/01.wnl.0000208408.98482.99. [DOI] [PubMed] [Google Scholar]
- Klohs J, Deistung A, Schweser F, Grandjean J, Dominietto M, Waschkies C, Nitsch RM, Knuesel I, Reichenbach JR, Rudin M. Detection of cerebral microbleeds with quantitative susceptibility mapping in the ArcAbeta mouse model of cerebral amyloidosis. J Cereb Blood Flow Metab. 2011;31:2282–2292. doi: 10.1038/jcbfm.2011.118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang S, Lou M, Liu T, Cui D, Chen X, Wang Y. Hematoma volume measurement in gradient echo MRI using quantitative susceptibility mapping. Stroke. 2013;44:2315–2317. doi: 10.1161/STROKEAHA.113.001638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haacke EM, Tang J, Neelavalli J, Cheng YC. Susceptibility mapping as a means to visualize veins and quantify oxygen saturation. J Magn Reson Imaging. 2010;32:663–676. doi: 10.1002/jmri.22276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan AP, Bilgic B, Gagnon L, Witzel T, Bhat H, Rosen BR, Adalsteinsson E. Quantitative oxygenation venography from MRI phase. Magn Reson Med. 2014;72:149–159. doi: 10.1002/mrm.24918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jain V, Abdulmalik O, Propert KJ, Wehrli FW. Investigating the magnetic susceptibility properties of fresh human blood for noninvasive oxygen saturation quantification. Magn Reson Med. 2012;68:863–867. doi: 10.1002/mrm.23282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Powers WJ, Grubb RL, Jr, Darriet D, Raichle ME. Cerebral blood flow and cerebral metabolic rate of oxygen requirements for cerebral function and viability in humans. J Cereb Blood Flow Metab. 1985;5:600–608. doi: 10.1038/jcbfm.1985.89. [DOI] [PubMed] [Google Scholar]
- Detre JA, Zhang W, Roberts DA, Silva AC, Williams DS, Grandis DJ, Koretsky AP, Leigh JS. Tissue specific perfusion imaging using arterial spin labeling. NMR Biomed. 1994;7:75–82. doi: 10.1002/nbm.1940070112. [DOI] [PubMed] [Google Scholar]
- An H, Lin W. Quantitative measurements of cerebral blood oxygen saturation using magnetic resonance imaging. J Cereb Blood Flow Metab. 2000;20:1225–1236. doi: 10.1097/00004647-200008000-00008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bulte DP, Kelly M, Germuska M, Xie J, Chappell MA, Okell TW, Bright MG, Jezzard P. Quantitative measurement of cerebral physiology using respiratory-calibrated MRI. Neuroimage. 2012;60:582–591. doi: 10.1016/j.neuroimage.2011.12.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gauthier CJ, Hoge RD. Magnetic resonance imaging of resting OEF and CMRO(2) using a generalized calibration model for hypercapnia and hyperoxia. Neuroimage. 2012;60:1212–1225. doi: 10.1016/j.neuroimage.2011.12.056. [DOI] [PubMed] [Google Scholar]
- Wise RG, Harris AD, Stone AJ, Murphy K. Measurement of OEF and absolute CMRO2: MRI-based methods using interleaved and combined hypercapnia and hyperoxia. Neuroimage. 2013;83:135–147. doi: 10.1016/j.neuroimage.2013.06.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J, Pei M, Liu T, Gupta A, Wisnieff C, Sanelli PC, Spincemaille P, Wang Y. Proceedings of the 21st Annual Meeting of ISMRM, Salt Lake City. Utah, USA: 2013. Quantitative susceptibility mapping (QSM) for high resolution quantitative cerebral metabolic rate of oxygen; p. 3334. [Google Scholar]
- Moos T, Morgan EH. The metabolism of neuronal iron and its pathogenic role in neurological disease: review. Ann NY Acad Sci. 2004;1012:14–26. doi: 10.1196/annals.1306.002. [DOI] [PubMed] [Google Scholar]
- Lee DW, Andersen JK, Kaur D. Iron dysregulation and neurodegeneration: the molecular connection. Mol Interv. 2006;6:89–97. doi: 10.1124/mi.6.2.6. [DOI] [PubMed] [Google Scholar]
- Zecca L, Youdim MB, Riederer P, Connor JR, Crichton RR. Iron, brain ageing and neurodegenerative disorders. Nat Rev Neurosci. 2004;5:863–873. doi: 10.1038/nrn1537. [DOI] [PubMed] [Google Scholar]
- Crichton RR. Iron metabolism : from molecular mechanisms to clinical consequences. Vol. 461. Chichester, UK: John Wiley & Sons; 2009. p. xx. [Google Scholar]
- Lim IA, Faria AV, Li X, Hsu JT, Airan RD, Mori S, van Zijl PC. Human brain atlas for automated region of interest selection in quantitative susceptibility mapping: Application to determine iron content in deep gray matter structures. Neuroimage. 2013;82:449–469. doi: 10.1016/j.neuroimage.2013.05.127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng W, Nichol H, Liu S, Cheng YC, Haacke EM. Measuring iron in the brain using quantitative susceptibility mapping and x-ray fluorescence imaging. Neuroimage. 2013;78:68–74. doi: 10.1016/j.neuroimage.2013.04.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oshiro S, Morioka MS, Kikuchi M. Dysregulation of iron metabolism in Alzheimer’s disease, Parkinson’s disease, and amyotrophic lateral sclerosis. Adv Pharmacol Sci. 2011;2011:378278. doi: 10.1155/2011/378278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crichton RR, Dexter DT, Ward RJ. Brain iron metabolism and its perturbation in neurological diseases. J Neural Transm. 2011;118:301–314. doi: 10.1007/s00702-010-0470-z. [DOI] [PubMed] [Google Scholar]
- Nunez MT, Urrutia P, Mena N, Aguirre P, Tapia V, Salazar J. Iron toxicity in neurodegeneration. Biometals. 2012;25:761–776. doi: 10.1007/s10534-012-9523-0. [DOI] [PubMed] [Google Scholar]
- Williams R, Buchheit CL, Berman NE, LeVine SM. Pathogenic implications of iron accumulation in multiple sclerosis. J Neurochem. 2012;120:7–25. doi: 10.1111/j.1471-4159.2011.07536.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dexter DT, Wells FR, Agid F, Agid Y, Lees AJ, Jenner P, Marsden CD. Increased nigral iron content in postmortem parkinsonian brain. Lancet. 1987;2:1219–1220. doi: 10.1016/s0140-6736(87)91361-4. [DOI] [PubMed] [Google Scholar]
- Riederer P, Sofic E, Rausch WD, Schmidt B, Reynolds GP, Jellinger K, Youdim MB. Transition metals, ferritin, glutathione, and ascorbic acid in parkinsonian brains. J Neurochem. 1989;52:515–520. doi: 10.1111/j.1471-4159.1989.tb09150.x. [DOI] [PubMed] [Google Scholar]
- Hirsch EC, Brandel JP, Galle P, Javoy-Agid F, Agid Y. Iron and aluminum increase in the substantia nigra of patients with Parkinson’s disease: an x-ray microanalysis. J Neurochem. 1991;56:446–451. doi: 10.1111/j.1471-4159.1991.tb08170.x. [DOI] [PubMed] [Google Scholar]
- Oakley AE, Collingwood JF, Dobson J, Love G, Perrott HR, Edwardson JA, Elstner M, Morris CM. Individual dopaminergic neurons show raised iron levels in Parkinson disease. Neurology. 2007;68:1820–1825. doi: 10.1212/01.wnl.0000262033.01945.9a. [DOI] [PubMed] [Google Scholar]
- Lotfipour AK, Wharton S, Schwarz ST, Gontu V, Schafer A, Peters AM, Bowtell RW, Auer DP, Gowland PA, Bajaj NP. High resolution magnetic susceptibility mapping of the substantia nigra in Parkinson’s disease. J Magn Reson Imaging. 2012;35:48–55. doi: 10.1002/jmri.22752. [DOI] [PubMed] [Google Scholar]
- Ulla M, Bonny JM, Ouchchane L, Rieu I, Claise B, Durif F. Is R2* a new MRI biomarker for the progression of Parkinson’s disease? A longitudinal follow-up. PloS One. 2013;8:e57904. doi: 10.1371/journal.pone.0057904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Youdim MB, Ben-Shachar D, Riederer P. Iron in brain function and dysfunction with emphasis on Parkinson’s disease. Eur Neurol. 1991;31(suppl 1):34–40. doi: 10.1159/000116719. [DOI] [PubMed] [Google Scholar]
- Jomova K, Vondrakova D, Lawson M, Valko M. Metals, oxidative stress and neurodegenerative disorders. Mol Cell Biochem. 2010;345:91–104. doi: 10.1007/s11010-010-0563-x. [DOI] [PubMed] [Google Scholar]
- Hashimoto M, Takeda A, Hsu LJ, Takenouchi T, Masliah E. Role of cytochrome c as a stimulator of alpha-synuclein aggregation in Lewy body disease. J Biol Chem. 1999;274:28849–28852. doi: 10.1074/jbc.274.41.28849. [DOI] [PubMed] [Google Scholar]
- Li W, Jiang H, Song N, Xie J. Oxidative stress partially contributes to iron-induced alpha-synuclein aggregation in SK-N-SH cells. Neurotox Res. 2011;19:435–442. doi: 10.1007/s12640-010-9187-x. [DOI] [PubMed] [Google Scholar]
- Ordidge RJ, Gorell JM, Deniau JC, Knight RA, Helpern JA. Assessment of relative brain iron concentrations using T2-weighted and T2*-weighted MRI at 3 Tesla. Magn Reson Med. 1994;32:335–341. doi: 10.1002/mrm.1910320309. [DOI] [PubMed] [Google Scholar]
- Gorell JM, Ordidge RJ, Brown GG, Deniau JC, Buderer NM, Helpern JA. Increased iron-related MRI contrast in the substantia nigra in Parkinson’s disease. Neurology. 1995;45:1138–1143. doi: 10.1212/wnl.45.6.1138. [DOI] [PubMed] [Google Scholar]
- Bartzokis G, Cummings JL, Markham CH, Marmarelis PZ, Treciokas LJ, Tishler TA, Marder SR, Mintz J. MRI evaluation of brain iron in earlier- and later-onset Parkinson’s disease and normal subjects. Magn Reson Imaging. 1999;17:213–222. doi: 10.1016/s0730-725x(98)00155-6. [DOI] [PubMed] [Google Scholar]
- Brass SD, Chen NK, Mulkern RV, Bakshi R. Magnetic resonance imaging of iron deposition in neurological disorders. Top Magn Reson Imaging. 2006;17:31–40. doi: 10.1097/01.rmr.0000245459.82782.e4. [DOI] [PubMed] [Google Scholar]
- Wallis LI, Paley MN, Graham JM, Grunewald RA, Wignall EL, Joy HM, Griffiths PD. MRI assessment of basal ganglia iron deposition in Parkinson’s disease. J Magn Reson Imaging. 2008;28:1061–1067. doi: 10.1002/jmri.21563. [DOI] [PubMed] [Google Scholar]
- Rossi M, Ruottinen H, Elovaara I, Ryymin P, Soimakallio S, Eskola H, Dastidar P. Brain iron deposition and sequence characteristics in Parkinsonism: comparison of SWI, T(2)* maps, T(2)-weighted-, and FLAIR-SPACE. Invest Radiol. 2010;45:795–802. doi: 10.1097/RLI.0b013e3181ec9c96. [DOI] [PubMed] [Google Scholar]
- Haacke EM, Ayaz M, Khan A, Manova ES, Krishnamurthy B, Gollapalli L, Ciulla C, Kim I, Petersen F, Kirsch W. Establishing a baseline phase behavior in magnetic resonance imaging to determine normal vs. abnormal iron content in the brain. J Magn Reson Imaging. 2007;26:256–264. doi: 10.1002/jmri.22987. [DOI] [PubMed] [Google Scholar]
- Zhang W, Sun SG, Jiang YH, Qiao X, Sun X, Wu Y. Determination of brain iron content in patients with Parkinson’s disease using magnetic susceptibility imaging. Neurosci Bull. 2009;25:353–360. doi: 10.1007/s12264-009-0225-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang XM, Sun B, Xue YJ, Duan Q. [Susceptibility-weighted imaging in detecting brain iron accumulation of Parkinson’s disease] Zhonghua Yi Xue Za Zhi. 2010;90:3054–3058. [PubMed] [Google Scholar]
- Zhang J, Zhang Y, Wang J, Cai P, Luo C, Qian Z, Dai Y, Feng H. Characterizing iron deposition in Parkinson’s disease using susceptibility-weighted imaging: an in vivo MR study. Brain Res. 2010;1330:124–130. doi: 10.1016/j.brainres.2010.03.036. [DOI] [PubMed] [Google Scholar]
- Jin L, Wang J, Zhao L, Jin H, Fei G, Zhang Y, Zeng M, Zhong C. Decreased serum ceruloplasmin levels characteristically aggravate nigral iron deposition in Parkinson’s disease. Brain. 2011;134:50–58. doi: 10.1093/brain/awq319. [DOI] [PubMed] [Google Scholar]
- Jin L, Wang J, Jin H, Fei G, Zhang Y, Chen W, Zhao L, Zhao N, Sun X, Zeng M, Zhong C. Nigral iron deposition occurs across motor phenotypes of Parkinson’s disease. Eur J Neurol. 2012;19:969–976. doi: 10.1111/j.1468-1331.2011.03658.x. [DOI] [PubMed] [Google Scholar]
- Schafer A, Forstmann BU, Neumann J, Wharton S, Mietke A, Bowtell R, Turner R. Direct visualization of the subthalamic nucleus and its iron distribution using high-resolution susceptibility mapping. Hum Brain Mapp. 2012;33:2831–2842. doi: 10.1002/hbm.21404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu T, Eskreis-Winkler S, Schweitzer AD, Chen W, Kaplitt MG, Tsiouris AJ, Wang Y. Improved subthalamic nucleus depiction with quantitative susceptibility mapping. Radiology. 2013;269:216–223. doi: 10.1148/radiol.13121991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langkammer C, Schweser F, Krebs N, et al. Quantitative susceptibility mapping (QSM) as a means to measure brain iron? A post mortem validation study. NeuroImage. 2012;62:1593–1599. doi: 10.1016/j.neuroimage.2012.05.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Acosta-Cabronero J, Williams GB, Cardenas-Blanco A, Arnold RJ, Lupson V, Nestor PJ. In vivo quantitative susceptibility mapping (QSM) in Alzheimer’s disease. PloS One. 2013;8:e81093. doi: 10.1371/journal.pone.0081093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okun MS. Deep-brain stimulation for Parkinson’s disease. N Engl J Med. 2012;367:10. doi: 10.1056/NEJMct1208070. [DOI] [PubMed] [Google Scholar]
- Fox SH, Katzenschlager R, Lim SY, Ravina B, Seppi K, Coelho M, Poewe W, Rascol O, Goetz CG, Sampaio C. The Movement Disorder Society Evidence-Based Medicine Review Update: treatments for the motor symptoms of Parkinson’s disease. Mov Disord. 2011;26(suppl 3):S2–S41. doi: 10.1002/mds.23829. [DOI] [PubMed] [Google Scholar]
- Bronstein JM, Tagliati M, Alterman RL, et al. Deep brain stimulation for Parkinson disease: an expert consensus and review of key issues. Arch Neurol. 2011;68:165. doi: 10.1001/archneurol.2010.260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deuschl G, Schade-Brittinger C, Krack P, et al. A randomized trial of deep-brain stimulation for Parkinson’s disease. N Engl J Med. 2006;355:896–908. doi: 10.1056/NEJMoa060281. [DOI] [PubMed] [Google Scholar]
- Burchiel KJ, McCartney S, Lee A, Raslan AM. Accuracy of deep brain stimulation electrode placement using intraoperative computed tomography without microelectrode recording. J Neurosurg. 2013;119:301–306. doi: 10.3171/2013.4.JNS122324. [DOI] [PubMed] [Google Scholar]
- Holl EM, Petersen EA, Foltynie T, Martinez-Torres I, Limousin P, Hariz MI, Zrinzo L. Improving targeting in image-guided frame-based deep brain stimulation. Neurosurgery. 2010;67(suppl operative 2):437–447. doi: 10.1227/NEU.0b013e3181f7422a. [DOI] [PubMed] [Google Scholar]
- Kelman C, Ramakrishnan V, Davies A, Holloway K. Analysis of stereotactic accuracy of the Cosman-Robert-Wells frame and nexframe frameless systems in deep brain stimulation surgery. Stereotact Funct Neurosurg. 2010;88:288–295. doi: 10.1159/000316761. [DOI] [PubMed] [Google Scholar]
- Balachandran R, Welch EB, Dawant BM, Fitzpatrick JM. Effect of MR distortion on targeting for deep-brain stimulation. IEEE Trans Biomed Eng. 2010;57:1729–1735. doi: 10.1109/TBME.2010.2043675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- D’Haese PF, Pallavaram S, Konrad PE, Neimat J, Fitzpatrick JM, Dawant BM. Clinical accuracy of a customized stereotactic platform for deep brain stimulation after accounting for brain shift. Stereotact Funct Neurosurg. 2010;88:81–87. doi: 10.1159/000271823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zrinzo L, van Hulzen AL, Gorgulho AA, Limousin P, Staal MJ, De Salles AA, Hariz MI. Avoiding the ventricle: a simple step to improve accuracy of anatomical targeting during deep brain stimulation. J Neurosurg. 2009;110:1283–1290. doi: 10.3171/2008.12.JNS08885. [DOI] [PubMed] [Google Scholar]
- Hamid NA, Mitchell RD, Mocroft P, Westby GW, Milner J, Pall H. Targeting the subthalamic nucleus for deep brain stimulation: technical approach and fusion of pre- and postoperative MR images to define accuracy of lead placement. J Neurol Neurosurg Psychiatry. 2005;76:409–414. doi: 10.1136/jnnp.2003.032029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simon SL, Douglas P, Baltuch GH, Jaggi JL. Error analysis of MRI and leksell stereotactic frame target localization in deep brain stimulation surgery. Stereotact Funct Neurosurg. 2005;83:1–5. doi: 10.1159/000083861. [DOI] [PubMed] [Google Scholar]
- Ferroli P, Franzini A, Marras C, Maccagnano E, D’Incerti L, Broggi G. A simple method to assess accuracy of deep brain stimulation electrode placement: pre-operative stereotactic CT + postoperative MR image fusion. Stereotact Funct Neurosurg. 2004;82:14–19. doi: 10.1159/000076655. [DOI] [PubMed] [Google Scholar]
- Shahlaie K, Larson PS, Starr PA. Intraoperative computed tomography for deep brain stimulation surgery: technique and accuracy assessment. Neurosurgery. 2011;68(suppl operative 1):114–124. doi: 10.1227/NEU.0b013e31820781bc. ; discussion 124. [DOI] [PubMed] [Google Scholar]
- Caire F, Gantois C, Torny F, Ranoux D, Maubon A, Moreau JJ. Intraoperative use of the Medtronic O-arm for deep brain stimulation procedures. Stereotact Funct Neurosurg. 2010;88:109–114. doi: 10.1159/000280823. [DOI] [PubMed] [Google Scholar]
- Fiegele T, Feuchtner G, Sohm F, Bauer R, Anton JV, Gotwald T, Twerdy K, Eisner W. Accuracy of stereotactic electrode placement in deep brain stimulation by intraoperative computed tomography. Parkinsonism Relat Disord. 2008;14:595–599. doi: 10.1016/j.parkreldis.2008.01.008. [DOI] [PubMed] [Google Scholar]
- Videen TO, Campbell MC, Tabbal SD, Karimi M, Hershey T, Perlmutter JS. Validation of a fiducial-based atlas localization method for deep brain stimulation contacts in the area of the subthalamic nucleus. J Neurosci Methods. 2008;168:275–281. doi: 10.1016/j.jneumeth.2007.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guridi J, Rodriguez-Oroz MC, Lozano AM, Moro E, Albanese A, Nuttin B, Gybels J, Ramos E, Obeso JA. Targeting the basal ganglia for deep brain stimulation in Parkinson’s disease. Neurology. 2000;55(suppl 6):S21–S28. [PubMed] [Google Scholar]
- Kerl HU, Gerigk L, Pechlivanis I, Al-Zghloul M, Groden C, Nolte I. The subthalamic nucleus at 3.0 Tesla: choice of optimal sequence and orientation for deep brain stimulation using a standard installation protocol: clinical article. J Neurosurg. 2012;117:1155–1165. doi: 10.3171/2012.8.JNS111930. [DOI] [PubMed] [Google Scholar]
- Abosch A, Yacoub E, Ugurbil K, Harel N. An assessment of current brain targets for deep brain stimulation surgery with susceptibility-weighted imaging at 7 tesla. Neurosurgery. 2010;67:1745–1756. doi: 10.1227/NEU.0b013e3181f74105. ; discussion 1756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cho ZH, Min HK, Oh SH, Han JY, Park CW, Chi JG, Kim YB, Paek SH, Lozano AM, Lee KH. Direct visualization of deep brain stimulation targets in Parkinson disease with the use of 7-Tesla magnetic resonance imaging. J Neurosurg. 2010;113:639–647. doi: 10.3171/2010.3.JNS091385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shah RS, Chang SY, Min HK, Cho ZH, Blaha CD, Lee KH. Deep brain stimulation: technology at the cutting edge. J Clin Neurol. 2010;6:167–182. doi: 10.3988/jcn.2010.6.4.167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Gorman RL, Shmueli K, Ashkan K, Samuel M, Lythgoe DJ, Shahidiani A, Wastling SJ, Footman M, Selway RP, Jarosz J. Optimal MRI methods for direct stereotactic targeting of the subthalamic nucleus and globus pallidus. Eur Radiol. 2011;21:130–136. doi: 10.1007/s00330-010-1885-5. [DOI] [PubMed] [Google Scholar]
- Deistung A, Schafer A, Schweser F, Biedermann U, Turner R, Reichenbach JR. Toward in vivo histology: a comparison of quantitative susceptibility mapping (QSM) with magnitude-, phase-, and R2*-imaging at ultra-high magnetic field strength. Neuroimage. 2013;65:299–314. doi: 10.1016/j.neuroimage.2012.09.055. [DOI] [PubMed] [Google Scholar]
- Liu T, Spincemaille P, de Rochefort L, Wong R, Prince M, Wang Y. Unambiguous identification of superparamagnetic iron oxide particles through quantitative susceptibility mapping of the nonlinear response to magnetic fields. Magn Reson Imaging. 2010;28:1383–1389. doi: 10.1016/j.mri.2010.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wong R, Chen X, Wang Y, Hu X, Jin MM. Visualizing and quantifying acute inflammation using ICAM-1 specific nanoparticles and MRI quantitative susceptibility mapping. Ann Biomed Eng. 2012;40:1328–1338. doi: 10.1007/s10439-011-0482-3. [DOI] [PubMed] [Google Scholar]
- Wang Y, Johnston DL, Breen JF, Huston J, 3rd, Jack CR, Julsrud PR, Kiely MJ, King BF, Riederer SL, Ehman RL. Dynamic MR digital subtraction angiography using contrast enhancement, fast data acquisition, and complex subtraction. Magn Reson Med. 1996;36:551–556. doi: 10.1002/mrm.1910360408. [DOI] [PubMed] [Google Scholar]
- Donahue KM, Weisskoff RM, Burstein D. Water diffusion and exchange as they influence contrast enhancement. J Magn Reson Imaging. 1997;7:102–110. doi: 10.1002/jmri.1880070114. [DOI] [PubMed] [Google Scholar]
- Roberts TP. Physiologic measurements by contrast-enhanced MR imaging: expectations and limitations. J Magn Reson Imaging. 1997;7:82–90. doi: 10.1002/jmri.1880070112. [DOI] [PubMed] [Google Scholar]
- Schabel MC, Parker DL. Uncertainty and bias in contrast concentration measurements using spoiled gradient echo pulse sequences. Phys Med Biol. 2008;53:2345–2373. doi: 10.1088/0031-9155/53/9/010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stanisz GJ, Henkelman RM. Gd-DTPA relaxivity depends on macromolecular content. Magn Reson Med. 2000;44:665–667. doi: 10.1002/1522-2594(200011)44:5<665::aid-mrm1>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]
- Bowen CV, Zhang X, Saab G, Gareau PJ, Rutt BK. Application of the static dephasing regime theory to superparamagnetic iron-oxide loaded cells. Magn Reson Med. 2002;48:52–61. doi: 10.1002/mrm.10192. [DOI] [PubMed] [Google Scholar]
- Terreno E, Geninatti Crich S, Belfiore S, Biancone L, Cabella C, Esposito G, Manazza AD, Aime S. Effect of the intracellular localization of a Gd-based imaging probe on the relaxation enhancement of water protons. Magn Reson Med. 2006;55:491–497. doi: 10.1002/mrm.20793. [DOI] [PubMed] [Google Scholar]
- Zurkiya O, Chan AW, Hu X. MagA is sufficient for producing magnetic nanoparticles in mammalian cells, making it an MRI reporter. Magn Reson Med. 2008;59:1225–1231. doi: 10.1002/mrm.21606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauffer RB. Magnetic resonance contrast media: principles and progress. Magn Reson Q. 1990;6:65–84. [PubMed] [Google Scholar]
- Kirsch JE. Basic principles of magnetic resonance contrast agents. Top Magn Reson Imaging. 1991;3:1–18. [PubMed] [Google Scholar]
- Toth E, Helm L, Merbach A. Relaxivity of MRI contrast agents. Contrast agents I. Topics in current chemistry, volume 221. Berlin, Germany: Springer; 2002. pp. 61–101. [Google Scholar]
- Xu B, Spincemaille P, Chen G, Agrawal M, Nguyen TD, Prince MR, Wang Y. Fast 3D contrast enhanced MRI of the liver using temporal resolution acceleration with constrained evolution reconstruction. Magn Reson Med. 2013;69:370–381. doi: 10.1002/mrm.24253. [DOI] [PubMed] [Google Scholar]
- Bonekamp D, Li X, Leigh R, Van Zijl PC, Barker PB. Proceedings of the 21st Annual Meeting of ISMRM, Salt Lake City. Utah, USA: 2013. Optimized processing of quantitative susceptibility mapping-based gadolinium perfusion MRI: correction of bulk susceptibility effects and comparison of arterial input function selection from deltaR2* and QSM data; p. 0585. [Google Scholar]
- Hammond KE, Metcalf M, Carvajal L, Okuda DT, Srinivasan R, Vigneron D, Nelson SJ, Pelletier D. Quantitative in vivo magnetic resonance imaging of multiple sclerosis at 7 Tesla with sensitivity to iron. Ann Neurol. 2008;64:707–713. doi: 10.1002/ana.21582. [DOI] [PubMed] [Google Scholar]
- Haacke EM, Makki M, Ge Y, et al. Characterizing iron deposition in multiple sclerosis lesions using susceptibility weighted imaging. J Magn Reson Imaging. 2009;29:537–544. doi: 10.1002/jmri.21676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagemeier J, Heininen-Brown M, Poloni GU, et al. Iron deposition in multiple sclerosis lesions measured by susceptibility-weighted imaging filtered phase: a case control study. J Magn Reson Imaging. 2012;36:73–83. doi: 10.1002/jmri.23603. [DOI] [PubMed] [Google Scholar]
- Eissa A, Lebel RM, Korzan JR, Zavodni AE, Warren KG, Catz I, Emery DJ, Wilman AH. Detecting lesions in multiple sclerosis at 4.7 tesla using phase susceptibility-weighting and T2-weighting. J Magn Reson Imaging. 2009;30:737–742. doi: 10.1002/jmri.21926. [DOI] [PubMed] [Google Scholar]
- Walsh AJ, Lebel RM, Eissa A, et al. Multiple sclerosis: validation of MR imaging for quantification and detection of iron. Radiology. 2013;267:531–542. doi: 10.1148/radiol.12120863. [DOI] [PubMed] [Google Scholar]
- Khalil M, Langkammer C, Ropele S, et al. Determinants of brain iron in multiple sclerosis: a quantitative 3T MRI study. Neurology. 2011;77:1691–1697. doi: 10.1212/WNL.0b013e318236ef0e. [DOI] [PubMed] [Google Scholar]
- Habib CA, Liu M, Bawany N, Garbern J, Krumbein I, Mentzel HJ, Reichenbach J, Magnano C, Zivadinov R, Haacke EM. Assessing abnormal iron content in the deep gray matter of patients with multiple sclerosis versus healthy controls. AJNR Am J Neuroradiol. 2012;33:252–258. doi: 10.3174/ajnr.A2773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao B, Bagnato F, Matsuura E, Merkle H, van Gelderen P, Cantor FK, Duyn JH. Chronic multiple sclerosis lesions: characterization with high-field-strength MR imaging. Radiology. 2012;262:206–215. doi: 10.1148/radiol.11110601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bagnato F, Hametner S, Yao B, van Gelderen P, Merkle H, Cantor FK, Lassmann H, Duyn JH. Tracking iron in multiple sclerosis: a combined imaging and histopathological study at 7 Tesla. Brain. 2011;134:3602–3615. doi: 10.1093/brain/awr278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langkammer C, Liu T, Khalil M, Enzinger C, Jehna M, Fuchs S, Fazekas F, Wang Y, Ropele S. Quantitative susceptibility mapping in multiple sclerosis. Radiology. 2013;267:551–559. doi: 10.1148/radiol.12120707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Al-Radaideh AM, Wharton SJ, Lim SY, Tench CR, Morgan PS, Bowtell RW, Constantinescu CS, Gowland PA. Increased iron accumulation occurs in the earliest stages of demyelinating disease: an ultra-high field susceptibility mapping study in clinically isolated syndrome. Mult Scler. 2013;19:896–903. doi: 10.1177/1352458512465135. [DOI] [PubMed] [Google Scholar]
- Chen W, Gauthier SA, Gupta A, Comunale J, Liu T, Wang S, Pei M, Pitt D, Wang Y. Quantitative susceptibility mapping of multiple sclerosis lesions at various ages. Radiology. 2014;271:183–192. doi: 10.1148/radiol.13130353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yablonskiy DA, Luo J, Sukstanskii AL, Iyer A, Cross AH. Biophysical mechanisms of MRI signal frequency contrast in multiple sclerosis. Proc Natl Acad Sci U S A. 2012;109:14212–14217. doi: 10.1073/pnas.1206037109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiggermann V, Hernandez Torres E, Vavasour IM, Moore GR, Laule C, Mackay AL, Li DK, Traboulsee A, Rauscher A. Magnetic resonance frequency shifts during acute MS lesion formation. Neurology. 2013;81:211–218. doi: 10.1212/WNL.0b013e31829bfd63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dixon WT. Simple proton spectroscopic imaging. Radiology. 1984;153:189–194. doi: 10.1148/radiology.153.1.6089263. [DOI] [PubMed] [Google Scholar]
- Reeder SB, Wen Z, Yu H, Pineda AR, Gold GE, Markl M, Pelc NJ. Multicoil Dixon chemical species separation with an iterative least-squares estimation method. Magn Reson Med. 2004;51:35–45. doi: 10.1002/mrm.10675. [DOI] [PubMed] [Google Scholar]
- Yu H, Reeder SB, Shimakawa A, Brittain JH, Pelc NJ. Field map estimation with a region growing scheme for iterative 3-point water-fat decomposition. Magn Reson Med. 2005;54:1032–1039. doi: 10.1002/mrm.20654. [DOI] [PubMed] [Google Scholar]
- Hernando D, Haldar JP, Sutton BP, Ma J, Kellman P, Liang ZP. Joint estimation of water/fat images and field inhomogeneity map. Magn Reson Med. 2008;59:571–580. doi: 10.1002/mrm.21522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernando D, Kellman P, Haldar JP, Liang ZP. Robust water/fat separation in the presence of large field inhomogeneities using a graph cut algorithm. Magn Reson Med. 2010;63:79–90. doi: 10.1002/mrm.22177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yablonskiy DA, Sukstanskii AL, Luo J, Wang X. Voxel spread function method for correction of magnetic field inhomogeneity effects in quantitative gradient-echo-based MRI. Magn Reson Med. 2013;70:1283–1292. doi: 10.1002/mrm.24585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duyn JH, van Gelderen P, Li TQ, de Zwart JA, Koretsky AP, Fukunaga M. High-field MRI of brain cortical substructure based on signal phase. Proc Natl Acad Sci U S A. 2007;104:11796–11801. doi: 10.1073/pnas.0610821104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhong K, Leupold J, von Elverfeldt D, Speck O. The molecular basis for gray and white matter contrast in phase imaging. Neuroimage. 2008;40:1561–1566. doi: 10.1016/j.neuroimage.2008.01.061. [DOI] [PubMed] [Google Scholar]
- He X, Yablonskiy DA. Biophysical mechanisms of phase contrast in gradient echo MRI. Proc Natl Acad Sci U S A. 2009;106:13558–13563. doi: 10.1073/pnas.0904899106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Gelderen P, de Zwart JA, Lee J, Sati P, Reich DS, Duyn JH. Nonexponential T(2) decay in white matter. Magn Reson Med. 2012;67:110–117. doi: 10.1002/mrm.22990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wharton S, Bowtell R. Fiber orientation-dependent white matter contrast in gradient echo MRI. Proc Natl Acad Sci U S A. 2012;109:18559–18564. doi: 10.1073/pnas.1211075109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sati P, van Gelderen P, Silva AC, Reich DS, Merkle H, de Zwart JA, Duyn JH. Micro-compartment specific T2* relaxation in the brain. Neuroimage. 2013;77:268–278. doi: 10.1016/j.neuroimage.2013.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dibb R, Li W, Cofer G, Liu C. Microstructural origins of gadolinium-enhanced susceptibility contrast and anisotropy. Magn Reson Med. 2014;72:1702–1711. doi: 10.1002/mrm.25082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu C, Li W. Imaging neural architecture of the brain based on its multipole magnetic response. Neuroimage. 2013;67:193–202. doi: 10.1016/j.neuroimage.2012.10.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen WC, Foxley S, Miller KL. Detecting microstructural properties of white matter based on compartmentalization of magnetic susceptibility. Neuroimage. 2013;70:1–9. doi: 10.1016/j.neuroimage.2012.12.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bakker CJ, Seppenwoolde JH, Vincken KL. Dephased MRI. Magn Reson Med. 2006;55:92–97. doi: 10.1002/mrm.20733. [DOI] [PubMed] [Google Scholar]
- Sukstanskii AL, Yablonskiy DA. On the role of neuronal magnetic susceptibility and structure symmetry on gradient echo MR signal formation. Magn Reson Med. 2014;71:345–353. doi: 10.1002/mrm.24629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu C. Susceptibility tensor imaging. Magn Reson Med. 2010;63:1471–1477. doi: 10.1002/mrm.22482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wisnieff C, Liu T, Spincemaille P, Wang S, Zhou D, Wang Y. Magnetic susceptibility anisotropy: cylindrical symmetry from macroscopically ordered anisotropic molecules and accuracy of MRI measurements using few orientations. Neuroimage. 2013;70:363–376. doi: 10.1016/j.neuroimage.2012.12.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X, Vikram DS, Lim IA, Jones CK, Farrell JA, van Zijl PC. Mapping magnetic susceptibility anisotropies of white matter in vivo in the human brain at 7 T. Neuroimage. 2012;62:314–330. doi: 10.1016/j.neuroimage.2012.04.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu C, Li W, Wu B, Jiang Y, Johnson GA. 3D fiber tractography with susceptibility tensor imaging. Neuroimage. 2012;59:1290–1298. doi: 10.1016/j.neuroimage.2011.07.096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee J, Shmueli K, Fukunaga M, van Gelderen P, Merkle H, Silva AC, Duyn JH. Sensitivity of MRI resonance frequency to the orientation of brain tissue microstructure. Proc Natl Acad Sci U S A. 2010;107:5130–5135. doi: 10.1073/pnas.0910222107. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Information.