Abstract
We estimate the trend in the transitory variance of male earnings in the U.S. using the Michigan Panel Study of Income Dynamics from 1970 to 2004. Using an error components model and simpler but only approximate methods, we find that the transitory variance started to increase in the early 1970s, continued to increase through the mid-1980s, and then remained at this new higher level through the 1990s and beyond. Thus the increase mostly occurred about thirty years ago. Its increase accounts for between 31 and 49 percent of the total rise in cross-sectional variance, depending on the time period.
I. Introduction
A substantial literature has accumulated on trends in various measures of instability in individual earnings and family income in the US over the last thirty or so years, with many studies finding increases in instability (Gottschalk and Moffitt 1994; Moffitt and Gottschalk 1995; Dynarski and Gruber 1997; Cameron and Tracy 1998; Haider 2001; Hyslop 2001; Stevens 2001; Moffitt and Gottschalk 2002; Dynan et al. 2008; Keys 2008; Jensen and Shore 2010; Shin and Solon 2010). Increases have also been found in Canada (Baker and Solon 2003; Beach et al. 2003; Beach et al. 2010; Ostrovsky 2010) and the U.K. (Dickens 2000). Interest in trends in instability, particularly instability that comes from an increase in the transitory variance of earnings, has arisen for many reasons. One reason is that Friedman (1957) argued in his classic treatise that transitory fluctuations should have little or no impact on consumption. A massive literature over the subsequent five decades has followed, showing that consumption and saving respond differently to permanent and transitory changes in income (Attanasio and Weber 2010). A recent contribution by Blundell, Pistaferri, and Preston (2008), for example, argues that considerable consumption smoothing takes place in response to transitory shocks but much less for permanent shocks. A second, more normative reason for interest in transitory variance is that shocks which cannot be smoothed generally impose welfare losses and, given the evidence that transitory fluctuations are more easily smoothed than permanent shocks, welfare losses are presumably smaller, the greater relative importance of transitory shocks compared to permanent ones. Third, and relatedly, many students of inequality have long noted that transitory shocks have little impact on the inequality of lifetime incomes, whereas permanent shocks do. This has normative implications for inequality (Atkinson and Bourguignon 1982; Cowell 2000; Gottschalk and Spolaore 2002; Sen 2000). Fourth, a literature which assumes that social welfare depends on whether it is possible for individuals to change their rank in the income distribution over their lifetimes argues that increases in the variance of permanent shocks, which move individuals farther apart in the distribution and hence makes changes in rank less likely are social-welfare-detracting. In contrast, transitory changes in income, which mix up the distribution and result in more changes in rank are social-welfare-improving (Shorrocks 1978; Gottschalk and Spolaore 2002).
A purely labor economics motivation for an interest in distinguishing permanent from transitory shocks relates to the well-known increase in cross-sectional inequality (Katz and Autor 1999). By definition, an increase in cross-sectional inequality has to arise from an increase in permanent shocks, transitory shocks, or both. The literature has put forth explanations for this trend in inequality (for example, skill-biased technical change) which all assume that permanent shocks have generated the cross-sectional increase, yet, statistically, a rising cross-sectional variance could also result from an increase in the transitory variance. Explanations for rising transitory variance are likely to be quite different. For example, the increase in the transitory variance could have been caused by an increase in product or labor market competitiveness, a decline in regulation and administered prices, a decline in union strength, increases in temporary work or contracting-out or self-employment, and similar factors. In addition, insofar as transitory fluctuations are more easily insured against than permanent fluctuations, as just noted, the welfare losses from increases in cross-sectional inequality might be smaller than would otherwise be supposed if transitory fluctuations have been an important source of the increase in cross-sectional inequality.
This paper reports new estimates of the trend in the transitory variance of male earnings in the U.S. over the period 1970–2004. We use several methods to estimate trends in transitory variances. The first is a formal error components model that is an extension of the model originally developed by Moffitt and Gottschalk (1995), but here adding several features that have since gained prominence in the literature. This is our preferred method since findings from this explicit statistical model map directly into well-defined statistical concepts of permanent and transitory variation. But we also use two simpler methods, one an extension of the method originally suggested by Gottschalk and Moffitt (1994) and the other a new nonparametric method that provides consistent estimates of the transitory variance while making weak assumptions about the structure of the earnings process. These two methods relax some of the strong parametric assumptions made in the error components model but at the cost of providing only approximate estimates. All three methods show rising transitory variances from the 1970s to the 1980s and a leveling off in the 1990s. Some ambiguity attaches to the precise dates at which the variance rises, and at which it levels off, as a result of cyclical events—which have a significant impact on transitory variances—that occur around the major turning points.
The first section briefly gives the intuition for how trends in transitory variances are identified with a panel data set. The next section describes the data set we construct and the third section lays out our methods and results. We then provide a section that compares our results to others in the literature and provides potential explanations for differences in findings. A brief summary concludes.
II. Identification of Trends in Transitory Variances
The intuition for identification of trends in a transitory variance can be seen from the canonical error components model with permanent and transitory components:
| (1) |
where yit is log earnings or residual log earnings for individual i at age t, μit is a time-invariant, permanent individual component, and νit is a transitory component. The typical assumptions are that E(μi) = E(νit) = E(μiνit) = 0, and . Identification and estimation of this basic random effects model has been known since the 1960s. However, typically these models assume E(νit νiτ) = 0 for t ≠ τ but this has been shown not to hold in most earnings applications. When it does not hold, identification is less obvious. Carroll (1992) was, to our knowledge, the first to point out explicitly that identification in this case can be obtained from “long” autocovariances. The covariance of yit between periods τ apart is
| (2) |
and hence is identified from Cov(yit, yi,t−τ), which is observed in the data, provided that Cov(νit, νi,t−τ) = 0.1 But Cov(νit, νi,t−τ) = 0 is essentially the definition of a transitory component in the first place, because this covariance represents the persistence of such a component--that is, whether a transitory shock at time t-τ is still present, even in reduced magnitude, by time t. If the definition of a transitory component is something that eventually goes away, the permanent variance must be identified at sufficiently high values of τ (more on this below).
Once the permanent variance is identified, the transitory variance is identified as the residual:
| (3) |
because Var(yit) is observed in the data. This exercise can be conducted in different calendar periods, thereby revealing whether transitory variances are changing.
This method of identification of permanent and transitory variances from the long autocovariances of yit is employed in the richer error components model as well as the nonparametric method described below. The data requirements are therefore for a sufficiently long panel which allows not only calculation of variances but also long autocovariances, and for different periods of calendar time.
III. Data
The Michigan Panel Study on Income Dynamics (PSID) satisfies these requirements, for it covers a long calendar time period (1968–2005 at the time this analysis was conducted) and, because it is a panel, we can compute autocovariances of earnings between periods quite far apart. We use the data from interview year 1971 through interview year 2005.2 Earnings are collected for the previous year, so our data cover the calendar years 1970 to 2004. The PSID skipped interviews every other year starting in interview year 1998, so our last five observations are for earnings years 1996, 1998, 2000, 2002, and 2004. The sample is restricted to male heads of households. Females are excluded in order to reduce the selection effects of the increasing number of females participating in the labor market. Only heads are included since the PSID earnings questions we use are only asked of heads of household. We take any year in which these male heads were between the ages of 30 and 59, not a student, and had positive annual wage and salary income and positive annual weeks of work. We include men in every year in which they appear in the data and satisfy these requirements. We therefore work with an unbalanced sample because of aging into and out of the sample in different years, attrition, and movements in and out of employment. Fitzgerald, Gottschalk, and Moffitt (1998) have found that attrition in the PSID has had little effect on its cross-sectional representativeness, although less is known about the effect of attrition on autocovariances. Measurement error in earnings reports is another potential problem when using survey data to estimate covariance matrices. However, Pischke (1995) has shown that measurement error in the PSID has little effect on earnings covariances and Gottschalk and Huynh (2010) show that this is a result of the non-classical structure of measurement error in earnings found in many surveys.3 We exclude men in all PSID oversamples (SEO, Latino). All earnings are put into 1996 CPI-U-RS dollars. The resulting data set has 2,883 men and 31,054 person-year observations, for an average of 10.8 year-observations per person. Means of the key variables are shown in Appendix Table 1––1.
Rather than form a variance-autocovariance matrix directly from these earnings observations, we work with residuals from regressions of log earnings on education, race, a polynomial in age, and interactions among these variables, all estimated separately by calendar year. Our analysis, therefore, estimates the transitory component of the within group variance of log earnings. We use these residuals to form a variance-autocovariance matrix indexed by year, age, and lag length. Thus, a typical element consists of the covariance between residual log earnings of men at ages a and a′ between years t and t′. Because of sample size limitations, however, we cannot construct such covariances by single years of age. Instead, we group the observations into three age groups--30–39, 40–49, and 50–59--and then construct the variances for each age group in each year, as well as the autocovariances for each group at all possible lags back to 1970 or age 20, whichever comes first. We then compute the covariance between the residual log earnings of the group in the given year and each lagged year, using the individuals who are in common in the two years (when constructing these covariances, we trim the top and bottom one percent of the residuals within age-education-year cells to eliminate outliers and top-coded observations4). The resulting autocovariance matrix represents every individual variance and covariance between every pair of years only once, and stratifies by age so that life cycle changes in the variances of permanent and transitory earnings can be estimated (the human capital literature has shown that there are life cycle patterns in earnings variances). The covariance matrix has 1,197 elements over all years, ages, and lag lengths. A few specimen elements are illustrated in Appendix Table 1–2.
After presenting our main results, we will report the results of sensitivity tests to a number of the more important of these data construction decisions.
IV. Models and Results
We present results on trends in transitory variances from three models: a parametric error components model; an approximate nonparametric implementation of that model; and an even simpler method used originally by Gottschalk and Moffitt (1994) which also only approximates the variances of interest.
A. Error Components Model
We first formulate an error components (EC) model of life cycle earnings dynamics process in the absence of calendar time shifts. There is a large literature on the formulation of such models (Hause 1977; Lillard and Willis 1978; Lillard and Weiss 1979; Hause 1980; MaCurdy 1982; Abowd and Card 1989; Baker 1997; Geweke and Keane 2000; Meghir and Pistaferri 2004; Guvenen 2009; see MaCurdy 2007 for a review). These models have suggested that the permanent component is not fixed over the life cycle but evolves, typically with variances and covariances rising with age. This pattern can be captured by a random walk or random growth process in the permanent effect. The literature has also shown that the transitory error is serially correlated, usually by a low-order autoregressive moving-average (ARMA) process. Our model contains all these features:
| (4) |
| (5) |
| (6) |
with E(μia) = E(δi) = E(ωia) = E(ζia) = 0, orthogonality between all four of these errors, and initial conditions μi0 ≠ 0, νi0 = 0 (the life cycle begins at a=1). Equation 4 again posits a permanent-transitory model but with an age-varying permanent effect (μia). The latter evolves over the life cycle from a random growth factor (δi) which allows each individual to have a permanently higher or lower growth rate than that of other individuals, and from a random walk factor (ωia) that arrives randomly but is a permanent shock in the sense that it does not fade out over time as the individual ages. The transitory error evolves according to a ARMA(1,1) process typically found in the literature, with the underlying transitory shock (ξia) fading out at rate ρ but deviating from that smooth fade-out rate by θ in the next period (the MA(1) parameter θ improves the fit of the lag process significantly). Our tests also show, consistent with other findings in the literature, that higher order ARMA parameters are not statistically significant. We assume all forcing errors to be i.i.d. except ξia, whose variance we assume to vary with age because transitory shocks are likely to be greater at younger ages. We allow μi0 and δi to be correlated in light of the Mincerian theory that they should be negatively related (those who have higher initial investments in human capital will start off low but rise at a faster rate). Hence and E(μi0δi) = σμδ. An important point to note is that, in this more realistic model, compared to the simple canonical model outlined previously, transitory shocks never completely fade out because of the AR(1) process, which implies that they fade out only asymptotically. Consequently, the variance of the permanent effect can never be exactly identified by the long autocovariances, as we argued it should be, above. The permanent variance (and hence the transitory variance as well) is therefore identified by extrapolation of the AR(1) curve to infinity. However, provided that ρ is not too high, the covariance will fall to a low value over the 34 years of our data, reducing the extrapolation problem to some degree.5
With this identification condition satisfied, the parameters of the model can be identified for a single cohort. Determining whether there are calendar time shifts can therefore be identified from changes in parameters across multiple cohorts, for that allows a comparison of variances and covariances at the same point in the life cycle but at different calendar time periods. Although all the parameters of the model could potentially shift with calendar time, for reasons of convenience and on the basis of past work testing for calendar-time shifts in the other parameters (Moffitt and Gottschalk 1995), we allow calendar time shifts in only two places in the model, in the permanent component and the forcing transitory component:
| (7) |
| (8) |
| (9) |
where t is calendar time. The parameter αt alters the variance of the permanent effect, which is now . This formulation coincides with an interpretation of μia as a flow of human capital services and αt as its time-varying price, consistent with the literature on changes in the returns to skill. We force it to be the same for all ages although this could be relaxed. The parameter αt likewise allows calendar time shifts in the variance of the transitory component, which is now .
The introduction of time-varying parameters introduces a problem of left-censoring because those parameters cannot be identified prior to 1970 yet their evolution prior to that year affects variances and covariances after 1970. To address this issue, we introduce an additional parameter γ which allows the transitory variances in 1970 to deviate from what they would be if βt = 1for t<1970, with γ = 0 implying no deviation. The details are given in Appendix 2.
For any set of values of the parameters, the model in (7)–(9) generates a set of predicted variances and covariances in each year and for each age and lag length, and therefore a predicted value for each of the 1,197 elements of our data covariance matrix. We estimate the parameters by minimizing the sum of squared deviations between the observed elements and elements predicted by the model, using an identity weighting matrix and computing robust standard errors. The formal statement of the model and estimating procedure appears in Appendix 2.6
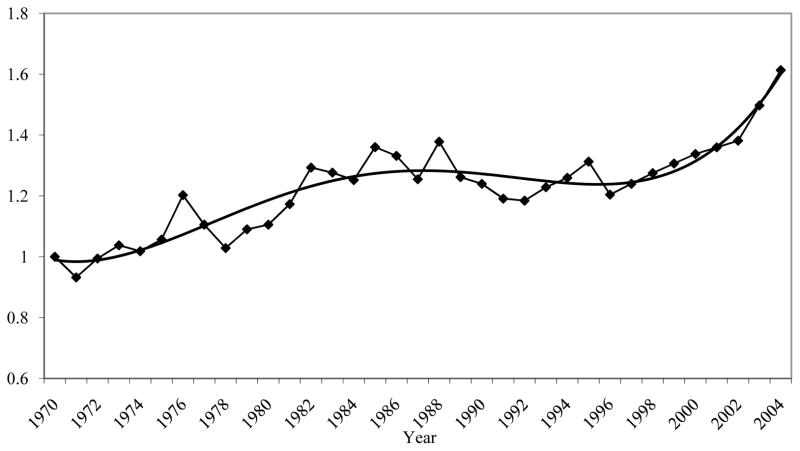
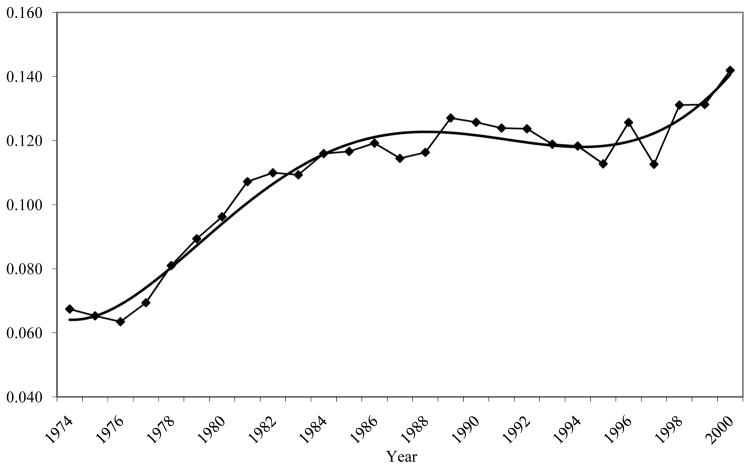
The estimates of the model parameters are given in Appendix Table 1–3. The transitory component is significantly serially correlated both through the AR(1) and MA(1) component, implying, as discussed before, that long autocovariances are needed to identify the model, and the variances of the random walk and random growth errors in the permanent component are both statistically significant; and the initial permanent and transitory components are indeed negatively correlated. However, our main interest is in the estimates of αt and βt which are shown graphically in Figures 1 and 2 along with smoothed trend lines (both are normalized to one in 1970).7 Figure 1 shows that the permanent variance rose starting in the early 1970s, continued to rise through to the mid-1980s, leveled off or declined slightly from then through the mid-1990s, and then started rising again in the mid-1990s. This pattern in within group permanent variance is roughly consistent with rises in the return to education and other indicators of skill differentials shown in the cross-sectional literature on inequality trends. This pattern reflects, as has already been emphasized and as will be shown explicitly below, trends in the long autocovariances in the data.8
Figure 1. Error Components (EC) Model Estimates of Alpha.
Notes: In this and subsequent figures, the four PSID non-interview years are interpolated from the two adjacent points. The trend line is fit from a fifth-order polynomial.
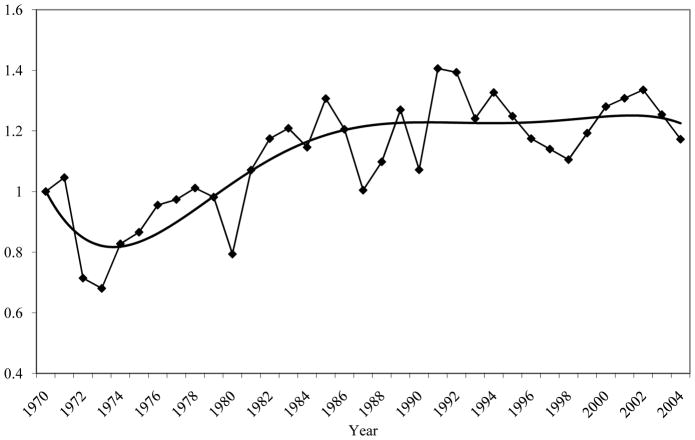
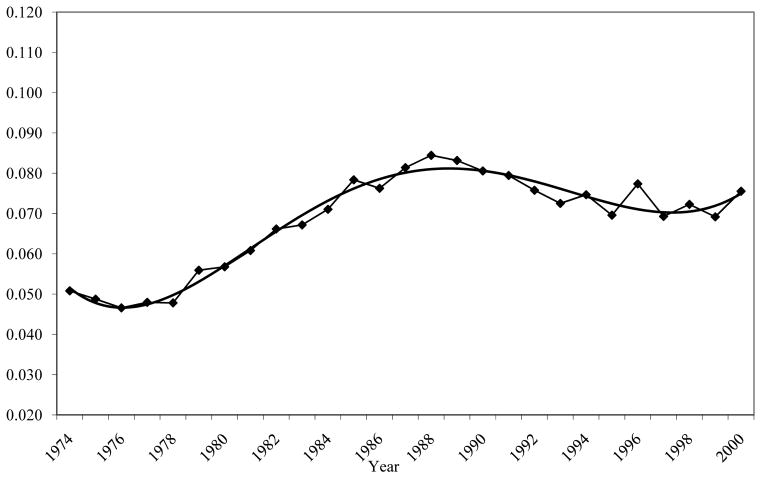
Figure 2.
Error Components (EC) Model Estimates of Beta
Of more direct interest to our focus on the transitory variance of earnings is Figure 2, which shows the estimated values of βt along with a trend line. The transitory variance rose sharply starting in the early 1970s, and then continued to rise, albeit at a slower rate, until the mid-1980s, after which time it has remained flat, although with major fluctuations (that is, it remained flat on average, as shown by the smoothed line). As we will show momentarily, recessions in the early 1980s, early 1990s, and early 2000s caused jumps in the transitory variance which prevent us from being precise about the exact dates at which some of the trends stopped rising or leveled off. Nevertheless, our general answer to the question we posed in the introduction is: the transitory variance of male earnings started to increase in the early 1970s, continued to rise through the mid-1980s, and then stabilized at a new higher level.
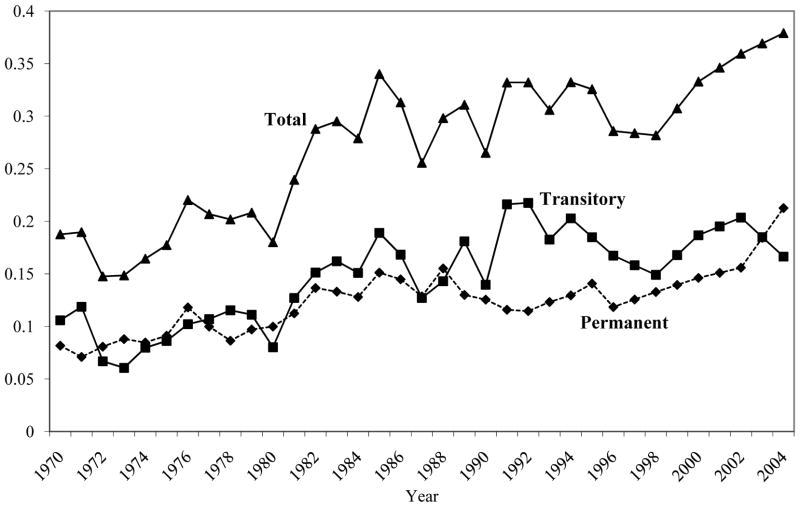
The evolution over time in the variance of the transitory component, whose formula is shown in Equation 9, is not quite the same as that of βt since the latter feeds into the transitory variance in future periods, and similarly for the permanent variance. Drawing the implications of our estimated parameters for the variances of αtμia and νiat requires applying the formulas in Appendix 2. Figure 3 shows the resulting pattern in permanent and transitory variances for those age 30–39 (the variances differ by age, but a similar time pattern obtains for other ages; plots for the other ages are available upon request). Both the permanent and transitory variances follow roughly the same pattern as αt and βt, as should be expected since these are the only calendar-time varying parameters in their formulas. From 1970 to 1984, the rise in the transitory variance accounted for 49 percent of the total rise in the cross-sectional variance, consistent with prior work on the 1980s by Gottschalk and Moffitt (1994) and Moffitt and Gottschalk (1995). However, from 1970 to 2004, it has accounted for only 31 percent of the total rise because of the increase in the permanent variance that started in the mid-1990s. In fact, all of the rise in the total variance over the last decade reflects an increase in the permanent variance. This points to a resumption in the rise in skill prices that started in the late 1970s and continued through the mid-1980s. This was followed by nearly a decade of little or no growth in the permanent variance. However, as Figure 3 shows, the permanent variance resumed its upward trend in the mid-1990s and continued through 2004.
Figure 3.
Fitted Permanent, Transitory, and Total Variances of Log Earnings Residuals, Age 30–39 (EC Model)
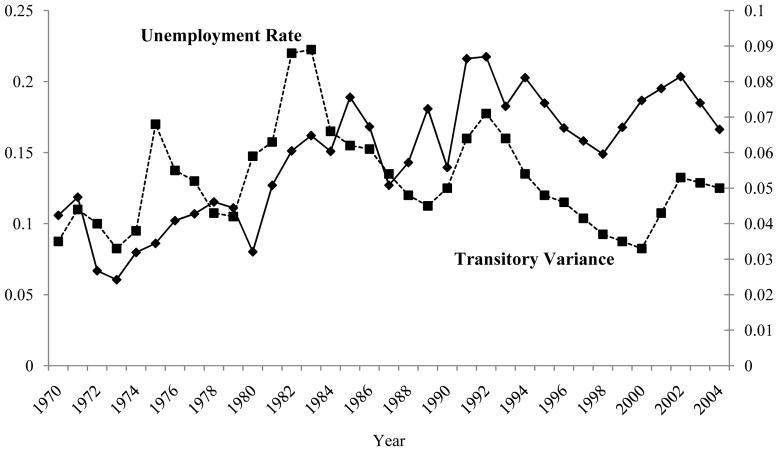
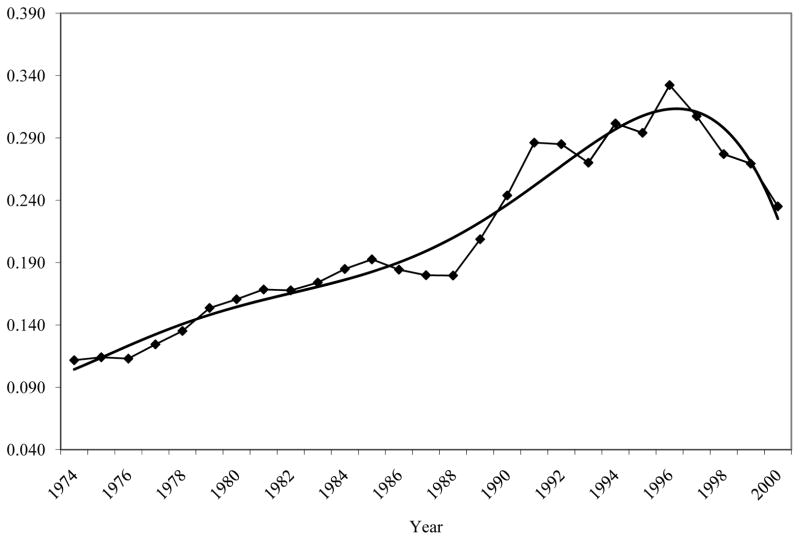
Much of the fluctuation in the transitory variance is business-cycle related. Figure 4 shows the same transitory variance but plotted along with the national unemployment rate for men 20 and over. The variance is clearly positively correlated with the unemployment rate, albeit with something of a lag in the first half of the period. The recession of the early 1980s appears to have been responsible for some of the transitory variance increase in the early 1980s, but the variance never returned to its pre-1980s levels in the late 1980s, when the unemployment had fallen. The transitory variance increase in the early 1990s appears to also have been partly business-cycle related, its decrease from the early 1990s to 1997 appears to be related to the decline in the unemployment rate (although, once again, it did not return to its former level), and the increase in the variance in the early 2000s corresponds to the recession in that period. Thus the fluctuations after approximately 1990 appear to be cyclically induced. However, the average level of the transitory variance during the decade of the 1990s was above its average level in the1980s, even the late 1980s. Thus our evidence also suggests, albeit with considerable uncertainty as to the exact timing, that the transitory variance in the 1990s may have been slightly higher than in the 1980s. Nevertheless, even if true, the size of the increase was much less than the size of the increase from the 1970s to the 1980s.
Figure 4. FittedTransitory Variance of Log Earnings Residuals forAge 30–39 (EC Model) and Unemployment Rate.
Notes: Male Unemployment Rate Age 20 and over
An important question for the credibility of these results is whether they can be demonstrated with simpler econometric methods which employ more flexible specifications of the permanent and transitory components than assumed in our parametric model. We consider two simpler methods to address this question.
B. Approximate Nonparametric Method
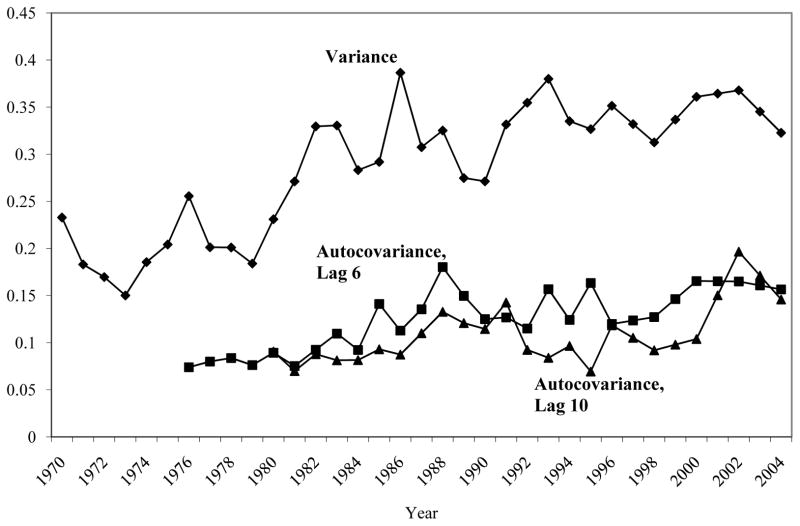
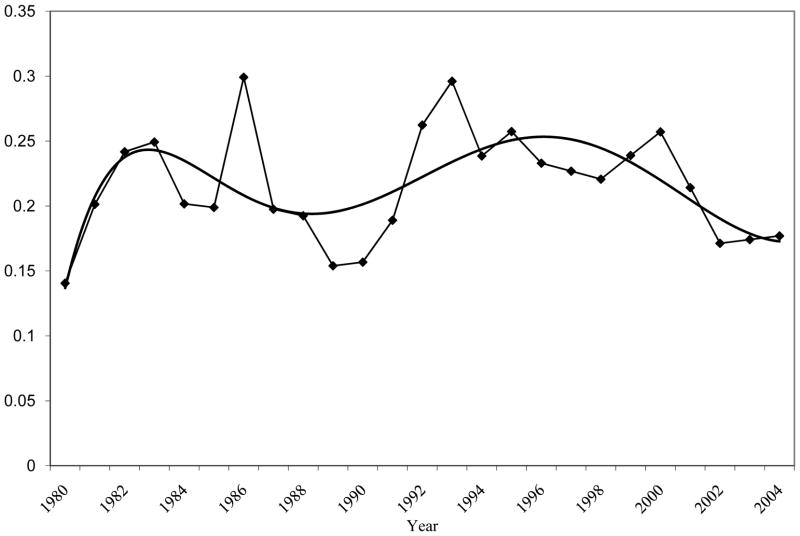
One approach is to follow the simple model described in Section I by using the long autocovariances to estimate the variance of the permanent effect and by then subtracting that value from the total variance to obtain an estimate of the transitory variance. Figure 5 shows the variance of log annual earnings residuals in each year for those 30–39, for illustration, along with the autocovariances between those residuals in each year and those in years six and ten years previous, which might be considered to be sufficiently long that the transitory shocks are no longer correlated. The figure shows this not to be the case for the lag-six autocovariance, which is above that at lag ten, indicating that the autocovariance is still falling between six and ten years previous (the lag-ten autocovariance may, of course, not be long enough either). Taking the difference between the upper line for the variance and the line for the lag-ten autocovariance results in an estimate of the transitory variance which is plotted in Figure 6 (it necessarily starts in 1980, since a ten-year lag is needed to compute it). These estimates show an increase in the transitory variance in the early 1980s followed by a reversal, and fluctuations but no clear trend over the entire period. This is quite different than the pattern shown in the EC model.
Figure 5.
Variances and Autocovariances, Age 30–39
Figure 6.
Implied Transitory Variance of Log Earnings Residuals Using 10-Lag Autocovariance, Age 30–39
However, this method has two flaws which imply that it should not be used, although we will modify it to correct these flaws. The first is that the more realistic model of the age-evolution of the permanent effect shown in Equation 4–6 with its random walk and random growth specifications implies that the relevant long autocovariance is no longer equal to the variance of the permanent component, as it was in the simple canonical model.9 The second is that the method does not work well when αt is evolving over the period covered by the long autocovariance, for in that case the autocovariance of yiat is
| (10) |
and therefore the long autocovariance will not equal because αt is changing over time. For example, Cov(yiat, yi,a−τ,t−τ) will rise at a faster rate than αt is rising if recent lagged αt−τ have also been rising. Specifically, the rise in αt in the 1970s and early 1980s shown in Figure 1 will cause later Cov(yiat, yi,a−τ,t−τ) to rise “too much,” leading to an excess decline in the transitory variance because it is obtained as the residual from subtracting Cov(yiat, yi,a−τ,t−τ) from the total variance.10
Nevertheless, Equation 10 forms a basis for a better method of applying the idea of using the long autocovariances to obtain an estimate of the permanent variance, which we term the approximate nonparametric (NP) method. Taking the logs of Equation 10, we have
| (11) |
an equation which should hold, again, if the lag order τ is high enough that the transitory errors are no longer correlated. Equation 11 can be estimated by OLS using year dummies to capture the logαt and logαt−τ and if (say) a polynomial approximation in a and τ is used to approximate log[Cov(μia, μi,a−τ)] nonparametrically. We denote that approximation as f(a,τ). The variance of the permanent component is then estimated by using the fitted Equation 11, evaluated at τ = 0.11 The influence of the lagged logαt−τ on the autocovariance is captured by the lagged year dummies. This method is nonparametric because it imposes no parametric model on the evolution of the permanent effect--random walk, random growth, or something else--with that evolution approximated by an arbitrary function of age and lag length; and because it imposes no parametric model on the evolution of the transitory component, except to assume that that component is not correlated after a sufficient length of time. But it is only approximate because the effects of past transitory shocks are never exactly zero because of the presence of the AR(1) process.
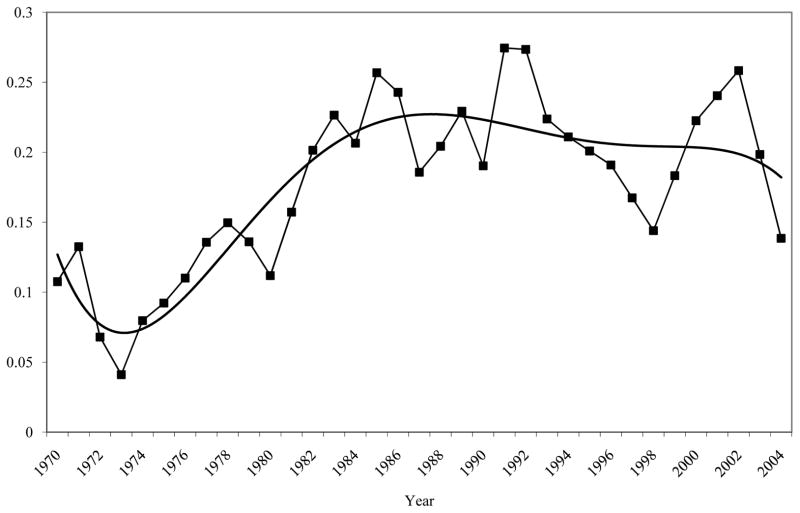
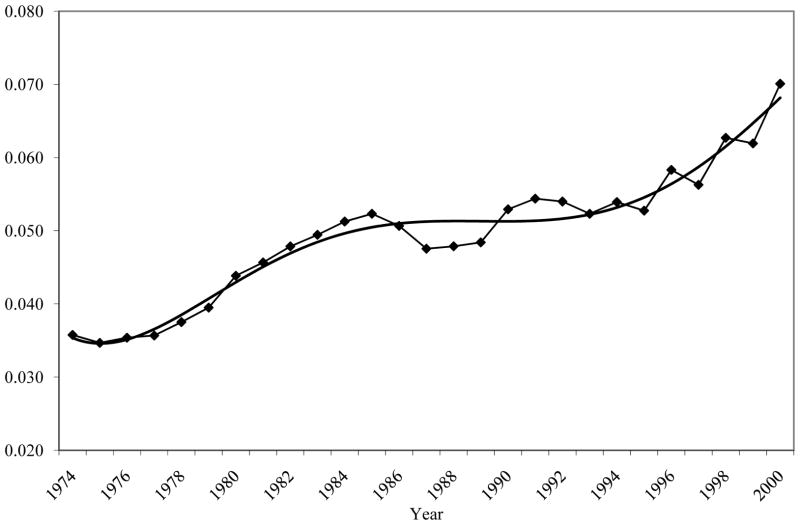
Figure 7 shows the estimates of the transitory variance obtained in this way using a second-order polynomial for a and τ for the function f(a,τ) and using all lags of order 10 and over in the regression Equation 11 (the predicted permanent variance from the fitted equation is then subtracted from the total variance). The pattern in the Figure is much closer to that obtained from the EC model, differing only in the period of the 1990s and after, when the variance indicated by the smoothed line gradually falls instead of flattening out, as the smoothed line in Figure 2 does. This latter difference is a result of the failure of the key assumption of negligible transitory autocovariance. At lag ten, that autocovariance is small but it is still trending upward (see Figure 5). The transitory autocovariance is trending upward because the transitory variances themselves are; and, because the transitory components are serially correlated, an increase in the variance of the underlying transitory shock necessarily increases all transitory autocovariances as well (see Equation 2-19). This spuriously pulls up the permanent variance when Equation 11 is estimated, pushing the transitory variance down. Nevertheless, this simple nonparametric method provides some support for the error components model by showing that approximately the same results are obtained without so much structure imposed on the autocovariance process.
Figure 7. Approximate Nonparametric (NP) Estimate of Transitory Variance of Log Earnings Residuals.
Notes: Averaged over all ages
C. Window Averaging Method
An even simpler method introduced by Gottschalk and Moffitt (1994) and applied in some subsequent studies is to estimate the permanent and transitory variances with standard random-effects formulas within moving calendar time windows of fixed length, which we denote the window averaging (WA) method.12 To estimate the transitory variance in year t, the 2w+1 residuals in the calendar time window [t−w, t+w] are averaged for each individual i to obtain an estimate of the individual’s permanent component. The difference between the residual for each individual in each year and the individual’s average residual constitutes an estimate of the transitory component. Then the textbook formulas for the random effects model are used to compute the variances of the two components.13 Repeating this process for each successive year t in the data—with a shift in the window each time--a trend in the estimated transitory variance is generated.
If the window is limited to two periods, the variance of transitory earnings computed in this way is closely related to the variance of the change in earnings (yiat − yi,a−1,t−1) between the periods. This can be seen by recognizing that when the window is limited to two periods, a transitory component calculated as the deviation of earnings in period t from the average earnings over periods t and t−1 is equal to one-half times the change in earnings between the periods. In this case the variance of transitory earnings is equal to one-quarter of the variance of the change in earnings. When the window is longer than two periods, this equivalence no longer holds.
The WA method produces consistent estimates of the transitory variance under the canonical model described in Section I because that model corresponds to the textbook random effects model whose estimator we use. However, in more general models the residuals used in the computation are not quite the right ones if the permanent and transitory components follow the more complex, serially-correlated process in our EC model. The method is also not well-suited to detecting exact turning points in trends because it averages over years. Nevertheless, it is an approximation which has the virtue of simplicity and transparency whose defects may not be quantitatively important.
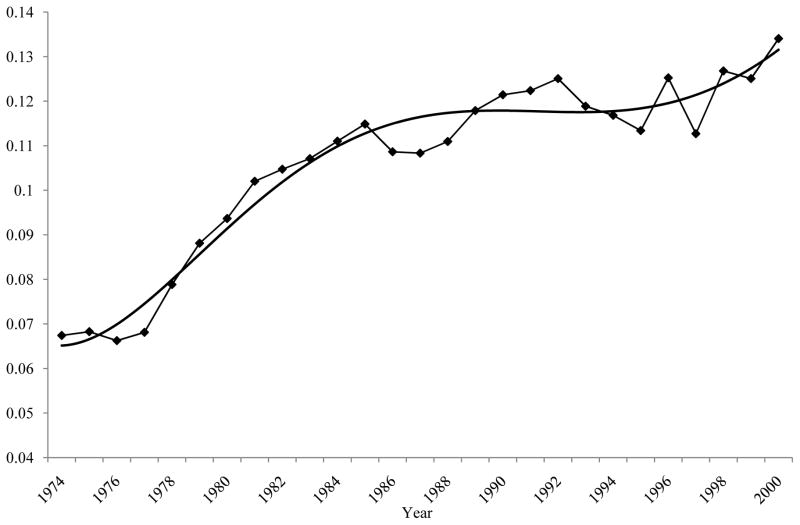
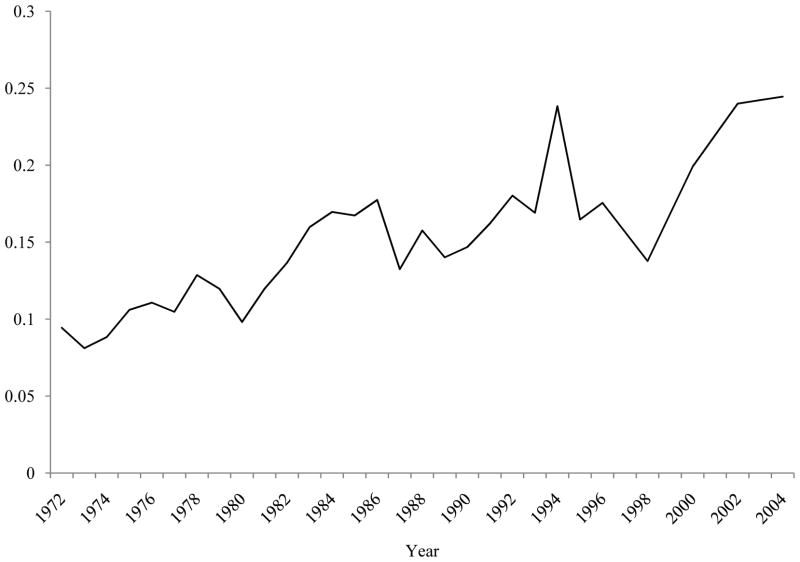
Figure 8 shows the WA estimates using a nine-year window. Thus the earliest date is 1974 and the latest is 2000 because of the requirement of four years of data on either side of the year in question. The results are quite similar to those from the EC model shown in Figure 4 and the NP model shown in Figure 7, rising from the 1970s to the 1980s and leveling off around 1990, a bit later than in the other methods but not drastically so. The variance turns up at the end, for the year 2000 window, but Figure 4 and Figure 7 show that this upturn is followed by a downturn in the years which follow. Because of the averaging that is part of this method, the series is much smoother than that of the other methods.
Figure 8.
Window Averaging (WA) Estimate of Transitory Variance, 9-Year Window
D. Sensitivity Tests
We conduct sensitivity tests to several of the more important data construction decisions we have made in this study. All sensitivity tests are conducted using the simplest method, the WA method, and all results are shown graphically in Appendix 3. We examine the effect on the results from (1) using residuals that do not take out age and education effects, (2) restricting the sample to those who worked 48 or more weeks per year, (3) trimming the data to lesser or greater degrees than in our base case, and (4) including nonworkers.
The residuals from our first-stage log earnings regression necessarily have a lower variance than if age and education effects were not taken out, and would probably be expected to result in lower permanent and transitory variances in terms of levels. However, the difference in the trend could be either positive or negative, for that depends on trends in the variance of age and education and trends in the transitory variance of the age and education coefficients, which fluctuate from year to year. Figure 3-1 shows estimates from the WA method of transitory variances using residuals which only take out year effects (which must be removed to avoid macro effects generating transitory fluctuations) and not age and education. The pattern is virtually identical to that shown in Figure 8.
It is of interest to know whether the increased transitory variance has been a result of increased transitory variance of wage rates or labor supply. A full investigation of this issue is beyond the scope of this paper, but a simple method often used to isolate something close to a wage rate is to select workers who work full year. Figure 3-2 shows the pattern of transitory variances based on a sample of men who worked at least 48 weeks in the year. The same pattern of sharply increased variances from the 1970s to the 1980s as in Figure 8 is exhibited, although the uptick in the late 1990s and early 2000s in that Figure does not appear, suggesting that the variance of weeks worked may have increased in that period. However, as we noted previously, our EC and NP methods imply that variances turned down subsequent to 2000, and it could easily be that the early-2000s recession generated a short-term increase in the variance of weeks worked. Further investigation of the issue is warranted.
Our main results are based on data in which the top and bottom one percent of earnings residuals within age-education-year cells are deleted, both to eliminate top-coded observations and to eliminate earnings observations with low and high values in general, which can have a disproportionate effect on logarithmic transformations. Figure 3--3(a) shows estimates when no trimming is done. Variances are much higher in this case (compare its vertical axis with that of Figure 8) but the same upward trend through the early 1990s is present, though the jump in the variance in the early 1990s is much larger, which may be a result of changes in PSID procedures in that period which we discuss further below. The transitory variance does turn down at the end, but this may also be traceable to the high rates of variances in the early 1990s. Figure 3--3(b) shows trends when five percent of each tail is trimmed and shows that the upward trend from the 1970s to 1980s continues to be robust to this additional trimming. However, there is a stronger increase in the late 1990s and early 2000s in this case, which must mean that the 95th to 99th percentiles or the 1st to 5th percentiles moderated the increase in the variance.
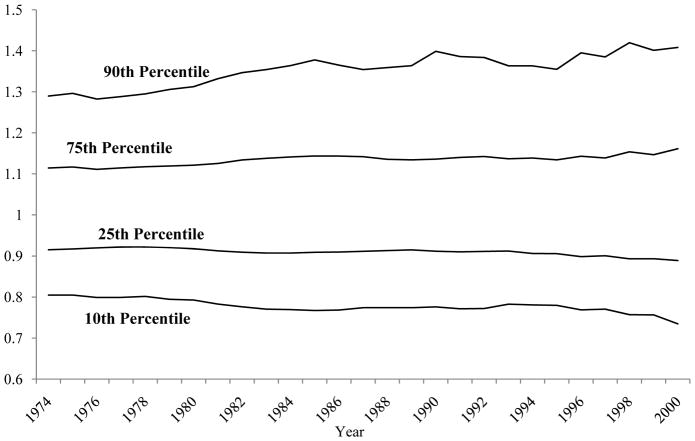
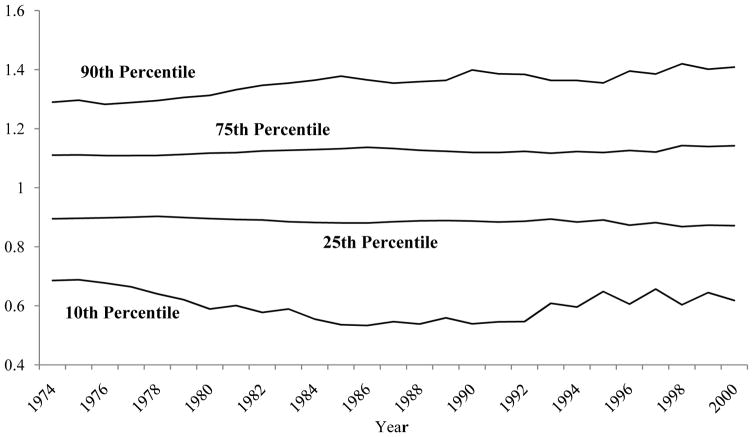
To include nonworkers, we must modify our method because log earnings cannot be used. We include nonworkers by changing from calculations of variances to calculations of percentile points, using percentile points of the non-logarithmic earnings distribution. To accomplish this, we select the log earnings residuals we have used thus far for each individual in each year and calculate the anti-logarithm of each.14 Following the WA method, we then compute the average of these transformed residuals for each individual in a nine-year window over working years only and, finally, we compute, for each year, an individual’s ratio of his transformed residual in that year to his mean. This ratio signifies the fraction by which (non-logged) earnings in the year is in excess of, or below, his mean over all years, and thus measures a relative transitory component. In years in which an individual is a nonworker, this fraction is zero by definition. We then compute the percentile points of the distribution of these fractions in each year.
Figure 3-4(a) shows percentile point trends excluding nonworkers to determine if this method yields the same result as our variance calculations above. All four percentile points in the figure show a marked spreading-out of the distribution from the 1970s to the 1980s. Thus the increase in variance we have found previously is not a result of a change in only one part of the distribution, but is rather widely spread across the entire distribution. The percentile points are stable through the late 1990s but, again consistent with the variance calculations, a slight spreading out of the distribution occurs at both high and low percentile points starting in the late 1990s. Figure 3-4(b) shows the trends including nonworkers (between 10 percent and 14 percent of these prime-age men were nonworkers, depending on the year). The upper three percentile point patterns are virtually the same as in Figure 3-4(a) but the 10th percentile point pattern shows a sharper rate of increased dispersion from the 1970s to the 1980s but then a narrowing in the 1990s, ending up in 2000 only slightly below its initial 1974 value. The inclusion of nonworkers, it should be noted, should increase cross-sectional dispersion but has no necessary implication for trends in the transitory variance, which will depend on the degree to which nonworking status has become more persistent rather than more unstable. If the rate of nonwork increases but becomes more persistent, this will not increase the transitory variance. The pattern in the figure suggests that nonworking did, in fact, become more persistent in the 1990s for the lower tail of the distribution, leading to a decline in transitory dispersion in those years.
V. Differences Across Studies
There have been several other studies in the literature which separate permanent from transitory components and have estimated whether the male earnings variance of the transitory component has increased with calendar time in the U.S. (Gottschalk and Moffitt 1994; Moffitt and Gottschalk 1995; Haider 2001; Stevens 2001; Hyslop 2001; Moffitt and Gottschalk 2002; Gottschalk and Moffitt 2006; Keys 2008; Jensen and Shore 2010). These studies all find increases in the transitory variance over time, particularly from the 1970s to mid-1980s. Those later studies which examined the period after the mid-1980s report different results, some finding no trend in the 1990s while others finding some decrease and others finding an increase. Moffitt and Gottschalk (2002), for example, find a decrease from the early 1990s to 1996, but our current results show that decrease to be temporary and probably a result of cyclical factors. Also, Gottschalk and Moffitt (2006) found a larger increase in the 1990s than we find in this study (as noted above, we find a small increase in that period), but this is a result of improvements in the model specification.15 Overall, however, this literature reinforces the view that transitory variance increases were greater in the 1970s and 1980s than anything in the 1990s.
Another strand in the literature does not attempt to separate permanent from transitory variances but instead focuses on trends in the variance of one-year or two-year changes in male annual earnings, often termed ‘volatility’. While most of these studies find, like us for transitory variances, increases in volatility in the 1970s and early 1980s (Dynarski and Gruber 1997; Cameron and Tracy 1998; Dynan et al. 2008; Shin and Solon 2010), the two studies which had data through the late 1990s and early 2000s showed an additional significant increase in that period (Dynan et al. 2008; Shin and Solon 2010), which we do not find despite using the same data; and one study found no increase at all in earlier periods, in contrast to our findings (U.S. Congressional Budget Office 2007; Dahl et al. 2010).16 These differences must be traced either to differences in the measures—transitory variances versus volatility—or to differences in data.
Regarding differences in the measures, the most obvious difference is that the volatility measure includes changes in the instability of permanent earnings as well as transitory earnings. The authors of these studies argue that there is considerable interest among policy-makers and others in volatility per se regardless of the permanent-transitory decomposition of such changes. We do not disagree with that view but believe that the classically-defined decomposition into these two components is of additional interest for the reasons noted in the Introduction. The inclusion of permanent earnings in the volatility measure explains one of the two differences in findings we noted above, namely, why Dynan et al. (2008) and Shin and Solon (2010) find significant increases in volatility in the late 1990s and early 2000s whereas our EC model finds no increase in the transitory variance in that period (aside from cycle). Since we find that there was a marked increase in the permanent variance in that period, as shown in Figure 1, a measure which aggregates increasing permanent variances and stable transitory variances should show an increase. Our data, indeed, show such an aggregate increase in the variance of two-year changes in log residual earnings in the last years of the data (see Appendix Figure 3-5; this result also holds for log earnings itself rather than residuals).17
As for differences with these two studies in treatment of the PSID data, while there are differences in age ranges, variable definitions, and related decisions that we would expect to have only minor effects, two differences could be important.18 One is that both studies included nonworkers in some of their volatility measures whereas we exclude nonworkers from our main transitory variance calculations. However, as we noted above in our discussion of sensitivity tests, including nonworkers does not change our results (Shin and Solon 2010) also calculated their estimates with and without nonworkers and found little difference). The other difference is that, as Dynan et al. (2008) emphasize, the introduction of Computer Assisted Telephone Interviewing in the PSID in 1992 and a shift to new data processing software in 1993 may also have led to a spurious one time shift in measures of instability. Dynan et al. (2008) find an unusually large increase in the number of individuals who change from positive earnings to zero earnings from 1991 to 1992, even though hours worked were reported in the latter year; they find that excluding those with zero earnings but positive hours leads to a reduction in estimated volatility over those years. More generally, they find an increase in the number of low earners in this period relative to previous years of the PSID. Once again, however, our results do not appear to be sensitive to this issue as far as we can determine, even though complete certainty about the effect of this change is not known. For example, we include in our sample only men with both positive earnings and positive weeks worked in our sample, thereby accomplishing the restriction imposed by Dynan et al. In addition, as we already noted, the inclusion of nonworkers does not affect our results when we use percentile point measures of transitory dispersion. Finally, as our discussion of sensitivity to trimming above indicated, our one-percent trim at both tails does indeed remove the major jump in transitory variance in the 1991–1993 period, and further trimming does not have much effect on reducing the size of the modest jump that remains.
As for the difference in findings with the U.S. Congressional Budget Office (2007) (CBO) and Dahl et al. (2010), who find no upward trend (if not a downward one) in volatility, we should immediately note that the latter study restricted its analysis to years 1985 and after on the grounds that the Social Security earnings data prior to those years—which were used in the earlier CBO report—had been discovered suspect and were no longer sufficiently trustworthy to use. However, our results and theirs for the years 1985 and after differ very little, for both Dahl et al. (2010) and we find no long-term trend in volatility or transitory variance after that year. Our results show that the major upward trend was completed by the mid-1980s.19
Of course, there is a major difference in the data used, for these studies use administrative earnings reports from the Social Security Administration whereas we use household survey data, which may contain response error. However, the two data sets also differ in their sample populations—the Social Security data contain non-heads and the PSID data only cover heads, and neither data set can replicate the other’s sample—and the Social Security data have somewhat different coverage than the PSID. Further, earnings recorded on Social Security records have some errors, and there are some items likely to be reported in a survey that are excluded from the relevant line on W-2 forms (Abowd and Stinson 2010). In addition, the simple presumption that the Social Security data contain less response error is not consistent with the finding in several studies that those data show greater cross-sectional dispersion than do survey data, not less (Abowd and Stinson 2010; Gottschalk and Huynh 2010), suggesting that there may be other differences in either the populations or the earnings measures than simple reporting error. The reasons for differences in the data sets certainly deserve further investigation.
VI. Summary
We have provided new estimates of the trend in the transitory variance of male earnings in the U.S. using the Michigan Panel Study of Income Dynamics through 2004. Our study uses the classical definition of a transitory component that fades out over time and eventually disappears altogether, as distinct from a permanent component that never goes away. Using both an explicit error components model as well as two simpler but more approximate methods, we find that the transitory variance increased substantially in the 1970s and early 1980s and then remained at this new higher level through 2004. We also find a strong cyclical component to the transitory variance which induced major jumps in the variance during the recessions of the early 1980s, early 1990s, and early 2000s. Our conclusion that the transitory variance was stable, net of cycle, after the mid-1980s results from our interpretation that the changes in the transitory variance were cyclical and that there was no trend after that time, although it is possible that that transitory variance was slightly higher than it was previously. The trend increase in the transitory variance accounts for about half of the increase in cross-sectional inequality through the late 1980s but only for about a third through 2004 because the permanent variance has been rising markedly since the mid-1990s. Since other research has shown that a significant proportion of transitory shocks can be smoothed, these findings imply that the welfare implications of the rise in cross-sectional inequality experienced in the U.S. are less serious than they might otherwise have been thought to be. Put differently, the rise in cross-sectional inequality corresponds to a smaller increase in lifetime inequality.
These results are robust both to the methodology used and to data construction decisions related to outliers and trimming, inclusion of non-workers, and related issues. We have also reconciled our results with most other studies, although there is some uncertainty whether findings from the PSID give the same results as those from administrative data drawn from Social Security earnings files which deserves further research.
In addition to further research on methods and data, it would be interesting to conduct more subgroup analysis to determine how these transitory variance trends vary by age, education, race, and other dimensions. The sample sizes in the PSID limit the amount of disaggregation that is possible, however, and other data sets might have to be brought to bear to fully conduct such an investigation.
Acknowledgments
The authors would like to thank two referees at this journal and the participants at many seminars and conferences for comments, Joe Tracy and John Abowd for discussant comments, and Tom DeLeire and Gary Solon for helpful conversations. Outstanding research assistance was provided by Yonatan Ben-Shalom, Kai Liu, Shannon Phillips, and Sisi Zhang.
Appendix 1. Supplementary Tables
Appendix Table 1––1.
Descriptive Statistics
| Mean | Standard Deviation | Minimum | Maximum | |
|---|---|---|---|---|
| Annual real earnings | $ 43,514.00 | $ 26,516.00 | $ 615.00 | $ 525,015.00 |
| Log annual real earnings | 10.51 | 0.62 | 6.42 | 13.17 |
| Log annual real earnings residual | 0.02a | 0.55 | −3.85 | 2.50 |
| Age | 42.80 | 8.40 | 30.00 | 59.00 |
| Year | 1985.70 | 9.60 | 1970.00 | 2004.00 |
Notes:
Means taken over all person-year observations (NT=30,424).
Means taken after 1-percent trimming within age-education-year cells for paired observations.
Multiplied by 10,000; residual mean is close to zero.
Appendix Table 1–2.
Specimen Elements of the Covariance Matrix: Year 1974
| Year | Age | Lag Year | Lag Age | Covariance |
|---|---|---|---|---|
| 1974 | 35 | 1970 | 31 | 0.0783 |
| 1974 | 35 | 1971 | 32 | 0.0941 |
| 1974 | 35 | 1972 | 33 | 0.1150 |
| 1974 | 35 | 1973 | 34 | 0.1211 |
| 1974 | 35 | 1974 | 35 | 0.1861 |
| 1974 | 45 | 1970 | 41 | 0.1117 |
| 1974 | 45 | 1971 | 42 | 0.1225 |
| 1974 | 45 | 1972 | 43 | 0.1283 |
| 1974 | 45 | 1973 | 44 | 0.1420 |
| 1974 | 45 | 1974 | 45 | 0.1945 |
| 1974 | 55 | 1970 | 51 | 0.0993 |
| 1974 | 55 | 1971 | 52 | 0.1075 |
| 1974 | 55 | 1972 | 53 | 0.1094 |
| 1974 | 55 | 1973 | 54 | 0.1196 |
| 1974 | 55 | 1974 | 55 | 0.1762 |
Notes:
Ages in the table denote midpoints of a ten-year group (35=30–39, 34=29–38, etc)
Covariance element values are after 1-percent trimming
A set of covariance elements of this type exist for each year, 1970–2004, for all three age groups in each, and for lags back to 1970 or age 25 (=20–29), whichever comes first.
Appendix Table 1–3.
Estimates of the Error Components Model
| Estimate | Standard Error | ||
|---|---|---|---|
| Alpha | |||
| 1971 | 0.9320 | 0.0471 | |
| 1972 | 0.9942 | 0.05158 | |
| 1973 | 1.0376 | 0.0590 | |
| 1974 | 1.0182 | 0.0658 | |
| 1975 | 1.0565 | 0.0748 | |
| 1976 | 1.2024 | 0.0896 | |
| 1977 | 1.1055 | 0.0819 | |
| 1978 | 1.0285 | 0.0752 | |
| 1979 | 1.0900 | 0.0905 | |
| 1980 | 1.1055 | 0.0892 | |
| 1981 | 1.1730 | 0.0928 | |
| 1982 | 1.2930 | 0.1030 | |
| 1983 | 1.2764 | 0.1040 | |
| 1984 | 1.2518 | 0.1006 | |
| 1985 | 1.3603 | 0.1097 | |
| 1986 | 1.3314 | 0.1077 | |
| 1987 | 1.2546 | 0.1024 | |
| 1988 | 1.3781 | 0.1141 | |
| 1989 | 1.2614 | 0.0998 | |
| 1990 | 1.2339 | 0.1010 | |
| 1991 | 1.1910 | 0.1023 | |
| 1992 | 1.1843 | 0.1019 | |
| 1993 | 1.2284 | 0.1036 | |
| 1994 | 1.2594 | 0.1082 | |
| 1995 | 1.3126 | 0.1127 | |
| 1996 | 1.2041 | 0.1094 | |
| 1998 | 1.2750 | 0.1205 | |
| 2000 | 1.3377 | 0.1327 | |
| 2002 | 1.3812 | 0.1465 | |
| 2004 | 1.6133 | 0.1715 | |
| Beta | |||
| 1971 | 1.0461 | 0.1328 | |
| 1972 | 0.7143 | 0.0880 | |
| 1973 | 0.6804 | 0.0974 | |
| 1974 | 0.8274 | 0.1165 | |
| 1975 | 0.8659 | 0.1234 | |
| 1976 | 0.9554 | 0.1424 | |
| 1977 | 0.9737 | 0.1340 | |
| 1978 | 1.0116 | 0.1414 | |
| 1979 | 0.9817 | 0.1394 | |
| 1980 | 0.7937 | 0.1131 | |
| 1981 | 1.0708 | 0.1578 | |
| 1982 | 1.1747 | 0.1709 | |
| 1983 | 1.2086 | 0.1736 | |
| 1984 | 1.1462 | 0.1594 | |
| 1985 | 1.3068 | 0.1789 | |
| 1986 | 1.2053 | 0.1675 | |
| 1987 | 1.0044 | 0.1370 | |
| 1988 | 1.0982 | 0.1560 | |
| 1989 | 1.2699 | 0.1692 | |
| 1990 | 1.0718 | 0.1439 | |
| 1991 | 1.4059 | 0.1963 | |
| 1992 | 1.3934 | 0.1860 | |
| 1993 | 1.2409 | 0.1676 | |
| 1994 | 1.3267 | 0.1778 | |
| 1995 | 1.2486 | 0.1770 | |
| 1996 | 1.1748 | 0.1592 | |
| 1998 | 1.1053 | 0.1552 | |
| 2000 | 1.2802 | 0.1847 | |
| 2002 | 1.3354 | 0.1942 | |
| 2004 | 1.1726 | 0.1807 | |
|
|
0.0901 | 0.0186 | |
|
|
0.2669 | 0.1430 | |
|
|
0.3830 | 0.2663 | |
|
|
−1.9033 | 0.6828 | |
| ρ | 0.8468 | 0.0510 | |
| θ | −0.5740 | 0.0495 | |
| π0 | 0.0625 | 0.0216 | |
| π1*100 | 0.1985 | 0.0859 | |
| γ | −0.0330 | 0.0348 | |
Notes:
R-squared = .105
Chi-squared = 5.27
Appendix 2. Model and Estimating Procedure
The model, restated, is
| (2-1) |
| (2-2) |
| (2-3) |
with the following normalizations, variance assumptions, and initial conditions:
| (2-4) |
| (2-5) |
| (2-6) |
| (2-7) |
| (2-8) |
| (2-9) |
and with a=1 defined as age 20. For the left-censored (1970) observations, define a70 as the individual’s age in 1970. Those with a70>1 are left-censored. We define the variance of the transitory component in 1970 for these left-censored observations in the following way (the variance of the permanent component does not require knowledge of αt prior to 1970):
| (2-10) |
| (2-11) |
| (2-12) |
Equation 2-10 is the ARMA(1,1) expression for the 1970 transitory component. Only the first and third terms are prior to 1970 and hence only they must be approximated. Equation 2-12 gives the formula for the variance of the transitory component for someone who is age a70 in 1970 and whose transitory component has followed its age evolution from age a=1 to that age with βt=1 in all those years. Equation 2-11 allows that age profile of transitory variances to be modified by the parameter γ, and it is assume that the deviation is a function of age--the lower the age, the fewer years prior to 1970 have occurred, and hence the smaller the expected deviation. We denote the expression in (2-11) as g(a70) for use in the formulas below.
An alternative treatment of the left-censored observations would simply allow the 1970 age-profile of transitory variances to be some unknown function of g(a70) whose parameters would be estimated. However, this approach would result in a misspecification in the present case because it would make all succeeding transitory variances a function of calendar time (we do not demonstrate this for brevity). As a result, even in a model with αt = βt = 1, the model would predict calendar time evolution of the variances and covariances. Thus true calendar time shifts after 1970 would be confounded with distance from the left-censoring point, generating incorrect estimates of αt and βt (see MaCurdy 2007, pp.4094-4098 for a related discussion).
The unknown parameters in the model are αt,βt,ρ,π0,π1,γ, , and . They generate the following variances and covariances for all years, ages, and lag lengths.
Total Variances zxand Covariances
| (2-13) |
| (2-14) |
Permanent Variances and Covariances
| (2-15) |
| (2-16) |
Transitory Variances and Covariances
If a70 ≤ 1 (non-left-censored)
| (2-17) |
| (2-18) |
| (2-19) |
If a70>1 (left-censored)
| (2-20) |
| (2-21) |
| (2-22) |
We estimate the model with minimum distance. Let sim = yij yik, where yij and yik are the log earnings residuals for individual i for age-year “locations” j and k, and where m=1,…,M indexes the moments generated by the product of residuals at all locations j and k. In our case, M=1,197. Write the model in generalized form as
| (2-23) |
where θ is a L×1 vector of parameters. Then the set of M equations in 2-23 constitutes an SUR system whose efficient estimation requires an initial consistent estimate of the covariance matrix of the εim. However, following the findings and recommendations of Altonji and Segal (1996) on bias in estimating covariance structures of this type, we employ the identity matrix for the estimation. Hence we choose θ to minimize the sum of squared residuals:
| (2-24) |
or, equivalently, since f is not a function of i,
| (2-25) |
where s̄im is the mean (over i) of sim (in other words, a covariance).
To obtain standard errors, we apply the extension of Eicker-White methods in the manner suggested by Chamberlain (1984), using the residuals from (B24), each of which we denote eim. Let Ω be the M×M covariance matrix of the eim, each element of which is estimated by:20
| (2-26) |
Define Δ as the NM×NM covariance matrix of individual residuals which is a block diagonal matrix with the matrix Ω on the diagonals. Then
| (2-27) |
where G is the NM×L matrix of gradients .
Appendix 3. Sensitivity Tests
Figure 3-1.
Window Averaging (WA) Estimate of Transitory Variance of Log Earnings Residuals, 9Year Window, Year Residuals Only
Figure 3-2.
Window Averaging (WA) Estimate of Transitory Variance of Log Residual Earnings, 9-Year Window, 48+ Weeks Worked
Figure 3-3.
Figure 3--3(a). WA Estimate of Transitory Variance, No Trimming
Figure 3--3(b). WA Estimate of Transitory Variance, Five Percent Trimming
Figure 3-4.
Figure 3-4(a). Percentile Points of the Relative Transitory Component Distribution, excluding Nonworkers
Figure 3-4(b). Percentile Points of the Relative Transitory Component Distribution, including Nonworkers
Figure 3-5.
Variance of Two-Year Difference in Log Residual Male Annual Earnings
Footnotes
The textbook random-effects ANOVA expression for the permanent variance, which involves the variance of the mean of y for each individual over time periods, should, under the assumptions of the model, equal this long autocovariance if that mean is taken over periods far apart.
We do not use earnings reported in 1969 or 1970 since wage and salary earnings, which is what we use, are reported only in bracketed form in those years.
In fact, Gottschalk and Huynh find that the cross-sectional variance of true earnings is greater, rather than smaller, than that variance in survey data, contrary to expectations (this is because measurement error is negatively correlated with true earnings). Nevertheless, we do expect some measurement error in the PSID data and expect this to affect our estimates. However, since our focus is on how the various variance estimates have changed over time, this should be a problem for our work only if PSID measurement error has changed. Aside from one possible instance of such a change, which we discuss below, we have no evidence of such changes.
If top-coding were the only motivation for trimming, a preferable procedure would be to top-trim the earnings variable directly rather than the residuals. However, our motivation is more general, to avoid distortion of log variances from outliers. The section below on sensitivity tests discusses trimming in more detail. In any case, in prior work (Moffitt and Gottschalk 2002), we tested trimming on the residuals versus trimming on earnings itself, and found no qualitative difference in the results.
In an AR(1) model, another way to state the identification condition for the permanent variance is that we require ρ<1. If ρ=1, transitory shocks are equivalent to permanent shocks and hence the two cannot be separately identified. In practice, we have found this sometimes to be an important issue because estimates of ρ can be close to 1.
We estimate the model in levels rather than differences. The individual effect μi0 does not cancel out in differences in our model because of the αt. In addition, the covariance matrix of the differences of yiat is a function of the same covariance matrix we are fitting with our levels model. Fitting in levels is more convenient for our purposes because we wish to decompose the trend in the cross-sectional variance of yiat into permanent and transitory variances.
To avoid clutter in the figures, we do not show confidence interval bands. The point estimates in both figures have standard errors that range from one-twentieth to one-tenth of those estimates (see Table 1–3), which means that the patterns of rising, falling, and stable variances we find are all significant.
We do not attempt to interpret the large increase in the permanent variance at the end of the period, which is mostly a result of one observation, that in 2004 (the 2003 point is interpolated). Given the volatility of this series, the estimate could easily drop in the next year. We will examine this further as more waves of the PSID are released.
See Appendix Equations (2-15) and (2-16): the autocovariance in (2-16) equals the permanent variance in (2-15) only if the random walk and random growth terms do not appear.
This problem was noted initially by Gottschalk and Moffitt (2006) and noted as well by Shin and Solon (2010) and in a prior 2008 version of their paper. Shin and Solon criticize us in their 2010 paper for using this method despite the fact that we have not used it since we uncovered the problem in 2006.
The permanent variance in Appendix equation (2-15) equals the autocovariance in equation (2-16) when at τ =0.
In a prior version of this paper, and in some other work, this method has been referred to as the “BPEA” method.
The exact formulas used for the permanent and transitory variance are given in Gottschalk and Moffitt (1994). The above description is only approximate because a term involving the deviations around individual means must be subtracted from the variance of the means to obtain consistent estimates of the permanent variance. Note that the residuals from a regression that controls for age are being averaged; if this were not done, normal life cycle growth would be misinterpreted as negative transitory earnings in the early period of the window and positive transitory earnings in the later period.
We also tested using unlogged earnings as the dependent variable in the first-stage regression, but this provided a very poor fit to the data, as earnings tend to grow in proportionate terms and to differ across age and education groups proportionately.
Specifically, the addition of the random growth term in the permanent variance lowers the growth rate of the transitory variance in the 1990s. This is because the random growth term accounts for part of the rise in the long autocovariance, and that is therefore attributed more now to the permanent variance, leaving less for the transitory variance. We should emphasize, however, that Gottschalk and Moffitt (2006) still found the increase in the 1970s and 1980s to be greater.
In addition, Shin and Solon (2010) find a slight decline in the 1990s rather than a flattening out or slight increase, as we find. This is a less important difference, but we remark on it below.
This also explains the difference in trends in the 1990s between our study and that of Shin and Solon (2010), who find a decline in volatility over that period instead of a flattening out, for we find that the permanent variance declined in that period (see Figures 1 and 3 above).
We have investigated changing our age ranges by up to 10 years at the bottom and top ends, and find no change in results. We should note that Shin-Solon exclude imputed values, whereas we do not. While we have not investigated this issue in this paper, an earlier investigation of ours found no difference in results whether imputations were included or excluded (Moffitt and Gottschalk 1995).
It is also surprising that the CBO report found no increase in the early 1980s despite the recession in those years, which all the PSID studies show temporarily increased instability. A possible reason for the lack of an increase in volatility even in that period, if the data are considered reliable, is that the variance of a change in earnings is not the simple sum of the variance of permanent and transitory earnings but is, rather, equal to that sum minus the covariance in earnings between the two periods. However, the two-year covariance trended upward over the 1970s and early 1980s (a figure showing this is available upon request), thus pulling down such a volatility measure relative to that for the transitory variance. This could also explain a decline in volatility but a stable trend in transitory variance (although a declining permanent variance can also explain that). Our EC model, by subtracting off long-term covariances instead of short-term ones, avoids this issue. We should also note that the CBO tested a variant of the WA method in their Appendix, however, and still did not find an increase in their measure in the early 1980s.
Each individual in our data set contributes to only a subset of the moments in Ω; we do not adjust the notation in (2-26) for this.
Contributor Information
Robert A. Moffitt, Professor of Economics at Johns Hopkins University
Peter Gottschalk, Research Professor of Economics at Boston College.
References
- Abowd John, Card David. On the Covariance Structure of Earnings and Hours Changes. Econometrica. 1989;57(2):411–45. [Google Scholar]
- Abowd John, Stinson Martha. Unpublished manuscript. Ithaca, NY and Washington, D.C: Cornell University and U.S. Census Bureau; 2010. Estimating Measurement Error in SIPP Annual Job Earnings: A Comparison of Census Survey and SSA Administrative Data. [Google Scholar]
- Altonji Joseph, Segal Lewis. Small Sample Bias in GMM Estimation of Covariance Structures. Journal of Business and Economic Statistics. 1996;14(3):353–66. [Google Scholar]
- Atkinson Anthony, Bourguignon Francois. The Comparison of Multidimensional Distributions of Economic Status. Review of Economic Studies. 1982;49(2):183–201. [Google Scholar]
- Attanasio Orazio, Weber Guglielmo. Consumption and Saving: Models of Intertemporal Allocation and Their Implications for Public Policy. Journal of Economic Literature. 2010;48(3):693–751. [Google Scholar]
- Baker Michael. Growth-Rate Heterogeneity and the Covariance Structure of Life-Cycle Earnings. Journal of Labor Economics. 1997;15(2):338–75. [Google Scholar]
- Baker Michael, Solon Gary. Earnings Dynamics and Inequality Among Canadian Men, 1967–1992: Evidence from Longitudinal Income Tax Records. Journal of Labor Economics. 2003;21(2):289–322. [Google Scholar]
- Beach Charles, Finnie Ross, Gray David. Earnings Variability and Earnings Instability of Women and Men in Canada: How Do the 1990s Compare to the 1980s? Canadian Public Policy. 2003;29(Supplement):S41–S63. [Google Scholar]
- Beach Charles, Finnie Ross, Gray David. Long-Run Inequality and Short-Run Instability of Men’s and Women’s Earnings in Canada. Review of Income and Wealth. 2010;56(3):572–96. [Google Scholar]
- Blundell Richard, Pistaferri Luigi, Preston Ian. Consumption Inequality and Partial Insurance. American Economic Review. 2008;98(5):1887–1921. [Google Scholar]
- Cameron Stephen, Tracy Joseph. Unpublished manuscript. New York: Columbia University and Federal Reserve Bank of New York; 1998. Earnings Variability in the United States: An Examination Using Matched-CPS Data. [Google Scholar]
- Carroll Christopher. The Buffer-Stock Theory of Saving: Some Macroeconomic Evidence. Brookings Papers on Economic Activity. 1992;2:61–135. [Google Scholar]
- Chamberlain Gary. Panel Data. In: Griliches Zvi, Intriligator Michael., editors. Handbook of Econometrics. Vol. 2. Amsterdam: North-Holland; 1984. pp. 1247–1318. [Google Scholar]
- Cowell F. Measurement of Inequality. In: Atkinson Anthony, Bourguignon Francois., editors. Handbook of Income Distribution. I. Amsterdam and New York: Elsevier North Holland; 2000. pp. 87–166. [Google Scholar]
- Dahl Molly, DeLeire Thomas, Schwabish Jonathan. Unpublished manuscript. Washington: Congressional Budget Office; 2010. Estimates of Year-to-Year Variability in Worker Earnings and in Household Incomes from Administrative, Survey, and Matched Data. [Google Scholar]
- Dickens Richard. The Evolution of Individual Male Earnings in Great Britain: 1975–95. Economic Journal. 2000;110(460):27–49. [Google Scholar]
- Dynan Karen, Elmendorf Douglas, Sichel Daniel. Unpublished manuscript. Washington: Brookings Institution; 2008. The Evolution of Household Income Volatility. [Google Scholar]
- Dynarski Susan, Gruber Jonathan. Can Families Smooth Variable Earnings? Brookings Papers on Economic Activity. 1997;1:229–303. [Google Scholar]
- Fitzgerald John, Gottschalk Peter, Moffitt Robert. An Analysis of Sample Attrition in Panel Data: The Michigan Panel Study of Income Dynamics. Journal of Human Resources. 1998;33(2):251–99. [Google Scholar]
- Friedman Milton. A Theory of the Consumption Function. Princeton: Princeton University Press; 1957. [Google Scholar]
- Geweke John, Keane Michael. An Empirical Analysis of Earnings Dynamics Among Men in the PSID: 1968–1989. Journal of Econometrics. 2000;96(2):293–356. [Google Scholar]
- Gottschalk Peter, Huynh Minh. Are Earnings Inequality and Mobility Overstated? The Impact of Non-classical Measurement Error. Review of Economics and Statistics. 2010;92(2):302–15. [Google Scholar]
- Gottschalk Peter, Moffitt Robert. The Growth of Earnings Instability in the U.S. Labor Market. Brookings Papers on Economic Activity. 1994;2:217–272. [Google Scholar]
- Gottschalk Peter, Moffitt Robert. Trends in Earnings Volatility in the US: 1970–2002. Paper presented at the Meetings of the American Economic Association; January 2007.2006. [Google Scholar]
- Gottschalk Peter, Spolaore Enrico. On the Evaluation of Economic Mobility. Review of Economic Studies. 2002;69(1):191–208. [Google Scholar]
- Guvenen Fatih. An Empirical Investigation of Labor Income Processes. Review of Economic Dynamics. 2009;12(1):58–79. [Google Scholar]
- Haider Steven. Earnings Instability and Earnings Inequality of Males in the United States, 1967–1991. Journal of Labor Economics. 2001;19(4):799–836. [Google Scholar]
- Hause John. The Covariance Structure of Earnings and the On-the-Job Training Hypothesis. Annals of Economic and Social Measurement. 1977;6(4):335–65. [Google Scholar]
- Hause John. The Fine Structure of Earnings and the On-the-Job Training Hypothesis. Econometrica. 1980;48(4):1013–1029. [Google Scholar]
- Hyslop Dean. Rising U.S. Earnings Inequality and Family Labor Supply: The Covariance Structure of Intrafamily Earnings. American Economic Review. 2001;91(4):755–777. [Google Scholar]
- Jensen Shane, Shore Stephen. Unpublished manuscript. Baltimore: Johns Hopkins University; 2010. Changes in the Distribution of Income Volatility. [Google Scholar]
- Katz Lawrence, Autor David. Changes in the Wage Structure and Earnings Inequality. In: Ashenfelter Orley, Card David., editors. Handbook of Labor Economics. 3A. Amsterdam and New York: Elsevier North-Holland; 1999. pp. 1463–1555. [Google Scholar]
- Keys Benjamin. Trends in Income and Consumption Volatility, 1970–2000. In: Jolliffe D, Ziliak J, editors. Income Volatility and Food Assistance in the United States. Kalamazoo, Michigan: W.E.Upjohn; 2008. pp. 11–34. [Google Scholar]
- Lillard Lee, Weiss Yoram. Components of Variation in Panel Earnings Data: American Scientists, 1960–1970. Econometrica. 1979;47(2):437–454. [Google Scholar]
- Lillard Lee, Willis Robert. Dynamic Aspects of Earnings Mobility. Econometrica. 1978;46(5):985–1012. [Google Scholar]
- MaCurdy Thomas. The Use of Time Series Processes to Model the Error Structure of Earnings in a Longitudinal Data Analysis. Journal of Econometrics. 1982;18(1):83–114. [Google Scholar]
- MaCurdy Thomas. A Practitioner’s Approach to Estimating Intertemporal Relationships Using Longitudinal Data: Lessons from Applications in Wage Dynamics. In: Heckman James, Leamer Edward., editors. Handbook of Econometrics. Part 1. 6A. Amsterdam: Elsevier; 2007. pp. 4057–167. [Google Scholar]
- Meghir Costas, Pistaferri Luigi. Income Variance Dynamics and Heterogeneity. Econometrica. 2004;72(1):1–32. [Google Scholar]
- Moffitt Robert, Gottschalk Peter. Trends in the Covariance Structure of Earnings in the U.S.: 1969–1987.” Unpublished Manuscript. Reprinted in. Journal of Economic Inequality. 1995 doi: 10.1007/s10888-010-9154-z. Forthcoming. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moffitt Robert, Gottschalk Peter. Trends in the Transitory Variance of Earnings in the United States. Economic Journal. 2002;112(478):C68–C73. [Google Scholar]
- Ostrovsky Yuri. Long-Run Earnings Inequality and Earnings Instability Among Canadian Men Revisited, 1985–2005. The BE Journal of Economic Analysis and Policy. 2010;10(1):Article 20, 1–32. [Google Scholar]
- Pischke S. Measurement Error and Earnings Dynamics: Some Evidence from the PSID Validation Study. Journal of Business and Economic Statistics. 1995;13(3):305–14. [Google Scholar]
- Sen A. Social Justice and the Distribution of Income. In: Atkinson Anthony, Bourguignon Francois., editors. Handbook of Income Distribution. I. Amsterdam and New York: Elsevier North Holland; 2000. pp. 59–85. [Google Scholar]
- Shin Donggyun, Solon Gary. Unpublished manuscript. East Lansing, Michigan: Michigan State University; 2010. Trends in Men’s Earnings Volatility: What Does the Panel Study of Income Dynamics Show? [Google Scholar]
- Shorrocks Anthony. The Measurement of Mobility. Econometrica. 1978;46(5):1013–24. [Google Scholar]
- Stevens Anne. Changes in Earnings Instability and Job Loss. Industrial and Labor Relations Review. 2001;55(1):60–78. [Google Scholar]
- U.S. Congressional Budget Office. Trends in Earnings Variability over the Past 20 Years. Washington DC: U.S. Congress; 2007. [Google Scholar]