Frequency response properties of primary afferent neurons in the posterior lateral line system of larval zebrafish

Abstract

The ability of fishes to detect water flow with the neuromasts of their lateral line system depends on the physiology of afferent neurons as well as the hydrodynamic environment. Using larval zebrafish (Danio rerio), we measured the basic response properties of primary afferent neurons to mechanical deflections of individual superficial neuromasts. We used two types of stimulation protocols. First, we used sine wave stimulation to characterize the response properties of the afferent neurons. The average frequency-response curve was flat across stimulation frequencies between 0 and 100 Hz, matching the filtering properties of a displacement detector. Spike rate increased asymptotically with frequency, and phase locking was maximal between 10 and 60 Hz. Second, we used pulse train stimulation to analyze the maximum spike rate capabilities. We found that afferent neurons could generate up to 80 spikes/s and could follow a pulse train stimulation rate of up to 40 pulses/s in a reliable and precise manner. Both sine wave and pulse stimulation protocols indicate that an afferent neuron can maintain their evoked activity for longer durations at low stimulation frequencies than at high frequencies. We found one type of afferent neuron based on spontaneous activity patterns and discovered a correlation between the level of spontaneous and evoked activity. Overall, our results establish the baseline response properties of lateral line primary afferent neurons in larval zebrafish, which is a crucial step in understanding how vertebrate mechanoreceptive systems sense and subsequently process information from the environment.

the lateral line system in fishes is used to sense water flow, which can originate from external stimuli as well as from self-motion. The importance of the lateral line in fishes has been demonstrated in a variety of behaviors, including orienting to current, prey capture, predator evasion and courtship (Coombs and Janssen 1989; McHenry et al. 2009; Montgomery et al. 1997; Olszewski et al. 2012; Stewart et al. 2013; Suli et al. 2012). Flow detection is made possible by clusters of mechanoreceptive hair cells called neuromasts distributed along the body of the fish, each of which are innervated by one or more primary afferent neurons (Münz 1985). It has long been known that, in most fishes, two types of neuromasts, one lying exposed on the skin surface (superficial) and the other recessed in fluid-filled openings in the scales (canal), are used to detect flow velocity and acceleration, respectively (Coombs et al. 1989; Dijkgraaf 1963). The use of a vibrating sphere stimulus has shown that these two neuromast types have different frequency responses that can strongly influence behavior, but most studies to date have been on adult species (Coombs et al. 1989). Larval zebrafish are emerging as a model vertebrate system to tackle questions on aspects of the lateral line system with unprecedented detail. While strong advances have been made in elucidating the development and organization of lateral line afferent neurons and their connected neuromasts (Alexandre and Ghysen 1999; Gompel et al. 2001; Liao 2010; Nagiel et al. 2008; Pujol-Marti et al. 2012; Raible and Kruse 2000; Sarrazin et al. 2010; Sato et al. 2010), physiological studies have lagged behind (Liao and Haehnel 2012; Trapani and Nicolson 2011). The ability to conduct electrophysiological recordings from identified neurons in vivo in an optically transparent, model genetic system opens the door to substantially advance our functional understanding this unique sensory modality.

The goal of this study is to provide the first comprehensive characterization of the physiological response properties of the primary afferent neurons to controlled neuromast deflections. To do so, we adopted an approach where we employed direct mechanical deflection of a neuromast and a simultaneous recording from its connected afferent neuron. Larval zebrafish only have a few dozen neuromasts, all of which are superficial at this early developmental stage. We focused on two stimulation protocols. The first stimulus was a sine wave to determine the range of frequencies that afferent neurons respond to most strongly. This type of stimulation protocol has been the gold standard for analyzing the frequency responses of afferent neurons and has been performed in many other species. Those studies most commonly employed a vibrating sphere located at a distance from the body to stimulate neuromasts (Coombs and Janssen 1990; Mogdans and Bleckmann 1999; Montgomery et al. 1988; Münz 1985; Weeg and Bass 2002; Wubbels 1992). We departed from this approach in favor of direct neuromast deflection to minimize boundary layer effects and complex fluid-structure interactions at small scales (Anderson and Grosenbaugh 2001; McHenry et al. 2008; McHenry and Liao 2014; Rapo et al. 2009; Windsor and McHenry 2009). The second stimulus was a series of pulses (pulse train) in which each pulse contained a broad frequency spectrum. Recent work has demonstrated that a single pulse stimulus to an individual neuromast can elicit a robust afferent response (Haehnel-Taguchi et al. 2014). Based on these results, we designed a stimulation protocol to evaluate the limitations of the spike generation capacity of individual afferent neurons. This was accomplished by driving afferent neurons to their physiological limitations by systematically increasing the pulse rate. Assessing the physiological capability of afferent neurons is crucial, given that how many spikes in a given time window an afferent is capable of generating is correlated to how well it can represent a complex stimulus.

Our results in wild-type larvae offer an essential physiological baseline, which promises to open the door to interpreting underlying molecular and transduction mechanisms and provide insight into how afferent properties may change with age or disease, or to which future studies of mutant hair cell lines can be compared.

METHODS

Fish.

Zebrafish (Danio rerio) were reared in an in-house facility at 28°C according to standard methods (Westerfield 2000). All research protocols were approved by the Institutional Animal Care and Use Committee at the University of Florida and followed the National Institutes of Health Guidelines for Use of Zebrafish (http://oacu.od.nih.gov/ARAC/documents/Zebrafish.pdf). Experiments were conducted on 4- to 6-day postfertilization wild-type larvae. This developmental stage was selected because it allowed for relatively easy visualization and in vivo recording of afferent neurons in the posterior lateral line ganglion without the need for invasive dissections. Larvae were raised in 10% Hank's solution (137 mM NaCl, 5.4 mM KCl, 0.25 mM Na₂H PO₄, 0.44 mM KH₂PO₄, 1.3 mM CaCl₂, 1.0 mM Mg SO₄, 4.2 mM NaHCO₃). Prior to experiments, larvae were paralyzed by immersion in 1 mg/ml α-bungarotoxin (Sigma) in 10% Hank's solution. Larvae were then placed in a Sylgard-bottom dish containing extracellular solution (134 mM NaCl, 2.9 mM KCl, 1.2 mM MgCl₂, 2.1 mM CaCl₂, 10 mM glucose, 10 mM HEPES buffer, adjusted to a pH of 7.8 with NaOH) and positioned on their side by pinning them through the dorsal notochord with four etched tungsten pins.

Stimulation.

Zebrafish larvae only have about a dozen superficial neuromasts on each side of the trunk, which allows for deflection of individual neuromasts (Fig. 1A). To stimulate a neuromast, the visible hair cell bundle (e.g., kinocilia) was deflected with a glass pipette attached to piezoelectric stimulator (30v300 model, Piezosystem, Jena, Germany; Fig. 1A). The device was driven by an analog output from Digidata 1440A (Molecular Devices, Sunnyvale, CA). We used sine wave and pulse train stimuli (Fig. 1B) at frequencies ranging from 1 to 100 Hz, which is within the frequency selectivity of superficial neuromasts (Kroese and Schellart 1987; Montgomery et al. 1988; Münz 1985; no. 3877). Both stimulation protocols employed constant amplitudes. Because of our direct deflection protocol, we were careful to set the amplitude of the stimulus to a minimum value that evoked a reliable afferent response without damaging the neuromasts.

Fig. 1.

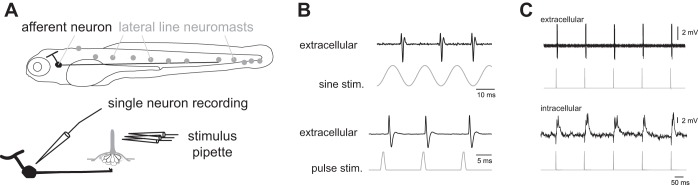
A: setup to record the response of a posterior lateral line afferent neuron to single neuromast deflections. B: extracellular loose-patch recordings reveal the response characteristics of single afferents to sinusoidal or pulse stimulations applied to individual neuromasts. C: additional pulse stimulations were performed to confirm that the activity patterns of extracellular recordings matched those of intracellular recordings.

Glass pipettes for stimulation were pulled from borosilicate glass (model G150-F-3; inner diameter, 0.86 mm; outer diameter, 1.5 mm; Warner Instruments) on a model P-97 Flaming/Brown micropipette puller (Sutter Instrument). Pipette tip diameters of 1–20 μM were used for all experiments.

Electrophysiology.

In this study, patch recordings were made from the somata of single afferent neurons. Patch electrodes were pulled from borosilicate glass (model G150-F-3; inner diameter, 0.86 mm; outer diameter, 1.5 mm; Warner Instruments) to 3–5 MΩ resistances on a model P-97 Flaming/Brown micropipette puller (Sutter Instrument).

Neuronal activity was amplified with Axoclamp 770B (Molecular Devices, Sunnyvale, CA) at 20 kHz and gain of 1,000 in AC mode and then filtered between 300 Hz and 6 kHz. The signal was digitized with Digidata 1440A and saved with pClampv10 (Molecular Devices, Sunnyvale, CA). To find the neuromast that was connected to the recorded afferent neuron, we systematically stimulated neuromasts along the rostro-caudal axis of the body. The afferent neurons of certain neuromasts (e.g., L₂ and L₃) were easier to record from than others (Haehnel et al. 2011).

For the majority of recordings, extracellular loose-patch recordings were used as they were more stable and therefore allowed us to record from more cells. We confirmed that these patch recordings were from individual afferent neurons by recording intracellularly from afferent neurons in a separate set of experiments. The timing of intracellular spikes with respect to pulse stimulation was identical to the timing seen in extracellular spikes (Fig. 1C).

Data analysis.

All error bars for the values associated with measured parameters were presented as standard error of the mean. Data were analyzed offline with customized scripts in Matlab (Mathworks, Natick, MA). A potential spike event was identified when voltage values fell between predetermined lower and upper thresholds. Spikes were then considered real if they exhibited a minimum duration of 0.1 ms and minimum interspike interval (ISI) of 1 ms. Spike times were estimated from the onset of each spike. Note that the spike duration was taken as the portion of the event above the lower threshold.

We first looked for natural groupings of afferent neurons based on their intrinsic spike activity (i.e., spontaneous activity). The ISIs were used to characterize spontaneous activity. The distributions of the ISIs were fitted with one or two exponential decay equations. For a more detailed inspection of the spike dynamics, we used ISI return maps, where ISI_n (where n is an index) is plotted against the preceding ISI_n−1 (Dekhuijzen and Bagust 1996). Based on the grouping of the data on the return map plot, distinctions can be made between regular and irregular spiking, as well as bursting activity and other spiking dynamics.

The afferent response to sine wave stimulation was quantified in terms of spike rate (number of spikes/s) and vector strength [phase locking between a periodic stimulus and a response (Gumbel et al. 1953)]. To calculate vector strength, a period was determined between two identical points in the stimulus. For each spike in the response, the delay from the period onset was measured and divided by the total period time to give a vector angle (phase) in radians from 0 to 2π. Vector strength was computed by averaging the vectors of all spikes in the response, where a perfectly synchronized response had a value of 1.

The gain of the frequency-response curve was evaluated by multiplying spike rate with vector strength (Coombs and Montgomery 1994; Montgomery and Coombs 1992). We used linear regression to quantify the slope of the frequency-response curve. We also individually analyzed spike rate and vector strength as a function of stimulation frequency. We modeled the relationship between spike rate and frequency by using the following equation:

$$y=\left[(a\cdot b\cdot x)/(1+b\cdot x)\right]+c$$ (1)

where c is the minimum spike rate which corresponds to spontaneous activity, the summation of a and c gives the maximum spike rate and b is the rate of increase in spike rate as a function of stimulation frequency. We also identified the frequency range (from the vector strength plot) in which phase locking was high (vector strength > 0.6). In this frequency range, we computed the average time delay between afferent response and stimulus from the slope of vector angle-stimulation frequency curve.

To investigate how the afferent response may change over time, we used long-duration sine wave stimulation that lasted 7 s. We divided the afferent response into 1-s bins and calculated spike rate for each bin. Note that the first and last time window was omitted from analysis to eliminate transition periods between stimulation and no stimulation. To analyze how temporal response changed as a function of stimulation frequency, we fit data points from each stimulation frequency with linear regression and analyzed the slope.

The afferent response to pulse train stimulation was also quantified in terms of spike rate and vector strength. To estimate the maximum spike rate that afferent neurons could consistently reach, we fit the relationship between spike and pulse rates to Eq. 1. We also identified the maximum pulse rate that an afferent neuron could follow in a reliable and precise manner. Reliability was evaluated as the ability of an afferent neuron to generate at least one spike for each pulse. Precision was evaluated as the phase-locking ability of an afferent neuron, where the maximum pulse rate for precision was identified based on the criteria of a vector strength > 0.9.

To analyze the response of afferent neurons to relatively long pulse train stimulation (7 s), we divided afferent response into time segments that represented 20% of the total response. Measurements of maximum spike rate and vector strength as well as their maximum pulse rates for reliable and precise response were evaluated for each portion.

Correlation between spontaneous and evoked activity.

We next evaluated the correlation of evoked responses to the spontaneous activity using a Pearson correlation. In particular, we tested whether afferent neurons with higher spontaneous spike rates could generate higher maximum spike rates, as well as evaluate their ability to follow higher pulse rates reliably and precisely. This correlation was evaluated for each time portion, with the corresponding correlation coefficients (r) and P values included.

The effect of water.

Frequency-response analysis of afferent neurons through direct mechanical deflections of individual neuromasts allowed us to isolate the physiological aspects of the system. However, under natural conditions, a stimulus signal must be transmitted through the fluid medium before reaching a neuromast. In this way, the response properties of the lateral line system should be strongly influenced by the filtering properties of water. To evaluate this effect, we moved the stimulus pipette ∼200 μm away from the neuromast (i.e., “indirect stimulation”), so that the pipette could only generate neuromast deflections by moving the water, and then repeated the sinusoidal stimulation protocol. We used the same frequency range, but the amplitude was increased to compensate for the attenuation due to the distance traveled in water. We compared the frequency responses with previous responses obtained by direct stimulation.

In several of our experiments, high-speed video was used to validate the effect of our stimulus pipette on neuromast deflection. We captured images with a Phantom Miro EX-4 video camera (500 frames/s, 384 × 512 pixel resolution, VisionResearch, Wayne, NJ) mounted on an upright Olympus BX51W1 fixed stage microscope fitted with a ×40 water-immersion lens. The captured images were then analyzed with custom program using image processing toolbox in Matlab.

RESULTS

Spontaneous firing.

We did not see evidence for more than one type of afferent neuron based on their spontaneous activity patterns. Afferent neurons fired spontaneously and irregularly in the absence of neuromast stimulation (average spike rate = 8.6 ± 6.0 Hz, n = 30 neurons). Figure 2A shows that the pattern of spontaneous activity behaved like a Poisson process (Trapani and Nicolson 2011). Specifically, ISI distribution revealed that the ratio between the standard deviation and the mean approached a value of 1 (0.7 ± 0.4), the falling phase of the distribution was well characterized by an exponential decay (Fig. 2B; r² = 0.95, n = 30), and the return maps of the ISIs revealed no bursting pattern in firing activity (Fig. 2C). We found that fitting the data with an equation with two exponential decays was no better than with one exponential decay (not shown; paired T-test, r² = 0.89, P > 0.05).

Fig. 2.

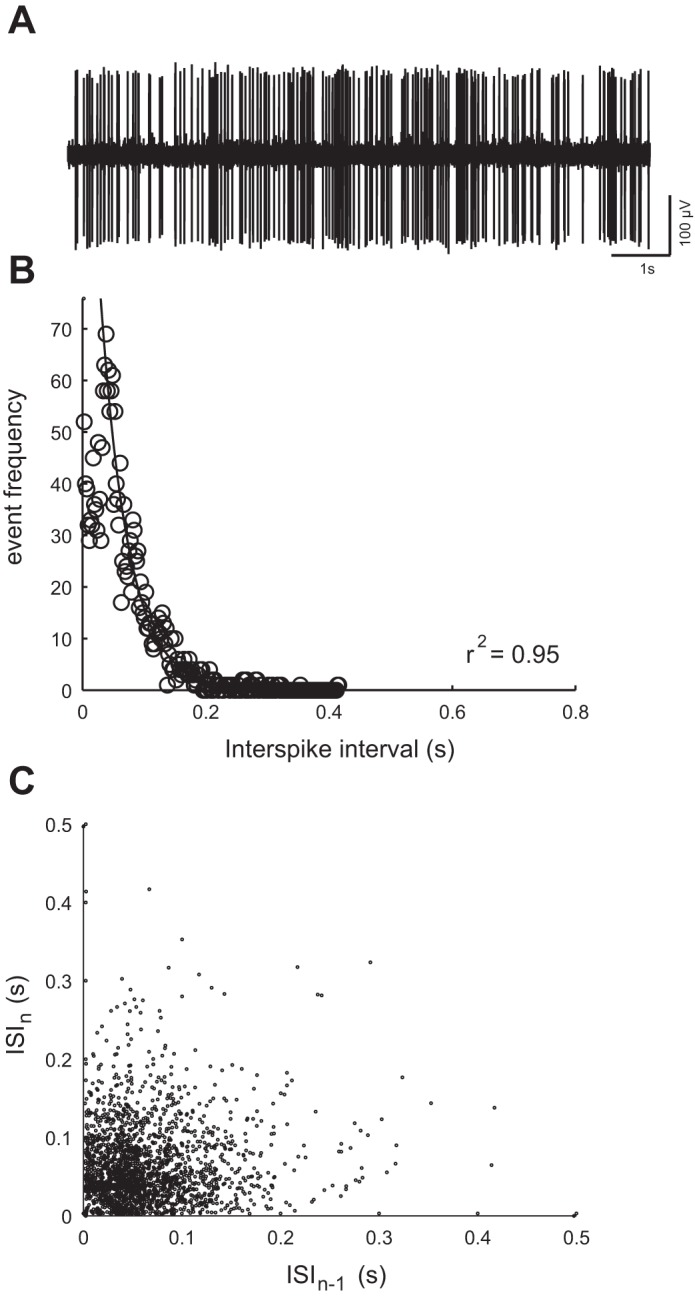
A: example of spontaneous activity of an afferent neuron (i.e., in the absence of neuromast deflection), as revealed by an extracellular loose patch recording. B: distribution of interspike intervals (ISIs) for the example shown in A shows that the falling part of the distribution follows a single exponential decay rate, which indicates that the pattern of spontaneous firing behaved like a Poisson process. C: ISI return maps, where ISI_n (n is an index) is plotted against the preceding ISI_n−1, shows that spontaneous spiking had no bursting firing patterns or other well-defined temporal structure.

Frequency response of afferent neurons revealed by sinusoidal stimulation of individual neuromasts.

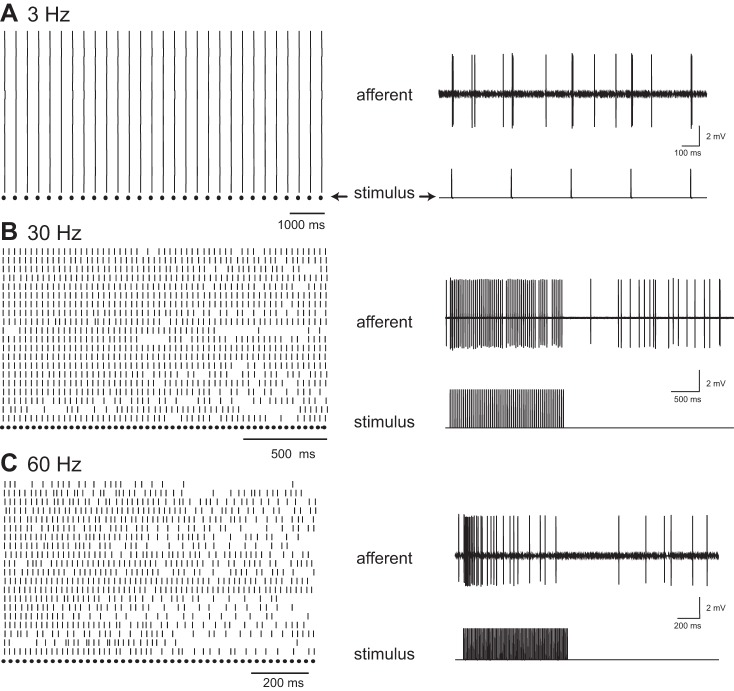
Afferent neurons show a frequency-dependent response to sine wave stimulation. Figure 3 shows examples of afferent responses for three stimulation frequencies. At 2 Hz, the overall spike rate did not increase from the level of spontaneous activity, but the majority of spikes fired during a specific phase of the stimulus. A few spikes still occurred, regardless of the stimulus phase, which we interpret as residual spontaneous activity and not a response to the stimulus. Note that these spikes would artificially lower the vector strength values. At 30 Hz, spikes became more synchronized to the stimulus, and residual spontaneous activity became less common. At 60 Hz, there was an increase in spike failure, especially at the end of the stimulus train.

Fig. 3.

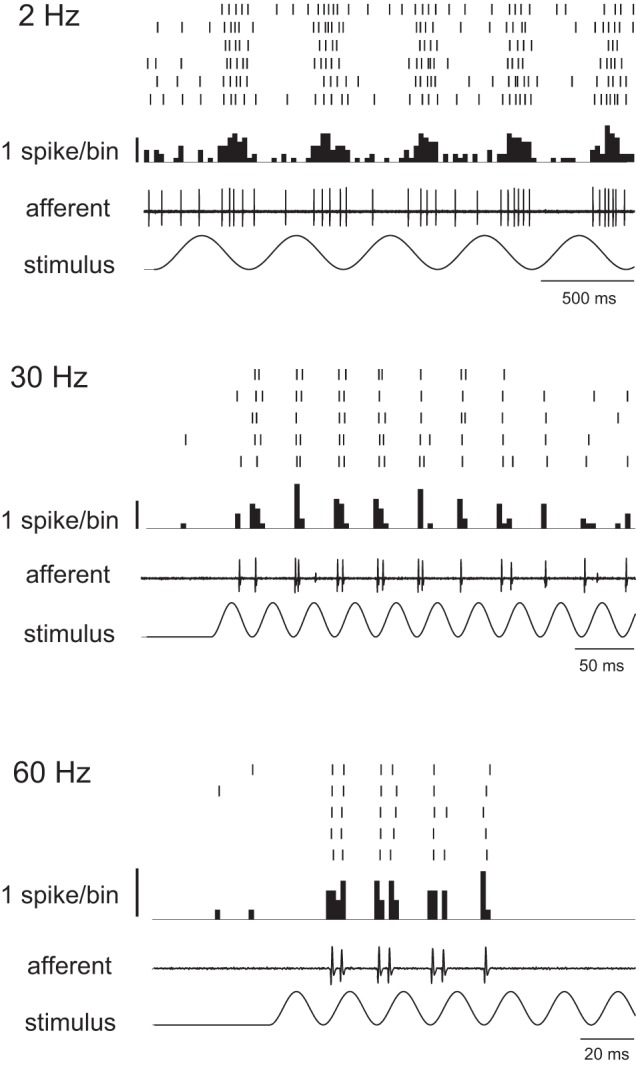
Response of afferent neurons to three sinusoidal neuromast stimulation frequencies. For each frequency, the stimulus is shown with an example of an afferent recording, with the peristimulus time histogram above. A raster plot on top is shown for several repeated responses.

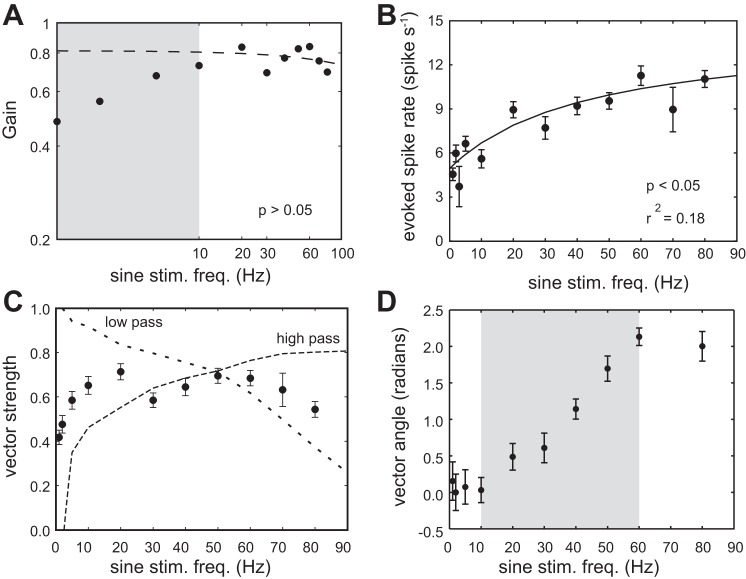
The overall gain of the system was plotted as a function of stimulation frequency (Fig. 4A). Because gain values were artificially depressed due to the residual spontaneous activity at low stimulation frequencies, we performed a linear regression analysis only for data associated with stimulation frequencies above 10 Hz and found no significant relationship (P > 0.05).

Fig. 4.

Response of afferent neurons to sine-wave stimulation across a range of frequencies. A: a log-log plot of response gain (spike rate × vector strength) as a function of stimulus frequency. The dashed line is a linear regression of the data for stimulation frequencies above 10 Hz. Note that the gain values are artificially depressed due to the residual spontaneous activity at stimulation frequencies below 10 Hz (gray region). B: evoked spike rate increases asymptotically as stimulation frequency increases, where the line is a fit of Eq. 1 (see methods). C: the ability to phase lock to the stimulus, as measured by vector strength, is highest at midrange frequencies (solid line). Dashed lines show examples of afferent neurons that display a low-pass filter and a high-pass filter (n = 1). D: a relatively linear increase in vector angle from 10 to 60 Hz (gray region) indicates that a constant time delay exists between the stimulus and the response.

To provide a more comprehensive picture of the gain, we also separately analyzed spike rate and vector strength curves as a function of stimulation frequency. The evoked spike rate increased asymptotically with frequency (Fig. 4B). This relationship is described by Eq. 1, where the coefficient values were a = 9.4, b = 0.02 and c = 4.9 (r² = 0.18, P < 0.05). From these values, we estimated an average spontaneous spike rate of 4.9 spikes/s, which was similar to our measured spontaneous spike rate value (Fig. 2). We also estimated the maximum spike rate to be 13.3 spikes/s. This was a relatively low value given what we know of the capacity of afferent neurons, which we evaluated by using the pulse train protocol (see later section).

The vector strength-frequency relationship shows that vector strength was high (>0.6) for an intermediate range of frequencies between 10 and 60 Hz (Fig. 4C). We found that the majority of afferent neurons (11 out of 17) followed this trend. However, we also observed other neurons (6 out of 17) with highest vector strength values at different ranges. Individual examples of a low- and high-pass afferent (0–10 Hz and 60–90 Hz, respectively) are shown in Fig. 4C.

Within intermediate frequencies, vector angle increased linearly with stimulation frequency, revealing a constant time delay (7.5 ± 2.5 ms) between the stimulus and an afferent response (Fig. 4D). This delay may be attributed to physiological processes (i.e., synaptic delay and axonal transmission) and cupular mechanics, but cannot be due to hydrodynamic properties, given our direct deflection protocol.

Temporal properties of afferent response to sinusoidal stimulation are frequency-dependent.

Figure 5A illustrates an example of an afferent response to 7 s of 60 Hz sine wave stimulation, where spike rate decreased over time. The rate of decrease (slope) depended on the stimulation frequency (Fig. 5B). A comprehensive slope-frequency response is given in Fig. 5C. At low stimulation frequencies (<10 Hz), there was no significant relationship between the slope and the stimulation frequency (P > 0.05 for all data points), suggesting that an afferent neuron can generate spikes for a long time period. In contrast, at high frequencies, the slope was significant (P < 0.05 for all data points) and approached −1.25. This transient response indicates a limited ability of the system to maintain constant firing to high-frequency stimulation.

Fig. 5.

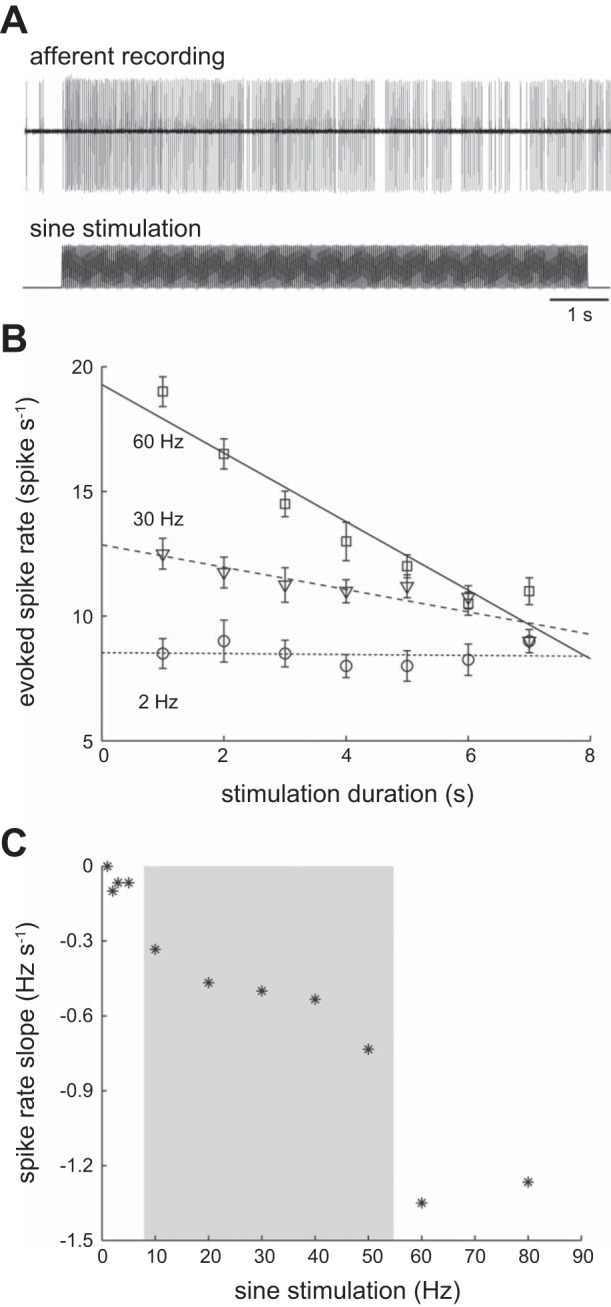
Afferent spike rate can decrease over time, depending on the stimulus frequency. A: an example of a typical afferent response illustrating the decrease in spike rate over the course of 7-s-long stimulation. B: linear regressions show that at a low stimulation frequency (2 Hz), a low spike rate is maintained throughout the stimulus duration. At higher stimulation frequencies (30 and 60 Hz), spike rates, which are initially higher in comparison, generally decrease over time. C: the slopes of spike rate change over time, measured from the curves in B, depend critically on stimulation frequency. Spike rate slope shows a decreasing trend within an intermediate range of frequencies (gray region).

Response of afferent neurons to pulse train stimulation.

Figure 6 shows examples of afferent responses for three pulse rates. At 3 pulses/s, each pulse elicited at least one spike that was strictly timed to the pulse onset (Fig. 6A). Similar to sine wave stimulation, we also observed residual spontaneous activity. At 30 pulses/s, the majority of afferent neurons were able to follow each pulse throughout the entire stimulus duration, firing one spike to each pulse (Fig. 6B). At 60 pulses/s, this one-to-one relationship was lost toward the end of the stimulation (Fig. 6C). During this portion of the stimulation, the phase-locking ability of afferent neurons was also reduced. We also observed that, for higher pulse rates, there was a recovery period after stimulation when spike activity was quiescent before it regained prestimulus levels of activity.

Fig. 6.

Response of afferent neurons to pulse stimulation across a range of frequencies. A: a raster plot (left) of the afferent response to low-frequency stimulation (3 pulses/s) is shown for repeated trials, with the stimulus pattern (dots) shown below. An example of an afferent trace (right) illustrates how each stimulus pulse can elicit a spike. Note that nonevoked spikes are also present. B: at 30 pulses/s, afferents generally spike to each stimulus pulse throughout the stimulus duration. C: at 60 pulses/s, spikes also follow pulses with a one-to-one pattern, but only for the initial portion of the stimulus. Spikes start to fail shortly after the initiation of the spike train.

Afferent spike rate increased asymptotically with pulse rate where the maximum measured spike rate was 60 spikes/s (Fig. 7A). We fit the data to Eq. 1 to obtained the following coefficient values: a = 71.30, b = 0.03, c = 7.06 (r² = 0.69, P < 0.05). From these coefficients, we estimated spontaneous and maximum spike rates to be 7.1 spikes/s and 78.4 spikes/s, respectively. The phase-locking ability of afferent neurons approached maximal (vector strength > 0.9) at pulse rates up to 40 pulses/s, which indicated that spikes were timed very precisely within the stimulus period (Fig. 7B). Once the pulse rate exceeded 70 pulses/s, the vector strength decreased to ∼0.6. The average latency between a synchronous spike and the onset of a pulse was ∼5 ms.

Fig. 7.

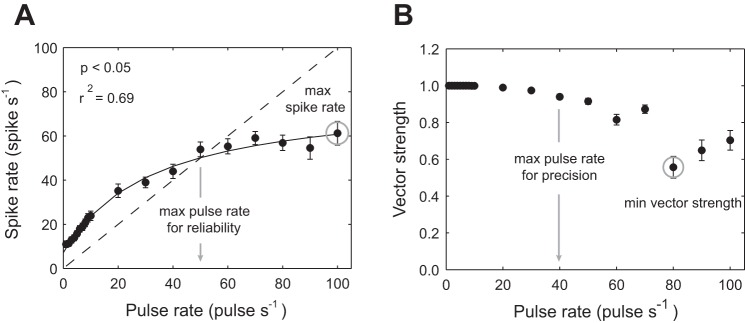
Measurements of spike rate and vector strength for afferent responses to pulse stimuli. A: solid line indicates fitted values for Eq. 1, showing that spike rate increases asymptotically with pulse rate. Dashed line represents the 1:1 ratio of spikes to pulses. Values that fall below this line indicate that, for the given pulse rate, each pulse does not elicit a spike response. Thus the intersection between the solid and dashed line sets the maximum pulse rate for which our definition of reliability in maintained (gray arrow). Gray circle represents the maximum spike rate observed. B: vector strength of the response (using the initial spike, see methods) across pulse rates, where the gray circle represents the minimum vector strength observed. All values are means ± SE. Equations are described in the methods.

Temporal properties of afferent response to pulse train stimulation are also frequency dependent.

The maximum spike rate and the maximum pulse rate at which neurons could still generate at least 1 spike/pulse decreased over stimulation time (Fig. 8A). Both measures were highest during the first 20% of the pulse train stimulus (100 spikes/s and 60 pulses/s). Note that these values were higher than the average values (80 spikes/s and 40 pulses/s). During the last 20% of the stimulus, maximum spike rate dropped to 40 spikes/s, which is less than one-half of its original value. Similarly, the maximum pulse rate decreased to fewer than 10 pulses/s, which is less than one-fifth of its original value.

Fig. 8.

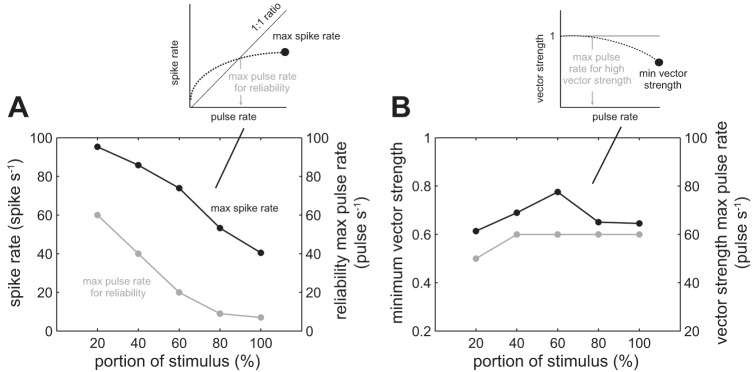
Measurements of change in maximum spike rate and vector strength over the portion of the pulse train stimulation duration. A: an afferent response to pulse stimulation can be characterized by 1) the maximum spike rate (black line), and 2) the maximum pulse rate for which an afferent can generate at least one spike for each pulse (gray line). The inset graph illustrates how the maximum spike rate (black circle) and maximum pulse rate (gray arrow) values were calculated. Both values decrease over time, represented as a percentage portion from the start of the stimulus, where 0% is the start of the stimulus and 100% is the end of the stimulus. B: the minimum vector strength (black line) and maximum pulse rate at which an afferent response is highly synchronized with the pulse train (vs. >0.9, gray line) does not show the consistent pattern of decrease seen in A. The inset graph illustrates how the minimum vector strength (black circle) and maximum pulse rate (gray arrow) values were calculated. The lines connecting the data points are for illustrative purposes.

When we looked at the phase-locking response, we saw a different pattern (Fig. 8B). The minimum vector strength and maximum pulse rate at which an afferent response is considered highly synchronized with the pulse train stimulation did not show a consistent pattern of decrease.

Correlation between the spontaneous spike rate of an afferent neuron and its frequency response.

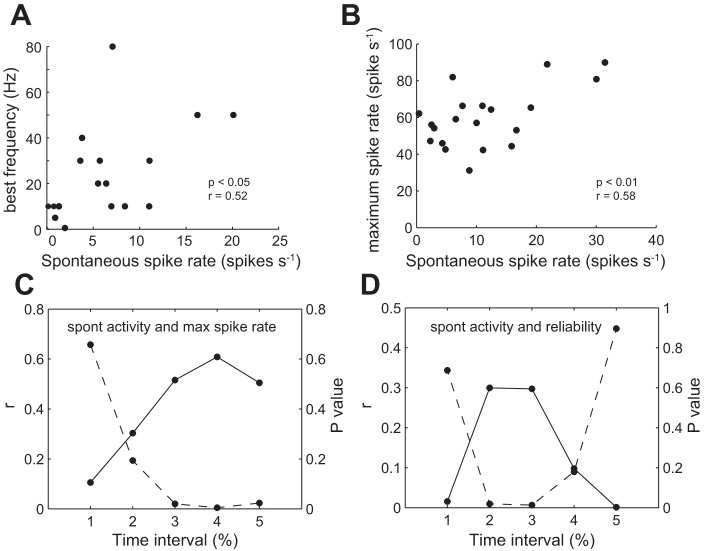
Given that response properties and spontaneous activity of afferent neurons depend on intrinsic physiological properties, we tested whether there was a correlation between the two. For sinusoidal stimulation, we analyzed the frequency that generated the highest vector strength (i.e., best frequency). Neurons that had higher spontaneous activity also tended to have higher best frequencies (Fig. 9A; r = 0.52, P < 0.05, Pearson correlation). For pulse stimulation, there was a correlation between spontaneous activity and the maximum spike rate (Fig. 9B; r = 0.58, P < 0.01, Pearson correlation). We followed this correlation over the duration of the stimulus (Fig. 9C). Correlation values were low at the beginning and increased significantly toward the end. In addition, we looked at the correlation between spontaneous activity and maximum pulse rate that an afferent neuron could reliably follow. We found that there was a certain time interval (40–80%) during which there was a significant correlation (Fig. 9D). This suggests that afferent neurons with higher spontaneous activity can keep up with higher frequency stimulation for longer time periods, although this effect may not be explicit at the beginning of the stimulation.

Fig. 9.

Correlation between spontaneous and evoked afferent activity. A: the best frequency of an afferent neuron (e.g., highest vector strength) in response to sinusoidal stimulation is correlated to its spontaneous spike rate. B: the maximum spike rate of an afferent neuron, as determined by pulse stimulation, increases with spontaneous spike rate. C: the correlation coefficient (r) between spontaneous activity and maximum spike rate (solid line) generally increases with time over the course of the stimulus, while the P value of the correlation (dashed line) decreases such that the relationship is significant only after the first 20% of the stimulus has been applied. D: the correlation (r) between spontaneous activity and reliability (e.g., maximum pulse rate that an afferent could reliably follow, solid line) is only significant between 20 and 80% of the portion of the stimulus (dashed line, P < 0.05). The lines connecting the data points are for illustrative purposes.

The fluid medium increases dynamic range and attenuates low-frequency signals.

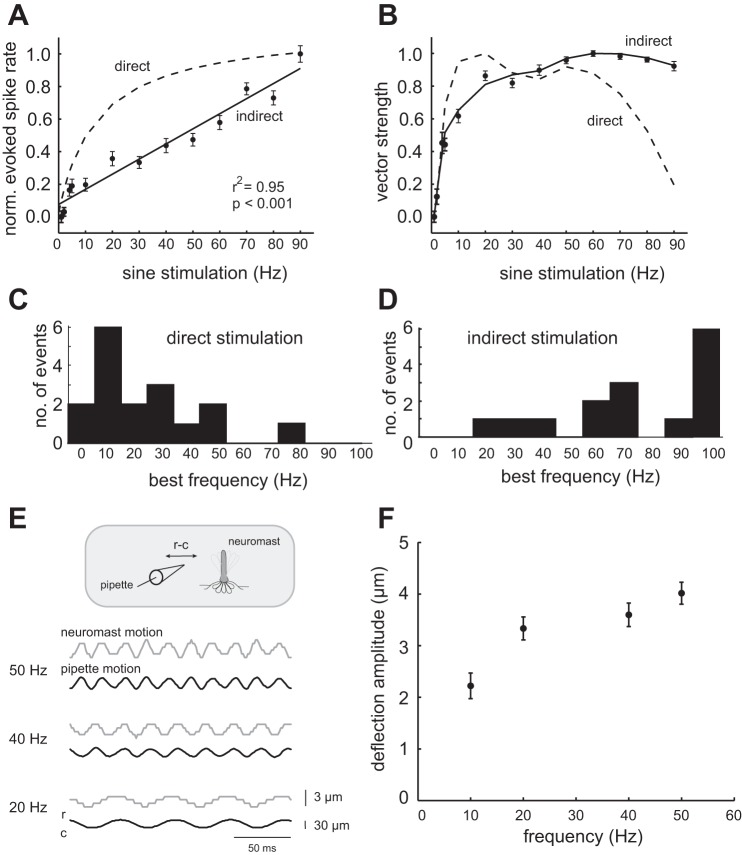
Unlike for direct stimulation, in which spike rate changed the most at low frequencies, during indirect stimulation spike rate increased linearly for the entire frequency range (r² = 0.95, P < 0.001; Fig. 10A). The normalized vector strength plots between direct and indirect stimulation were also different (Fig. 10B). At low stimulus frequencies (0–30 Hz), vector strength values for indirect stimulation were lower than those for direct stimulation, indicating that water may attenuate low-frequency signals. Note that, at high stimulus frequencies (60–90 Hz), the vector strength values for indirect stimulation were higher than those for direct stimulation. We attributed this to the higher stimulus intensities that were used for indirect stimulation. The higher stimulus intensity was required to compensate for signal attenuation as we moved the pipette farther away from the neuromast. It is worth mentioning that had we not compensated for signal attenuation, the filtering of low-frequency signals would be even more evident. This is because, even with a smaller intensity compensation, the entire curve would be shifted down substantially, resulting in an even greater difference between the curves at low frequencies. The low-frequency attenuation becomes more evident when individual response curves are examined more closely. Best frequency distributions shifted to higher frequencies when moving from direct to indirect stimulation (from an average of 24 ± 20 Hz to 74 ± 28 Hz, P < 0.01, Student t-test, Fig. 10, C and D).

Fig. 10.

Comparing the effect of direct stimulation to indirect stimulation on the neuromast. A: indirect neuromast stimulation, in which a sinusoidal motion must be transmitted through the fluid medium before influencing the neuromast, results in a lower evoked spike rate (solid line) compared with direct mechanical stimulation of the neuromast (dashed line). B: vector strength differs during indirect (solid line) vs. direct (dashed line) stimulation. C: when neuromasts are directly stimulated, most afferent neurons exhibited low best frequencies. D: when neuromasts are indirectly stimulated, the same cells shifted to higher best frequencies. E: simultaneous tracking of the stimulation pipette and hair cell bundle of a single neuromast, showing the displacement of hair cell bundle (gray trace) in response to the rostrocaudal (r-c) displacement of the stimulation pipette (black trace) at three frequencies. F: the deflection amplitude of the hair cell bundle increases with stimulation frequency (P < 0.05, Wilcoxon rank-sum test).

We experimentally confirmed that our physiological results originated from smaller hair cell movements at low frequencies. To do so, we simultaneously recorded the motions of a pipette placed ∼30 μm from the hair cell bundle of a single neuromast with a high-speed video camera. Figure 10E shows that the amplitude of the hair cell bundle had a tendency to decrease with decreasing stimulus frequencies. This result was quantified in Fig. 10F for multiple stimulation cycles and found to have a significant correlation (P < 0.05, Wilcoxon rank-sum test). Since afferent neuron activity simply reflects the motion of the hair cell bundle, it is no surprise that afferent activity was attenuated more at low stimulation frequencies (Flock 1965; Hudspeth et al. 2000; Van Trump and McHenry 2008).

DISCUSSION

One central tenet in the lateral line field is that the two types of neuromasts, superficial and canal, have distinct frequency response characteristics (Coombs and Janssen 1990; Kroese and Schellart 1987; Montgomery et al. 2001; Münz 1985). Within a neuromast type, investigating the variation of frequency sensitivity along the body can be challenging and requires a good approximation of the location of a neuromast. The advantages of using larval zebrafish are that they only possess a limited number of superficial, stereotypically located neuromasts, which connect to afferent neurons that can be recorded from in vivo. Thus it is possible to identify an afferent neuron that specifically innervates an individual neuromast at a known location along the body. This neuromast can be identified and mechanically deflected in a controlled manner, and its influence on the afferent neuron directly evaluated.

Lateral line studies that employ stimulation by transmitting a signal through the fluid medium have demonstrated that superficial neuromasts are sensitive to flow velocity (Coombs and Janssen 1989; Kroese and Schellart 1992). More accurately, due to the spatial variation in velocity created by the hydrodynamic boundary layer, superficial neuromasts are sensitive to the associated shear stress at the surface of the skin (Kalmijn 1988; McHenry and Liao 2014; Rapo et al. 2009). It is important to remember that, at the neuromast level, flow velocity is translated to hair bundle deflection. Our deflection protocol, which bypasses the effect of the boundary layer, demonstrates in vivo that the afferent neurons which contact superficial neuromasts of larval zebrafish are sensitive to hair bundle displacement. Specifically, we show that the frequency-response curve of afferent neurons is flat up to 100 Hz (Fig. 4A). This is consistent with the response of hair cell receptor potentials to mechanical deflection in other hair cell systems (Hudspeth and Corey 1977).

Our results show that lateral line afferent neurons connected to midbody neuromasts show some degree of frequency specialization in zebrafish larvae. Even though the majority of afferent neurons have a frequency sensitivity range between 10 and 60 Hz, we also observed some afferent neurons with distinct sensitivity ranges. While it is known that the number of hair cells and the height and viscoelastic properties of the neuromast cupula can all influence sensitivity (Van Trump and McHenry 2008), we consider it probable that these distinct sensitivity ranges are physiological and not mechanical in nature. Consistent with this, differences in afferent physiology, such as spontaneous spiking and excitability, have been shown to be correlated to the age and size of the neuron (Liao and Haehnel 2012). Although there are currently no data on the frequency sensitivity of superficial neuromasts for adult zebrafish, there is evidence for frequency specialization in adults of other species (Radford and Mensinger 2014; Weeg and Bass 2002). If adult zebrafish do show frequency specialization, then one potential interpretation of our findings is that specialization starts at a very early age. The picture remains inconclusive; however, for in other adult species there is no evidence for frequency specialization (Coombs and Montgomery 1994; Montgomery et al. 1994; Montgomery and Coombs 1992). Another scenario, while speculative, is that the different physiological responses we document stem from the fact that we are recording from a subset of superficial neuromasts which are actually a population of presumptive canal neuromasts.

The potential ability of larval zebrafish to distinguish relative stimulus frequencies can be used to identify biologically relevant signals in nature. In particular, this may provide a mechanism to distinguish large predatory fish from smaller sized fish by analyzing their wakes, which have been shown to persist in the environment for many seconds (Hanke et al. 2000; Hanke and Bleckman 2004). In adult fishes, an inverse relationship that exists between fish length and tail-beat frequency has been established (Webb et al. 1984). Moreover, the tail-beat frequency of larval fishes is much higher than that of adults (Müller and van Leeuwen 2004). This frequency sensitivity may also aid in the identification of other sources of periodic wakes, such as from prey or stationary objects in flow (Fields and Yen 2002; Liao et al. 2003; Tritico and Cotel 2010). At this stage, larval zebrafish already have a rich behavioral repertoire involving slow and fast swimming, struggling, turns and escape maneuvers (Budick and O'Malley 2000; Liao and Fetcho 2008; Müller and van Leeuwen 2004). Recent behavioral studies on freely swimming larvae have shown the critical role of the lateral line in mediating avoidance responses, which presumably increases survivability (McHenry et al. 2009; Stewart et al. 2013).

Based on an analysis of spontaneous activity, we found evidence for only one type of afferent neuron. However, within this cell type, the spontaneous spike rate varied significantly. We found that afferent neurons with higher spontaneous spike rate are more tolerant to prolonged stimuli at higher frequencies. Put another way, the slope of the spike rate decay is less steep for neurons with higher spontaneous activity. Several attributes of the system may facilitate this phenomenon. Hair cells specialized for high-frequency stimuli have a greater number of vesicles and calcium currents (Obholzer et al. 2008; Schnee et al. 2005; Sheets et al. 2012; Trapani et al. 2009). They also have a greater ease of vesicle release, a faster recycling of vesicles and more efficient docking (Fuchs et al. 2003; Khimich et al. 2005; Moser et al. 2006; Schnee et al. 2005). The mechanism of spontaneous activity proceeds as a random process due to neurotransmitter leakage. Therefore, it follows that an afferent neuron more adapted to high-frequency stimuli is more likely to leak more glutamate and thus will have a higher spontaneous activity (Fuchs and Parsons 2006; Trapani and Nicolson 2011). This pattern of spontaneous activity may serve another function, as a substrate to guide connections into different hindbrain regions during development, similar to the auditory system (Katz and Shatz 1996).

Previous work has demonstrated a correlation between the average maximum spike rate and spontaneous activity (Coombs and Janssen 1990; Kroese and Schellart 1992). However, when this correlation is analyzed as a function of stimulus duration, we see a surprising result. We found that cells with a higher spontaneous activity did not generate a higher initial spike rate, but that later in the stimulus these cells maintained their higher spike rate for a longer period. At this point, we do not know the functional relevance of this to the organism.

Complex signals can be encoded by the sequence of spikes within a given time period. We found that afferent neurons in larvae are capable of a generating up to 80 spikes/s for an extended time period, which is similar to adult fishes (Coombs et al. 1998; Kroese and Schellart 1992; Weeg and Bass 2002). We know from previous studies related to mechanoreception that complex signals such as white noise may be represented with a spike train with much lower average spike rate (Bale et al. 2013; Chagnaud et al. 2006; Fox et al. 2010; Goulet et al. 2012; Johnson 1980; Mogdans and Bleckmann 1999; Rieke et al. 1995). In addition to having the potential to encode complex stimuli, larval afferent neurons also respond distinctly to a variety of mechanical stimuli applied to neuromasts (Haehnel-Taguchi et al. 2014). This demonstrates that, even at this early developmental stage, the lateral line system of larval zebrafish may already generate a rich representation of stimuli.

We found that afferent neurons are tuned to respond to transient rather than sustained signals. Afferent response strength decreased over time, but only to high-frequency stimulation. In other words, the higher the stimulus frequency, the lower the ability for an afferent neuron to maintain a tonic response. Why are lateral line responses to high frequency temporary? One reason may be because high frequencies do not typically exist in the aquatic environment (Dijkgraaf 1963; Kalmijn 1988). When high-frequency signals do exist, they are typically transient, as during a predator attack, so there would be minimal value to devote attention to it for a sustained time period. Transient responses can help the system filter out constant signals like background flow (Engelmann et al. 2000). These responses may also result from filtering mechanisms that take place at higher brain centers (Montgomery et al. 1996). The mechanism responsible for this transient response is not known, but seems similar to the plasticity seen in other hair cell systems (Eatock 2000). In zebrafish, plasticity has been shown to arise at the level of hair cells, from calcium-dependent changes acting on the mechanoreceptor channel directly (Holt and Corey 2000; Ricci et al. 2013). Plasticity could also be contributed at afferent synapses, as the time course of the change is consistent with synaptic vesicle depletion (Flock and Russell 1976; Furukawa et al. 1972; Furukawa and Matsuura 1978). One mechanism, motor model plasticity entailing a physical translocation of receptors on the hair cell bundle, seems unlikely given the bidirectional nature of our stimulus and the time course of the change (Gillespie and Corey 1997; Hudspeth and Gillespie 1994). Experimental studies use a vibrating sphere cannot separate the effect of water from the physiological responses of the lateral line (Coombs and Janssen 1990; Mogdans and Bleckmann 1999; Montgomery et al. 1988; Münz 1985; Weeg and Bass 2002; Wubbels 1992). Our direct deflection protocol allowed us to experimentally determine the effect of the fluid medium on afferent responses. We were able to show that the fluid medium shifts the response profile of an afferent neuron to higher frequencies and affects spike rate and synchronization. This frequency-dependent signal attenuation has been predicted by theoretical work which has shown that signals generated by low-frequency stimuli are attenuated more by the hydrodynamic boundary layer (McHenry et al. 2008; Windsor and McHenry 2009). We show here, for the first time, physiological confirmation from afferent recordings that the presence of water filters out information at the lower frequencies.

Our results in larvae occur at a dynamic developmental stage where not all afferent neurons are fully developed and are still in the process of making contacts with proliferating neuromasts. Nevertheless, we expect the general principles of frequency detection to be preserved in adults. We also expect similarities to extend to other vertebrate hair cell systems, since the lateral line system is structurally and molecularly similar to the mammalian vestibular and auditory system (Nicolson 2005). Even though hair cell systems show marked differences in their receptor sensitivity, dynamic properties and frequency responses, the underlying mechanisms that govern these attributes can be expected to share common principles. Our findings, therefore, lay the foundation for a better understanding of an important hair cell system in a model vertebrate organism.

GRANTS

This work was supported by National Institute on Deafness and Other Communications Disorders Grant RO1-DC-010809 and National Science Foundation Grant IOS1257150 to J. C. Liao.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: R.L. and J.C.L. conception and design of research; R.L. and A.B. performed experiments; R.L., O.A., and A.B. analyzed data; R.L., O.A., and J.C.L. interpreted results of experiments; R.L., O.A., and J.C.L. prepared figures; R.L., O.A., and J.C.L. drafted manuscript; R.L., O.A., and J.C.L. edited and revised manuscript; R.L., O.A., and J.C.L. approved final version of manuscript.