Progressive glucose stimulation of islet beta cells reveals a transition from segregated to integrated modular functional connectivity patterns

Abstract

Collective beta cell activity in islets of Langerhans is critical for the supply of insulin within an organism. Even though individual beta cells are intrinsically heterogeneous, the presence of intercellular coupling mechanisms ensures coordinated activity and a well-regulated exocytosis of insulin. In order to get a detailed insight into the functional organization of the syncytium, we applied advanced analytical tools from the realm of complex network theory to uncover the functional connectivity pattern among cells composing the intact islet. The procedure is based on the determination of correlations between long temporal traces obtained from confocal functional multicellular calcium imaging of beta cells stimulated in a stepwise manner with a range of physiological glucose concentrations. Our results revealed that the extracted connectivity networks are sparse for low glucose concentrations, whereas for higher stimulatory levels they become more densely connected. Most importantly, for all ranges of glucose concentration beta cells within the islets form locally clustered functional sub-compartments, thereby indicating that their collective activity profiles exhibit a modular nature. Moreover, we show that the observed non-linear functional relationship between different network metrics and glucose concentration represents a well-balanced setup that parallels physiological insulin release.

Beta cells secrete insulin in response to stimulation by energy rich molecules in a regulated manner and play a central role in whole-body energy homeostasis¹. In vivo, beta cells are organized into microorgans called islets of Langerhans. All beta cells of an islet of Langerhans are coupled into a single functional unit by means of the gap junction protein Connexin 36 (Cx36) that allows for electrical coupling and exchange of small signaling molecules between physically adjacent cells. One of these small signaling molecules being calcium ions². In this way, a coordinated activity in a large number of cells can be established, thereby leading to a regulated exocytosis of insulin³,⁴.

The mechanisms that govern insulin secretion at the single-cell level have been studied extensively. An increase in extracellular glucose concentration leads to an increased entry of glucose into the beta cell, an increased metabolic production of ATP and a decrease in the open probability of ATP-sensitive potassium ion channels. Consequently, the beta cell depolarizes and the voltage-sensitive calcium ion channels open to increase the intracellular calcium concentration ([Ca²⁺]_i) that triggers the calcium-sensitive exocytosis of insulin granules. This calcium-induced exocytosis is believed to be augmented via a less well known amplifying pathway⁵. The changes in membrane potential, [Ca²⁺]_i as well as exocytosis occur in the form of synchronous oscillations⁶,⁷,⁸,⁹,¹⁰. Insulin acting on different target cells in the body subsequently reduces glucose concentration to stop the stimulation of insulin release and prevent hypoglycemia by means of a negative feedback loop.

At the tissue level however, the relationship between the collective activity of cell populations and hormone release is not completely understood¹¹. This is mainly due to the fact that until recently, our ability to study the physiology of many cells simultaneously had largely been limited by the existing experimental methods¹². The investigations of the intercellular communication between beta cells had mostly relied on imaging changes in [Ca²⁺]_i in isolated islets. These measurements, using either CCD cameras with limited temporal resolution and a height of the focal plane larger than a single cell⁸,¹³ or confocal microscopy with limited uptake of [Ca²⁺]_i-sensitive fluorescent dyes, constrained the number of simultaneously studied cells to a few cells from the mantle of the islet¹⁴,¹⁵. Recently, the drawbacks of the existing experimental techniques were circumvented by applying high spatial and temporal resolution confocal functional multicellular calcium (fMCI) and membrane potential imaging to the islets of Langerhans in tissue slices⁷,¹⁶. Additionally, two-photon confocal microscopy in combination with extracellular polar fluorescent dyes enables the study of exocytosis from all beta cells within a focal plane¹⁷,¹⁸. Therefore, from a technical point of view, it is now possible to study the collective behavior of cell populations, such as the islet of Langerhans, and more specifically the degree of coupling and residual heterogeneity in such populations.

The heterogeneity of beta cells is most pronounced when cells are dispersed or uncoupled, thereby completely or partially losing their social context within the functional syncytium of the islet¹²,¹⁹. Early studies proposed that such individual beta cells exhibit differences in glucose metabolism²⁰,²¹ and insulin secretion²². More recent works on the dynamics of [Ca²⁺]_i in isolated or uncoupled cells further confirmed heterogeneity of beta cells. In isolated beta cells, [Ca²⁺]_i responses were elicited at very different threshold concentrations of glucose, with a significant proportion of cells responding only to unphysiologically high concentrations of glucose or tolbutamide²³. In uncoupled cells, [Ca²⁺]_i responses to a given concentration of glucose were unsynchronized²⁴,²⁵.

In an intact islet, these heterogeneities are largely attenuated and the islet functions more homogeneously than isolated or uncoupled cells¹². The cells within an islet respond metabolically over a more confined glucose concentration range²¹,²⁶ and the membrane potential and [Ca²⁺]_i oscillations of cells within an islet are, in contrast to single and uncoupled cells, in phase⁶,¹⁰,¹⁵. Finally, it has long been known that intact islets display a higher glucose stimulated insulin release than isolated and reaggregated, but not coupled beta cells²⁷.

However, the activity of beta cells within an islet is not completely synchronized and the islet shall not be regarded as a single large cell. Namely, the membrane potential and [Ca²⁺]_i changes spread over the islet in a wave-like manner⁷,¹³,¹⁶. Moreover, it was recently shown that in terms of exocytosis, upon stimulation with glucose, not all beta cells within an islet respond at the same time but are progressively recruited with increasing levels of stimulation¹⁷. Thus, in an islet there is a considerable degree of heterogeneity between individual beta cells.

It is important to focus on and quantify the level of heterogeneity among beta cells, since it was demonstrated that a larger-than-normal degree of heterogeneity, possibly due to disruptions to the normal intercellular communication, could play a role in type 2 diabetes mellitus²⁵,²⁸,²⁹,³⁰. Thus, studying how the activity of a large number of heterogeneous beta cells is aligned functionally, how the functional syncytium breaks down, and determining where the increasing heterogeneity results in disease, is of great importance.

However, before embarking on this journey, it is important to reevaluate the parameters on which our predictions about the heterogeneity of beta cells are based and assess a possibly present and physiologically important residual heterogeneity between beta cells in normal islets in a quantitative manner. We believe that such a reevaluation would make it possible to draw a line between normal and pathological function and predict or detect the development of diabetes mellitus.

From the analytical point of view, one possible way to better understand interactions between cells and the functioning of complex biological systems relies on the modern theory of complex networks³¹. Network concepts have been successfully applied on various scales of living organisms ranging from the organization of single cells³² to that of entire ecosystems³³. From the viewpoint of clinical applications, the greatest progress in this context has been done in the field of neuroscience³⁴. The modern neuroimaging technologies allow the acquisition of comprehensive datasets of anatomical or functional connection patterns in the human brain, thereby providing new insights into the structure and functionality of healthy human brain as well as new insights into many brain disorders³⁵. Impaired and disrupted complex brain networks were reported in autism³⁶, schizophrenia³⁷, and multiple sclerosis³⁸. Moreover, recent investigations of functional network analysis exceed the stationary representation by focusing on dynamical tracking of the changes in brain activity associated with task performance. It has been shown that the brain's network organization reconfigures due to cognitive efforts³⁹, dynamic changes in the sensory environment⁴⁰, learning processes⁴¹, and during stroke recovery processes⁴².

While being well acknowledged in the field of neuroscience, the application of network concepts has not yet received very much attention at the tissue level, where individual cells represent the nodes of a network. Several tissues are often organized as networks, they evolve in time and their cells can be regarded as dynamic systems, which interact with each other. But they have not been studied as such, predominantly due to a lack of experimental techniques that would enable the necessary assessment of function in a large number of cells simultaneously, as noninvasively as possible, and over longer periods of time. First endeavors combining fMCI and graph-theoretical approaches were conducted on pituitary endocrine cells⁴³,⁴⁴,⁴⁵. We and others succeeded in applying these methodologies to study the activity of beta cell populations¹¹,²⁴,⁴⁶. In particular, in our previous study we showed that the functional connectivity extracted on the basis of [Ca²⁺]_i dynamics exhibits small-world topological features, which are most pronounced in the regime of high glucose stimulation⁴⁶. This finding was later confirmed by Hodson and coworkers¹¹. Recently, these techniques were also successfully applied at uncovering the functional cellular connectivity in a network of astrocytes⁴⁷.

In the present study, we continue our quest to explore functional heterogeneity in beta cells in islets of Langerhans in situ by applying advanced analytical tools from the realm of complex network theory. The tools have been applied on long temporal traces obtained by confocal fMCI of beta cells stimulated in a stepwise manner with a range of glucose concentrations from the substimulatory concentration of 6 mM to the above-physiological, but traditionally often used 12 mM glucose. Employing this experimental approach, we demonstrate a modular nature of mouse islets, revealing a multiunit organizational principle in a structure with an apparently homogeneous microanatomy and even largely synchronous activity in terms of traditional physiological measures.

Results

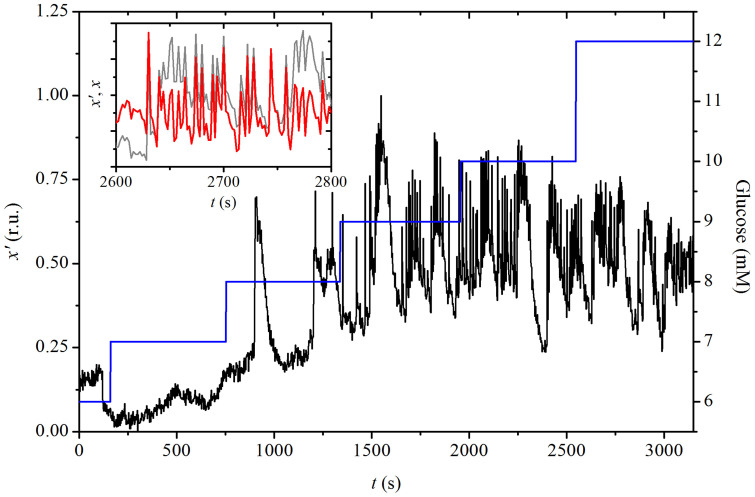
Confocal fMCI imaging was used to monitor [Ca²⁺]_i signals emanating from Oregon Green 488 BAPTA-1 (OGB-1)-loaded beta cells in acute tissue slices (see Methods). The temporal evolution of [Ca²⁺]_i in a typical beta cell under progressive stepwise stimulation with glucose from 6 mM to 12 mM is shown in Fig. 1. As expected, the frequency of oscillations [Ca²⁺]_i as well as the basal [Ca²⁺]_i level increase with increasing concentrations of glucose. The inset shows a segment of the [Ca²⁺]_i trace of the same cell x(t) after subjecting it to ensemble empirical mode decomposition (EEMD) (see Methods).

Figure 1. Experimentally measured temporal evolution of [Ca²⁺]_i in a typical beta cell x′(t) in response to different concentrations of glucose expressed in relative units (r.u., black line).

The blue line denotes stepwise increases in glucose concentration with the respective axis located on the right. In the inset, a segment of the original signal (grey line) and the corresponding EEMD x(t) (red line) are shown.

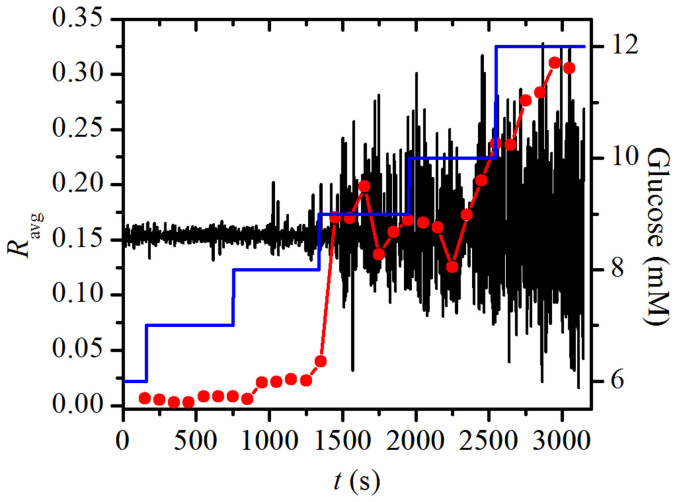
We proceeded with the sliding window correlation analysis of beta cell dynamics in order to examine the temporal evolution of the average correlation coefficient R_avg. Results shown in Fig. 2 reveal that the level of correlation progressively increases with increasing concentrations of glucose. For the calculation of correlations and for the following network constructions we used, [Ca²⁺]_i traces that were subjected to EEMD in order to exclude baseline trends. These variations of the baseline activity are the so called slow [Ca²⁺]_i oscillations and most probably reflect glycolytic oscillations in some cells of the islet and not the rapid [Ca²⁺]_i oscillations that spread from cell to cell by means of depolarization waves and are the subject of this study⁴⁸. In addition, fluctuations in baseline trends could be an experimental artefact due to drifts in the perifusion chamber. Furthermore, we verified if a similar behavior can be observed also in other islets, subjected to similar protocols. Indeed, results shown in Fig. S1 reveal that a very similar temporal evolution of the average correlation coefficient R_avg can be observed in three other islets as well, when the concentration of glucose is progressively increased.

Figure 2. The temporal evolution of the average correlation coefficient (red line with symbols) and the mean-field signal of EEMD processed [Ca²⁺]_i activity of beta cells (black line).

The blue line denotes the concentration of glucose. In the calculation of the sliding window correlation analysis (see Methods), Δτ was set to 300 s and step Δn to 100 s.

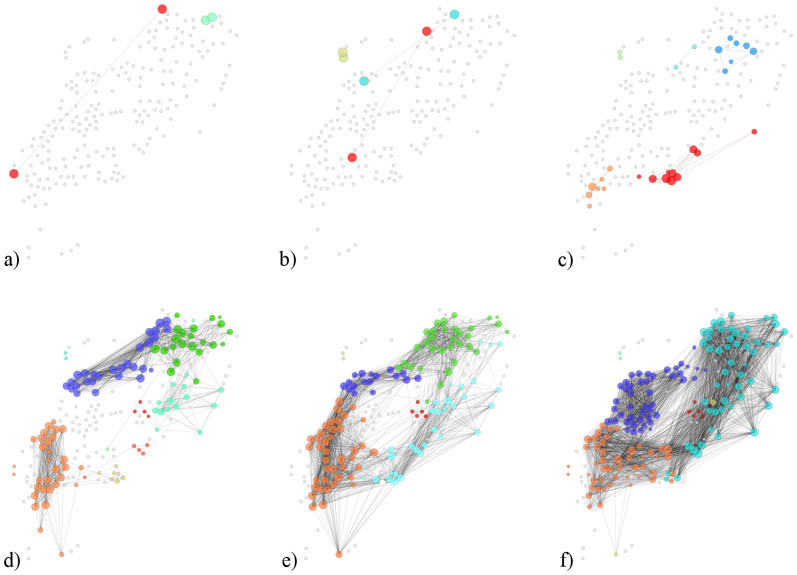
Functional connectivity maps were constructed on the basis of pairwise correlations between [Ca²⁺]_i signals of individual cells. Two cells were considered to be connected if their Pearson product-moment correlation over a certain time interval Δτ exceeded a predetermined threshold value R_th (see Methods). Fig. 3 features the beta cell functional network architectures for different concentrations of glucose. We can observe that for low stimulation levels (≤8 mM) only isolated and rarely synchronized activities are detected. With increasing concentrations of glucose, the network becomes denser, which reflects the increase of the average correlation coefficient shown in Fig. 2. Furthermore, it can be observed that the beta cell functional network is modular. Namely, well pronounced local communities are identified in which mostly interactions between nearest neighbors are present. It appears that the beta cell syncytium is structured in several sub-networks in each of which the degree of synchronization between the cells is very high. These sub-compartments are strongly segregated at lower concentrations of glucose, whereas for high concentrations they become more integral, yet still well expressed and localized. Thus, it appears that for different levels of stimulation the synchronization activity of beta cells is regulated in segregated local clusters. Furthermore, this localized organization suggests that physical constraints drive the structure of the beta cell functional network. A more precise tracking of the temporal evolution of the beta cell functional network by progressively increasing concentrations of glucose can be observed in the Supplementary video S1. In order to further corroborate our findings, we show in Fig. S2 beta cell functional networks of three additional islets (the same as in Fig. S1) subjected to similar protocols, under 8 mM and 12 mM glucose stimulation. Evidently, in all three cases the networks are sparse and very segregated in 8 mM glucose, whereas in 12 mM glucose they are much more dense and interconnected, but with well-expressed localized communities.

Figure 3. Functional networks of beta cells at different concentrations of glucose: a) 6 mM, b) 7 mM, c) 8 mM, d) 9 mM, e) 10 mM, f) 12 mM.

Colors of circles denote the modularity classes (communities). Grey circles signify unconnected cells. The threshold for functional connectivity R_th was set to 0.7. The number of cells in the examined slice was 200. The positions of nodes correspond to physical positions of cells within the examined islet of Langerhans.

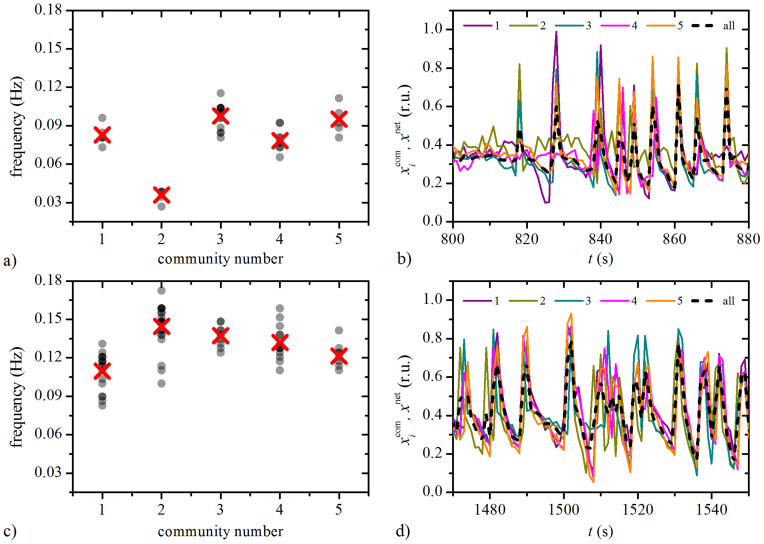
It remains of interest to identify the reasons for the segmentation into functional sub-compartments. For this purpose we calculated the frequencies in five largest communities in the network, the corresponding EEMD-processed [Ca²⁺]_i mean-field signals within individual communities 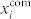, and the mean-field signal of the whole network x^net, at 9 mM and 12 mM glucose. The results for the islet analyzed and shown in Figs. 2 and 3 are presented in Fig. 4. It can be observed that the average frequencies under both stimulation levels are not completely unified. These discrepancies in the frequencies are principally not a consequence of uncoordinated intercellular activity, but rather a result of unexecuted oscillations in particular groups of cells, as it can be seen from the courses of individual mean-field signals. Furthermore, an inspection of the mean-field signals (Figs. 4(b) and 4(d)) reveals, that the amplitude of x^net is for the most of the time noticeably lower than the amplitude of signals in individual communities 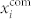, thereby indicating that the [Ca²⁺]_i dynamics among communities is not completely phase synchronized. To conclude, the existence of communities in the beta cell functional network can be attributed to a more simultaneous activity as well as to a better phase synchronization within other three individual groups of cells. The same behavior is observed also in the three other islets.

Figure 4.

Frequency distributions within 5 largest communities under 9 mM (a) and 12 mM (c) glucose. Grey dots denote frequencies of individual cells and the red crosses signify the average frequency in the given community. It can be observed that the frequencies are in average higher under 12 mM glucose stimulation, and that the average values in different communities are not exactly the same. The corresponding mean-field signals of individual communities 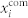(colored lines) and of the whole network x^net (black dotted line) under 9 mM and 12 mM glucose are shown in panels (b) and (d), respectively. The amplitude of the whole-network mean-field signal x^net is lower than the amplitude in individual communities, thereby indicating that individual signals are not completely phase synchronized.

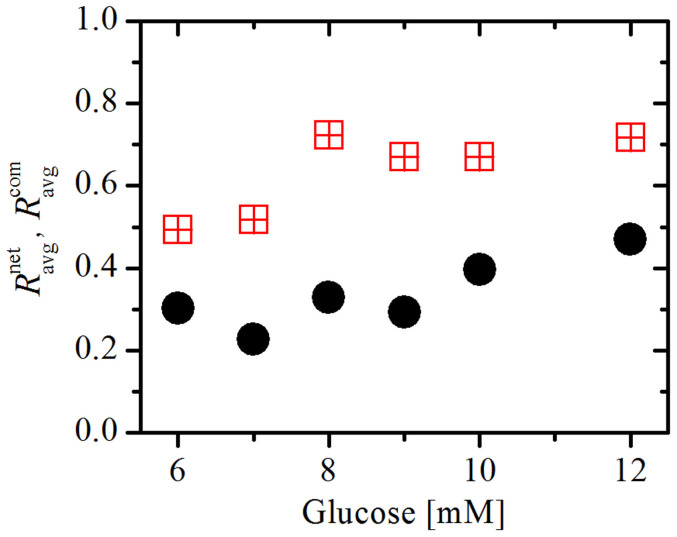
To further analyze the organization of interconnected modules of beta cells, we computed the average correlation coefficient between cell pairs within each of the communities, 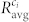. The overall average correlation in communities 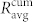was then defined as the average 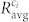for all communities. The results presented in Fig. 5 feature the values of 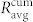for different concentrations of glucose. For comparison, we additionally calculate the average correlation between all cell pairs in the network, 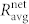. The values of 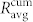and 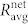represent the averages of four different functional networks having altogether 722 nodes (slices shown in Figs. 3 and S2). Evidently, the correlations between cell pairs in individual communities are much higher than the correlation at the level of the whole slice, which further supports the idea of segregated synchronization activities in the islet. These findings are qualitatively independent of the choice of the connectivity threshold R_th (see Fig. S3).

Figure 5. Average correlation between cell pairs in individual communities 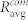(red squares) and between all connected cells in the network 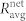(black circles) at different concentrations of glucose.

In the calculation the connectivity threshold R_th was set to 0.7. The results are based on the average of four different functional networks (slices presented in Figs. 3 and S2) having altogether 722 nodes.

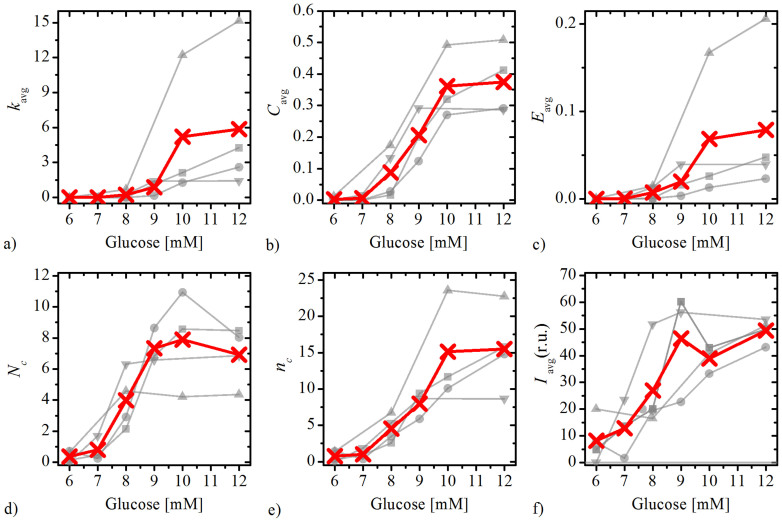
To describe the temporal evolution of the network characteristics more quantitatively, we calculated several network measures (see Methods) at different concentrations of glucose. For a more precise and reliable quantification, the calculations were performed for four different islets (the same as shown in Figs. 3 and S2). In Fig. 6 we present the results showing the network measures for each concentration of glucose. The light grey lines with symbols denote values in individual islets and the thick red line with symbols signifies the average over all four functional networks. Quite considerable discrepancies in absolute values of network metrics can be observed, which reflect the inter-islet variability, whereas most notably, the functional relationship between different network metrics and glucose concentration is very similar in all four islets.

Figure 6. Different network measures at different concentrations of glucose for four islets (the same as shown in Figs. 3 and S2).

a) average degree, b) average clustering coefficient, c) global efficiency, d) average number of communities, e) average size of communities, f) average length of functional connections. Light grey line with symbols denote the values in individual islets, whereas the thick red lines with crosses indicates the average. In all calculations the connectivity threshold R_th was set to 0.7.

In Fig. 6(a), the average degree of cells k_avg is shown as a function of glucose concentrations. Its increase at higher concentrations of glucose is related to a greater level of synchronization between beta cells (see Fig. 2), as the correlation coefficient between more and more cell pairs exceeded the threshold and consequently the network became denser. We believe that the higher network degree is a result of a more pronounced communication via electrical synapses and possibly also other more long-range-oriented communication mechanisms. The average clustering coefficient C_avg is a measure for the network's functional segregation and is indicative of small-worldness of the network⁴⁹. Results in Fig. 6(b) show that in the beta cell network a prevalence of clustered connectivity around individual cells was detected, but only for high enough stimulation levels reaching a plateau value at a glucose concentration of >9 mM. Another measure of interest is the global efficiency E, which reflects the functional integration of the tissue such as the traffic capacity of a network in the form of signal-propagation speed and degree of synchronizability. Fig. 6(c) features the results for different glucose concentrations. It can be noticed that for high stimulation levels (≥10 mM) an efficient information exchange throughout the entire network was achieved.

We also focused on the evolution of the modular structure of the beta cell network. Figs. 6(d) and (e) show the number N_c and average size n_c of communities that change with increasing concentrations of glucose. Notably, for glucose concentrations >8 mM the networks are in average composed of around 7 densely interconnected groups of cells. The size of these communities increases markedly with increasing concentrations of glucose, but reaches a plateau at 10 mM. Finally, we examined the average length of functional connections I_avg as a function of glucose concentration. This parameter reflects either prevalent adjacent cell-to-cell communication in case of short distances or, alternatively, cell-to-cell communication spanning over several cells that is mediated either by postganglionic nerve axons within islet or diffusible paracrine factors such as NO. Fig. 6(f) reveals that I_avg, similarly to other network metrics, rises between 7 mM and 10 mM glucose, while for concentrations >10 mM the average link length remained more or less constant. Notably, at high levels of stimulation, the average range of interactions between beta cells is around 45 μm.

Finally, to be able to ascribe the observed effects upon network metrics to increasing concentrations of glucose, we had to assess whether there are any time-dependent increases in parameter values in constant glucose. For this purpose, we analyzed eight additional islets. Four of them were stimulated with 8 mM and four of them with 12 mM of glucose for the entire period of stimulation. For all of them we calculated the temporal evolution of the same network metrics as presented in Fig. 6. Results in Fig. S4 reveal that the values obtained during constant stimulation with 8 mM and 12 mM glucose were comparable with the values obtained for the respective concentrations during stepwise stimulation. Additionally, with the exception of N_c, on average all parameters displayed lower values in 8 mM glucose than in 12 mM glucose throughout the entire period of stimulation. Finally, although beyond the scope of this paper, a clear trend toward decreasing parameter values with time was detected for constant long-term stimulation with 12 mM glucose.

Discussion

Individual or uncoupled beta cells have been found to be intrinsically heterogeneous and as such incapable of collectively adjusting their insulin secretion rates in accordance with blood glucose levels. Intercellular communication via gap junctions attenuates the heterogeneous nature of beta cells by synchronizing their activity and suppressing any subtreshold responses as well as recruiting high glucose responders of individual beta cells, thereby representing the fundamental mechanism ensuring whole body energy homeostasis²⁵,²⁶,⁵⁰,⁶⁵. In this study we obtained additional insight into these issues by analysing how the functional network of beta cells changes during step-wise elevations of stimulatory glucose levels, ranging from 6 mM (basal) to 12 mM (high). We showed that for basal glucose levels the collective dynamics is poorly synchronized resulting in a sparsely connected functional network. With increasingly stimulatory glucose levels, the multicellular system gets more synchronized and evolves into a more densely connected network with increasingly expressed small-world topological features, characterized by high global efficiency (short internodal distances) and a highly clustered organization⁴⁹. This is in agreement with our previous study where we found that the functional network of beta cells, when exposed to high glucose levels, exhibits small-worldness⁴⁶. In terms of the real network of an islet of Langerhans, the degree of small worldness probably contributes to the robustness of the network in terms of its secretory response and determines its resilience to metabolic and immune perturbations occurring during onset of diabetes mellitus. Furthermore, for glucose values above 10 mM, the network characteristics seem to saturate. This could be caused by spatial constraints which prohibit the establishment of too long connections and hence hinder additional improvements of the evolving functional network. The origin of the spatial constraints could be similar to those discussed in neuronal networks. In the brain it is believed that its small-world functional network is the outcome of an optimization mechanism based on minimizing wiring cost and maximizing efficiency³⁴. Since long-range connections are related to higher cost, this causes spatial constraints. Since in our study, the connectedness of two cells depends on the similarity of their signals, which in turn conceivably depends on the degree of their electrophysiological coupling that is expected to be high at low membrane and high gap junctional conductance, the abovementioned spatial constraint could have its mechanistic substrate in the fact that at a certain level of stimulation, in this case at 10 mM glucose, the membrane conductance reaches its minimum or the junctional conductance its maximum.

Through the process of stimulus-secretion coupling in beta cells, membrane potential changes in the form of bursts of depolarizations are translated to oscillations of [Ca²⁺]_i and finally to pulses of insulin secretion. To assess beta cell activity, all three parameters can be used. Thus, we need to justify the choice of [Ca²⁺]_i as a proxy for beta cell function in our study and comment briefly on the generalizability of our findings. First, from the technical point of view, due to the commercial availability of [Ca²⁺]_i sensitive fluorescent dyes, their ease of use and high signal-to-noise ratio, especially as compared to currently available voltage sensitive fluorescent dyes, [Ca²⁺]_i seems a logical choice. Second, [Ca²⁺]_i is a trigger for exocytosis also in other tissues, where an increase in [Ca²⁺]_i is not brought about by electrical activity and influx of [Ca²⁺]_i, but by secretagogue induced release of Ca²⁺ from internal stores. Some of these tissues are accessible to fMCI and the use of [Ca²⁺]_i in our case facilitates comparison between different tissues. Finally and most importantly, in previous studies by us and other groups employing a wide array of experimental approaches, it was demonstrated that in islets of Langerhans, the relationship between the changes in membrane potential and changes in [Ca²⁺]_i⁷,⁸,¹⁰ as well as between changes in [Ca²⁺]_i and pulses of insulin secretion⁶,⁹,¹⁷,¹⁸ are straightforward. Thus, we are confident that changes in [Ca²⁺]_i are a representative measure of beta cell activity.

In addition, the binding of Ca²⁺ to [Ca²⁺]_i sensitive dyes with different affinities could influence the nature of the observed changes in [Ca²⁺]_i to depart from the ones occurring in vivo or even lead to cell death. Employing an armamentarium of [Ca²⁺]_i sensitive fluorescent dyes with different affinities, we and others have shown largely comparable [Ca²⁺]_i changes, even after prolonged periods of recording⁶,⁷,⁸,⁹,¹⁰,¹⁵,¹⁶,⁴⁶.

In general, in all four analyzed islets, all the network measures obeyed a similar response with respect to increasing concentrations of glucose; a steep increase occurred between 8 mM and 10 mM, whereas above these values a saturation of the network properties was detected. It seems that within these physiological ranges of glucose, the beta cell network exhibits a high level of plasticity, reflected by gradual adjustments of the global efficiency and local organization with respect to the external stimulus. This is in an agreement with the role of beta cells as primary glucose sensors matching their dynamic range with normal physiological fluctuations of plasma glucose. For high concentrations of glucose (10 mM and above), on the other hand, a saturation of the network characteristics occurs, thereby indicating the realization of the maximal operating ability. A similar non-linear behavior within the same physiological range of stimulatory glucose concentrations was experimentally observed from dynamic glucose stimulated insulin release perifusion studies with isolated islets⁵¹. In our experimental setup, it is currently impossible to study insulin secretion simultaneously with [Ca²⁺]_i signals due to the exceedingly small amount of insulin released by an islet within tissue slice in the physiological glucose range.

One of our most important findings is the modular nature of the extracted functional networks, which indicates that beta cells inside the islet of Langerhans form functional sub-compartments. Cells within sub-compartments are clustered and their activity is much more correlated in comparison to the islet as a whole. For low levels of glucose, only completely segregated local areas occasionally responded to stimulation. With increasing levels of the stimuli, a higher number of communities were recruited which got more and more interconnected, thereby making the whole functional network more efficient. The modular behavior of the beta cell functional syncytium was predicted by previous experimental data⁴⁶. Stepwise glucose stimulation progressively recruited cells that were organized in multicellular groups. Recruitment was shown on the level of glucose metabolism⁵², insulin synthesis⁵³ and insulin secretion¹⁷. Since the global efficiency indicates shorter path lengths among nodes, it is also referred to as a measure of functional integration³⁵. This suggests that the islet of Langerhans is capable to continuously improve from a highly segregated into a more integrated functional network. Since cell-to-cell communication coordinates the activities of individual cells, the modular nature of the islets could represent an additional spatially regulated insulin secretion mechanism.

Our control experiments with constant stimulation confirmed that the effects upon network metrics observed during stepwise stimulation can indeed be ascribed to increasing concentrations of glucose. In 8 mM glucose, the parameter values continued to increase after the initial 500 seconds (this was the time period used for each concentration of glucose during stepwise stimulation), but this additional increase was clearly insufficient to raise the parameter values to levels attained in 12 mM glucose. The trend toward a decrease in parameter values in 12 mM glucose warrants further investigation, since it might be a network correlate of glucotoxicity, previously observed in concentrations of glucose higher than 10 mM⁵⁴. Exploring the effects of constant stimulation with high concentrations of glucose upon network metrics seems especially compelling in the light of a recent study demonstrating that lipotoxicity can target beta cell connectivity²⁴.

Recent studies analyzing mouse and human islets with a complex network approach, that have produced largely compatible results regarding the general connectivity patterns in mouse islets, have not explicitly detected any communities¹¹,¹⁶,²⁴. First, this might be due the fact that these studies have not specifically looked for the presence of communities analytically in a way we did in our present study. One of the reasons that communities have not been detected before might be that glucose concentration of 11 mM¹¹,²⁴ or 12 mM¹⁶ has been used to evoke [Ca²⁺]_i responses. As demonstrated in the present study, at this high concentrations of glucose, the activity of cells belonging to different communities is most aligned, i.e. the networks are quite dense, and this might have caused that the functional compartmentalization has escaped our attention.

It was shown that rodent islets are of polyclonal origin and that the cells stemming from the same progenitor remain spatially clustered⁵⁵. Thus, it is tempting to speculate that the functional subunits of an islet of Langerhans might overlap with the embryological subunits defined by a common progenitor. This awaits further elucidation, possibly involving human tissue, since recently, a polyclonal origin of beta cells was also demonstrated for human islets of Langerhans⁵⁶.

It was pointed out that a balanced combination of segregated and integrated information processing, established via efficient small-word topological features, ensures normal brain functioning⁵⁷. Disruptions to this balance can lead for instance to autism, in case of predominantly segregated information processing⁵⁸, or schizophrenia in case of predominantly integrated information processing³⁷. It is reasonable to speculate that anomalies in the functional connectivity could results in pathological conditions of islets, leading to diabetes mellitus. Hence, additional experimental and theoretical studies are needed in order to gain knowledge about how this multicellular system regulates its functioning through cell-to-cell communication in disease states.

Finally, in our study beta cells exhibited greatest responsiveness at a range of glucose concentrations commonly experienced by animals in vivo and significantly below the ones traditionally used in electrophysiological, [Ca²⁺]_i imaging and insulin secretion experiments, where in our hands, the network parameters typically reached their maxima and stabilized. Perhaps, the supraphysiological concentrations were classically used due to lower inter-specimen variability and greater reproducibility of results. This study suggests, however, that in order to learn more about the physiology of beta cells and their heterogeneity, in future work, lower, more physiological stimulatory concentrations of glucose should be used.

Methods

Ethics statement

All methods and animal protocols were performed in strict accordance with all national regulations and ethical guidelines approved by the Ministry of Agriculture and Environment, Republic of Slovenia (Permit Number: 34401-61-2009/2).

Experimental protocol

Experimental protocols for preparation of acute pancreas tissue slices and confocal [Ca²⁺]_i imaging were described in detail previously¹⁶. In brief, tissue slices were cut from pancreata of 10–20 week old NMRI mice of either sex. After sacrificing the animals by cervical dislocation, low-melting point 1.9% agarose in extracellular solution (ECS, consisting of (in mM) 125 NaCl, 26 NaHCO₃, 6 glucose, 6 lactic acid, 3 myoinositol, 2.5 KCl, 2 Na pyruvate, 2 CaCl₂, 1.25 NaH₂PO₄, 1 MgCl₂, 0.5 ascorbic acid) at 40°C was injected into the proximal common bile duct clamped at the papilla of Vater. Small blocks of tissue from the agarose-injected pancreas were cut with vibratome (Leica vt1000) into 140 μm-thick slices in an ice-cold ECS continuously bubbled with a gas mixture (95% O₂ and 5% CO₂, pH of 7.4). Slices were incubated in a calcium dye loading solution composed of 6 μM Oregon Green 488 BAPTA-1 AM, 0.03% Pluronic F-127 (w/v) and 0.12% dimethylsulphoxide (DMSO, v/v) in HEPES-buffered saline (HBS, consisting of (in mM) 150 NaCl, 10 HEPES, 6 glucose, 5 KCl, 2 CaCl₂, 1 MgCl₂; titrated to pH = 7.4 using 1 M NaOH) for 50 minutes at room temperature and protected from light.

Confocal [Ca²⁺]_i imaging using OGB-1 was performed on a Leica TCS SP5 AOBS Tandem II upright confocal system using a Leica HCX APO L 20× water immersion objective (NA = 1.0). The dye was excited by an argon 488 nm laser. The emitted fluorescence in the range of 500–700 nm was collected by Leica HyD detector. Individual slices were imaged in a temperature-controlled bath chamber at 37°C (TC05, Luigs & Neumann) mounted on the microscope and continuously perifused with ECS. Sampling rate was 0.5–1 Hz at 512 × 512 pixels. The [Ca²⁺]_i oscillations were analyzed off-line employing custom-made scripts.

Analysis of time series

Ensemble empirical mode decomposition

The recorded time series were subject to Huang-Hilbert type empirical model decomposition⁵⁹ in order to retrieve baseline trends. In this manner, we were able to extract undistorted [Ca²⁺]_i dynamics of individual cells. In particular, we used the upgraded ensemble empirical mode decomposition (EEMD) proposed by Torres et al.⁶⁰. The recorded time series 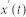were decomposed into the so called intrinsic mode functions (IMFs). Initially, white noise w_i(t) in the range w_i(t) ∈ [−0.1,0.1] is added to the original time series: 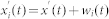, where i refers to the i-th realization of white noise at time t. Then, local maxima and minima are detected in the signal 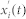. We separately interpolated cubic spline lines through the detected maxima and minima and created an upper and lower envelope through them. Their mean value m₁(t) and the difference h₁(t) between the time series 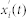and the mean m₁(t) was calculated. The process was repeated to ensure more symmetric wave profiles⁵⁸. In the next repetition h₁(t) was treated as the input. Again the upper and lower envelopes were constructed on the basis of the detected minima and maxima, and the difference h₁₁(t) was calculated between the mean of the envelopes m₁₁(t) and h₁(t). In general, the process was defined as follows:

where k stands for the k-th repetition of the procedure described above. The process was repeated until the standard deviation (SD) in the difference between h_1k and h_1(k−1) was above a predefined threshold (in our case 0.0001). Afterwards, h_1k became the first intrinsic mode during the i-th generation of white noise 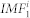. This mode contained the fastest time scale. In order to calculate other intrinsic modes of the signal, we took the signal 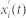and calculated the residue 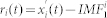. Since 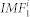was excluded from r_i(t) we repeated the process described above on the signal r_i(t) and generated the second mode 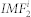. One can continue the process of decomposition until the residual becomes a monotonic function r_i,n(t). Hence the signal 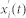can be expressed as:

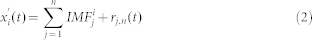The true IMFs of the signal 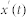were than calculated as the average over all m realizations of white noise as:

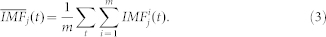The true monotonic characteristics 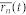of the signal 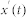were calculated in the same manner:

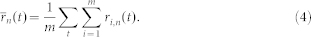Once all the true IMFs and monotonic characteristics of the original signal were determined, we excluded all the modes except the modes that possessed relevant dynamical features. Thus, the time series used for subsequent analysis x(t) was calculated as:

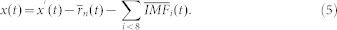Analysis of time series correlations

For the characterization of dynamical correlations between beta cells we calculated the correlation coefficient between the signals of the i-th and j-th cell, defined as follows:

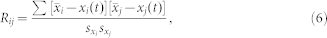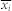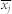where and are the mean values of the time series x_i(t) and x_j(t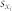), and and 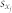the corresponding standard deviations. The correlation coefficient R_ij indicates the linear relationship between the dynamics of the i-th and the j-th cell. Values of R_ij are bounded within [−1,1], whereby −1, 0 and 1 signify anti-correlation, no-correlation and complete correlation, respectively. In order to describe the level of global correlation in the whole slice, we calculated the average correlation coefficient:

For the visualization of the temporal evolution of the average correlation coefficient, we made use of the sliding window correlation analysis. In particular, we calculated the average correlation coefficient between all pairs of cells in the interval Δτ and shifted it throughout the time series with a step Δn.

Construction and characterization of functional beta cell networks

Extraction of functional networks from Ca²⁺ signals

The adjacency matrix d(t) of the evolving functional network was constructed according to the correlation coefficients R_ij(t) between cells pairs. Two cells i and j were regarded as connected in a given time interval Δτ if the correlation coefficient R_ij(t) exceeded or equaled a threshold value R_th. The value of R_th was selected in accordance to the corresponding R², in such a way, that at least 50% of the variation in system, can be explained with a linear relationship among a cell pair (we use R_th = 0.7 in the most of the calculations). These thresholding of the correlation matrix leads to a time-dependent connectivity matrix, whose ij-th element d_ij(t) equals 1 if the nodes i and j are connected in the interval Δτ and 0 otherwise. A similar methodology was used for extraction of the functional connectivity patterns elsewhere³⁴,⁴⁶.

Node degree and average degree

In an undirected network the degree of a node k_i equals the number of direct edges connecting it to its neighbors. By knowing the individual node degrees we computed the overall degree k_avg of the network as the average over all k_i.

Edges among individual nodal pairs reflect well synchronized mutual dynamical behavior. Therefore, the degree of a cell k_i corresponds to the number of cells with similar time courses. Higher average degree signifies a more synchronized collective behavior of the system.

Clustering coefficient

Functional segregation occurs within highly interconnected groups of nodes. A common way to find such groups is to compute the local clustering coefficient C_i of individual nodes. We implemented the method introduced by Watts and Strogatz⁶¹. The local clustering coefficient C_i of the i-th node is defined as:

whereby n_e stands for the number of existing edges between the neighbors of the i-th node and the term k_i(k_i − 1)/2 reflects the maximal number of possible edges between all its neighbors. The average clustering coefficient C_avg was then computed as the mean value of all C_i.

Global efficiency

A commonly used measure to characterize a network's integration of individual nodes is the network's global efficiency E_avg. In order to compute E_avg, one shall compute all the shortest paths lengths l_ij between all pairs of nodes in the network. Afterwards, E_avg is computed as follows⁴⁹:

Community structure

A community is a partition of a network or a sub-graph in which the nodes are more densely interconnected as in the rest of the network. We will refer to the i-th community of the network as c_i. We implemented the algorithm introduced in ref. 62 to arrange nodes into partitions that maximized a measure called modularity Q. Modularity Q is commonly used as a measure that quantifies how successful the partitioning of a network was refs. ^{63, 64} and is defined as:

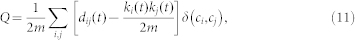where 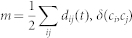, δ(c_i,c_j) is 1 if c_i = c_j and 0 otherwise and k_i(t) is the i-th node degree at time t. The aim of the algorithm is to maximize the modularity by continuously reshaping the community structure of the network. A new configuration is accepted if the gain in modularity ΔQ is positive. The process is repeated until no further improvement in ΔQ is achieved and the most likely community structure of the network is found.

Author Contributions

A.S., J.D. and M.S.R. conceived and designed the experiments. A.S. and J.D. performed the experiments. R.M., M.G. and M.M. designed analysis tools and performed the calculations. R.M., A.S. and M.G. wrote the main manuscript text and prepared the figures. All authors reviewed the manuscript.

Supplementary Material

Supplementary Information

Supplementary information

Supplementary Information

Supplementary video S1