Ion Selectivity in the Selectivity Filters of Acid-Sensing Ion Channels

Abstract

Sodium-selective acid sensing ion channels (ASICs), which belong to the epithelial sodium channel (ENaC) superfamily, are key players in many physiological processes (e.g. nociception, mechanosensation, cognition, and memory) and are potential therapeutic targets. Central to the ASIC's function is its ability to discriminate Na⁺ among cations, which is largely determined by its selectivity filter, the narrowest part of an open pore. However, it is unclear how the ASIC discriminates Na⁺ from rival cations such as K⁺ and Ca²⁺ and why its Na⁺/K⁺ selectivity is an order of magnitude lower than that of the ENaC. Here, we show that a well-tuned balance between electrostatic and solvation effects controls ion selectivity in the ASIC1a SF. The large, water-filled ASIC1a pore is selective for Na⁺ over K⁺ because its backbone ligands form more hydrogen-bond contacts and stronger electrostatic interactions with hydrated Na⁺ compared to hydrated K⁺. It is selective for Na⁺ over divalent Ca²⁺ due to its relatively high-dielectric environment, which favors solvated rather than filter-bound Ca²⁺. However, higher Na⁺-selectivity could be achieved in a narrow, rigid pore lined by three weak metal-ligating groups, as in the case of ENaC, which provides optimal fit and interactions for Na⁺ but not for non-native ions.

Acid sensing ion channels (ASICs) are weakly voltage-dependent, Na⁺-selective channels that belong to the degenerin or epithelial Na⁺ channel (ENaC) superfamily of ion channels¹,²,³. They are devised to sense extracellular protons and open when the external pH decreases, due very often to tissue acidosis resulting from inflammation, muscle ischemia or stroke⁴,⁵,⁶. Largely expressed in the central and peripheral nervous systems⁷, ASICs play pivotal roles in several physiological processes such as nociception, mechanosensation, fear-related behavior, seizure termination, modulation of synaptic plasticity, cognition, and memory⁶. They are potential therapeutic targets for painkillers and drugs against ischemic stroke and panic disorder⁶.

Central to the function of ASICs is their ability to selectively conduct the cognate Na⁺ against a background of competing ions, in particular K⁺ with the same net charge and Ca²⁺ with nearly identical ionic radius as Na⁺ for the same coordination number. ASICs exhibit Na⁺:K⁺ selectivity ranging from 3 to 30:1⁸,⁹,¹⁰ and generally do not conduct divalent ions. However, ASIC1a, unlike other subtypes, is also permeable to Ca²⁺ with a Na⁺:Ca²⁺ permeability ratio of ~18⁸. Interestingly, although the ASIC channels are Na⁺-selective, their Na⁺:K⁺ selectivity is an order of magnitude lower than that of the ENaC (the namesake originator of the ENaC/degenerin superfamily), which ranges from 100–500:1³,¹¹.

The metal ion selectivity of an ion channel is largely determined by its selectivity filter (SF), the narrowest part of an open pore lined with amino acid residues that face the pore lumen and interact specifically with the passing ion(s). The recent X-ray structure (PDB entry 4ntw, 2.07 Å) of an open-state ASIC1a in complex with snake toxin derived from Na⁺-soaked crystals¹² has suggested a putative structure of an ASIC1a homotrimeric SF lined by Gly443 backbone peptide groups from the conserved Gly-Ala-Ser (“GAS”) motif. However, it lacks electron density for Na⁺ in the SF; nevertheless, the distance between the Gly443 backbone oxygen atoms of 6.2 Å, equivalent to a SF pore radius of ~3.6 Å, fits nicely fully hydrated Na⁺ whose hydration radius has been estimated to be 3.58 Ź³. The ASIC1a SF seems to be relatively flexible as it can adjust its geometrical parameters to accommodate the bulkier Cs⁺: the mean distance between the Gly443 backbone oxygen atoms increases from 6.2 Å in the Na⁺-soaked crystals to 7.1 Å in the Cs⁺-bound SF (PDB entry 4nty, 2.65 Å)¹².

Because the SF pore radius is compatible with hydrated Na⁺, the ASIC1a is thought to recognize fully hydrated metal ions and to discriminate among cations on the basis of the hydration ion size¹². Thus, hydrated K⁺ with a radius of ~4.2 Å would be too large to fit in the ASIC1a SF¹²,¹⁴. This raises the following intriguing questions: (1) Is the ion hydration sphere size the sole determinant of metal ion selectivity in ASICs? (2) Do other factors influence the competition between Na⁺ and other monovalent (K⁺) or divalent (Ca²⁺) ions in these systems? If so, how do they control ion selectivity in the ASIC1a SF? Do the key determinants of Na⁺ vs. K⁺ selectivity in the ASIC1a SF differ from those of Na⁺ vs. Ca²⁺ selectivity? (3) Why is the ASIC1a SF less Na⁺/K⁺-selective compared to the ENaC SF?

Here, we endeavor to address these questions by evaluating the metal selectivity properties of model trimeric SFs of various pore sizes and compositions (see Methods). Since the interactions between the metal ions and ligands in the first and second coordination shell play a key role in the Na⁺/K⁺ and Na⁺/Ca²⁺ competition, the structures of the metal-bound model SFs were subjected to all-electron geometry optimization without constraints using density functional theory. The fully optimized geometries were then used to compute the free energy for replacing K⁺ or Ca²⁺ bound inside a model SF, [K⁺/Ca²⁺(H₂O)_n-filter], characterized by an effective dielectric constant x, with Na⁺:

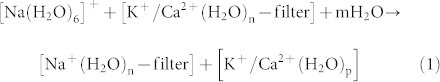where n = 0, 6 or 7, m = 0 or 1, and p = 6 or 7. As the most common hydration number is six for Na⁺ or K⁺ and seven for Ca²⁺ in aqueous solution¹⁵,¹⁶,¹⁷,¹⁸, hexahydrated Na⁺ or K⁺ and heptahydrated Ca²⁺ aqua complexes were modeled. The ion exchange free energy for eq 1 was computed as a sum of the gas-phase free energy ΔG¹ (electronic effects) and the solvation free energy difference between the products and reactants (solvation effects); i.e.,

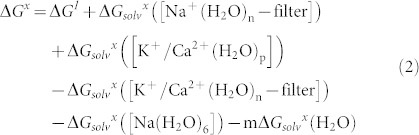A positive ΔG^x implies a K⁺/Ca²⁺-selective filter, whereas a negative value implies a Na⁺-selective one. This approach (eq 2) has yielded trends in the free energy changes with varying parameters (e.g., the metal type, the metal hydration number, the ligand type, and the pore size) that are consistent with experimental findings¹⁹,²⁰,²¹,²²,²³,²⁴,²⁵,²⁶,²⁷. Note that the contributions from other segments of the pore, kinetic barriers, or other ions in the surrounding baths to ion selectivity fall outside the scope of this work, as the aims herein are to identify the key determinants of Na⁺/K⁺ and Na⁺/Ca²⁺ selectivity in the ASIC1a and ENaC SFs.

Results

Binding mode of metal hydrates to a model ASIC1a SF

Na⁺ complexes

The model trimeric ASIC1a SF lined by three backbone peptide groups can bind hexahydrated Na⁺ in two distinct modes (Figure 1): In the first binding mode, each of the three backbone oxygen atoms from the SF forms a hydrogen bond with a Na⁺-bound water molecule, yielding three backbone–water hydrogen bonds (denoted as Na-GGG-3, Figure 1a). This binding mode requires a wide SF pore: the mean distance between backbone oxygen atoms for the Na-GGG-3 complex is 6.8 Å. In the second binding mode, each SF backbone oxygen forms bifurcated hydrogen bonds with two Na⁺-bound water molecules, yielding altogether six backbone–water hydrogen bonds (denoted as Na-GGG-6, Figure 1b). Relative to the Na-GGG-3 complex, the increased number of hydrogen bonds in the Na-GGG-6 complex increases the strength of electrostatic interactions and results in a more compact structure: the mean O–O distance between the SF backbone ligands decreases from 6.8 Å in the Na-GGG-3 complex to 5.1 Å. Notably, the average backbone O–O distance in the Na-GGG-3 and Na-GGG-6 configurations (~6.0 Å) is close to the respective distance (6.2 Å) in the 4ntw crystal structure¹². As the conformation with six hydrogen bonds (Na-GGG-6, Figure 1b) is energetically more favorable (by ~11 kcal/mol) than that with three hydrogen bonds (Na-GGG-3, Figure 1a), it was used for further evaluations (see below).

Figure 1.

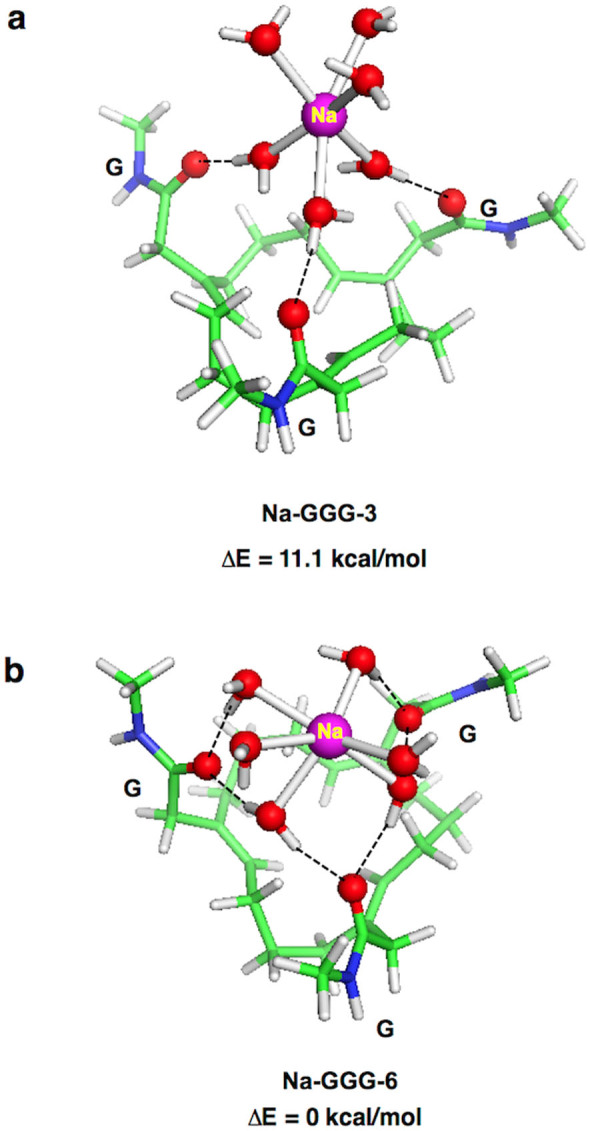
B3LYP/6-31+G(3d,p) optimized structures and relative energies of formation (in kcal/mol) of [Na(H₂O)₆]⁺-GGG SF complexes, characterized with (a) three and (b) six H₂O…O = C hydrogen bonds.

K⁺ complexes

As for the Na⁺ complexes, two distinct binding modes of hexahydrated K⁺ to the model ASIC1a SF were also found with the binding mode containing three hydrogen bonds (K-GGG-3, Figure 2a) less stable than that with four hydrogen bonds (K-GGG-4, Figure 2b). Because K⁺ is larger than Na⁺ with longer K⁺–O(water) bonds²⁸, only one of the backbone oxygen atoms can form bifurcated hydrogen bonds with two K⁺-bound water molecules in the K-GGG-4 complex (Figure 2b), hence the K-GGG-4 complex contains four instead of six hydrogen bonds seen in the Na-GGG-6 complex (Figure 1b). Consequently, the electronic energy of K-GGG-4 is only ~4 kcal/mol lower than that of K-GGG-3, as compared to an energy difference of ~11 kcal/mol for the respective Na⁺ complexes in Figure 1. Furthermore, the contraction of the SF upon [K(H₂O)₆]⁺ binding in the K-GGG-4 rather than the K-GGG-3 complex is less than that upon [Na(H₂O)₆]⁺ binding: the mean backbone O–O distance difference between K-GGG-3 and K-GGG-4 is 0.5 Å, whereas that between Na-GGG-3 and Na-GGG-6 is 1.7 Å. This suggests that the number of HOH---O = C contacts is an important determinant of the structure and energetics of these systems.

Figure 2.

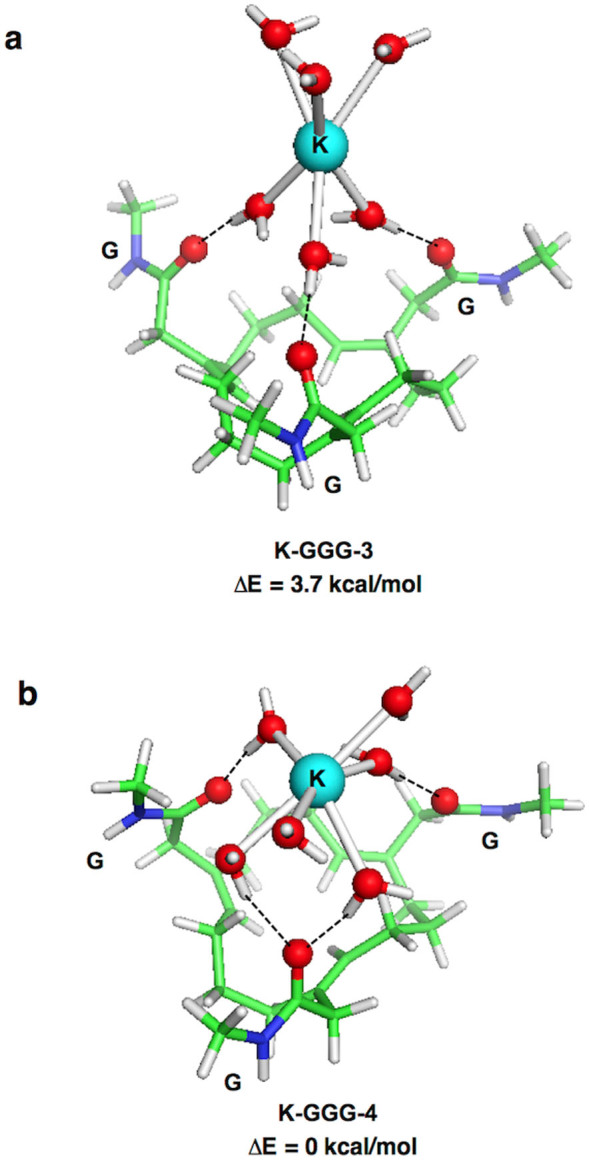
B3LYP/6-31+G(3d,p) optimized structures and relative energies of formation (in kcal/mol) of [K(H₂O)₆]⁺-GGG SF complexes, characterized with (a) three and (b) four H₂O…O = C hydrogen bonds.

Ca²⁺ complexes

As the ionic radius of hexa or heptacoordinated Ca²⁺ (1.00 or 1.06 Å) is similar to that of Na⁺ (1.02 Å)²⁹, each of the three SF backbone oxygen atoms should be able to form bifurcated hydrogen bonds with water molecules. Indeed, each of the SF carbonyl oxygen atoms formed two hydrogen bonds with water ligands in the fully optimized structure of hexahydrated Ca²⁺ in the GGG SF (Ca-GGG-6, Figure 3a), but one of the carbonyl oxygen atoms formed hydrogen bonds with three water molecules in the optimized structure of heptahydrated Ca²⁺ in the GGG SF (Ca-GGG-7, Figure 3b), which thus has an additional HOH---O = C hydrogen bond. Because of the stronger Ca²⁺–OH₂---O = C electrostatic interactions, the Ca²⁺-bound structures are quite compact with a mean SF O–O distance of 5.4 Å for Ca-GGG-6 and 5.5 Å for Ca-GGG-7.

Figure 3.

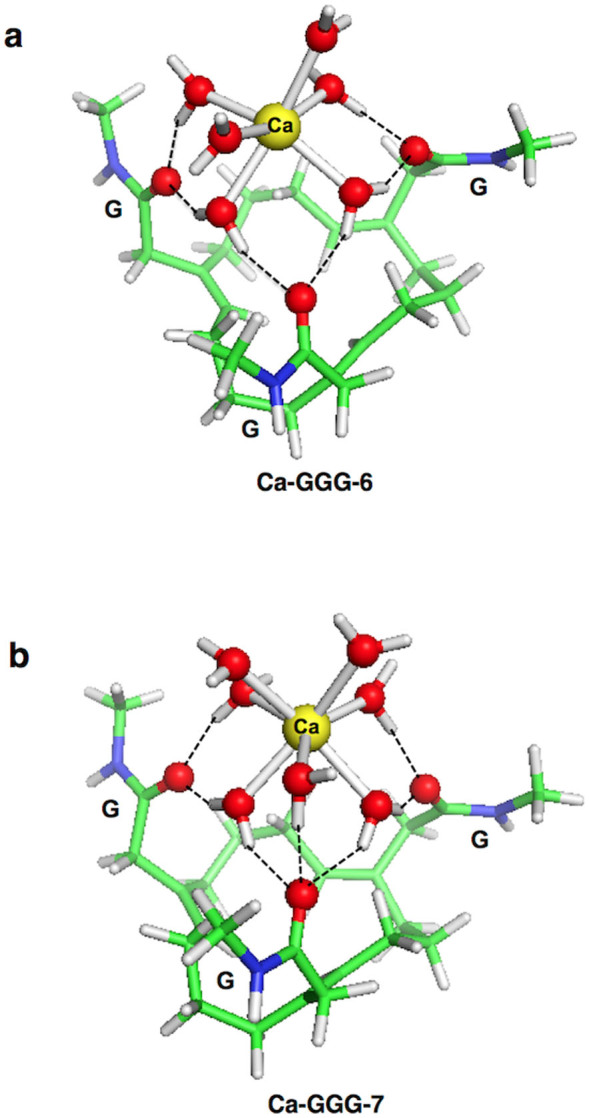
B3LYP/6-31+G(3d,p) optimized structures of (a) [Ca(H₂O)₆]²⁺-GGG SF and (b) [Ca(H₂O)₇]²⁺-GGG SF complexes.

Competition among metal ions in the model ASIC1a SF

Na⁺ vs. K⁺

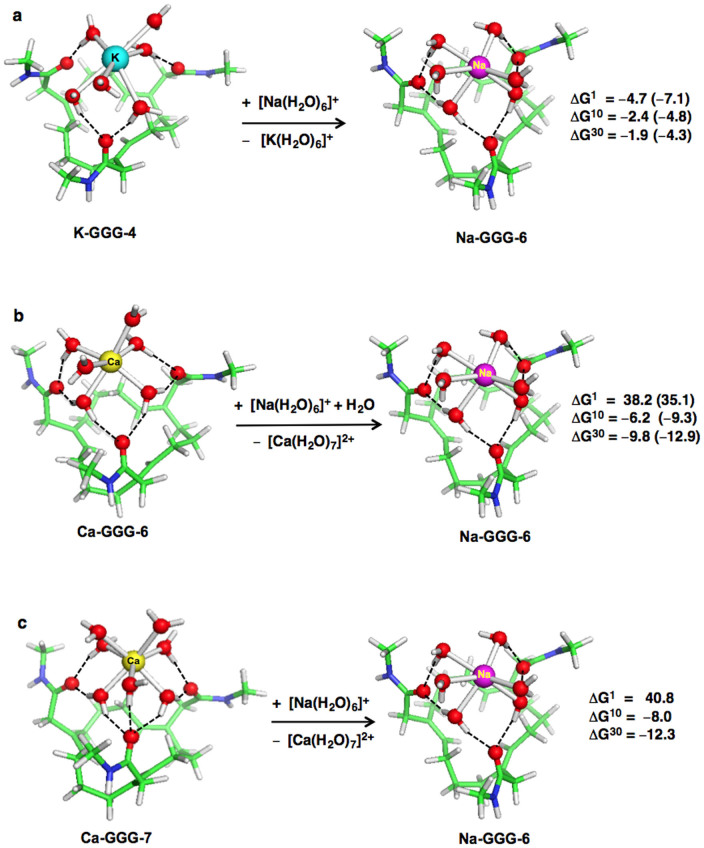
Substituting hydrated K⁺ for hydrated Na⁺ in the model ASIC1a SF is thermodynamically favorable: The ion exchange free energies are negative for an effective dielectric constant x ranging from 1 to 30 (–4.7 to –1.9 kcal/mol, Figure 4a), implying a Na⁺-selective SF. Rigidifying the model ASIC1a SF, whose pore is optimized to fit hydrated Na⁺, further disfavors the bulkier hydrated K⁺ from binding, thus enhancing the competitiveness of Na⁺: The metal exchange free energies in a Na⁺-optimized GGG filter that is prohibited from relaxing upon binding K⁺ (numbers in parentheses, Figure 4a) are even more negative (by 2.4 kcal/mol) than those in a GGG filter that can adjust to accommodate K⁺. Since solvation effects (x > 1) diminished Na⁺/K⁺ selectivity (less negative ΔG^x with increasing x, Figure 4a), electronic factors favor binding of Na⁺ over K⁺ and govern the Na⁺ vs. K⁺ competition in the ASIC1a SF: Compared to K⁺, Na⁺ is a stronger Lewis acid and forms more polar and shorter bonds with water molecules. The much shorter Na⁺–OH₂ (2.45 Å) bonds compared to K⁺–OH₂ (2.82 Å) bonds allow the trimeric SF to gain more hydrogen-bond contacts with Na⁺ than with K⁺. This along with the more polarized Na⁺–bound water molecules result in stronger electrostatic interactions with the SF carbonyl moieties.

Figure 4.

The free energies, ΔG^x (in kcal/mol), for replacing (a) K⁺ bound to 6 water molecules, (b) Ca²⁺ bound to six water molecules, and (c) Ca²⁺ bound to seven water molecules with Na⁺ in the GGG ASIC model SF (eq 1). ΔG¹refers to the metal exchange free energy in the gas phase, whereas ΔG¹⁰ and ΔG³⁰ refer to the metal exchange free energies in an environment characterized by an effective dielectric constant of 10 and 30, respectively. The free energies for metal exchange in a rigid Na⁺-optimized GGG filter prohibited from relaxing upon K⁺/Ca²⁺ binding are in parentheses.

Na⁺ vs. Ca²⁺

As the Ca²⁺ hydration number varies from 6 to 10 depending on the water:salt ratio, two Ca²⁺ hydration numbers were considered in the Ca²⁺ vs. Na⁺ competition in the GGG SF: (1) hexahydrated Ca²⁺, whose hydration number matches that of Na⁺ (Ca-GGG-6, Figure 4b) and (2) heptahydrated Ca²⁺ (Ca-GGG-7, Figure 4c). Electronic effects again favor the better electron acceptor cation; i.e., divalent Ca²⁺ over monovalent Na⁺ (positive ΔG¹ in Figures 4b,c). This is because divalent hydrated Ca²⁺ has stronger electrostatic interactions with the SF carbonyl moieties than hydrated Na⁺. Thus, unlike the Na⁺ vs. K⁺ competition in the GGG SF, electronic effects disfavor the native Na⁺ in the competition with Ca²⁺.

Instead, a relatively high-dielectric environment in the ASIC1a SF is the key determinant of the Na⁺/Ca²⁺ selectivity: Whereas the ion exchange free energy is positive in the gas phase (x = 1), it is negative for an effective dielectric constant x ranging from 10 to 30 (–6.2 to –12.3 kcal/mol, Figures 4b,c). A high-dielectric environment in the ASIC1a SF favors binding of Na⁺ over Ca²⁺ due mainly to the low desolvation penalty of the incoming Na⁺ and the high free energy gain on solvating the outgoing Ca²⁺: For x = 30 in eq 2, the solvation free energy difference between Ca²⁺ and Na⁺ hydrates, ΔG_solv^x[Ca²⁺(H₂O)₇] − ΔG_solv^x[Na⁺(H₂O)₆] = −136 kcal/mol, outweighs the difference between hydrated Na⁺ and Ca²⁺ bound to the SF, ΔG_solv^x[Na⁺(H₂O)₆-filter] − ΔG_solv^x[Ca²⁺(H₂O)₇-filter] = 83 kcal/mol, and the gas-phase free energy, ΔG¹ = 41 kcal/mol. Increasing the SF rigidity and metal hydration number both enhance Na⁺/Ca²⁺ selectivity, albeit to a lesser extent than medium effects: The metal exchange free energies in a rigid Na-GGG-6 pore (numbers in parentheses, Figure 4b) are more negative (by ~3 kcal/mol) than those in a flexible SF that can adjust to the geometrical requirements of hydrated Ca²⁺. Furthermore, the free energies for replacing heptahydrated Ca²⁺ with Na⁺ in the GGG SF (Figure 4c) are more negative (by ~2 kcal/mol) than those for replacing hexahydrated Ca²⁺ (Figure 4b).

Competition among metal ions in a model ENaC SF

Although ENaC and ASIC belong to the same superfamily of ion channels, the size and structure of their trimeric SFs appear to be quite different: Unlike the wide ASIC1a SF, the highly Na⁺-selective asymmetric ENaC SF is lined by conserved Ser residues and has a rigid, narrow pore (radius <2.5 Å) that fits dehydrated metal ions³⁰,³¹,³². How does the ENaC SF select its cognate ion and achieve a Na⁺/K⁺ selectivity ratio (100–500) that is an order of magnitude greater than that exhibited by the ASIC SF (3–30)? No crystal structures are available for ENaC. Kellenberger et al.³³ proposed that the Ser backbone oxygen atoms interact with the permeating ion, whereas Sheng et al.³² differ in proposing the α subunit's Ser hydroxyl oxygen to coordinate Na⁺. Since it is unclear whether backbone or sidechain oxygen atoms or a combination of both coordinate the permeating ions, we modeled dehydrated ions bound in the two “limits” of the ENaC SFs: a BBB SF containing three backbone groups (Figure 5a) and a SSS SF lined by three Ser hydroxyl groups (Figure 5b). We then computed the free energies ΔG^x for Na⁺ to displace K⁺ (numbers in black) and Ca²⁺ (numbers in blue) in these two types of model SFs.

Figure 5.

The free energies, ΔG^x (in kcal/mol), for Na⁺ to displace K⁺ (numbers in black) and Ca²⁺ (numbers in blue) bound to (a) 3 –CONHCH₃ ligating groups (representing backbone peptide groups denoted by B) in the BBB filter and (b) 3 OH-ligating groups (representing Ser side chains) in the SSS filter (eq 1). ΔG¹refers to the metal exchange free energy in the gas phase, whereas ΔG¹⁰ and ΔG³⁰ refer to the metal exchange free energies in an environment characterized by an effective dielectric constant of 10 and 30, respectively. The free energies for metal exchange in a rigid Na⁺-optimized SSS and BBB filters prohibited from relaxing upon K⁺ or Ca²⁺ binding are in parentheses. Shown are B3-LYP/6-31+G(3d,p) fully optimized structures of Na⁺ bound to the model SFs.

Na⁺ vs. K⁺

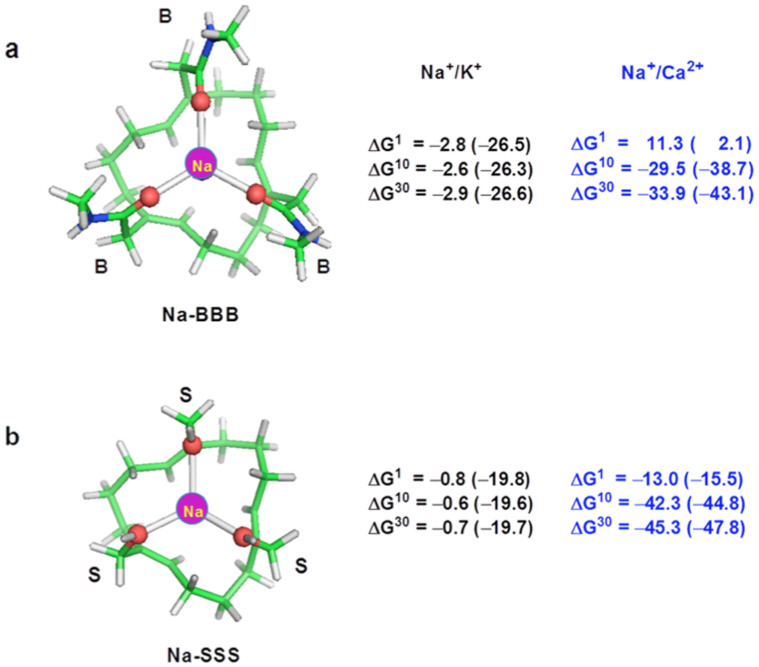
Higher Na⁺/K⁺ selectivity is achieved if backbone rather than Ser side chain oxygen atoms coordinate the metal cation: The free energies for replacing K⁺ in the BBB SF with Na⁺ (Figure 5a) are more favorable than those in the SSS SF (Figure 5b) by ~2 kcal/mol. Compared to the hydroxyl group, the carbonyl group has stronger charge-donating ability and interacts more favorably with Na⁺ than K⁺, thus helping to offset the larger Na⁺ dehydration penalty. For both types of filters, Na⁺/K⁺ selectivity is dramatically enhanced if the ENaC SF were rigid. A rigid ENaC SF pore optimized to fit bare Na⁺ strongly disfavors binding of the bulkier K⁺, as evidenced by the much more negative Na⁺ → K⁺ free energies (numbers in parentheses, Figure 5): A rigid, Na⁺-optimized BBB SF enhances Na⁺/K⁺-selectivity by ~24 kcal/mol, whereas a rigid, Na⁺-optimized SSS SF has a smaller effect (~19 kcal/mol).

In line with experimental findings, a rigid ENaC SF is more Na⁺/K⁺-selective than a rigid ASIC1a SF (the numbers in parentheses in Figure 5a are more negative than those in Figure 4a). Making the Na⁺-binding site rigid in the ENaC structure enhanced Na⁺/K⁺-selectivity by an order of magnitude greater than rigidifying the Na⁺-binding site in the ASIC1a structure: Na⁺/K⁺-selectivity is enhanced by ~24 kcal/mol in a rigid, constricted ENaC pore (Figure 5a), but by 2.4 kcal/mol in the rigid, wide ASIC1a pore (Figure 4a). This difference is mainly due to the smaller binding cavity in the ENaC SF compared to the ASIC1a one, as the same three backbone groups line the SFs of both types of channels.

Na⁺ vs. Ca²⁺

Unlike the competition between Na⁺ and K⁺, higher Na⁺/Ca²⁺ selectivity was found in a SSS SF rather than a BBB SF: The Na⁺ → Ca²⁺ free energies in the SSS SF (Figure 5b) are more favorable than those in the BBB SF (Figure 5a). This is mainly because the three weakly ligating Ser hydroxyl groups lining the narrow SSS SF “undercoordinate” Ca²⁺, resulting in feeble interactions that cannot compensate for the cost of stripping the Ca²⁺-bound water molecules, as evidenced by a ΔG¹ = –13 kcal/mol, Figure 5b. As for the ASIC1a SF, the higher dielectric environment of the SF favors the permeating ion with the smaller dehydration penalty, thus Na⁺ is preferred over Ca²⁺ in both BBB and SSS SFs (negative ΔG^x, x ≥ 10, in Figure 5). Thus, a relatively high-dielectric SF providing suboptimal interactions for the rival dication can bestow high Na⁺/Ca²⁺ selectivity.

Even though solvation effects favor Na⁺ over Ca²⁺ in both the ENaC and ASIC1a SFs, the ENaC SF is more Na⁺/Ca²⁺-selective than the ASIC1a one. This is because in the wide ASIC1a SF, (i) there is no dehydration penalty and (ii) Ca²⁺ is no longer “undercoordinated” but is bound to six (Ca-GGG-6, Figure 4b) or seven (Ca-GGG-7, Figure 4c) water molecules³⁴,³⁵. Thus, the gas-phase ΔG¹ free energy for replacing Ca²⁺ with Na⁺ in the constricted ENaC SF (11 kcal/mol, Figure 5a) is less positive than that in the wide ASIC1a SF (38–41 kcal/mol, Figures 4b,c); consequently, in the higher dielectric SF (x ≥ 10), the ΔG^x in Figure 5a (–30 to –34 kcal/mol) are more favorable than those in Figures 4b,c (–6 to –12 kcal/mol).

Discussion

Since the open-state structures with the native Na⁺ ion bound in the SFs of the ASIC1a and ENaC have not yet been solved, we have examined the outcome of the competition among Na⁺, K⁺, and Ca²⁺ in models of these channel SFs, which were designed in accord with available experimental data (see Methods). Nevertheless, the results obtained are in line with experimental findings: The computed SF pore size, estimated by the area of the triangle formed by the metal-ligating oxygen atoms lining the SF, is consistent with the respective experimental estimate: (i) The calculated pore area of the model ENaC SF (6.3 Ų for Na-BBB or 6.9 Ų for Na-SSS, Figure 5) is consistent with the experimental estimate of <8.1 Å^{2 31}. (ii) The mean pore area of the Na-GGG-3 and Na-GGG-6 SFs in Figure 1 (15.7 Ų) is also close to the respective area (16.6 Ų) determined from the Na⁺-bound ASIC1a/snake toxin crystal structure¹². In accord with experiment, the calculations predict that the ASIC SF is selective for Na⁺ over both K⁺ and Ca²⁺ and is more Na⁺/Ca²⁺-selective than Na⁺/K⁺-selective (more negative ΔG¹⁰/ΔG³⁰ in Figures 4b,c than in Figure 4a). Indeed, the experimentally measured permeability ratios for the ASIC1a channel reveal that the Na⁺-selective pore is less permeable to Ca²⁺ (Na⁺:Ca²⁺ permeability ratio = 18.5) than to K⁺ (Na⁺:K⁺ permeability ratio = 7.8)⁸. The model ENaC SF is also found to be much more discriminatory toward Ca²⁺ than K⁺ (the Na⁺ → Ca²⁺ ΔG^x numbers are an order of magnitude more negative than the Na⁺ → K⁺ ΔG^x in Figure 5). This is in line with the experimental finding that ENaC exhibits a Na⁺:K⁺ permeability ratio of 100–500³,¹¹, but Ca²⁺ is not permeable¹¹. The calculations also predict that a rigid ENaC SF (numbers in parentheses, Figure 5) is much more selective for Na⁺ over K⁺ and Ca²⁺ than its ASIC counterpart (which exhibits less negative ΔG^x values). This is in agreement with the greater Na⁺:K⁺ permeability ratio for the ENaC (100–500)³,¹¹ compared to that for the ASICs (3–30)⁸,⁹, and the fact that ENaC is impermeable to Ca²⁺, but the ASIC1A is slightly permeable to Ca²⁺.

Selectivity in the large ASIC1a pore is not solely based on the hydrated ion size and its compatibility with the SF pore size¹⁰. Rather, it is a fine balance between electronic effects, which favor the cation that is a better electron acceptor (i.e., Ca²⁺ > Na⁺ > K⁺) and solvation effects, which favor the ion with smaller dehydration penalty binding (i.e., K⁺ > Na⁺ > Ca²⁺). Electronic factors favor Na⁺ over K⁺ in the ASIC1a SF, because the shorter and more polar Na–OH₂ bonds compared to K⁺–OH₂ bonds enable more hydrogen-bond contacts and stronger electrostatic interactions with the ligands lining the ASIC1a SF (Figure 4a). On the other hand, solvation effects favor binding of Na⁺ over Ca²⁺ because Na⁺ has a much smaller dehydration penalty than Ca²⁺ (Figure 4c). Changes in the metal hydration number inside the ASIC1a SF could be considered a second-order selectivity determinant. Consistent with the fact that hydrated Na⁺ as well as the bulkier Cs⁺ can be bound to the ASIC1a SF in the crystal structure, the pore rigidity does not play a major role in controlling metal ion competition, unlike the narrower ENaC SF pores (see below).

Compared to the ASIC1a SF, the ENaC SF has adopted a different selectivity strategy to achieve Na⁺ selectivity³⁶: Unlike the ASIC1a SF, the ENaC SF has a narrow and rigid pore that fits dehydrated metal ions, which bind directly to three SF ligands (Figure 5). Protein matrix effects that rigidify and constrict the SF pore so that the bulkier K⁺ cannot fit optimally help to achieve high Na⁺/K⁺ selectivity. This is in line with experimental studies showing that the ENaC pore is rigid and narrow: In the series of monovalent ions, Na⁺, K⁺, Rb⁺, Cs⁺, NH₄⁺, (CH₃)NH₃⁺, (CH₃)₂NH₂⁺, (CH₃)₃NH⁺, and guanidine, the ENaC channel is permeable to only Na⁺ and impermeable to the larger cations³³. Backbone oxygen atoms interacting with the permeating ion in lieu of the weaker metal-ligating Ser hydroxyl group would further enhance Na⁺/K⁺ selectivity. This is consistent with mutagenesis data suggesting that a conserved Gly from the β subunit of the ENaC SF is important in restricting K⁺ permeation³². On the other hand, the filter's trimeric structure and absence of strong metal-ligating groups such as Asp/Glu carboxylates favor Na⁺ over Ca²⁺. Thus, the pore's rigidity and undercoordination of the permeable ion by only three weak metal-ligating SF groups appear to be the key selectivity determinants of the ENaC SF (see Figure 5 and Ref. 24). Departing from these physical principles in the case of the ASIC1a SF; i.e., a hydrated metal ion with coordination number of six bound to a large and less rigid pore, diminishes the Na⁺/K⁺ and Na⁺/Ca²⁺ selectivity and renders the ASIC channels less Na⁺ selective than their ENaC counterparts (see above).

Methods

Selectivity Filter Models

Since crystallographic studies indicate a ASIC1a SF providing a ring of three carbonyl oxygen atoms with a pore radius that matches hydrated cations¹², we modeled hydrated cations bound in a SF containing three –CONHCH₃, representing peptide backbone groups (see Figures 1–4). On the other hand, experimental studies indicate that the ENaC transports completely dehydrated ions³⁷, but there is no consensus as to whether the backbone carbonyl or Ser hydroxyl oxygen atoms line a trimeric ENaC SF³⁰,³¹,³². Hence, we modeled dehydrated metal cations bound in both BBB and SSS SFs lined with three –CONHCH₃ and three –OH groups, respectively (Figure 5). Models of the SFs were built using GaussView version 3.09 following the guidelines from our previous work²³. The metal ligating groups were coordinated to the permeating bare/hydrated ion (Na⁺, K⁺ or Ca²⁺) and attached to a carbon–hydrogen ring scaffold via flexible methylene spacers.

Justification of the Model SF Structures

The models of the ASIC1a and ENaC SFs were designed to maximize their resemblance with the channel's SF. They were constructed on the basis of the following considerations: (a) The ring mimics the oligomeric state and overall symmetry of the ion channel pore. (b) The ring scaffold prevents the metal ligands from drifting away or assuming unrealistic, pore-occluding positions during geometry optimization. If the metal ligands were detached from the ring scaffold, the fully optimized structure of the resulting metal-ligand complex would lose the pore-like shape, as one or more ligands would be positioned along the ion permeation pathway, thus occluding the pore³⁵. Hence, the ring scaffold reflects the effects of the protein matrix in orienting the metal-ligating groups to interact with the permeating ions without obstructing the conduction pathway. (c) The metal-ligating groups and their connection to the ring are flexible enough to allow them to optimize their positions upon metal binding: the optimized metal–O distances in the model SF complexes were similar to those in metal complexes containing the free ligands without the ring scaffold²³. (d) The shape and C–H orientations of the ring do not obstruct the pore lumen. Notably, the metal–O distances and pore sizes of the model SFs were found to be consistent with experimental estimates, as discussed above.

Gas-Phase Free Energy Calculations

Among several combinations of different ab initio/density functional theory methods (HF, MP2, S-VWN and B3-LYP) and basis sets (6-31+G(d,p), 6-31+G(2d,2p), 6-31+G(3d,p), 6-31+G(3d,2p), 6-311++G(d,p) and 6-311++G(3df,3pd)), the B3-LYP/6-31+G(3d,p) method has been shown to be the most efficient in yielding dipole moments of the metal ligands that are closest to the respective experimental values; it can also reproduce (within experimental error) the metal–oxygen bond distances in aqua and crown ether complexes, which resemble metal-occupied ion channel pores²³. Hence, the B3-LYP/6-31+G(3d,p) method was used to optimize the geometry of each metal complex and to compute the electronic energies, E_el, using the Gaussian 09 program. Frequency calculations for each optimized structure were performed at the same level of theory. No imaginary frequency was found for the lowest energy configurations of the optimized structures. The B3-LYP/6-31+G(3d,p) frequencies were scaled by an empirical factor of 0.9613³⁸ and used to compute the thermal energies (E_th), including zero-point energy, and entropies (S). The differences ΔE_el, ΔE_th, ΔPV (work term) and ΔS between the products and reactants in eq 1 were used to calculate the gas-phase ΔG¹ free energy at T = 298.15 K according to:

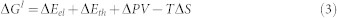Solution Free Energy Calculations

The ΔG_solv^x (x = 10 or 30) values were estimated by solving Poisson's equation using finite difference methods³⁹,⁴⁰ with the MEAD (Macroscopic Electrostatics with Atomic Detail) program⁴¹, as described in previous works⁴². Natural Bond Orbital atomic charges, which are known to be numerically quite stable with respect to basis set changes⁴³, were employed in the calculations. The effective solute radii were obtained by adjusting the CHARMM (version 22)⁴⁴ van der Waals radii to reproduce the experimental hydration free energies of Na⁺, K⁺ and Ca²⁺, and model ligand molecules to within 1 kcal/mol²³,³⁵,⁴⁵. The resulting values (in Å) are: R_Na = 1.72, R_K = 1.90, R_Ca = 1.75, R_C = 1.95, R_N = 1.75, R_O(−CONHCH₃) = 1.72, R_O(H₂O) = 1.85, R_O(−CH₂OH) = 1.90, R_H = 1.50, R_O(Na/K–H₂O) = 1.85, R_O(Ca–H₂O) = 1.84, R_H(H₂O−Na) = 1.26, R_H(H₂O−K) = 1.20, R_H(H₂O−Ca) = 1.053.

Author Contributions

T.D. performed the calculations. T.D. and C.L. designed the project and wrote the manuscript text. All authors reviewed the manuscript.