Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Jan 19;5:7876. doi: 10.1038/srep07876

Experimental and Theoretical Investigation of Macro-Periodic and Micro-Random Nanostructures with Simultaneously Spatial Translational Symmetry and Long-Range Order Breaking

Haifei Lu 1,*, Xingang Ren 1,*, Wei E I Sha 1, Jiajie Chen 2, Zhiwen Kang 2, Haixi Zhang 2, Ho-Pui Ho 2,a, Wallace C H Choy 1,b
PMCID: PMC4297977  PMID: 25597407

Abstract

Photonic and plasmonic quasicrystals, comprising well-designed and regularly-arranged patterns but lacking spatial translational symmetry, show sharp diffraction patterns resulting from their long-range order in spatial domain. Here we demonstrate that plasmonic structure, which is macroscopically arranged with spatial periodicity and microscopically constructed by random metal nanostructures, can also exhibit the diffraction effect experimentally, despite both of the translational symmetry and long-range order are broken in spatial domain simultaneously. With strategically pre-formed metal nano-seeds, the tunable macroscopically periodic (macro-periodic) pattern composed from microscopically random (micro-random) nanoplate-based silver structures are fabricated chemically through photon driven growth using simple light source with low photon energy and low optical power density. The geometry of the micro-structure can be further modified through simple thermal annealing. While the random metal nanostructures suppress high-order Floquet spectra of the spatial distribution of refractive indices, the maintained low-order Floquet spectra after the ensemble averaging are responsible for the observed diffraction effect. A theoretical approach has also been established to describe and understand the macro-periodic and micro-random structures with different micro-geometries. The easy fabrication and comprehensive understanding of this metal structure will be beneficial for its application in plasmonics, photonics and optoelectronics.

Plasmons are collective oscillations of electrons in matter stimulated by incident light. Manipulating light-matter interaction in periodic plasmonic nanostructures has received a lot of attention due to its unprecedented ability to harness both far-field interference and near-field coupling of plasmonic waves by Plasmon-Floqet modes. Intriguing physical effects including Bragg scattering, plasmonic band gap and edge, Fano resonance, zero-index metamaterials, super-radiance, etc. can be supported in periodic plasmonic nanostructures1,2,3,4,5,6,7. In terms of practical applications, they can be used for optoelectronic devices, surface enhanced Raman scattering, biosensing, microscopy and spectroscopy8,9,10,11,12,13,14,15,16,17,18,19,20. Meanwhile, random (disordered) plasmonic nanostructures were also explored to efficiently transport and localize light by manipulating plasmonic scattering channels. Emerging physical phenomena, such as extremely strong hot spots, Anderson location, and anomalous transmission enhancement have been reported21,22,23,24. Random plasmonic nanostructures have found potential applications in random laser, sensing, and nonlinear optics25,26,27,28.

Recently, structures, lying between periodic and random patterns, have shown new physical effects, governing the wave transport and interference. Quasi-crystals made from building blocks that are arranged using well-designed patterns but lack of translational symmetry, are one of the representatives. The fundamental description of quasi-crystal in mathematical aspect has been systematically studied29,30. Physically, quasi-crystals show sharp diffraction patterns that confirm the existence of wave interference resulting from their long-range order in the spatial domain31,32,33. For instance, different types of quasi-crystal structures, such as Fibonacci, Thue-Morse, and Rudin-Shapiro, have been developed to realize controllable optical properties for surface enhanced Raman scattering and sensing applications31,34,35,36,37,38,39. Moreover, stable lasing modes have been demonstrated on such kind of quasi-crystal structures32,40,41,42,43. Additionally, contributed from rich spatial frequencies, broadband field enhancement can be achieved by quasi-crystal structures and their performances on light management are superior to both periodic and random structures44,45,46,47,48.

Here, we present a macroscopically periodic (macro-periodic) and microscopically random (micro-random) plasmonic structure, which also lies between periodic and random structures. The nanoplate-based silver structure is realized through a seed-initiated photochemical growth process using a light source with low photon energy and a low optical power density of 4.7 mW/cm2. Because the structure is macroscopically arranged with a spatial periodicity and microscopically constructed by randomly distributed metal nanostructures, both translational symmetry and long-range order are broken. Surprisingly, the diffraction effect can be experimentally demonstrated in the structure. We also develop a theoretical model to understand the diffraction effect. It is believed the plasmonic nanostructures with tunable macro- and micro-geometries would provide an alternative approach to manipulate light-matter interaction for lasing, energy harvesting, and sensing applications.

Results

Macro-periodic and micro-random patterns fabrication

A simple scheme was introduced for fabricating the silver nanoplate-based macro-periodic and micro-random structures as shown in Fig. S1, which are chemically grown from strategically immobilized nano-seeds upon light irradiation (detail will be discussed in methods section). It is important to note that without the nano-seed on substrate, no silver structure will form even through the sample is irradiated by a high optical power density of light. While there are nano-seeds on substrate, light with a very low optical power density (4.7 mW/cm2) would be able to trigger the growth; and the pattern can be easily fabricated in large area.

The macro-periodic and micro-random nanostructure show different colors by varying tilted angles as shown in Fig. 1a, which confirms the macro-periodic characteristics of the sample. As SEM images of three typical samples illustrated in Figs. 1b–1d, macro-periodic structures with different periodicities can be obtained by changing the incident angles of light for fabrication. It can be observed that the samples are composed of one-dimensional (1D) periodic pattern and the periodicity increases with the increasing incident angle. Finally, six samples of different periodicities have been prepared from six incident angles (30, 35, 40, 43, 45 and 50 degree) of the fabrication light, whose periodicities have been measured and summarized in Fig. S2 in supplementary information. As demonstrated, the experimental results have a good agreement with the calculated curve, which describes a relationship between periodicity of optical interference pattern on the glass substrate and incident angles. It implies that growth of the silver nanostructure is driven by a photon-excited chemical process. Meanwhile, it also indicates that our robust approach can be feasibly programmable for fabricating various macro-periodic nanopatterns. In supplementary information, two dimensional macro-periodic nanopatterns fabricated from similar approach have been demonstrated in Fig. S3.

Figure 1.

Figure 1

Open in a new tab

(a) Photographs showing the diffracted colors of the silver nanoplate-based periodic structure at different tilted angles. Three representative SEM images of samples fabricated with light source at incident angles of (b) 35 degree, (c) 45 degree, and (d) 50 degree. Inset in (b) shows a magnified area.

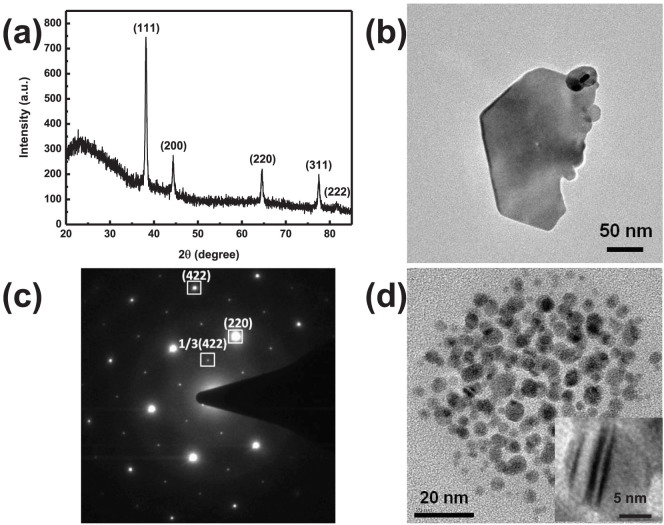
As the enlarged SEM image shown in the inset of Fig. 1b, the macro-periodic nanostructure is made from random distributed silver nanoplates, which have anisotropic geometries. Since no silver nanostructure grows on the glass substrate when there is no pre-formed nano-seed, it is believed that the nanoplates are grown from the seeds under the excitation of 632.8 nm light. X-ray diffraction (XRD) and selected area electron diffraction (SAED) patterns in Fig. 2 have proven that, the nanoplates are {111} planes dominated structures and some {111} stacking fault planes lying parallel to the bottom and top surfaces. Under the illumination of 632.8 nm light, having lower photon energy than UV or blue light, the growth would more easily occur at the high potential energy sites. While the twinned defects generally have high potential energy and have been commonly observed in the nano-seeds as the transmission electron microscope (TEM) image shown in Fig. 2d, the nano-seeds would grow along the twinned planes and transform into nanoplates49,50,51,52,53. As the seeds layer on the glass substrate is formed through chemical bonding approach, their twinned directions on the substrate would be randomly distributed, which induces the formation of the random silver nanoplates structures. Despite of the periodic arrangement of the macropattern, the translational symmetry and long range order have broken due to random-nanoplates comprised strips. Besides the tunable periodicity and pattern of the macro-periodic structure, the micro-random geometry can be further modified through thermal annealing. As evidenced by the SEM image in Fig. S4, the macro-periodic and micro-random structure after 150°C annealing in vacuum is mainly made from silver nanodots, which are attributed to the shrinkage of silver nanoplates upon heating.

Figure 2.

Figure 2

Open in a new tab

(a) The XRD plot of the nanoplate based macro-periodic and micro-random structure. (b) The TEM and (c) SADE images of a silver nanoplate collected from substrate. (d) TEM image of small silver nanoparticle seeds. The inset TEM image shows stacking faults inside a nano-seed.

Observing diffraction effect from macro-periodic and micro-random structure

The macro-periodic and micro-random structure has been intuitively explained and compared with completely-random and perfect-periodic structures by spatial-frequency spectra of SEM images in Figs. 3a, 3c and 3e. Regarding completely-random structures by silver nanoplates, uniformly distributed spatial frequencies with comparable amplitudes in the k-space can be observed in Fig. 3b. Therefore, neither constructive nor destructive wave interference appears in the completely-random structures. On the contrary, only several bright spots in the k-space, which is similar to the reciprocal space concept, exist for the perfectly-periodic strip grating (See Fig. 3d), where plasmon-Floquet modes coherently interact with each other. For the k-space image of the macro-periodic and micro-random structure in Fig. 3f, it is contributed from a superposition of the k-space image of perfectly-periodic structure and that of completely-random structure. Consequently, wave interferences are maintained in the structure.

Figure 3.

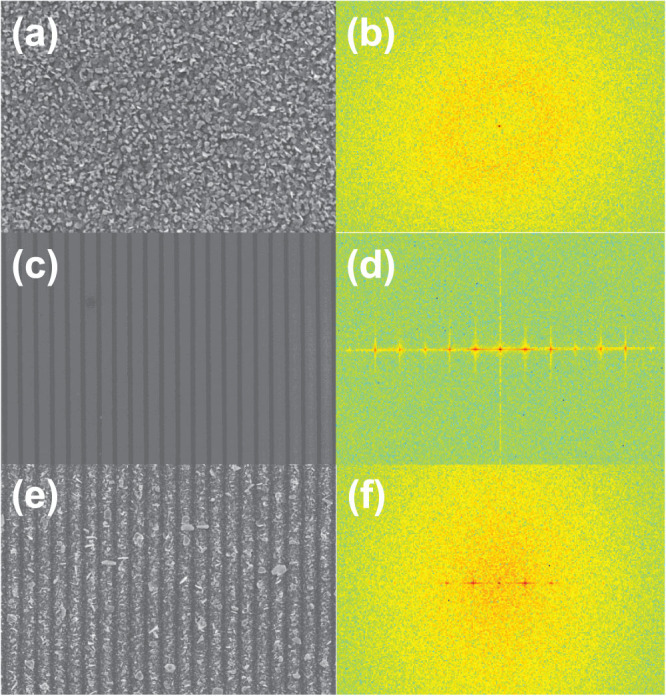
Figure 3

Open in a new tab

SEM images and Fourier transformation spectra of (a) (b) random, (c) (d) periodic and (e) (f) macro-periodic and micro-random structures.

The experimental optical extinction spectra also strongly suggest the structure has a hybridized optical property of periodic and random structures. As depicted in Figs. 4a and S5, all the samples exhibit broad extinction spectra covering from visible to NIR under both TE and TM excitations. That can be attributed to the collective effect of multiple localized plasmon resonances from the micro-random nanoplates. On the other hand, distinct resonance peaks (indicated by red arrows) have been found in all the samples under TM excitation, and these peaks red-shift as the macro-periodicities increase which can be more clearly indicated by the extinction difference between TM and TE in Fig. 4b.

Figure 4.

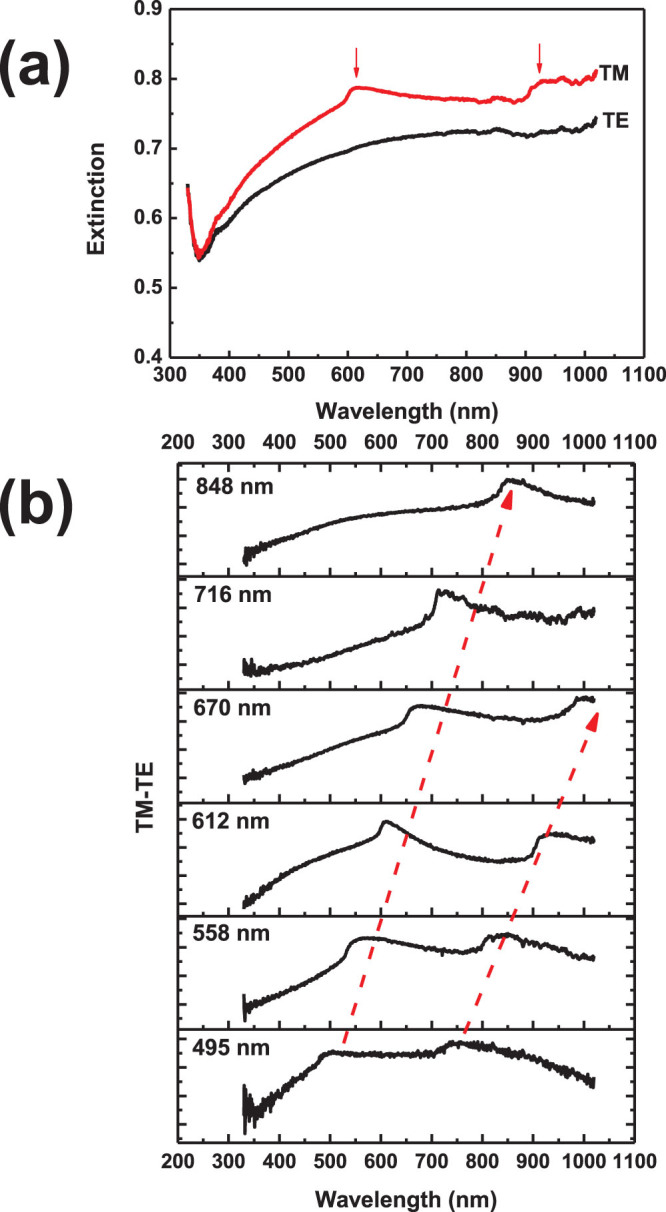
Figure 4

Open in a new tab

(a) Extinction spectrum of a representative silver macro-periodic and micro-random structure (P = 612 nm) under two polarized light: TM (red, electric field perpendicular to the periodic strips) and TE (black, electric field parallel to the periodic strips) and (b) the extinction difference (TM-TE) of the structures with different periodicities.

Discussion

Theoretical investigation of the diffraction effect

As indicated in the experimental extinction spectra of Fig. 4, our nanostructures: (1) maintain the first diffraction order; (2) weaken and broaden high-order resonance peaks. It would be highly desirable to develop an effective approach to understand the optical responses of nanostructures with both translational symmetry and long-range order breaking. The analysis tools such as fast Fourier transform (FFT)31 and concept of scattering centers54,55 can be utilized to intuitively understand maintenance of diffraction order and predict diffraction directions (hotspots in k space). However, the quantitative description of far-field responses (absorption, scattering, and extinction spectra, etc.) of the class of macro-periodic and micro-random nanostructures cannot be achieved by these intuitive analysis tools. Full-wave solvers can be adopted to obtain localized near-fields for one sampling of the nanostructure56, but they require a great number of simulations with repeated random samplings to capture the ensemble average effects, which is similar to Monte Carlo method57. Hence, we aim at developing an efficient tool to quantitatively model the far-field response of the macro-periodic and micro-random nanostructures through rigorously solving Maxwell's equations. As a mode matching method58, rigorous coupled wave analysis (RCWA) method59,60,61, could solve Maxwell's equations rigorously and efficiently. It has been an indispensable tool to simulate periodic and multilayer structures in areas of plasmonics and photonics. Here, a modified RCWA is developed to simulate the evolution of extinction spectra for the nanostructures simultaneously preserving properties of periodicity and randomness. To the best of our knowledge, it is the first time RCWA has been introduced to simulate such unusual nanostructures.

Firstly, we investigate the perfect silver strip grating. Through expanding the field components in Fourier series in terms of space harmonic fields as well as using mode matching condition and Floquet-Bloch theorem, one can rigorously solve Maxwell's equations by determining eigenvalues and eigenmodes in each unit cell. RCWA method has been briefly described in supplementary information. From red triangles curve of Fig. S5 (b) obtained by RCWA method, four resonance peaks can be found in the extinction spectrum of the silver strip grating. Peaks 1 and 2 are the plasmonic modes excited by high-order Floquet modes. Peaks 3 and 4 are the first-order diffraction from the interfaces of Ag-air and Ag-glass, respectively.

Secondly, the RCWA method can be extended to the structure if we set the periodicity of the macro-periodic and micro-random grating to be infinity. However, that would be not computationally useful and lose physical insights. Alternatively, we adopt the ensemble averaging concept from random signal analysis62. In the new RCWA: (1) the macro periodicity (macro translational symmetry) is maintained; (2) Floquet spectra of spatial distribution of refractive indices are modified to describe the influence of both translational symmetry and long-range order breaking microscopically. Through convoluting a Gaussian fluctuation function and the permittivity distribution, equivalently damping the high-order Floquet spectra due to the ensemble averaging effect, we can approximately evaluate the extinction spectra of the nanostructure. Mathematically, we have

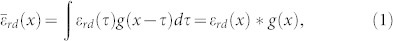graphic file with name srep07876-m1.jpg

where εrd is the permittivity distribution of grating ridge materials, and 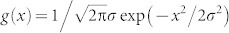Inline graphic is the Gaussian function with a zero mean and variance of σ. As indicated by our initial results in Fig. S6 (blue curve), the first-order diffraction from the interfaces of silver-air and silver-glass are well resolved, whereas the high-order diffraction modes are weakened or broadened. Most importantly, the extinction peaks are caused by the first-order diffractions rather than zero-order diffractions from a planar structure. As shown in Fig. S7 (denoted by the red dot curve), by setting all the high-order Floquet spectra of refractive indices to be zero while only including the zero-order component, we get a smooth curve without any peaks in the extinction spectrum. However, after adding the first-order component, the perfectly periodic structure exhibits diffraction effect analogous to the structure. Consequently, the surprising diffraction effect from the structure is originated from the maintained first-order Floquet spectra of permittivity and the corresponding first-order Floquet eigenmode, which is fundamentally different from the reflection effect induced by the zero-order Floquet spectra (eigenmode) supported in the planar multilayer structures.

Thirdly, although the extinction obtained by the modified RCWA resembles the experimental results, it still cannot accurately describe the optical property of the macro-periodic and micro-random structure. The peak shape of the simulated extinction spectra is different from the experimental one. Since the structure is composed of random distributed nanoplates and contains a great amount of air holes, the strip building block should be treated as a composite material of silver and air. This is also the reason why a direct usage of Ag permittivity shows some derivations between theoretical model and experimental results. Here, the effective medium theory (EMT) is employed for modeling the composite strip by Bruggeman's model63,64:

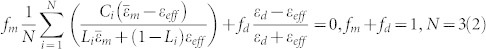graphic file with name srep07876-m2.jpg

where εd and 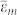Inline graphic are respectively the permittivity of the dielectric (here is air) and metal (here is silver). Ci is the oscillator strength which has been valued as C1 = C2 = C3 = 1 / 3 for simplicity here. fd and fm are the corresponding filling fractions of air and silver. L1, L2, L3are the depolarization factors, which depend on shapes of the random materials and satisfying L1 + L2 + L3 = 1 (for instance, spherical nanostructure has L1 = L2 = L3 = 1 / 3). εeff is the effective permittivity of the composite strip material.

After integrating the effective medium theory and Gaussian filtering process into the RCWA, the whole and detailed numerical procedures are given in Fig. 5. The modified RCWA enables the extinction spectrum of the structure to be accurately predicted. As shown in Fig. 6, the theoretical result well matches our experimental result of the nanoplates comprised macro-periodic structure. Furthermore, the macro-periodic structure after thermal annealing, which is mainly composed of nanodots, has been also simulated using the same model. Compared to nanoplates with a geometrical asymmetry, nanodots are more isotropic, which shows different values of L1, L2, and L3 in Eq. (2). As depicted in the blue curve of Fig. 6, with the modification of depolarization factors for nanodots, the simulated spectrum is also coincident with the experimental result of the macro-periodic structure after thermal annealing (red curve of Fig. 6). Nanoplates comprised structures have broader spectral response in comparison with nanodots comprised structures. Consequently, besides varying the periodicity length for controlling the diffraction effect, the optical property of the structure can be further tuned by modifying the geometrical symmetry of nanoparticles.

Figure 5. The permittivity evolution of macro-periodic and micro-random structure in frequency and Fourier domains after combining the effective medium theory (EMT) with the Gaussian fluctuation from perfect strip grating.

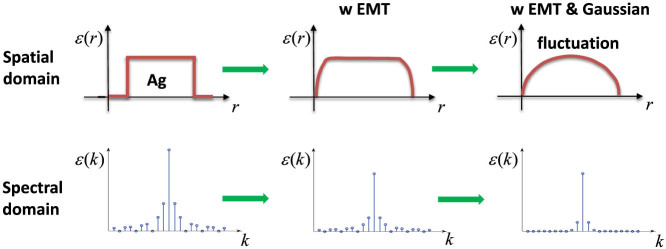
Figure 5

Open in a new tab

Figure 6. Experiment (exp.) and simulation (sim.) extinction spectra silver nanoplate and nanodot based macro-periodic structure.

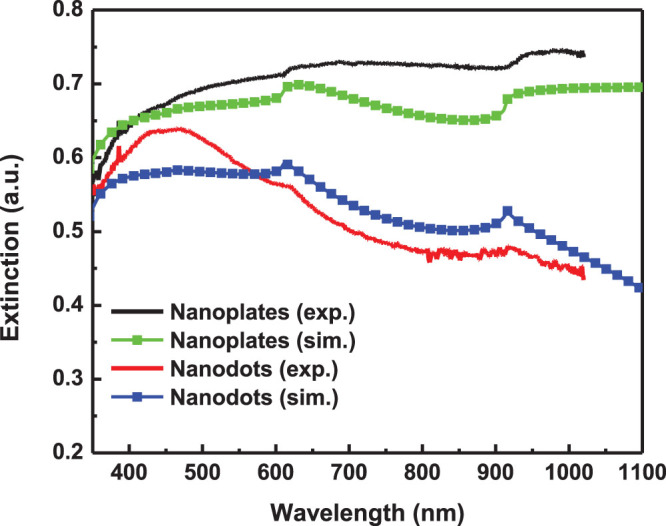
Figure 6

Open in a new tab

The black and red curves are the experimental results results of periodicity 610 nm before and after annealing respectively. The green and blue square curves are the simulated extinction spectra (σ = 0.15; fd = 0.6; and L1 = L2 = 0.2, L3 = 0.6 for silver nanoplate, L1 = L2 = L3 = 1 / 3 for silver nanodots). The periodicity, width and height of silver strips in simulation are 610 nm, 400 nm and 50 nm, respectively.

In conclusion, we have proposed and demonstrated the fabrication of macro-periodic and micro-random silver nanoplate structures with the pre-formed silver nano-seeds and photon driven growth using the light of low photon energy and a low optical power density. The structures offer the features of both random and periodic structures, which have been confirmed by the extinction spectra and Fourier transform of the SEM image of nanopattern. Induced by the random distributed silver nanostructures, both translational symmetry and long-range order are simultaneously broken in the spatial domain, which have not been investigated in previous literatures. A broadband optical response together with an interesting diffraction effect is supported in the structures. The experimentally observed optical responses can be well predicted by our newly-developed RCWA. Consequently, the macro-periodic and micro-random plasmonic structure, providing the freedom of controllable macro-patterns and micro-geometries, could be an excellent candidate to manipulate light-matter interaction for various plasmonic, photonic and optoelectronic applications.

Methods

The growth of silver nanoplate-based macro-periodic and micro-random structure was realized through two stages. The first stage was to prepare metal nano-seeds on substrate. Here, a monolayer of solution prepared silver nanoparticles with diameter smaller than 10 nm were immobilized on the glass substrate using the strong bonding between silver atom and NH2- groups of 3-aminopropyltrimethoxysilane (3-APTMS) which were pre-functionalized on the substrate. In the second stage, the treated glass substrate was fixed on a glass prism with the metal nano-seeds layer faced the reaction solution filling between the treated substrate and glass cover slide separated confirmed by a PDMS spacer as shown in Fig. S1. The reaction solution was a mixture of silver nitrate (0.4 mM) and sodium citrate (2.5 mM) aqueous solution. Matching oil was added between the glass prism and glass substrate, and a rotation stage was used to adjust the incident angle of the expanded 632.8 nm laser beam. After light exposure, 1D periodic nanostructure with periodic strips parallel to the right-angled rim of the glass prism will gradually form on glass substrate. Thermal annealing of the sample was carried out in a MILA-3000 furnace (ULVAC-RIKO), and the chamber was kept in vacuum during the process.

The sample morphology and crystallization structure were investigated by using LEO 1530 FEG scanning electron microscopes and FEI Tecnai G2 20 S-TWIN scanning transmission electron microscope, respectively. The crystallization phases were investigated by a Siemens D5005 X-ray diffraction system (CuKα radiation, λ = 1.54056 Å). The optical extinction spectra were obtained from a home built goniometer.

Author Contributions

H.L. and X.R. contributed equally to the work. H.L. and H.P.H. conceived and designed the experiment. H.L. conducted experiments. X.R. and W.E.S. conceived and carried out the theoretical part. J.C., Z.K. and H.Z. provided valuable discussion on the experiment and manuscript. W.C.C. and W.E.S. improved the manuscript presentation. W.C.C. supervised the whole project. All authors discussed the progress of research and reviewed the manuscript.

Supplementary Material

Supplementary Information

Supplementary Informations

srep07876-s1.doc (4.9MB, doc)

Acknowledgments

This work is supported by the General Research Fund (grants: HKU711813 and HKU711612E), the RGC-NSFC grant (N_HKU709/12), and CRF grant (CUHK1/CRF/12G) from the Research Grants Council (RGC) of Hong Kong Special Administrative Region, China, as well as CAS-Croucher Funding Scheme for Joint Laboratories from Croucher Foundation.

References

  1. Tsai M. W., Chuang T. H., Chang H. Y. & Lee S. C. Bragg scattering of surface plasmon polaritons on extraordinary transmission through silver periodic perforated hole arrays. Appl. Phys. Lett. 88, 213112 (2006). [Google Scholar]
  2. Sha W. E. I., Meng L. L., Choy W. C. H. & Chew W. C. Observing abnormally large group velocity at the plasmonic band edge via a universal eigenvalue analysis. Opt. Lett. 39, 158–161 (2014). [DOI] [PubMed] [Google Scholar]
  3. Christ A., Tikhodeev S. G., Gippius N. A., Kuhl J. & Giessen H. Waveguide-plasmon polaritons: Strong coupling of photonic and electronic resonances in a metallic photonic crystal slab. Phys. Rev. Lett. 91 183901 (2003). [DOI] [PubMed] [Google Scholar]
  4. Luk'yanchuk B., Zheludev N. I., Maier S. A., Halas N. J. & Nordlander P. et al. The Fano resonance in plasmonic nanostructures and metamaterials. Nat. Mater. 9, 707–715 (2010). [DOI] [PubMed] [Google Scholar]
  5. Soukoulis C. M. & Wegener M. Past achievements and future challenges in the development of three-dimensional photonic metamaterials. Nat. Photonics 5, 523–530 (2011). [Google Scholar]
  6. Suchowski H., O'Brien K., Wong Z. J., Salandrino A. & Yin X. B. et al. Phase Mismatch-Free Nonlinear Propagation in Optical Zero-Index Materials. Science 342, 1223–1226 (2013). [DOI] [PubMed] [Google Scholar]
  7. Dorofeenko A. V., Zyablovsky A. A., Vinogradov A. P., Andrianov E. S. & Pukhov A. A. et al. Steady state superradiance of a 2D-spaser array. Opt. Express 21, 14539–14547 (2013). [DOI] [PubMed] [Google Scholar]
  8. Atwater H. A. & Polman A. Plasmonics for improved photovoltaic devices. Nat. Mater. 9, 205–213 (2010). [DOI] [PubMed] [Google Scholar]
  9. Green M. A. & Pillai S. Harnessing plasmonics for solar cells. Nat. Photonics 6, 130–132 (2012). [Google Scholar]
  10. Li X. H., Choy W. C. H., Huo L. J., Xie F. X. & Sha W. E. I. et al. Dual Plasmonic Nanostructures for High Performance Inverted Organic Solar Cells. Adv. Mater. 24, 3046–3052 (2012). [DOI] [PubMed] [Google Scholar]
  11. Li X. H., Choy W. C. H., Ren X. G., Xin J. Z. & Lin P. et al. Polarization-independent efficiency enhancement of organic solar cells by using 3-dimensional plasmonic electrode. Appl. Phys. Lett. 102, 153304 (2013). [Google Scholar]
  12. You J. B., Li X. H., Xie F. X., Sha W. E. I. & Kwong J. H. W. et al. Surface Plasmon and Scattering-Enhanced Low-Bandgap Polymer Solar Cell by a Metal Grating Back Electrode. Adv. Energy Mater. 2, 1203–1207 (2012). [Google Scholar]
  13. Wang W., Wu S. M., Reinhardt K., Lu Y. L. & Chen S. C. Broadband Light Absorption Enhancement in Thin-Film Silicon Solar Cells. Nano Lett. 10, 2012–2018 (2010). [DOI] [PubMed] [Google Scholar]
  14. Bantz K. C., Meyer A. F., Wittenberg N. J., Im H. & Kurtulus O. et al. Recent progress in SERS biosensing. Phys. Chem. Chem. Phys. 13, 11551–11567 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Hoppener C. & Novotny L. Exploiting the light-metal interaction for biomolecular sensing and imaging. Q. Rev. Biophys. 45, 209–255 (2012). [DOI] [PubMed] [Google Scholar]
  16. Okamoto K., Niki I., Shvartser A., Narukawa Y. & Mukai T. et al. Surface-plasmon-enhanced light emitters based on InGaN quantum wells. Nat. Mater. 3, 601–605 (2004). [DOI] [PubMed] [Google Scholar]
  17. Kwon M. K., Kim J. Y., Kim B. H., Park I. K. & Cho C. Y. et al. Surface-plasmon-enhanced light-emitting diodes. Adv. Mater. 20, 1253–1257 (2008). [Google Scholar]
  18. Bi Y. G., Feng J., Li Y. F., Zhang X. L. & Liu Y. F. et al. Broadband Light Extraction from White Organic Light-Emitting Devices by Employing Corrugated Metallic Electrodes with Dual Periodicity. Adv. Mater. 25, 6969–6974 (2013). [DOI] [PubMed] [Google Scholar]
  19. Ferry V. E., Munday J. N. & Atwater H. A. Design Considerations for Plasmonic Photovoltaics. Adv. Mater. 22, 4794–4808 (2010). [DOI] [PubMed] [Google Scholar]
  20. Munday J. N. & Atwater H. A. Large Integrated Absorption Enhancement in Plasmonic Solar Cells by Combining Metallic Gratings and Antireflection Coatings. Nano Lett. 11, 2195–2201 (2011). [DOI] [PubMed] [Google Scholar]
  21. Conley G. M., Burresi M., Pratesi F., Vynck K. & Wiersma D. S. Light transport and localization in two-dimensional correlated disorder. Phys. Rev. Lett. 112, 143901 (2014). [DOI] [PubMed] [Google Scholar]
  22. Segev M., Silberberg Y. & Christodoulides D. N. Anderson localization of light. Nat. Photonics 7, 197–204 (2013). [Google Scholar]
  23. Strudley T., Zehender T., Blejean C., Bakkers E. P. A. M. & Muskens O. L. Mesoscopic light transport by very strong collective multiple scattering in nanowire mats. Nat. Photonics 7, 413–418 (2013). [Google Scholar]
  24. Wiersma D. S. Disordered photonics. Nat. Photonics 7, 188–196 (2013). [Google Scholar]
  25. Bozhevolnyi S. I., Beermann J. & Coello V. Direct observation of localized second-harmonic enhancement in random metal nanostructures. Phys. Rev. Lett. 90, 197403 (2003). [DOI] [PubMed] [Google Scholar]
  26. Kauranen M. & Zayats A. V. Nonlinear plasmonics. Nat. Photonics 6, 737–748 (2012). [Google Scholar]
  27. Redding B., Liew S. F., Sarma R. & Cao H. Compact spectrometer based on a disordered photonic chip. Nat. Photonics 7, 746–751 (2013). [Google Scholar]
  28. Zhai T. R., Zhang X. P., Pang Z. G., Su X. Q. & Liu H. M. et al. Random Laser Based on Waveguided Plasmonic Gain Channels. Nano Lett. 11, 4295–4298 (2011). [DOI] [PubMed] [Google Scholar]
  29. Steinhardt P. & Ostlund S. The Physics of Quasicrystals. (World Scientific Publishing Company, Singapore., 1987). [Google Scholar]
  30. Baake M. & Moody R. V. Directions in Mathematical Quasicrystals. (American Mathematical Society, Centre de Recherches Mathematiques, R.I., 2000). [Google Scholar]
  31. Dal Negro L. & Boriskina S. V. Deterministic aperiodic nanostructures for photonics and plasmonics applications. Laser Photonics Rev. 6, 178–218 (2012). [Google Scholar]
  32. Mahler L., Tredicucci A., Beltram F., Walther C., Faist J. et al. Quasi-periodic distributed feedback laser. Nat. Photonics 4, 165-169 (2010). [Google Scholar]
  33. Vardeny Z. V., Nahata A. & Agrawal A. Optics of photonic quasicrystals. Nat. Photonics 7, 177–187 (2013). [Google Scholar]
  34. Gopinath A., Boriskina S. V., Feng N. N., Reinhard B. M. & Dal Negro L. Photonic-plasmonic scattering resonances in deterministic aperiodic structures. Nano Lett. 8, 2423–2431 (2008). [DOI] [PubMed] [Google Scholar]
  35. Gopinath A., Boriskina S. V., Premasiri W. R., Ziegler L. & Reinhard B. M. et al. Plasmonic Nanogalaxies: Multiscale Aperiodic Arrays for Surface-Enhanced Raman Sensing. Nano Lett. 9, 3922–3929 (2009). [DOI] [PubMed] [Google Scholar]
  36. Gopinath A., Boriskina S. V., Reinhard B. M. & Dal Negro L. Deterministic aperiodic arrays of metal nanoparticles for surface-enhanced Raman scattering (SERS). Opt. Express 17, 3741–3753 (2009). [DOI] [PubMed] [Google Scholar]
  37. Lee S. Y., Amsden J. J., Boriskina S. V., Gopinath A. & Mitropolous A. et al. Spatial and spectral detection of protein monolayers with deterministic aperiodic arrays of metal nanoparticles. PNAS 107, 12086–12090 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Yan B., Thubagere A., Premasiri W. R., Ziegler L. D. & Dal Negro L. et al. Engineered SERS Substrates With Multiscale Signal Enhancement: Nanoplarticle Cluster Arrays. ACS Nano 3, 1190–1202 (2009). [DOI] [PubMed] [Google Scholar]
  39. Yang L. L., Yan B., Premasiri W. R., Ziegler L. D. & Dal Negro L. et al. Engineering Nanoparticle Cluster Arrays for Bacterial Biosensing: The Role of the Building Block in Multiscale SERS Substrates. Adv. Funct. Mater. 20, 2619–2628 (2010). [Google Scholar]
  40. Kim S. K., Lee J. H., Kim S. H., Hwang I. K. & Lee Y. H. et al. Photonic quasicrystal single-cell cavity mode. Appl. Phys. Lett. 86, 031101 (2005). [Google Scholar]
  41. Noh H., Yang J. K., Liew S. F., Rooks M. J. & Solomon G. S. et al. Control of Lasing in Biomimetic Structures with Short-Range Order. Phys. Rev. Lett. 106, 183901 (2011). [DOI] [PubMed] [Google Scholar]
  42. Notomi M., Suzuki H., Tamamura T. & Edagawa K. Lasing action due to the two-dimensional quasiperiodicity of photonic quasicrystals with a Penrose lattice. Phys. Rev. Lett. 92, 123906 (2004). [DOI] [PubMed] [Google Scholar]
  43. Yang J. K., Boriskina S. V., Noh H., Rooks M. J. & Solomon G. S. et al. Demonstration of laser action in a pseudorandom medium. Appl. Phys. Lett. 97, 223101 (2010). [Google Scholar]
  44. Dolev I., Volodarsky M., Porat G. & Arie A. Multiple coupling of surface plasmons in quasiperiodic gratings. Opt. Lett. 36, 1584–1586 (2011). [DOI] [PubMed] [Google Scholar]
  45. Ferry V. E., Verschuuren M. A., van Lare M. C., Schropp R. E. I. & Atwater H. A. et al. Optimized Spatial Correlations for Broadband Light Trapping Nanopatterns in High Efficiency Ultrathin Film a-Si:H Solar Cells. Nano Lett. 11, 4239–4245 (2011). [DOI] [PubMed] [Google Scholar]
  46. Academic RadiologyMartins E. R., Li J. T., Liu Y. K., Depauw V. & Chen Z. X. et al. Deterministic quasi-random nanostructures for photon control. Nat. Commun. 4, 2665 (2013). [DOI] [PubMed] [Google Scholar]
  47. Pala R. A., Liu J. S. Q., Barnard E. S., Askarov D. & Garnett E. C. et al. Optimization of non-periodic plasmonic light-trapping layers for thin-film solar cells. Nat. Commun. 4, 2095 (2013). [DOI] [PubMed] [Google Scholar]
  48. Vynck K., Burresi M., Riboli F. & Wiersma D. S. Photon management in two-dimensional disordered media. Nat. Mater. 11, 1017–1022 (2012). [DOI] [PubMed] [Google Scholar]
  49. Jin R. C., Cao Y. C., Hao E. C., Metraux G. S. & Schatz G. C. et al. Controlling anisotropic nanoparticle growth through plasmon excitation. Nature 425, 487–490 (2003). [DOI] [PubMed] [Google Scholar]
  50. Lu H. F., Kang Z. W., Zhang H. X., Xie Z. L. & Wang G. H. et al. Synthesis of size-controlled silver nanodecahedrons and their application for core-shell surface enhanced Raman scattering (SERS) tags. RSC Adv. 3, 966–974 (2013). [Google Scholar]
  51. Lu H. F., Zhang H. X., Yu X., Zeng S. W. & Yong K. T. et al. Seed-mediated Plasmon-driven Regrowth of Silver Nanodecahedrons (NDs). Plasmonics 7, 167–173 (2012). [Google Scholar]
  52. Xue C. & Mirkin C. A. pH-switchable silver nanoprism growth pathways. Angew. Chem. Int. Edit. 46, 2036–2038 (2007). [DOI] [PubMed] [Google Scholar]
  53. Wu X. M., Redmond P. L., Liu H. T., Chen Y. H. & Steigerwald M. et al. Photovoltage mechanism for room light conversion of citrate stabilized silver nanocrystal seeds to large nanoprisms. J. Am. Chem. Soc. 130, 9500–9506 (2008). [DOI] [PubMed] [Google Scholar]
  54. Pinel N. & Boulier C. Electromagnetic Wave Scattering from Random Rough Surfaces: Asymptotic Models. (John Wiley & Sons, Inc., Hoboken, 2013). [Google Scholar]
  55. Ishimaru A. Wave Propagation and Scattering in Random Media. (IEEE Press, New York, 1997). [Google Scholar]
  56. Tsangarides C. P., Yetisen A. K., Vasconcellos F. D., Montelongo Y. & Qasim M. M. et al. Computational modelling and characterisation of nanoparticle-based tuneable photonic crystal sensors. RSC Adv. 4, 10454–10461 (2014). [Google Scholar]
  57. Sadiku M. N. O. Monte Carlo methods for electromagnetics. (CRC Press, Boca Raton, 2009). [Google Scholar]
  58. Chew W. C. Waves and Fields in Inhomogenous Media. (Wiley-IEEE Press, Hoboken, 1999). [Google Scholar]
  59. Chandezon J., Maystre D. & Raoult G. A New Theoretical Method for Diffraction Gratings and Its Numerical Application. J. Opt. 11, 235–241 (1980). [Google Scholar]
  60. Moharam M. G., Grann E. B., Pommet D. A. & Gaylord T. K. Formulation for Stable and Efficient Implementation of the Rigorous Coupled-Wave Analysis of Binary Gratings. J. Opt. Soc. Am. A 12, 1068–1076 (1995). [Google Scholar]
  61. Liu H. T. & Lalanne P. Microscopic theory of the extraordinary optical transmission. Nature 452, 728–731 (2008). [DOI] [PubMed] [Google Scholar]
  62. Norton M. P. & Karczub D. G. Fundamentals of Noise and Vibration Analysis for Engineers. 2nd edn, (Cambridge University Press, Cambridge, 2003). [Google Scholar]
  63. Landauer R. Electrical conductivity in inhomogeneous media. AIP Conf. Proc. 40, 2–45 (1978). [Google Scholar]
  64. Reynolds J. A. & Hough J. M. Formulae for Dielectric Constant of Mixtures. Proc. Phys. Soc. London, Sect. B 70 769–775 (1957). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Informations

srep07876-s1.doc (4.9MB, doc)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES