Determination of the second virial coefficient of bovine serum albumin under varying pH and ionic strength by composition-gradient multi-angle static light scattering

Abstract

Composition-gradient multi-angle static light scattering (CG-MALS) is an emerging technique for the determination of intermolecular interactions via the second virial coefficient B₂₂. With CG-MALS, detailed studies of the second virial coefficient can be carried out more accurately and effectively than with traditional methods. In addition, automated mixing, delivery and measurement enable high speed, continuous, fluctuation-free sample delivery and accurate results. Using CG-MALS we measure the second virial coefficient of bovine serum albumin (BSA) in aqueous solutions at various values of pH and ionic strength of a univalent salt (NaCl). The systematic variation of the second virial coefficient as a function of pH and NaCl strength reveals the net charge change and the isoelectric point of BSA under different solution conditions. The magnitude of the second virial coefficient decreases to 1.13 x 10⁻⁵ ml*mol/g² near the isoelectric point of pH 4.6 and 25 mM NaCl. These results illuminate the role of fundamental long-range electrostatic and van der Waals forces in protein-protein interactions, specifically their dependence on pH and ionic strength.

Electronic supplementary material The online version of this article (doi:10.1007/s10867-014-9367-7) contains supplementary material, which is available to authorized users.

Introduction

Long range interactions (LRIs) are important not only in nanoscale science [1] but also in biomolecular systems [2, 3] such as protein solutions. LRIs dictate protein recognition, crystallization, and self association, as well as more general phenomena such as aggregation and self-assembly [4, 5]. In mesoscale science, proteins, peptides, viral nanoparticles and other colloidal materials are utilized as building blocks for the assembly of hierarchical materials incorporating functional entities or self-healing properties [Hemminger Quanta 2012], the design of which is based on the understanding of long- and short-range interactions between the building blocks. The basic principles of protein-protein interactions and protein aggregation in aqueous solutions [6, 7] are also important for the manufacture and delivery of protein drugs [8], for structural biology and crystallography [9], as well as for understanding the basis of certain diseases [10]. Protein-protein interactions can be characterized by standard principles of nanoscale stability theory that identify direct long-range and solvent-mediated short-range interactions [1] that together govern the molecular recognition and assembly of macromolecules [2].

LRIs include electrostatic interactions [11] that depend on the specific nature of molecular charges and the net charge on a body, polar interactions [12] arising from dipolar and higher order charge multipoles, and van der Waals-London dispersion (vdW-Ld) interactions, which are driven by quantum and thermal fluctuations and depend on the dielectric response properties of the molecular materials [13]. Polar interactions in particular seem to be important for proteins because their charged groups are unevenly distributed in patches, creating a complex mosaic of charges on the protein surface [4] with dipolar and higher multipolar moments that affect the interaction in an essential way [14]. In aqueous solutions, non-specific LRIs, which play critical role in harnessing the assembly and disassembly of general nanoscale systems, are often modified by quite specific short-range water-mediated interactions such as hydration, hydrophobic, and steric interactions [15].

LRIs between molecules can be measured and characterized in different ways. At thermodynamic equilibrium the particle-particle, or in this case protein-protein, interaction potential (the potential of mean force) is related to thermodynamics via the osmotic second virial coefficient B₂₂, which characterizes the pairwise interactions [16]. For relatively weak interactions the second virial coefficient quantifies the deviation of a solution from thermodynamic ideality. Positive values of B₂₂ indicate a predominant mutual repulsive interaction, and negative values a predominant attractive interaction. The connection is not direct, however, since the second virial coefficient is proportional to an integral of the potential of mean force over all separations (as well as orientations) and though it is relatively insensitive to its detailed nature, it can nevertheless reveal many important details of the protein-protein interactions [17].

The potential of mean force between biomolecular or colloidal materials can be decomposed [11] into the additive contributions of different LRIs including the attractive vdW-Ld interaction (W_A(r)) [18] and repulsive electrostatic interaction (W_R(r)) [19] in combination with a hard core/steric W_HC(r). The protein-protein potential of mean force can then be approximated as [20]

$$W\left(r\right)=W_A\left(r\right)+W_R\left(r\right)+W_{\mathit{HC}}\left(r\right)=W_{\mathit{DLVO}}\left(r\right)+W_{\mathit{HC}}\left(r\right),$$ 1

where we combine the vdW-Ld and electrostatic LRIs into the DLVO potential [11, 20]. Here r is the center-to-center separation, and orientational averaging is already implied. The second virial coefficient B₂₂ then enters the osmotic pressure (Π) virial equation of state as [21]

$$\Pi \left(c\right)/\mathit{RT}=c/M+B_{22}{c}^2+B_{33}{c}^3+\mathrm{...}$$ 2

where c is the molecular or colloidal materials concentration in solution, M is their molecular mass, B₃₃ is the third virial coefficient, R is the ideal gas constant, and T is temperature. In some communities, the second virial coefficient B22 is referred to as A2 or B2 [24, 27, 40, 46]. Consequently, the second virial coefficient can be written explicitly as a functional of the interaction potential in the form [20]

$$B_{22}{M}^2=2\pi N_A{\int }_a^{\infty }\left(1-e^{-W\left(r\right)/k_{B}T}\right)r^2\mathit{dr}$$ 3

where a is the hard core radius, k_B is the Boltzmann constant, N_a is the Avogadro number, r is the center-to-center separation, and M is molecular mass.We did not differentiate between the apparent second virial coefficient and the B₂₂, the appropriate connection being thoroughly discussed in the works of Roberts and coworkers [23].

Various experimental techniques have been developed to determine the second virial coefficient with differing limitations and caveats. Traditionally, membrane osmometry has been a widely-used technique [24–28]. The osmometry system consists of a solvent and a protein chamber equipped with a pressure gauge. The osmotic pressure of the solution is measured at the equilibrium state of the system (which can take several hours to reach). The second virial coefficient is determined from the slope of the osmotic pressure dependence on the concentration. This measurement method usually needs high protein concentrations (tens to hundreds mg/mL) and long measurement times (a few hours are needed to determine a single B₂₂ value).

Both small-angle X-ray scattering [29–31] and small-angle neutron scattering [32, 33] methods have been used to monitor the second virial coefficient of proteins in aqueous solutions. The determination of the second virial coefficient is based on the equivalence between the structure factor at the origin of the reciprocal space and the normalized osmotic compressibility. The main drawback of the scattering methods is that in order to maintain high accuracy, access to the synchrotron and/or neutron source is necessary; therefore this experiment would demand extensive resources and would be rather time consuming. Another approach to the determination of the second virial coefficient uses isopycnic ultracentrifugation, based on the radial concentration distribution profile of the solute at the sedimentation equilibrium [34, 35].

Self-interaction chromatography (SIC) [36, 37] and frontal chromatography [38] were also used in the characterization of the protein solution second virial coefficient. In SIC, the protein is covalently immobilized on chromatographic particles, the particles are packed into a column, and the retention time of a pulse of the same protein through the SIC column is measured. This method requires prior immobilization of the protein, thereby affecting its structure [39]. Frontal chromatography requires large amounts of protein because the solute concentration in the column needs to be constant. While some efforts have been made to use size exclusion chromatography (SEC) as a tool to study the second virial coefficient [40], this method assumes that there is no difference in the solute-solute interactions in the mobile and stationary phase, as well as a linear dependence of the logarithm of the activity coefficients of solute molecules on the protein concentration even at high concentration [41]. Furthermore, though the eluting concentrations of protein are comparable for SEC and static light scattering (SLS), the injected concentrations of the protein must be much higher for SEC than SLS experiments [9, 33, 42–44], which could create problems, and, finally, at these concentrations the column could get saturated, precluding interpretable measurement.

Many of these techniques have been applied to the characterization of bovine serum albumin (BSA). For example, the osmotic pressure of BSA solutions at pH = 4.5, 5.4, 7.4 and 0.15 M NaCl ionic strength were measured [20, 24]. Subsequent osmometry on BSA investigated the second virial coefficient as a function of pH and ammonium sulfate concentrations [26, 27]. More recent studies using osmometry investigated the effect of pH and various monovalent ions (sodium, potassium, lithium) on the second virial coefficient of BSA [28]. SIC [37], SEC [39, 40, 45], and frontal chromatography [38] were also used to determine the second virial coefficient of BSA.

Recent progress in the SLS techniques, specifically the advent of composition-gradient multi-angle static light scattering (CG-MALS) [22, 46–48], has enabled a more accurate and nondestructive determination of the second virial coefficient of protein solutions. With CG-MALS, detailed studies of the second virial coefficient can be carried out using only limited amounts of protein samples (a low-moderate protein concentration of 1.5 - 35 mg/mL is appropriate for the chemical conditions of this work) and within a reasonable time (five A2 measurements can be completed in three hours). In CG-MALS, the Rayleigh scattering of real solution is related to deviations from ideal solution as [49]

$$\frac{R(c,\theta )}{K^{\ast }c}=\mathit{MP}(r_g,\theta )-2B_{22}c{M}^2{P}^2{r}_g,\theta ),$$ 4

or alternatively in its reciprocal form as [46, 50]

$$\frac{K^{\ast }c}{R(c,\theta )}=\frac{1}{\mathit{MP}\left(r_g,\theta \right)}+2B_{22}c,$$ 5

where R(c, θ) is the excess Rayleigh ratio, c is the concentration of the species, M is the molar mass, θ is the scattering angle, K^∗ is a constant that depends on the illumination wavelength solvent refractive index and refractive index increment, r_g is the root mean square radius and P(r_g, θ) is the angular dependence of the scattered light, and B₂₂ is the apparent second virial coefficient recovered from SLS. Though the real second virial coefficient and the apparent second virial coefficient retrieved from the classical light scattering equation are in general different when the protein concentration is too high [23], we assume that in the regime relevant for the present work the limit of small concentrations is valid and the two are equivalent.

In the present work we use CG-MALS with Calypso and Dawn Heleos II tools (Wyatt Technology, Santa Barbara, CA) to measure the second virial coefficient of protein solutions as a function of the bathing conditions. Since BSA has served as a validated standard to measure and interpret second virial coefficient data [39, 51, 52] for many years, we assumed that BSA would be a good model for our approach. We determined the second virial coefficient of BSA in aqueous solutions at various pH (pH 3.6 - 7.4) and ionic strength (25 - 150 mM NaCl) in Na₂HPO₄-citric acid buffer. The Calypso automated mixing and delivery hardware enables high-speed, continuous, fluctuation-free sample delivery, allowing us to focus on the detailed effects of fine variations of pH as well as the ionic strength of the univalent (NaCl) salt solution on the second virial coefficient of BSA aqueous solutions.

Methods

Buffer and sample preparation

BSA, citric acid anhydrate, Na₂HPO₄ anhydrate, and NaCl were all purchased from Sigma Aldrich and used as received. Citric acid-Na₂HPO₄ buffers of varying pH (pH 3.07-6.68) were prepared through addition of 50 mM citric acid solution to a 50 mM citric acid-Na₂HPO₄ buffer pH 7.50±0.03 stock solution; this mixing was carried out using the in-line Calypso hardware for CG-MALS. NaCl was dissolved into the stock solution of 50 mM citric acid solution and 50 mM citric acid-Na₂HPO₄ pH 7.50+/-0.03 buffer to adjust the ionic strength and yield buffers containing 0 mM, 25 mM, 50 mM, 75 mM, and 150 mM NaCl. We measured the pH (pH meter, Sper Scientific) of each buffer solution prepared before and after addition of NaCl (see Supporting Data, Figure S1). We refer to the nominal pH as the pH of the buffer before the addition of NaCl, and the solvent pH as the pH of the buffer after the NaCl addition. BSA (1.5 - 35 mg/mL) in 50 mM citric acid-Na₂HPO₄ buffer with additional NaCl was also mixed in using the in-line Calypso hardware. It is known that the pH of BSA solution is dependent on the protein concentration [53] and thus we also tested the deviation of the pH of 1 mg/mL BSA and 35 mg/mL BSA solutions with respect to the solvent pH. All solutions were filtered through a 0.1 um syringe filter followed by a 0.02 um syringe filter to remove aggregates and possible contaminants prior to CG-MALS analysis.

Hardware System Description and CG-MALS Method

The measurements of the second virial coefficient were carried out using a Wyatt Dawn Heleos II, a composition gradient-multiangle static light scattering (CG-MALS) detector in conjunction with Wyatt Calypso automating delivery system and Waters 2487 Dual Absorbance Detector [46]. The CG-MALS batch mode measurement consists of a buffer flush to obtain initial baseline light scattering intensity, several sample injections with gradient concentrations, and finally a buffer flush to obtain another baseline. The scattered light from the solution is obtained by 18 detectors distributed around the flow cell. The sample concentration is measured by the in-line UV detector and transmitted to the CG-MALS detector. The utilization of the Calypso automating mixing and delivery hardware guarantee a continuous, fluctuation-free sample delivery. Calypso software was used to collect and analyze the UV absorbance and light scattering data. These data are then fitted to equation (4), obtaining in the process the second virial coefficient, molar mass M, and root mean square radius (for particles with radius larger than 10 nm). Specifically, the value of the second virial coefficient is determined by the slope of the concentration dependence of the excess Rayleigh ratio.

Fast protein liquid chromatography (FPLC)

To determine the overall yield of BSA monomers vs. dimers and multimers, BSA samples were analyzed by size exclusion chromatography (SEC) using a Superose 6 column on the $Ä$KTA Explorer chromatography system (GE Healthcare). BSA (100 μg/100 μL) was analyzed at a flow rate of 0.5 mL/min using citric acid-Na₂HPO₄ buffer with pH 3.78 and 150 mM NaCl.

Dynamic light scattering (DLS)

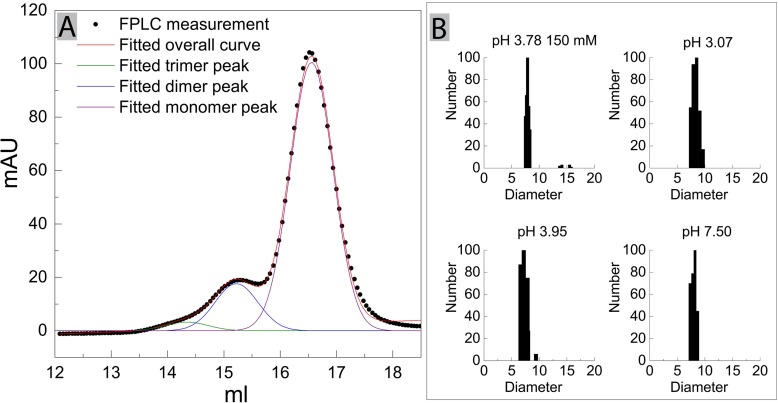
A 90 Plus Particle Size Analyzer (Brookhaven Instruments Corporation, Holtsville NY) Dynamic Light Scattering (DLS) instrument (at 25^oC) was used to measure the hydrodynamic diameter of 1 mg/ml of BSA at pH 3.78 with 150 mM NaCl, as well as pH 3.07, 3.95, and 7.50 without NaCl. Five 1-min measurements were made, and each sample was measured in triplicate; Fig. 1B reports representative data. The software version 5.57 used solid sphere assumptions in its calculations.

Fig. 1.

A) Fractional composition of the BSA polydispersity in solution. BSA (100 μg/100 μL) was analyzed at a flow rate of 0.5 mL/min using citric acid-Na₂ HPO ₂ buffer with 150 mM NaCl at pH 3.78. The experimental result is presented as black dots. The data were fitted with a second-derivative plot. The fitted monomer, dimer, trimer peaks and overall curve are presented as colored lines. B) The hydrodynamic diameter of BSA determined by DLS method; BSA at 1 mg/mL in citric acid-Na₂ HPO ₂ buffer at pH 3.78 with 150 mM NaCl, and pH 3.07, 3.95, and 7.50 without NaCl

Results

Determination of fractional polydispersity and hydrodynamic diameter

BSA has a molecular weight of ∼ 66.5 kDa. The average molecular weight of BSA as determined by SLS was indicated to lie at 90 - 100 kDa, which implies the presence of BSA dimers and oligomers. We therefore used SEC to identify and separate the fraction of monomers, dimers, etc. Size exclusion chromatography elution profiles obtained by FPLC were analyzed with a second-derivative plot, resolving into three Gaussian peaks (Fig. 1A). These peaks are considered as monomers, dimers and trimers, respectively, because BSA in solution is known to exist as these three structures [54, 55]. By calculating the area of the fitted monomer, dimer, and trimer peaks, the fraction of monomers is determined to be 83%. Consistent with FPLC measurements, DLS data (Fig. 1B) indicate that the monomer is by far the dominating species. The averaged BSA hydrodynamic diameter was determined to lie at approximately 7.8 ± 5% nm, which is consistent with previous literature reports [53] and also with the BSA structure, which has a heart shape that can be approximated to an equilateral triangles with sides of ∼8 nm and a depth of ∼3 nm [56].

Measurement of pH

To investigate the effect of pH on the interaction between proteins, it is important to determine the pH value of the buffers under investigation accurately. One should consider uncertainties arising from the sample handing (weighing and pipetting) and pH measurement itself, which may lead to errors in the pH values. Therefore, we prepared buffer solutions before and after the addition of NaCl that were then measured manually multiple times (at least in triplicates). From this we determined an average pH uncertainty value of 0.03 (see Supporting Information, Figure S1). Further, measurement of pH before and after the NaCl addition was carried out to determine the influence of NaCl on pH. We determined a cross-correlation coefficient of -0.00116 between pH and NaCl concentration (see Supporting Information, Figure S1). By dissolving 1 mg/mL and 35 mg/mL BSA into the buffer solution containing NaCl and measuring the pH change, it was observed that the addition of 35 mg/mL BSA would lead to a pH increase of 0.72 units on average; the pH difference caused by an addition of 1 mg/mL BSA is too slight to be measured.

Zimm plot and the determination of the second virial coefficient

The static light scattering data of a set of BSA samples (which comprise one concentration gradient) is represented as a Zimm Plot (Fig. 2) [49]. Detector 1 is physically blocked by the flow cell and should not be used; since large particles will scatter more light to the detectors at low angles (such as detectors 2 and 3), these detectors are more sensitive to the presence of contaminants. Detectors at high angle (such as detector 18) can be affected by particles causing poor normalization. As a result, these detectors are prone to show noisy signal due to particle contamination and may be excluded from data analysis. The value of the second virial coefficient is determined by the slope of the concentration dependence of R/K^∗c for each scattering angle.

Fig. 2.

Zimm plot for the static light scattering data of a set of BSA samples that comprise one concentration gradient (bathing condition is: pH 4.25 buffer with 150 mM NaCl). Symbols with the same color correspond to the angle-dependent scattered light signal of one step among the BSA concentration gradient. Black color represents the highest concentration, and orange color represents the lowest concentration. Squares represent experimental data, whereas the fitted data are shown as lines. In this case, detectors 4 - 17 were included; 1, 2, 3, and 18 were excluded. The six sample concentrations were determined to be: 17.6, 14.9, 12.3, 9.7, 7.0, and 4.4 (mg/mL)

A2 vs. actual pH at each ion strength; A2 vs. ionic strength at each nominal pH

The second virial coefficients data are listed in Table 1. Figure 3A represents the second virial coefficient of BSA versus the actual pH of 35 mg/mL BSA solution at each NaCl concentration; Figure 3B illustrates the second virial coefficient of BSA versus NaCl concentration at each nominal pH.

Table 1.

The second virial coefficients of BSA under various pH and NaCl strength. The unit is ml*mol/g². The pH of the actual BSA solution is shown

25 mM NaCl		50 mM NaCl		75mM NaCl		150mM NaCl
pH	B22*105	pH	B22*105	pH	B22*105	pH	B22*105
3.76	15.30	3.73	10.80	3.70	9.94	3.62	6.97
4.64	1.13	4.61	1.62	4.58	1.63	4.50	3.16
4.89	1.92	4.86	2.16	4.83	3.11	4.75	3.27
5.11	3.18	5.08	3.62	5.05	3.02	4.97	3.47
5.47	3.34	5.44	4.25	5.41	3.60	5.33	3.39
6.39	6.30	6.36	5.19	6.33	4.78	6.25	6.16
7.37	8.60	7.34	6.93	7.31	6.86	7.23	6.64

Fig. 3.

Variation of the second virial coefficient as a function of the pH and the ionic strength of the NaCl. A) B₂₂ vs. actual pH value of BSA solution. B) B₂₂ vs. NaCl concentration. The size of the data symbols are designed to include the error bars of pH (0.03 as determined through experiments, see Supporting Information, Figure S1) and the second virial coefficient (1.8 x10⁻⁶ ml*mol/g²). Dashed line indicates the value of the ideal hard sphere second virial coefficient as in Sahin et al. [22]

Discussion

Though it is not the primary intention of this work to deconvolute the second virial coefficient data into the underlying components of the interactions potential of mean force, (1), we do comment upon this connection. From the measured values of the second virial coefficient and its connection with the potential of mean force, (3), it is clear that the pH and the salt concentration have a significant effect on the intermolecular interactions. The second virial coefficient minimum is observed at pH of ∼ 4.6. Previous zeta potential measurements on BSA indicate an isoelectric point ranging from pH 4.13 to pH 5.0 [17, 53, 57], depending on the buffer condition and BSA concentration. Other studies employing methods of osmometry and electrophoresis have reported isoelectric points of 4.40 and 4.72 [24, 58].

Overall, the changes in the second virial coefficient for the BSA samples with high salt concentration are less profound, which indicates that there is strong screening of the electrostatic repulsion at these solution conditions [19]. The small increase of the second virial coefficient as a function of the salt concentration in the regime of nominal pH 3.95 - 4.20 could be interpreted to indicate the effect of screening on the vdW-Ld interactions, specifically on the zero frequency term in the Hamaker coefficient [13], leading to a small decrease in the effective attraction between the proteins. While the screening effect is standardly acknowledged in the electrostatic interactions, it is seldom considered in the vdW-Ld interactions. We note that in particular for the aqueous solvent the zero (Matsubara) frequency contribution to the total Hamaker coefficient can amount to about 50% of the total value [59, 60] and its screening makes a big change in the Hamaker coefficient. The higher (Matsubara) frequency contributions to the Hamaker coefficient are not screened as their frequency is way above any electrolyte relaxation processes.

For over 30 years [24–28], osmotic pressure measurements of BSA have been reported from the fit to (2). Additionally, other measurements of the second virial coefficient for BSA solutions have been quantified by the solute retention time used in chromatography [37–40, 45]. Although these techniques are valid for the determination of the second virial coefficient, the CG-MALS method offers a direct way to retrieve a large amount of angle-dependent data for many simultaneous fits and thus turns out to be a more efficient and accurate method for determining the second virial coefficient of BSA under different salt concentrations and pH values. With the analysis of the B₂₂ variation in Fig. 3 and verification of the high monomer percentage in our sample with FPLC measurements, we find that CG-MALS is to be preferred as a method for determining the second virial coefficient with low error, providing more information on each BSA sample than the previous experimental techniques.

The comparison between the measurements of the second virial coefficient of BSA under different univalent salt conditions is presented in Fig. 4, showing four published data sets for BSA in monovalent salt solutions [24, 28, 40, 46] together with present data at 150 mM NaCl strength. The methods used in the determination of the solution parameters and the range of bathing solution conditions vary. The scatter in the various experimental data is surprisingly large and the data taken by SLS technique tend to be at the lower boundary of the measured values. However, it is in general difficult to compare various methods and estimate the pertinent errors. We note that often it is not at all clear from the described protocols what pH value is quoted in the pH scans of the second virial coefficient, i.e., no attention was paid in the previous work to the coupling between the pH and the ionic strength of the bathing solution as well as the pH and the BSA concentration. In the present work, we specifically consider the variation of pH with the explicit addition of NaCl and BSA, thus enabling a more precise determination of the second virial coefficient and the pertinent isoelectric point of BSA. It should be noted that the accuracy in the determination of the second virial coefficients can be improved further using BSA samples with higher monomer percentage. The current measured values are more or less affected by the 17% dimers and trimers in the BSA solution.

Fig. 4.

Comparison between the measured second virial coefficients under different univalent salt bathing solution conditions. Data labelled [Park], [Vilker], [Bloustin], and [Some], is taken from references [24, 28, 40], and [46], respectively. [Park]: BSA in sodium phosphate buffer with various univalent salts as indicated in the figure, measured by osmometry. [Vilker]: BSA in distilled water with 0.15M NaCl, measured by osmometry. [Bloustin]: BSA in potassium phosphate buffer, measured by size exclusion chromatography. [Some]: BSA in standard phosphate buffer with 0.05M NaCl, measured by CG-MALS. The present work: BSA in citric acid-Na₂HPO₄ buffer with 0.15M NaCl. Lines are to guide the eyes

Robust and fast techniques for measuring the second virial coefficients of complex systems are important for the accurate study of the properties of the underlying fundamental LRIs between solutes. In principle, accurate determination of the second virial coefficient allows differentiation of the specific and non-specific interactions in multi-component systems. We have reached an accuracy in the determination of the second virial coefficient that allows the study of subtle phenomena such as the interdependence of the screening properties of vdW-Ld and electrostatic interactions in proteins.The study methodology can be expanded to more complex inorganic and biomolecular moieties in realistic and well defined bathing conditions.

Conclusion

The second virial coefficients of BSA at multiple univalent salt (NaCl) strengths and pH bathing solution conditions were measured with a CG-MALS detector in conjunction with a Calypso automating delivery system and UV detector. The second virial coefficient data were obtained with low error bars. Comparison of CG-MALS with traditional experimental techniques indicates that CG-MALS is an effective and precise method for determining the second virial coefficient of molecules and can be used to study subtle effects that require high precision of the experiment such as the combined vdW-Ld and electrostatic screening. The accurate second virial coefficient data indicate its strong dependence on pH and salt, as well as their coupling, thus giving insight into the isoelectric point of BSA, and the close relationship between the electrostatic and vdW-Ld interactions.This experimental method can be applied to determine second virial coefficients and consequently for characterization of molecular interactions in even more complex biomolecular systems encompassing solutions of different viral nanoparticles. The accuracy provided by this experimental method will be particularly useful when studying large parameter spaces (pH, ionic strength, PEGylation, counter-ion identity etc.) as is the case in virus capsids and virus nanoparticles [61].