When maths trumps logic: probabilistic judgements in chimpanzees

Abstract

When searching for hidden food, do chimpanzees take into account both the number of hidden items and the number of potential hiding locations? We presented chimpanzees with two trays, each of them containing a different food/cup ratio and therefore a different likelihood of finding a baited cup among empty alternatives. Subjects' performance was directly influenced by the relative difference (probability ratio (PR)) between the two given probabilities. Interestingly, however, they did not appreciate the special value of a truly safe option (with P = 1.0). Instead, they seemed to ‘blindly’ rely on the PR between the two options, systematically preferring the more likely one once a certain threshold had been reached. A control condition ruled out the possibility of low-level learning explanations for the observed performance.

1. Introduction

Several quantitative abilities including quantity discrimination [1–5], numerical ordering [6] and even basic arithmetic operations [7] have been documented in various animal species. Moreover, the importance of relative rather than absolute quantity assessments has been reported both in laboratory and in natural settings. For example, in intergroup encounters, lions [8] and chimpanzees [9] chose to approach or withdraw from intruders depending on the relative (not the absolute) number of intruders and defenders present. However, little is known about how individuals spontaneously respond when confronted with options with identical absolute values (i.e. same amount of food in each option) that differ in the probability of success prior to learning the reward contingencies.

In this study, subjects searched for food hidden underneath one of up to six cups placed on two different trays. Chimpanzees had to pick one cup from one of the two trays, with each tray representing a different likelihood of finding a food-baited cup. Crucially, we administered only a few trials per food/cup constellation to minimize the likelihood of learning to respond according to the reward contingencies experienced during the test. Moreover, we confronted subjects with another condition identical to the previous condition except that all cups were empty. This empty condition allowed us to assess whether subjects had learned to focus on those food/cup constellations that were more frequently followed by positive outcomes without resorting to any probabilistic judgement. If this were the case, no difference between the conditions should be expected because both the baited and empty condition followed identical reinforcement regimes.

2. Material and methods

(a). Subjects

We tested eight chimpanzees (four females) with estimated ages between 10 and 15 years (mean = 12.6, s.d. = 1.7). All chimpanzees were wild-born, orphaned at a young age, and rescued and sent to the Ngamba Island Sanctuary, Uganda, where they lived in a social group at the time of testing. All subjects were tested individually and were never food or water deprived.

(b). Material

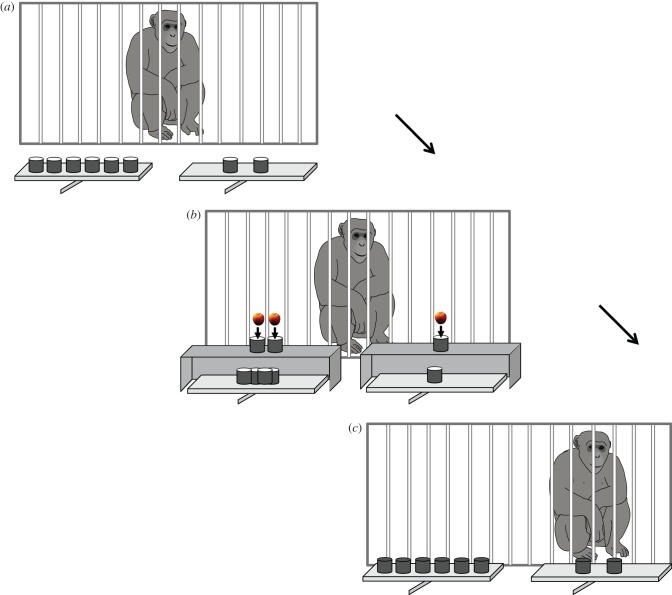
Twelve identical metal cups (7 cm in diameter and 5 cm deep) served as hiding locations. They were distributed on top of two wooden trays (80 × 20 cm) presented side-by-side 10 cm apart from each other on the floor directly in front of the subject (figure 1). Two half-open cardboard boxes served as occluders that served to block the subject's view while shuffling the cups on each tray.

Figure 1.

Experimental set-up used: (a) starting position of empty cups on each tray; (b) after the occluders were put up, an assigned number of cups were baited; (c) after both occluders were lifted, subjects were allowed to choose. (Online version in colour.)

(c). Procedure

Subjects sat facing the experimenter, separated by metal bars. Each session began with four warm-up trials to acquaint subjects with the testing procedure and to ensure that they could keep track of a baited cup. During a warm-up trial, only two cups were used, each placed on one tray. Subjects witnessed the experimenter baiting one of the cups, while the other was left empty. Both cups were then covered by an occluder and they were turned upside down. Upon removing the occluders, subjects chose one of the cups by touching it. Only subjects who chose the baited cup (4/4 times) moved on to the test phase.

(i). Baited condition

Each trial started by showing subjects that all cups (varying in number from 1 to 6) on both trays were empty. After placing the occluders on the trays and over the cups (figure 1a), the experimenter moved a pre-determined number of cups (varying from 1 to 4) from the tray to the top of each occluder and subjects witnessed how he baited each cup with one apple piece (figure 1b). We used the food/cup ratios shown in table 1. After the baiting, all cups were put back on their respective trays behind the occluders, turned upside down and shuffled. Finally, both occluders were lifted and the trays were simultaneously moved into the subject's reach (figure 1c). Subjects could choose one cup from either tray, and always received its contents.

Table 1.

The food/cup ratio depicts how many food pieces are distributed among how many cups on a given tray. The probability ratio (PR) relates the likelihood of finding the food on the ‘risky tray’ to the likelihood of finding the food on the ‘safe(r) tray’. Correct choice corresponds to the percentage of trials in which the ‘safe(r) tray’ is chosen.

food/cup ratio on each tray	1/1 versus 1/2	1/1 versus 1/3	1/1 versus 1/4	1/1 versus 1/5	1/1 versus 1/6	1/1 versus 2/4	1/1 versus 2/3	1/2 versus 1/4	1/2 versus 2/6	1/3 versus 1/6	2/3 versus 3/6	2/2 versus 4/6	2/2 versus 3/6
probability ratio (PR) between trays (Plow/Phigh)	0.5	0.33	0.25	0.2	0.17	0.5	0.67	0.5	0.67	0.5	0.75	0.67	0.5
correct choice (%)	44	69	78	75	84	38	41	63	34	44	38	44	42

(ii). Empty condition

The procedure was identical to the baited condition except that prior to putting the cups back behind the occluder, the experimenter removed the food from the cups and placed it into a bucket. Both the baiting as well as the subsequent food removal took place in full view of the subject. All (now empty) cups were placed back on the respective trays behind the occluders and the procedure continued in the same way as the baited condition except that all cups remained empty. Whenever a subject chose a cup that was assigned ‘baited’, it received one apple piece from the bucket, whereas when it chose a cup that was assigned ‘empty’, it received nothing. This rewarding scheme followed exactly the baiting scheme of the baited condition, so that the reward contingencies in the baited and empty condition were identical.

Subjects received five consecutive sessions per condition (one daily session of 10–12 trials). Half of the subjects (group 1) started with the baited condition (52 trials) followed by the empty condition (52 trials), whereas the other half of the subjects (group 2) received the two conditions in the opposite order. Out of the 18 possible options to distribute one to four food pieces between one and six cups, we decided to present subjects with the following 12 food/cup ratios: 1/1, 1/2, 1/3, 1/4, 1/5, 1/6, 2/2, 2/3, 2/4, 2/6, 3/6 and 4/6. These 12 food/cup ratios represent seven different probabilities of finding the baited cup among all cups on each tray (P = 1.00, 0.66, 0.50, 0.33, 0.25, 0.20, 0.17). The 12 possible food/cup ratios per tray resulted in 144 potential left tray/right tray constellations, out of which we presented only 13 to the subjects (table 1). Each of the 13 left tray/right tray constellations was presented four times in total per condition, with the higher probability of finding a baited cup appearing two times on each tray. To avoid a decisional deadlock, there were no cases in which both trays provided the same probability of finding a baited cup.

(d). Data scoring and analysis

All trials were videotaped. Our dependent variable was the percentage of trials in which subjects selected a cup from the tray with the higher likelihood of finding the hidden food item (i.e. the tray with the better food/cup ratio). Subjects chose by touching one of the cups with their fingers. A second observer scored 20% of all sessions to assess inter-observer reliability, which was excellent (Cohen's κ = 0.99).

3. Results

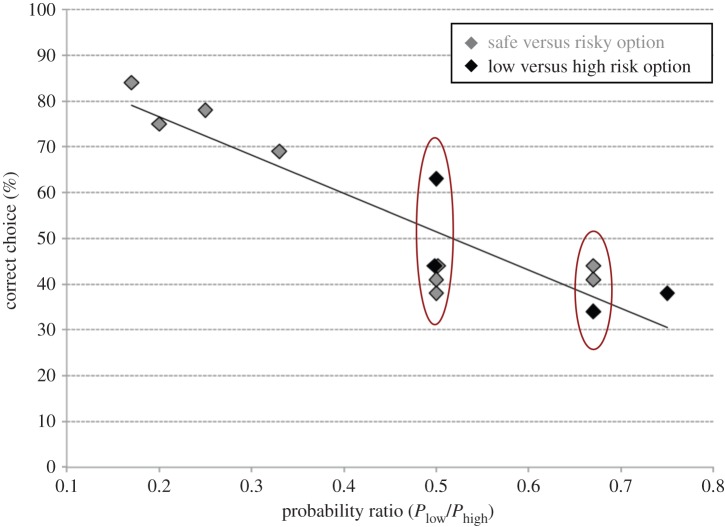
The percentage of correct responses significantly increased as a linear function of the probability ratio (PR) in the baited condition (Pearson's r₁₁ = 0.90, p < 0.001, figure 2) but not in the empty condition (Pearson's r₁₁ = 0.36, p = 0.229). All subsequent analyses are based on the baited condition. Comparing performance against chance (50%) revealed that subjects only performed above chance level in those trials with a PR that was smaller than 0.50 (one-sample t-test: t₇ > 2.99, p < 0.05 in all cases). Six of the 13 constellations involved trials in which the number of food items differed between trays. This means that the difference in food quantities between trays, not just the probability associated with them, may have also influenced subjects' choices. Therefore, we calculated the percentage of trials in which subjects chose the tray with the larger food quantity for each of those six constellations. Subjects showed a significant preference for the tray with the larger food quantity only in the 1/2 versus 2/6 constellations (one-sample t-test: t₇ = 2.65, p = 0.033; t₇ < 1.94, p > 0.05 in all other cases). However, pooling together all constellations revealed a slight but consistent preference for the tray with the larger food quantity (one-sample t-test: t₇ = 4.18, p = 0.004; mean = 60.4%, s.e.m. = 2.5). This means that the number of food items may have also influenced subjects' choices. However, it still cannot explain the results of those trials with the same food quantity on both trays (54% of the trials), which still evidenced a strong relationship between the percentage of correct responses and the ratio between probabilities (Pearson's r₅ = 0.804, p = 0.029).

Figure 2.

Percentage of trials in which subjects chose the tray with the higher likelihood of finding the hidden food item. Grey-filled symbols represent decisions between a safe and a risky option; black symbols represent decisions between two risky options. (Online version in colour.)

Two of the PRs (PR = 0.50, PR = 0.67) were represented by trials differing in the number of cups and food pieces used. However, there was no significant difference in the percentage of correct responses between the different food/cup constellations within each of the probabilities (PR = 0.50: F_4,28 = 1.80, p = 0.16; PR = 0.67: F_2,14 = 0.34, p = 0.72). Pooling the trials representing the same probabilities and re-analysing the data confirmed the significant relationship between the percentage of correct responses and the ratio between probabilities (Pearson's r₅ = 0.97, p < 0.001). Moreover, focusing exclusively on those trials where one of the options offered a certain reward (P = 1; e.g. two apples in two cups) produced comparable results (Pearson's r₇ = 0.92, p < 0.001).

There was no indication that subjects learned over time, as their performance during the first and the last 25% of trials did not differ (paired-sample t-test: t₇ = 0.37, P = 0.72). In fact, the relationship between PR and subjects' preference for the better likelihood tray was already apparent during the first exposure to each of the different food/cup constellations (Pearson's r₁₁ = 0.73, p < 0.04). Additionally, there was no indication that subjects spied the reward under the baited cups because their observed success did not differ from chance in those trials in which they picked a tray with P < 1.0 (paired-sample t-test: t₇ = 1.18, p = 0.28).

4. Discussion

Subjects' performance increased as a linear function of the PR. The higher the discrepancy between trays, the easier it became for chimpanzees to choose the tray associated with the larger chance of finding the hidden food. Furthermore, this result held even when we only considered (i) the first trials of each constellation and (ii) those trials with identical food quantities on both trays. This finding is consistent with previous work on quantity discrimination and risk estimation in great apes [2,5,10] and supports the idea of an analogue magnitude system that is engaged in decision-making involving quantities [11,12].

Two additional findings are important. First, subjects did not differentiate between the individual food/cup constellations as long as they belonged to the same PR (e.g. PR = 0.50 is represented by 1/1 versus 2/4 and 1/3 versus 1/6 choice). Although subjects' performance gradually increased with a decreasing PR, it reached significance level only when the PR between the trays was less than or equal to 0.33. We found some indication that the food quantity on each tray may have also influenced subjects' choices. However, this factor, unlike the PR, left the performance in trials with identical food quantities unexplained.

Second, a rather unexpected outcome was that subjects applied the described ratio calculation quite rigidly, which in some cases became counterproductive. We found no evidence that they appreciated the special status of a completely safe option (P = 1). Instead their decisions were influenced by the relative difference between two probabilities (PR) and not by the fact that one of the probabilities was 1.0 and therefore completely safe (figure 2). By contrast, human adults have a strong preference for options that offer a safe reward compared with any other option, provided the maximum outcome is the same [13,14]. In a sense, the chimpanzees tested here seemed to be strictly guided by (intuitive) mathematics—‘How much do the two likelihoods differ?’—rather than by (intuitive) logic—‘Is one of the options safe?’.

Crucially, all the patterns described above only applied to the baited condition. By contrast, subjects' performance in the empty condition did not differ from chance for any given probability, even though the reward contingencies were identical. These differences in performance between the baited and the empty conditions, which appeared between and within subjects, after only a few trials, and under the same reinforcement schedule, make any associative learning explanation quite implausible and support the view that subjects applied a simple form of probabilistic reasoning here.

Ethics statement

In accordance with the recommendations of the Weatherall report ‘The use of non-human primates in research’ subjects are allowed to roam freely on the 40 ha island covered with tropical rainforest during the day and spend the night in seven interconnected sleeping rooms (approx. 140 m²) with regular feedings and water ad libitum. Subjects voluntarily participated in the study and were never food or water deprived.

No medical, toxicological or neurobiological research of any kind is conducted at Ngamba Island. Research was non-invasive, strictly adhered to the legal requirements of Uganda and was approved and reviewed by the Ugandan Wildlife Authorities and the Ugandan National Council for Science and Technology. The study was ethically approved by committees of the Max Planck Institute for Evolutionary Anthropology and the Chimpanzee Sanctuary & Wildlife Conservation Trust. Animal husbandry and research comply with the ‘PASA Primate Veterinary Healthcare Manual’ and the ‘Guidelines for the Treatment of Animals in Behavioral Research and Teaching’ of the Association for the Study of Animal Behavior.