Abstract
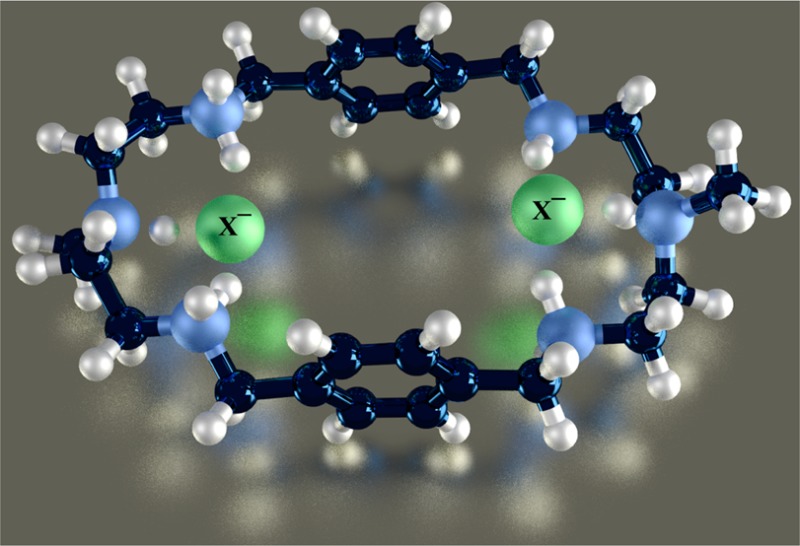
A p-xylyl-based macrocycle L has been synthesized and its binding properties with halides have been investigated by 1H NMR titrations, single crystal X-ray diffraction analysis, and density functional theory (DFT) calculations. As investigated by 1H NMR titrations, the ligand preferentially binds a halide in a 1:2 binding mode, with the association constants (in log K2) of 2.82, 2.70, 2.28, and 2.20 for fluoride, chloride, bromide, and iodide, respectively. The overall binding trend was found to be in the order of fluoride > chloride > bromide > iodide, reflecting that the binding strength correlates with the relative basicity and size of the respective halide. Crystallographic studies indicate that the ligand forms 1:2 complexes with chloride, bromide and iodide. In the chloride complex, the ligand is hexaprotonated and each chloride is held via three NH···Cl– bonds. The ligand is tetraprotonated for the other complexes, where each halide is H-bonded to two secondary ammonium NH+ groups via NH···X– bonds. The results of DFT calculations performed on [H6L]6+ at M062x/6-311G (d,p) level in both gas and solvent phases, suggest that the ligand binds halides with the binding energy in the order of F– > Cl– > Br– > I–, supporting the experimental data obtained from 1H NMR studies. Results from DFT calculations further indicate that a 1:2 binding is energetically more favorable than a 1:1 binding of the ligand.
Introduction
The coordination chemistry of anions is a major field of research in supramolecular chemistry because of the key roles played by anions in chemistry, biology, medicine, catalysis, and environment.1−4 Halides are common inorganic anions performing many important functions in environment and life.5 For example, fluoride is used in toothpaste and in city water to prevent tooth decay; however, the high concentration of fluoride is harmful causing dental fluorosis.6 An excess amount of chloride and fluoride in water has been implicated in high incidences of lymphoma.7 In biology, chloride has an important role, which is transported to different organs including kidney and pancreas through cystic fibrosis transmembrane conductance regulator (CFTR), while the disruption of chloride-transport may cause a fatal genetic disease known as cystic fibrosis.8 The presence of bromide in water could be harmful, since it can be converted during water purification process into bromate, which is suspected to be a genotoxic carcinogen.9 The presence of iodide in drinking water causes an unpleasant odor due to the formation of iodoform with natural organic matter.10 In human, iodide is known to block the release of thyroid hormone, and is used to treat patients with hyperthyroidism.11 Therefore, there is an increasing interest in understanding interactions of halides with synthetic receptors both by experimental and theoretical approaches.12−16 Because the ionic size in the halide series increases from F– to I–, both the charge densities and the basicity decrease from F– to I–. Thus, their binding and selectivity to synthetic receptors depends on a number of factors including sizes, binding sites, charges and geometries of host molecules.5
Historically, polyamine-based receptors are the first17 and most extensively investigated synthetic receptors for the recognition of halides in solution as well as in solid states.5,18,19 In particular, monocyclic polyamines that are known to be conformationally flexible, bind halides by both sides of their macrocycles, forming ditopic complexes in different fashions.20 For instances, [18]N621 and metacyclophanes22 were reported to form chloride, bromide, and iodide complexes in a 1:2 binding mode. However, a larger m-xylyl-based macrocycle containing propylene chains was shown to adopt a chairlike conformation, with six bromides located outside the macrocyclic cavity via NH···Br– interactions.23 A series of experimental and theoretical studies revealed that hydrogen bonding and electrostatic interactions are the primary binding forces in such receptors for the stabilization of anion complexes.24−27 In such complexes the binding patterns and selectivity can be influenced by the variation of spacers as well as linking amine groups.24−27 Recently, we developed a structurally simple monocyclic polyamine (L) incorporated with N-methyl-2,2′-diaminodiethylamine as an amine linker (Scheme 1), coordinating two bromides in its tetraprotonated form.28 Upon further investigation on chloride anions, the receptor was shown to encapsulate two chlorides in the macrocyclic cavity.20 We were further interested in exploring this receptor for halides in solution and solid states and corroborate the data with results from theoretical calculations. Herein is the full report of the halide binding studies of L using 1H NMR titrations, X-ray crystallography, and DFT calculations.
Scheme 1. Chemical Structures of L and [H6L]6+.
Experimental Section
General Information
The chemicals used for this work were purchased from Aldrich as reagent grades and used as received. Nuclear magnetic resonance (NMR) spectra were recorded at 25 °C on a Varian Unity INOVA 500 FT-NMR. Chemical shifts for NMR were expressed in parts per million (ppm), and calibrated against trimethylsilane (TMS) or sodium salt of 3-(trimethylsilyl)propionic-2,2,3,3-d4 acid (TSP) as an external reference used in a sealed capillary tube. All NMR data were processed and analyzed with MestReNova Version 6.1.1–6384. Mass spectral data were obtained at ESI-MS positive mode on a FINNIGAN LCQDUO. Elemental analysis was done from Columbia Analytical Service (Tucson, AZ).
Synthesis
L
The synthesis of L was carried out following the procedure described earlier.28 In a typical reaction, N-methyl-2,2′-diaminodiethylamine (0.74 g, 6.3 mmol) and terephthaldehyde (0.85 g, 6.3 mmol) were dissolved separately in CH3OH (250 mL). The solutions were simultaneously added in CH3OH (400 mL) at 0 °C over 6 h. The resulting mixture was further stirred overnight at room temperature. After evaporating the solvent under reduced pressure, the oily product was redissolved in CH3OH (100 mL) and NaBH4 (1.2 g, 31.7 mmol) was added to reduce the product into an amine. The mixture was stirred overnight at room temperature. The solvent was evaporated, and the residue was dissolved in water (100 mL). The aqueous phase was extracted by CH2Cl2 (3 × 100 mL), and the organic layers were dried by the addition of MgSO4 (2.0 g). The organic portions were separated by filtration and were concentrated. The crude oily product was purified by column chromatography on a neutral-alumina column (2% CH3OH in CH2Cl2) to yield L as a white powder. Yield: 0.80 g, 1.82 mmol, 58%. Mp: 88 °C. 1H NMR (500 MHz, CDCl3, TMS): δ 7.19 (s, 8H, ArH), 3.75 (s, 8H, ArCH2), 2.77 (t, J = 5.5 Hz, 8H, NHCH2), 2.54 (t, J = 5.5 Hz, 8H, NHCH2CH2), 2.16 (s, 6H, CH3). 13C NMR (125 MHz, CDCl3,): δ 138.9 (Ar–C), 128.0 (Ar–CH), 56.5 (NHCH2), 53.9 (NHCH2), 47.0 (NHCH2CH2), 42.2 (CH3). ESI-MS: m/z (+) 439.5 [MH]+. Anal. Calcd for C26H42N6: C, 71.19; H, 9.65; N, 19.16. Found: C, 71.28; H, 9.66; N, 19.19.
[H6L]·(TsO)6
The protonated ligand was prepared by reacting L (70 mg, 0.16 mmol) with 8-fold p-toluenesulfonic acid (243.48 mg, 1.28 × 10–3 mol) in methanol (5 mL). The addition of diethyl ether resulted in a white microcrystalline product that was filtered and washed by diethyl ether. Yield: 188 mg, 0.13 mmol, 80%. NMR (500 MHz, CDCl3, TMS): δ 7.65 (s, 8H, ArH), 7.40 (Ts–ArH), 7.35 (Ts–ArH), 4.24 (s, 8H, ArCH2), 3.55(8H, NHCH2), 3.03 (8H, NHCH2CH2), 2.42 (s, 6H, CH3) 2.37 (s, 3H, Ts–CH3). 13C NMR (125 MHz, CDCl3,): δ 145.35 (Ts–Ar–C), 142.25 (Ar–C), 134.99 (Ts–Ar–C) 133.10 (Ar–CH), 132.30 (Ts–Ar–CH), 128.20 (Ts–Ar–CH), 56.47 (NHCH2), 53.34 (NHCH2), 48.05 (NHCH2CH2), 41.17 (CH3), 23.33 (Ts–CH3) Anal. Calcd for C68H90N6O18S6: C, 55.49; H, 6.16; N, 5.71. Found: C, 55.41; H, 6.17; N, 5.73.
[H6L(Cl2)]Cl4·2.34H2O, 1
The free amine L (30 mg, 0.068 mmol) was mixed with 6 N HCl (0.1 mL) in methanol (2 mL) to give a white precipitate. The salt was redissolved in water/methanol mixture (1:1, v/v; 1 mL), and X-ray quality crystals were grown from this solution by slow evaporation after 5 days. Yield: 26 mg, 0.051 mmol, 75%. Anal. Calcd for C26H52.67Cl6N6O2.34: C, 44.64; H, 7.59; N, 12.01. Found: C, 44.67; H, 7.56; N, 12.03.
[H4L(Br2)]Br2, 2
The free amine L (30 mg, 0.068 mmol) was mixed with 48% aqueous HBr (0.1 mL) in methanol (2 mL) to give a white precipitate. The salt was redissolved in water/methanol mixture (1:1, v/v; 1 mL), and X-ray quality crystals were grown from this solution by slow evaporation after 3 days. Yield: 37 mg, 0.049 mmol, 72%. Anal. Calcd for: C26H46Br4N6: C, 40.97; H, 6.08; N, 11.02. Found: C, 40.91; H, 6.06; N, 11.05.
[H4L(I2)(CH3OH)2]I2, 3
The free amine L (30 mg, 0.068 mmol) was mixed with 47% aqueous HI (0.1 mL) in methanol (2 mL) to give a white precipitate. The salt was redissolved in water/methanol mixture (1:1, v/v; 1 mL), and X-ray quality crystals were grown from this solution by slow evaporation after 3 days. Yield: 48 mg, 0.048 mmol, 70%. Anal. Calcd for C28H54I4N6O2: C, 33.15; H, 5.37; N, 8.28. Found: C, 33.12; H, 5.39; N, 8.25.
NMR Studies
Binding constants were obtained by 1H NMR (500 MHz Bruker) titrations of H6L·6TsO with the anions (A– = F–, Cl–, Br– and I–) as their sodium salts in D2O. The pH was adjusted to 2.1 by adding TsOH and NaOD. Initial concentrations were [L]0 = 2 mM, and [A]0 = 20 mM. Sodium salt of 3-(trimethylsilyl)propionic-2,2,3,3,-d4 acid (TSP) in D2O was used as an external reference in a sealed capillary tube. Each titration was performed by 15 measurements at room temperature, and repeated three times. The association constants (K) were calculated by fitting of several independent NMR signals using EQNMR.29 Error limit in K was less than 10% which was based on the curve fitting analysis for each anion.
X-ray Crystallography
The crystallographic data and details of data collection for the crystals (1 - 3) are given in Table 1. Intensity data for 1 and 2 were collected using Nonius KappaCCD diffractometer and graphite-monochromated MoKα radiation (λ = 0.71073 Å at 90.0 K), while that for 3 was collected using a diffractometer with a Bruker APEX ccd area detector and graphite-monochromated MoKα radiation (λ = 0.71073 Å).30 The data were corrected for absorption by the semiempirical method giving minimum and maximum transmission factors of 0.878 and 0.914 for 1, 0.300 and 0.356 for 2 and 0.383 and 0.778 for 3.31 The space groups were determined by statistical tests and verified by subsequent refinement. The structures were solved by direct methods and refined by full-matrix least-squares methods on F2.32 The position of hydrogens bonded to carbons were refined by a riding model, while those of hydrogens bonded to nitrogens were located on a difference map, and their positions were refined independently. Non-hydrogen atoms were refined with anisotropic displacement parameters. Hydrogen atom displacement parameters were set to 1.2 times the isotropic equivalent displacement parameters of the bonded atoms. Hydrogen-bonding interactions are shown in Table 2.
Table 1. Crystallographic data for [H6L(Cl2)]Cl4·2.34H2O (1), [H6L(Br2)]Br2 (2), and [H6L(I2)(CH3OH)]I2 (3).
| compound 1 | compound 2 | compound 3 | |
|---|---|---|---|
| empirical formula | C26H52·67Cl6N6O2·34 | C26H46Br4N6 | C28H54I4N6O2 |
| formula weight | 699.47 | 762.33 | 1014.37 |
| crystal system | monoclinic | triclinic | triclinic |
| a/Å | 10.925(3) | 5.7991(5) | 7.361(4) |
| b/Å | 12.736(2) | 9.5238(10) | 9.964(5) |
| c/Å | 12.453(3) | 14.7954(14) | 14.366(8) |
| α/deg | 90 | 74.360(5) | 70.123(14) |
| β/deg | 98.413(9) | 84.001(6) | 81.812(15) |
| γ/deg | 90 | 88.462(6) | 70.667(16) |
| V/Å3 | 1714.1(7) | 782.58(13) | 934.5(9) |
| T/K | 90.0(5) | 90.0(5) | 100(2) |
| space group | P21/c | P1̅ | P1̅ |
| Z | 2 | 1 | 1 |
| radiation type | Mo Kα | Mo Kα | Mo Kα |
| μ/mm–1 | 0.536 | 5.168 | 3.366 |
| no. of reflns measured | 18451 | 33284 | 15238 |
| no. of indept reflns | 4083 | 7513 | 4672 |
| Rint | 0.066 | 0.023 | 0.0624 |
| R1 (I > 2σ(I)) | 0.054 | 0.028 | 0.0431 |
| GOF on F2 | 1.061 | 1.053 | 1.005 |
Table 2. Binding Data of the Ligand for Halides in D2O at 298 K.
| anion | log K1 (1:1 binding) | log K2 (1:2 binding) | log β2 (β2 = K1K2) | ΔδH1 | ΔδH2 |
|---|---|---|---|---|---|
| fluoride | 1.23 | 2.82 | 4.05 | 0.304 | 0.283 |
| chloride | 1.30 | 2.70 | 4.00 | 0.038 | 0.034 |
| bromide | 1.41 | 2.28 | 3.69 | 0.032 | 0.030 |
| iodide | 1.46 | 2.20 | 3.66 | 0.027 | 0.023 |
Computational Studies
The density functional theory (DFT) with the hybrid meta exchange-correlation functional M06-2X33 was applied in all the calculations. The standard valence triple-ζ basis set, augmented with d-type polarization functions for heavy elements and p-type polarization functions for hydrogen, namely 6-311G(d,p), and LanL2DZ34−37 basis set for iodide, were used. All calculations were performed with the Gaussian 09 package of programs.38 The solvent (water) effects were evaluated by the polarizable continuum model (PCM) self-consistent reaction field of Tomasi and co-workers.39 The geometries of all the models have been fully optimized in both the gas phase and in the solvent by analytical gradient techniques. The local minimum energy structures are found by ascertaining that all of the harmonic frequencies are real. The Atoms In Molecule (AIM) theory was also applied to characterize the hydrogen bonds for the complexes.40 The relative binding energies (ΔEZPE) and the Gibbs free energy changes (ΔΔG) were calculated with zero-point correction both in the gas phase and in the PCM model. The calculations include both 1:1 binding (H6L(X)]5+) and 1:2 ([H6L(X)2]4+) binding of the motif [H6L]6+ using the respective halides (X– = F–, Cl–, Br–, I–) in both gas and solvent phases.
Result and Discussion
Synthesis
The synthesis of L was readily accomplished from the Schiff base condensation of dialdehyde and diamine, followed by the reduction with sodium borohydride.28 The chloride (1), bromide (2), and iodide (3) complexes were prepared by mixing of the free ligand with respective inorganic acids in water/methanol mixture. All the salts yield good quality crystals from slow evaporation of the solution. However, attempts to prepare crystals of the free ligand and that of fluoride complex were unsuccessful. All the isolated crystals were fairly stable at room temperature, and characterized by single crystal X-ray diffraction.
NMR Studies
The binding affinities of [H6L]6+ for halides (F–, Cl–, Br– and I–) were evaluated by 1H NMR titrations using their sodium salts dissolved in D2O at pH = 2.1. The pH for the solution was adjusted with TsOH and NaOD. As shown in Figure 1, the addition of halide anions to [H6L]6+ in D2O resulted in a downfield shift of NCH3 (H1) and CH3NCH2 (H2) protons. Negligible shifts were observed for other protons.
Figure 1.
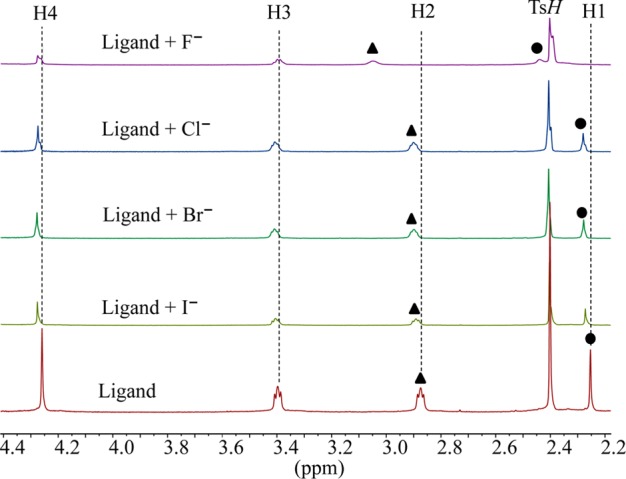
Partial 1H NMR spectra of H6L(TsO)6 in the presence of 5 equiv of various halides in D2O at pH = 2.1.
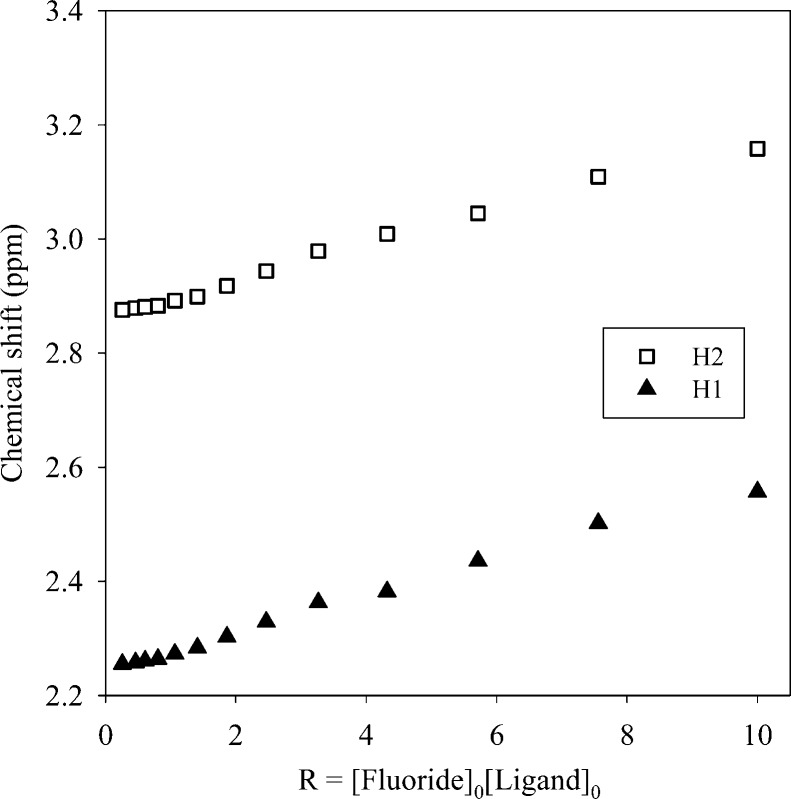
The highest shift of the proton signals was observed for fluoride, as compared with other anions. For the larger halides (chloride, bromide and iodide), the shifting patterns were almost similar. Figure 2 displays the stacking of 1H NMR titration spectra of the ligand obtained after the increasing amount of fluoride anion (0–10 equiv), showing a gradual change of proton resonances at room temperature. The changes in the chemical shift of the aliphatic protons H1 and H2 as a function of the fluoride concentration are displayed in Figure 3. The titrations spectra for other halides are included in the Supporting Information (Figures S4, S6, and S8). The changes in the chemical shift of the ligand as recorded with an increasing amount of anionic solution provided the best fit for a 1:2 binding model for each anion (Figures S5, S7, and S9). The binding data is listed in Table 1, showing that the binding process involves the formation of both a 1:1 (ligand:anion) complex and a 1:2 (ligand:anion) complex for each anion. However, it is obvious that a 1:2 complex is much stronger than a 1:1 complex, supporting both crystallographic and theoretical data (discussed later). The ligand form 1:2 complexes with halides with the binding constants (in log K2) of 2.82, 2.70, 2.28, and 2.20 for fluoride, chloride, bromide, and iodide, respectively. The overall binding constants (in log β2) are 4.05, 4.00, 3.69, and 3.66 for fluoride, chloride, bromide, and iodide, respectively. In the case of 1:2 complexes, the binding trend follows the order: fluoride > chloride > bromide > iodide, reflecting that the binding strength roughly correlates with the relative basicity of halides. Further, this binding order is also an indication that the larger anions may experience a stronger electrostatic repulsion in a single cavity. It is assumed that each anion is held by hydrogen bonding interactions in an axial pocket formed by one N+ and two NH+ groups. In contrast, the binding trend in a 1:1 complexation follows the order of fluoride (log K1 = 1.23) < chloride (log K1 = 1.30 < bromide (log K1 = 1.42 < iodide (log K1 = 1.46), suggesting that the 1:1 binding is favored for the large anion, which is most likely due to the complementarity in size of the cavity and an anion. A cryptand-based ligand with p-xylyl spacers was found to form a 1:1 complex with chloride and bromide with the binding constants (in log K) of 3.37 and 3.34, respectively, measured at pH = 5.41
Figure 2.
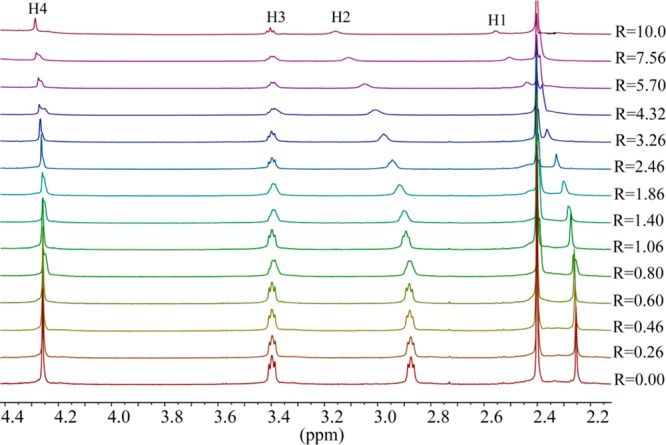
1H NMR titrations of H6L(Ts)6 (2 mM) with the increasing amount of NaF (R = [NaF]0/[ligand]0) in D2O at pH = 2.1.
Figure 3.
Change in the chemical shifts of NCH3 (H1) and CH3NCH2 (H2) against the increasing ratio of NaF in D2O at pH = 2.1.
Crystal Structure Analysis
[H6L(Cl2)]Cl4·2.34H2O, 1
Single crystal X-ray diffraction analysis reveals that the chloride complex 1 crystallizes in the monoclinic system with a space group of P21/c. All six nitrogens in the macrocycle are protonated and the cavity contains by two symmetry chlorides. Other four chlorides and crystalline water molecules remains outside the cavity. As shown in Figure 4, two encapsulated chlorides are almost coplanar with the macrocycle, each being held via three strong hydrogen bonding interactions with NH···Cl– distances of 3.0674(18) to 3.146(2) Å (Table 3). These distances are comparable to the reported NH···Cl– distances of 3.048(3) and 3.10 Å observed in thiophene-based azacryptand42 and tiny octaazacryptand,43 respectively (Table 3). The two encapsulated chlorides are separated by 4.433 Å and lie above just at 0.588 Å from the axis of the two central nitrogen atoms. Presumably, the chloride-chloride repulsion between the encapsulated chlorides is offset by the decreased charge of the negative anions due to the formation of strong hydrogen bonds with ammonium groups. The other four chlorides remain outside the cavity, each being held by a protonated secondary amine via single NH···Cl– bond. Therefore, all ten protons (eight from secondary and two from tertiary nitrogens) on the charged nitrogen centers are fully utilized in anion binding. The macrocycle in the complex is almost flat and quite different than that observed in related macrocycles showing a chair conformation.23 In the chloride complex of L, two aromatic units are parallel to each other at a distance of 7.842 Å (centroid-to-centroid), while the distance between the two tertiary nitrogens is 10.338 Å, forcing the macrocycle to adopt an ellipsoid which is suitable to host two chlorides (Figure 4C).
Figure 4.
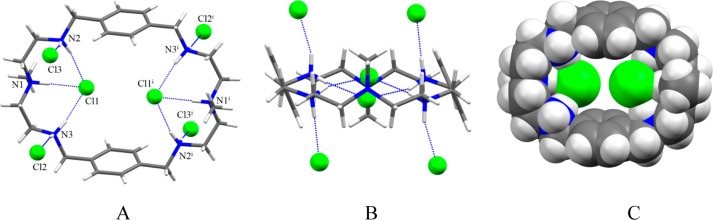
Crystal structure of the chloride complex, 1: (A) perspective side view of [H6L(Cl2)]Cl4 showing atom labeling on N and Cl; (B) perspective view down the two central amines and (C) space filling model of [H6L(Cl2)]4+ (water molecules are omitted for clarity).
Table 3. Selected Hydrogen Bonding Parameters (Å, deg) for the Halide Complexes of La.
| D–H···A | D···A | H···A | ∠D–H···A |
|---|---|---|---|
| 1 | |||
| N1–H1···Cl1 | 3.0674(18) | 2.14 | 178.1 |
| N2–H22···Cl1 | 3.126(2) | 2.25 | 159.5 |
| N3–H32N···Cl1 | 3.146(2) | 2.23 | 170.6 |
| 2 | |||
| N2–H21N···Br1 | 3.3398(12) | 2.48(2) | 168.0(19) |
| N3–H31N···Br1 | 3.3622(12) | 2.52(2) | 167.2(19) |
| 3 | |||
| N(4)–H(4A)···I(2) | 3.827(5) | 3.22(6) | 129(4)) |
| N(13)–H(13B)···I(2)i | 2.76(5) | 3.573(5) | 159(5) |
| N(4)–H(4B)···O(1S) | 2.13(6) | 2.935(6) | 157(5) |
| N(13)–H(13A)···O(1S)i | 2.10(6) | 2.948(6) | 178(5) |
| O(1S) −H(1S) ···I(1) | 2.87(6) | 3.539(4) | 148(6) |
(i) Symmetry code: 1 – x + 1, −y + 1, −z.
[H4L(Br2)]Br2, 2
The bromide salt of the ligand prepared from the reaction of L with HBr in water crystallizes in the triclinic P1̅ space group. The macrocycle is tetraprotonated instead of hexaprotonated observed in 1. The tertiary amines remain unprotonated. As shown in Figure 5A, two symmetry related bromides (Br1 and Br1i) are bonded to N2 and N3 with N···Br– distances 3.3398(12) and 3.3622(12) Å, respectively, forming a ditopic complex. The N···Br– distances are comparable with those observed previously in the bromide complexes of [18]N6 (N···Br– = 3.343(8) – 3.416(8) Å)21 and [14]metacyclophane (N···Br– = 3.279(16)–3.437(17) Å).22 Each bromide lies 2.454 Å from the plane of four secondary nitrogen atoms, thus the two bromides are partially encapsulated and slightly different than 1 where two chlorides are completely encapsulated. The two bromides are separated by 7.717 Å from each other, which is much longer than 4.433 Å observed for two encapsulated chlorides in 1. The longer distance between two bromides is an indication of the significant bromide–bromide repulsion due the lack of the participation of tertiary amines in hydrogen bonding. The remaining two symmetry related bromides (Br2 and Br2i) are coordinated to protonated amine (N2 and N2i), each with one NH···Br– bond with a distance of 3.2614 (12) Å. The distance between two tertiary nitrogens (N1 and N1i) is 11.115 Å. Two aromatic groups are parallel to each other facing to the cavity center, and separated by a distance, Arcentroid···Arcentroid = 5.560 Å. No intramolecular aromatic stacking is observed. The macrocycle is elongated as compared to that with 1. In an extended structure, each internal bromide is further coordinated by one hydrogen bond from a neighboring macrocycle, thereby forming a three coordinate bromide complex with regard to the internal bromide (Figure 5B) as also observed in the chloride complex. As can be seen in Figure 5C, two internal bromides (each from one macrocycle) are connected by two parallel macrocycles forming a sandwich type complex.
Figure 5.
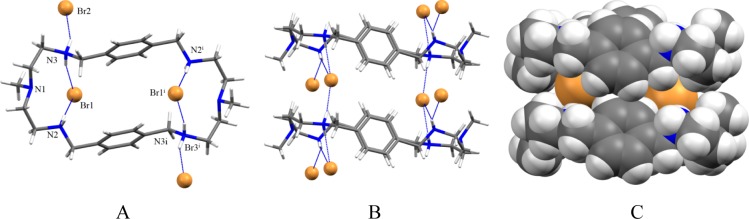
Crystal structure of the bromide complex, 2: (A) perspective side view of [H4L(Br2)]Br2 showing atom labeling on N and Br; (B) perspective view showing three coordinate bromide between two macrocycles; (C) space filling model showing two bromide between two macrocycles.
[H4L(I2)(CH3OH)2]I2, 3
Single crystal X-ray diffraction studies of 3 indicate that the complex crystallizes with four iodides and two molecules of methanol per macrocycle. The macrocycle sits on a crystallographic center of symmetry, and the structure is similar to that with 2 except two methanol molecules bonded to the macrocyclic cavity in 3 (Figure 6). The macrocycle is tetraprotonated adopting an elliptical shape, with the tertiary amines at opposite ends of the main axis of an approximate ellipsoid with a distance of N1···N1i = 11.156 Å (Figure 6A). The symmetry related two iodides are bonded at the opposite side of the methanol molecules, each with two NH···I– bonds (Figure 6B). The distance between the bonded iodides is fairly large (8.848 Å) to minimize the electrostatic repulsion between these two anions. This distance is longer than that of the corresponding distance in the bromide complex (7.717 Å), which is probably the effect of larger iodide anion. Other two iodides are directly linked with methanolic OH with a distance of OH···I– of 3.539(4) Å. In the complex, there are two symmetry related methanol molecules, each with two hydrogen bonds to the opposite sides of the ellipsoid. As shown in Figure 6C, two methanol molecules are almost encapsulated within the cavity. The encapsulation of methanol in the presence of an anion was unexpected and could be due to the effect of crystallization and packing forces in crystals. We previously observed the similar effect in thiophene-based cryptands in the presence of sulfate.44
Figure 6.
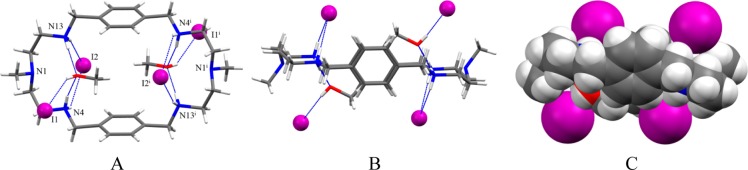
Crystal structure of the iodide complex, 3: (A) perspective side view of [H4L(I2)(CH3OH)2]I2 showing atom labeling on N, I and O; (B) perspective view down the two aromatic units and (C) space filling model of [H4L(I2)(CH3OH)2]I2.
DFT Calculations
Crystallographic data of 1 demonstrates that the azamacrocycle [H6L]6+ containing six protonated amines is proton capable to encapsulate two chloride anions on each side of the azamacrocycle cavity.20 Based on the experimental data from the solid state, the azamacrocyclic motif [H6L]6+ was constructed for studying halide binding. Although, the macrocycle was tetraprotonated in the bromide and iodide complexes observed in X-ray structures, the hexaprotonated species was used in all cases for the direct comparison. As shown in the optimized structure of [H6L]6+ (Figure 7), all six nitrogens of the azamacrocycle are protonated. The methyl-linked two ammonium centers are connected by ethyl chains spaced with two para-substituted aromatic groups. The macrocycle adopts an ellipsoid shape, where the two aromatic rings are parallel. In the gas phase, the distance between N2 and N5 is found to be 9.79 Å, while the distance between the two aromatic rings is 8.75 Å. However, in solvent (water), the distance between N2 and N5 is shortened to 7.42 Å, but the distance between the two planes of benzene rings is increased to 9.63 Å, which could be the effect of interactions of the macrocycle with the solvent modeled in the calculations. The detailed hydrogen bonding interactions for 1:1 complexes ([H6L(F)]5+, [H6L(Cl)]5+, [H6L(Br)]5+ and [H6L(I)]5+) and 1:2 complexes ([H6L(F)2]4+, [H6L(Cl)2]4+, [H6L(Br)2]4+, and [H6L(I)2]4+) are shown in Table 4 and Table 6, respectively. Whereas, the thermodynamic parameters for 1:1 and 1:2 complexes are given in Table 5 and Table 7, respectively.
Figure 7.
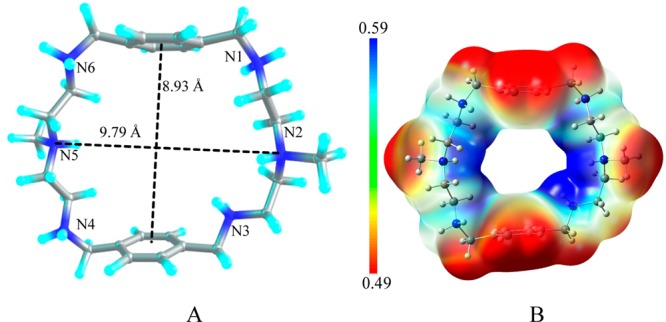
(A) Structure of the azamacrocycle, [H6L]6+; (B) electrostatic potential map for [H6L]6+ calculated at the M06-2X/6-311G(d,p) level of theory (red = less positive potential, blue = more positive potential).
Table 4. Hydrogen Bond Parameters for [H6L(X)]5+ in the Gas Phasea.
| structure | HB parameters | HB1 | HB2 | HB3 |
|---|---|---|---|---|
| [H6L(F)]5+ | N···F (Å) | 2.57(2.65) | 2.50(2.44) | 2.57(2.64) |
| H···F (Å) | 1.56(1.64) | 1.52(1.33) | 1.56(1.64) | |
| ∠NHF (deg) | 156.6(157.1) | 151.5(171.3) | 156.6(156.8) | |
| ρ (au) | 0.057(0.046) | 0.067(0.110) | 0.057(0.047) | |
| Δ2ρ (au) | 0.047(0.041) | 0.052(0.050) | 0.047(0.041) | |
| [H6L(Cl)]5+ | N···Cl (Å) | 3.11(3.18) | 3.06(3.10) | 3.11(3.19) |
| H···Cl (Å) | 2.09(2.16) | 2.06(2.05) | 2.09(2.17) | |
| ∠NHCl (deg) | 163.8(166.3) | 160.1(180.0) | 163.8(166.6) | |
| ρ (au) | 0.033(0.028) | 0.037(0.037) | 0.033(0.027) | |
| Δ2ρ (au) | 0.019(0.018) | 0.019(0.019) | 0.019(0.018) | |
| [H6L(Br)]5+ | N···Br (Å) | 3.26(3.33) | 3.24(3.25) | 3.26(3.35) |
| H···Br (Å) | 2.24(2.29) | 2.23(2.21) | 2.24(2.32) | |
| ∠NHBr (deg) | 165.8(170.4) | 161.3(172.8) | 165.7(168.6) | |
| ρ (au) | 0.029(0.027) | 0.032(0.034) | 0.029(0.025) | |
| Δ2ρ (au) | 0.015(0.014) | 0.015(0.015) | 0.015(0.014) | |
| [H6L(I)]5+ | N···I (Å) | 3.53(3.58) | 3.54(3.51) | 3.53(3.59) |
| H···I (Å) | 2.52(2.55) | 2.52(2.48) | 2.52(2.56) | |
| ∠NHI (deg) | 163.6(170.9) | 165.1(168.5) | 163.6(171.0) | |
| ρ (au) | 0.029(0.027) | 0.032(0.034) | 0.029(0.025) | |
| Δ2ρ (au) | 0.015(0.014) | 0.015(0.015) | 0.015(0.014) |
PCM model data are shown in parentheses.
Table 6. Hydrogen Bond Parameters for [H6L(X)2]4+ in the Gas Phasea.
| structure | HB parameters | HB1 | HB2 | HB3 | HB4 | HB5 | HB6 |
|---|---|---|---|---|---|---|---|
| [H6L(F)2]4+ | N···F (Å) | 2.58(2.61) | 2.45(2.47) | 2.58(2.61) | 2.57(2.60) | 2.45(2.48) | 2.57(2.60) |
| H···F (Å) | 1.58(1.60) | 1.40(1.38) | 1.58(1.60) | 1.57(1.58) | 1.41(1.40) | 1.57(1.58) | |
| ∠NHF (deg) | 154.7(157.5) | 156.1(171.7) | 154.7(157.4) | 155.5(160.7) | 158.6(171.4) | 155.4(160.4) | |
| ρ (au) | 0.055(0.052) | 0.092(0.099) | 0.055(0.052) | 0.055(0.056) | 0.089(0.094) | 0.055(0.055) | |
| Δ2ρ (au) | 0.047(0.044) | 0.055(0.051) | 0.047(0.044) | 0.047(0.046) | 0.055(0.052) | 0.047(0.046) | |
| [H6L(Cl)2]4+ | N···Cl (Å) | 3.07(3.16) | 2.99(3.11) | 3.07(3.16) | 3.07(3.15) | 3.00(3.10) | 3.07(3.18) |
| NH···Cl (Å) | 2.05(2.13) | 1.93(2.07) | 2.05(2.14) | 2.04(2.12) | 1.95(2.05) | 2.04(2.16) | |
| ∠NHCl (deg) | 164.7(168.4) | 173.1(176.5) | 164.6(167.4) | 165.7(168.9) | 172.0(174.5) | 165.7(165.9) | |
| ρ (au) | 0.037(0.030) | 0.051(0.037) | 0.037(0.029) | 0.037(0.030) | 0.050(0.037) | 0.037(0.028) | |
| Δ2ρ (au) | 0.019(0.018) | 0.018(0.018) | 0.019(0.018) | 0.019(0.018) | 0.018(0.019) | 0.019(0.018) | |
| [H6L(Br)2]4+ | N···Br (Å) | 3.22(3.31) | 3.16(3.27) | 3.22(3.33) | 3.22(3.31) | 3.16(3.27) | 3.22(3.33) |
| H···Br(Å) | 2.19(2.28) | 2.10(2.23) | 2.19(2.30) | 2.19(2.28) | 2.10(2.23) | 2.19(2.30) | |
| ∠NHBr (deg) | 166.6(169.4) | 175.1(171.1) | 166.5(169.1) | 166.0(169.4) | 174.3(171.1) | 166.0(169.0) | |
| ρ (au) | 0.033(0.028) | 0.043(0.033) | 0.033(0.027) | 0.033(0.027) | 0.043(0.033) | 0.033(0.028) | |
| Δ2ρ (au) | 0.016(0.014) | 0.015(0.014) | 0.016(0.014) | 0.016(0.014) | 0.015(0.014) | 0.016(0.014) | |
| [H6L(I)2]4+ | N···I (Å) | 3.46(3.57) | 3.41(3.52) | 3.46(3.59) | 3.46(3.56) | 3.40(3.53) | 3.46(3.57) |
| H···I (Å) | 2.43(2.54) | 2.36(2.50) | 2.42(2.56) | 2.43(2.52) | 2.35(2.50) | 2.43(2.53) | |
| ∠NHI (deg) | 168.0(170.0) | 178.1(167.5) | 168.4(170.5) | 168.5(172.4) | 179.3(169.7) | 168.6(171.8) | |
| ρ (au) | 0.029(0.029) | 0.037(0.037) | 0.029(0.029) | 0.029(0.029) | 0.037(0.037) | 0.029(0.029) | |
| Δ2ρ (au) | 0.015(0.014) | 0.014(0.014) | 0.015(0.015) | 0.015(0.015) | 0.014(0.014) | 0.015(0.015) |
PCM model data are shown in parentheses.
Table 5. Thermodynamic Parameters for 1:1 Binding Mode of the Complexes in the Gas Phasea.
| parameters | ΔE, kcal·mol–1 | ΔEZPE, kcal·mol–1 | ΔH, kcal·mol–1 | ΔΔG, kcal·mol–1 |
|---|---|---|---|---|
| [H6L(F)]5+ | –466.9(−76.4) | –467.2(−78.9) | –467.8(−79.3) | –459.9(−71.4) |
| [H6L(Cl)]5+ | –399.2 (−27.5) | –399.0(−28.6) | –399.3(−29.4) | –393.6(−19.7) |
| [H6L(Br)]5+ | –395.6(−26.8) | –395.6(−27.3) | –395.7(−27.6) | –389.3(−18.8) |
| [H6L(I)]5+ | –389.9(−25.0) | –389.8(−26.3) | –389.8(−26.4) | –384.7(−18.0) |
PCM model data are shown in parentheses.
Table 7. Thermodynamic Parameters for 1:2 Binding Mode of the Complexes in the Gas Phasea.
| parameters | ΔE, kcal·mol–1 | ΔEZPE, kcal·mol–1 | ΔH, kcal·mol–1 | ΔΔG, kcal·mol–1 |
|---|---|---|---|---|
| [H6L(F)2]4+ | –905.1(−158.5) | –904.3(−163.0) | –906.0(−163.8) | –887.7(−147.6) |
| [H6L(Cl)2]4+ | –761.3 (−56.2) | –760.2(−61.6) | –761.3(−61.8) | –744.4(−46.8) |
| [H6L(Br)2]4+ | –752.8 (−57.6) | –752.8 (−59.9) | –752.2 (−59.9) | –737.4 (−44.8) |
| [H6L(I)2]4+ | –737.9(−55.0) | –737.9(−57.4) | –738.5(−57.3) | –721.8(−43.0) |
PCM model data are shown in parentheses.
1:1 Complexes of [H6L]6+ with Halides
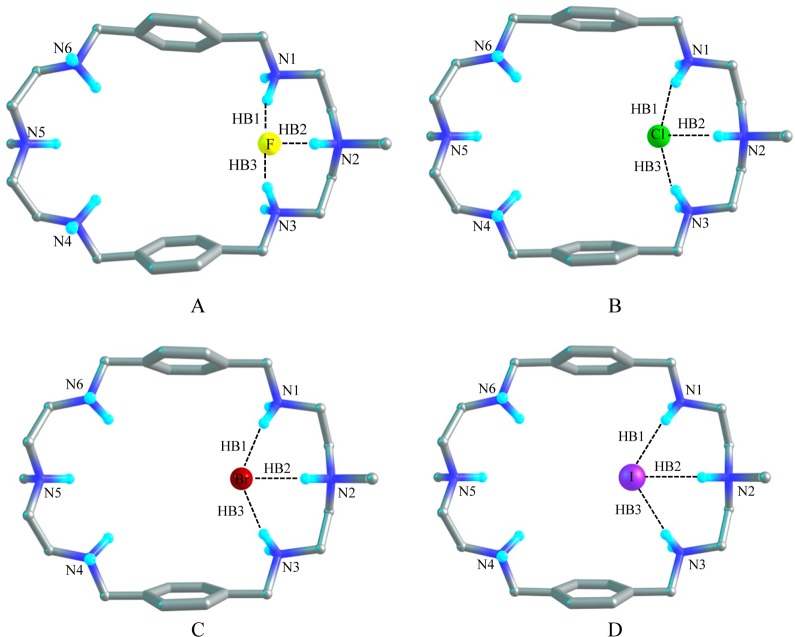
Fluoride Complex
Figure 8A shows the optimized structure of [H6L(F)]5+ in the gas phase, which illustrates the binding of one fluoride anion with [H6L]6+. As compared to [H6L]6+, the distance between N2 and N5 is elongated to 11.16 Å and the distance between the two benzene rings is shortened to 7.60 Å for [H6L(F)]5+. The fluoride anion is located at one corner of the cavity of [H6L]6+. Three hydrogen bonds are formed between F– and three NH+ of [H6L]6+, which are HB1, HB2, and HB3 with the H···F– distances of 1.56 Å, 1.52 Å, and 1.56 Å, respectively. The corresponding distance between the donor–acceptor (N···F) groups are 2.57 Å, 2.50 and 2.57 Å in the gas phase. The bond angles of F–···HN are approximately 156°. The geometry of [H6L(F)]5+ shows a similar hydrogen bonding structure in solvent. However, the atomic distances of HB1 and HB3 are lengthened to 1.64 Å (with the bond angles of 157°), while the distance of HB2 is shortened to 1.33 Å (with the F···HN bond angle of 171°). In PCM model, the donor–acceptor (N···F) distances are 2.65 Å, 2.44 and 2.64 Å, respectively. In solvent, the distance between N2 and N5 is found to be 10.73 Å which is shorter by 0.43 Å than that found in the gas phase. Meanwhile, the distance between the two aromatic rings is slightly larger (7.69 Å). The AIM results show that in the gas phase the electron density (ρ) at the bond critical point (BCPs) of HB1and HB3 are 0.057 au and the Laplacian of the electron density (Δ2ρ) are 0.047 au, while the corresponding parameters are 0.065 and 0.052 au for HB2, respectively. In solvent, the electron density (ρ) are 0.046 au, 0.011 au, and 0.047 au for HB1, HB2, and HB3 and the Laplacian of the electron density (Δ2ρ) are 0.041 au for both HB1and HB3 and 0.050 au for HB2. The results suggest that the hydrogen bonds are slightly stronger in the gas phase than those in the solvent due to the effect of solvent–receptor interactions. The binding energy (ΔEZPE) between F– and [H6L]6+ is calculated to be −467.2 kcal/mol in the gas phase, and −78.9 kcal/mol in solvent. The Gibbs free energy change (ΔΔG) amounts to −459.9 kcal/mol (gas phase) and −71.4 kcal/mol (solvent) respectively (Table 5).
Figure 8.
Optimized structures of 1:1 complexes showing hydrogen bonds in [H6L(F)]5+ (A), in [H6L(Cl)]5+ (B), in [H6L(Br)]5+ (C), and [H6L(I)]5+ (D) in the gas phase at the M06-2X/6-311G(d,p) level.
Chloride Complex
The optimized structure of [H6L(Cl)]5+ with one chloride binding with the hexaprotonated L is depicted in Figure 8B. Similar to the model [H6L(F)]5+, the chloride anion is encapsulated by the azamacrocycle at one corner of the cavity. The distance between N2 and N5 is about 0.8 Å which is longer than that of [H6L]6+ and is 0.5 Å shorter than that of [H6L(F)]5+. However, the distance between the two benzene rings is 8.24 Å, which is 0.5 Å shorter than that of [H6L]6+ and 0.64 Å longer than that of [H6L(F)]5+. The distances of all three Cl–···HN hydrogen bonds are 2.09 Å and the bond angles of Cl–···HN are 163° in the gas phase. The distance between the donor–acceptor (N···Cl–) groups are 3.11 Å, 3.06 and 3.11 Å, respectively. The model [H6L(Cl)]5+ shows a similar geometry in the solvent (with the distance of N2 and N5 to be 10.43 Å and the distance between the two aromatic rings to be 8.16 Å). It has three HN···Cl– pattern hydrogen bonds with the distances of 2.1 Å and the H-bond angles of 170°. The donor–acceptor (N···Cl) distance is around 3.15 Å. The topological analysis demonstrates that the electron densities (ρ) at BCPs are 0.033 au for HB1 and HB3 and 0.037 au for HB2. The Laplacian of the electron density (Δ2ρ) are 0.019 au for all of the H-bonds in the gas phase, while 0.028 au for HB1 and HB3 and 0.037 au for HB2 in solvent phase. The binding energy (ΔEZPE) between Cl(−) and the [H6L]6+ is calculated to be −399.0 kcal/mol in the gas phase, while only −28.6 kcal/mol) in solvent phase. The change of the Gibbs free energy (ΔΔG) is found to be −393.6 kcal/mol in the gas phase and −19.7 kcal/mol in the solvent.
Bromide Complex
Figure 8C shows the complex of [H6L(Br)]5+ where the bromide binds with the azamacrocycle through three hydrogen bonds at one side of the cavity in the similar ways as found in the fluoride and chloride complexes. Three Br–···HN hydrogen bonds (HB1, HB2, and HB3) have been observed with the distances of 2.2 Å and the bond angles of 165° in the gas phase. The AIM calculations indicate that electron density of the BCPs are 0.03 au and the Laplacian of the electron density are 0.015 au in the gas phase. In solvent the electron density (ρ) and the Laplacian of the electron density (Δ2ρ) at the BCPs are slightly reduced to 0.028 au and 0.014, respectively (Table 4). In the gas phase the atomic distance of N2 to N5 is 10.49 Å which is 0.7 Å longer than that in [H6L]6+. However, the distance between the two aromatic rings is 8.39 Å which is 0.4 Å shorter than that in [H6L]6+. In the complex, [H6L(Br)]5+, these distances are predicted as 10.32 and 8.20 Å, respectively in the PCM model. The distance from donor atom to acceptor atom is roughly 3.28 Å. The binding energy for the bromide complex is calculated to be −395.6 kcal/mol in the gas phase and −27.3 kcal/mol in solvent. The change of Gibbs free energy (ΔΔG) is −389.3 kcal/mol for gas phase and −18.8 kcal/mol in the PCM model.
Iodide Complex
Model [H6L(I)]5+ as displayed in Figure 8D illustrates that one iodide is bounded by three NH···I– hydrogen bonds at one side of the cavity. The distance between N2 and N5 in the optimized [H6L(I)]5+ structure is 10.20 Å which is longer than that of [H6L]6+ but shorter than that of [H6L(Br)]5+. Whereas the distance between two benzene rings is 8.63 Å which is shorter than that of [H6L]6+ but slightly longer than that of [H6L(Br)]5+. In solvent the distance between N2 and N5 is 10.22 Å which is almost the same as in the gas phase. But the distance between the two planes of the aromatic rings is 8.33 Å which is 0.3 Å smaller than that in the gas phase. The distances for H-bonds (HB1, HB2 and HB3) are approximately 2.52 Å and the bond angles are almost 163° in the gas phase whereas in the PCM model these values are 2.56 Å and 170° respectively. The distance between the donor–acceptor (N···I) atom are nearly 3.55 Å in both phases. The electron density(ρ) and the Laplacian of the electron density(Δ2ρ) at the bond critical points are nearly 0.030 au and 0.014 au respectively both in the gas phase and in the PCM model (Table 4). In gas phase the binding energy between iodide and [H6L]6+ is estimated to be −389.8 kcal/mol and the Gibbs free energy change (ΔΔG) amounts to −384.7 kcal/mol. It is noted that these values are reduced drastically to −26.3 kcal/mol and −18.0 kcal/mol, respectively, in the PCM model.
1:2 Complexes of [H6L]6+ with Halides
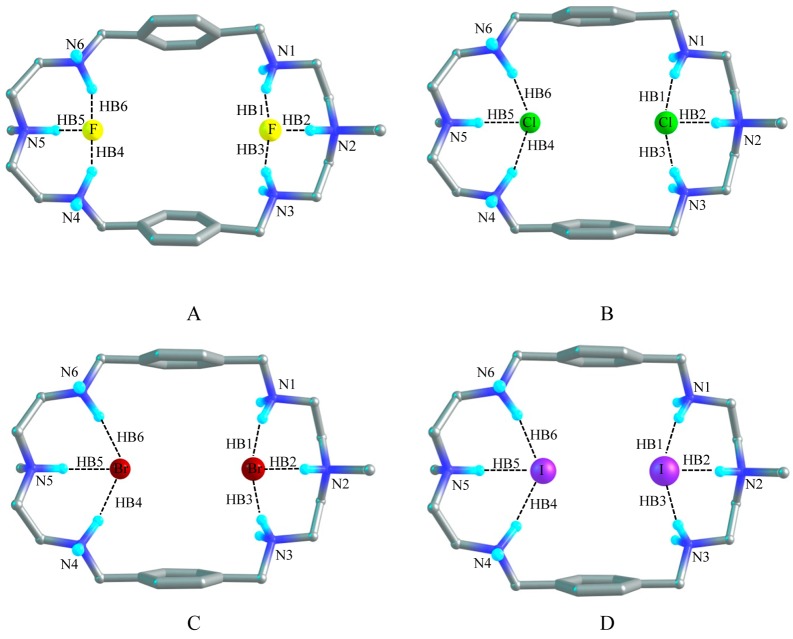
Fluoride Complex
Figure 9A shows the optimized structure of model [H6L(F)2]4+ which demonstrates the 1:2 binding of the azamacrocycle with fluoride. The distance between N2 and N5 of the optimized [H6L(F)2]4+ model is 11.38 Å which is 1.6 and 0.2 Å longer than that of [H6L]6+ and [H6L(F)]5+ respectively. While the two aromatic rings are separated by 7.10 Å which is 1.6 and 0.5 Å shorter than that of [H6L]6+ and [H6L(F)]5+, respectively. Two fluoride anions are located at two corners of the host cavity with a distance of 6.57 Å in the gas phase and 6.68 Å in the PCM model. Each fluoride anion is held with three strong NH···F– hydrogen bonds with the three protonated amines at each corner. HB1, HB2, and HB3 are formed by HN1, HN2, and HN3 with one F– anion with the atomic distance of 1.58, 1.40, and 1.58 Å, respectively, in the gas phase. And the other F– anion also forms three hydrogen bonds (HB4, HB5, and HB6) with HN4, HN5, and HN6 with F–···H distances of 1.57, 1.41, and 1.57 Å, respectively. The bond angles of F–···HN are around 155°. The structure in solvent is similar to the structure of [H6L(F)2]4+ in the gas phase. The distances between the donor–acceptor (N···F) groups in HB1, HB3, HB4, and HB6 are the same which is equal to 2.58 Å in the gas phase, whereas in solvent this distance is 2.60 Å. However, the donor–acceptor distance in HB2 and HB5 is shortened about to 2.46 Å in both phases. In PCM model the distance between N2 and N5 is 11.23 Å and the distance between the two planes of the benzene rings is 7.00 Å. Both distances are shortened by 0.15 Å than that in the gas phase. The bond angles of HB2 and HB5 are almost 171.5° and the short NH···F– distance (Table 6), suggests the strong hydrogen bonds in solvent.45 Both in the gas phase and solvent, the topological analysis demonstrates that the electron density (ρ) and the Laplacian of the electron density (Δ2ρ) at the BCPs are approximately 0.052 and 0.045 au for HB1, HB3, HB4, and HB6, respectively (Table 6). However, these parameters are about 0.090 and 0.052 au for HB2 and HB5, respectively. The binding energy of the fluoride complex of [H6L]6+ is −904.3 kcal/mol in the gas phase. In solvent the binding energy is estimated to be −163.0 kcal/mol. The change of Gibbs free energy (ΔΔG) is −887.7 kcal/mol in the gas phase and −147.6 kcal/mol in the PCM model. As expected the binding energy for the complex with two fluorides is higher than that for the complex with a single fluoride anion in the gas phase or in the PCM model.
Figure 9.
Optimized structures of 1:2 complexes showing hydrogen bonds in [H6L(F)2]4+ (A), in [H6L(Cl)2]4+ (B), in [H6L(Br)2]4+ (C), and [H6L(I)2]4+ (D) in the gas phase at M06-2X/6-311G(d,p) level.
Chloride Complex
The X-ray analysis of chloride complex reveals that the host encapsulates two chlorides inside the cavity via six hydrogen bonds. Figure 9B shows the optimized structure of [H6L(Cl)2]4+ with two encapsulated chlorides. This structure is almost similar to that observed in the crystal structure. In the optimized structure, the distance of axial nitrogens (N2 and N5) is 10.80 Å as compared to the experimental value (10.338 Å). In gas phase, the N2–N5 distance (10.80 Å) in [H6L(Cl)2]4+ is longer by 1.0 and 0.18 Å than those calculated in [H6L]6+ and [H6L(Cl)]5+, respectively. In PMC model, the atomic distance between N2 and N5 is 10.57 Å. Meanwhile, two aromatic rings in the optimized model are parallel to each other with a distance of 7.78 Å, which is 0.97 and 0.46 Å shorter than those of [H6L]6+ and [H6L(Cl)]5+, respectively, and fairly correlates with corresponding value obtained from the X-ray data (7.842 Å). The calculated result in the gas phase shows that two chloride anions are apart by 5.23 Å and six H-bonds are formed in [H6L(Cl)2]4+. HB1, HB2, and HB3 bonds are formed by one chloride with HN1, HN2, and HN3 at one side, while the other chloride is bonded to N4, N5, and N6 via HB4, HB5, and HB6 hydrogen bonds at the other side of the cavity. The distances of HB1, HB3, HB4, and HB6 are around 2.0 Å and bond angles of Cl–···HN are around 165° in the gas phase. In solvent the atomic distances and bond angles for the HB1, HB3, HB4, and HB6 are 2.1 Å and 168°, respectively. The X-ray data shows that each chloride is bonded by three hydrogen bonds at one side with the N···Cl– distances of 3.07 Å, 3.13 and 3.15 Å. According to our calculation, those N···Cl– bond distances are 3.00 (HB2), 3.07 (HB1), and 3.07 (HB3) Å in the gas phase. In the PCM model these values are calculated to be 3.10, 3.15, and 3.18 Å. This implies that our calculated data are comparable with the experimental data. The calculated electron density (ρ) and the Laplacian of the electron density (Δ2ρ) at these BCPs are 0.037 au and 0.019 au, respectively, in the gas phase; while these parameters are reduced to approximately 0.030 au and 0.018 au, respectively, in solvent. Alternatively, in the gas phase HB2 and HB5 are predicted with the distance of 1.9 Å and the bond angles of Cl–···HN around 172° which are slightly increased to 2.0 Å and 175° respectively, in the PCM model. The electron density (ρ) at these two BCPs are around 0.050 and 0.037 au in the gas phase and in solvent, respectively. The Laplacians of the electron density (Δ2ρ) are 0.018 au in both phases. This indicates that HB2 and HB5 form stronger hydrogen bonds both in the gas phase and in solvent.45 According to the bond distance and electron density at bond critical point, the hydrogen bonds are slightly stronger in the gas phase than those in the PCM model. In the gas phase, the binding energy and the free energy change (ΔΔG) are −760.2 and −744.4 kcal/mol, respectively. In the PCM model the binding energy and the Gibbs free energy changes for [H6L(Cl)2]4+ model are significantly lowered to −61.6 and −46.8 kcal/mol, respectively. The quantum mechanical calculation shows that the binding energy (both in the gas phase and solvent) for the encapsulation of two chlorides is significantly higher than that for the encapsulation of single chloride anion, suggesting that the 1:2 complex is energetically more stable than 1:1 complex.
Bromide complex
The optimized structure of [H6L(Br)2]4+ is shown in Figure 9C in which two bromide anions are separated by 5.10 Å and bonded by six hydrogen bonds in the gas phase. In [H6L(Br)2]4+, the atomic distance between N2 and N5 is extended to 10.74 Å which is 0.95 Å longer than that of [H6L]6+ but the distance between the two planes of benzene rings is condensed to 7.89 Å which is 0.86 Å shorter than that of [H6L]6+ in the gas phase. The analogous distances are 0.25 Å bigger and 0.5 Å smaller respectively than those in [H6L(Br)]5+. The structure [H6L(Br)2]4+ in solvent can be compared to the structure in the gas phase. In solvent the distance of N2 to N5 is 10.6 Å which is reduced by 0.1 Å compared to that of in the gas phase. The distance between two planes of the aromatic rings is 7.84 Å which is slightly shorter than that in the gas phase. HB1, HB3, HB4 and HB6 hydrogen bonds are formed and characterized by the atomic distances of approximately 2.19 Å with the bond angles of Br–···HN around 167° in the gas phase. The corresponding donor–acceptor distances are 3.22 Å. In PMC model, the HB bond distances, donor–acceptor distances and the bond angles for the same HBs are raised to 2.28 Å, 3.32 Å and 171°, respectively. The electron density (ρ) and the Laplacian of the electron density (Δ2ρ) at these four BCPs are approximately 0.030 au and 0.015 au, respectively, both in the gas phase and in solvent. On the other hand, HB2 and HB5 are predicted with the atomic distance of 2.10 Å (with the bond angles of 175°, donor–acceptor distances 3.16 Å) in the gas phase and 2.23 Å (with the bond angles of 171°, donor–acceptor distances 3.27 Å) in the PCM model. Meanwhile, the electron density and the Laplacian of the electron density at BCPs are about 0.043 au and 0.015 au, respectively, for these two bonds in the gas phase. In solvent these values are narrowed to 0.033 and 0.014 au, respectively. The calculated binding energy between two bromides and [H6L]6+ is −752.8 kcal/mol and the free energy change is −737.4 kcal/mol. In PCM model the binding energy is −59.9 kcal/mol and the free energy change amounts to −44.8 kcal/mol. The large value of binding energy is again an indication of strong electrostatic interactions between the highly positive charged azamacrocycle and the negatively charged anions.
Iodide Complex
The optimized structure of [H6L(I)2]4+ with two iodide anions by [H6L]6+ is shown in Figure 9D. In gas phase the atomic distance between N2 and N5 is 10.57 Å, which is 0.78 and 0.37 Å longer than those of [H6L]6+ and [H6L(I)]5+, respectively. However, the distance between two planes of aromatic rings is 8.09 Å, which is 0.66 and 0.54 Å shorter than those of [H6L]6+ and [H6L(I)]5+, respectively. Six hydrogen bonds are formed between two iodide anions and [H6L]6+. The average distance in HB1, HB3, HB4, and HB6 is 2.43 Å with the average bond angle of 168° in the gas phase. The donor–acceptor distance in these HBs is 3.45 Å. Similar structure has been revealed in PMC model; however, the distance between N2 and N5 is slightly shortened to 10.30 Å. The distance between the two aromatic rings is 8.13 Å which is only 0.04 Å longer than that in the gas phase. In solvent the distances and the bond angles for the HBs (HB1, HB3, HB4, and HB6) are found to be 2.53 Å and 171°, respectively. The donor–acceptor distance is predicted to be 3.57 Å. The electron density (ρ) and the Laplacian of the electron density (Δ2ρ) for these four HBs are nearly 0.03 and 0.015 au, respectively, both in the gas phase and in the PCM model. The other two hydrogen bonds HB2 and HB5 are formed with the atomic distances of 2.35 Å and the bond angle values of 179° (donor–acceptor distances of 3.40 Å) in the gas phase, where the average distance and angle are 2.50 Å and 169° (donor–acceptor distance is 3.52 Å), respectively, for I–···HN in solvent. Also, the electron density (ρ) and the Laplacian of the electron density (Δ2ρ) at these two BCPs are 0.037 and 0.014 au both in the gas phase and solvent, indicating that among the six H-bonds these two bonds are slightly stronger than others. The calculated H-bond parameters of the [H6L(I)2]4+ complex are listed in Table 6. As shown in Table 7, the binding energy of [H6L]6+ for two iodides is estimated as −737.9 kcal/mol in the gas phase and −57.4 kcal/mol in solvent. The Gibbs free energy change (ΔΔG) in the gas phase is −721.8 kcal/mol and is −43.0 kcal/mol in the PCM model. The binding energy is significantly higher for two iodide anions compared with a single iodide (−389.8 kcal/mol in the gas phase and −26.3 kcal/mol in the PCM model). The lower value of binding energy in solvent than that in the gas phase demonstrates that solvent has a huge effect on the formation of a guest–host complex.
Conclusions
A simple polyazamacrocycle has been synthesized and thoroughly studied for binding of halide anions by both experimental and computation techniques. The study demonstrates that the ligand serves as an effective host for halides at low pH. Results from solution studies suggest that with smaller halide ions the ligand preferentially forms a 1:2 complex rather than a 1:1 complex. However, for a larger halide, the preferential binding mode is 1:1, which is attributed to the complementarity in size of the cavity and an anion. The overall trend of the strength of ligand binding for halides follows in the order: fluoride > chloride > bromide > iodide, indicating that the binding strength depends on the relative size and basicity of halides. Three anion complexes including chloride, bromide and iodide have been isolated and their structures have been characterized crystallographically, showing the formation of 1:2 complexes for all three anions. In the chloride complex, two chlorides are found fully encapsulated in the cavity being held strongly by hydrogen bonding interactions. In contrast, larger bromide or iodide anions interact with both sides of the macrocycle instead of being full encapsulation. This is due to the possible repulsion of two anions. DFT calculations performed on [H6L]6+ at M062x/6-311G (d,p) level to evaluate halide binding in gas and PMC models suggest that after binding with a halide anion by L, the distance between the apical nitrogens (N2 and N5) in both 1:1 and 1:2 binding models is elongated by 0.4 to 1.6 Å compared with [H6L]6+. Whereas, the distance between the two planes of the two benzene rings is shortened by 0.1 to 1.9 Å. In both gas phase and solvent, the binding strength increases in the order: fluoride > chloride > bromide > iodide for either 1:1 or the 1:2 binding mode, supporting the experimental data obtained from the 1H NMR studies. DFT calculations further indicate that a 1:2 binding is energetically more favorable than a 1:1 binding of the ligand.
Acknowledgments
The National Science Foundation is acknowledged for a CAREER award (CHE-1056927) to MAH. NMR core facility at Jackson State University was supported by the National Institutes of Health (G12MD007581). We thank for the support of the NSF CREST Interdisciplinary Nanotoxicity Center, Grant No. HRD-0833178. The authors thank the Louisiana Board of Regents for funds to acquire the diffractometers used in this work. The computation work described in this paper was supported by the National Science Foundation under award number EPS 0903787.
Supporting Information Available
Crystallographic data in CIF format, spectroscopic data and NMR titrations, and Cartesian coordinates for optimized structures in PDF. This material is available free of charge via the Internet at http://pubs.acs.org.
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- Bianchi A.; Bowman-James K.; García-España E.. Supramolecular Chemistry of Anions; Wiley-VCH: New York, 1997. [Google Scholar]
- Wichmann K.; Antonioli B.; Söhnel T.; Wenzel M.; Gloe K.; Gloe K.; Price J. R.; Lindoy L. F.; Blake A. J.; Schröder M. Polyamine-Based Anion Receptors: Extraction and Structural Studies. Coord. Chem. Rev. 2006, 250, 2987–3003. [Google Scholar]
- Amendola V.; Esteban-Gómez D.; Fabbrizzi L.; Licchelli M. What Anions Do to N–H-Containing Receptors. Acc. Chem. Res. 2006, 39, 343–353. [DOI] [PubMed] [Google Scholar]
- Wenzel M.; Hiscock J. R.; Gale P. A. Anion Receptor Chemistry: Highlights From 2010. Chem. Soc. Rev. 2012, 41, 480–520. [DOI] [PubMed] [Google Scholar]
- Hossain M. A. Inclusion Complexes of Halide Anions with Macrocyclic Receptors. Curr. Org. Chem. 2008, 12, 1231–1256. [Google Scholar]
- Colquhoun J. Why I Changed My Mind about Water Fluoridation. Perspect. Biol. Med. 1997, 41, 29–44. [DOI] [PubMed] [Google Scholar]
- Ward M. H.; Cerhan J. R.; Colt J. S.; Hartge P. Risk of Non-Hodgkin Lymphoma and Nitrate and Nitrite from Drinking Water and Diet. Epidemiology 2006, 17, 375–382. [DOI] [PubMed] [Google Scholar]
- Akabas M. H. Cystic Fibrosis Transmembrane Conductance Regulator: Structure and Function of an Epithelial Chloride Channel. J. Bio. Chem. 2000, 275, 3729–3732. [DOI] [PubMed] [Google Scholar]
- Bonacquisti T. P. A Drinking Water Utility’s Perspective on Bromide, Bromate, and Ozonation. Toxicology 2006, 221, 145–148. [DOI] [PubMed] [Google Scholar]
- Bichsel Y.; von Gunten U. Oxidation of Iodide And Hypoiodous Acid in the Disinfection of Natural Waters. Environ. Sci. Technol. 1999, 33, 4040–4045. [Google Scholar]
- Andersson M.; Zimmermann M. B. Influence of Iodine Deficiency and Excess on Thyroid Function Tests. Thyroid Function Testing 2010, 28, 45–69. [Google Scholar]
- Pramanik A.; Powell D. R.; Wong B. M.; Hossain M. A. Spectroscopic, Structural, and Theoretical Studies of Halide Complexes with a Urea-Based Tripodal Receptor. Inorg. Chem. 2012, 51, 4274–4284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaumont A.; Wipff G. Macrotricyclic Quaternary Tetraammonium Receptors: Halide Anion Recognition and Interfacial Activity at an Aqueous Interface. A Molecular Dynamics Investigation. J. Comput. Chem. 2002, 23, 1532–1543. [DOI] [PubMed] [Google Scholar]
- Turner D. R.; Paterson M. J.; Steed J. W. A Conformationally Flexible, Urea-Based Tripodal Anion Receptor: Solid-State, Solution, and Theoretical Studies. J. Org. Chem. 2006, 71, 1598–1608. [DOI] [PubMed] [Google Scholar]
- Chen Y. Theoretical Study of Interactions between Halogen-Substituted S-Triazine and Halide Anions. J. Phys. Chem. A 2013, 117, 8081–8090. [DOI] [PubMed] [Google Scholar]
- Révész Á.; Schröder D.; Svec J.; Wimmerová M.; Sindelar V. Anion Binding by Bambus[6]Uril Probed in the Gas Phase and in Solution. J. Phys. Chem. A 2011, 115, 11378–11386. [DOI] [PubMed] [Google Scholar]
- Park C. H.; Simmons H. E. Macrobicyclic Amines. III. Encapsulation of Halide Ions by In,In-1,(k + 2)-Diazabicyclo[k.l.m.]alkane Ammonium Ions. J. Am. Chem. Soc. 1968, 90, 2431–2432. [Google Scholar]
- Llinares J. M.; Powell D.; Bowman-James K. Ammonium Based Anion Receptors. Coord. Chem. Rev. 2003, 240, 57–75. [Google Scholar]
- García-España E.; Díaz P.; Llinares J. M.; Bianchi A. Anion Coordination Chemistry in Aqueous Solution of Polyammonium Receptors. Coord. Chem. Rev. 2006, 250, 2952–2986. [Google Scholar]
- Hossain M. A.; Saeed M. A.; Fronczek F. R.; Wong B. M.; Dey K. R.; Mendy J. S.; Gibson D. Charge-Assisted Encapsulation of Two Chlorides by a Hexaprotonated Azamacrocycle. Cryst. Growth Des. 2010, 10, 1478–1481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warden A. C.; Warren M.; Hearn M. T. W.; Spiccia L. Anion Binding To Azamacrocycles: Synthesis and X-Ray Crystal Structures of Halide Adducts of [12]anen4 and [18]anen6. New J. Chem. 2004, 28, 1160–1167. [Google Scholar]
- Ilioudis C. A.; Steed J. W. Polyaza Metacyclophanes as Ditopic Anion Receptors. Organ. Biomol. Chem. 2005, 3, 2935–2945. [DOI] [PubMed] [Google Scholar]
- Llobet A.; Reibenspies J.; Martell A. E. Oxydiacetic Acid and Copper(II) Complexes of a New Hexaaza Macrocyclic Dinucleating Ligand. Inorg. Chem. 1994, 33, 5946–5951. [Google Scholar]
- Valencia L.; Bastida R.; García-España E.; de Julián-Ortiz J. V.; Llinares J. M.; Macías A.; Pérez Lourido P. Nitrate Encapsulation within the Cavity of Polyazapyridinophane. Considerations on Nitrate–Pyridine Interactions. Cryst. Growth Des. 2010, 10, 3418–3423. [Google Scholar]
- Juwarker H.; Lenhardt J. M.; Castillo J. C.; Zhao E.; Krishnamurthy S.; Jamiolkowski R. M.; Kim K.-H.; Craig S. L. Anion Binding of Short, Flexible Aryl Triazole Oligomers. J. Org. Chem. 2009, 74, 8924–8934. [DOI] [PubMed] [Google Scholar]
- Chauhan S. M. S.; Garg B.; Bisht T. Synthesis and Anion Binding of 2-Arylazo-meso-octamethylcalix[4]pyrroles. Supramol. Chem. 2009, 21, 394–400. [Google Scholar]
- Rhaman M. M.; Ahmed L.; Wang J.; Powell D. R.; Leszczynski J.; Hossain M. A. Encapsulation and Selectivity Of Sulfate With A Furan-Based Hexaazamacrocyclic Receptor in Water. Organ. Biomol. Chem. 2014, 12, 2045–2048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mendy J. S.; Pilate M. L.; Horne T.; Day V. W.; Hossain M. A. Encapsulation and Selective Recognition of Sulfate Anion in an Azamacrocycle in Water. Chem. Commun. 2010, 46, 6084–6086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hynes M. J. Eqnmr: A Computer Program for the Calculation of Stability Constants from Nuclear Magnetic Resonance Chemical Shift Data. J. Chem. Soc., Dalton Trans. 1993, 311–312. [Google Scholar]
- Van der Sluis P.; Spek A. L. BYPASS: An Effective Method for The Refinement of Crystal Structures Containing Disordered Solvent Regions. Acta Crystallogr., Sect. A 1990, 46, 194–201. [Google Scholar]
- Data Collection: SMART Software Reference Manual; Bruker-AXS: Madison, WI, 1998 [Google Scholar]
- Sheldrick G. M. A Short History of SHELX. Acta Crystallogr. 2008, A64, 112–122. [DOI] [PubMed] [Google Scholar]
- Zhao Y.; Truhlar D. The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Dunning T. H. Jr.; Hay P. J.. Gaussian Basis Sets for Molecular Calculations. In Methods of Electronic Structure Theory. Modern Theor. Chem.; Schaefer H. F., III, Ed.; Plenum, New York, 1977; Vol. 3; pp 1–27. [Google Scholar]
- Hay P. J.; Wadt W. R. Ab Initio Effective Core Potentials for Molecular Calculations. Potentials for the Transition Metal Atoms Sc to Hg. J. Chem. Phys. 1985, 82, 270–283. [Google Scholar]
- Wadt W. R.; Hay P. J. Ab Initio Effective Core Potentials for Molecular Calculations. Potentials for Main Group Elements Na to Bi. J. Chem. Phys. 1985, 82, 284–298. [Google Scholar]
- Hay P. J.; Wadt W. R. Ab Initio Effective Core Potentials for Molecular Calculations. Potentials for K to Au Including the Outermost Core Orbitals. J. Chem. Phys. 1985, 82, 299–310. [Google Scholar]
- Frisch M. J.et al. Gaussian 09, Revision B.01. Wallingford CT, 2009.
- Tomasi J.; Mennucci B.; Cammi R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [DOI] [PubMed] [Google Scholar]
- Koch U.; Popelier P. L. A. Characterization of C-H-O Hydrogen Bonds on the Basis of the Charge Density. J. Phys. Chem. 1995, 99, 9747–9754. [Google Scholar]
- Hossain M. A.; Morehouse P.; Powell P. D.; Bowman-James K. Tritopic (Cascade) and Ditopic Complexes of Halides with an Azacryptand. Inorg. Chem. 2005, 44, 2143–2149. [DOI] [PubMed] [Google Scholar]
- Saeed M. A.; Fronczek F. R.; Hossain M. A. Encapsulated Chloride Coordinating with Two In-In Protons of Bridgehead Amines in an Octaprotonated Azacryptand. Chem. Commun. 2009, 6409–6411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hossain M. A.; Llinares J. M.; Miller C.; Seib L.; Bowman-James K. Further Insight to Selectivity Issues in Halide Binding in a Tiny Octaazacryptand. Chem. Commun. 2000, 2269–2270. [Google Scholar]
- Hossain M. A.; Saeed M. A.; Gryn’ova G.; Powell D. R.; Leszczynski J. Unusual Complexes of Trapped Methanol with Azacryptands. CrystEngComm. 2010, 12, 4042–4044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grabowski S. J.Hydrogen Bonding: New Insights. Springer: Dordrecht, The Netherlands, 2006. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.