The neglected tool in the Bayesian ecologist's shed: a case study testing informative priors' effect on model accuracy

Abstract

Despite benefits for precision, ecologists rarely use informative priors. One reason that ecologists may prefer vague priors is the perception that informative priors reduce accuracy. To date, no ecological study has empirically evaluated data-derived informative priors' effects on precision and accuracy. To determine the impacts of priors, we evaluated mortality models for tree species using data from a forest dynamics plot in Thailand. Half the models used vague priors, and the remaining half had informative priors. We found precision was greater when using informative priors, but effects on accuracy were more variable. In some cases, prior information improved accuracy, while in others, it was reduced. On average, models with informative priors were no more or less accurate than models without. Our analyses provide a detailed case study on the simultaneous effect of prior information on precision and accuracy and demonstrate that when priors are specified appropriately, they lead to greater precision without systematically reducing model accuracy.

Introduction

Ecological data are hard to acquire. This limits the rate at which ecologists can develop and apply understanding of phenomena. Some ecological parameters are more difficult to learn about than others, particularly those that occur sparsely in space or time. For example, for a given time and budget, mortality rates are harder to learn about than growth rates because deaths are relatively rare compared to observations of incremental growth. Therefore, it is important to find ways to accelerate learning so that more precise ecological parameter estimates can be acquired more quickly.

Modeling using Bayesian inference can increase the precision of model parameter estimates because it combines previous knowledge (a prior) with newly collected data (the likelihood) to produce a posterior distribution. Bayesian methods are now commonplace in ecological research (Clark 2005), but typically, models using Bayesian inference are fit with vague, relatively uninformative priors, negating what is seen as an important benefit of Bayesian statistics (Kéry 2010). Sometimes, weakly informative priors are used (e.g., Gelman 2006; Gelman et al. 2008) but in such cases, the motivation derives from statistical concerns rather than an attempt to incorporate existing ecological knowledge. The aim of using a vague prior is to maximize the contribution of the data to the posterior distribution. But, this stance implies that nothing was known about the model parameters before the data were collected. Assuming complete ignorance of all model parameters is unlikely to be justified. In almost all cases, something is known about the model parameters before collecting new data. Despite this, informative priors are almost never used for ecological models.

The application of Bayesian methods in ecology has increased in frequency by almost an order of magnitude over the past decade (McCarthy 2007). Why then, is true Bayesian updating, using empirical data-derived priors, still so rare in ecology? There are several potential, nonexclusive reasons ecologists may find it difficult to express prior knowledge as a probability distribution. The perception that informative priors must be subjective may be off-putting. Another reason may be a concern that more informative priors could reduce model accuracy because priors influence the location of the posterior estimate. Priors affect the location of the posterior because the posterior is a weighted average of the prior and likelihood. The relative influence of the prior and likelihood are driven by the variance (i.e., the inverse of precision) of each distribution, with the posterior being closer in location to the one with the less variance (Gelman et al. 2004).

Accuracy and precision are two important properties that can be used to assess the value of a model. Both concepts relate to a model's ability to make predictions, but differ in the aspect of prediction they affect. Accuracy is the ability of a model to make unbiased predictions. Precision is the inverse of variance and describes the confidence ascribed to the predictions a model makes. Precision increases with sample size if regularity conditions hold. Accuracy, however, does not necessarily increase concurrently with an increase in sample size. Precision is an intrinsic property of a model and can easily be compared between models by contrasting the variance of common parameters. Accuracy is a property external to the model and can only be assessed with respect to data. Those data may be the same data that were used to train the model, but a stronger test of model accuracy is to compare model predictions to an external data set and perform external model validation (Rykiel 1996).

Increased precision of estimates from using informative priors is well known, and the extent of improvement in ecological contexts has been demonstrated (e.g., McCarthy and Masters 2005; McCarthy et al. 2008; Morris et al. 2013). The increase in precision is uncontroversial and unsurprising as it is an inherent feature of using most informative priors. Possible adverse effects of informative priors on accuracy are less clear and have not been analyzed for Bayesian models of ecological data. To fill this gap in the literature, we present an empirical assessment of the effect of using empirical data-derived priors on a set of ecological models.

To explore the simultaneous effect of empirical data-derived priors on model precision and accuracy by validating models with new data, we used a large, long-term forest dynamics data set from western Thailand containing records of growth and mortality for >80,000 trees over 15 years. This allowed us to develop empirical data-derived priors for species-specific mortality models based on species-specific growth patterns and then compare them to species-specific mortality models that used vague priors and assess model accuracy and precision. We specifically tested the following hypotheses: (1) mortality models developed with empirical data-derived priors would be more precise, having greater effective sample sizes (not to be confused with the effective sample size used to measure dependence in the Markov chains) than those with vague priors; and (2) mortality models with empirical data-derived priors would have equivalent or greater accuracy to models based on vague priors.

Materials and Methods

To test the effect of empirical data-derived priors on model accuracy requires fitting a large number of equivalent models with and without empirical data-derived priors and validating them against independent data. Our data come from a 50-ha permanent forest dynamics plot at the Huai Kha Khaeng (HKK) Wildlife Sanctuary in Uthai Thani province in western Thailand. The HKK plot is a collaborative project of the Royal Forest Department and National Parks Wildlife and Plant Conservation Department of Thailand, and the Smithsonian Tropical Research Institute's Center for Tropical Forest Science ((Bunyavejchewin et al. 2009) and see Appendix S1 for further details).

We used a three-step modeling process to assess the effect of empirical data-derived priors on predictions of tree mortality rate (Fig.1). Here, we briefly outline each of the three steps (see also Appendix S1 in Supporting Information for further details). Each of the three steps was performed multiple times for different species and over multiple census intervals with the data from the HKK forest dynamics plot.

Figure 1.

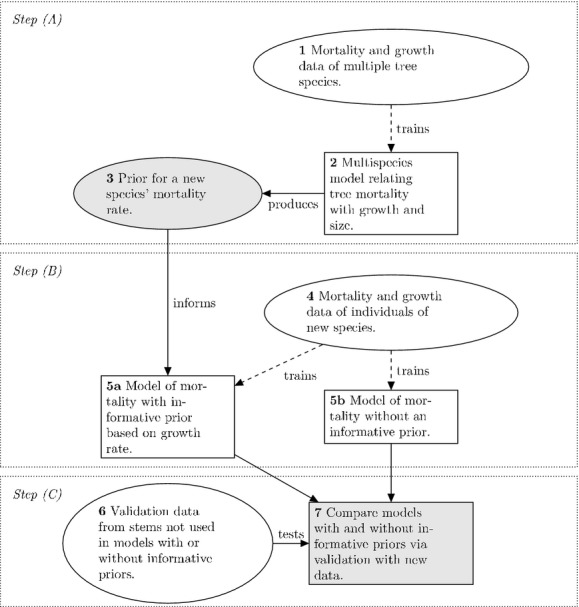
Schematic showing the major components of constructing an informative prior (Step A), fitting models with and without informative priors (Step B) and validating each model (Step C). The schematic outlines the components leading to a single comparison of the effect of an empirical data-derived prior versus a vague prior. In total, there were 90 such comparisons. Components 1 and 2 were initially repeated 15 times. And for each of the repetitions of component 2, there were three informative priors produced at component 3. This resulted in 45 (3 15) repetitions of components 4 through 6. The whole process was carried out twice producing a total of 90 comparisons at component 7.

Prior specification (Step A)

Correlations among biological rates can be used as a source of prior information. Here, we take advantage of the well-known correlation between mortality rate and growth rate (Condit et al. 1995). Typically, species with fast intrinsic growth rates will also have high mortality rates and vice versa. Therefore, knowing something about the growth rate of a species will tell us something about the same species' mortality rate. With data on the growth and mortality of many species, a general relationship between these rates can be inferred and used to specify a prior probability of mortality for a new species with known growth rates.

We developed empirical data-derived priors for single-species mortality models based on the posterior predictive distributions of a hierarchical model that related mortality rates to the growth rates of multiple species. The hierarchical model used mortality as the response, growth rate as a predictor and species as the grouping factor. To construct the empirical data-derived priors for average mortality rate, we produced predictive distributions given the multispecies model estimates, conditional on the relative growth rate of the new species used in the single-species models.

Model fitting (Step B)

The priors derived from the hierarchical model were then applied to single-species models based on a sample of 98 individual stems of each species. The species used in the single-species mortality models were not present in the data sets used to fit the hierarchical models. Like the hierarchical model, the single-species models also considered mortality rate as the response but did not include species growth rate as a predictor. To compare empirical data-derived priors with vague priors, each single-species model was run twice – once using the empirical data-derived prior based on growth rate and again using the same mortality data but with a vague prior that did not include any growth rate-based information.

Model validation (Step C)

Last, we validated both versions of the single-species models with and without empirical data-derived priors. To validate the predictions of the single-species models, we compared predictions to additional external mortality data not used to train the single-level models.

We used the effective number of samples to compare precision of models with and without empirical data-derived priors. We describe the uncertainty around our estimates using a beta distribution. Using moment matching, we estimated the effective number of binomial samples (i.e., tree stems monitored), 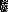, it would take to achieve a given level of certainty with, 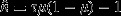, where μ and τ are the mean and precision of the estimated mortality rate parameter. When comparing models with and without informative priors, models with larger effective sample sizes are those with greater precision. This measure of precision was preferred over simply using the posterior variance (or some transformation) as it can be directly interpreted as a measure of sampling effort.

To assess the accuracy of each single-species model with and without empirical data-derived priors, we compared the observed proportion of dead stems in the validation data set, q^val, to the expected proportion of dead individuals predicted by the models given the covariate data, 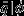. We calculated by averaging over each individual stem's (in the validation set) posterior predictive probability of death, conditional on the covariate data. Then for each species we could compare the magnitude of the difference between, q^val and for both models, with and without informative priors. More accurate models would have lower absolute error, .

All models were fit using Markov Chain Monte Carlo sampling (see Appendix S1 for details) with the open-source software package JAGS version 3.1.0 (Plummer 2003) run through the statistical software environment R version 2.14 (R Development Core Team 2010) with the package R2jags (Su and Yajima 2011).

Results

We developed single-species models for 45 tree species from the HKK forest dynamics plot using growth and mortality data collected between 1994 and 2009. Incorporating the informative priors in the single-species models increased precision of average mortality rate estimates. On average, the precision was four times greater when an empirical data-derived prior was included – equivalent to increasing the sample size by 20 trees (Fig.2: right panel). For most models, the empirical data-derived prior itself was a less precise estimate than the estimate based only on single-species training data, meaning the likelihood had greater influence on the posterior estimates than the prior (see Appendix S1). The average standard deviation of the empirical data-derived priors was 0.7 (range 0.5–0.8), while the standard deviation of the likelihood estimate was typically around 0.5, though more variable (range 0.2–4.3). The effective number of samples (stems measured) of an empirical data-derived prior was typically 15–20 stems. Despite always being based on a sample of 98 real stems, the effective number of samples of the models without empirical data-derived priors was highly variable, but typically <98, because the trees were not treated in the model as being independent samples of mortality. The effective number of samples for estimates made without empirical data-derived priors was typically around 50 stems and less than the estimate made with an empirical data-derived prior.

Figure 2.

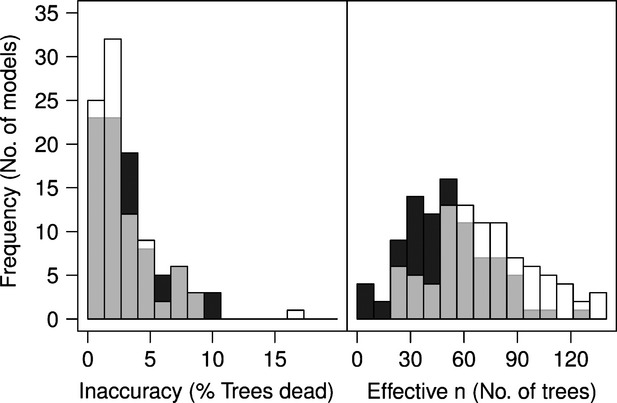
Left panel: histograms of accuracy of single-species models, |(|ϕ) − q^val|. Right panel: Histograms of effective sample size, , of single-species models. Dark grey bars in background are for models with vague priors. Transparent white bars in foreground are for models with empirical data-derived priors.

Adding prior information did not systematically sacrifice the accuracy of models with respect to the validation data set. Models with or without informative priors could usually predict the proportion of dead trees within <5% of the observed value and nearly all within 10% (Fig.2: left panel). Neither group of models was more or less likely to over-or underpredict mortality in the validation sets (see Appendix S1). The predictions of models with informative priors were more often (56 of 90) closer to the validation mortality rate than models with vague priors. There was no relationship between the accuracy lost or gained in having an informative prior and the increase in precision (see Appendix S1). In general, models with large increases in precision due to their informative priors were no more or less likely to be more accurate than models that had only modest increases in precision. One exception was the understory species Murraya paniculata (Rutaceae), which we discuss in greater detail below.

For most species, prior point estimates of average mortality rate were similar to the estimates made for the models fit without informative priors with both prior and likelihood estimates at around 10–20% of stems dying for an average 5-year census period. Prior estimates of mortality tended to be slightly greater than estimates based only on the likelihood, particularly when the likelihood estimate was <10%. One of the 45 (single-species model) species, Murraya paniculata (Rutaceae), a short tree, common in the understory and lower midstory of the forest, had large disagreement between prior and likelihood (Figs.2, 3). In both time periods, its prior estimate of average mortality was ∼10%, but the training data indicated a mortality rate of ∼80% (see Discussion for further details). Across single-species models, the posterior estimates of average mortality for the models with and without informative priors were more similar to each other than the prior was to the posterior of the model without an informative prior. Therefore, for most models, the data had a greater influence on the posterior estimates, than did the prior.

Figure 3.

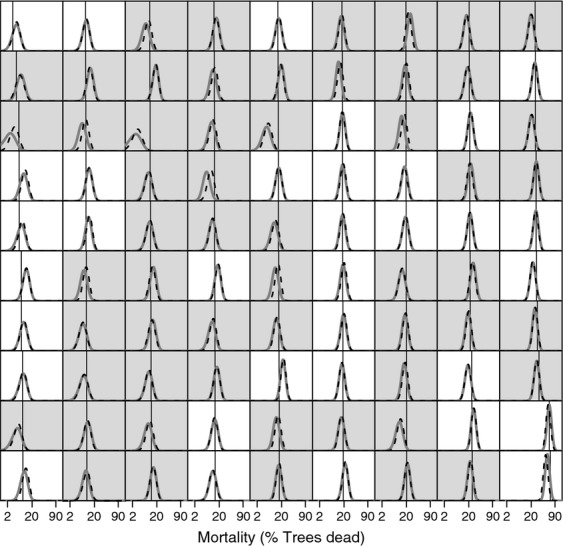
Posterior predictive distributions and observed rate for overall mortality in the validation datasets of the 90 single-species models. Straight black lines show the observed proportion of dead individuals for each validation data set. Thick gray unbroken curves in the background are the posterior predictive distribution produced by models with vague priors. Thin black broken curves are posterior predictive distributions for equivalent models that included empirical data-derived priors. A gray background to the panel indicates the empirical data-derived prior improved model accuracy with respect to the validation data, while a white background indicates that the model with vague priors was more accurate. The horizontal axes are plotted on the complementary log–log scale to aid visualization of the probability distributions. Panels are ordered by increasing observed mortality in the validation set from top to bottom then from left to right.

Discussion

Our analyses illustrate that the type of data-derived priors we used increase model precision and effective sample size without forgoing accuracy. In 56 of 90 cases, the prior drew the posterior of the predicted mortality rate toward the mortality rate observed in the validation data. In these instances, the prior and training data estimates agreed and the prior simply increased the confidence in the estimated mortality rate. But in the remaining cases, the prior estimate made the posterior estimate less accurate than the estimate without an data-derived prior. Overall, though, there was no evidence that a prior, constructed in the manner we have here, would lead to systematic bias and inaccurate models. In a model using Bayesian inference, both the prior and the data influence the location of parameter estimates and therefore model accuracy (Gelman et al. 2004). The influence on parameter location is proportional to the precision of the prior and data. To ensure unbiased parameter estimates, one should take as much care in specifying the prior distribution as when collecting the data (McCarthy and Masters 2005).

The use of Bayesian statistics for ecology has sometimes been criticized (e.g., Dennis 1996; Lele and Dennis 2009). Much of this sentiment stems from the idea that Bayesian priors are overly subjective. Subjective priors can be used and have been demonstrated to work effectively when data are scarce and experts are available to provide information (e.g., Choy et al. 2009). But, a prior need not be subjective. There are a number of examples of ecological studies where the same level of objectivity used to collect the model training data has been used to formulate the prior (e.g., McCarthy and Masters 2005; Dupuis and Joachim 2006; McCarthy et al. 2008).

The method of forming a prior we have used here is a clear example of an non-subjective empirical data-derived prior. The well-established relationship between species potential growth and mortality holds across many taxonomic groups and ecosystems (Condit et al. 1995; Benrey 1997; McCoy and Gillooly 2008) and the species-rich data set used here was no exception. Collecting information on growth rate could be of great benefit when mortality data are scarce or costly to collect, which is typically the case for long-lived organisms that occur at low densities such as tree species. However, this approach could be extended to link functional traits (e.g., wood density, leaf mass area) and demographic rates (e.g., Poorter et al. 2008) to construct priors.

In our study, an empirical data-derived prior only introduced bias in an extreme situation in which the informative prior made the mortality rate prediction less accurate. We observed this bias for the species M. paniculata, which had a large disagreement between prior and likelihood. The reason for the disparity highlights the varied impacts of different agents of mortality and shows that care must be taken to ensure that prior information is relevant to the data that are being modeled. In this case, the prior ignored the extreme sensitivity of M. paniculata to low-intensity ground fires. A fire that burnt through the forest in 1998 increased mortality in the smallest size classes for most species (Baker et al. 2005). However, for M. paniculata ∼80% of the stems died as a direct or indirect consequence of the fire. The species' thin bark meant that the fires directly killed many individuals, but a widespread fungal infection associated with fire-induced basal wounding led to further widespread mortality across the population. The high mortality rate and associated fungal infection also coincided with a population-wide slowing of growth rate. Thus, the relative growth rate for this species was far lower than it would have been under normal circumstances. This low relative growth rate, according to the generalization on which the prior was based, indicated that future mortality would be low, so the prior shifted the mortality lower and away from the mortality rates observed in both the training and validation data sets. This circumstance only arose as the decrease in relative growth rate was so great that the relative growth rate for this species was misleading with respect to the mortality data.

The reluctance of ecologists to use informative priors despite an increase in the use of Bayesian methods is surprising given the increasing use of hierarchical models, which have a similar logic to Bayesian informative priors. The use of hierarchical/mixed modeling (utilizing Bayesian or non-Bayesian inference) is becoming increasingly common in ecology (Bolker et al. 2009). Hierarchical models are a type of formal inductive reasoning, as they enable us to make transparent and general inference from many specific cases coherently. In hierarchical models, whether Bayesian or non-Bayesian, the group-varying parameters operate like a prior and likelihood in a single-level model (Gelman and Hill 2007). If researchers are comfortable with the use of hierarchical models, they should be comfortable with using informative priors. Using priors as we have here is an extension of the logic of hierarchical modeling. For any given individual-group parameter (a parameter associated with a particular group in a hierarchical model), the data of the group form the likelihood, and the prior is the global (across group) mean and associated variance. Each group in a hierarchical data set contributes to the global mean estimate proportionally to the group sample size. For groups with relatively large sample sizes, the data dominates the parameter estimate for that group and will have a value with much the same location and precision as if the estimate was made without the influence of other groups. But for groups with very small sample sizes, the global-average-derived prior contributes far more to the posterior estimate. Small-sample-size group estimates are often very different from the estimates made if their data were modeled with a simpler single-level model. A group with few data would be dominated by the global-average-derived prior and informed by the greater precision of the global-average-derived prior relative to the lower precision of the small-sample-size group. A hierarchical model estimate would be closer to the global, across-group average, and more precise than a single small-sample-size group model estimate. Groups not present in a data set at all operate at the extreme of low sample size.

Our work empirically tests the effect of empirical data-derived priors on model accuracy for the first time. Adding prior information increased the precision of our estimates without systematically biasing model estimates. When priors are appropriately formulated, they should not introduce bias and will increase precision. Here, we have shown the gain in precision possible by recognizing the general link between growth and mortality. Alhough, on average, accuracy was neither greater nor less for the models with empirical data-derived priors, in some cases, we identified a bias introduced by the prior because the information used to form the prior was atypical. Our findings contribute to a motivation for the use of Bayesian methods for ecology. This work provides powerful incentive to use empirical data-derived priors in models for ecology by overcoming a perception that priors could lead to systematic biases.

Conflict of Interest

None declared.