Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Jan 20;5:7906. doi: 10.1038/srep07906

Functional Loop Dynamics of the Streptavidin-Biotin Complex

Jianing Song 1, Yongle Li 4, Changge Ji 1,2,3,a, John Z H Zhang 1,3,b
PMCID: PMC4298722  PMID: 25601277

Abstract

Accelerated molecular dynamics (aMD) simulation is employed to study the functional dynamics of the flexible loop3-4 in the strong-binding streptavidin-biotin complex system. Conventional molecular (cMD) simulation is also performed for comparison. The present study reveals the following important properties of the loop dynamics: (1) The transition of loop3-4 from open to closed state is observed in 200 ns aMD simulation. (2) In the absence of biotin binding, the open-state streptavidin is more stable, which is consistent with experimental evidences. The free energy (ΔG) difference is about 5 kcal/mol between two states. But with biotin binding, the closed state is more stable due to electrostatic and hydrophobic interactions between the loop3-4 and biotin. (3) The closure of loop3-4 is concerted to the stable binding of biotin to streptavidin. When the loop3-4 is in its open-state, biotin moves out of the binding pocket, indicating that the interactions between the loop3-4 and biotin are essential in trapping biotin in the binding pocket. (4) In the tetrameric streptavidin system, the conformational change of the loop3-4 in each monomer is independent of each other. That is, there is no cooperative binding for biotin bound to the four subunits of the tetramer.

As we know, the loop element is a basic structure of folded protein, connecting the secondary structures such as helix or sheet units. Far from just being “connectors”, loops often form parts of the functionally important binding or enzymatic sites. For example, the activity of the protein kinases is regulated by a DFG loop flip mechanism1,2. In another example, the extracellular loops of GPCR are involved in the activation of GPCR3,4. The loops are often located on the solvent-exposed surface of proteins and often have highly flexible conformations. The flexibility of the loops allows them to have more than one local conformation, often corresponding to “open” and “closed” positions that act as a gate to control the protein's function. Thus, it is quite important to study the dynamics of these dynamical loops in order to understand the gating mechanism. A recent study5 of our work on an ECF-transporter showed that the flexible Loop5′ is found to be a gate controlling the binding of vitamin B2 to the S-component of ECF-transporter.

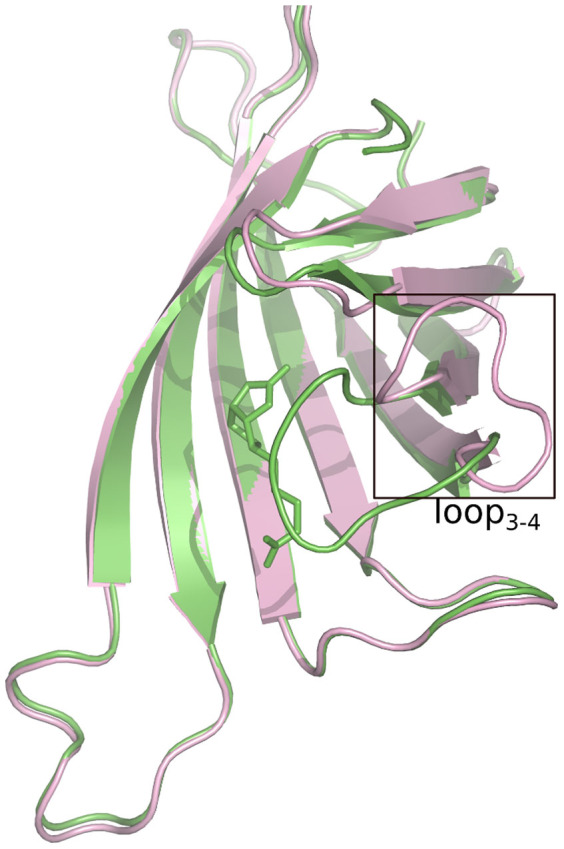
Wild-type streptavidin is a tetramer, with each subunit binding to one biotin6,7. There are complex interactions that dominate the biotin binding process. Among these interactions, the one that involves the flexible loop3-4 between β-strand 3 and β-strand 48,9,10 is quite important. Previous crystal structure studies8,11,12 found that the loop3-4 remains open in the Apo-state but closes after biotin binding, like a “lid” over the binding pocket (shown in Figure 1). Thus, it is important to study the conformational dynamics of the loop3-4 with or without biotin binding.

Figure 1. The loop-open (pink color) and loop-closed (green color) conformation of monomer streptavidin.

Figure 1

Open in a new tab

In our current work, we perform MD simulations to study the conformational dynamics of this flexible loop. Because the time scale for conformational change of loop3-4 is beyond the scope of current standard MD simulation, accelerated Molecular Dynamics (aMD) simulation is adopted to study the conformational dynamics of this loop. Accelerated molecular dynamics is an enhanced sampling MD simulation approach proposed by Voter13,14 and developed by J. A. McCammon15. The philosophy of aMD simulations is to add an external potential either to the dihedrals or the potential of proteins. Compared to other enhanced sampling methods, aMD approach enlarges sampling without any advance knowledge of end states or a pre-defined “reaction coordinates”15,16,17,18,19,20,21,22,23,24,25,26,27. Thus, it allows for greater freedom in sampling diverse reaction pathways. Recently, aMD simulation has been successfully applied to study the conformational changes of soluble protein28,29,30,31 in a shorter time, or to the bilayer lipids32 in 2011 and membrane protein33 system in 2013.

In this work, we apply aMD simulation to study the dynamics of the flexible loop3-4 in streptavidin. Firstly, an external potential is added to the dihedrals of monomer streptavidin in its open-state. Then, aMD simulation is also applied to the monomer of streptavidin in its closed state with or without biotin binding. Thirdly, the conformation of open loop3-4 is exchanged to the closed-state streptavidin with biotin binding. Finally, an external potential is applied to the tetramer streptavidin in its open-state. Conventional molecular (cMD) simulation is also applied for comparison. Details of our work will be stated in the following sections.

Methods

System Setup

The crystal structure of open-state tetramer streptavidin (PDB ID1SWC8) is used for the open-to-close transition simulation. Chain C is chosen for the monomer simulation. The Chain A in the crystal structure of closed-state tetramer streptavidin (PDB ID 1MK534) is used for the monomer close-to-open transition simulation. The parameter for biotin is built from antechamber as follows. Firstly, the structure of biotin is optimized at HF/6-31G* level, and then its atomic charges are fitted through RESP35 at MP2/6-31G* level. The quantum chemical calculations are performed by Gaussian. Finally, GAFF36 force field is used to generate the parameters for biotin simulation. Tleap in AMBER1237,38,39 suit is used to build all the simulation systems. 12 Å TIP3P40 water is added to the simulation system in an octahedron box. Counter-ions are added to neutralize the entire simulation systems. The average size of monomer simulations is around 28000 atoms. The size of tetramer simulation is about 37154 atoms.

Conventional and Accelerated MD simulation

All MD simulations are performed using pmemd.cuda in AMBER12 with amber12 force field for protein, and GAFF force field for biotin. The particle mesh Ewald41 (PME) is used to treat the long-range electrostatic interactions. A cutoff of 12 Å is applied to treat van der Waals interactions. Periodic boundary condition (PBC) is imposed on all directions. Time-step is 2fs with SHAKE42 used to constrain all the hydrogen atoms. Langevin43 dynamics is applied to control the temperature, with a collision frequency of 1.0 ps−1. Berendsen' weak coupling44 is used to control the pressure. Firstly, the system is minimized with protein constrained to equilibrate the solvent. Secondly, protein is released to minimize the whole simulation system. Thirdly, the system is slowly heated to 300 K, followed by a 10 ns equilibration of the whole system in an NPT ensemble. The equilibrated systems are subjected to cMD and aMD simulation protocols at constant temperature (300 K).

Five separate simulations are carried out and they can be grouped into monomer and tetramer simulations, respectively. These five simulations are chosen to be as follows. The first one starts with the open-state streptavidin (Apo-state) as the initial structure. The second one starts with the closed-state streptavidin but with the biotin removed from the crystal structure of the complex. The third one uses the closed streptavidin-biotin complex structure as the initial structure. In the fourth simulation, the conformation of the closed state loop3-4 is artificially replaced by its open state conformation in the streptavidin-biotin complex structure (see Figure S3). In the last simulation study, the tetramer streptavidin in its open-state is used as the initial structure and subjected to an 800 ns simulation study. Details of all the simulations are listed in Table 1.

Table 1. Summary of Conventional MD (cMD) and Accelerated MD (aMD) simulation.

Bio-system Simulation length (ns) Biotin binding Constant c
Monomer cMD aMD    
Open-close 300 200 No 0.4
Close-open 500 120 No 0.4
Close-open 300 300 Yes 0.4
Change loop 100 / Yes 0.4
Tetramer        
Open-close / 800 No 0.5
Open in a new tab

The aMD protocol modifies the initial potential energy surface of biomolecules, by adding a non-negative bias potential, and allows the system sample the conformational space more efficiently. By adding an external dihedral potential ΔV(r) to the original dihedral potential V(r), the modified V*(r) could be expressed as the following equations15.

V*(r) = V(r) + ΔV(r)

And

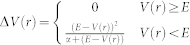graphic file with name srep07906-m1.jpg

where E is the “boost energy” specified by the user, which determines the level of the potential surface affected by the bias potential. α is the “boost factor” tuning the shape of the modified potential.

Thus, it is quite important to choose an appropriate E and α for the transition from one state to another state. In this work, the value E and α come from the following equation suggested by J. A. McCammon in the membrane protein33 simulation job: E = Vav + Vav*c, where Vav is the average dihedral energy from 10 ns cMD simulation and c is a constant and should be specified by the user. We test four constants (0.2, 0.3, 0.4, 0.5) and find that the constant 0.4 produces the open-to-close conformational changes, while retains the protein fold and reasonable secondary structure. Thus E0.4 = Vav + Vav*0.4 and α = E0.4/5 is chosen to conduct all the monomer simulation with random velocities. For tetramer, the constant 0.5 is more reasonable and is used to perform the tetramer simulation of open-state and closed-state streptavidin.

Result and Discussion

Open-to-close transition in Apo-streptavidin captured by aMD simulation

The high affinity of streptavidin-biotin complex provides the basis for many biomedical applications. This tight binding has motivated a variety of biophysical experiments, and has been the model system for binding free energy studies45,46,47,48,49,50. It is known that the major conformational change of the protein associated with biotin binding is the closure of the loop3-4, and the open-close transition process is beyond the time frame of standard MD simulation. In this work, aMD simulation protocol is used, hoping to capture dynamic characteristics of this open-close transition. The monomer of the open-state streptavidin is subjected to a 200 ns aMD simulation and a 300 ns cMD simulation, respectively. To compare the conformational sampling of the flexible loop3-4 in cMD and aMD simulations, we analyzed the distribution of torsional angles of the eight residues in the loop (shown in Figure S1). The analysis shows that the sampled distributions of the torsions in cMD simulations are concentrated near open-state conformations of streptavidin (red balls in Figure S1). However, the distributions in aMD simulations have extended to the closed-state conformations of streptavidin (green balls in Figure S1).

PCA analysis

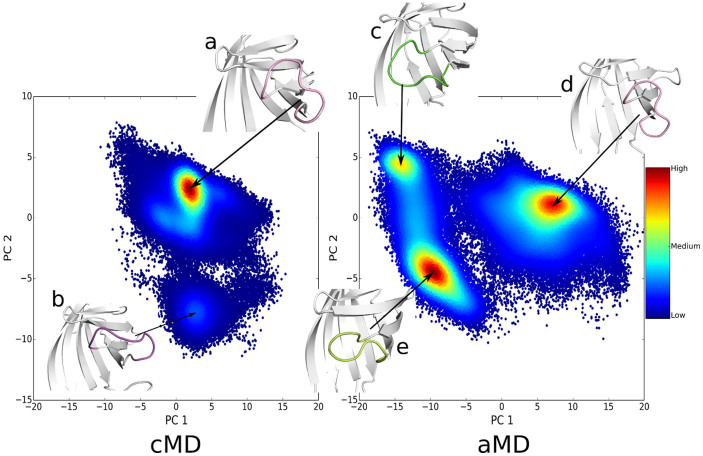
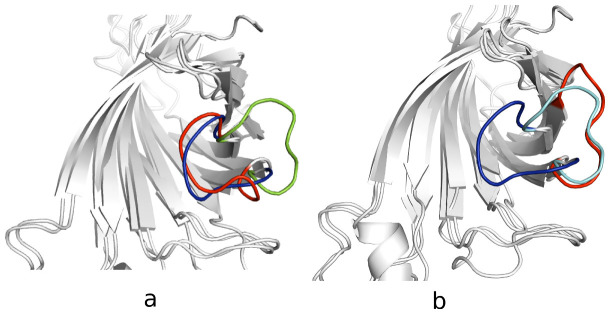
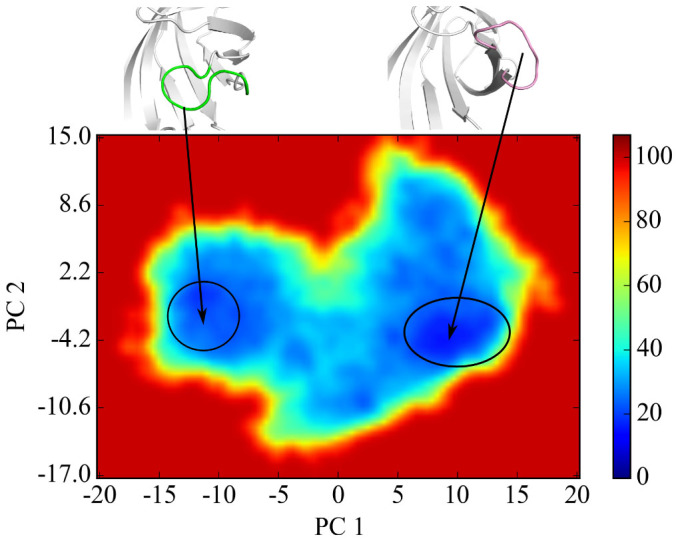
In addition, the principal component analysis (PCA) is performed to both cMD and aMD trajectories. The ptraj in AMBERTools suit and the R-based package Bio3d51 are used to obtain the PCs for further analysis. Firstly both trajectories are combined to be one single trajectory, named meta-trajectory. This procedure is to ensure that all the comparisons of data are in the same subspace. Then the alpha carbons of the rigid part (beta-sheets and alpha-helices only) of the protein in each frame in the meta-trajectory are superposed. After the superposition, the PCA of the alpha carbon of loop3-4 is performed. Once the eigenvectors are obtained, the meta-trajectory is projected onto the two largest PCs (principal components). Then the projected meta-trajectory is split back to two sets. The two-dimensional distributions of trajectories projected to the first and second principal components (PCs) are shown in Figure 2. In our 300 ns cMD simulation, the open-loop conformation (structure a in left plot of Figure 2) as well as another open-loop conformation (structure b) is observed, but no other conformations are found. The situation is quite different for PCA based on aMD trajectory. There are three major distributions, namely, structure c, structure d, and structure e, in the right plot of Figure 2. Specifically, structure c stands for the closed-state of loop3-4 and structure d represents the open-state of loop3-4, while an intermediate state (structure e) is observed under an external potential. Although structure a sees lower distributions than the other states, it clearly shows that open-to-close transition is captured in our aMD simulation. The PC1 and PC2 account for 72.2% of the variance in the original distribution, as shown in Figure S2. The first PC mode is just the loop open/closing motion, shown in Figure S3.

Figure 2. Projection of the loop3-4 conformational space simulated by cMD (left panel) and aMD (right panel) onto the two principal components (PC1 and PC2) produced from the PCA analysis of cMD and aMD trajectories.

Figure 2

Open in a new tab

The distributions of components are depicted with density-colored points, redder points denote higher density, while bluer points denote lower density. Matplotlib59 is used to generate these density-colored points. Structure a in the left panel indicated the open-loop conformation in cMD simulation, and structure b for an intermediate state. Structure c in the right panel represents the closed-loop conformation in aMD simulation, structure d for the loop-open state and structure e for an intermediate state sampled by aMD simulation.

Pocket and structure analysis

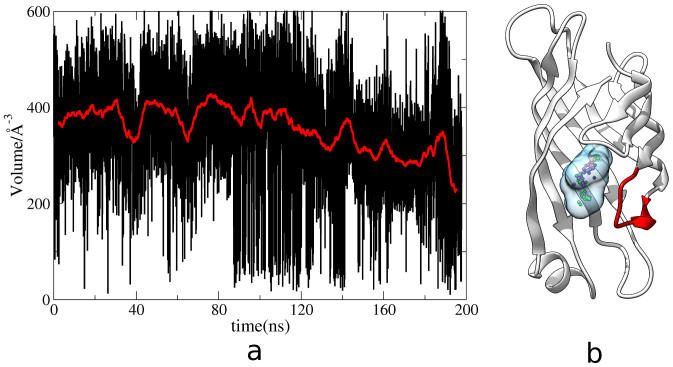
To further examine the transition, pocket analysis has been performed based on the aMD trajectory using the software Fpocket52. Figure 3a shows the change of pocket volume as a function of time. The initial volume is around 400 Å3 and is reduced to 200 Å3 at the end of simulation. Clearly, the loop3-4 closes during the aMD simulation. Figure 3b displays a snapshot at 170th ns from aMD simulation. The loop (red color in Figure 3b) now almost covered the binding pocket and became a closed-state of streptavidin. For comparison, this closed-structure is superimposed onto the open or closed-state crystal structures of streptavidin. Figure 4a shows that the conformation of loop3-4 in aMD simulation (red color) almost completely overlaps the closed-state XRD structure, consistent with the analysis of the torsions. Furthermore, the final conformation from aMD simulation is also superimposed onto the open and closed-state XRD structures of streptavidin (Figure 4b). It is observed that the conformation of loop3-4 is largely the same with the open-state XRD structure of the loop. Thus, the closed-loop opens within a short time of simulation, which concludes that the loop3-4 is not stable in the closed-state streptavidin without biotin binding, consistent with PCA analysis of the lower distributions of closed-state loop3-4.

Figure 3.

Figure 3

Open in a new tab

a, The changes of the binding pocket volumes in aMD simulation as a function of time.Red line indicates the average changes of the volumes. b, the 170th ns simulated structure from aMD simulation. Transparent ball indicates the binding pocket, and red color shows the location of the loop3-4.

Figure 4.

Figure 4

Open in a new tab

a, the 170th ns aMD simulated structure (red color) superimposed onto the loop-open (green color) and loop-closed (blue color) crystal structure.b, the final aMD simulated structure superimposed to the loop-open (cyan color) and loop-closed (blue color) crystal structure.

Free energy landscape analysis

We reweighted the biased distributions derived from aMD simulation to recover the unperturbed free energy landscape of open-to-close transition. The results are shown in Figure 5. The free energy of the open-state is set to zero as a reference energy (PC1: 5~10, PC2: −4.2~2.2) and the closed-state (PC1: −15~−10, PC2: 2.2~8.6) is found to be 5 kcal/mol higher. Thus the open-state is more stable than the closed-state conformation of loop3-4, in the absence of biotin binding.

Figure 5. Free energy landscape calculated for the open-to-close transition, with the right cycle for the open-state (set to be zero point of the free energy), and left cycle for the closed-state (5 kcal/mol).

Figure 5

Open in a new tab

In summary, PCA and pocket analyses show that aMD captures the open-to-close transition. Furthermore, our detailed structure and energetic analysis indicates that the closed-state streptavidin is not stable in the absence of biotin binding. Our result is consistent with experimental observations in which no closed-state of loop3-4 in Apo-protein complex is observed. The free energy analysis shows that the open state is 5 kcal/mol more stable than the closed state. Although an earlier crystallographic study8 observed an tetramer with three open conformations of loop3-4 and a closed-state loop3-4, but it is believed that this apo-closed-state subunit of loop3-4 is due to the effect of crystal-packing interactions in “freezing” out various conformational states of proteins9.

Closed-streptavidin simulation without biotin binding

To further examine the stability of the loop3-4, we carried out cMD/aMD simulations for the closed-state monomer of streptavidin by removing biotin from the binding pocket directly. That is, closed–state streptavidin without biotin binding is used as the initial simulation structure and subjected to a 120 ns aMD simulation and a 500 ns cMD simulation, respectively.

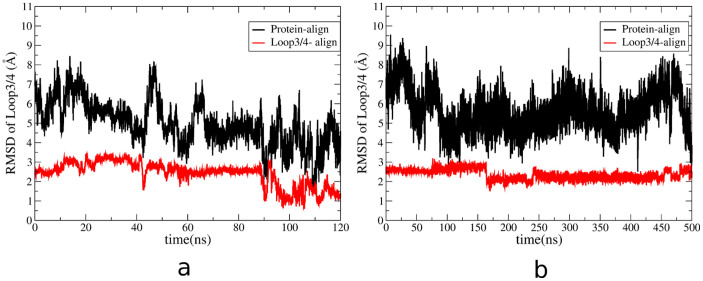
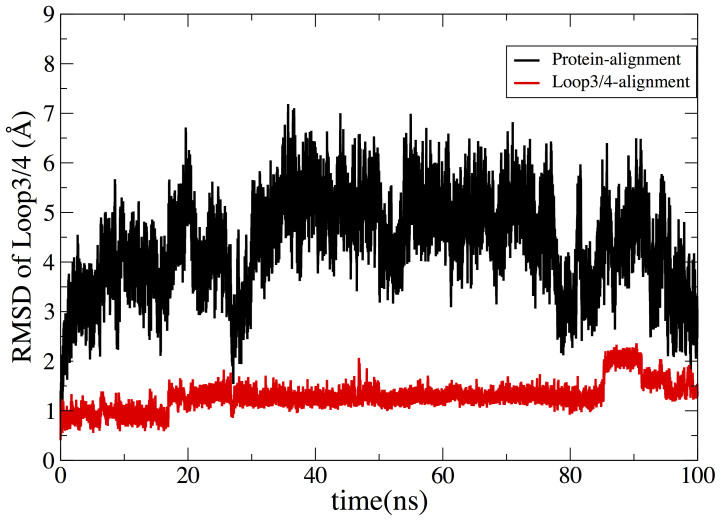
Two different root mean square deviations (RMSD) of loop3-4 analyses are performed to study the conformation changes of loop3-4. The closed-state crystal structure of streptavidin is as the reference conformation. First, RMSD of loop3-4 is calculated based on the alignment of the entire protein backbone (protein-alignment). Secondly, alignment is only applied to the loop3-4 to remove the effect of translation and rotation on the conformation changes of the loop (loop-alignment). Figure 6a shows the results of aMD simulation. For protein-alignment (black color in Figure 6a), the initial RMSD is around 8 Å and is reduced to 3 Å at the end of 120 ns simulation. The dramatic decrease in RMSD shows the structure of the loop3-4 is quite different from the initial closed-state. The situation remains the same when loop-alignment method is used. The RMSD of loop3-4 is reduced from 2.5 Å to 1 Å, showing the conformation changes of this surface loop.

Figure 6. Changes of RMSD of loop3-4 as a function of time, calculated from aMD simulation (a) and cMD simulation (b).

Figure 6

Open in a new tab

Black line indicates the RMSD of loop3-4 based on the alignment of the entire protein. Red line shows the RMSD of loop3-4 based on the alignment of the loop3-4.

For comparison, the above RMSD analyses are also applied to the 500 ns cMD trajectory. Figure 6b shows that the RMSD of loop3-4 decreases to 3 Å from the initial value of 8 Å using protein-alignment analysis. The dramatic decrease in RMSD again shows that the structure of loop3-4 is quite different from the initial closed-state in cMD simulation. When using loop-alignment method, the RMSD of loop3-4 is stabilized at 2.5 Å, which is close to the RMSD value of 2.2 Å between the open and closed loop in XRD structure.

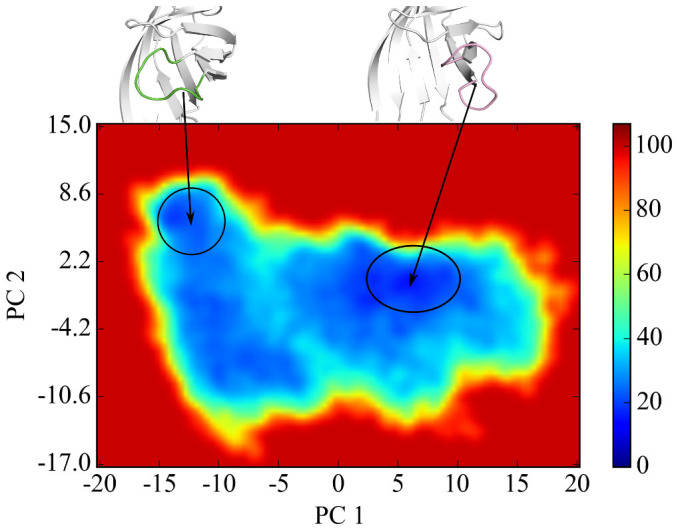
The RMSD analysis shows that the conformation of loop3-4 underwent large changes. In order to examine detailed structural differences of the flexible loop3-4 before and after MD simulation, the simulated final aMD and cMD snapshots are superimposed onto the open/closed state crystal structures. Figure 7 shows that the initial closed loop3-4 is opened in aMD simulation. In cMD simulation, this loop is not fully opened due to a short simulation time.

Figure 7. The final simulated cMD structure (pink color) and aMD structure (red color) superimposed onto the loop-open crystal structure (green color) and closed-loop (blue color) of streptavidin.

Figure 7

Open in a new tab

We reweighted the biased distributions to recover the unperturbed free energy landscape of close-to-open transition and the results are shown in Figure 8. In this close-to-open simulation, the free energy (ΔG) difference between these two states is 7 kcal/mol, about 2 kcal/mol higher than that from the open-to-close simulation. The 2 kcal/mol difference from two stimulations is within the numerical error bar. Thus, these two calculations are consistent with each other.

Figure 8. Free energy landscape calculated for the close-to-open transition, with the right cycle for the open-state loop3-4 (set to be zero point of the free energy), and left cycle for the closed-state (7 kcal/mol).

Figure 8

Open in a new tab

In summary, the initial closed loop3-4 is opened in aMD simulation and is almost opened in cMD simulation as well. Thus, in the absence of biotin binding, the open-state streptavidin is more stable than closed streptavidin, consistent with the mentioned PCA analysis. However, aMD simulation is quite useful in speeding up the transition, based on the fact that the transition happens during 120 ns aMD simulation, while more than four time (500 ns) is needed in cMD simulation to observe this close-to-open transition.

Closed-streptavidin simulation with biotin binding

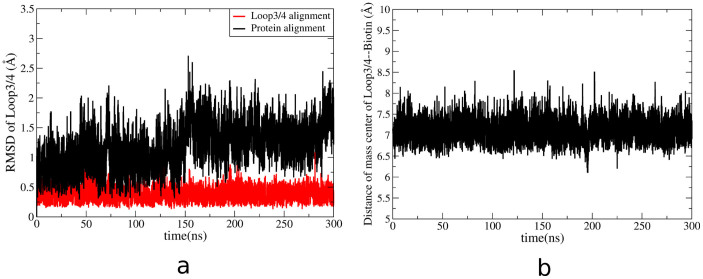
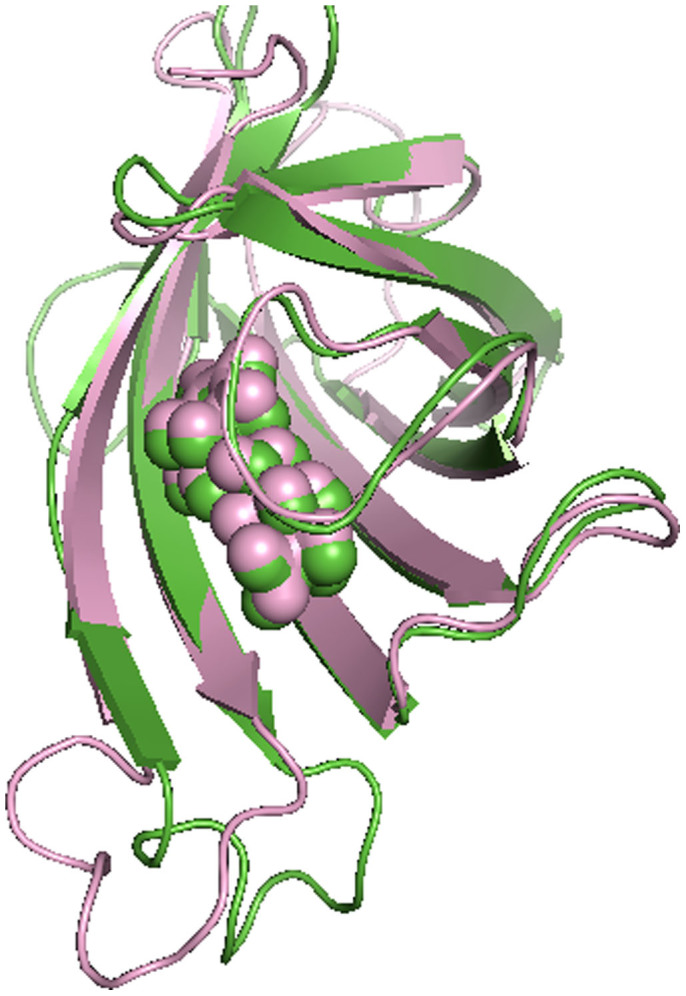
For comparison, streptavidin with biotin binding is also subjected to MD simulation to study the dynamics of the loop3-4 in this tight binding complex. Specifically, we have carried out a 300 ns cMD simulation and a 300 ns aMD simulation. Figure 9a shows the RMSD from cMD simulation. The closed-state crystal structure of streptavidin is as the reference conformation. Using protein-alignment analysis, RMSD of loop3-4 only sees very small changes (from 1 Å to 2 Å), and the situation is similar using loop-alignment analysis with the value of RMSD stabilized at 0.25 Å. Further, the distance between the loop3-4 and biotin is calculated and is shown in Figure 9b. It is observed that the distance remains stable at 7 Å. In another word, RMSD and distance analysis show that the conformation of loop3-4 remains unchanged during the entire 300 ns cMD simulation. The final cMD simulated structure is superimposed onto the initial closed-state streptavidin-biotin complex for detailed structure analysis. Figure 10 shows that biotin and the loop3-4 both overlap well with their initial locations in the XRD structure, indicating stable binding between loop3-4 and biotin.

Figure 9.

Figure 9

Open in a new tab

a, RMSD analysis of loop3-4 in the closed-to-open cMD simulation with biotin binding.Black line indicates the RMSD of loop3-4 based on the alignment of the entire protein. Red line shows the RMSD of loop3-4 based on the alignment of the loop3-4. b, the changes of the distances between the center mass of the loop3-4 and biotin plotted as a function of time in the closed-to-open cMD simulation.

Figure 10. The final cMD simulated structure (green color) superimposed to the crystal streptavidin-biotin complex structure (pink color).

Figure 10

Open in a new tab

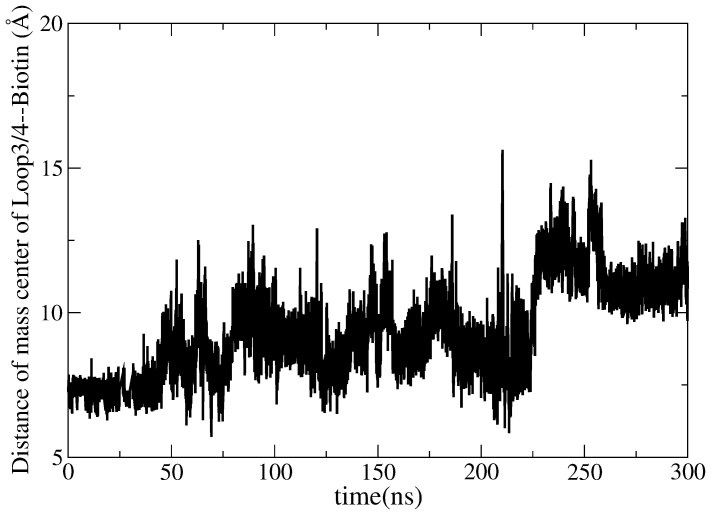
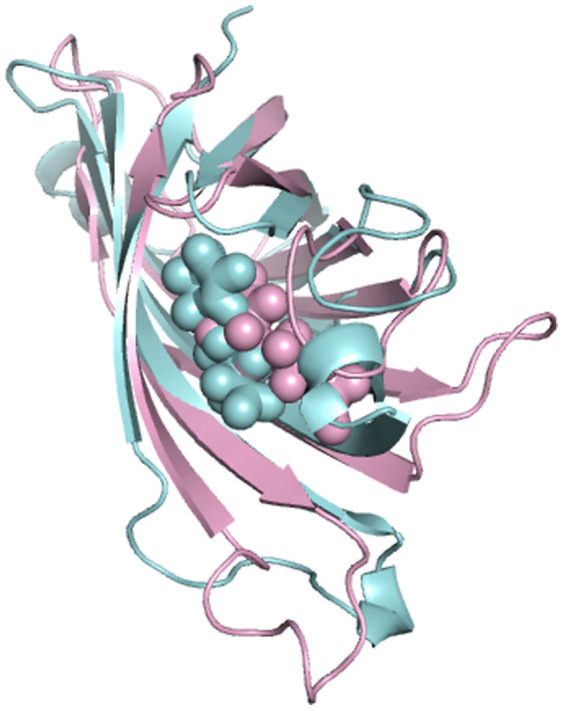
The situation is only slightly different in aMD simulation of streptavidin-biotin complex. Figure 11 plots the change of the distance between loop3-4 and biotin as a function of time. It is observed that the distance is increased from 7 Å to 13 Å. It seems that the loop experienced conformation changes. To further examine this case, the final aMD simulated structure is superimposed onto the initial closed-state streptavidin-biotin complex as shown in Figure 12. The Figure shows that although some conformational changes occurred in loop3-4 and both biotin and loop3-4 drift away from their initial crystal structure, the loop3-4 is still in a closed-state. This result shows that loop3-4 did not change to the open-state even under an external potential. Thus, both cMD and aMD simulations conclude that the loop3-4 of streptavidin is quite stable with biotin binding.

Figure 11. The changes of the distances between the center mass of the loop3-4 and biotin plotted as a function of time in the closed-to-open aMD simulation.

Figure 11

Open in a new tab

Figure 12. The final aMD simulated structure (cyan color) superimposed to the crystal streptavidin-biotin complex structure (pink color).

Figure 12

Open in a new tab

Cooperative binding of Biotin and the loop3-4

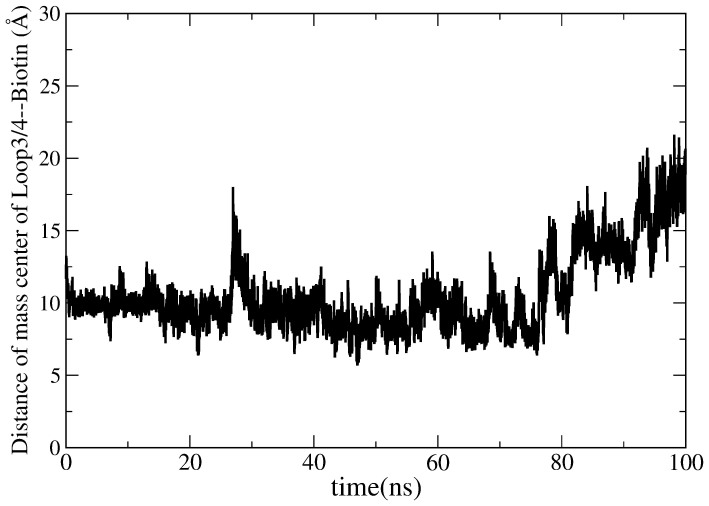
The loop3-4 is stable in Apo-state, but its closed-state becomes stable upon biotin binding. To investigate the dynamics of the open loop3-4 with biotin binding, the initial structure of the closed state loop3-4 is artificially replaced by its open state conformation (Figure S6) in MD simulation. And from this modified initial structure, a 100 ns cMD simulation is performed to study the dynamics of biotin and loop3-4. The RMSD of loop3-4 is plotted as a function of time and shown in Figure 13, with the artificially modified initial structure mentioned above as the reference conformation. Using protein-alignment, the RMSD is increased to 6.5 Å and then decreased to 3 Å at the end of 100 ns simulation. This shows that the conformation of the loop fluctuates a lot. The RMSD is increased to 2 Å using loop-alignment. The RMSD analysis reveals the changes of the conformation of the loop3-4 during our simulation. The distance of biotin and loop3-4 is again calculated as a function of time and shown in Figure 14. It is observed that this distance keeps increasing to 20 Å from 10 Å. This indicates that biotin is not stable during our simulation. Additionally, the final cMD simulated structure is superimposed onto the initial simulation structure to see the conformational differences in details. Figure 15 shows that the loop3-4 partially closes in comparison with the open-conformation. Biotin moves out of its binding pocket and moves away from the loop3-4, shifting to the location of the loop7-8. This kind of cMD simulation is repeated three times. All of them show that biotin moves away from the binding pocket.

Figure 13. RMSD analysis of loop3-4 in the replaced-loop cMD simulation.

Figure 13

Open in a new tab

Black line indicates the RMSD of loop3-4 based on the alignment of the entire protein. Red line shows the RMSD of loop3-4 with the alignment of the loop3-4.

Figure 14. The changes of the distances between the center mass of the loop3-4 and biotin plotted as a function of time in the replaced-loop cMD simulation.

Figure 14

Open in a new tab

Figure 15. Superposition of the final simulated structure (cyan color, in the replaced-loop cMD simulation) and the crystal streptavidin-biotin complex structure (pink color).

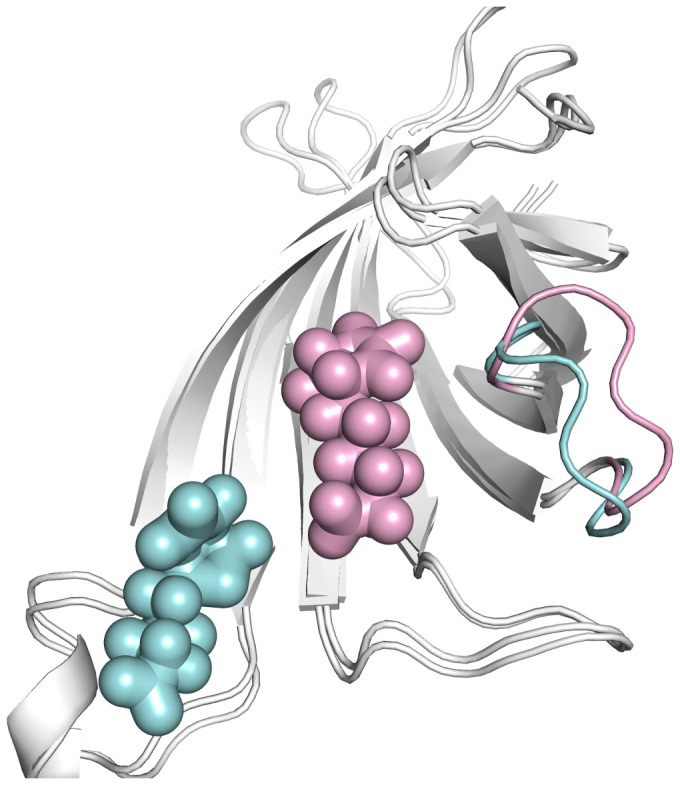
Figure 15

Open in a new tab

As has been stated, S4553 forms a hydrogen bond with the nitrogen atom in biotin while N49 forms another hydrogen bond with the carbonyl oxygen in the aliphatic tail of biotin. The other three residues (V47, G48, A50) interact with biotin through hydrophobic interactions with the aliphatic part of the tail. When the conformation of the loop in the closed-state is artificially changed to that in the open-state, the strong hydrogen bonds interactions and hydrophobic interactions between biotin and the loop3-4 are all interrupted, and this results in the shift of biotin from its binding pocket. This result shows that the interaction between the loop3-4 and biotin is essential in trapping biotin in the binding pocket and the closure of loop3-4 is necessary for stable binding of biotin to streptavidin. The binding process closely correlates with the closure of the loop3-4. That is, as biotin binds to the pocket step by step, the loop3-4 closes simultaneously.

The closure of loop3-4 in each subunit is independent of each other

The above simulations have provided useful information regarding the dynamics of loop3-4 in its monomer state. In order to study any difference in the dynamical behavior of loop3-4 in individual subunits within the tetramer structure, we performed another 800 ns aMD simulation in which the open-state streptavidin (PDB ID 1SWC) in its tetramer conformation is used as the initial simulation structure.

Figure 16 shows the final aMD simulated structure of each subunit. One can see that the conformational change of loop3-4 in the four subunits is not synchronized. Specifically, the loop3-4 in subunit B has already closed at the end of the 800 ns simulation, while the one in subunit A just started to close. The loop3-4 is semi-closed in subunit C, while the one in subunit D is about 75% closed. This analysis concludes that the closure of the loop3-4 in each subunit is independent of each other, and may not happen at the same time.

Figure 16. The final simulated aMD structure for tetramer streptavidin is superimposed onto the crystal structure.

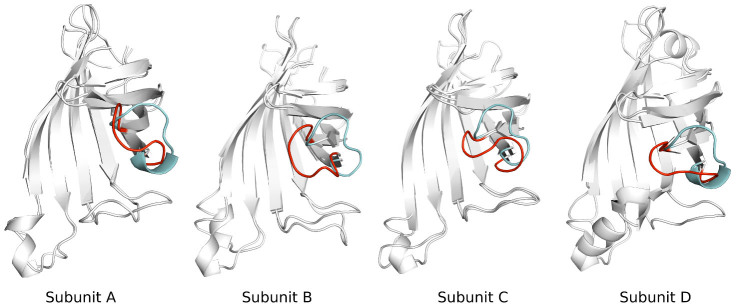
Figure 16

Open in a new tab

Four chains are shown as Subunit A, Subunit B, Subunit C and Subunit D, respectively. Cyan color stands for the conformation of the loop in the open crystal structure, red color for the simulated structure.

To further investigate the correlation among the motion of loop3-4 in the tetramer, the mutual information54,55,56,57 (MI) between each pair of loops is calculated using their principal components (PC). And to avoid the convergence problem of histogram, the kernel density estimation58 (KDE) is used for binning. The results are shown in Table 2. From the table, all MI values are small enough (with maximum 0.07 for IAD and minimum 0.03 for IBC), so it is clear that there is little correlation among the motions of the loops, thus the transition of the loop3-4 in each subunit of the tetramer is independent of each other. That is, there is no cooperative binding of biotin to the four subunits of the tetramer.

Table 2. The mutual information (MI) for the first principal component (PC) of loop3-4 in each subunit of the tetramer.

Loop pair MI
IAB 0.06
IAC 0.04
IAD 0.07
IBC 0.03
IBD 0.06
ICD 0.05
Open in a new tab

Additionally, we have performed a 200 ns aMD and a 200 ns cMD simulation with the closed streptavidin-biotin complex as the initial simulation structure. The distance between loop3-4 and biotin is measured and the results are shown in Figure S9. The distances in cMD simulations are all stabilized at 7 Å. The conformational changes of loop3-4 are somewhat different in the four subunits in aMD simulation. This distance fluctuates in subunit A between 7 Å and 12 Å. In subunit D, the distance in subunit D first increases to 10 Å and then drops to about 7 Å. In contrast, this distance is quite stable near 7 Å in subunits B and C. The loop3-4 (green color in structure a in Figure S9) displays the conformation at a distance of 12 Å, and it is clearly seen that the loop3-4 is partially open at this conformation, which is quite different from the closed-state conformation (structure b in Figure S9). These observations also indicate that the motions of the four loops in the subunits are independent of each other, consistent with that observed in the 800 ns open-state simulation discussed previously in the paper.

Conclusion

The high binding affinity makes it difficult to study the open-to-close transition process of the loop3-4 in streptavidin-biotin system using conventional molecular dynamics (cMD) simulation. In the present work, accelerated molecular dynamics (aMD) simulation is adopted to study the dynamics of flexible loop3-4 of streptavidin in both Apo- and bound states. Five separate simulations have been carried out including both monomer and the tetramer systems. Additionally, cMD simulation is also performed for comparison. The followings are major findings from the present work.

  1. The transition of loop3-4 from open to closed states is observed in our 200 ns aMD simulation. Furthermore, the detailed structure analysis indicates that the closed-state monomer streptavidin is not quite stable in the absence of biotin binding. The relative free energy (ΔG) difference between the open and closed states of apo-streptavidin is found to be about 5~7 kcal/mol.

  2. The closed-to-open transition of loop3-4 is observed in aMD simulations and the loop3-4 is almost open in cMD simulation.

  3. Our simulation study shows that in the absence of biotin binding, the open-state streptavidin is more stable, which is consistent with experimental evidences. But with biotin binding, the closed state is more stable due to electrostatic and hydrophobic interactions between the loop3-4 and biotin.

  4. The closure of loop3-4 is necessary for stable binding of biotin to streptavidin. When the loop3-4 is in its open-state, biotin moves out of the binding pocket. This shows that the interaction between the loop3-4 and biotin is essential in trapping biotin in the binding pocket. The binding process correlates with the closure of the loop3-4.

  5. In the tetramer system of streptavidin, the conformational change of the loop3-4 in each monomer is independent of each other. That is, there is no cooperative binding of biotin to the four subunits of the tetramer.

The present simulation study helps elucidate the functional dynamics of the loop3-4. In our current study, we have quantified relative stability of the open and closed conformations of the active site loop of streptavidin system. Our study may shed light on uncovering important roles of flexible loops in protein-ligand binding and developing practical methods for accounting protein flexible effects in drug design.

Author Contributions

J.S. performed MD simulation, data analysis, and wrote the main manuscript text and prepared most of he figures. Y.L. wrote the part named PCA analysis, and prepared Figure2, Figure5, Figure 8, FigureS1, Figure S2, Figure S3, Figure S5, Figure S6, and Table2. C.J. and J.Z.H.Z. discussed the results and revised the final draft of the paper. All authors reviewed the manuscript.

Supplementary Material

Supplementary Information

Supporting info

srep07906-s1.doc (3.4MB, doc)

Acknowledgments

We thank the National Natural Science Foundation of China (Grants No. 21003048, 21433004) and Shanghai Natural Science Foundation (14ZR1411900) for financial support. CGJ is also supported by “the Fundamental Research Funds for the Central Universities” and Open Research Fund of the State Key Laboratory of Precision spectroscopy, East China Normal University. We also thank the Computer Center of ECNU for providing us computational time.

References

  1. Schindler T. Structural Mechanism for STI-571 Inhibition of Abelson Tyrosine Kinase. Science 289, 1938–1942 (2000). [DOI] [PubMed] [Google Scholar]
  2. Kufareva I. & Abagyan R. Type-II Kinase Inhibitor Docking, Screening, and Profiling Using Modified Structures of Active Kinase States. J. Med. Chem. 51, 7921–7932 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Moro S., Hoffmann C. & Jacobson K. A. Role of the Extracellular Loops of G Protein-Coupled Receptors in Ligand Recognition:A Molecular Modeling Study of the Human P2Y1 Receptor. Biochemistry 38, 3498–3507 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Peeters M. C., van Westen G. J. P., Li Q. & Ijzerman A. P. Importance of the extracellular loops in G protein-coupled receptors for ligand recognition and receptor activation. Trends Pharmacol. Sci. 32, 35–42 (2011). [DOI] [PubMed] [Google Scholar]
  5. Song J., Ji C. & Zhang J. Z. Unveiling the gating mechanism of ECF transporter RibU. Sci Rep 3, 3566 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Stayton P. S. et al. Streptavidin-biotin binding energetics. Biomol. Eng 16, 39–44 (1999). [DOI] [PubMed] [Google Scholar]
  7. O'Sullivan V. J. et al. Development of a tetrameric streptavidin mutein with reversible biotin binding capability: engineering a mobile loop as an exit door for biotin. PloS one 7, e35203 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Freitag S., LeTrong I., Klumb L., Stayton P. S. & Stenkamp R. E. Structural studies of the streptavidin binding loop. Protein Sci. 6, 1157–1166 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Le Trong I. et al. Streptavidin and its biotin complex at atomic resolution. Acta Crystallogr. Sect. D-Biol. Crystallogr. 67, 813–821 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Chu V., Freitag S., Le Trong I., Stenkamp R. E. & Stayton P. S. Thermodynamic and structural consequences of flexible loop deletion by circular permutation in the streptavidin-biotin system. Protein Sci. 7, 848–859 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. General I. J. & Meirovitch H. Relative stability of the open and closed conformations of the active site loop of streptavidin. J. Chem. Phys. 134, 025104–025120 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Weber P. C., Ohlendorf D. H., Wendoloski J. J. & Salemme F. R. Structural origins of high-affinity biotin binding to streptavidin. Science (New York, N.Y.) 243, 85–88 (1989). [DOI] [PubMed] [Google Scholar]
  13. Voter A. F. Hyperdynamics: Accelerated molecular dynamics of infrequent events. Phys. Rev. Lett. 78, 3908–3911 (1997). [Google Scholar]
  14. Voter A. F. A method for accelerating the molecular dynamics simulation of infrequent events. J. Chem. Phys. 106, 4665–4677 (1997). [Google Scholar]
  15. Hamelberg D., Mongan J. & McCammon J. A. Accelerated molecular dynamics: A promising and efficient simulation method for biomolecules. J. Chem. Phys. 120, 11919–11929 (2004). [DOI] [PubMed] [Google Scholar]
  16. Hamelberg D., de Oliveira C. A. F. & McCammon J. A. Sampling of slow diffusive conformational transitions with accelerated molecular dynamics. J. Chem. Phys. 127, 155102–155110 (2007). [DOI] [PubMed] [Google Scholar]
  17. Adcock S. A. & McCammon J. A. Molecular Dynamics: Survey of Methods for Simulating the Activity of Proteins. Chem. Rev. 106, 1589–1615 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Hamelberg D., Shen T. & McCammon J. A. Phosphorylation Effects on cis/trans Isomerization and the Backbone Conformation of Serine−Proline Motifs: Accelerated Molecular Dynamics Analysis. J. Am. Chem. Soc. 127, 1969–1974 (2005). [DOI] [PubMed] [Google Scholar]
  19. Hamelberg D., de Oliveira C. A. F. & McCammon J. A. Sampling of slow diffusive conformational transitions with accelerated molecular dynamics. J. Chem. Phys. 127, 155102 (2007). [DOI] [PubMed] [Google Scholar]
  20. Fajer M., Hamelberg D. & McCammon J. A. Replica-Exchange Accelerated Molecular Dynamics (REXAMD) Applied to Thermodynamic Integration. J. Chem. Theory Comput. 4, 1565–1569 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. de Oliveira C. A. F., Hamelberg D. & McCammon J. A. Estimating kinetic rates from accelerated molecular dynamics simulations: Alanine dipeptide in explicit solvent as a case study. J. Chem. Phys. 127, 175105 (2007). [DOI] [PubMed] [Google Scholar]
  22. Markwick P. R. L. & McCammon J. A. Studying functional dynamics in bio-molecules using accelerated molecular dynamics. Phys. Chem. Chem. Phys. 13, 20053–20065 (2011). [DOI] [PubMed] [Google Scholar]
  23. Wang Y., Harrison C. B., Schulten K. & McCammon J. A. Implementation of accelerated molecular dynamics in NAMD. Comput. Sci. Discovery 4, 015002 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. de Oliveira C. A. F., Hamelberg D. & McCammon J. A. Coupling Accelerated Molecular Dynamics Methods with Thermodynamic Integration Simulations. J. Chem. Theory Comput. 4, 1516–1525 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Markwick P. R. L., Pierce L. C. T., Goodin D. B. & McCammon J. A. Adaptive Accelerated Molecular Dynamics (Ad-AMD) Revealing the Molecular Plasticity of P450cam. J. Phys. Chem. Lett. 2, 158–164 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Sinko W., de Oliveira C. A. F., Pierce L. C. T. & McCammon J. A. Protecting High Energy Barriers: A New Equation to Regulate Boost Energy in Accelerated Molecular Dynamics Simulations. J. Chem. Theory Comput. 8, 17–23 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Markwick P. R. L., Bouvignies G. & Blackledge M. Exploring Multiple Timescale Motions in Protein GB3 Using Accelerated Molecular Dynamics and NMR Spectroscopy. J. Am. Chem. Soc. 129, 4724–4730 (2007). [DOI] [PubMed] [Google Scholar]
  28. Grant B. J., Gorfe A. A. & McCammon J. A. Ras Conformational Switching: Simulating Nucleotide-Dependent Conformational Transitions with Accelerated Molecular Dynamics. Plos Comput. Biol. 5, e1000325–e1000334 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. de Oliveira C. A. F., Grant B. J., Zhou M. & McCammon J. A. Large-Scale Conformational Changes of Trypanosoma cruzi Proline Racemase Predicted by Accelerated Molecular Dynamics Simulation. Plos Comput. Biol. 7, e1002178–e1002184 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Bucher D., Grant B. J., Markwick P. R. & McCammon J. A. Accessing a Hidden Conformation of the Maltose Binding Protein Using Accelerated Molecular Dynamics. Plos Comput. Biol. 7, e1002034–e1002043 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Wereszczynski J. & McCammon J. A. Nucleotide-dependent mechanism of Get3 as elucidated from free energy calculations. Proc. Natl. Acad. Sci. U. S. A. 109, 7759–7764 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Wang Y., Markwick P. R. L., de Oliveira C. A. F. & McCammon J. A. Enhanced Lipid Diffusion and Mixing in Accelerated Molecular Dynamics. J. Chem. Theory Comput. 7, 3199–3207 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Tikhonova I. G., Selvam B., Ivetac A., Wereszczynski J. & McCammon J. A. Simulations of Biased Agonists in the beta(2) Adrenergic Receptor with Accelerated Molecular Dynamics. Biochemistry 52, 5593–5603 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Hyre D. E. et al. Cooperative hydrogen bond interactions in the streptavidin-biotin system. Protein Sci. 15, 459–467 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Bour P. & Keiderling T. A. Ab initio simulations of the vibrational circular dichroism of coupled peptides. J. Am. Chem. Soc. 115, 9602–9607 (1993). [Google Scholar]
  36. Wang J. M., Wolf R. M., Caldwell J. W., Kollman P. A. & Case D. A. Development and testing of a general amber force field. J. Comput. Chem. 25, 1157–1174 (2004). [DOI] [PubMed] [Google Scholar]
  37. Pearlman D. A. et al. AMBER, a package of computer programs for applying molecular mechanics, normal mode analysis, molecular dynamics and free energy calculations to simulate the structural and energetic properties of molecules. Comput. Phys. Commun. 91, 1–41 (1995). [Google Scholar]
  38. Case D. A. et al. The Amber biomolecular simulation programs. J. Comput. Chem. 26, 1668–1688 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Salomon-Ferrer R., Case D. A. & Walker R. C. An overview of the Amber biomolecular simulation package. Wiley Interdiscip. Rev. Comput. Mol. Sci. 3, 198–210 (2013). [Google Scholar]
  40. Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W. & Klein M. L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79, 926–935 (1983). [Google Scholar]
  41. Darden T., York D. & Pedersen L. Particle mesh Ewald: an N.log(N) method for Ewald sums in large systems. J. Chem. Phys. 98, 10089–10092 (1993). [Google Scholar]
  42. Ryckaert J.-P., Ciccotti G. & Berendsen H. J. C. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 23, 327–341 (1977). [Google Scholar]
  43. Pastor R. W., Brooks B. R. & Szabo A. An analysis of the accuracy of Langevin and molecular dynamics algorithms. Mol. Phys. 65, 1409–1419 (1988). [Google Scholar]
  44. Berendsen H. J. C., Postma J. P. M., van Gunsteren W. F., DiNola A. & Haak J. R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81, 3684–3690 (1984). [Google Scholar]
  45. Miyamoto S. & Kollman P. A. Absolute and relative binding free energy calculations of the interaction of biotin and its analogs with streptavidin using molecular dynamics/free energy perturbation approaches. Proteins 16, 226–245 (1993). [DOI] [PubMed] [Google Scholar]
  46. Kuhn B. & Kollman P. A. A ligand that is predicted to bind better to avidin than biotin: Insights from computational fluorine scanning. J. Am. Chem. Soc. 122, 3909–3916 (2000). [Google Scholar]
  47. Kuhn B. & Kollman P. A. Binding of a diverse set of ligands to avidin and streptavidin: An accurate quantitative prediction of their relative affinities by a combination of molecular mechanics and continuum solvent models. J. Med. Chem. 43, 3786–3791 (2000). [DOI] [PubMed] [Google Scholar]
  48. Tong Y., Mei Y., Li Y. L., Ji C. G. & Zhang J. Z. H. Electrostatic Polarization Makes a Substantial Contribution to the Free Energy of Avidin-Biotin Binding. J. Am. Chem. Soc. 132, 5137–5142 (2010). [DOI] [PubMed] [Google Scholar]
  49. Ye M., Li Y. L., Juan Z. & Zhang J. Z. H. Electrostatic polarization is critical for the strong binding in streptavidin-biotin system. J. Comput. Chem. 33, 1374–1382 (2012). [DOI] [PubMed] [Google Scholar]
  50. Juan Z., Xiangyu J., Zhang J. Z. H. & Ye M. The F130l Mutation in Streptavidin Reduces Its Binding Affinity to Biotin through Electronic Polarization Effect. J. Comput. Chem. 34, 2677–2686 (2013). [DOI] [PubMed] [Google Scholar]
  51. Grant B. J., Rodrigues A. P. C., ElSawy K. M., McCammon J. A. & Caves L. S. D. Bio3d: an R package for the comparative analysis of protein structures. Bioinformatics 22, 2695–2696 (2006). [DOI] [PubMed] [Google Scholar]
  52. Le Guilloux V., Schmidtke P. & Tuffery P. Fpocket: An open source platform for ligand pocket detection. Bmc Bioinformatics 10, 168–178 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Hyre D. E., Le Trong I., Freitag S., Stenkamp R. E. & Stayton P. S. Ser45 plays an important role in managing both the equilibrium and transition state energetics of the streptavidin-biotin system. Protein Sci. 9, 878–885 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Shukla D., Meng Y., Roux B. & Pande V. S. Activation pathway of Src kinase reveals intermediate states as targets for drug design. Nat. Commun. 5, 3397–3407 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Steuer R., Kurths J., Daub C. O., Weise J. & Selbig J. The mutual information: Detecting and evaluating dependencies between variables. Bioinformatics 18, S231–S240 (2002). [DOI] [PubMed] [Google Scholar]
  56. Kolmogorov A. Logical basis for information theory and probability theory. IEEE Trans. Inf. Theory 14, 662–664 (1968). [Google Scholar]
  57. Shannon C. E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 27, 379–423 (1948). [Google Scholar]
  58. Moon Y.-I., Rajagopalan B. & Lall U. Estimation of mutual information using kernel density estimators. Phys. Rev. E 52, 2318–2321 (1995). [DOI] [PubMed] [Google Scholar]
  59. Hunter J. D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 9, 90–95 (2007). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supporting info

srep07906-s1.doc (3.4MB, doc)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES