Cohort of birth modifies the association between FTO genotype and BMI

Significance

Our finding of a significant gene-by-birth-cohort interaction adds a previously unidentified dimension to gene-by-environment interaction research, suggesting that global changes in the environment over time can modify the penetrance of genetic risk factors for diverse phenotypes. This result also suggests that presence (or absence) of a genotype–phenotype correlation may depend on the period of time study subjects were born in, or the historical moment researchers conduct their investigations.

Abstract

A substantial body of research has explored the relative roles of genetic and environmental factors on phenotype expression in humans. Recent research has also sought to identify gene–environment (or g-by-e) interactions, with mixed success. One potential reason for these mixed results may relate to the fact that genetic effects might be modified by changes in the environment over time. For example, the noted rise of obesity in the United States in the latter part of the 20th century might reflect an interaction between genetic variation and changing environmental conditions that together affect the penetrance of genetic influences. To evaluate this hypothesis, we use longitudinal data from the Framingham Heart Study collected over 30 y from a geographically relatively localized sample to test whether the well-documented association between the rs993609 variant of the FTO (fat mass and obesity associated) gene and body mass index (BMI) varies across birth cohorts, time period, and the lifecycle. Such cohort and period effects integrate many potential environmental factors, and this gene-by-environment analysis examines interactions with both time-varying contemporaneous and historical environmental influences. Using constrained linear age–period–cohort models that include family controls, we find that there is a robust relationship between birth cohort and the genotype–phenotype correlation between the FTO risk allele and BMI, with an observed inflection point for those born after 1942. These results suggest genetic influences on complex traits like obesity can vary over time, presumably because of global environmental changes that modify allelic penetrance.

The rise in obesity in the United States and other Western countries is a major public health concern, and obesity is known to have both genetic and environmental determinants (1–3). Changes in the population distribution of body mass index (BMI), a common measure of obesity, have attracted the attention of researchers from disciplines across the health and social sciences. Social scientists have attributed changes in obesity to macroenvironmental developments, such as urban design, occupational shifts, dietary modifications, and social effects (4–10). Many of these arguments are plausible and hold considerable intuitive appeal. In parallel, research in the health sciences provides significant evidence to suggest that genetic factors, notably the FTO gene, play an important role in BMI over the lifespan (11–14). Although these research studies were typically not designed to assess interactions between genetic variants and environmental factors, it is likely that environmental effects are modulated by genetic pathways, causing some individuals or population groups to be differentially affected by changes in the environment (7).

To date, gene–environment interaction studies have primarily examined within-birth-cohort differences among individuals with varying environmental exposures in a narrow time period (3). The foregoing research design uses a cross-sectional approach to sample environmental variation and focuses on whether the effects of a single specific environmental variable (e.g., childhood maltreatment) with respect to some outcome (e.g., adult depression) depend on a specific genetic polymorphism (15). This empirical strategy has prompted some debate regarding its ability to detect g-by-e effects (16, 17).

On the other hand, using between-birth-cohort differences is different, allowing for the testing of hypotheses related to time-varying changes in the whole of the environment affecting a population. To our knowledge there have been no longitudinal population studies that seek to determine whether there are between-birth-cohort differences in genotype–phenotype associations. Disentangling the extent to which historical versus contemporaneous environmental factors interact with genetic features, and how these in turn differ from simple aging, can shed light on the mechanisms underlying the rise in obesity (and similar phenomena).

Here, we extend the statistical approach used for decades by epidemiologists and social scientists to understand temporal trends in health outcomes. This approach, known as “age–period–cohort analysis” (18), presumes that the patterns of obesity rates across people of different ages at one point in time do not solely reflect the physiological effects associated with aging but also the accumulation of varied experiences over the lifecycle. These experiences include external factors (such as technological innovations or cultural changes) that influence multiple birth cohorts simultaneously (albeit at different moments in their lives)—known as “period effects” —but that also, in addition, differentially affect specific groups of individuals born within the same era—known as “cohort effects”. This distinction is important because, for example, younger cohorts might be more likely to either embrace new technologies and their corresponding modes of work and leisure or be exposed to a sophisticated marketing campaign at more impressionable ages.

Our approach allows for differential responses to age, period, and cohort factors depending on the genetic markers one carries, thereby providing insights into the source of gene–environment interactions. In addition, we use an estimation strategy that statistically determines the optimal breakpoint (if any) at which the effects of the explanatory variables differ by genetic variant (13). This allows us to directly examine the hypothesis that genetic effects on a phenotype vary meaningfully according to the era of birth of an individual (i.e., the specific cohort to which people belong). Specifically, using a unique dataset, we test the hypothesis that a particular genetic variant with an established association with BMI may have differential influence on the phenotype of BMI depending on when, exactly, an individual was born, suggesting a gene-by-birth cohort (g-by-c) interaction.

To quantify the separate effects of age, period, and cohort (APC) and their interactions with genetic variation, we analyze longitudinal data from the Offspring Cohort of the Framingham Heart Study (FHS) collected between 1971 and 2008 (www.framinghamheartstudy.org/participants/offspring.php). To evaluate statistically which environmental or demographic factors interact with rs9939609 to affect BMI, we estimate augmented versions of age–period–cohort models. These models partition the time-related variation in obesity to the three distinct sources. Intuitively, age effects represent the influence of a person’s current age on obesity, thereby reflecting biological and social processes of maturation and aging internal to individuals. Period effects represent temporal variations in obesity rates over time affecting all age groups simultaneously and subsume a complex set of historical events and environmental factors. In our case, period is quantified as the subintervals of time captured by the eight waves of data collection from 1971 through 2008. Cohort effects represent differences in obesity across groups of individuals born in different eras, implying that members of a given group encounter the same historical and social events at the same ages. Thus, to argue for a g-by-c interaction (the idea that the genotype–phenotype relationship varies by era of birth), it becomes necessary to show, through results and reasoned arguments, that one of the other interactions is not confounding our results. In this case, we argue that g-by-p (gene-by-period) effects are minimal using empirical and circumstantial evidence.

Our main analyses (described in Materials and Methods) begin with a simple descriptive analysis and then postulate a linear model for associations between BMI of person i in family f at time t with a particular age, period (i.e., wave), and cohort (YOB). That is,

$${\text{BMI}}_{ift}={\mathrm{\beta }}_0+{\mathrm{\beta }}_1{\text{age}}_{ift}+{\mathrm{\beta }}_2{\text{wave}}_{it}+{\mathrm{\beta }}_3{\text{YOB}}_i+{\mathrm{\beta }}_4{\text{gene}}_i+{\mathrm{\beta }}_5{\text{X}}_{ift}+{\mathrm{\mu }}_{ift},$$ [1]

where age and wave are a series of indicators for an individual’s age in 5-y intervals when the measurement occurred, respectively, and YOB is the year of birth. We also include a genetic main effect for each genetic variant being investigated (gene), controls for relevant covariates including sex (X), and µ_ift, which is a random error term with a mean of zero. This model makes an assumption of stationarity by assuming the parameters β are constant across APC. To address the research question posed above, we first augment Eq. 1 by interacting each of the key variables with indicators for genotype (gene_i), thus allowing for differential coefficients by genotype. A nonzero interaction of age, period, or cohort with the genetic factors would indicate differential effects for individuals at a given age, in a different period, or in a different cohort group, identification of which is described in detail in Supporting Information, though it is important to note that our identification is inherently constrained as in any APC model due to collinearity. We used a previously developed estimator (19) to identify whether there is a change point in the parameters that represents a discontinuity in the genotype–phenotype relationship. By allowing the parameters for YOB to undergo a structural shift in an unspecified year, this allows us to test for a structural break of unknown timing. Our approach assumes that birth cohort effects, as well any of their interactions with genetic markers, are homogenous before and after the year of the identified structural break, but allows the effects to vary between the pre- and postbreak periods.

The main advantage of this approach is that we can conduct specification tests to determine whether future research should focus on genetic interactions with specific historical influences (cohort effects) and/or contemporaneous influences (period effects), and/or exposure accumulation (age effects). Our approach requires restrictions to be placed on two parameters of the model because it is well known that no statistical model can simultaneously estimate all of the linear APC effect parameters in Eq. 1, given their collinearity (i.e., cohort = period − age). Thus, we followed earlier research relating to identification of these effects (detailed in Supporting Information) and used graphical data describing the obesity trends by period, age, and cohort to establish the choice of constraints for this model; and we investigated whether the results were sensitive to the chosen constraints. Our preferred estimates are obtained by selecting the first age and period groups as the reference categories and also restricting any linear birth cohort effect to be zero, allowing only for a nonlinear effect of cohort. We argue that it is natural in our setting to set the linear cohort effect to zero because, in a model with separable age and time effects and only a linear cohort effect, we would only observe parallel shifts of the cross-sectional age profiles over time. This is unlikely to be the case for BMI, and we wish to observe how these responses varied across genetic markers using the most common genotype (TT) at rs9939609 as the reference category in the underlying regression specifications.

By restricting the first age and period groups as well as the most common genotype to be reference categories, we can identify unique parameter estimates. The choice of which restrictions that constrain any two specific APC variables to serve as reference categories does affect the estimated coefficient values and SEs. Unfortunately, there is no empirical method of differentiating between alternative variables whose effects are constrained because, irrespective of the restrictions, all estimated models yield identical fits of the data. Thus, to investigate the sensitivity of our estimated g-by-c effects, we conducted numerous robustness exercises including (i) fixing alternative age or period effects to be zero allowing for only a nonlinear cohort effect, (ii) treating birth year as a continuous variable so that the function of the cohort variable does not have a perfect linear relationship with the discrete age and period effects we condition upon, and (iii) constraining a set of parameters (i.e., the effect of two age effects) to be equal. In general, these alternative models placed different constraints that were also chosen using external information on obesity prevalence over time. However, these alternative models placed restrictions that were more difficult to justify in our setting based on a graphical examination of our data that showed rising rates of obesity both across time and age. That said, our analyses led to identical findings of a significant g-by-c interaction irrespective of the constraints and restrictions imposed.

Results

We first undertook a primarily descriptive analysis by reviewing the average BMI in cells of a two-way table presented in Table 1. Each cell denotes the age–period combination where the rows represent categories of subject age and the columns define categories of year when the measurement was taken. The diagonal of Table 1 (going from upper left to lower right) defines the patterns of mean BMI for successive cohorts of the FHS Offspring sample who were born together and hence age together. Looking across rows, columns, and the diagonal, we generally see increased values for BMI. For example, moving down each column, we document the well-established age profile that generally reflects rising BMI over the lifecycle. The trajectories observed across waves and lifecycle documented in Table 1 also justify setting the first age and period categories as reference groups; and, looking across the diagonal, there does not appear to be a linear relationship between BMI and cohort. This suggests that restricting the first age and period groups to be reference categories is acceptable. Caution should be exercised in reaching any further conclusions from this table, however, because it simply provides a general qualitative impression about APC rate patterns and does not decompose their separate effects. To more rigorously assess these effects we use the methods described below.

Table 1.

Average BMI by subject age and period measured in the full sample used in our estimation

	Wave 1	Wave 2	Wave 3	Wave 4	Wave 5	Wave 6	Wave 7	Wave 8
Age, years	30 Aug 1971	26 Jan 1975	20 Dec 1983	22 Apr 1987	23 Jan 1991	26 Jan 1995	11 Sep 1998	10 Mar 2005
27–29.99	24.36	24.37	24.57	25.12	30.38
30–34.99	24.74	24.26	25.08	26.05	26.53	26.80	22.41
35–39.99	25.44	25.07	25.19	25.41	26.64	28.13	28.99
40–44.99	25.83	25.68	25.86	26.31	26.39	27.80	28.79	29.97
45–49.99	26.09	26.05	26.55	26.90	27.13	27.40	27.81	29.19
50–54.99	26.27	26.50	26.52	27.48	27.71	27.98	27.72	28.65
55–59.99	26.38	26.28	26.82	27.16	27.79	28.55	28.59	28.41
60–63	28.13	26.45	26.67	27.15	27.77	28.00	28.73	28.60

Each cell contains the average BMI of individuals measured in the age and period denoted by the row and column and for the sample denoted by the panel.

Modeling birth year as a continuous variable, we find evidence from estimates of the augmented version of Eq. 1 of a significant change in the relationship between FTO genetic variants and BMI in the early 1940s (Table S1). That is, we use an estimation approach (Supporting Information) that finds the point at which the genotypes have the greatest overall difference in their effect on BMI between subgroups of the population born before and after this threshold. The change points supported by estimating various models ranged from 1942 to 1945. We chose 1942 as the change point in further models that treated the YOB as a discrete variable, but results were insensitive to alternative values from 1942 to 1945.

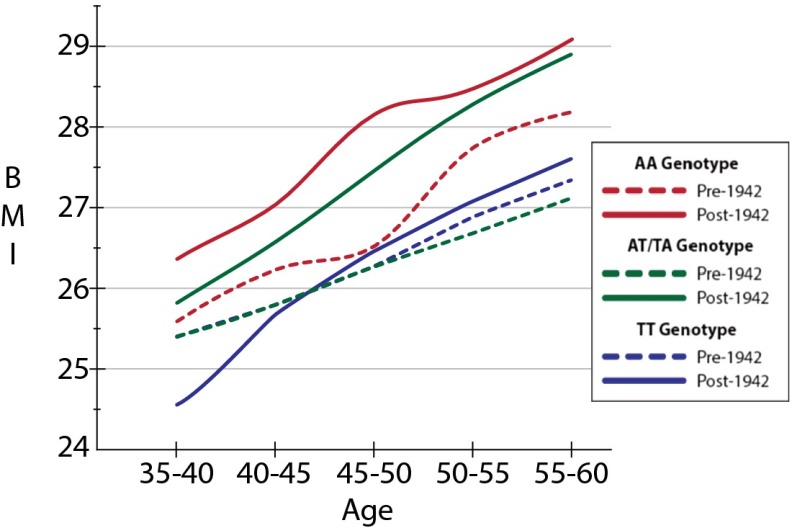
As shown in Fig. 1, mean BMI evolves over the lifecycle for individuals with the same genotype, comparing the pre- and post-1942 birth cohorts in the full dataset. However, mean BMI differs across the three genotypes in the later birth cohort compared with the pre-1942 cohort. The between-birth-cohort differences in mean BMI are statistically significant (P < 0.017) for individuals with one or two of the risk (“A”) FTO allele, particularly during early middle age. This difference (and the lack of difference between cohorts without the risk allele) suggests that differences between BMI growth curves from different birth cohorts are more pronounced among individuals carrying A alleles.

Fig. 1.

BMI over the ages of 35–60 by birth cohort for AA, TT, and AT/TA genotypes by general birth cohort (born before or during/after 1942).

Table 2 presents estimates from our preferred specification of the age–period–cohort regression models, allowing for differential relationships between the genetic effects and BMI on the basis of sex and APC variables (for details, see Materials and Methods). Tests of the joint significance of regression parameter estimates indicate a highly significant cohort-gene interaction [F statistic for joint effects, F(2, 19,617) = 17.51, P = 2.54 × 10⁻⁸] controlling for age–gene and period–gene interactions. This suggests that the effect of FTO varies across cohorts or eras. More specifically, we find a highly significant interaction between the post-1942 birth cohort indicator and genotype, with the more efficient random effects estimator (Supporting Information) showing interactions with both AA and AT genotypes compared with the TT genotype. The results indicate that, among individuals in the cohort born after 1942, the AA and AT genotypes are associated with an additional average gain in BMI of 1.04 units [95% confidence interval (CI) 0.15–2.03, P = 0.023] and 1.14 units (95% CI 0.50–1.77, P = 0.0005), respectively, relative to individuals with the same genotype born before 1942 (Table S2). Our results provide evidence that only AA homozygosity is associated with a statistically significant BMI difference for both cohorts born before and after 1942. Further, our estimates indicate that the AT genotype is characterized by different rates of increase in BMI between cohorts; and, for homozygous TT subjects, there was little change in BMI across cohorts. Several of the period–genetic variant interactions are individually statistically significant at conventional levels, but they are jointly insignificant (F = 0.59, P = 0.69), suggesting that these effects are likely to be artifacts of multiple testing.

Table 2.

Random effect estimates of factors influencing BMI from a specification using discrete variables to indicate birth cohort differences and their interactions with genetic factors

Explanatory variables	Random effects estimates
Subject is male	1.641*** (0.146)
Age 30–34.99	0.477*** (0.174)
Age 35–39.99	0.608*** (0.174)
Age 40–44.99	1.011*** (0.188)
Age 45–49.99	1.199*** (0.212)
Age 50–54.99	1.231*** (0.238)
Age 55–59.99	1.272*** (0.269)
Age 60–63	1.229*** (0.300)
Subject was born after 1942	−1.360*** (0.280)
AA genotype	0.708* (0.398)
AT genotype	−0.412 (0.282)
Born after 1942 by AA genotype	1.041** (0.459)
Born after 1942 by AT genotype	1.135*** (0.326)
Constant	24.01*** (0.250)
Observations	19,617
R2	0.106
No. of individuals	3,720

Presented are the estimates of the age–period–cohort model where the cohort variable is treated as discrete. Each entry refers to the effect of the variable listed in the first column on BMI holding all other factors constant. SEs are presented in parentheses. Specifications also include gene-by-age (g-by-a) interactions and the estimates of all other factors included in this model as well as other estimators are presented in Table S2. See Table S6 for the calendar time corresponding to examinations in each wave. Note that our main results of birth cohort and genotype interactions are not sensitive to the method by which the model was estimated. The following indicate statistical significance of each explanatory variable: ***P < 0.01, **P < 0.05, and *P < 0.1.

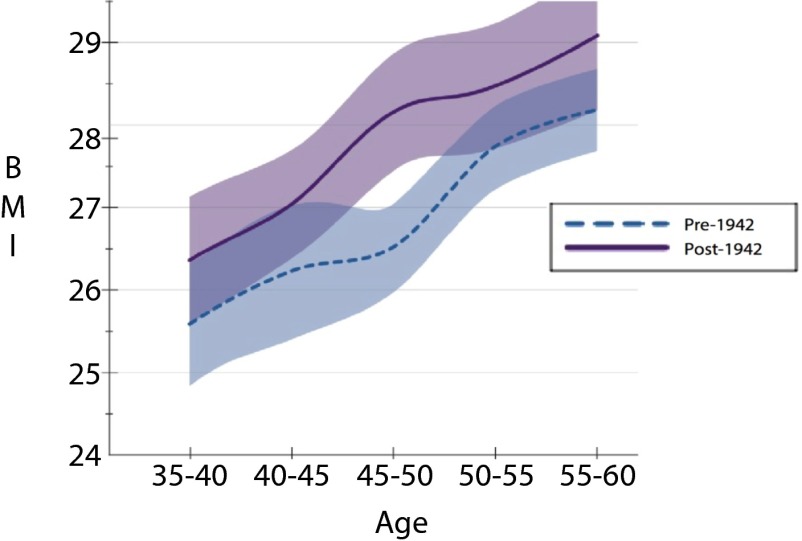
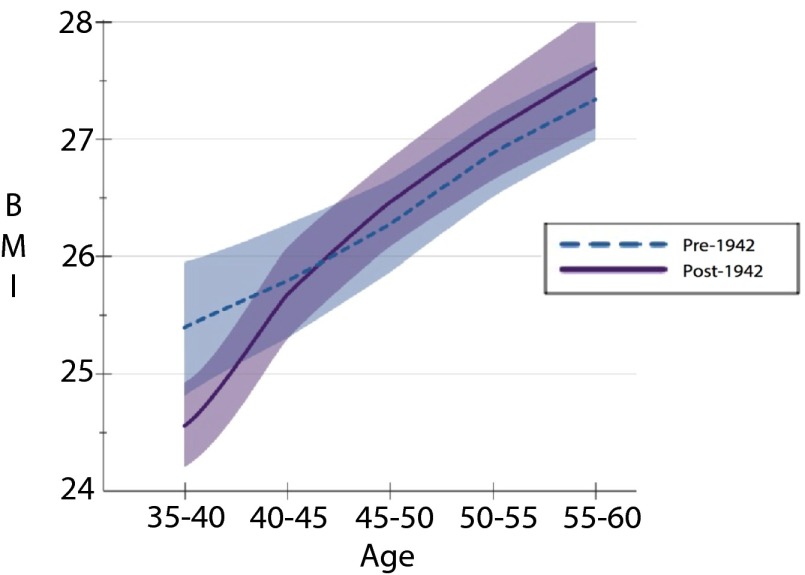
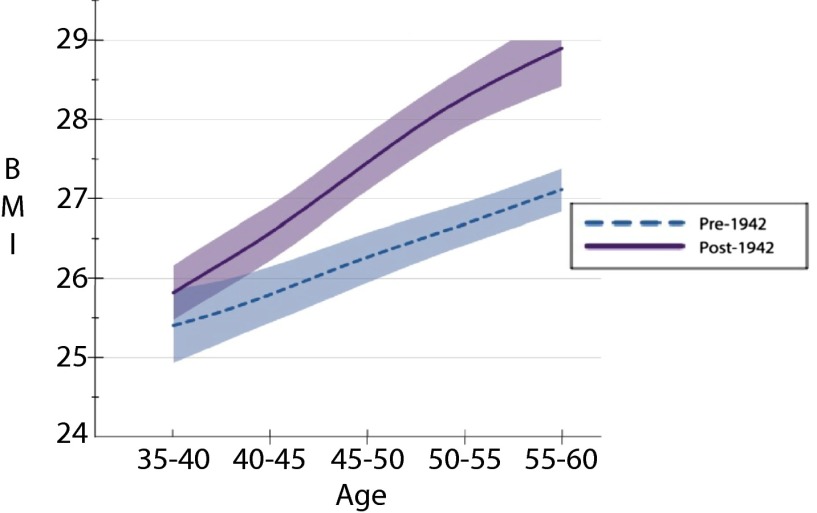
In Figs. 2–4, we demonstrate that the age gradient in BMI does not significantly differ for individuals with the TT genotype across birth cohorts (Fig. 4). In contrast, we not only observe a significantly different FTO–BMI relationship across ages for those with the AT genotype, but the age gradient documented in Fig. 3 becomes steeper in the post-1942 cohort. Last, whereas the estimates in Table 2 showed that individuals with the AA polymorphism had significantly higher BMI in both the pre- and post-1942 cohorts, we did not find a significant difference in the BMI age gradient between cohorts (Fig. 2), although this may be due to low power resulting from the smaller sample size. Taken together, the set of Figs. 2–4 illustrate that there is an age gradient across all genotypes, but it does not point to an overall steepening of the age gradient. The results continue to point out differences in the estimated relationships between those born before and after 1942, and, given our sample size, it would not be surprising if, with additional data, we would see the observed difference in the BMI age gradient for the AA genotype become statistically significant. Last, we note that the statistically significant differences in BMI between and within birth cohorts on the basis of genotype do not arise due to the specification of our linear model and are also observed when simply comparing the unconditional sample means of BMI across genetic variant, birth cohorts, and 5-y age intervals (as reported in Table S3).

Fig. 2.

BMI over the ages of 35–60 by birth cohort for the AA–FTO genotype.

Fig. 4.

BMI over the ages of 35–60 by birth cohort for the TT–FTO genotype.

Fig. 3.

BMI over the ages of 35–60 by birth cohort for AT/TA–FTO genotype.

We conducted several robustness exercises that exploit the familial structure of the FHS data by estimating a further augmented age–period–cohort model that incorporates family-specific unobserved heterogeneity through random effects, as suggested in ref. 20 (Tables S1, S2, and S4). This allows us to control for family effects shared by siblings, including childhood diet and other aspects of physical and social environment as well as similarities of genetic endowment other than the target gene. In addition, in Table S2, we consider alternative estimators for our preferred model, and, in Table S4, we explore sex differences in the magnitude and statistical significance of the interaction of birth cohort and genotype with BMI by testing sex differences in sample means and in coefficients of sex-stratified regression models. Consistent with previous studies, our longitudinal family fixed-effect model (Table S1) finds a significant main effect for rs9939609 both for AA and AT genotypes indicating an average increase of 0.88 (95% CI 0.26–1.50, P = 0.006) and 0.49 (95% CI 0.075–0.93, P = 0.017) units of BMI, respectively, relative to those with the TT genotype.

Discussion

Our results suggest that the well-documented rise in BMI in the United States over the past 40 y may have been disproportionately driven by individuals for whom genetic factors interacted with environmental changes encountered in their development due to their era of birth—in this case, being born later. Although our approach, by its nature, cannot ever rule out a g-by-p interaction, tests of joint significance of these interactions (F = 0.59, P value = 0.69) are fairly suggestive of a minimal g-by-p contribution, holding all else constant. Furthermore, the lack of any g-by-p findings over the time period studied, and the fact that our study focused on adults (who, according to previous research, have already incorporated differential genetic contributions to BMI) (1, 21–25), all provide strong suggestive evidence of limited g-by-p influence on our results.

Our results also help to disentangle the impact(s) of FTO genotype, age, and generational environment on BMI. As discussed above, previous GWAS (genome-wide association studies) and g-by-e work has generally examined interactions of genotype with a specific environmental change or attributed all changes in phenotype to changes in environment, assuming that genotype effects did not change in the period studied. However, such analyses do not make it possible to distinguish effects of contemporaneous and lifetime environmental shocks as well as maturation effects, a limitation of single birth cohort and cross sectional studies.

More generally, these findings raise the possibility that genetic associations may differ across birth cohorts due to variation in prevailing environmental contexts. If so, a genetic association detected by a gene-by-environment (g-by-e) study performed today might not be detectable in future generations. Conversely, effects not seen at this time may appear as environmental changes occur that affect entire populations. This general point could certainly extend beyond the particular case of FTO and obesity; and although the odds that a gene discovery effort would be successful increase with larger sample sizes, the results of such studies (and even their ability to detect a genotype–phenotype relationship) may be influenced by the within-sample birth cohort distribution or the time when such research was undertaken (26). The fact that allelic penetrance could vary across over time (e.g., across birth cohorts) may have implications for the interpretation of genetic risk data. This idea, that genetic effects could vary by geographic or temporal context is somewhat self-evident, yet has been relatively unexplored and raises the question of whether some association results and genetic risk estimates may be less stable than we might hope.

The concept of time-dependent genetic penetrance has been raised in the past. The so-called thrifty-gene hypothesis suggested that genetic variants selected for energy conservation have contributed to increased obesity prevalence in modern environments where food has become more plentiful, although recent empirical tests of the hypothesis have not supported it (27, 28). This work raises the question of whether broad environmental changes might have differential impacts on the BMI of individuals based on genotype. Many hypothesized environmental influences on the rise in obesity did indeed occur after the early 1940s, including technological advances reducing energy expenditure at work as well as increases in the caloric content of processed foods (4), whose effect may be experienced most strongly by individuals whose tastes and habits would be influenced at a young age (1).

Although our work shows a general g-by-c effect, we do not attempt to identify the particular environmental factor(s) whose change(s) might be driving these results. Understanding which specific historical influences alter the penetrance of genetic variants across cohorts is beyond the scope here, but is an important avenue of research that is worth additional comment. Because many of the environmental changes between birth cohorts hypothesized to be responsible for the rise in obesity are correlated over both time and geographic space, well-powered studies will be required. Although other research designs, such as natural experiments, can in principle help identify the particular environmental factors that might interact with specific genotypes, they require that the specific gene–environment interaction being investigated not be confounded with other potential gene and environment interactions (29–31). Implementing such an approach would be challenging: spatial variation in the price of calories may be correlated with spatial variation in the rate of change in sedentary lifestyles or other environmental changes that have been hypothesized to be linked with obesity. In addition, the large number of potential g-by-e hypotheses creates a large number of testable hypotheses, thereby reducing the statistical power of the study and increasing the multiple-testing burden.

To overcome these challenges, we propose that future research into these effects could estimate age–period–cohort models with samples defined on the basis of geographic regions. Regional environmental changes that track with regional differences in the timing of breakpoints would be candidate mediators of g-by-c effects. This approach would be well suited for other large-scale longitudinal databases that are now beginning to genotype subjects (32).

There are some notable limitations to our study. First, given the unique nature of the FHS, it is not yet possible to find an appropriate replication sample for the time period of birth years studied and our genetic variant of interest, both of which would be required to test the specific FTO–variant–birth-cohort interaction results (33–37). The special circumstances of the FHS with localized, longitudinal data over a large birth cohort range, means that it would be hard to perform a traditional replication study (16, 17). However, with the advent of more studies that include genetic data in longitudinal samples, the conceptual approach we are proposing, if not this particular finding, will likely be testable in additional settings soon (32).

A second limitation of our study is that all of the observations in our analyses were of adults; hence, we cannot examine critical periods of growth and development where many environmental factors particular to given birth cohorts may have been influential. Because most evidence suggests that the genetic influences on BMI heterogeneity are first seen in childhood and may relate to food intake levels in that developmental period (1, 38–41), studies of younger subjects may elucidate which particular environmental influences might be interacting with genetic factors. Third, our observation that the 95% confidence bands for those with the AA genotype overlap between the two cohorts in Fig. 2 may reflect limited power to detect an effect and/or the stronger relative impact of birth-cohort-associated-factors on heterozygotes. However, in addition to sample size differences, nonlinearity in the effects of the A allele on BMI is also a possibility (42). Fourth, there remains the possibility of sample selection bias arising from subjects in the older cohort dying before the time when they would have been genotyped, particularly if those who died were disproportionately heavier or of a certain genotype, although we saw no evidence of this in measured attributes.

In sum, we have outlined what we believe to be a useful application of age–period–cohort modeling to improve population genetic research. Our findings are suggestive of a previously unidentified factor to consider when assessing time trends in obesity, as well as the interpretation of genetic association findings more broadly. The phenotypic expression of individual-level genetic variation and our ability to detect it may depend on historical contingencies.

Materials and Methods

The FHS was initiated in 1948 when 5,209 people were enrolled in the original cohort; since then, the study has come to be composed of four separate but related populations. The Framingham Offspring Study began in 1971, consisting of 5,124 individuals who represented the children of the original cohort population and their spouses. Participants in the offspring study were given physical examinations and detailed questionnaires at regular intervals starting in 1972, with a total of eight waves completed through 2008. BMI was calculated from measured height and weight. Notably, the offspring cohort was born over a 40-y period, with participants ranging in age from their teens to their late 50s at the time of study onset in 1971. In addition to providing survey and examination data, a large fraction of participants (73.0%, 3,742 individuals) had their DNA genotyped using the 100KAffymetrix array (43). Genotypes at the rs9939609 allele were extracted using PLINK (44) from data contained in the Framingham SHARe database accessed through the dbgap system (www.framinghamheartstudy.org/researchers/description-data/genetic-data.php).

For simplicity, we elected to focus attention on the rs9939609 polymorphism although a large number of variants have been associated with BMI across large-scale genome-wide studies (and/or been in strong linkage disequilibrium with other FTO variants) (6). For example, in the large GIANT (Genome-wide Investigation of Anthropomophic Traits) consortium (n = 249,794), the less common A allele rs1558902 (in strong linkage disequilibrium with rs9939609 r² = 0.901) on the FTO gene was strongly associated with BMI (P = 4.8 × 10⁻¹²⁰) with a per-allele change associated with an increase in BMI of 0.39 (7).

To minimize the possibility that the g-by-c effects would be capturing differences in age ranges of the participants across cohorts, we focus our analyses on observations between the ages of 27 and 63. That is, by excluding observations collected during examinations when subjects were at younger and older ages, we ensure that individuals who are unique to the earliest and latest cohorts (for who we cannot use as self-controls) respectively are removed from the analyses, thereby mitigating potential bias from model misspecification (26). These restrictions ensured that age is balanced between cohorts and brought the sample size to 19,617 phenotypic observations regarding 3,720 individuals.

Summary statistics for the variables used in the regression analysis reported in the main text and SI Materials and Methods and Tables S1–S5, S7, and S8 are shown in Table S6. Although only 3,724 of 5,124 individuals in the FHS Offspring sample were genotyped and not every subject attended each medical examination, χ² tests of differences in proportions indicate that neither specific genotypes nor birth cohort were associated with missing data from our sample, Χ²(2) = 2.91 and P[X > Χ²(2) = 0.23], reducing concerns about nonresponse.

We also compare the distribution of genetic variants for those born before and after the identified structural breakpoint (of 1942) in the relationship with BMI. Specifically, at the base of Table S5, we present evidence that the differences in genetic variant association with BMI across cohorts were not due to differences in sample characteristics before and after 1942 (26) (P = 0.1550).

In motivating our specification of a modified age–period–cohort model, we initially hypothesized that the significance of the association between the FTO genetic variant and BMI may be significantly stronger for individuals born in later years due to environmental changes in the United States following World War II that influenced food availability, the overall levels of physical activity, and other factors that could affect bodily metabolism, all previously noted in a number of studies as potential modifiers of FTO expression (42, 45, 46). Table S3 presents some descriptive evidence supporting a g-by-c effect. Each entry corresponds to 5-y age-intervals of a person’s life and presents the sample means of BMI across genetic variants and birth cohorts. Thus, participants born in 1940 would have belonged to the 30–34.99 age group in 1974 and the 40–44.99 age group in 1984. Within these g-by-a bins, we conducted simple hypothesis tests to assess whether there were differences in BMI between the pre- and post-World War II cohorts. Table S3 presents evidence that, unconditionally, there are statistically significant differences in BMI between and within birth cohorts on the basis of genotype, particularly for those with the risk allele.

Although tests of differences in means can be used to look at broad trends over time, the participant’s age or commonly shared environmental changes (such as the invention of television or a price shock in food) might also trigger interactions if their impacts are modified by specific genetic variants. The full specification of our modified age–period–cohort models, and methods used to identify the separate effects where the cohort variable is treated as either linear or continuous, is detailed in Supporting Information. Our modified version of Eq. 1 includes a full set of interactions with genetic variants where the TT genotype is the reference category; this full set of interactions is not considered in earlier, distinct age, period, or cohort analyses of the evolution of obesity prevalence, although we have made similar assumptions as those in prior studies (47). To reduce additional concerns that we were restricting the relationship between the explanatory variables (including age and period) and BMI to be linear, we converted all of our data, including age, period of examination, era of birth, and genetic variants, to indicator variables, coding responses as “1” if the characteristic of the individual observation fell in that category, and “0” otherwise. By generating the indicator variables in this way, we are reducing functional form assumptions. We also used YOB as a continuous cohort variable with a single linear term in some specifications.

Finally, all CIs and significance tests reported here accounted for correlations over time due to repeated observations of the same individual or family group, using a standard clustered robust variance estimator (48), and the errors are assumed to be independently distributed across clusters and correlated within clusters. Throughout, we did not impose any distributional assumptions on µ_ift, and we note that whereas the weighted least-squares estimates of the random effects estimator were virtually identical to a maximum likelihood estimator that imposes more structure on the data, both the ordinary least squares and family fixed-effect estimates are identical to maximum likelihood estimates where µ_ift is assumed to be normally distributed.