Abstract
The ability to accurately develop subject-specific, input causation models, for blood glucose concentration (BGC) for large input sets can have a significant impact on tightening control for insulin dependent diabetes. More specifically, for Type 1 diabetics (T1Ds), it can lead to an effective artificial pancreas (i.e., an automatic control system that delivers exogenous insulin) under extreme changes in critical disturbances. These disturbances include food consumption, activity variations, and physiological stress changes. Thus, this paper presents a free-living, outpatient, multiple-input, modeling method for BGC with strong causation attributes that is stable and guards against overfitting to provide an effective modeling approach for feedforward control (FFC). This approach is a Wiener block-oriented methodology, which has unique attributes for meeting critical requirements for effective, long-term, FFC.
Introduction
Diabetes is characterized by an inability to synthesize, secrete, and/or, in some cases, respond to insulin. Without this vital hormone, cells and tissues cannot absorb glucose, and the patients’ cells can starve to death, despite high levels of glucose in the bloodstream. Among the two major types of diabetes, Type 1 diabetes is characterized by the inability to produce insulin. Type 1 diabetics often experience extreme variations in blood glucose concentration (BGC), which can have adverse long- and short-term effects such as severe hypoglycemia, hyperglycemia, and organ destruction. Studies have established that there is a need to maintain glucose levels within a normal range (e.g., 80–150 mg/dL) to avoid complications caused by diabetes.1−4 Therefore, Type 1 diabetics require daily exogenous insulin infusion for survival. Current injection treatment usually involves an insulin pump with manually controlled bolus infusion and preprogrammed basal infusion. However, oftentimes the patient is still not able to mimic a normally occurring insulin profile using insulin pumps or/and insulin injections, which leads to inadequate regulation of blood glucose concentration (BGC), possibly causing hyperglycemia, hypoglycemia, or various complications.5,6
Consequently, what is needed is an automatic insulin delivery system (i.e., artificial pancreas) with the ability to determine continuously the amount of insulin required to provide optimum closed-loop glucose control (i.e., to minimize the variability around a desired glucose level) and to eliminate the individual from the insulin dosage decision making in this control loop.
The development of a closed-loop artificial pancreas has the potential to simultaneously reduce the risks of hypoglycemia and hyperglycemia while also enabling individuals with Type 1 diabetes mellitus to maintain a normal lifestyle.7 To create a closed-loop artificial pancreas, three crucial components are needed: a continuous glucose sensor, an insulin pump, and a robust controller.7−11
For effective long-term control of BGC, the control system must be capable of tight control under critical disturbances with extreme changes such as food, activity, and stress. While feedback control (FBC) and model predictive control (MPC) have shown promise under mild changes (e.g., overnight) in disturbances,12−15 these approaches have not shown strong promise for long-term tight control under extreme changes in disturbances. Due to recent technological advancements of body monitoring devices,30,31 activity-, stress-, circadian rhythm-related disturbances16−19 can be monitored in real time, which makes feedforward control (FFC) a possibility. Given that FFC directly models the relationship between disturbances and the control variable, BGC in this context, an accurate modeling approach that can produce stable causation relationships between critical disturbances and BGC has the potential to make a significant advancement in the development of an effective long-term artificial pancreas.
Hence, the focus of this article is strictly model development for effective FFC. The maximization of cause-effect relationship between critical disturbances and BGC is the goal of this model. Mathematically, a viable and general FFC law based on the model ŷt = fx(xt; θ̂) is given below by eq 1:
| 1 |
where B is constant systematic model biased such that B = fx(0; θ̂) – Yset, Yset is the target value of the controlled variable (i.e., the set point), ŷt is the modeled estimate of BCG at current time t, fx is the fitted function; xt is a vector of measured input variables at t, θ̂ is the vector of estimated parameters, and xI,t is the insulin infusion rate at t that is required to satisfy eq 1 (i.e., the inlet flow rate needed so that eq 1 is satisfied at t). Equation 1 gives the estimated insulin infusion rate to compensate for the all modeled input changes. Thus, the goal and scope of this work is to obtain a model for fx that is able to significantly tighten BGC in an automatic FFC scheme. Note that under eq 1, large systematic modeling bias does not impede effective FF control because B cancels out, as shown. Physically, this means that eq 1 estimates the amount of insulin infusion at each time instant (i.e., xI,t) needed to dynamically compensate for deviations of modeled inputs from their initial values where the model was at the target BGC level. Modeling errors in estimating xI,t will exist and will be compensated for under FB control. Note that any modeling approach that contains outputs, such as k-steps-ahead prediction models, does not meet the requirement of fx in eq 1 and is, therefore, not in the scope of this work. Moreover, the only types of models that have relevance to our scope are those that depend on inputs only.
There are a number of studies in the literature involving the development of models in BGC for real type 1 diabetic subjects.20−26 There are models that used measured BGC only,20−23 ones that use BGC and food consumption, namely carbohydrates only,24 and ones that use BGC, food, and activities variables.25,26 However, we have not found any approach that gives modeling results for only inputs and thus, the results reported in these studies are not in this scope of this work, as they do not meet our criteria under eq 1.
Therefore, the goal of this work is the development of a FF modeling approach that has the characteristics mentioned above under eq 1. The outline for this article is as follows. Specific mathematical details of the proposed approach are given in the next section. Next, the details of the study in this paper to evaluate the proposed method are given. Following this section are the results of this study on 15 2 week outpatient data collection cases, followed by concluding remarks including future work.
Modeling Methodology
The proposed modeling approach is a critical advancement over the modeling method proposed by Rollins et al.,27 which is an extension of the Wiener method developed by Rollins and Bhandari.28 The Rollins et al. technique was developed in the context of noninsulin dependent Type 2 diabetics. For modeling Type 1 diabetics, it becomes necessary to refine this approach due to the incorporation of insulin infusion as an input. This refinement or extension involves the development of a new parameter estimation procedure that guards better against overfitting and is better able to handle a large input set. Before introducing this new procedure, we present the modeling equations under a general Wiener framework that is the foundation to this approach.
Mathematical Models
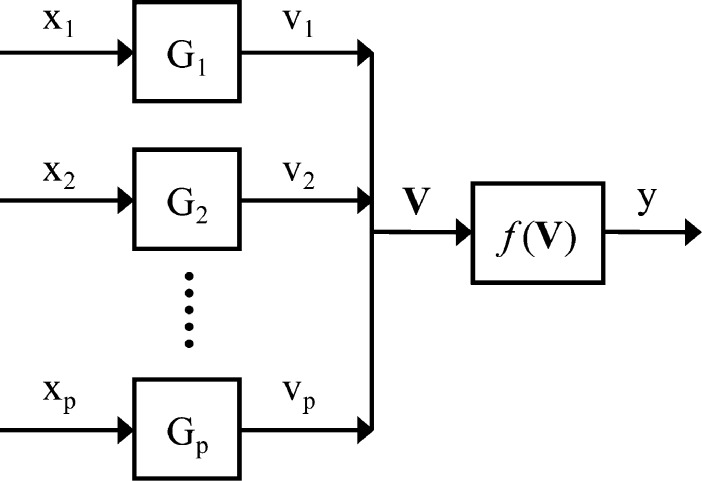
Wiener modeling follows a block-oriented model structure formed by a series and/or parallel arrangement of unrestricted static functions and linear dynamic blocks. A block diagram with p inputs and one output is given in Figure 1.
Figure 1.
Block diagram for a general Wiener network with p inputs and one output. Each input, xi, is passed through their own linear dynamic block, Gi(s), after which these unobservable intermediate outputs are collected and passed through a single unrestricted static gain function, f(V), to produce the output, y.
The inputs, xi for i = 1, ..., p, of the Wiener network are the measured noninvasive variables or disturbances (i.e., food, activity, and stress) and the output, y, is BGC. Each input has its own linear dynamic block, Gi, and each dynamic block has an intermediate unobservable, output vi, which represents the independent dynamic response of its corresponding input. All the intermediate vi’s are collected and passed through a nonlinear static gain block, f(V), to produce the final output, y. The linear dynamic blocks are essentially linear ordinary differential equations, a second-order-plus-lead with dead time (SOPLDT) form, as shown in eq 2.
| 2 |
where i = 1, ..., p, p is the total number of inputs, τi is the time constant, ζi is the
damping coefficient, τai is the
lead parameter, and θi is the dead
time. Using a backward difference approximation
(e.g., 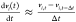 ), applied to a sampling
interval of Δt, Rollins et al.27 obtained
an approximate discrete-time form of eq 2.
), applied to a sampling
interval of Δt, Rollins et al.27 obtained
an approximate discrete-time form of eq 2.
| 3 |
where, to satisfy the unity gain constraint, ω2,i = 1 – δ1,i – δ2,i – ω1,i and
| 4 |
| 5 |
| 6 |
As described in Rollins et al.,27 this discrete form provides several strengths. First, the function form does not change as values of the parameters change, unlike the continuous form that can change as ζi changes. Second, one does not have to be concerned about applying a fading memory algorithm that is needed for the continuous form to truncate terms after a certain period in the past. Third, eqs 4–6 are highly nonlinear in the dynamic parameters (τai, τi, and ζi) and these intelligent complex structures aid in strengthening input-causation relationships by restricting parameters estimates to regions that are phenomenologically sound. A detail discussion is given in Rollins et al.27 using the information matrix to explain the strengths of this nonlinear model identification approach over a linear one where the coefficients in eq 3 would be estimated directly. Lastly, the physical constraints, namely unity gain, ζi > 0 and τi > 0, also provide intelligence that aids in strengthening modeled relationships in input-causation.
The engineering community tends to define a linear model based on the time dependent variables in the model. For example, eq 2 is linear in v(t) and the transfer functions represented by this equation are said to be “linear” (but in the variables). However, this paper defines a nonlinear model based on the statistical definition, which in Bates and Watts,32 is defined as “at least one of the derivatives of the expectation function with respect to the parameters depends on at least one of the parameters.” Thus, the statistical definition is based on the form of the parameters in the model and not the variables. If the proposed approach estimated the parameters in eq 3 directly, the model would be linear and would fall in the scope of the study by Garnier et al.33 for linear multiple-input, single output (MISO) structures. However, because the parameters estimated in this work are the ones given in eqs 4–6 (i.e., the dynamic parameters), the proposed model is nonlinear, and not in the scope of the models in Garnier et al.,33 which is deliberate and is a unique strength of this approach.
After eq 3 is obtained for each i, the modeled glucose value is determined by substituting these results into the static function, f(V), such as a second-order regression form shown below:
| 7 |
where ai, bi, and ci,j, denote the linear, quadratic and interaction parameters for i = 1, ..., p-1, and j = 2, ..., p. The measurement model is given as
| 8 |
where yt is the modeled glucose concentration at time instant t and εt is the error term under the assumptions of independence, normality, and constant variance (i.e., εt ∼ N(0, σ2), ∀ t). Under these assumptions, Rollins et al.27 proposed the following estimator for BGC under this measurement model:
| 9 |
Thus, eq 9, along with eqs 3–6 give the functional form with its supporting equations for the proposed FF controller under this work. Later, in the Results Section, this control law is given as a differential equation.
Modeling Procedure
The proposed modeling procedure is a novel approach to maximize input-causation, guard against overfitting, and maximize long-term stability. As discussed above, we attempt to maximize input-causation through the use of highly nonlinear structures and physical constraints. Cross-validation, in a novel fitting strategy, is used to guard against overfitting. We do not use a k-fold cross validation procedure with the testing data randomly split into k equal groups as this is not a realistic evaluation since in practice the model can only be applied to data collected after the model is built. Thus, our cross-validation procedure uses only testing data obtained after any data (i.e., Training and Validation data) used to influence model building. We seek to enhance long-term stability by obtaining consistent performance under significant changes in unmeasured disturbances. Our cross validation procedure aids in this goal by seeking to achieve similar fitting results on all data sets. In addition, we evaluate the models using testing data several days after the Training data, so that unmeasured disturbances are more likely to be correlated differently with measured inputs.
The proposed modeling methodology is an extension and enhancement of the procedure proposed by Rollins et al.27 due to the larger number of inputs (13 variables) including the addition of two exogenous insulin inputs and the additional complexities they bring. For simplicity and to provide the best fit for mild extrapolation, this work used a reduced form of eq 9 that is given by eq 10. As shown, eq 10 eliminates all second-order and interaction terms of eq 9 and consists only of the first-order, a, terms.
| 10 |
where v̂i,t is the estimate of vi,t obtained by substituting the estimated dynamic parameters (i.e., τ̂i, τ̂ai, ζ̂i and θ̂i) into eqs 3–6 for all i. Note that the linear form of eq 10 makes this particular network structure equivalent to a general class of transfer functions where the gains for each one is contained in eq 10 by ai, i = 1, ..., 13. Also, note that a model is completely specified when the dynamic parameters in eqs 4–6 have estimates for obtaining eq 3; then for each input these equations are incorporated into eq 10 along with estimates for the a’s.
As stated in Rollins et al.,27 the modeling
objective is simply to maximize the true but unknown correlation coefficient
between measured and fitted BGC. This quantity is represented by 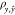 and estimated
by rfit. Thus, under this criterion, as
a minimum, a model is considered
useful, if, and only if
and estimated
by rfit. Thus, under this criterion, as
a minimum, a model is considered
useful, if, and only if
| 11 |
Because the degree of usefulness
increases
with 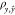 , the
goal is to obtain the largest (as
close to the upper limit of 1) value as possible. Due to the highly
complex mapping of the parameters into the response space of rfit, the following criterion is used in obtaining
the parameter estimates:
, the
goal is to obtain the largest (as
close to the upper limit of 1) value as possible. Due to the highly
complex mapping of the parameters into the response space of rfit, the following criterion is used in obtaining
the parameter estimates:
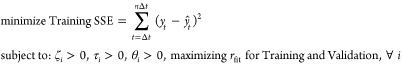 |
12 |
The objective criterion, eq 12, is written to address the effect of unmeasured disturbances, which is an artifact of real modeling as opposed to hypothetical simulated data modeling without unmeasured disturbances. The Validation data set helps to guard against fitting the Training data to unmeasured input variables that are correlated with measured input variables during training but differently during validation. This is done by seeking to obtain similar fitted correlation for Training and Validation sets, which is a goal of the proposed modeling approach. The systematic bias that appears in the Validation set is largely due to level changes in unmeasured inputs. However, as eq 1 shows, the proposed approached is not affected by this type of systematic bias and thus, can be effective in the presence of level changes for unmeasured disturbances. This is a critical attribute for long-term effective FF control.
For FF model evaluation, of the statistics commonly used for evaluating model fit, rfit is premier, as supported by the discussion earlier in regards to eq 1. As discussed, a FF model needs to be accurate for the change in inputs and rfit is the best statistical measure of this ability. Statistics that are affected by model bias are not relevant as measures of performance in this context as discussed earlier.
The novelty of the proposed modeling procedure lies
in a two level
decomposition of the parameter estimation problem. The first level
decomposes the static and dynamic problem. That is, the dynamic parameters
(i.e., the parameters in eq 2) are estimated
first and separately from the static parameters (i.e., the âi’s in eq 10). The second level decomposes dynamic parameter
estimation into p = 13 separate (i.e., sub-) problems,
one for each input. For this approach to be possible, a modeling structure
must allow these decompositions. Under a SOPLDT dynamic model structure,
the Wiener network is the only one that does as opposed to other common
networks like the autoregressive moving-average exogenous input (ARMAX)
model.27,29 For this approach to be effective, with
only one input, xi, in
each dynamic estimation problem, rfit must
depend only on the dynamic parameters to obtain the best set. That
is, the value of rfit must be solely controlled
by the values of the dynamic parameters irrespective of the values
of static parameters. Fortunately, this is the case because with only
one input, xi,  , the correlation coefficient
for yt and v̂i,t (see the Appendix for the mathematical proof). Thus, for
the simple linear regression model (SLRM) (i.e., eq 10 with one input), since v̂i,t depends only on the dynamic parameters, rfit depends only on the dynamic parameters.
Although a formal proof is given in the Appendix, one can prove this in practice quite easily by changing the static
parameters for a fixed set of dynamic parameters and verifying that
the value of rfit does not change by observation.
, the correlation coefficient
for yt and v̂i,t (see the Appendix for the mathematical proof). Thus, for
the simple linear regression model (SLRM) (i.e., eq 10 with one input), since v̂i,t depends only on the dynamic parameters, rfit depends only on the dynamic parameters.
Although a formal proof is given in the Appendix, one can prove this in practice quite easily by changing the static
parameters for a fixed set of dynamic parameters and verifying that
the value of rfit does not change by observation.
In the proposed procedure, models are developed from Training and Validation data sets. The Training set is used to determine the value of SSE and in adjusting the values of the parameters directly to minimize this value. The Validation set calculates rfit for each adjustment on the values of the parameters, and is used to stop the minimization process for SSE if rfit for the Training set increases significantly and causes a significant drop in rfit for the Validation set. This is the practical way that we feel that cross validation is done in practice as mentioned above. In addition, the proposed procedure includes a more stringent condition, that is, rfit for both sets to be close to one another. Thus, for each input, the goal is not just for high values of rfit for Training and Validation but also for their values to be close. Moreover, this procedure will lower the value of rfit in the Training data to bring its value close to the Validation data and vice versa. We impose this condition because we have found from modeling many cases that when this condition is met that the final fit of the static model at the fixed set of dynamic values produces rfit values in Training, Validation, and Testing sets that are very close together to minimize overfitting and maximum long-term stability as discussed above.
After finding the dynamic parameters, the next step in the procedure is to obtain the static parameters under eq 10. With the dynamic parameters fixed, this becomes a linear regression problem that has a global minimum as the solution. However, because we have a validation set, we observe its rfit performance under an iterative approach to the global minimum using an iterative optimization process. We have found that most of the time, the global minimum is the optimal solution but sometimes we find a slightly better solution based on the validation set that is not too far away from the global minimum.
The final process in the proposed procedure is the elimination of inputs that adversely affect the final model when fitting the combined set of inputs under the static model. Each input is removed from the model with all the other inputs kept in the model. If rfit increases when an input is removed, this input is taken out of the final model. After completing this process for all the inputs, the inputs that passed this test are used to obtain the fit of the final model under the static model. It should be noted that in most cases all the activity inputs were retained in the model and if any were eliminated this number was only a few. Rollins et al. obtained this set from an extensive study in type 2 modeling involving all 22 of the armband inputs. Given that most of the inputs were retained in this work for each subject, this set appears to be quite acceptable. Also, note that the final set of inputs for a given model is not of concern in this work since we have no use for the models beyond model building to evaluate this approach.
Study
Subjects in this study followed a 2 week free-living outpatient protocol in which no constraints or conditions were placed on their daily diet or lifestyle. The subjects in this study were all healthy young adults from the ages of 18 to 25 with type 1 diabetes and on insulin pump therapy with a body mass index (BMI) from 20.8 to 27.6. To obtain a sufficiently fast sampling rate necessary for discrete-time (DT) dynamic glucose modeling, the iPro continuous glucose monitor (CGM) (Medtronic MiniMed, Inc., Northridge, California) was used to provide glucose measurements. Use of the CGM requires the insertion of a short flexible sensor (by needle) into the subcutaneous tissue of the abdominal/supra-iliac area (i.e., between the umbilicus and the hip). The sensor samples the surrounding interstitial glucose, which is then used to infer an individual’s blood glucose levels with a reporting frequency of every 5 min. Following FDA recommendations, the sensors were replaced every 3 days. A period of 1 to 2 h of missing measurements resulted during initialization of the new sensor after each insertion. To maximize sensor reading accuracy, the sensor must be calibrated with at least four finger-stick measurements daily from the subject’s personal blood glucose lancet meter.
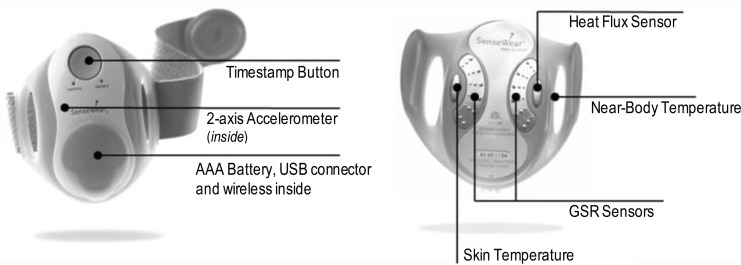
Activity information was collected using the SenseWear Pro3 body monitoring system (BodyMedia Inc., Pittsburgh, Pennsylvania) shown in Figure 2, which is wore on the triceps of the subject’s arm. The SenseWear armband utilizes pattern detection algorithms30,31 that employ physiologic signals from a unique combination of sensors to generate values for 20 activity variables. The armband collects data using a two-axis accelerometer and four sensors that are used to determine heat flux, skin temperature, near body temperature, and galvanic skin response (GSR). The two-axis accelerometer provides information about body position and tracks upper arm movement. The heat flux sensor calculates the amount of heat being dissipated from the body by measuring the amount of heat lost along a thermally conductive path between the skin and a vent on the side of the armband. Skin temperature and near-body temperature are measured by sensitive thermistors and GSR is measured via the conductivity of the subject’s skin as it varies due to physical and emotional stimuli.31 The SenseWear armband samples at a rate of once per minute; however, measurements at 5 min intervals were used to match the sampling rate of the CGM used in this study. The armband was typically only removed once a day while the subject was showering. Finally, to represent circadian rhythm (i.e., the body’s internal clock), we used a variable that we called the time of day (TOD), which is simply 24 h clock time.
Figure 2.
BodyMedia, Inc. SenseWear Pro3 body monitoring system.
Food information was collected using food logs. For Subjects 1–6, and 11, detailed food logs were kept on the actual food consumed and, for Subjects 7–10, meals were logged based on the size of the meal with small =1, medium =2, and large =3. As part of the detailed protocol, subjects recorded the approximate serving size and the time they started eating, for all of the food they consumed, into a PDA, which used Weightmania Pro software (Edward A. Greenwood, Inc., Cambridge, Massachusetts) to determine the carbohydrate, fat, and protein content of their meals. In addition, the subjects’ insulin pumps were downloaded on biweekly basis to retrieve their daily bolus and basal insulin infusion rate data. The 13 variable input set for this study is given in Table 1.
Table 1. Input Variables.
| food | activity | circadian rhythm | insulin |
|---|---|---|---|
| 1. carbohydrates | 4. transverse accel - peaks | 11. time of day (TOD) | 12. bolus |
| 2. fats | 5. heat flux - average | 13. basal | |
| 3. proteins | 6. longitudinal accel - average | ||
| 7. near body temperature | |||
| 8. transverse accel - MAD | |||
| 9. GSR - average | |||
| 10. energy expenditure |
Based on
results in Rollins et al.27 for a Type
2 subject and in Beverlin et al.34 for
20 noninsulin dependent Type 2 diabetics, a goal was set for rfit to be greater than 0.40 with a value greater
than 0.60 considered excellent. Note that this goal of rfit may not seem very high. However, one must recognize
that this is an application in FF model development for inputs only
and not a model prediction application requiring high model accuracy.
Our objective function, eq 11, is defined in
terms of “usefulness”, which essentially means any model
that has the potential to significantly tighten BGC for a given subject.
For a given subject, it is not likely necessary for  to be
too high to achieve usefulness when
input model causation is strong. However, ultimately, the only way
to truly evaluate the effectiveness of a given model is its use in
FFC. Models with strong input-causation fitting can actually do better
than models with weaker input-causation and higher rfit results.
to be
too high to achieve usefulness when
input model causation is strong. However, ultimately, the only way
to truly evaluate the effectiveness of a given model is its use in
FFC. Models with strong input-causation fitting can actually do better
than models with weaker input-causation and higher rfit results.
The first half of this study involved splitting the data into 1 week of Training data and 1 week of Validation data. The second half of the study split the data into 1 week of training data, 4 days of Validation data, and 3 days of test data.
Although correlation is the premier performance statistic as mentioned above, three other statistics were determined that are affected by model bias. Because bias can be neutralized as shown in eq 1, these statistics are irrelevant as FF model performance measures, but are included to give an indication of how well rfit holds its level in Validation and Testing data under conditions when model bias can be significant. These additional statistics are the average deviation (AD), the average absolute deviation (AAD) and mean relative absolute deviation (MRAD). The AD is simply the average of the residuals and is an estimate of model bias, B, as shown below:
| 13 |
where n is the number of observed blood glucose measurements in the statistic being calculated. A check that the aforementioned convergence criterion is met is the AD value equaling 0.0 mg/dL. A model with a significantly large absolute value of AD or model bias will tend to raise AAD values. The equation for AAD is similar to AD except AAD takes the absolute value of the residuals before finding the average.
| 14 |
The spread in BCG can vary widely among T1Ds, and AAD will tend to be large when the BGC spread is large. Therefore, MRAD, a relative ADD value, is defined as follows
| 15 |
Results
Tables 2 and 3 contain results for 15 subject-specific models and Tables 4 and 5 for 11 subject-specific models. The data for Subjects 1–11 were collected by an experienced graduate student that left the project after completing the first phase of the study. The other ones (Subjects 12–15) were collected by a new, less experienced, graduate student in the second phase of the study. This lack of experience is revealed in the tables by the number of days of modeling data. Although data collection for each subject was about 2 weeks, the amount of useful modeling data was much less for Subjects 12–15 because of missing BGC data that the CGMS did not give. Thus, for a given subject, the data in Tables 2 and 3 had a split of 1/2 for Training and 1/2 for Validation and in Tables 4 and 5 the split was 1/2 Training, 2/7th Validation, and 3/14th Testing.
Table 2. Model Results for 1 Week (or 7/14th) of Training and 1 week (or 7/14th) of Validation with All Inputs Includeda.
| training |
validation |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| subject | days | AD | AAD | MRAD | rfitb | AD | AAD | MRAD | rfitb |
| 1 | 14.0 | 0.00 | 44.8 | 0.44 | 0.61 | 20.4 | 50.5 | 0.33 | 0.68 |
| 2 | 13.0 | 0.00 | 72.1 | 0.62 | 0.49 | –18.0 | 68.5 | 0.72 | 0.51 |
| 3 | 13.9 | 0.00 | 48.0 | 0.37 | 0.68 | –0.1 | 49.3 | 0.33 | 0.66 |
| 4 | 10.7 | 0.00 | 31.6 | 0.38 | 0.53 | 33.4 | 48.4 | 0.39 | 0.55 |
| 5 | 14.0 | 0.00 | 62.6 | 0.47 | 0.56 | 15.1 | 73.6 | 0.53 | 0.55 |
| 6 | 13.9 | 0.00 | 50.1 | 0.31 | 0.67 | 24.9 | 45.6 | 0.23 | 0.68 |
| 7 | 14.0 | 0.00 | 46.7 | 0.43 | 0.69 | 37.1 | 56.5 | 0.36 | 0.64 |
| 8 | 14.0 | 0.00 | 32.7 | 0.36 | 0.45 | 10.8 | 43.2 | 0.42 | 0.43 |
| 9 | 13.9 | 0.00 | 51.8 | 0.37 | 0.63 | –35.2 | 64.2 | 0.62 | 0.56 |
| 10 | 16.8 | 0.00 | 47.4 | 0.30 | 0.57 | 14.0 | 46.8 | 0.30 | 0.73 |
| 11 | 15.1 | 0.00 | 33.7 | 0.23 | 0.72 | –24.3 | 47.2 | 0.43 | 0.79 |
| 12 | 8.9 | 0.00 | 56.3 | 0.25 | 0.63 | –33.0 | 83.0 | 0.57 | 0.72 |
| 13 | 8.2 | 0.30 | 55.4 | 0.47 | 0.54 | 52.5 | 76.9 | 0.41 | 0.58 |
| 14 | 7.9 | –0.10 | 48.2 | 0.39 | 0.56 | –30.1 | 48.6 | 0.59 | 0.61 |
| 15 | 13.6 | 0.00 | 23.1 | 0.21 | 0.56 | 20.7 | 45.2 | 0.35 | 0.56 |
| Mean | 12.8 | 0.0 | 47.4 | 0.37 | 0.60 | 7.1 | 56.5 | 0.44 | 0.62 |
AE and AAE values are in mg/dL.
The mean Validation rfit for the detailed food logged cases, 1–6, and 11–15, is 0.63. The mean Validation rfit for the nondetailed food logged cases, 7–10, is 0.59.
Table 3. Model Results for 1 Week (or 7/14th) of Training and 1 Week (or 7/14th) of Validation without Armband Inputs Includeda.
| training |
validation |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| subject | days | AD | AAD | MRAD | rfitb | AD | AAD | MRAD | rfitb |
| 1 | 14.0 | 0.0 | 49.2 | 0.47 | 0.52 | 26.9 | 56.8 | 0.36 | 0.57 |
| 2 | 13.0 | 0.0 | 65.4 | 0.55 | 0.58 | –13.1 | 64.4 | 0.64 | 0.56 |
| 3 | 13.9 | 0.0 | 61.0 | 0.48 | 0.46 | 18.2 | 56.6 | 0.35 | 0.42 |
| 4 | 10.7 | 0.0 | 32.2 | 0.38 | 0.48 | 32.6 | 32.6 | 0.38 | 0.49 |
| 5 | 14.0 | 0.0 | 66.1 | 0.51 | 0.50 | 11.3 | 81.7 | 0.62 | 0.44 |
| 6 | 13.9 | 0.0 | 62.8 | 0.40 | 0.39 | 13.9 | 50.8 | 0.26 | 0.35 |
| 7 | 14.0 | 0.0 | 58.3 | 0.55 | 0.52 | 21.3 | 51.5 | 0.34 | 0.57 |
| 8 | 14.0 | 0.0 | 35.8 | 0.41 | 0.25 | 15.1 | 46.6 | 0.46 | 0.34 |
| 9 | 13.9 | 0.0 | 59.3 | 0.43 | 0.52 | –21.8 | 64.4 | 0.63 | 0.43 |
| 10 | 16.8 | 0.0 | 48.8 | 0.31 | 0.55 | 13.3 | 49.8 | 0.32 | 0.67 |
| 11 | 15.1 | 0.0 | 33.5 | 0.23 | 0.70 | –23.5 | 48.3 | 0.43 | 0.77 |
| 12 | 8.9 | 0.2 | 58.4 | 0.26 | 0.61 | –37.6 | 87.7 | 0.61 | 0.61 |
| 13 | 8.2 | 0.0 | 61.5 | 0.53 | 0.40 | 54.9 | 82.0 | 0.45 | 0.45 |
| 14 | 7.9 | –0.1 | 48.2 | 0.39 | 0.56 | –30.1 | 48.6 | 0.59 | 0.61 |
| 15 | 13.6 | 0.0 | 25.2 | 0.24 | 0.50 | 26.4 | 48.5 | 0.37 | 0.50 |
| Mean | 12.8 | 0.0 | 51.1 | 0.41 | 0.50 | 7.2 | 58.0 | 0.45 | 0.52 |
AE and AAE values are in mg/dL.
The mean Validation rfit for the detailed food logged cases, 1–6, and 11–15, is 0.52. The mean Validation rfit for the nondetailed food logged cases, 7–10, is 0.50.
Table 4. Model Results for 1 Week (or 7/14th) of Training, 4 Days (or 4/14th) of Validation, and 3 Days (or 3/14th) of Testing with All Inputs Includeda.
| 7 days training |
4 days validation |
3 days testing |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| subject | days | AD | AAD | MRAD | rfitb | AD | AAD | MRAD | rfitb | AD | AAD | MRAD | rfitb |
| 1 | 14.0 | 0.00 | 45.0 | 0.45 | 0.60 | 20.1 | 52.9 | 0.36 | 0.66 | 16.7 | 46.9 | 0.30 | 0.66 |
| 2 | 13.0 | 0.00 | 67.2 | 0.55 | 0.57 | –33.3 | 62.6 | 0.74 | 0.67 | 2.9 | 64.8 | 0.47 | 0.54 |
| 3 | 13.9 | 0.00 | 50.9 | 0.39 | 0.64 | –12.9 | 60.7 | 0.37 | 0.53 | –21.3 | 53.0 | 0.37 | 0.68 |
| 4 | 10.7 | 0.00 | 31.9 | 0.38 | 0.53 | 31.1 | 52.5 | 0.45 | 0.52 | 35.4 | 40.5 | 0.29 | 0.57 |
| 5 | 14.0 | 0.00 | 63.3 | 0.48 | 0.55 | 31.4 | 87.3 | 0.63 | 0.54 | –15.0 | 55.9 | 0.44 | 0.67 |
| 6 | 13.9 | 0.00 | 52.8 | 0.33 | 0.65 | 37.9 | 59.8 | 0.29 | 0.60 | –0.1 | 34.0 | 0.20 | 0.60 |
| 7 | 14.0 | 0.00 | 56.4 | 0.53 | 0.56 | 25.6 | 52.6 | 0.32 | 0.58 | –1.7 | 58.7 | 0.48 | 0.56 |
| 8 | 14.0 | 0.00 | 36.5 | 0.41 | 0.21 | 26.7 | 46.1 | 0.38 | 0.28 | –0.1 | 48.7 | 0.59 | 0.30 |
| 9 | 13.9 | 0.00 | 53.2 | 0.38 | 0.61 | –19.4 | 51.8 | 0.41 | 0.65 | –54.9 | 75.8 | 0.90 | 0.55 |
| 10 | 16.8 | 0.00 | 44.9 | 0.29 | 0.62 | 15.0 | 43.6 | 0.25 | 0.68 | 0.8 | 50.9 | 0.37 | 0.70 |
| 11 | 15.1 | 0.00 | 30.4 | 0.21 | 0.79 | –22.3 | 41.8 | 0.36 | 0.81 | –25.3 | 60.8 | 0.56 | 0.63 |
| Mean | 13.9 | 0.0 | 48.4 | 0.40 | 0.58 | 9.1 | 55.6 | 0.41 | 0.59 | –5.7 | 53.6 | 0.45 | 0.59 |
AD and AAD values are in mg/dL.
The mean Testing rfit for the detailed food logged cases, 1–6, and 11, is 0.62. The mean Testing rfit for the nondetailed food logged cases, 7–10, is 0.53.
Table 5. Model Results for 1 Week (or 7/14th) of Training, 4 Days (or 4/14th) of Validation, and 3 Days (or 3/14th) of Testing without Armband Inputsa.
| 7 days training |
4 days validation |
3 days testing |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| subject | days | AD | AAD | MRAD | rfitb | AD | AAD | MRAD | rfitb | AD | AAD | MRAD | rfitb |
| 1 | 14.0 | 0.00 | 49.2 | 0.47 | 0.52 | 22.1 | 56.5 | 0.39 | 0.56 | 31.5 | 57.1 | 0.33 | 0.58 |
| 2 | 13.0 | 0.00 | 68.0 | 0.58 | 0.56 | –28.2 | 65.1 | 0.79 | 0.55 | 6.5 | 71.7 | 0.52 | 0.48 |
| 3 | 13.9 | 0.00 | 60.6 | 0.48 | 0.47 | 13.3 | 51.7 | 0.30 | 0.47 | 25.1 | 64.2 | 0.42 | 0.36 |
| 4 | 10.7 | 0.00 | 32.1 | 0.38 | 0.49 | 31.7 | 52.4 | 0.44 | 0.49 | 34.2 | 40.6 | 0.29 | 0.52 |
| 5 | 14.0 | 0.00 | 66.0 | 0.51 | 0.49 | 27.3 | 92.5 | 0.71 | 0.48 | –12.4 | 65.3 | 0.51 | 0.45 |
| 6 | 13.9 | 0.00 | 63.5 | 0.40 | 0.38 | 23.7 | 62.8 | 0.32 | 0.27 | –3.4 | 37.1 | 0.21 | 0.52 |
| 7 | 14.0 | 0.00 | 60.7 | 0.58 | 0.47 | 22.6 | 47.8 | 0.29 | 0.60 | –2.9 | 55.1 | 0.44 | 0.54 |
| 8 | 14.0 | 0.00 | 33.6 | 0.38 | 0.39 | 23.8 | 42.9 | 0.36 | 0.47 | –4.6 | 45.5 | 0.54 | 0.48 |
| 9 | 13.9 | 0.00 | 63.8 | 0.48 | 0.44 | –6.0 | 62.6 | 0.44 | 0.47 | –44.1 | 69.0 | 0.85 | 0.49 |
| 10 | 16.8 | 0.00 | 48.3 | 0.31 | 0.56 | 15.2 | 42.7 | 0.25 | 0.70 | 11.8 | 54.1 | 0.37 | 0.67 |
| 11 | 15.1 | 0.00 | 31.5 | 0.22 | 0.77 | –20.6 | 38.7 | 0.33 | 0.83 | –14.5 | 59.0 | 0.51 | 0.58 |
| Mean | 13.9 | 0.0 | 52.5 | 0.44 | 0.50 | 11.4 | 56.0 | 0.42 | 0.54 | 2.5 | 56.2 | 0.45 | 0.51 |
AD and AAD values are in mg/dL.
The mean Testing rfit for the detailed food logged cases, 1–6, and 11, is 0.50. The mean Testing rfit for the nondetailed food logged cases, 7–10, is 0.55.
As mentioned, Tables 2 and 3 equally split the data into Training and Validation sets. In Table 2, all the inputs are included in the models and in Table 3, the armband inputs are not included. Thus, a comparison of these tables indicates the modeling improvement from use of the armband inputs. The average rfit with and without the armband for Validation are 0.62 and 0.52, respectively, indicating a very significant improvement from use of the armband. The Training and Validation rfit values are in general quite close together and thus, supporting the effectiveness of the proposed modeling approach to obtain similar values to guard against overfitting. Note that the mean Training and Validation values are 0.60 and 0.62, respectively, and 0.50 and 0.52, respectively, for Tables 2 and 3, respectively. Although the three biased indicating statistics are quite larger for the Validation results in several cases, rfit is quite consistent given that it is an estimate of fitted correlation with significant standard error. Thus, the approach appears to be maintaining its level of fit quite well from Training to Validation results. The fit of model for Subject 11 is given in Figure 3. As shown, the input-only model tracks the observed BGC quite well in terms of correlation. The systematic bias of the Validation fit is quite evident as well as the apparent shift in the average BGC level from Training to Validation data.
Figure 3.
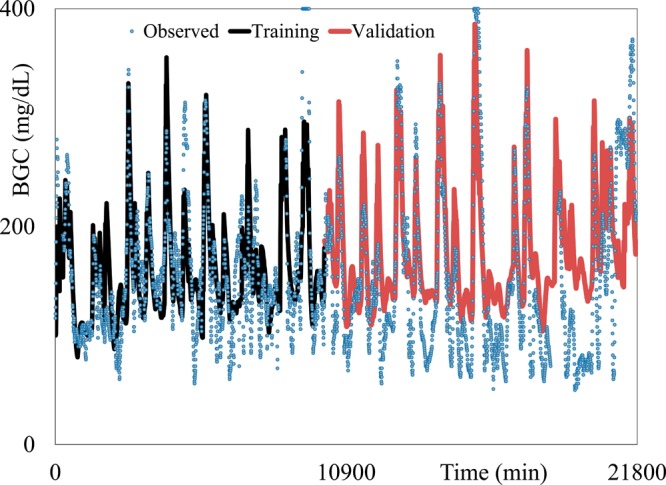
Fitted and observed BGC versus time for Subject 11 in Table 2.
Tables 4 and 5 include test data. In Table 4, all the inputs are included in the models and in Table 5, the armband inputs are not included. The average rfit with and without the armband for Testing are 0.59 and 0.51, respectively. These results are very similar to the previous ones in Tables 2 and 3 and support a significant improvement from use of the armband. The Training, Validation, and Testing rfit values are, in general, quite close together and thus, supporting the effectiveness of the proposed modeling approach to obtain similar values to guard against overfitting. Note that the mean Training, Validation, and Testing values are 0.58, 0.59, and 0.59, respectively, and 0.50, 0.54, and 0.51, respectively, for Tables 4 and 5, respectively. The AAD and MRAD values in these tables are similar to the ones in Tables 2 and 3 and the analysis of model bias is the same as before. That is, although they are larger for the Validation and Testing results in several cases, rfit is quite consistent, Thus, the approach appears to be maintaining its level of rfit quite well from Training to Validation to Testing results.
In comparing rfit results of detailed food log cases (Subjects 1–6, 11–15) versus meal size (nondetailed) food log cases (Subjects 7–10), it is not conclusive how much the detailed food logs improve the fit, if at all. Averaged rfit Validation results in Tables 2 and 3 for detailed and nondetailed cases are 0.63 versus 0.59 and 0.52 versus 0.50, respectively. In Tables 4 and 5, averaged rfit Testing results for detailed and nondetailed cases are 0.62 versus 0.53 and 0.50 versus 0.55, respectively. If Subject 8 is removed in Table 4, the averaged rfit, for the 3 remaining subjects, increases from 0.53 to 0.60, and it is very close to the detailed result of 0.62. Thus, it seems that if detailed food log are improving the fit, it does not appear to be very significant.
The FF model can be obtained by application of eq 1. Note that from eq 10 at the initial steady state when xt = vt = 0 and ŷ = Yset + B̂, then âo = Yset + B̂. For simplicity, we use only two inputs, one for say, carbohydrates, for example, x1, and one for insulin infusion, say x2. Thus, eq 1 in continuous time is
| 16 |
In the Laplace domain, eq 16 becomes
| 17 |
By taking θ̂i = 0, for simplicity, in the s-domain, eq 2 becomes
| 18 |
Substituting eq 18 into eq 17, rearranging and writing as a differential equation, one gets the following form for the proposed FF controller:
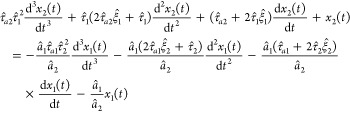 |
19 |
As shown by eq 19, the FF control law contains the numerator and denominator dynamics of both the load variable and the manipulated variable, the insulin infusion rate. This equation can be solved numerically using a technique such as Euler’s method to give the insulin infusion rate at each time instant to satisfy eq 1.
For an ARMAX model, the FF controller would be (the derivation is not shown for space considerations)
| 20 |
Note that this controller only has numerator dynamics for the inputs. Because inputs in this context will have very different denominator dynamics (e.g., very different residence times of carbohydrates and fats), it is not reasonable to use a model with this restriction when it is unnecessary. Thus, ARMAX and its related structures such as ARX are not considered based on the goals of this research work.
Concluding Remarks
This work proposed an input-only, multiple-input, outpatient free-living, modeling methodology for T1D subjects for FFC. We have not found any input-only models for real T1D subjects in the literature and thus, none that meet the requirements for FF controller development under eq 1, our scope. The proposed methodology extends the one developed by Rollins et al.27 for Type 2 diabetic subjects to include insulin infusion. It decomposes the static and dynamic parameter estimation problems and then decomposed the dynamic parameter estimation problem into a separate one for each input. This strategy seeks to guard against overfitting and to strengthen long-term stability by producing Training, Validation, and Testing fitted correlations (rfit) that are similar as evidence of achieving these goals. The activity inputs provided by the armband were shown to be quite valuable in improving model fit. For several subjects, the fits were excellent (rfit ≥ 0.6) even though they were developed from free-living data and totally from noninvasive inputs. This work makes a major step toward the goal of the development of a long-term automatic insulin delivery system for T1Ds.
The goal of a FF controller is to determine the insulin infusion rate that will cancel the effects of measured input changes on BGC. Thus, the FF model used to build the FFC system can have large model bias and be quite effective as long as it is able to accuracy determine the insulin infusion rate to cancel out changes of measured and modeled inputs. Consequently, a FF model can be quite biased and still very effective in this application.
Given that of model bias does not matter in this application, the premier performance measure is rfit, as it is not affected by model bias and gives an indication of model fit. However, high correlation does not necessarily mean high causation. Moreover, under free-living data collection, and this context of modeling real subjects, input model causation cannot be determined and can only, ultimately, be evaluated under real subject FFC. Nonetheless, our approach has attempted to strengthen input causation in model building by using highly structure nonlinear models with physically interpretable dynamic parameters and a model identification strategy to minimize over fitting. We sought to accomplish the latter by a cross-validation strategy that used sequential data for training, validation, and testing sets and obtains similar values of rfit for all the data sets. In addition, by using a sequential cross-validation approach as opposed to a k-fold approach, ones is able to evaluate how rfit maintains it level under a model with changing bias due to changes in unmeasured disturbances and this is more realistic in terms of practice because the model will be used in practice on data that is collected after the model is built.
In the future, we will continue to improve the accuracy of the method and evaluate its suitability for FF control in real data studies. Although the Wiener structure has unique strengths, it is still limited. Consequently, we will continue to look for other types of structures that have better phenomenological attributes, especially for the incorporation of unmeasured blood insulin. We feel this accomplishment has the potential for a significant advancement in model-based FFC applications as it should provide the insulin infusion rate to compensate for multiple and simultaneous input changes in a dynamic fashion.
Acknowledgments
The authors thank BodyMedia, Inc. of use of the SenseWear® Pro3 Body Monitoring System and Nisarg Vyas from BodyMedia, Inc. for his assistance with the study. Financial support from the National Institutes of Health (Grant 1R01DK085611) through Illinois Institute of Technology and the Juvenile Diabetes Research Foundation (Grant 5-2010-7) is gratefully acknowledged.
Appendix
The purpose of this appendix is to provide a mathematical proof for rfit, under simple linear regression (i.e., eq 10) with one input. Let η̂t = â0 + âiv̂i,t; in this context, rfit is mathematically given by
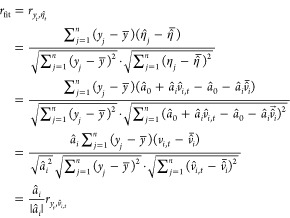 |
21 |
Thus, with âi > 0, rfit = 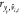 and for âi <
0, rfit =
and for âi <
0, rfit = 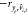 . This result means that
if the correlation
of measured blood glucose concentration (BGC) and v̂i,t is positive, âi can be set at any
positive value and rfit, which will be
>0, will depend only of the behavior of v̂i,t, which is independently
controlled by the values of the dynamic parameters associated with vi,t. Conversely, if the correlation
of BGC and v̂i,t is negative, âi can be set at any negative value and rfit will be >0 and independently controlled by the
values
of the dynamic parameters associated with vi,t.
. This result means that
if the correlation
of measured blood glucose concentration (BGC) and v̂i,t is positive, âi can be set at any
positive value and rfit, which will be
>0, will depend only of the behavior of v̂i,t, which is independently
controlled by the values of the dynamic parameters associated with vi,t. Conversely, if the correlation
of BGC and v̂i,t is negative, âi can be set at any negative value and rfit will be >0 and independently controlled by the
values
of the dynamic parameters associated with vi,t.
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
References
- The effect of intensive treatment of diabetes on the development and progression of long-term complications in insulin-dependent diabetes mellitus. N Engl. J. Med. 1993, 329, 977–986. [DOI] [PubMed] [Google Scholar]
- Ohkubo Y.; Kishikawa H.; Araki E.; et al. Intensive insulin therapy prevents the progression of diabetic microvascular complications in Japanese patients with non-insulin-dependent diabetes mellitus: a randomized prospective 6-year study. Diabetes Res. Clin. Pract. 1995, 28, 103–117. [DOI] [PubMed] [Google Scholar]
- Intensive blood-glucose control with sulphonylureas or insulin compared with conventional treatment and risk of complications in patients with type 2 diabetes (UKPDS 33). Lancet 1998, 352, 837–853. [PubMed] [Google Scholar]
- Effect of intensive blood-glucose control with metformin on complications in overweight patients with type 2 diabetes (UKPDS 34). Lancet 1998, 352, 854–865. [PubMed] [Google Scholar]
- Hermanides J.; Phillip M.; DeVries J. H. Current application of continuous glucose monitoring in the treatment of diabetes: Pros and cons. Diabetes Care 2011, 342197–201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan J. C. N. Diabetes and noncommunicable disease: Prevent the preventables. JAMA, J. Am. Med. Assoc. 2013, 3109916. [DOI] [PubMed] [Google Scholar]
- Bequette B. W. A critical assessment of algorithms and challenges in the development of a closed-loop artificial pancreas. Diabetes Technol. Ther. 2005, 7128–47. [DOI] [PubMed] [Google Scholar]
- Hovorka R.; Canonico V.; Chassin L. J.; Haueter U.; Massi-Benedetti M.; Federici M. O.; Pieber T. R.; Schaller H. C.; Schaupp L.; Vering T.; Willinska M.E. Nonlinear model predictive control of glucose concentration in subjects with type 1 diabetes. Physiol. Meas. 2004, 25, 905–920. [DOI] [PubMed] [Google Scholar]
- Hovorka R. Continuous glucose monitoring and closed-loop systems. Diabetic Med. 2005, 23, 1–12. [DOI] [PubMed] [Google Scholar]
- Steil G. M.; Clark B.; Kanderian S.; Rebrin K. Modeling insulin action for development of a closed-loop artificial pancreas. Diabetes Technol. Ther. 2005, 7194–108. [DOI] [PubMed] [Google Scholar]
- Magni L.; Raimondo D. M.; Bossi L.; Dalla Man C.; De Nicolao G.; Kovatchev B.; Cobelli C. Model predictive control of type 1 diabetes: An in silico trial. J. Diabetes Sci. Technol. 2007, 1, 804–812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinzimer S. A.; Steil G. M.; Garry M.; Swan K. L.; Dziura J.; Kurtz N.; Tamborlane W. V. Fully automated closed-loop insulin delivery versus semiautomated hybrid control in pediatric patients with type 1 diabetes using an artificial pancreas. Diabetes Care 2008, 315934–936. [DOI] [PubMed] [Google Scholar]
- Hovorka R.; Allen J. M.; Elleri D.; Chassin L. J.; Harris J.; Xing D.; et al. Manual closed-loop insulin delivery in children and adolescents with type 1 diabetes: A phase 2 randomised crossover trial. Lancet 2010, 375, 743–51. [DOI] [PubMed] [Google Scholar]
- Kovatchev B.; Cobelli C.; Renard E.; Anderson S.; Breton M.; Patek S.; Clarke W.; et al. Multinational study of subcutaneous model-predictive closed-loop control in type 1 diabetes mellitus: Summary of the results. J. Diabetes Sci. Technol. 2010, 461374–1381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cobelli C.; Renard E.; Kovatchev B. Artificial pancreas: Past, present, future. Diabetes 2011, 60, 2672–2682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berlin K. S.; Rabideau E. M.; Hains A. A. Empirically derived patterns of perceived stress among youth with type 1 diabetes and relationships to metabolic control. J. Pediatr. Psychol. 2012, 379990–998. [DOI] [PubMed] [Google Scholar]
- Mommersteeg P. M. C.; Herr R.; Zijlstra W. P.; Schneider S.; Pouwer F. Higher levels of psychological distress are associated with a higher risk of incident diabetes during 18 year follow-up: Results from the British household panel survey. BMC Public Health. 2012, 12, 1109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cagampang F. R.; Bruce K. D. The role of the circadian clock system in nutrition and metabolism. Br. J. Nutr. 2012, 1083381–392. [DOI] [PubMed] [Google Scholar]
- Van Cauter E.; Polonsky K. S.; Scheen A. J. Roles of circadian rhythmicity and sleep in human glucose regulation. Endocr Rev. 1997, 185716. [DOI] [PubMed] [Google Scholar]
- Sparacino G.; Zanderigo F.; Corazza S.; Maran A.; Facchineti A.; Cobelli C. Glucose concentration can be predicted ahead in time from continuous glucose monitoring sensor time-series. IEEE Trans. Biomed. Eng. 2007, 545931–937. [DOI] [PubMed] [Google Scholar]
- Eren-Oruklu M.; Cinar A.; Quinn L.; Smith D. Estimation of future glucose concentrations with subject-specific recursive linear models. Diabetes Technol. Ther. 2009, 114243–253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gani A.; Gribok A. V.; Rajaraman S.; Ward W. K.; Reifman J. Predicting subcutaneous glucose concentration in humans: Data-driven glucose modelling. IEEE Trans. Biomed. Eng. 2009, 562246–254. [DOI] [PubMed] [Google Scholar]
- Perez-Gandia C.; Facchinetti A.; Sparacino G.; Cobelli C.; Gomez E. J.; Rigla M.; de Leiva A.; Hernando M. E. Artificial neural network algorithm for online glucose prediction from continuous glucose monitoring. Diabetes Technol. Ther. 2010, 12181–88. [DOI] [PubMed] [Google Scholar]
- Mougiakakou S. G.; Prountzou A.; Iliopoulou D.; Nikita K. S.; Vazeou A.; Bartsocas C. S. Neural network based glucose-insulin metabolism models for children with type 1 diabetes. IEEE Eng. Med. Biol. Soc. 2006, 3545–3548. [DOI] [PubMed] [Google Scholar]
- Pappada S. M.; Cameron B. D.; Rosman P. M.; Bourey A. E.; Papadimos T. J. Neural network-based real-time prediction of glucose in patients with insulin-dependent diabetes. Diabetes Technol. Ther. 2011, 132135–141. [DOI] [PubMed] [Google Scholar]
- Georga E. I.; Protopappas V. C.; Ardig’o D.; Marina M.; Zavaroni I.; Polyzos D.; Fotiadis D. I. Multivariate prediction of subcutaneous glucose concentration in Type 1 diabetes patients based on support vector regression. IEEE J. Biomed. Health Inf. 2013, 17171–81. [DOI] [PubMed] [Google Scholar]
- Rollins D. K.; Bhandari N.; Kleindler J.; Kotz K.; Strohbehn A.; Boland L.; Murphy M.; Andre D.; Vyas N.; Welk G.; Franke W. E. Free-living inferential modeling of blood glucose level using only noninvasive inputs. J. Process Control 2010, 20195–107. [Google Scholar]
- Rollins D. K.; Bhandari N. Constrained MIMO dynamic discrete-time modeling exploiting optimal experimental design. J. Process Control 2004, 146671–683. [Google Scholar]
- Rollins D. K.; Bhandari N.; Kotz K.. Critical modeling issues for successful feedforward control of blood glucose in insulin dependent diabetics. American Control Conference, Seattle, WA, June 11–13, 2008.
- Andre D.; Teller A. Health care anywhere today. Stud. Health Technol. Inf. 2005, 118, 89–110. [PubMed] [Google Scholar]
- Welk G.; Blair S. N.; Woof K.; Jones S.; Thompson R. W. A comparative evaluation of three accelerometry-based physical activity monitors. Med. Sci. Sports Exercise 2000, 329489–497. [DOI] [PubMed] [Google Scholar]
- Bates D. M.; Watts D. G.. Nonlinear Regression Analysis and Its Applications; Wiley: New York, 1988. [Google Scholar]
- Garnier H.; Gilson M.; Young P. C.; Huselstein E. An optimal IV technique for identifying continuous-time transfer function model of multiple input systems. Control Eng. Pract. 2007, 15, 471–486. [Google Scholar]
- Beverlin L. P.; Rollins D. K.; Vyas N.; Andre D.. An algorithm for optimally fitting a Wiener model. Math. Probl. Eng. 2011, 2011, Article ID: 570509. [Google Scholar]