T-RECS: STABLE SELECTION OF DYNAMICALLY FORMED GROUPS OF FEATURES WITH APPLICATION TO PREDICTION OF CLINICAL OUTCOMES

Abstract

Feature selection is used extensively in biomedical research for biomarker identification and patient classification, both of which are essential steps in developing personalized medicine strategies. However, the structured nature of the biological datasets and high correlation of variables frequently yield multiple equally optimal signatures, thus making traditional feature selection methods unstable. Features selected based on one cohort of patients, may not work as well in another cohort. In addition, biologically important features may be missed due to selection of other co-clustered features We propose a new method, Tree-guided Recursive Cluster Selection (T-ReCS), for efficient selection of grouped features. T-ReCS significantly improves predictive stability while maintains the same level of accuracy. T-ReCS does not require an a priori knowledge of the clusters like group-lasso and also can handle “orphan” features (not belonging to a cluster). T-ReCS can be used with categorical or survival target variables. Tested on simulated and real expression data from breast cancer and lung diseases and survival data, T-ReCS selected stable cluster features without significant loss in classification accuracy.

1. introduction

Identifying a minimal gene signature that is maximally predictive of a clinical variable or outcome is of paramount importance for disease diagnosis and prognosis of individual patient outcome and survival. However, biomedical datasets frequently contain highly correlated variables, which generate multiple, equally predictive (and frequently overlapping) signatures. This problem is particularly evident when sample size is small and distinguishing between necessary and redundant variables becomes hard. This raises the issue of signature stability, which is a measure of a method’s sensitivity to variations in the training set. Lack of stability reduces confidence to the selected features. Traditional feature selection algorithms applied on high-dimensional, noisy systems are known to lack stability (2).

In this paper we propose a new feature selection algorithm, named Tree-guided Recursive Cluster Selection (T-ReCS), which addresses the problem of stability by performing feature selection at the cluster level. Clusters are determined dynamically as part of the predictive signature selection by exploiting a hierarchical tree structure. Formed clusters are of varying sizes depending on user-defined p-value thresholds. Selecting clusters of variables provides an additional potential benefit. Biologically meaningful biomarkers may not be maximally discriminative, but could be correlated with strongly discriminative features that lack biological interpretation. T-ReCS was tested on simulated and real data with categorical and survival outcome variables. T-ReCS can efficiently process large datasets with tens of thousands of variables, thus making it ideal for selecting predictive signatures for patient stratification and for development of personalized medicine strategies.

1.1. Related work

To our knowledge, this is the first method for group variable selection with dynamic formation of the groups as part of the feature selection procedure. Group-lasso (3) is the closest method to T-ReCS, but it requires prior knowledge of the groups, while ideally one wants to be able to determine clusters dynamically and the cluster formation to be part of the feature selection process. Localzo and colleagues used subsampling of the training set to identify consensus feature groups, and then perform feature selection on these groups (4). This method is valuable but the determination of clusters precedes the feature selection as well. Ensemble methods have been proposed to address the problem of stability by agreegating the results of different runs of conventional feature selection algorithms. Haury et al. (1) conducted a comprehensive comparative study of many of those methods. Jacob et al. (5) have presented a method on enforcing clustering structure on multi-task regression problems and these techniques can be adapted to cluster features. Another problem that is somewhat related to feature selection stability (but T-ReCS does not address it) is the selection of multiple signatures (6, 7), because in some cases the members of the signatures may belong to the same clusters.

2. Methods

2.1. Description of T-ReCS

T-ReCS is a modular procedure, which selects group variables in a multi-step process by combining elements of hierarchical clustering with traditional feature selection algorithms. First, the algorithm performs an initial standard feature selection. Suppose the single variables selected are {A,B,C}. Next, it constructs a hierarchical tree structure from the data that represents the similarity associations between variables. Leafs, at the bottom of the tree, are the single variables. Each internal node in the tree represents a group of variables (genes). The lower in the tree a node is, the more similar the patterns of its members are. Next, the algorithm climbs the tree up one level at a time per selected variable. If, for example, {A,D,E} are clustered together it creates a new feature A′ representing the cluster. If the representative of A′ is informationally equivalent for predicting T, then A is replaced by A′ in the set of selected variables which becomes {A′, B, C}. Essentially, the set of selected variables is now {{A,D,E},B,C}. The procedure continues for all selected variables until no informationally equivalent features can be constructed by climbing up the tree. Stability increases since a small perturbation of the data may lead to different initial features to be selected (e.g., {D,B,C}), but cluster-based selection will still be {{A,D,E},B,C}.

Any appropriate algorithm can in principle be employed for these steps. In our case, for the initial feature selection, we adopt the causal structure finding algorithm Max-Min Parents Children (MMPC) (8). MMPC assumes that the data distribution can be faithfully represented by a Bayesian Network where each variable and the target T serve as nodes. MMPC identifies the parents and children of T (i.e., the adjacencies with T), PC(T), in that network efficiently, without fully reconstructing the network. The output of the MMPC is an approximation (subset) of the Markov Blanket of T, i.e., a minimal subset of variables that renders all other variables conditionally independent and thus can optimally predict T. It was shown that under certain broad conditions, the Markov Blanket is the solution to the variable selection problem (8). Furthermore, Tsamardinos and colleagues have sown that the PC(T) set, in practice, leads to models that are close to optimal for predicting T, while it is significantly less computationally expensive than the full Markov Blanket (9). Therefore, primary feature selection here is equivalent to discovering the PC(T). For generating the tree structure we use ReKS (Recursive K-means Spectral Clustering), which was shown to outperform other methods in terms of speed or efficiency and outputs more balanced trees when applied to heterogeneous clinical data (10). Finally, to create the representative features of a cluster we tested the first Principal Component of the cluster, the medoid, and the centroid of the clustered variables.

MatLab was used for implementation of T-ReCS and comparison to other methods. The complexity of T-ReCS is roughly O(|φ |²). Specifically, ReKS is O(|φ |²) (10), MMPC is O(|φ |•|PC(T)|•k), and conditional independence tests for ascending the tree is O(log |φ |•|PC(T)|). We note, however, that selection of different methods for single feature selection and tree construction can alter this complexity.

2.2. Deciding informational equivalence

A key innovation of the algorithm is how to determine whether a cluster representative X′ at level k of the tree is informationally equivalent to X at a lower level k+1. Intuitively, we test whether X should be substituted with X′, a representative of a cluster of variables while maintaining predictive accuracy. We require two conditions to be satisfied: Condition (C1) Dep(X′ ; T | S), for every S ⊆ {PC(T)\{X}}, where Dep(X ; T | S) denotes the conditional dependence of X with T given variables S. This condition needs to be satisfied by MMPC to select a variable in the output. Thus, if (C1) is satisfied MMPC could have selected X′ instead of X in the original set of variables if it was available. Intuitively, the test determines that X′ carries unique information for predicting T in any context (subset) of the other selected variables. This is justified by Bayesian Network theory: if the data distribution is faithful to some Bayesian Network, then this condition is satisfied by the parents and children of T. This condition dictates that in the absence of X, a representative X′ of a cluster of variables should be selected, which increases stability. Thus, this condition is responsible for increasing stability. Condition (C2) is Ind(X ; T | X′), denoting the conditional independence of X with T given X′. This second condition implies that the original variable X is rendered superfluous (redundant) once X′ is selected. Thus, X and X′ are informationally equivalent for predicting T (at least, when no other variables are considered). Thus, this condition aims at ensuring that predictive performance is maintained when replacing X with X′.

2.3. Statistical tests of conditional independence

T-ReCS, like MMPC, uses conditional independence tests to determine inclusion in the final output, based on a corresponding p-value, denoted as P(X ; T | S). If this p-value is below a user-defined threshold (typically, 10⁻² to 10⁻⁴; see below) we accept dependence, and if it is larger than a threshold (not necessarily the same) we accept independence. The pseudo-code of the algorithm is presented in Suppl Fig S1. We emphasize that the procedure constructs new features, corresponding to clusters of variables, adaptively and dynamically. It may or may not decide to substitute a variable in the output of MMPC with a representative of a larger cluster. A common framework for constructing hypothesis tests is the framework of a Likelihood Ratio test (11). The Likelihood Ratio computes the deviance D = −2 · ln(P₀/P₁), where P₀ and P₁ are the null and the alternative model, respectively. D asymptotically follows the chi-square distribution with degrees of freedom equal to the difference in the number of parameters between the two models. From this distribution we can obtain the p-value of the test. For testing the hypothesis Ind(X;T | Z) the null model is a predictive model for T given Z and the alternative model is a predictive model for T given Z and X. Thus, the ratio tests whether the likelihood for T when X is added is statistically significantly different compared to when X is not given. If yes, then indeed X provides additional information for T given Z and the null hypothesis of independence is rejected. In the following experiments, when T is continuous, we employ linear models (equivalent to testing the partial correlation of X and T given Z); when T is discrete, we employ logistic models; and when T is a right-censored survival variable, we employ the proportional Hazard Cox Regression model) as we did before (12, 13).

2.4. Group variable representation

There are many ways to construct a group variable X' from its members. In this paper, we tested the centroid, medoid and the first component of the principal component analysis (PCA) as cluster representatives since they have been successfully applied on gene expression data before (14–16).Other latent variable representations can be used instead.

2.5. Methods for measuring predictive performance

In this paper, we measured the predictive quality of the sets of selected features either directly (when the network was known, i.e., synthetic data) or indirectly by using the selected features in a regression or classification method.

For binary target variables, we used Support Vector Machine (SVM) (17), which takes continuous predictors as input and outputs a label assignment. SVMs are practical, scalable, and have competitive performance for this type of data (9). We evaluated the performance in terms of (1) classification accuracy rate defined as the sum of number of true positives and true negatives over total number instances and (2) stability as it is defined below.

For time-to-event target variables (a.k.a. survival data) we used the Cox regression (Cox Proportional Hazards Model) (18), which relates the predictor variables to the time that passes before an event of interest occurs. Time-to-event data are typically right-censored, i.e., for some patients we do not know the time of occurrence of the event, but only know that they were event-free up to a time point. Measuring the predictive performance of a survival regression model is also not straightforward as the prediction error can be computed exactly only for the uncensored cases (i.e. when the time to event is known). Several measures have been proposed to measure performance for survival analysis (19–22). We select the Concordance Index (CI) (19) as it is one of the most commonly used measures for survival models. Intuitively, the CI measures the fraction of all pairs of patients, whose predicted survival time is correctly ordered by the regression model. Scenarios in which the order of observed survival cannot be determined due to censorship are excluded from the calculation.

2.6. Methods for measuring stability

For this paper, stability is a measure of how consistently the same variables are selected across different cross validation runs. Typically, a measure like Tanimoto set-similarity (23) is used to characterize the agreement or percentage of overlap between two sets of features. In our case, however, each set of features can contain single- or group-variables, and the Tanimoto setsimilarity alone would not suffice. For example, F_i = {{A,B,C}, {D,E}} may be selected in cross-validation fold i and F_j = {{A,C}, {B,D}} may be the selection at fold j. Before computing set-similarities between elements of F_i and F_j, the elements of these sets need to be matched. In this example, one question is whether {A,B,C} in F_i should be matched with {B,D} or {A,C} in F_j? To find the best matching, we use maximum weight matching (24) to build a bipartite graph between elements of F_i, and F_j. The weights on the edges correspond to the Tanimoto set-similarity S(s, w) = |s ∩ w| / |s ∪ w|, where s ∈ F_i and w ∈ F_j. In this example, {A,B,C}_i is matched to {A,C}_j, and {D,E}_i to {B,D}_j where the indexes denote membership in F_i and F_i respectively. After the optimal matching is found, the weights normalized to a total sum of 1, and we take the sum of normalized weights of the selected edges of this matching as a metric of stability between the selected variables in each pair of folds. The overall stability is the average pair-wise stability over all pairs of cross-validation folds and ranges between zero (no stability) and one (absolute stability). Note that, when only single variables are selected, this definition of stability reduces to the average Tanimoto similarity of the selected variables over each pair of folds.

2.7. Datasets used in this paper

2.7.1. Synthetic data

Simulated gene expression data were created using the linear Gaussian Bayesian network structure shown in Suppl Fig S2. The network includes the target variable T, a set of 25 variables that are ancestors of T, a set of 25 variables that are descendants of T, and 44 variables that do not have a path to T. Parents are nodes 26–28, children are nodes 29–31, connected variables are nodes 1–25 and 32–56 and unconnected variables are nodes 57–100. The non-immediate relatives to T have an average out-degree of 2. Each node has continuous values analogous to that of gene expression data. The target variable we observe is binary; this is akin to case/control studies or observing two disease subtypes in patients. To generate the data, we model the value of each variable as a linear function of its parents with equal weights, with a Gaussian noise. In order to simulate the effects of co-linearity between variables, for every variable in the dataset we created a total of 10 datasets × 1,000 samples each. Each dataset had an increasing amount of Gaussian noise, ranging from N(0, 0.05) to N(0, 2.5). In addition, we similarly created one test set with 5000 samples.

2.7.2. Biological data

Large scale biomedical datasets

We used three large-scale biomedical datasets. Haury et al. (1) study used gene expression data from four metastatic breast cancer cohorts (GEO numbers GSE1456, GSE2034, GSE2990, GSE4922)., each with >125 patient samples to a total of 819 samples. The second is a breast cancer cell line dataset (25), which contains mRNA expression in 60 breast cancer cell lines (24 basal and 36 luminal). The third dataset is miRNA expression data from the Lung Genomics Research Consortium (LGRC) (26), which includes samples from patients with chronic obstructive pulmonary disease (COPD; 210 patients) and idiopathic pulmonary fibrosis (IPF; 249 patients). In all these datasets, T-ReCS was used to identify gene signatures predictive of the particular target variable (relapse or not, breast cancer type and COPD or IPF, respectively).

Censored dataset

We used the censored benchmarking datasets from (12) which consisted of six publicly available gene expression datasets (27–32). The six sets of censored survival data range in size from 86 to 295 cases with 70 to 8,810 variables, and the events of interests are either metastasis or survival.

3. Results

We tested T-ReCS on (1) a set of simulated data, (2) a set of six benchmarking gene expression datasets, and (3) one set of biological (cell lines) and two of biomedical (clinical) data. These datasets were selected to cover cases with either binary or survival target variables. We compare T-ReCS performance to a baseline produced by single variable selection. We also compare it against ensembles constructed from features selected from different folds of cross validation data. We perform 10-fold cross validations when the sample size allows. For datasets with sample size less than 200, we perform two repetitions of 5-fold cross validation. For a fair comparison, on all instances, the single variable MMPC component was run with the same significance threshold a=0.05 and size of maximum conditioning set k=5.

3.1. Evaluation of T-ReCS

3.1.1. T-ReCS evaluation on synthetic data and comparison to other methods

On the synthetic dataset MMPC recovered on average 5.5 out of 6 PC(T) members, with 0.8 false positives that are almost always the least significant selected variables. This confirms that the single variable MMPC is successfully recovering the planted variables. We also note that the spectral clustering method (ReKS) clusters together most of the noisy copies of the variables. Non-singleton clusters are often connected by an edge, indicating that there is high correlation between them and the clustering is justified. In fact, 75.7% of all the unique clusters that were selected under the most lenient parameter combination contain copies of a single “seed” variable; while another 18.6% contain “foreign” variables seeded from a different variable; and a mere 5.7% of the selected clusters have copies of variables from more than one foreign seed variables. This result confirms that ReKS is indeed creating valid data partitions for T-ReCS.

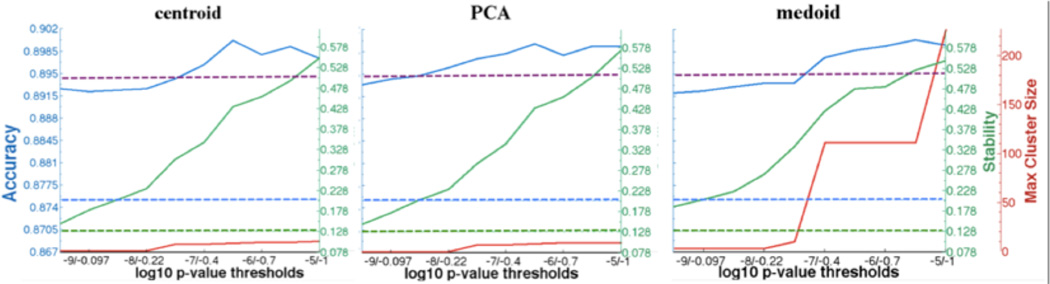
The average cross validation accuracy, stability, and cluster size for different thresholds are plotted in Fig 1 for three methods for cluster definition. As expected, we see a trend of increasing stability and cluster size toward the top of the tree (left to right), with the accuracy displaying more subtle variations with a slight spike in the middle region. We plot the baseline stability and accuracy in dotted lines in corresponding colors. These are the average performance of single variable MMPC across the cross validation runs. Both T-ReCS accuracy and stability are improved over the corresponding baselines. For comparison purposes, we plot the baseline of the ensemble consisting of the union of single variables selected from all the 10 cross validation runs, which we use to train SVM models across the 10 training sets. The average test accuracy is plotted in purple dotted line, and we can see that in the more permissive half of the parameter range, T-ReCS performs the same or better than simple ensemble average. Lastly, we observe that centroid and PCA methods produce very similar results, while medoid allows for larger clusters to be formed, possibly because the same member continues to be the “medoid” of the cluster as it advances up the tree, masking the “noise” that other cluster members may otherwise introduce.

Fig. 1. T-ReCS performance on synthetic data.

Accuracy (blue), Stability (green) and Cluster size (red) across 10 parameter combinations (left to right, most stringent to most permissive) for three different cluster representation methods applied on simulated data. Plotted in dotted lines in corresponding colors are single variable selection baseline results. The purple dotted line is the ensemble baseline accuracy.

T-ReCS run on 10 subsets of the synthetic dataset and it identified a total of 66 group features, 58 of which contained representatives of at least one of the six members of the PC(T) (nodes 26–31). Three others contained only distantly connected nodes and five contained unconnecred nodes. Out of the ten testing sets, T-ReCS recovered all 6 PC(T) nodes in six, 5 PC(T) nodes in three and 4 PC(T) nodes in one. The results were the same regardless of the method used for representing the cluster. We compare T-RECS to SVM Recursive Feature Elimination (RFE), lasso and Elastic Net (E-Net) methods on 10 subsets. For comparison, we retained the top seven features of each run (total: 70 features for each method). SVM RFE recovered instances of nodes 27, 29, 30, 31 only two times and representatives of nodes 29, 30, 31 eight times. Lasso recovered instances of nodes 27, 29, 30, 31 four times and instances of nodes 27, 29, 31 six times. E-Net only recovered instances of nodes 29, 31 on all runs. The detailed results are presented in Suppl Table S1.

3.1.2. Comparison of T-ReCS to other feature selection methods on biological datasets

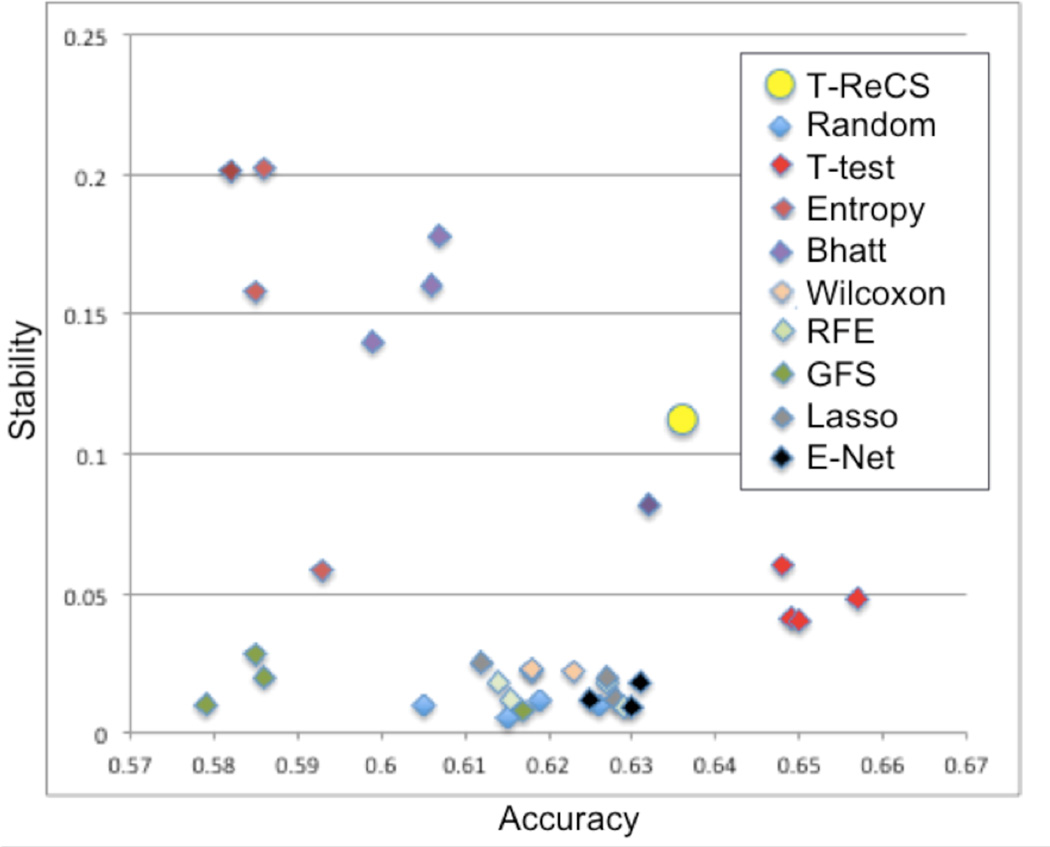
Haury et al. (1) performed a comprehensive study on the influence of feature selection on accuracy and stability of molecular signatures. They compared eight filter and wrapper feature selection methods, including E-Net, RFE and Lasso in single run or ensemble runs. We also run T-ReCS on the same four public datasets (33–36) and we calculated the same measure of accuracy and stability. We found that T-ReCS strikes a very good balance between accuracy and stability compared to these methods (Fig 2). Perhaps more importantly, the figure shows that T-ReCS is on the pareto frontier, i.e., it is never simultaneously dominated in both stability and accuracy; thus, T-ReCS offers a new trade-off point of stability vs accuracy not found in any other method.

Fig. 2. Comparison of T-ReCS with other feature selection methods.

Accuracy and stability tradeoff is calculated as in Haury et al. (1) from which the other results are obtained. RFE: recursive feature elimination; GFS: greedy forward selection; E-Net: elastic network.

3.2. Application of T-ReCS to biomedical datasets

3.2.1. T-ReCS on breast cancer cell line data

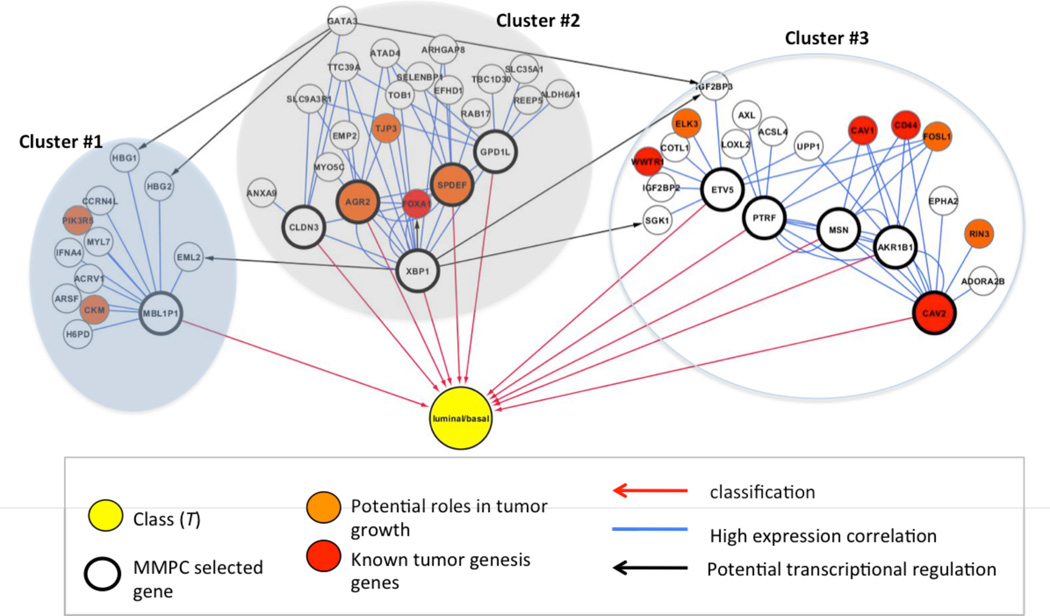
T-ReCS run on a set of 60 Basal and Luminal breast cancer cell lines (25) and identified three groups of genes that differentiate the two subtypes (Fig 3). MMPC identified several genes as predictive of basal vs luminal in one or more rounds of cross-validation (Fig 3, “MMPC selected genes”, bold cycles), but most are not known to be involved with breast cancer. However, their clusters contain members such as FOXA1 (known to be involved in ESR-mediated transcription in breast cancer cells) and GATA3 (a known marker of luminal breast cancer). Additionally, when we examined the local potential regulatory relationships between the selected genes and their group variables, we found potential XBP1 and GATA3 transcription factor binding sites in other members as evidenced by the fact that these two genes are the two regulatory hubs in this network (Fig 3). This observation suggests that a method like T-ReCS that performs variable selection on groups of variables and additionally provides contextual information around the selected groups could provide more biologically robust and meaningful biomarkers.

Fig. 3. T-ReCS applied on breast cancel cell line expression data.

Selected gene groups predictive of Basal vs. Luminal subtypes are presented.

3.2.2. T-ReCS on lung patient data

miRNA expression data from LGRC were analyzed with respect to disease diagnosis (COPD vs ILD). MMPC, ran on the 210 COPD and 249 ILD samples, returned seven miRNAs as maximally predictive of diagnosis, none of which was reported as associated with COPD or IPF on a recent comprehensive review article (37). When T-ReCS performed cluster selection starting from these seven miRNAs, it identified 33 additional miRNAs, (Suppl Fig S3; each miRNA label marks the cluster that includes it). Four of the 33 had distinct role in these diseases according to the Sessa et al. review (p-value=10⁻⁴). miR-1274a, is the most highly induced miRNA in smoker COPD patients compared to normal smoker individuals (38). miR-146a is believed to participate in a feedback loop with its target, COX2, that limits prostaglandin E₂ production and thus controls inflammation. In fibroblasts from COPD patients, miR-146a is induced at lower levels than in normal fibroblasts (39). miR-21 has been strongly associated to IPF via the TGF-β signaling pathway (40). miR-154 is a SMAD3 regulated miRNA, whose expression is increased in IPF lung fibroblasts leading to increases in cell proliferation and migration (41). Transfection with miR-154 leads to the activation of the WNT pathway in NHLF cells. WNT and TGF-β are the two most important pathways involved in IPF (41). Further literature search showed that other MMPC/T-ReCS selected miRNAs that have also been reportedly associated with COPD or IPF are miR-24 (COPD) (38), miR-135b (COPD) (42) and miR-376a (IPF) (43). Interestingly, T-ReCS cluster #7 includes seven of the nine miRNAs with confirmed high expression in both IPF lungs and embryonic lungs (41): miR-127, miR-299-5p, miR-382, miR-409-3p, miR-410, as well as miR-154, and miR-487b. Overall, twelve of the 40 T-ReCS selected miRNAs as diagnostic to COPD or IPF are known to be associated with these diseases. The targets of 25 of the 40 miRNAs, as defined by the mirConnX (44) prior network, are presented in Suppl Fig S4.

3.2.3. T-ReCS on survival (censored) data

We evaluated T-ReCS on survival data by comparing it with the Survival MMPC (SMMPC) algorithm (13) on the same six clinical data sets that were in the 2010 publication (27–32). In general, stability improves from the baseline by a substantial margin, while accuracy (in terms of CI) hovers around baseline, with small increase or decrease across parameter combinations (Table 1). The size of the chosen group variables largely stays within the range of 10 members. This indicates that our method gains in stability without severe loss of accuracy, compared to the single variable selection baseline.

Table 1.

Benchmarking censored datasets used in T-ReCS evaluation.

	#Cases			% Improvement
Dataset	(Cens)	#Vars	Event	Stability	CI
Vijver	295 (207)	70	metastasis	+19~28%	−1.2~1.7%
Veer	78 (44)	4751	metastasis	+0~9%	−1.8~11%
Ros02	240 (102)	7399	survival	+23.5~41%	−2.7~0.6%
Ros03	92 (28)	8810	survival	+100~194%	−5.3~1.2%
Bullinger	116 (49)	6283	survival	+6.7~19%	−1.3~3%
Beer	86 (62)	7129	survival	+39~80%	−7.3~8.5%

3.3. Discussion

T-ReCS main novelty is on the dynamic nature of cluster formation, by statistically evaluating their predictive equivalence. Compared to other methods it was able to recover more of the true parents and children of the target variable. We believe this is because T-ReCS will cluster together most of the instances of a node. In addition, it was able to uncover more biological information than single feature selection methods. A body of work has been accumulating on structured sparsity using sparsity-inducing regularizers. Such approaches impose a hierarchy of group structure on the variables and penalties apply on the groups (45). Typically, the group structure stems from prior knowledge, while in T-ReCS it is learned dynamically. But, the main difference between T-ReCS and structured regularization methods is that the former is based on statistical tests of independence, while the latter on regularization and optimization theory. The former has the advantage of theoretically guaranteeing an optimal (and minimal) solution under certain conditions. On the other hand, T-ReCS only includes a subset of the variables in each independence test, which may lead to sub-optimal solutions if the conditions are not met. Overall, we believe T-ReCS addresses an important problem in biomedicine in a robust way. Below we explain some details of the algorithm, which we feel require further clarification.

3.3.1. Group vs single variable selection

We demonstrated the stability improvement of the algorithm over single variable selection and ensemble baseline on simulated data. Significant improvement of stability was achieved with minimum change in accuracy. This is somewhat expected, but this is the first time that the cluster structure is determined dynamically as part of the search process. T-ReCS uses two conditions to achieve this. One condition is designed to enhance stability by substituting single or group variables with larger group variables. The other condition is designed to maintain the predictive accuracy of the initial variables as they are substituted by group variables. Besides improved stability T-ReCS selected group variables contained more biological information than the single ones as we showed in the breast cancer and the biomedical datasets.

3.3.2. Selection of p-value threshold

Varying the thresholds of the two conditions affects the output cluster sizes and subsequently the accuracy and stability of the algorithm. A stringent set of thresholds would prevent the procedure from advancing far beyond the initial set of single variables (reducing stability), while moderate thresholds allow larger group variables to be selected (possibly, at the expense of accuracy). As we relax the parameters the expected gain in stability was observed, but the loss in accuracy was minimal at the p-value threshold range of 10⁻² to 10⁻⁴, suggesting that this may be a parameter region that is more suitable for biological data. The accuracy reflects a tradeoff between overfitting (from the more stringent range of the parameters) and loss of predictive signals (in the more relaxed range of the parameters). A closer look in the distribution of p-values of these two tests also confirms that this parameter range is most effective in thresholding the clusters in the bottom portion of the tree. Alternatively, cross validation can be performed on all input datasets and the parameters selected based on best combined accuracy and stability.

3.3.3. Group variable representation methods

We also investigated its performance over a range of parameter combinations using three distinctive cluster representation methods. Similar performance was observed between centroid and PCA, while medoid tends to produce slightly more dissimilar behaviors. We suspect that this is because a medoid does not represent an “average” behavior of a cluster; it is merely a member of the cluster that is most similar to everyone else. As the cluster size increases, the identity of this member could remain unchanged, in which case the cluster may be allowed to grow very large without affecting the predictive performance, and too many noisy members could be erroneously recruited. On the other hand, medoid could also be susceptible to fluctuations of the member composition in the scenario that a current cluster joins with a larger, dissimilar cluster and the identity of medoid switches all of a sudden. For this reason, we recommend centroid as the preferred collapsing method since it produces more gradual change in stability across many parameter ranges, but unlike PCA it has also a straightforward interpretation.

3.3.4. Future work

We have also begun systematically applying our method on a number of large-scale studies (e.g., TCGA datasets, METABRIC (46), LGRC (26)). While our method was tested only on gene expression datasets in this study, it can be easily adapted to other high-dimensional systems such as methylation and SNP data to provide predictive models as well as biological intuition. Additionally, the modular structure of the algorithms paves the way for a novel group feature selection framework in which alternative clustering step, hypothesis tests, and different variants of the causal discovery algorithm can be employed. The results presented here are promising both in terms of computational performance as well as biological implications.