Abstract
The 70 kDa Heat Shock Proteins (Hsp70) are a family of molecular chaperones involved in protein folding, aggregate prevention, and protein disaggregation. They consist of the substrate binding domain (SBD) that binds client substrates, and the nucleotide-binding domain (NBD), whose cycles of nucleotide hydrolysis and exchange underpin the activity of the chaperone. To characterize the structure-function relationships that link the binding state of the NBD to its conformational behavior, we analyzed the dynamics of the NBD of the Hsp70 chaperone from Bos taurus (pdb 3C7N:B) by all-atom canonical molecular dynamics simulations. It was found that essential motions within the NBD fall into three major classes: the mutual class, reflecting tendencies common to all binding states, and the ADP- and ATP-unique classes, which reflect conformational trends that are unique to either the ADP- or ATP-bound states, respectively. ‘Mutual’ class motions generally describe ‘in-plane’ and/or ‘out-of-plane’ (‘scissor-like’) rotation of the subdomains within the NBD. This result is consistent with experimental nuclear magnetic resonance data on the NBD. The ‘Unique’ class motions target specific regions on the NBD, usually surface loops or sites involved in nucleotide-binding and are, therefore, expected to be involved in allostery and signal transmission. For all classes, and especially for those of the ‘Unique’ type, regions of enhanced mobility can be identified; these are termed ‘hot-spots,’ and their locations generally parallel those found by NMR spectroscopy. The presence of magnesium and potassium cations in the nucleotide-binding pocket was also found to influence the dynamics of the NBD significantly.
Keywords: molecular chaperones, molecular dynamics, principal component analysis
Introduction
The Hsp70 chaperones constitute a family of 70 kDa heat shock proteins, occurring ubiquitously at the cellular level in all domains of life.1-3 As molecular chaperones, Hsp70 members are involved in protein folding, re-naturation, and the prevention of agglomerates. They chaperone proteins during their import into organelles,4 during the disassembly and assembly of complexes,5 and modulate protein-protein interactions6. Further functions include assistance in protein degradation and subcellular vesicle/protein transport,7 as well as signal transduction, protein regulation8 and maintenance.
Hsp70 chaperones are composed of two domains, an N-terminal nucleotide-binding domain (NBD), also referred to as the ATP-ase domain, and a C-terminal substrate-binding domain (SBD), being ~44 kDa and ~25 kDa in size, respectively.9 The various functions of the chaperone are achieved through a basic binding and unbinding mechanism, in which short hydrophobic stretches of substrate bind re-iteratively to the SBD.9 The small region on the potential substrate may originate from a linear polypeptide, a partially unfolded species, or a fully folded protein.9 In its substrate-free conformation, the SBD is open; its α-helical section (SBD-α) binds to one and its β-sheet section (SBD-β) to another side of the NBD. In the substrate-bound conformation, the SBD is closed, holding the substrate within it. In this conformation, the SBD and NBD do not bind to each other, and so the two domains constitute fully independent units. The hydrolysis of ATP in the NBD is essential to the Hsp70 cycle, and the ATP-ase activity of the NBD is critical to allosteric communication between the NBD and SBD domains. The binding of ATP results in the formation of the SBD-open conformation, while the transition to the SBD-closed conformation with concurrent substrate binding is initiated by ATP hydrolysis.
The global arrangement and interactions between the NBD and the SBD have been the subject of much experimental research, and structures of the chaperone in various nucleotide-binding states have been identified.3 The SBD-closed (ADP-bound) structure of the DnaK Hsp70 chaperone from E. coli was determined by Zuiderweg and coworkers10 by NMR spectroscopy (PDB: 2KHO). Recently,11 we carried out molecular dynamics simulations, using the coarse-grained UNRES force field12-15 developed in our laboratory, of the conformational transition of DnaK, starting from the SBD-closed 2KHO structure. We determined a probable structure of the SBD-open conformation11, which was unknown at the time, and which turned out to be very close to the x-ray structure of the SBD-open (ATP-bound) form of DnaK, which was determined by Mayer and coworkers3 after the results of our simulations had been published. Starting from a homology model of the SBD-open conformation of bovine Hsp70, and using all-atom molecular dynamics with the GROMOS force field, Senet, Ripoll, and coworkers16 simulated the initial stage of the dissociation of SBD-β from the NBD. Very recently, using the GROMACS17 [with the GROMOS96 (ff43a1)18 force field], Chiappori et al.19 carried out simulations aimed at reproducing the transitions from the SBD-closed to the SBD-open structure of DnaK, and vice versa. Their first series of simulations was started from the SBD-closed conformation of DnaK, in which ADP was replaced with ATP, while their second series of simulations was started from an SBD-open conformation of 2KHO that was obtained by homology modeling, with bound ADP. However, both simulations resulted in similar intermediate structures, with SBD-α separated from SBD-β, but with SBD-α not docked to the NBD (Figure 2 in ref 19).
A study of the effect of nucleotide binding to the structure of the NBD has generated a largely nucleotide-based state-dependent description of this domain3,20. Circular Dichroism thermal melt and Electrospray Ionization Mass Spectroscopy experiments have suggested that, relative to the nucleotide-free state, the binding of ADP compacts the NBD.4 A comparison of ATP-ase domain crystal structures indicates that the central cleft of this domain is indeed more closed in its ADP-bound form than in the nucleotide-free species with co-crystallized nucleotide-exchange factor (NEF).4,20,21 Solution Nuclear Magnetic Resonance studies of the NBD without an NEF also verified cleft opening by rotation of the IIB subdomain.20 Upon binding of ATP, as suggested by an overlay of crystal structures from the ADP- and ATP-bound forms of the chaperone, small sub-domain rearrangements are produced, which open and close crevices on the surface of the NBD,3,20 thereby remodeling its SBD or cochaperone-accessible surface. Residual dipolar coupling (RDC) analyses have also pointed towards subdomain rotation as a function of the ADP- and ATP-analogue bound states;22 certainly, such reported rotations are quite significant, with sub-domain IIB rotating by up to 20°.22 Moreover, these rotations were found to be characteristic of the domain, visible even without nucleotide exchange factor cochaperones such as BAG (Bcl-2 associated athanogene) or GrpE (GroP-like gene E).22 Woo et al.23 carried out long molecular-dynamics simulations of ADP- and ATP-bound NBD of the Hsp70 from Bos taurus (PDB code: 3C7N:B) and found that the inter-domain angle δ (see Figure 1C for illustration) became smaller after the simulation with ATP-bound compared to the ADP-bound 3C7N (chain B) structure, which agrees with the experiment.22
Figure 1.

A. Domain division of the Hsp70 Nucleotide Binding Domain (3C7N:B). B. Illustration of the coordinate system of the NBD domain of Hsp70. The origin of the coordinate system is taken as the center of mass of the NBD, and the x, y, and z axes of the coordinate system are the principal axes of the NBD. C. Illustration of the δ angle. D. Illustration of the τ angle.
The concept of inherent NBD function20 therefore arises, which enables cooperation in a complex allosteric mechanism with the SBD. Although allosteric communication between the domains occurs in a two-way dialogue,24 the structure of the NBD provides ‘functional handles’ or ‘hot-spots’21 which serve as key allosteric and subsequently function-generating sites. This is exemplified by activation of the ATP-ase without the presence of the SBD,8,24 which was demonstrated by binding a fragment of the inter-domain linker to a cleft between subdomains IA and IIA (see Figure 1A for a definition of the domains).8,20,24 On the other hand, ATP binding to the NBD radically alters the character of the SBD, decreasing its affinity for the client protein8; the ATP-ase domain therefore demonstrates a strong innate functional behavior that contributes an essential building block to the allosteric pathway of the chaperone. Fluorescence experiments by Mapa et al.25 also pointed towards different SBD-NBD inter-domain distance distributions for the ADP- and ATP- bound chaperone.
The NBD has also been reported to bear a proline switch, whose response differs with respect to the identity of the nucleotide and enables the domain to assume an appropriate open or closed conformation;26 this proline is universally conserved among all Hsp70s.26 Moreover, the concept of such engrained functionality is considered a common quality for all nucleotide binding domains,20 with subdomain re-organization being an intrinsic function-permitting feature and signal transduction medium.20 It has been suggested that allosteric communication by means of the NBD occurs by a network of allosteric regions, which manifest themselves as residues on selected subdomain interfaces.20 Nucleotide binding enables internal conformational changes, which then trigger these sites for signal transduction.20 The idea of allosteric sites as domain-inherent attributes is further exemplified by the binding of a drug compound that incited ATP-ase and protein-folding activity;27 the investigated drug target thereby mimicked the behavior of Hsp40, a cochaperone,27 and further modification of the drug molecule generated an inhibitor for the prokaryotic Hsp70, DnaK.27 The NBD binding region of the drug included a sector on the upper IIA (Figure 1A) subdomain intersurface,27 an area already flagged as belonging to a zone of allosteric ‘hot spots’.21
Given the fact that the structures of both ATP-3 and ADP-bound10 Hsp70 chaperone DnaK are known, and that the structures of isolated domains from various Hsp70’s were known even earlier,22 the effect of ADP and ATP binding on NBD conformation has been well determined. However, the dynamics of conformational changes, which are critical for understanding the mechanism of allosteric communication (as pointed out by experimental22 and theoretical11,16 studies), remains to be explained. From the FRET (Förster resonance energy transfer) study by Mapa et al.25, it is known that the ADP-bound conformation exhibits a bimodal distance distribution, which suggests conformational transitions between the SBD-open and SBD-closed form; however, FRET cannot provide fine details of the dynamics of conformational changes. The comparative simulation study by Woo et al.23 consisted of only single simulations of the ATP-bound and ADP-bound 3C7N:B chaperone. The work presented here attempts to determine the behavior of the NBD, in nucleotide-unbound and nucleotide-bound states, in terms of its protein dynamics, and identifies sites of allosteric potential. Employing molecular dynamics simulations, simulated trajectories of the isolated NBD (Hsp70 from Bos taurus, PDB code 3C7N:B), in its free (no-nucleotide), ADP-, and ATP-bound forms, were analyzed by essential dynamics in an effort to characterize the protein dynamics of the NBD in different binding states. Important motions in each of the states, in addition to mutual trends, are presented. Target regions of characteristic mobility in the NBD in response to bound nucleotide are also portrayed, which could serve as potential Hsp70 allosteric sites.
Methods
Simulation Details
Canonical MD simulations were performed on the crystal structure of the Bos Taurus Hsp70 NBD (PDB code 3C7N:B), as taken from residues 1 to 384 (with missing N-terminal residues built with the LEAP utility of the AMBER package). The AMBER 11 force-field28 and model were employed with explicit TIP3P water29 as solvent. Production trajectories ranged in length from 1.8 to 2.0 μs. All simulations were carried out in an NPT ensemble with the Berendsen thermostat/barostat30 at a temperature of 300 K and a 2.0 fs time step. Production calculations were carried out using the ANTON supercomputer located in the Pittsburgh Supercomputer Center, while preparatory simulations were carried out by using the Beowulf cluster at the Faculty of Chemistry, University of Gdańsk. With these facilities, initial minimization and equilibration for ~20 ns were performed locally, with subsequent production runs accomplished on ANTON. Production snapshots were recorded at 240 ps intervals. Three series of systems were simulated: the NBD with no bound nucleotide (2 trajectories), and with either bound ADP or ATP in the nucleotide-binding pocket (6 trajectories each). The ADP-bound active site contained one magnesium and two potassium ions, while the ATP-bound active site included one magnesium and three potassium ions, consistent with the experimental structures of the ADP- and ATP-bound NBD. Nucleotide-free simulations contained a free sodium ion, which did not necessarily associate with the nucleotide binding pocket during the trajectory. ADP systems contained 53244 waters (with box dimensions of 94.80 Å, 71.96 Å, 86.84 Å), ATP systems contained 52731 waters (with box dimensions 100.91 Å, 71.82 Å, 85.31 Å), and systems with no nucleotide contained 52437 waters (with box dimensions 95.51 Å, 71.82 Å, 85.31 Å).
Essential Dynamics (Principal Component Analysis)
Snapshot conformations from individual trajectories were aligned to the respective average structure (averaged over the whole trajectory). Subsequently, the coordinate frame of each trajectory was exchanged for a centralized frame in which the origin was taken as the center of mass of the NBD, and the principal axes of the molecule were taken as the x, y, and z axes of the coordinate system with respect to which the Cα atoms of the backbone were then described (Figure 1B). A principal component analysis was then conducted on the Cα backbone for residues 5-378, according to the methods described in the literature.31-34 The initial and terminal few residues (1-4, 379-384) of the protein were omitted from the Essential Dynamics procedure for clarity, since these regions are highly mobile and undergo essentially random motions because of their direct exposure to solvent. Depending on system and trajectory, 5-30 eigenvectors captured over 80% of the variation of the conformation of the protein (Figure S1); therefore, only the first 100 eigenvectors were considered.
To find similarities between the dynamic behavior of the three systems studied, we first compared the essential dynamics vectors across all trajectories. Two vectors were considered similar if they satisfied the similarity criterion, namely that the absolute value of the cosine of the angle between them was ≥ 0.45. Degrees of similarity therefore arose, with a value of 1 corresponding to the parallel/antiparallel (highly similar) extreme.
To define the classes of similar vectors used in further analysis of trajectories, each vector from a given trajectory of a give type, i.e., each vector of the six ADP-bound trajectories, each vector of the six ATP-bound trajectories, and each vector of the two no-nucleotide-bound trajectories, was compared with vectors of the other trajectories of the same type or of the trajectories of a different type, respectively, according to the similarity criterion defined above. Vector pairs that passed the similarity criterion and components of these pairs were grouped type-wise into sets, as described below. These sets correspond to modes of motion, characteristic to the set type.
Set ADPγ ADP. This is a set of vector pairs whose members originate from ADP-bound trajectories. The similarity criterion holds for each pair. ADPγ ADP denotes all individual ADP vectors from this set; i.e., such ADP vectors that each of them is similar to at least one ADP vector from a different ADP trajectory.
Set ATPγ ATP. This is the set of vectors pairs from ATP-bound trajectories for which the similarity criterion holds. ATPγ ATP denotes all individual ATP vectors from this set; i.e., such ATP vectors that each of them is similar to at least one ATP vector from a different trajectory.
Set NNγ NN. This is the set of vector pairs from trajectories with no bound nucleotide (experimentally known as the Apo form of the protein, which we refer to as the NN form) for which the similarity criterion holds. NNγ NN denotes all individual NN vectors from this set; i.e., such NN vectors that each of them is similar to at least one NN vector from a different trajectory.
Set ADPγ ATP. This is the set of vector pairs taken from ADP-bound and ATP-bound trajectories for which the similarity criterion holds; ADPγ ATP and ADPγ ATP denote all individual ADP and ATP vectors from this set, respectively, i.e., such vectors that each of them is similar to at least one ATP (ADP) vector, respectively.
Set ADPγ NN. This is the set of vector pairs satisfying the similarity criterion that originate from ADP-bound trajectories and trajectories with no nucleotide bound. ADPγ NN and ADPγ NN symbolize all individual ADP and NN vectors from this set, respectively, i.e., such vectors that each of them is similar to at least one NN (ADP) vector, respectively.
Set ATPγ NN. This is the set of vector pairs from ADP-bound and trajectories with no nucleotide bound for which the similarity criterion holds. ATPγ NN and ATPγ NN symbolize all individual ATP and NN vectors from this set, respectively, i.e., such vectors that each of them is similar to at least one NN (ATP) vector, respectively.
With the above definitions of sets, we define the following classes of vectors:
ADP-unique vectors. These are the set of vectors from ADPγ ADP that do not appear in either ADPγ ATP or ADPγ NN. These reflect motion that is unique to the ADP-bound state.
ATP-unique vectors. These are the set of vectors from ATPγ ATP that do not appear in either ATPγ ADP or ATPγ NN. These reflect motion that is unique to the ATP-bound state.
NN (no bound nucleotide) -unique vectors. These are the set of vectors from NNγ NN that do not appear in ADPγ NN or ATPγ NN. These reflect motion that is unique to the NN state.
Nucleotide-mutual vectors (NUC-mutual). These are those vectors from ADPγ ADP and ADPγ ATP that do not appear in ADPγ NN; or analogously, those from ATPγ ATP and ATPγ ADP that do not appear in ATPγ NN. These describe the behavior of the NBD upon the binding of nucleotide, regardless of its identity.
No bound nucleotide-mutual vectors (NN-mutual). These are those vectors from ADPγ ADP and ADPγ NN that do not belong to ADPγ ATP; or analogously, those from ATPγ ATP and ATPγ NN that do not belong to ATPγ ADP. These vectors describe the basal behavior of the NBD when no nucleotide is bound.
All-mutual vectors. These are those vectors that appear simultaneously in ADPγ ADP and ADPγ ATP and ADPγ NN, or analogously, those that appear simultaneously in ATPγ ATP and ATPγ ATP and ATPγ NN, or analogously, those that appear simultaneously in NNγ NN and ATPγ NN and ADPγ NN. These vectors describe the basal behavior of the NBD, in all its binding states.
In addition, we defined the active-site or fragment vectors. An active-site or fragment vector was defined as a vector containing only a subset of the parent principal component coefficients, in which only the residues of the active site or fragment of interest were included. Two such active-site vectors were considered similar if the absolute value of the cosine of the angle between them was ≥ 0.40. The ‘active-site’ was taken as the set of the following residues (including the cross-helices): 9-18, 35-38, 70-72, 145-149, 174-184, 197-206, 230-235, 265-276, 335-343, and 365-378. These residues were selected either because of their location in the active site or due to previous implication in Hsp70 function as suggested by the literature.8,9,20,24,26,35-37
Rotational Component, ρ, of an Eigenvector
In Essential Dynamics, each eigenvector describes a particular mode of motion, which may be observed visually by projecting the vector onto the coordinates of the protein. The displacement of a given Cα atom, resulting from the projection of such an eigenvector, can be thought to contain a certain degree of rotational motion about a principal axis in its parent sub-domain. The net rotational component of an eigenvector, termed ρ here, about a selected sub-domain principal axis, then becomes the average of such rotational contributions from all the Cα atoms in the sub-domain of interest, as expressed by equation (1).
| (1) |
where are the x, y, and z components, respectively, of the part of the ith eigenvector corresponding to atom Cαj, is the component of the position vector of atom Cαj, perpendicular to the principal (rotation) axis, n is the number of residues, and ∥o∥ denotes the Euclidean norm of a vector. The mean structure (averaged over all snapshots) employed in the calculation of all quantities ρ was the mean structure from a reference ADP trajectory (arbitrarily selected as trajectory ADP1).
Weighted Coefficient Average Vector: vω
Each vector class may be analyzed by the use of a weighted coefficient vector, vω, which identifies the Cα atoms that are predominantly affected by the member vectors of a given eigenvector class. In forming vω, each member, vi, is split into three-coordinate sub-vectors, which correspond to the Cα coefficients of atoms in the parent eigenvector, vi. A new vector, , is then formed, whose elements are the magnitudes of the sub-vectors in vi. A weighted average of all the vectors, using normalized λ values from the parent eigenvectors as weights, forms the vector , which is then itself normalized to produce the vector vω, as expressed by equations (2-4).
| (2) |
| (3) |
with
| (4) |
where the meaning of ∥vij∥ is explained after equation (1), λi is the eigenvalue corresponding to the ith eigenvector and the sum is calculated over the first 100 eigenvector sorted by their eigenvalues in the descending order.
The magnitude of each position within this latter vector (vω) reflects a combination of both the frequency and loading of principal coordinate values for each Cα atom within the protein structure, as imposed by the vector class of interest. The weighted coefficient vector vω therefore identifies those regions within the protein that are collectively most affected by a given vector class.
Class Fragment Vectors, fr
A fragment vector fr, may be obtained for a selected fragment with a given secondary structure r within the NBD, for a chosen vector class. Taking the sum of eigenvector components for a given structural element produces a ‘net’ vector that illustrates the effect of the eigenvector on the element when taken as a simplified unit. Scaling by a normalized λ value for all such elements across the members of a class and averaging provides the fragment vector fr. The fragment vector reflects the net influence of the class on the structural element, and inherently contains aspects of the direction, magnitude, and λ contribution of its member vectors.
Results and Discussion
A Global Perspective of the NBD
A preliminary analysis of the 14 molecular dynamics trajectories (6 with bound ADP, 6 with bound ATP, and 2 without nucleotide) revealed a similar time-averaged structure of the NBD, with moderate or small changes in the local state of the nucleotide-binding pocket. Table 1 summarizes the RMSDs, as measured between the average structure for runs of like-binding state (averaged over the last 60% of trajectory frames for runs of the same state), with respect to the crystal structure of the Bos taurus NBD domain (pdb code 3C7N:B); The apparently similar conformation mutually shared by these binding states, and especially between the ATP- and ADP-bound forms, reflects the general difficulty experienced over the past 20 years in experimentally pin-pointing broad structural differences between the ATP- and ADP-bound variants of the domain.3,20-22
Table 1.
RMSD of mean structures with respect to crystal structure
| Structure | RMSD to crystal structure* [Å] | τ angle (deg) compared to 48.2° in the crystal | δ angle (deg) compared to 67.1° in the crystal. |
|---|---|---|---|
| Mean of ADP trajectories | 2.77 | 53.7 | 59.4 |
| Mean of ATP trajectories | 2.84 | 52.9 | 58.4 |
| Mean of NN trajectories | 2.86 | 54.8 | 58.8 |
Bos Taurus 3C7N:B, residues 5-378
Histograms of the δ and τ angles (where the angles are defined in Figures 1C and 1D) for each state are illustrated in Figure 2. Both ATP- and ADP-bound trajectories display the same range of possible δ/τ angles. For nucleotide-bound states, the τ angle exhibits the largest breadth, lying in a range of ~30° -65°; the δ angle generally lies in a smaller window of 50° - 65°. Although the no-nucleotide trajectories lie in the expected range of δ and τ angles, they display a narrower (by ~10°) range of δ and τ, especially towards low values of δ and τ. It should be noted, though, that only two non-nucleotide trajectories were simulated, as opposed to six trajectories for each of the other two systems.
Figure 2.
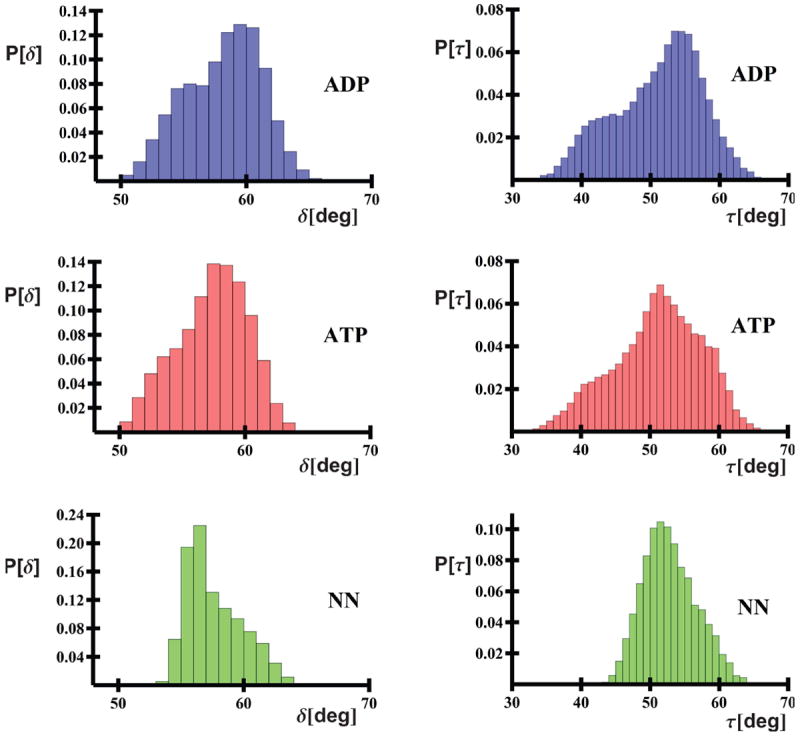
Histograms of τ and δ angles collected from the last 60% of trajectories as a function of state.
An analysis of histograms for individual trajectories (Figure S2) indicates that the distributions of the τ angle for the ATP-bound systems are unimodal, with their centers located either at low or mid τ angle values. Conversely, the τ angle distributions are often bimodal for ADP-bound systems (Figure S2). This greater flexibility of the τ angle is confirmed in Figure 3, which shows the potentials of mean force for ATP- and ADP-bound systems, plotted in terms of their δ and τ angles; these surfaces cover data from all trajectories of the respective binding type. It can be seen that the PMF contours of the ATP-bound system form a ravine with bottom forming an about 45° angle with the δ axis (Figure 3A), which indicates that, for the ATP-bound system, domain motion occurs in a highly correlated manner. Conversely, the PMF contours for the ADP-bound system, form a more round basin (Figure 3B) this indicating that the δ and τ angles vary in a more independent manner, indicating that a larger breadth of both in-plane and out-of-plane motions are simultaneously possible. It can also be noted that the low PMF region has a broader basin at larger δ/τ values for the ADP-bound system than for the ATP-bound system, which is consistent with the results of earlier MD simulations by Woo et al.23 Nonetheless, it should be noted that the differences between the ranges of the δ and τ angles reported here are less substantial than those suggested by Woo et al.23, whose work analyzed data from only one much shorter trajectory for each system.
Figure 3.

PMF surfaces of (A) the ATP-bound and (B) ADP-bound NBD (right) in the τ and δ angles (degrees) collected from the last 60% of trajectories. The PMF values of the contours (in kcal/mol) are indicated.
Fine Movements of the NBD
The analysis of the δ and τ angles in the previous section suggests that the NBD domain does not undergo drastic conformational changes in different binding states, but, to various extents, remains similar in each form. Such a conclusion suggests that a change in binding state evokes subtle rather than gross structural changes; these structural tendencies become apparent with a more detailed analysis of the behavior or the NBD.
Generally, the first several eigenvectors of highest eigenvalue (λi) are sufficient to almost completely characterize the variation of the system at hand in an essential dynamics analysis. Interestingly, the number of vectors necessary to describe at least 70% of the fluctuations of the protein was not the same across the various binding states of the NBD. For the ADP-bound systems, 70% of the net variation is reached after a progressive sum of the first 1 to 10 eigenvectors, while for the ATP-bound trajectories, 70% fluctuation is accounted for by 6 to 12 eigenvectors; this point is attained for the NN system after 8 to 10 vectors. This would suggest that the behavior of the ADP state is least complex, requiring the fewest vectors to describe the behavior adequately. This is in accord with the previously observed freedom of the values of the τ/δ pair value for the ADP-bound state (Figure 3). The ATP state, on the other hand, requires the most eigenvectors. Indeed, multiple-component dominance could readily provide a mechanism for allosteric communication and control within the NBD. In particular, several principal components of moderate size could work together differentially in order to elicit local structural changes, without the necessity of drastic domain remodeling, supporting the aforementioned concept of subtle rather than gross state-dependent structural change. This is consistent with the experimentally suggested hypothesis that the allosteric network is triggered by small sub-domain re-orientations and interface perturbations,20 motions that clearly do not entail major domain re-organization. Several moderate eigenvectors also enable tuning of and communication within the system: motions can be brought into significant principal coordinate values through modulation by co-chaperones or the SBD, effectively dominating the functionally-important modes of motion. Indeed, such momentary dominance of principal coordinates is especially notable for the ATP system (see Figures S3-S5). This agrees with the idea of a functionality-inherent NBD landscape from which conformational selections are made.20 Moreover, the necessity of multiple (and not two or three) such eigenvectors indicates the existence of a complex allosteric network that largely operates through a combinatorial mechanism.
Classifying Motions of the NBD
Given the general structural similarity among the three states of the NBD studied, certain eigenvectors should be expected to mutually re-appear in similar forms across trajectories. On the other hand, trajectories of the same state should express certain characteristic vectors that are not present in other states. Vectors between trajectories were compared by the absolute value of the cosine of the angle between them, which reflects their degree of likeness: with 1 and 0 being the parallel (highly similar) and perpendicular (non-similar) extremes, respectively. Following such logic, five different groups of vectors were identified: those particular to each of the ATP-bound, ADP-bound, and NN-states, those mutual to only nucleotide-bearing trajectories, those mutual to the NN state, and finally, those mutual to all states of the NBD. For brevity, these will be referred to as the ADP-unique, ATP-unique, NN-unique, NUC-mutual, NN-mutual, and All-Mutual classes.
Figure S6 presents a graphical representation of the distribution of vectors among the ADP-unique, NN-mutual, NUC-mutual, and All-Mutual groupings for ADP-bound trajectories. As foreshadowed, vectors of lower number (corresponding to larger values of λ) generally identify with the All-Mutual or nucleotide-mutual vector classes. This supports the hypothesis that the behavior of the NBD is generally analogous in all states, and that the binding of a nucleotide induces small-scale to moderate-sized structural changes. In hindsight, this also supports the previous difficulty in experimentally distinguishing the various states of the NBD.3,20,22 ADP-unique vectors occur at higher vector numbers, consistent with the concept that the nucleotide state does not play a role in defining the protein dynamics, but rather in its regulation; given that 70% fluctuation is accounted for after 1 to 10 components in these systems, the position of ADP-unique eigenvectors near the tail-end of this threshold places them in an ideal position for allosteric regulation, wherein such motions could be activated and thereby participate in periodically occurring coordinate value maxima or by regulation through co-chaperones or the SBD. Figure S7 portrays that this is also the case for ATP-bound trajectories; taking from 6 to 12 first vectors to reach 70% variation, more vectors naturally appear in the description of the system, although the same relationship holds, i.e., the majority of vectors are of the All-mutual or NN-mutual type, with ATP-unique vectors appearing towards the 70% threshold. An analogous distribution of eigenvectors is also exhibited for the NN state (Figure S8).
Sub-Domain Rotation: A Common Theme
Sub-domain rotation was found to be the predominant theme in the dynamics of the NBD. Aside from the individual characteristics of an eigenvector, the rotational components of the vecotr, ρ, about each of the sub-domain principal axes illustrates that the dynamics of the NBD is dominated by local re-orientations and rotations of its subdomains. This is illustrated in Figure 4, which plots the total rotational component (along the three major principal axes) for each domain as a function of eigenvector number, for an ADP-bound trajectory; over-lain are the rotational components as calculated for a set of normalized vectors with random coefficients. The random set naturally represents a system that undergoes no net rotation, and serves to define a baseline ρ value above which an eigenvector may be classified as inducing rotation. For any domain, net rotation decreases with increasing eigenvector number. Eventually, rotation is no longer distinguishable at distant eigenvectors; for the first 12 or so eigenvectors, this decrease is not prominent, and the rotational components clearly exhibit interplay of magnitude as a function of eigenvector number. Adjacent eigenvectors produce various degrees of rotation for each sub-domain. A given combination of eigenvectors can therefore be expected to produce different rotational behaviors: an important conclusion that corroborates the afore-mentioned combinatorial mechanism of domain behavior and allosteric control. Furthermore, Figure 4 illustrates that the sub-domains do not rotate to the same extent. Early eigenvectors produce the most rotation in the Ib and IIb sub-domains, which is consistent with experimental reports stating significant rotation of the IIb subdomain.20,22 The IIa subdomain reflects a lesser degree of rotation, with domain Ia following last. The rotational mobility of the subdomains thus follows the order: IIb> Ib > IIa > Ia. This same relationship holds for all trajectories (Figure S9). These findings support the experimentally observed module-like behavior of subdomains in the NBD, wherein subdomain rotation was highlighted as a key motion that furthermore enables allostery by sites located at interfaces.3,20,22 The above-mentioned order of rotational mobility, and especially the significant mobility of the IIb subdomain, is further corroborated by residual dipolar coupling experiments of the NBD22 and by crystal structures38, in which the binding of BAG induced conformational changes in the II subdomain of the NBD.
Figure 4.
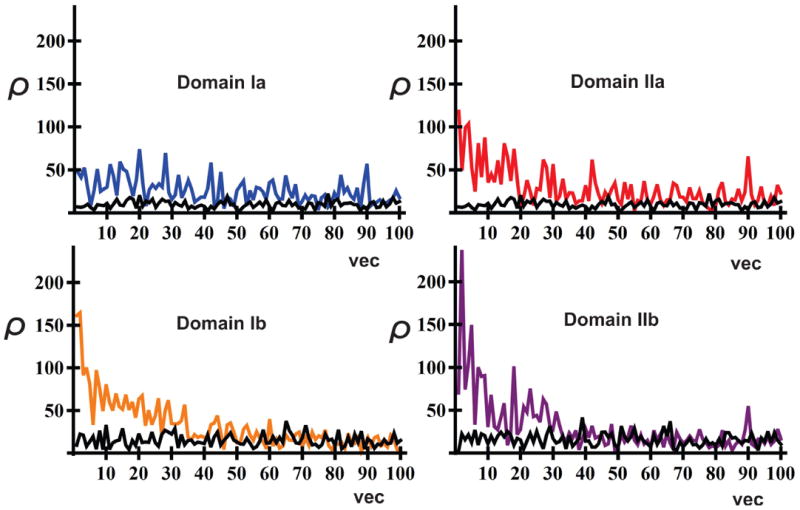
The net rotational component (ρ; see section “Rotational Component, ρ, of an Eigenvector” for definition) about the three major principal axes for each NBD sub-domain as a function of eigenvector (vec), for the ADP-bound trajectory ADP1. For comparison, the total rotational component (ρ) for a set of random vectors is shown in black.
From a vector-class perspective, this rotational tendency is also reproduced across the All-mutual, NUC-mutual and NN-mutual vector classes. As mentioned earlier, these three classes reflect the underlying character of the NBD domain. Figure 5 illustrates the distributions of the rotational components, ρ, for eigenvectors from all six vector classes. In general, each class covers a broad range of ρ values. Looking at mutual-type vectors (Figure 5A), high ρ rotation (which is manifested in this Figure by the appearance of histogram bars at high values of ρ) is induced in the IIb subdomain, supporting the aforementioned rotational order. All-mutual vectors produce high-end rotation in all three of the IIa, Ib, and IIb domains (IIb > Ib> IIa). NN-mutual vectors produce a parallel extended ρ pattern, however, Ib rotation is less prominent and rotation in the remaining domains does not occur over a broad range, but rather at select ρ values. NUC-mutual vectors show parallel but diminished rotation in the Ib, IIa, and IIb domains. In contrast to mutual-type vectors, the ATP-, ADP-, and NN-unique classes (Figure 5B) do not exhibit high-lying ρ ranges, and induce comparable rotations in all domains, with the IIb domain being most active for the ATP-unique class. Subdomain rotation is therefore an innate feature of the NBD, and is not the target effect of nucleotide binding.
Figure 5.
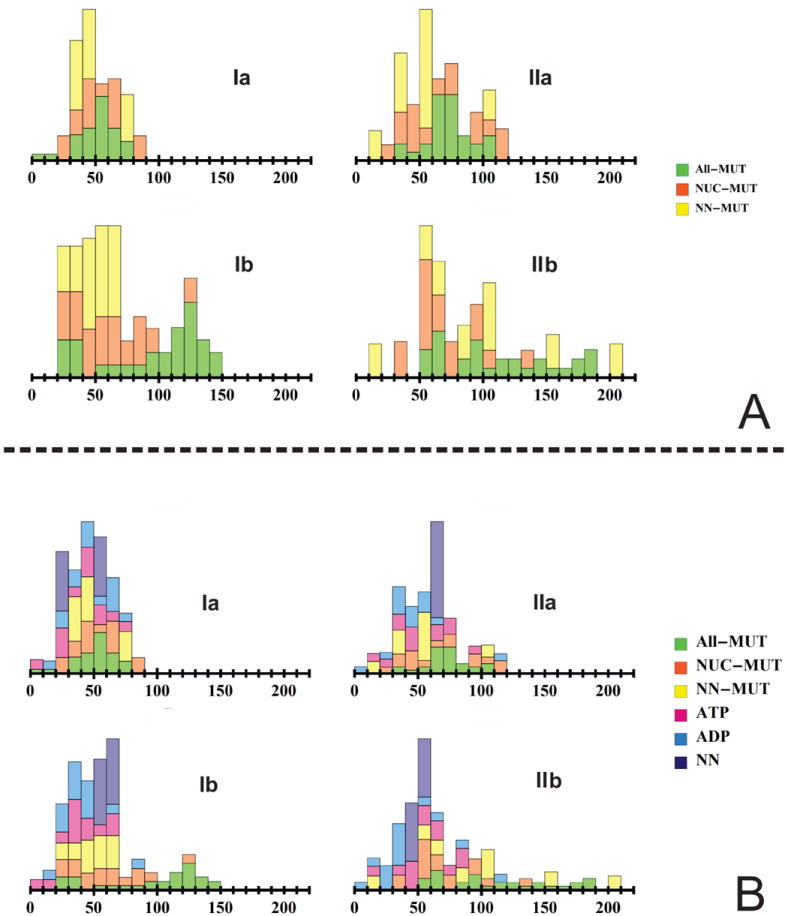
Stacked probability histograms of the net rotational component, ρ, for eigenvectors from each vector class, on a sub-domain basis. Bar lengths indicate the relative fractions of vectors in the vector class that fall within the given ρ window. A. All-mutual, NUC-mutual and Apo-mutual vectors. B. ATP-unique, ADP-unique and Apo-unique vectors.
All-Mutual and NN-Mutual Themes
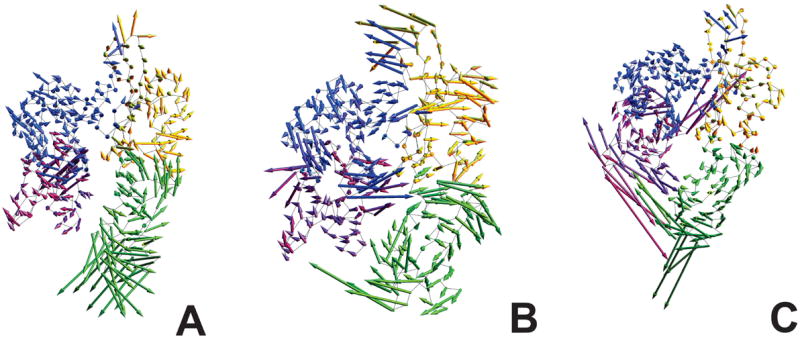
Figure 6 projects the motion of a vector in the All-mutual class onto an average ADP structure. This vector describes the internal rotation of the I and II subdomains, with the IIb subdomain being most affected. As suggested experimentally,20 the sub-domains act as ‘units’, with motion occurring internally in terms of the movement and re-orientation of, in general, whole sub-domain compartments. Anti-correlated rotation occurs along the II subdomain, effectively splitting it into two, namely, the IIB sub-domain rotates downwards, while the IIA subdomain rotates upwards. The IA and IIA subunits rotate in synchrony, in an anti-direction to the IIB domain. The net motion may be categorized as an opening of the domain in the out-of-plane x direction (Figure 1B). The greatest rotation occurs for the IA, IB and IIB sub-domains. The key α-helix (approx. residues 268-276) guarding entry into the active site is effectively displaced with the downward motion of the IIB domain. As expected from the behavior of the all-mutual class, this all-mutual vector induces large-scale module-like rotation of the subdomains of the NBD. A similar behavior is observed for ATP.
Figure 6.

Projection of the motion of an ADP-derived all-MUTUAL class vector onto an average ADP structure shown in the Cα-trace representation. The motions of the Cα atoms are represented by arrows anchored at the respective Cα’s. Each arrow points to the direction in which the Cα atom moves upon the motion along the respective eigenvector and its length is proportional to the relative extent of this motion. Front (A), left (B), and right (B) views of the projected motion of the vector. [ADP5: vector 2, 14% of Σλ].
The contribution of each atom to the vectors of the All-mutual class is illustrated in Figure 7A. Here, a visualization of the weighted coefficient vector for the all-mutual class indicates that this class describes the joint motion of whole sub-domains; vectors do not target individual Cα positions, but rather encompass the motion of whole blocks of atoms. Accordingly, each domain is marked by a relatively uniform distribution of vω components throughout the volume of each sub-domain. Subdomains Ib and IIb display the largest component vω values, indicating that All-mutual class vectors largely concentrate their dynamics into the motion of these two subdomains. In synergy with the previously discussed rotational analysis, the vω coefficient vector for the All-mutual class therefore confirms that All-mutual behavior entails the block-like rotation of the subdomains of the NBD, with motion being concentrated in Ib and IIb subunits. Since All-MUTUAL vectors generally occupy high λ values, these vectors dominate the dynamics of the NBD. This is in accord with experimental work3,20,22 that highlighted sub-domain rotation as a key feature of the NBD. In addition to these major features, short stretches of particularly active Cα atoms were also found on the protein surface; these include some exterior loops on the Ib and IIb sub-domains, and a helix located on the backside of the Ib subdomain.
Figure 7.

Illustration of vω for each of the: A. All-mutual, B. NUC-mutual, C. NN- mutual, D. ADP-unique, E. ATP-unique, and F. Apo-unique classes. Sphere size and color reflect the magnitude of the contribution of an atom to the class.
The NN-mutual class of vectors contains those vectors that are shared with the no-nucleotide binding state. Although these vectors do not appear across all states as did the vectors of the all-mutual class, different binding states of the NBD may contain various NN-mutual vectors, as was demonstrated in Figures S6 to S8. In fact (in addition to the NUC-mutual class for nucleotide-containing trajectories), vectors from the All-mutual and NN-mutual classes account for the bulk of the low number (high λ-value) eigenvectors that are present in each system. The weighted coefficient vector, vω, for these vector classes is presented in Figure 7C; as expected, the NN-mutual class predominantly describes the motion of the IIb subdomain. Interestingly, several coefficient ‘hot-spots’ for this class are located opposite the IIb subdomain, as expressed by prominent sphere size in Figure 7C. The motion of these sites can therefore be implicated in concurrent trends in IIb subdomain behavior, suggesting that these locations are hot-spots for allosteric regulation and are cooperative. Moreover, the motion of domain IIb appears to be correlated to that of the Ia domain. This is in agreement with Figure 5A, which revealed the occurrence of specific ρ bars in both the IIa and IIb subdomains, suggesting that the rotation of both domains is correlated. Indeed, Figure S2 produces ‘pairs’ of τ and δ angles, which would be in accord with such ρ-value rotational interdependency. Thus, NN-mutual class vectors describe the rotation of the whole IIb sub-domain, with a concurrent rotation of lesser magnitude occurring in subdomain Ia. This is exemplified by vector 4 of trajectory NN1 (6% of Σλ), which illustrates an out-of-plane rotation of the II subdomain (around the y axis, see Figure S10).
Nucleotide-Bound Themes
The NUC-mutual class vectors describe the behavior of nucleotide-bound trajectories, regardless of the identity of the nucleotide. Rotationally, subdomains are less active than in the NN-mutual or All-mutual classes, although the rotational order of the subdomains (IIb> Ib > IIa > Ia) is conserved (Figure 7A). Figure 7B illustrates the weighted coefficient vector, vω, for this vector class, more detailed plots for the ADP- and ATP-bound NBD are shown in Figures S11-S13. Although modest coefficient magnitudes are uniformly dispersed within each sub-domain (in accord with the moderate rotational potential), this vector class highlights the motion of ‘hot-spots’ within the NBD; these are depicted in Figure 8A. The helix behind subdomain I (residues ~78- 91) bears the largest weighted coefficient magnitude, even when compared to the magnitudes observed throughout the NBD in other classes; this implies significant movement of this helix. This region is directly behind residue LYS 71–a residue presumed to be involved in the hydrolysis of ATP.36,37 Indeed, structural changes in this region would be expected to modulate hydrolysis potential and, in retrospect, be sensitive to the presence of nucleotide. This area is furthermore within the binding site mapped out for the α-SBD indicated in X-ray ADP- and ATP-bound structures,3 and houses residue ARG 155, a residue critical for inter-domain communication.8 Although several of these hot-spots re-occur in other classes, the combined set of sites affected is not the same—further supporting a combinatorial mechanism of allosteric control. Projecting a NUC-mutual vector onto the structure of the NBD (Figure 9) does indeed reveal that sub-domain rotation is diminished, and that the demonstrated eigenvector describes the displacement of hot-spot atoms predominantly.
Figure 8.

Stretches of highly active Cα atoms, shown in red, per vector class. A. NUC-mutual hot-spots. B. ADP-unique hot-spots. C. ATP-unique hot-spots. D. NN-unique hot-spots.
Figure 9.
Projection of the motion of a NUC-mutual class vector onto an average ADP structure shown in the Cα-trace representation. The motions of the Cα atoms are represented by arrows anchored at the respective Cα’s. Each arrow points to the direction in which the Cα atom moves upon the motion along the respective eigenvector and its length is proportional to the relative extent of this motion. Front (A), left (B), and right (C) views of the projected motion of the vector. [ADP5: vector 7, 1% of Σλ].
Figure 7D illustrates the weighted coefficient vector, vω, for ADP-unique vectors. These vectors target certain loops/regions on the surface of the NBD, and further uniformly encompass fragments of the IIa and IIb subdomains with moderate coefficient values. The IIb domain is again most affected. Nonetheless, as Figure 7B indicates, the affected fragments do not induce considerable sub-domain rotation. Instead, this vector class predominantly describes either non-rotational movement of NBD fragments, or, in particular, ‘hot-spots’ at key locations on the NBD. The regions within the II subdomain, namely the terminal loops at its base, active-site shielding fragments on the I subdomain (red, Figure 8B), and along a set of main helices that run the long axis of the II domain (yellow, Figure 8B) are of distinct mobility. Indeed, principal vectors were identified that targeted this region in general causing the active (nucleotide-binding) site to open, and the IIB domain to translate away from the core of the protein (vector 7, ADP3, 2.6% of Σλ; vector 11, ADP3, 1.8% of Σλ). The region behind LYS 71 was also found to move away from body of the NBD. Such motions could provide an avenue for ADP loss, enabling active site access for nucleotide exchange by nucleotide exchange factors (NEFs)). The yellow helices that run the length of the II domain (Figure 9B) are fully unique to this class, and likely act as a transmission medium for hot-spot modulation at three sites: the base of the IIb domain, the external loops of IIa, and at the IIa/IIb boundary, which binds to the hydrophobic rings of a bound nucleotide.
Figure 7E illustrates the weighted coefficient vector, vω, for ATP-unique vectors. This class of vectors acts almost exclusively on ‘hot-spots’ within the NBD. The coefficient contributions for the remainder of the protein are significantly smaller than in any other class: ATP-unique vectors target specific fragments while holding the rest uninfluenced. Figure 5B indicates that rotation is not a central theme. Affected ‘hot-spots’ are illustrated in Figure 8C. The projection of ATP-unique principal components on the structures of ATP-bound trajectories confirms that motion is concentrated in fragment ‘hot-spots’, with minimal motion elsewhere. Such apparent ‘rigidity’ may play a role in functional reactivity, since gross protein dynamics is at least temporarily non-induced when ATP-vector contributions are high—a situation that may favor external protein-protein interactions or the conformational alignment of ATP for hydrolysis to occur successfully at a higher rate. Accordingly, residue LYS 71 is present in a hotspot at the boundary of the Ia and Ib subdomains, a catalytic residue involved in ATP hydrolysis.26,36
NN-Unique Themes
Figure 7F illustrates the weighted coefficient vector, vω, for NN-unique vectors. This class of vectors resembles the ADP-unique class at first glance: similar hot-spots are activated, and contributions to the IIb subdomain are prominent. As in all unique-class vectors, rotation is not a central theme (Figure 5B). The enhanced mobility of two fragments at the boundary of the Ia and IIb subdomains (yellow tubes in Figure 8D) are characteristic of the NN-unique class. The top fragment contains the residue ARG 155, which has already been identified as important for inter-domain communication.8,26 In fact, it has been suggested that the presence of a nucleotide is transmitted by LYS 71 (involved in the hydrolysis of ATP) to PRO 147 in an adjacent helix (Figure 7F, 9D); the latter acts as a molecular switch, and conformational information is passed to the surface-exposed residue ARG 155.26 The corresponding fragment encompassing LYS 71 is also implicated as significant to the NN-unique class (Figure 8D). The mobility of these fragments in the NN state may therefore duly act as a flag for the empty state of the active site.
Vector Classes: Hotspots
The various hot-spots across all classes are summarized in Figure 8. Certain hot-spots reoccur, and are shared among classes. Nonetheless, each class bears a unique combination of such regions, which supports a combinatorial mechanism to the dynamics of the NBD, and consequently, to its allosteric control. Many of these hot spots coincide with sites already implicated in protein-protein or allosteric interactions. For example, the two helices of the IIb subdomain have already been suggested as allosteric ‘hot-spots’ by NMR analysis.20 Furthermore, the terminal loops of the IIb subdomain have already been identified as the binding site for the nucleotide-exchange factor Bag2.38 Accordingly, the afore-mentioned helix and contiguous β-sheet of the IIb domain also serve as the binding site for the NEF GrpE.9
Fragment Vectors
The investigation of principal components presented to date generally focused on the motion of relatively external regions of the NBD, with moderate to small emphasis on the nucleotide-binding site. This is concordant with external (usually solvent-exposed) placement of these fragments and, thereby, a fairly unrestricted space in which they can move compared to the core residues. Nonetheless, although smaller in magnitude, motion within the core of the protein, and specifically within the active site, should be expected to play a role in the dynamics of the NBD, especially in an ATP-ase, in which changes in binding state dictate the function of the protein. Figure 10 illustrates the fragment vectors for active site structures as a function of class. As expected, mutual-class vectors entail the movement of large blocks of atoms within the NBD (in accord with its module-like tendency for sub-domain rotation). This sweeps along atoms in the active site, and so large fragment vectors are seen across mutual-class vectors. Interestingly, the helices forming the upper cross-helix at the boundary of the Ia and IIa subdomain (cyan, Figure 10:A-C) show a tendency for synchronous motion: both fragment vectors move together in the same direction. Unique-type vectors, on the other hand, demonstrate an anti-correlated behavior. The motion of these helices occurs in a piston-like fashion for the ATP-unique class. Moreover, despite the greater coefficient loading of the active site for the ADP-class (Figure 7D), the ATP-class (Figure 10E) presents longer active-site fragment vectors, which means that the active-site in the ADP-bound state undergoes significantly more random motion than in the ATP-bound state, which expresses rather a restricted/directional behavior. The ATP-unique class also activates and suppresses a distinct set of active site vectors, in contrast to the ADP-unique class, which suppresses most, and the NN-unique class, which heavily activates all.
Figure 10.
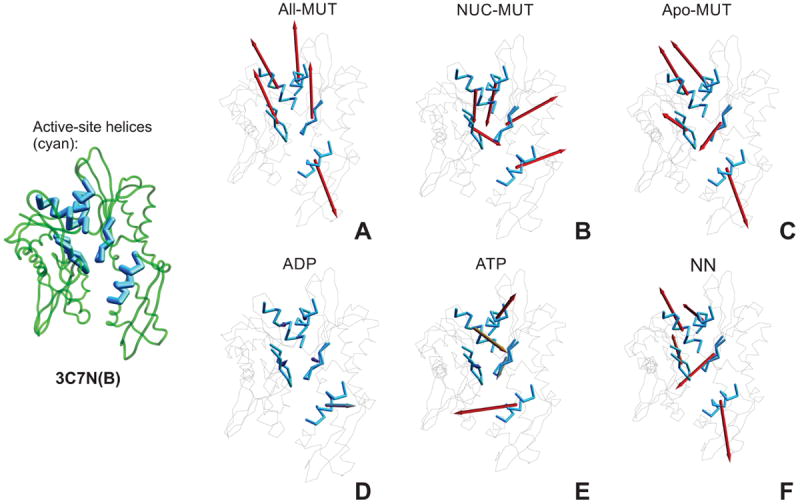
Active-site fragment vectors, per vector class: A. All-mutual, B. NUC-mutual, C. NN- mutual, D. ADP-unique, E. ATP-unique class, and F. NN-unique. Each vector is shown as an arrow anchored in the center of the corresponding fragment, with direction and length corresponding to the direction and extent of the motion of this fragment follwing the respective eigenvector. The active site and its immediate periphery are shown in blue. The length of vectors reflects their magnitude, to a maximal cut-off. For clarity, the structure of the NBD with active-site components shown in thicker lines is included on the left to panels A – E.
The Nucleotide-Binding Site: The Influence of ADP and ATP Binding
Inspection of the ADP-unique principal components and their descendant active site vectors reveals that the ADP-bound active site shows consistent behavior. A key feature includes the outward opening of the IIB helix that over-shadows the active-site (cyan, Figure 11B), whose displacement efficiently opens the binding site for ADP loss or NEF access. The two crossing helices (bridging the IA and IIA subdomains) perpendicular to the plane of the domain, which could serve as an allosteric transmission mechanism to other regions of the I and II subdomains, or externally, to the SBD or cochaperones undergo a concomitant motion. The crossing helices (forming part of a hydrophobic cleft between the I and II subdomains) have already been suggested to play a role in the latter,20,22 and lie in the binding region of the inter-domain linker, which has been implicated in state-influenced sub-domain rotation.20 Indeed, this region serves as the binding site of DnaJ, a cochaperone that is involved in regulating ATP hydrolysis.20 Related ADP-unique vectors accentuate the motion of the right, C-terminal, crossing helix in regards to the other. Figure 11A depicts the active site of a trend of the ATP-unique principal component. Here, the crossing helices are roughly equally engaged, and demonstrate a motion in the plane of the domain. The pronounced motion of LYS 71 and that of the notorious proline switch,26 PRO 147 are coincident. The motion of LYS 71 and PRO 147 appear synchronized, with LYS 71 approaching the phosphate tail of the ATP molecule; this likely presents an approach mechanism enabling ATP hydrolysis. Related ATP-unique active site vectors depict conserved dominance of both cross helices, with additional influence of residues along the active-site loops, whose role could serve in the facilitation of hydrolysis by nucleotide re-orientation.
Figure 11.
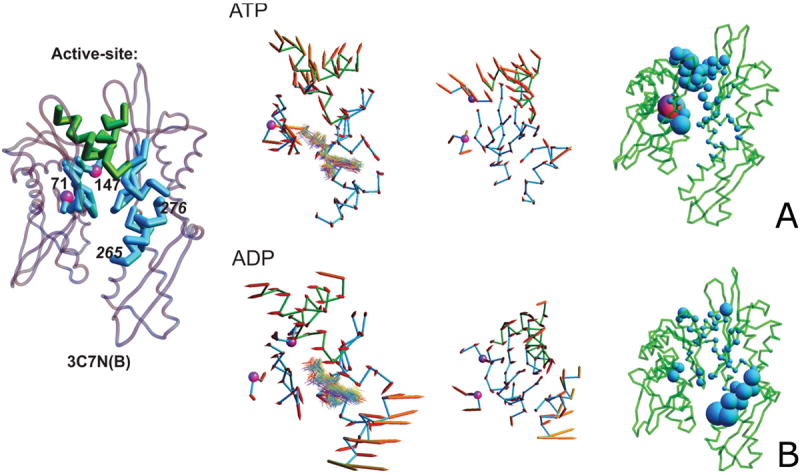
A. Projection of a vector that describes the trend of the motion of the active site, derived from similar ATP-unique principal components. Residues PRO 147 and LYS 71 are shown as purple spheres. The left and middle picture in the panel are front and top view with vectors displayed by arrows anchored in the Cα atoms, with directions and lengths corresponding to the directions and extent of motions of the corresponding Cα atoms following the trend motion; in the right section, the magnitudes of displacements of individual residues are represented as blobs. In the left section of the panel, snapshots of the nucleotide molecule (in wireframe representation) are superposed on the picture. B. Same for the ADP-unique principal component. For clarity, in panels A and B, the structure of the NBD with active-site components shown in thicker lines and the numbers of the residues referred to in the text are included on the left to panels A and B.
The Active Site: The Presence of Ions
The active site of ADP- and ATP-bound systems exhibited variant sensitivity to the presence of ions. Ion loss from the active site was a frequent phenomenon. Mg2+ was lost in 4 out of 6 ADP trajectories (trajectories 2-5); on the other hand, K+ ions were not lost in these trajectories. For ATP trajectories, both Mg2+ and K+ were lost in 3 trajectories (trajectories 4-6) and, additionally, only K+ was lost in one more trajectory (trajectory 2). For one ATP trajectory, magnesium ions were present in both magnesium-binding sites. Consequences of ion loss appeared in the hierarchy of state-unique eigenvectors. ATP eigenvectors (Figure S7) are effectively pushed to higher principal component numbers (lower λ value) upon disturbance of the active-site’s ionic structure. Trajectories 1 and 2 therefore retain ATP-unique vectors at lower principal component numbers, while a shift in magnesium binding site or its complete loss results in an up-shift of ATP-unique vector positions for the remaining trajectories. The ATP-bound active site is thus most sensitive to the correct coordination of the magnesium ion, as loss of potassium, with the concurrent retention of Mg2+, does not produce this up-shift (Figure S7). Indeed, it has been verified experimentally20 and by simulation17 that ATP hydrolysis is critically dependent on the correct placement of ions within the active site. ADP-bound systems, on the other hand, did not suggest this sensitivity to magnesium, with potassium playing a key role in stabilizing the system, as no trajectories depicted loss of the latter. Understandably, with the hydrolysis reaction having already taken place, magnesium no longer plays a key mechanistic role. Figure 12 illustrates the positioning of ions in the active sites of ADP- and ATP-bearing trajectories, respectively.
Figure 12.

The active sites from a sample (A) ADP-bound and (B) ATP-bound trajectory, respectively. Snapshots of the nucleotide molecule (in wireframe representation) and ions (represented as spheres; red: Mg2+, blue: K+) are superposed on the pictures.
On the other hand, despite the fact that ions move in and out of the binding site, it can be seen from Figure 12 that the nucleotide molecule stays nearly in place and does not change its conformation. This feature results from tight binding of the nucleotide molecule to the amino-acid side chains of the nucleotide-binding site.
Conclusions
Following all-atom canonical molecular dynamics simulations of the Hsp70 NBD on a time scale of 1.0-2.0 μs, an essential dynamics analysis of this domain was conducted for each of its free, ADP-, and ATP-bound forms. Essential Dynamics allowed the behavior of the NBD to be described as a combination of principal component vectors, which were divided into 6 classes of motion, three of which were binding-state specific.
In general, the behavior of the NBD is described predominantly by motions from the All-mutual and NN-mutual classes, which represent basal tendencies that are binding-state independent. All-mutual and NN-mutual motions describe the block-like rotation of individual subdomains (Ia, IIa, Ib, and IIb) which, when taken collectively, form various δ (in-plane) and τ (out-of-plane) angles between the I and II subdomains. The defining property of the NBD is therefore subdomain rotation, which is concordant with the experimental work of Mayer and coworkers,3 Zuiderweg and coworkers,22 and Gierasch and coworkers.20,24,35 Rotation of individual subdomains can occur along individual or multiple local principal axes. The magnitude of executed rotation is subdomain-dependent, and follows the order: IIb> Ib >IIa > Ia. The character of relative domain rotation in the ADP-bound state differs from that in the ATP-bound state, as seen from the respective PMF contours (Figure 3), indicating more concerted scissor-like (out-of-plane) motion for the ATP-bound state and a larger component of the in-plane (“sideways”) motion for the ADP-bound state (as in loose scissors).
The motions specific for the nucleotide-binding state (the ATP-, ADP-, and NN-unique- motions) occur to a smaller extent and affect mainly relatively localized surface regions of individual subdomains (the hot spots) that have a large content of loops. Loop motions in the context of protein functionality were recently investigated by Jernigan and coworkers based on a simplified Gaussian Network Model (GNM).39,40 Remarkable differences in the localization of hot spots corresponding to ‘unique’ class motions are observed between different nucleotide-bound states. From Figure 7 it can be seen that the ADP-unique (Figure 7D) motions affect mainly NBD-Ia and NBD-IIa, which are closer to the linker, while the ATP-unique motion (Figure 7E) affects NBD-Ib and NBD-IIb, which are farther from the linker (residues V389–D393) between the NBD and the SBD. It should be noted that this region was found to undergo remarkable changes upon ATP binding by chemical-shift experiments.20 Apart from the rotation of the whole NBD-I and NBD-II with respect of each other, part of the allosteric control of the dissociation of SBD-α from the NBD after ATP hydrolysis might involve increased motions near the linker region, resulting in its dissociation from the β-sheet it forms with the top section of NBD-IIa in the ATP-bound state (residue K214 – V218). The loose linker could then pull SBD-α, resulting in its dissociation from the NBD. A reverse process could occur upon the replacement of ADP with ATP in the binding site, which would thus partially immobilize NBD-IIa.
Specific hot-spots may re-occur from one class to another. However, the set of hot-spots active in a given vector class is unique and characteristic of that binding state. This supports a combinatorial description of allosteric control, wherein several handles are activated simultaneously.
It should be noted that all the above conclusions were drawn based on MD simulations carried out for the isolated nucleotide-binding domain of the Hsp70 chaperone and the picture of motions might change when the whole chaperone is considered. The presence of of the substrate-binding domain will probably not affect NBD motion in the ADP-bound form in which the two domains do not interact10 but might be important in the ATP-bound form where the two domains are tightly packed.3
The arrangement of ions in the active site is important for the expression of binding state-specific behavior. Indeed, a shift in magnesium ion binding site or its complete loss pushed ATP-unique vectors to lower λ values. The ATP-bound active site was most sensitive to the correct coordination of the magnesium ion, as loss of potassium, with concurrent retention of Mg2+, did not produce this up-shift. ADP-bound systems did not display this sensitivity to magnesium but potassium played a key stabilizing role, as no trajectories depicted its loss.
Supplementary Material
Acknowledgments
We thank Dr. Jarosław Marszałek (Intercollegiate Faculty of Biotechnology, University of Gdańsk and Medical University of Gdańsk, Poland) for helpful comments on the manuscript. This work was supported by grants from the Foundation for Polish Science (grant MPD/2010/5), National Institutes of Health (GM-14312), the National Science Foundation (MCB10-19767), and the Polish National Science Center (DEC-2012/06/A/ST4/00376). Computational resources were provided by (a) Pittsburgh Supercomputer Center through use of the 512-node ANTON supercomputer (grant PSCA10025P), which was made possible through the NIH Award (NIH RC2GM093307) awarded to CMU through the NRBSC (b) Argonne Leadership Computing Facility at Argonne National Laboratory, which is supported by the Office of Science of the U.S. Department of Energy under contract DE-AC02-06CH11357, (c) the Informatics Center of the Metropolitan Academic Network (IC MAN) in Gdańsk, and (d) Interdisciplinary Center of Mathematical and Computer Modeling (ICM) at the University of Warsaw. Our Beowulf clusters at Baker Laboratory of Chemistry, Cornell University and at the Faculty of Chemistry, University of Gdańsk, were also used to run calculations and perform trajectory analysis.
References
- 1.Bukau B, Mayer MP. Hsp70 chaperones: Cellular functions and molecular mechanism. Cell Mol Life Sci. 2005;62:670–684. doi: 10.1007/s00018-004-4464-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bukau D, Weissman J, Horwich A. Molecular chaperones and protein quality control. Cell. 2006;125:443–451. doi: 10.1016/j.cell.2006.04.014. [DOI] [PubMed] [Google Scholar]
- 3.Kityk R, Kopp J, Sinning I, Mayer MP. Structure and dynamics of the ATP-bound open conformation of Hsp70 chaperones. Molecular Cell. 2012;48:863–874. doi: 10.1016/j.molcel.2012.09.023. [DOI] [PubMed] [Google Scholar]
- 4.Gierasch LM, Swain JF, Dinler G, Sivendran R, Montgomery DL, Stotz M. Hsp70 chaperone ligands control domain association via an allosteric mechanism mediated by the interdomain linker. Molecular Cell. 2007;26:27–29. doi: 10.1016/j.molcel.2007.02.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Craig EA, Marszalek J. eLS. John Wiley & Sons Ltd; Chichester: 2011. Hsp70 Chaperones. http://www.els.net. [DOI] [Google Scholar]
- 6.Kampinga HH, Craig EA. The HSP70 chaperone machinery: J proteins as drivers of functional specificity. Nature Reviews Mol Cell Biol. 2010;11:579–592. doi: 10.1038/nrm2941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gestwicki JE, Evans CG, Chang L. Heat shock protein 70 (Hsp70) as an emerging drug target. J Med Chem. 2010;53:4585–4602. doi: 10.1021/jm100054f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Vogel M, Mayer MP, Bukau B. Allosteric Regulation of Hsp70 Chaperones Involves a Conserved Interdomain Linker. J Biol Chem. 2006;281:38705–38711. doi: 10.1074/jbc.M609020200. [DOI] [PubMed] [Google Scholar]
- 9.Bukau B, Horwich AL. The Hsp70 and Hsp60 chaperone machines. Cell. 1988;92:351–366. doi: 10.1016/s0092-8674(00)80928-9. [DOI] [PubMed] [Google Scholar]
- 10.Bertelsen EB, Chang L, Gestwick JE, Zuiderweg ERP. Solution conformation of wild-type E. coli Hsp70 (DnaK) chaperone complexed with ADP and substrate. Proc Natl Acad Sci USA. 2009;106:8471–8476. doi: 10.1073/pnas.0903503106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gołaś E, Maisuradze GG, Senet P, Ołdziej S, Czaplewski C, Scheraga HA, Liwo A. Simulation of the opening and closing of Hsp70 chaperones by coarse-grained molecular dynamics. J Chem Theory Comput. 2012;8:1750–1764. doi: 10.1021/ct200680g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Liwo A, Czaplewski C, Ołdziej S, Rojas AV, KaŸmierkiewicz R, Makowski M, Murarka RK, Scheraga HA. Simulation of protein structure and dynamics with the coarse-grained UNRES force field. In: Voth G, editor. Coarse-Graining of Condensed Phase and Biomolecular Systems. Taylor & Francis; 2008. pp. 107–122. [Google Scholar]
- 13.Kozłowska U, Maisuradze GG, Liwo A, Scheraga HA. Determination of side-chain-rotamer and side-chain and backbone virtual-bond-stretching potentials of mean force from AM1 energy surfaces of terminally-blocked amino-acid residues, for coarse-grained simulations of protein structure and folding. 2. Results. Comparison with statistical potentials, and implementation in the UNRES force field. J Comput Chem. 2010;31:1154–1167. doi: 10.1002/jcc.21402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sieradzan AK, Hansmann UE, Scheraga A, Liwo A. Extension of UNRES force field to treat polypeptide chains with D-amino acid residues. J Chem Theory Comput. 2012;8:4746–4757. doi: 10.1021/ct3005563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Krupa P, Sieradzan AK, Rackovsky S, Baranowski M, Ołdziej S, Scheraga HA, Liwo A, Czaplewski C. Improvement of the treatment of loop structures in the UNRES force field by inclusion of coupling between backbone- and side-chain-local conformational states. J Chem Theory Comput. 2013;9:4620–4632. doi: 10.1021/ct4004977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Nicolaï A, Senet P, Delarue P, Ripoll DR. Human inducible Hsp70: Structures, dynamics, and interdomain communication from all-atom molecular dynamics simulations. J Chem Theory Comput. 2010;6:2501–2519. doi: 10.1021/ct1002169. [DOI] [PubMed] [Google Scholar]
- 17.Hess B, Kutzner C, van der Spoel D, Lindahl E. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J Chem Theory Comput. 2008;4:435–447. doi: 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- 18.van Gunsteren WF, Billeter SR, Eising AA, Hunenberger PH, Krüger PP, Mark AE, Scott WRP, Tironi IG. Biomolecular Simulation: The GROMOS96 manual and user guide. Zurich, Switzerland: Hochschulverlag AG an der ETH Zurich; 1998. [Google Scholar]
- 19.Chiappori F, Merelli I, Colombo G, Milanesi L, Morra G. Molecular Mechanism of Allosteric Communication in Hsp70 Revealed by Molecular Dynamics Simulations. PLoS Comput Biol. 2012;8:e1002844. doi: 10.1371/journal.pcbi.1002844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zhuravleva A, Gierasch LM. Allosteric signal transmission in the nucleotide-binding domain of 70-kDa heat shock protein (Hsp70) molecular chaperones. Proc Natl Acad Sci USA. 2011;108:6987–6992. doi: 10.1073/pnas.1014448108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Schuler H, Wisniewska M, Karlberg T, Lehtio L, Johansson I, Kotenyova T, Moche M. PLOS. 2010;5:e8625. doi: 10.1371/journal.pone.0008625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Zuiderweg ERP, Bhattacharya A, Kurochkin AV, Yip GNB, Zhang Y, Bertelsen EB. Allostery in Hsp70 chaperones is transduced by subdomain rotations. J Mol Biol. 2009;388:475–490. doi: 10.1016/j.jmb.2009.01.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Woo HJ, Jiang J, Lafer EM, Sousa R. ATP-induced conformational changes in Hsp70: molecular dynamics and experimental validation of an in silico predicted onformation. Biochemistry. 2009;48:11470–11477. doi: 10.1021/bi901256y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zhuravleva A, Clerico EM, Gierasch LM. An interdomain energetic tug-of-war creates the allosterically Active State in Hsp70 Molecular Chaperones. Cell. 2012;151:1296–1307. doi: 10.1016/j.cell.2012.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Mapa K, Sikor M, Kudryavtsev V, Waegemann K, Kalinin S, Siedel CA, Neupert W, Lamb DC, Mokranjac D. The conformational dynamics of the mitochondrial Hsp70 chaperone. Mol Cell. 2010;38:89–100. doi: 10.1016/j.molcel.2010.03.010. [DOI] [PubMed] [Google Scholar]
- 26.Mayer MP, Bukau B, Vogel M. Allosteric Regulation of Hsp70 Chaperones by a Proline switch. Molecular Cell. 2006;21:359–367. doi: 10.1016/j.molcel.2005.12.017. [DOI] [PubMed] [Google Scholar]
- 27.Wisen S, Bertelsen EB, Thompson AD, Patury S, Ung P, Chang L, Evans CG, Walter GM, Wipf P, Carlson HA, Brodsky JL, Zuiderweg ERP, Gestwicki JE. Binding of a Small Molecule at a Protein-Protein Interface Regulates the Chaperone Activity of Hsp70-Hsp40. ACS Chem Biol. 2010;5:611–622. doi: 10.1021/cb1000422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Roitberg A, Seabra G, Kolossváry I, Wong KF, Paesani F, Vanicek J, Liu J, Wu X, Brozell SR, Steinbrecher T, Gohlke H, Cai Q, Ye X, Hsieh M, Cui G, Roe D, Mathews D, Seetin M, Sagui C, Babin V, Luchko T, Gusarov S, Kovalenko A, Kollman PA. Amber 11 Users’ Manual Univ Calif. 2010:300. [Google Scholar]
- 29.Mark P, Nilsson L. Structure and Dynamics of the TIP3P, SPC, and SPC/E water models at 298 K. J Phys Chem A. 2001;105:9954–9960. [Google Scholar]
- 30.Berendsen HJC, Postma JPM, van Gunsteren WF, DiNola A, Haak JR. Molecular dynamics with coupling to an external bath. J Chem Phys. 1984;81:3684–3690. [Google Scholar]
- 31.De Groot BL, Hayward S. Methods in Molecular Biology. In: Kukol A, editor. Molecular Modeling of Proteins. Vol. 443. 2008. pp. 89–103. [Google Scholar]
- 32.Amadei A, Linssen ABM, Berendsen HJC. Essential Dynamics of Proteins. Proteins: Struc Func Genet. 1993;17:412–425. doi: 10.1002/prot.340170408. [DOI] [PubMed] [Google Scholar]
- 33.Leitner GM, Maisuradze GG. Free Energy Landscape of a biomolecule in a dihedral principal component space: sampling convergence and correspondence between structures and minima. Proteins: Struct Funct Genet. 2007;67:569–578. doi: 10.1002/prot.21344. [DOI] [PubMed] [Google Scholar]
- 34.Scheraga HA, Liwo A, Maisuradze GG. Principal component analysis for protein folding dynamics. J Mol Biol. 2009;385:312–329. doi: 10.1016/j.jmb.2008.10.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.McKay DB, Flaherty KM, Sigurd MW, DeLuca-Flaherty C. Structural basis of the 70-kilodalton heat shock cognate protein ATP hydrolytic activity. J Biol Chem. 1994;269:12899–12907. [PubMed] [Google Scholar]
- 36.McKay DB, O’Brien M, Flaherty KM. Lysine 71 of the chaperone protein Hsc70 is essential for ATP hydrolysis. J Biol Chem. 1996;271:15874–15878. doi: 10.1074/jbc.271.27.15874. [DOI] [PubMed] [Google Scholar]
- 37.Smock RG, Rivoire O, Russ WP, Swain JF, Leibler S, Ranganathan R, Gierasch LM. An interdomain sector mediating allostery in Hsp70 molecular chaperones. Mol Sys Biol. 2010;6:414. doi: 10.1038/msb.2010.65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Xu Z, Page RC, Gomes MM, Kohli E, Nix JC, Herr AB, Patterson C, Misra S. Structural basis of nucleotide exchange and client binding by the Hsp70 cochaperone Bag2. Nat Struc Mol Biol. 2008;15:1309–1317. doi: 10.1038/nsmb.1518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Skliros A, Jernigan RL, Kloczkowski A. Models to approximate the motions of protein loops. J Chem Theory Comput. 2010;6:3249–3258. doi: 10.1021/ct1001413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Skliros A, Zimmermann MT, Chakraborty D, Saraswathi S, Katebi AR, Leelananda SP, Kloczkowski A, Jernigan RL. The importance of slow motions for protein functional loops. Phys Biol. 2012;9:014001. doi: 10.1088/1478-3975/9/1/014001. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


