Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Jan 21;5:7933. doi: 10.1038/srep07933

Unusual ferromagnetic critical behavior owing to short-range antiferromagnetic correlations in antiperovskite Cu1-xNMn3+x (0.1 ≤ x ≤ 0.4)

Jianchao Lin 1, Peng Tong 1,a, Dapeng Cui 1, Cheng Yang 1, Jie Yang 1, Shuai Lin 1, Bosen Wang 1, Wei Tong 2, Lei Zhang 2, Youming Zou 2, Yuping Sun 1,2,3,b
PMCID: PMC4300457  PMID: 25604754

Abstract

For ferromagnets, varying from simple metals to strongly correlated oxides,the critical behaviors near the Curie temperature (TC) can be grouped into several universal classes. In this paper, we report an unusual critical behavior in manganese nitrides Cu1-xNMn3+x (0.1 ≤ x ≤ 0.4). Although the critical behavior below TC can be well described by mean field (MF) theory, robust critical fluctuations beyond the expectations of any universal classes are observed above TC in x = 0.1. The critical fluctuations become weaker when x increases, and the MF-like critical behavior is finally restored at x = 0.4. In addition, the paramagnetic susceptibility of all the samples deviates from the Curie-Weiss (CW) law just above TC. This deviation is gradually smeared as x increases. The short-range antiferromagnetic ordering above TC revealed by our electron spin resonance measurement explains both the unusual critical behavior and the breakdown of the CW law.

Phase transition is a core concept of current condensed matter physics. The analysis of the critical behavior provides significant information about the thermodynamic observables near the transition1. As a classic example to address the critical behavior, the continuous paramagnetic (PM) to ferromagnetic (FM) transition has been extensively studied. In the vicinity of a second-order FM transition, the universal scaling laws apply to the spontaneous magnetization (Ms) and the initial magnetic susceptibility (χ0) due to the divergence of the correlation length. Namely, Ms just below the Curie temperature (TC) is described by the relation, Ms ~ (1 − T/TC)β, and χ0 just above TC follows the relation2, 1/χ0 ~ (T/TC − 1)γ. Accordingly, the critical isothermal M(H) at TC is described by M(H) ~ H1/δ. The three critical exponents, β, γ and δ, fulfill the Widom scaling relation3, δ = 1 + γ/β. The critical exponents, obtained in a wide variety of FM material systems, can be grouped into a few well-known universal classes4, such as the mean field (MF) model (β = 0.5, γ = 1.0 and δ = 3.0), 3D Heisenberg (3DH) model (β = 0.365, γ = 1.386 and δ = 4.80), and 3D Ising (3DI) model (β = 0.325, γ = 1.241 and δ = 4.82). Unusual critical behaviors, characterized by critical exponents out of the expected ranges of the universal classes, challenge the scaling theory of the critical phenomena and thus have attracted considerable attention5,6,7,8,9,10,11.

When the temperature is well above TC, the magnetic susceptibility χ(T) of a ferromagnet can be well illustrated by the Curie-Weiss (CW) law; namely, 1/χ(T) is linearly dependent on temperature12. However, the breakdown of the CW law has been widely observed, as evidenced by either an upturn or a downward deviation from the linear temperature dependence of 1/χ(T) upon cooling. The first case, a downward deviation on 1/χ(T), has frequently been observed in many materials, such as perovskite manganites11,13,14. This situation is usually attributed to the Griffiths phase15, where short-range (SR) FM clusters16 occur, grow upon cooling, and finally become long-range (LR) ordered below TC. By contrast, there are relatively few studies on the upturn deviation on 1/χ(T) above TC. Thus far, for this type of deviation, no well-accepted explanations of the driving force have been presented, although a few mechanisms, such as FM clusters17,18, strong exchange interaction between long-wavelength spin fluctuations19, spin lattice coupling20, and antiferromagnetic (AFM) correlations21 have been proposed. The unusual critical behaviors and the deviations of the magnetic susceptibility from the CW law have attracted much research interest separately, but it is unknown whether and how the two issues are related.

Manganese nitride CuNMn3 is a prototype antiperovskite compound (see Supplementary Figure S1(a) online for the antiperovskite structure). This compound and related chemically doped compounds have received considerable attention because of their various functionalities22,23, such as negative or zero thermal expansion24,25,26,27,28, nearly zero temperature coefficient of resistance29,30,31, large magnetocaloric effect32, giant magnetostriction33, and FM shape memory effect34. Upon cooling, a weakly first-order FM transition was observed at TC ~ 143 K in CuNMn3, accompanied by a cubic-tetragonal structural transition31. Our recent study found that, by substituting Cu sites with Mn, the FM transition and structural transformation are decoupled in Cu1-xNMn3+x35. With increasing x, the structural transition is gradually suppressed and disappears for x > 0.4. In addition, TC increases with increasing x. Here, we report the critical behavior for Cu1-xNMn3+x with 0.1 ≤ x ≤ 0.4. An upturn deviation against the CW law was observed in the 1/χ(T) curves above TC, which is gradually smeared as x increases. For low values of x, the critical behavior below TC follows the MF model well, whereas enhanced critical fluctuations beyond the theoretical prediction of the 3DH model were observed above TC. The critical fluctuations become weakened as x increases, and consequently, for x = 0.4, the critical behavior both below and above TC can be described by the MF model. Furthermore, our electron spin resonance (ESR) results indicate the existence of SR AFM ordering above TC, which provides the physical background for the unusual critical behavior and the deviation from the CW law observed in the 1/χ(T) curves.

Results

Inverse magnetic susceptibility: deviation from the Curie-Weiss behavior

Figure 1(a) shows 1/χ(T) measured at a magnetic field of 0.1 kOe under the zero-field-cooled mode for Cu1-xNMn3+x with x = 0.1, 0.2, 0.3 and 0.4. The CW law, namely the linear dependence on temperature, holds at temperatures well above TC. As the temperature decreases, the CW behavior breaks down because 1/χ(T) exhibits an upward departure from the linear dependence. The onset temperature of the deviation is denoted as T*. The gap between TC and T* decreases as x increases, that is, the upward deviation in x = 0.4 is less pronounced than in x = 0.1. We note that for the parent sample CuNMn3, no clear deviation from the CW law can be observed in the 1/χ(T) curve31. Figure 1(b) shows a comparison of 1/χ(T)s for x = 0.2 measured at 0.1 kOe, 1 kOe, 3 kOe and 10 kOe. It is apparent that all the 1/χ(T) curves exhibit an upward departure from the CW behavior. Moreover, T* appears to be insensitive to the applied field. This behavior contradicts the well-known Griffiths phase, in which a downward deviation in 1/χ(T) is usually observed at low magnetic field and disappears at high magnetic field because of the enhanced background PM signal and/or the saturation of the FM components14.

Figure 1. Inverse magnetic susceptibility 1/χ(T) for Cu1-xNMn3+x (x = 0.1, 0.2, 0.3 and 0.4).

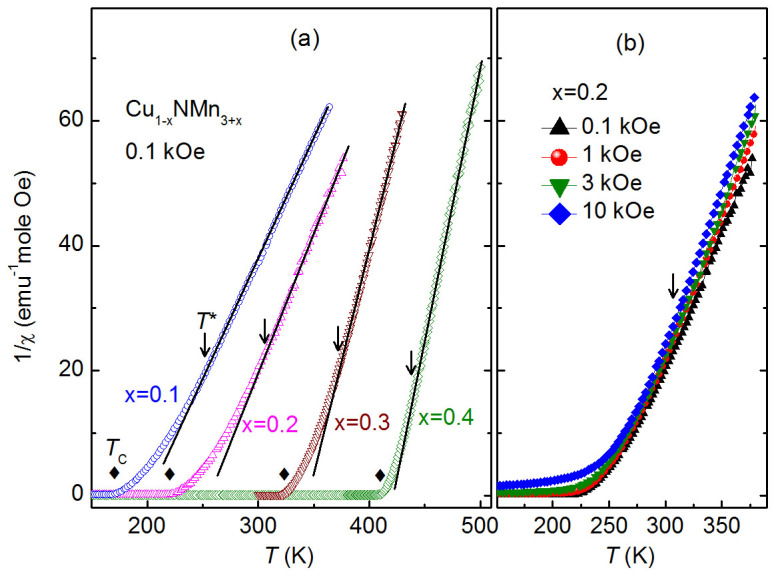
Figure 1

Open in a new tab

(a) 1/χ(T) at 0.1 kOe for all samples. (b) 1/χ(T) measured at 0.1 kOe, 1 kOe, 3 kOe and 10 kOe for the x = 0.2 sample. The onset temperatures (T*) where 1/χ(T) deviates from the linear temperature dependence (solid lines) are indicated by the arrows. The ferromagnetic transition for each composition at TC is marked as a solid diamond in (a).

Critical behavior around TC

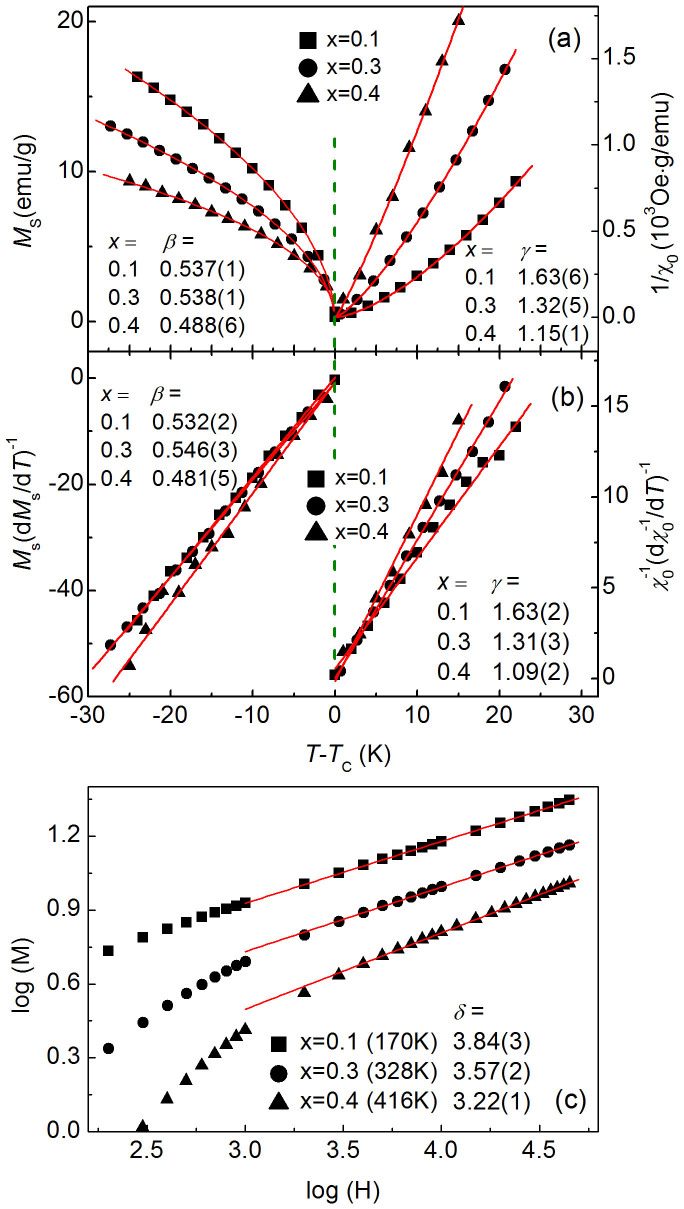
To better understand the magnetic behavior around TC, critical behavior analysis was performed for Cu1-xNMn3+x with x = 0.1, 0.3 and 0.4. The isothermal magnetization M(H) was measured in the vicinity of TC, and Arrott plots (M2-H/M) were derived (see Supplementary Figure S2 online). The high-field isotherms of the Arrott plots were fitted with a polynomial function and then extrapolated to the H/M = 0 and M2 = 0 axes to obtain Ms and χ0−1, respectively6. By fitting Ms(T) with the relation Ms ~ (1 − T/TC)β and χ0−1(T) with the relation 1/χ0 ~ (T/TC − 1)γ, we obtained the values of β and γ, respectively. Modified Arrott plots were then obtained as M1/β versus (H/M)1/γ, which were fitted again to obtain new values of β and γ. Then, the new critical exponents were used to make modified Arrott plots again. The above procedure was continued until the critical exponents converged to stable values. The final values of Ms and χ0−1 are plotted in Figure 2(a) as a function of reduced temperature (T-TC). The obtained exponent γ decreases from ~1.63 for x = 0.1, clearly larger than the value suggested by the 3DH model (1.386) or by the 3DI model (1.24), to a value of ~1.15 for x = 0.4, which is similar to the MF magnitude of unity (1)5. Nevertheless, the β values (0.537, 0.538 and 0.488 for x = 0.1, 0.3 and 0.4, respectively) are very close to the value (0.5) predicted by the MF theory. The large γ values for x = 0.1 and 0.3 are likely unrelated to the 3DH or 3DI model because the β values do not match these models. The critical exponents can also be obtained by using a Kouvel-Fisher (KF) plot36, in which MS(dMS/dT)−1 vs. T and χ0−1(dχ0−1/dT)−1 vs. T generate straight lines with slopes 1/β and 1/γ, respectively. The KF plots for x = 0.1, 0.3 and 0.4 are displayed in Figure 2(b). The estimated values for β and γ are consistent with those derived from the modified Arrott plots shown in Figure 2(a), indicating that the results of the critical behavior analysis are reliable.

Figure 2. Critical behavior analysis for Cu1-xNMn3+x (x = 0.1, 0.3 and 0.4).

Figure 2

Open in a new tab

(a) The spontaneous magnetization Ms (left) and inverse initial magnetic susceptibility 1/χ0 (right) vs. (T-TC) along with the fit (solid lines) to the power laws (see the text for details). The obtained critical exponents (β, γ) are shown. (b) The Kouvel-Fisher plot of Ms (left) and 1/χ0 (right) as a function of T-TC. The solid lines represent the linear fitting of the data. The obtained critical exponents (β, γ) are shown. (c) Critical isotherm M(H) on log-log scale at the temperature closest to TC for Cu1-xNMn3+x (x = 0.1, 0.3 and 0.4). The solid lines are linear fits, and the obtained critical exponent δ is shown for each sample.

The critical exponent δ can be either derived from the critical isothermal magnetization curve using the relation M(H) ~ H1/δ or estimated by the Widom scaling relation given the values of β and γ. For each composition, M(H) at the temperature closest to TC is plotted in Figure 2(c) in the form of log(H)-log(M). Based on the linear fitting to the high-field data, the δ values are found to be 3.84, 3.57 and 3.22 for x = 0.1, 0.3 and 0.4, respectively. The δ values estimated by taking the β and γ values from the modified Arrott plot method are 4.04, 3.45 and 3.35 for x = 0.1, 0.3 and 0.4, respectively. Similarly, by utilizing the β and γ values obtained from the KF method, the δ values are estimated to be 4.06, 3.39 and 3.26 for x = 0.1, 0.3 and 0.4, respectively. The δ values obtained using the three different strategies are very close, confirming the reliability of the critical behavior analysis. The δ value for x = 0.1 is remarkably larger than the value (3) predicted by the MF theory due to the large γ value. As x increases to 0.4, the δ value decreases and approaches the magnitude of the MF model. The scaling hypothesis1 predicts that the scaled isothermals m = M|(T − TC)/TC|−β vs. h = H|(T − TC)/TC|−(β+γ) fall onto two different curves, one for T > TC and the other for T < TC. As shown in Supplementary Figure S3 online, the scaling hypothesis is valid for the current samples, which further confirms that the obtained critical exponent values are reliable10,37.

Results of electron spin resonance

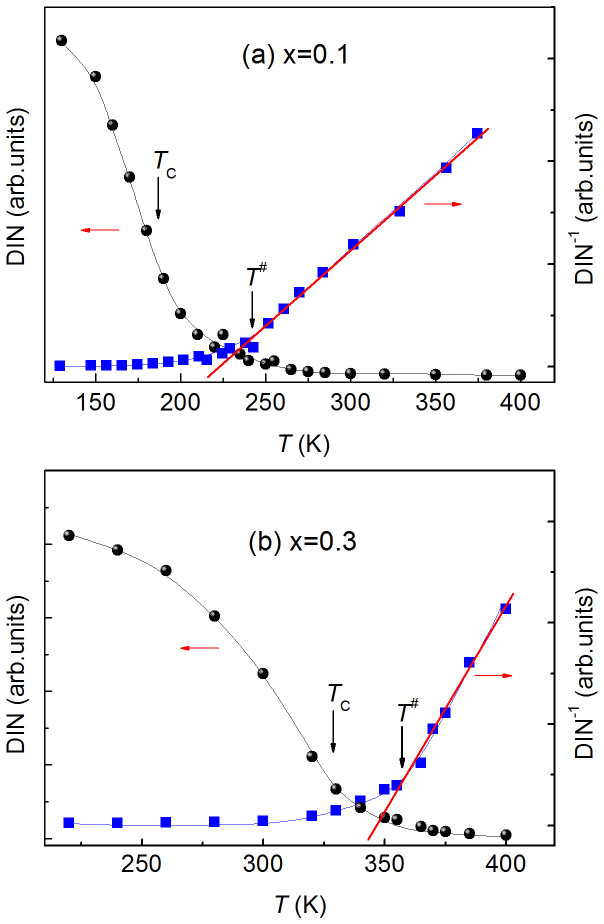
ESR has been demonstrated to be an effective tool to probe the local and microscopic magnetic states of materials. To elucidate the nature of the critical behavior around TC, temperature-dependent derivative ESR spectra (dP/dH) were measured for x = 0.1 and x = 0.3 samples and are presented in Figure 3(a) and (b), respectively. Here, the dP/dH data were normalized to the positive peak value and then shifted accordingly such that the evolution of the line shape could be easily seen. As shown in Figure 3(a) for x = 0.1, the dP/dH spectrum is asymmetrically distorted below TC. When approaching TC, the dP/dH spectrum makes a small shift toward higher fields and becomes less asymmetrical. Once above TC, however, the spectrum broadens and distorts again with increasing temperature. Synchronously, a shoulder-like feature appears on the right side of the original peak and finally evolves into a sharp peak above 235 K. Above this temperature, the two resonant peaks are clearly distinguishable in the dP/dH spectra with very different peak widths. Hereafter, the original peak is denoted as P1, whereas the new peak is denoted as P2. As shown in Figure 3(a), P1 keeps broadening as the temperature is further increased and eventually becomes invisible above 350 K, where only P2 is left. As displayed in Figure 3(b), the ESR spectra for x = 0.3 recorded with a bigger temperature interval than for x = 0.1 show a similar evolution with temperature, even though the wide peak (P1) still exists at 400 K.

Figure 3. ESR spectra, dP/dH, as a function of temperature for Cu1-xNMn3+x.

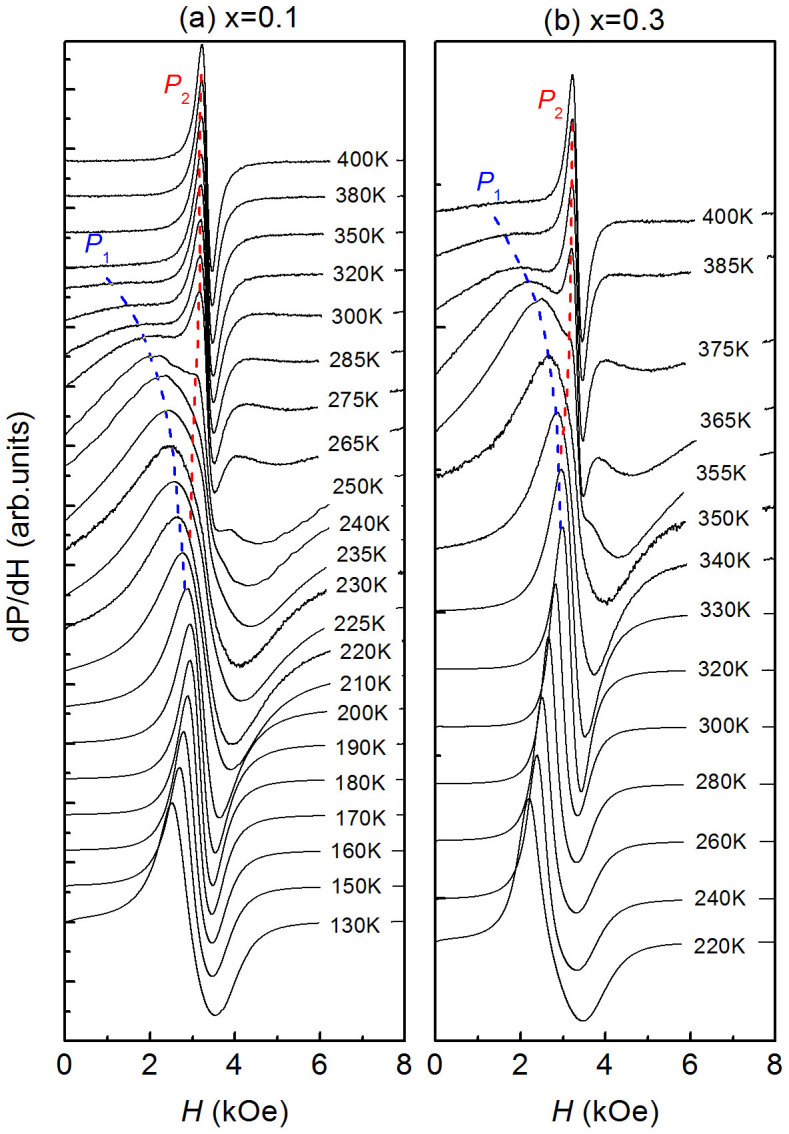
Figure 3

Open in a new tab

(a) dP/dH for x = 0.1. (b) dP/dH for x = 0.3. Note that the spectra plotted here were normalized and shifted (see the text for details). The dashed lines indicate the evolutions of resonant peaks (P1 and P2) with temperature above TC.

The transitions in the ESR spectra discussed above can also be found in the double integrated intensity (DIN) of the original dP/dH data plotted in Figure 4(a) and (b) for x = 0.1 and x = 0.3, respectively. For both compounds, the DIN increases remarkably as the temperature approaches TC from above. However, the inverse DIN shows an upturn at T# (~240 K and 355 K for x = 0.1 and 0.3, respectively), which is clearly higher than the Curie temperature, TC. Above T#, the inverse DIN is linearly temperature dependent, suggesting a CW behavior in accordance with that observed for 1/χ(T) (Figure 1).

Figure 4. Double integrated intensity (DIN) of the original ESR spectra for Cu1-xNMn3+x.

Figure 4

Open in a new tab

(a) for x = 0.1 and (b) for x = 0.3. The inverse DIN is also shown in each panel. The solid line (red) on DIN−1(T) curve indicates a linear fit. The temperatures (T#s) at which DIN−1 departs from the linear dependence on temperature and the Curie temperature TC are indicated by the arrows.

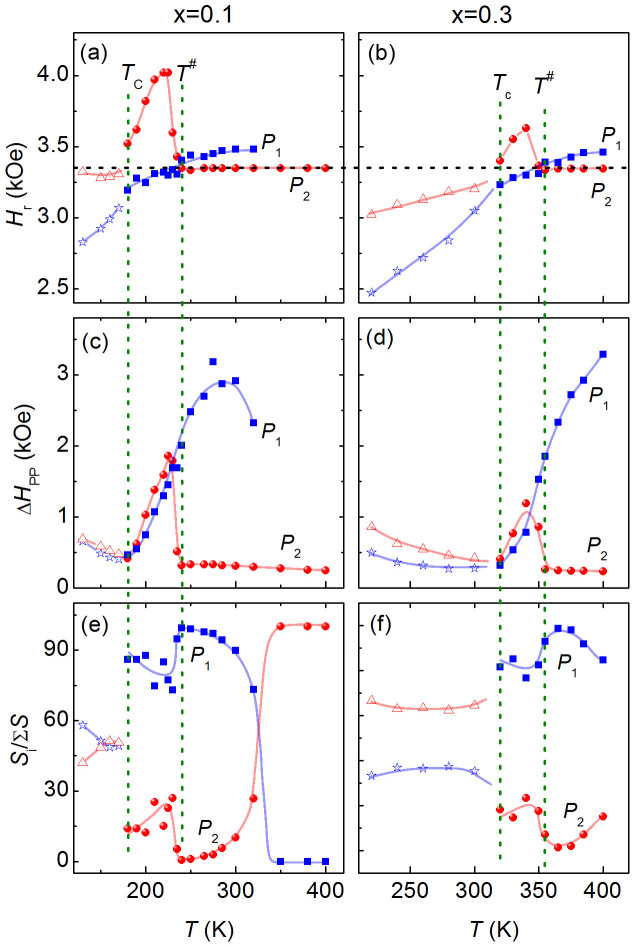
All the dP/dH data for the samples with x = 0.1 and 0.3 can be well fitted by a sum of two Lorentzian shape functions38, except for the data above 350 K for x = 0.1, where a single Lorentzian function fits the data well. The fitting profiles at typical temperatures are shown in Supplementary Figure S4 online. The fitted parameters, i.e., the resonant field (Hr), peak-to-peak distance (ΔHPP) and intensity ratio of each peak to the total intensity (Si/ΣS) for x = 0.1 and 0.3 are presented as a function of temperature in Figure 5(a)–(f). These parameters exhibit similar trends in both compounds. As shown in Figure 5(a) and 5(b), the two ESR peaks are well separated below TC because the Hr values are quite different. Above TC, Hr for P1 increases slightly as the temperature increases and becomes nearly independent of temperature above T#. Meanwhile, Hr for P2 increases rapidly with temperature to a peak value and then decreases upon further increasing the temperature up to T#. Above T#, Hr for P2 maintains a constant value of 3345 Oe (g ~ 2), which is attributable to PM resonance. As displayed in Figure 5(c) and (d), the ΔHPP values for both peaks show a similar dependence on temperature below TC. Above TC, ΔHPP for P1 keeps increasing with temperature, whereas ΔHPP for P2 increases initially with temperature and then dramatically decreases at T#, beyond which this parameter varies little with temperature. The Si/ΣS values for x = 0.1 and x = 0.3 are shown in Figure 5(e) and (f), respectively. Below TC, the Si/ΣS values for both peaks are comparable. Si/ΣS for P1 is stronger than that for P2 between TC and T#. When crossing T# from below, Si/ΣS for P1 jumps to a more dominant position at the expense of P2 and then decreases gradually as the temperature increases further. Eventually, the P1 peak for x = 0.1 disappears when T > 350 K (Figure 5(e)). Whereas for x = 0.3, the P1 peak still persists even at 400 K with a reduced relative intensity (Figure 5(f)).

Figure 5. Temperature dependence of the fit parameters, i.e., the resonant field (Hr), peak-to-peak distance (ΔHPP) and intensity ratio of each peak to the total intensity (Si/ΣS) of the ESR spectra for Cu1-xNMn3+x.

Figure 5

Open in a new tab

(a) Hr for x = 0.1. (b) Hr for x = 0.3. (c) ΔHPP for x = 0.1. (d) ΔHPP for x = 0.3. (e) Si/ΣS for x = 0.1. (f) Si/ΣS for x = 0.3. The temperatures TC and T# are indicated by the vertical dotted lines. The solid lines are guides to the eyes. P1 and P2 refer to the resonant peaks above TC.

Discussion

The slightly upward deviation of 1/χ(T) from the CW behavior has often been observed in normal FM materials showing stronger critical fluctuations than predicted by the MF model37,39. Alternative mechanisms associated with SR magnetic orders have also been proposed. In manganite oxides, this behavior has often been ascribed to the existence of SR FM clusters18. Phenomenologically, it is somewhat surprising because FM clusters enhance the susceptibility beyond the PM background and, in turn, lead to a reduced inverse susceptibility. In double perovskite La2NiMnO6, the AFM correlations among the neighboring FM clusters were proposed to account for the observed upward deviation in the 1/χ(T) curve21. Because of the existence of FM clusters, the downward deviation in the 1/χ(T) curve appears when a low measurement field is employed40. This interpretation was used to explain the upward deviation in the 1/χ(T) curves observed in perovskite cobaltites La1-xSrxCoO3, for which clear evidence of SR FM clusters has been demonstrated17. By contrast, as shown in Figure 1(b), the insensitivity of the upward deviation in 1/χ(T) to the applied magnetic field in Cu1-xNMn3+x implies that the AFM correlations may be responsible for the deviation alone.

The peak values (~4020 Oe and 3630 Oe for x = 0.1 and 0.3, respectively) of the resonant field Hr for P2 between TC and T# are much larger than the value of PM resonance (~3350 Oe), as demonstrated in Figure 5(a) and 5(b). Such high resonant fields suggest the related magnetic coupling is AFM-type that requires a stronger magnetic field to generate the ESR resonance than the PM-type does38,41. However, the AFM correlations should be SR ordered because for LR AFM ordering, the strong AFM spin coupling requires a resonance field that is much stronger than the magnitude of ~10 kOe42. Above T#, the resonant fields for P1 and P2 are close to each other, thereby making them indistinguishable through bulk magnetic susceptibility measurements. As plotted in Figure 5(e) and 5(f), P1 is predominantly stronger than P2 in terms of intensity just above T#. This result implies that the magnetic coupling corresponding to P1 actually provides a PM background rather than an AFM one. The upturn in DIN−1(T) below T# (Figure 4) is a signature of the subtle reduction of DIN, which is barely visible in DIN(T). The reduction of the ESR intensity can be ascribed to the appearance of AFM couplings43. Therefore, the SR AFM correlations observed here can explain the upturn below T# in DIN−1(T). The values of T# below which the SR AFM correlations appear coincide well with T* (~250 K and 365 K for x = 0.1 and 0.3, respectively), below which the magnetic susceptibility departs from the CW law, indicative of the same underlying physics for both cases. Therefore, it is the SR AFM correlations (or say, ordering) that reduce the magnetic susceptibility lower than the PM background and hence lead to the upward deviation of 1/χ(T) below T*, in sharp contrast to the Griffith phase case.

How do the SR AFM correlations/ordering influence the critical behavior? Ostensibly, γ represents the divergence of the initial magnetic susceptibility upon approaching TC from above, with smaller values yielding sharper divergence10. In physics, γ is in fact a measurement of the FM interaction range8,44. Based on the γ values shown in Figure 2(b), the FM exchange interaction is estimated to decay as J(r) ~ 1/r5.12±0.02, ~1/r4.87±0.03 and ~1/r4.63±0.02 for x = 0.1, 0.3 and 0.4, respectively. Clearly, the range of FM exchange interaction increases with x and approaches the anticipation of the MF model8 (slower than ~1/r4.5) for x = 0.4. The FM exchange interaction for x = 0.1 decays even faster than expected by the 3DH model with J(r) ~ 1/r5, suggesting very strong critical fluctuations6,37. The SR AFM coupled spins would force the surrounding spins to be antiferromagnetically coupled through the proximity effect45, which prohibits the formation of FM interactions among those spins. The affection of the proximity effect on the FM magnetic couplings would decay with distance. Spatially, the SR AFM interactions associated with chemical doping should be randomly distributed. It is therefore difficult for the FM couplings to develop globally when the system is cooled toward TC. As a result, the divergence of the magnetic susceptibility slows down, yielding an enhanced critical component γ. For TC < T < T#, Hr for P2, which is related to the strength of the SR AFM coupling, is smaller for x = 0.3 (Figure 5(b)) than for x = 0.1 (Figure 5(a)). Moreover, the temperature span between TC and T# where the SR AFM correlations appear is remarkably reduced for x = 0.3 (~30 K) in comparison to x = 0.1 (~60 K). This finding indicates that the SR AFM correlations are significantly weakened relative to the FM interactions with increasing x, leading to a reduced influence on the FM transition and hence to the suppressed critical fluctuations. Therefore, it is readily understandable that the MF-like critical behavior above TC can be restored in x = 0.4.

An unusually large critical component γ has been reported in a few FM materials. In weak itinerant-electron Zr1-xNbxZn2, γ increases from the MF magnitude to 1.33 when x approaches the critical concentration xc = 0.083, at which a quantum phase transition occurs9. However, β always takes the value of unity as expected by the MF model. The large γ value was also reported in perovskite BaRuO3 under high pressure6. At ambient pressure, BaRuO3 behaves as expected by the 3DH model with β = 0.348 and γ = 1.41. By applying a hydrostatic pressure, γ increases gradually to ~1.8 under 0.8 GPa, whereas there is no obvious change of β. This implies enhanced critical fluctuations under pressure; however, the detailed mechanism remains elusive. In the Invar system Fe100-xPtx, the critical exponent γ was observed to be enhanced by increasing the metallurgical site disorder when the concentration was close to the stoichiometric composition Fe75Pt25; however, β is insensitive to the disorder8. It was speculated that the random site disorder causes a strong broadening of the distribution of the local exchange fields owing to the competition between the strong AFM Fe-Fe exchange interaction and the dominating FM Fe-Pt and Pt-Pt interactions8. For manganese nitrides Cu1-xNMn3+x with antiperovskite structure, our results clearly suggest that the SR AFM couplings appearing above TC significantly affect the critical behavior. To the best of our knowledge, the influence of SR AFM orders on the critical behavior has not been addressed in the literature. We hope the present findings can stimulate further study in this direction both experimentally and theoretically.

Figure 6 is a phase diagram for Cu1-xNMn3+x with x up to 0.5 based on our previous measurements of the bulk magnetic susceptibility and temperature-dependent X-ray diffraction35. When x increases, the structural transition temperature TS decreases and finally disappears above x = 0.4; however, TC shifts toward higher temperatures. Similar trends were reported by Takenaka et al in nitrogen-deficient CuN1-δMn334, where the nitrogen deficiency causes a reduction of TS and an increase of TC. Based on the results discussed above, a temperature zone of SR AFM ordering against the PM background can be added to the phase diagram, which isolates the low-temperature FM ordered state from the high-temperature PM state.

Figure 6. Phase diagram for Cu1-xNMn3+x with 0 ≤ x ≤ 0.5.

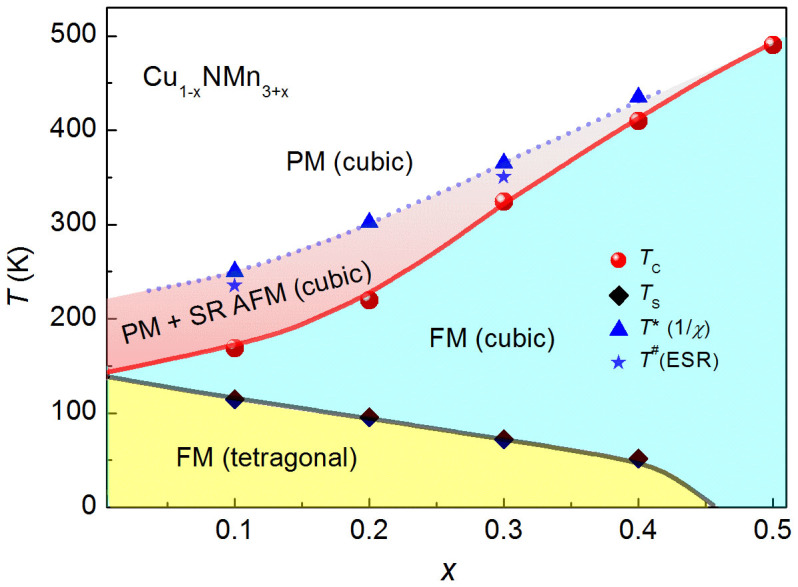
Figure 6

Open in a new tab

TC represents the ferromagnetic (FM) Curie temperature, and TS represents the tetragonal-cubic structural transition temperature. T* denotes the temperature below which 1/χ(T) deviates from the Curie-Weiss law, and T# is the onset temperature below which short-range antiferromagnetic ordering (SR AFM) occurs and coexists with the paramagnetic (PM) matrix.

The cubic antiperovskite lattice is composed of corner-sharing Mn6N octahedra (see Supplementary Figure S1(a) online) and contains 3D geometrical frustration in terms of AFM interactions46. In most cases, the AFM structure in cubic antiperovskite manganese nitrides takes triangular configurations47,48, where Mn moments on the (111) plane point 120° away from each other (see Supplementary Figure S1(b) online as an example). Complex AFM structures, e.g., a square configuration along with a FM component in a tetragonal crystal lattice or the existence of two sets of collinear AFM configurations, were observed in a very small number of compounds47,48. For the current case, the complex AFM structures may be excluded because only a single AFM signal was observed in addition to the PM background in the ESR spectra. Moreover, the AFM structures reported thus far in chemically doped CuNMn3 compatible with a cubic crystal structure are all in triangular configurations48. In this context, the SR AFM ordering observed in Cu1-xNMn3+x probably takes a triangular configuration. Although it is not favored by the geometrical frustration, the SR AFM ordering can still be expected if frustration is locally relieved by the lattice deformation due to the random substitution of Cu sites with Mn atoms. The local structural distortion upon doping has been verified to play a very important role in determining the physical properties and functionalities of antiperovskite manganese nitrides23,24,49,50,51. As reported in Ref. 23, strong frustration is suggested to be associated with lattice contraction in the PM state. According to our previous work35, the lattice constant keeps decreasing with increasing x, suggestive of strengthening geometrical frustration globally. Separately, the corner-site Mn atoms that replace the Cu sites are suggested to be magnetically coupled with the face-center-site Mn atoms by isotropic exchange interactions, which may disturb the AFM interactions within the (111) plane52. Because of the strengthening geometrical frustration and the disturbance from the corner-site Mn atoms, the local AFM ordering is unable to survive at higher doping levels, and the MF-type critical behavior is finally recovered at x = 0.4. For further study, local structural probes, such as neutron or X-ray pair distribution function and X-ray absorption fine structure spectra, are desirable. As in the situation of strongly correlated perovskite oxides, our result along with previous reports on local structure distortion suggests that the intrinsic magnetic, electronic and structural inhomogeneity on the microscopic scale is crucial for comprehending the bulk physical properties of antiperovskite manganese nitrides.

In summary, we studied the magnetic properties of Cu1-xNMn3+x (x = 0.1, 0.2, 0.3 and 0.4) using magnetic susceptibility and ESR measurements. We found that the inverse magnetic susceptibility 1/χ(T) exhibits an upward deviation from the CW behavior above TC, which was attributable to the existence of SR AFM correlations, as demonstrated by the ESR result. For all compositions, the critical behavior below TC was well described by the MF model. However, the critical fluctuations in compounds with small x values were much stronger than predicted by the MF model. As x increases, the critical fluctuations were suppressed gradually, and the MF-like behavior was recovered for x = 0.4. SR AFM correlations were proposed as the cause of the faster decay of the FM interaction length than that expected by the MF model, leading to the unusual critical behavior above TC.

Methods

Polycrystalline samples of Cu1-xNMn3+x with x = 0.1, 0.2, 0.3 and 0.4 were prepared via a direct solid-state reaction. Powders of Cu (4 N), Mn (4 N) and homemade Mn2N were mixed in the desired ratios, pressed into pellets, sealed in evacuated quartz tubes (~10−6 torr) and sintered at 750°C for 3 days, followed by annealing at 800°C for 5 days. After quenching the tubes to room temperature, the products were ground carefully, pressed into pellets, sealed in evacuated tubes and annealed again at 800°C for an additional 8 days. The Mn2N powders were prepared using the following sequence. First, the Mn (4N) powders were wrapped with Ta foil and placed into a high-pressure pipe furnace made of nickel-based stainless steel. Next, the pipe furnace was repeatedly cleaned using high-purity nitrogen gas (5N) before being sealed with high-purity nitrogen gas inside. Then the furnace was heated to 750°C and held for 60 hours while the inside-tube gas pressure was maintained as 5 MPa. Finally, high-quality Mn2N powders were obtained. From X-ray diffraction, all the samples exhibited the antiperovskite structure (group symmetry, 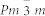Inline graphic) without a detectable second phase. For the x = 0.1 and 0.3 samples, the magnetic measurements were performed on a Quantum Design superconducting quantum interference device (SQUID). For the sample with x = 0.4, the measurements were carried out on a vibrating sample magnetometer with an oven attached on a Quantum Design physical property measurement system (PPMS). The isothermal magnetizations (M-H curves) were measured after the samples were cooled down to each measurement temperature from well above TC. The electron spin resonance (ESR) spectra were recorded using an X-band Bruker EMX plus 10/12 cw spectrometer operating at 9.4 GHz. ESR detects the power P absorbed by a sample from a transverse microwave magnetic field. The signal-to-noise ratio of the spectra was improved by recording the first derivative of P (dP/dH) using a lock-in technique.

Author Contributions

J.C.L. prepared the samples and performed the characterization. J.C.L., D.P.C., C.Y., S.L. and B.S.W. performed the magnetic susceptibility experiments. P.T. and L.Z. carried out the critical behavior analysis and data interpretation. W.T., Y.M.Z. and J.Y. assisted with the ESR measurement and contributed to the data analysis and interpretation. P.T. and Y.P.S. designed the experiments and guided the work. P.T. wrote the manuscript with help from the co-authors. All the authors discussed the results and reviewed the manuscript.

Supplementary Material

Supplementary Information

Supplementary information

srep07933-s1.pdf (1.6MB, pdf)

Acknowledgments

This work was supported by the National Key Basic Research under Contract No. 2011CBA00111; the National Natural Science Foundation of China under Contract Nos. 51322105, 11174295, 51301167, 51171177 and 91222109; the Joint Funds of the National Natural Science Foundation of China and the Chinese Academy of Sciences' Large-Scale Scientific Facility (Grant No. U1232138); and the Foundation of Hefei Center for Physical Science and Technology under Contract No. 2012FXCX007. The authors thank Dr. Chen Sun for her assistance in editing the manuscript.

References

  1. Stanley H. E. Introduction To Phase Transitions and Critical Phenomena (Oxford university press, Lodon, 1971). [Google Scholar]
  2. Fisher M. E. The theory of equilibrium critical phenomena. Rep. Prog. Phys. 30, 615 (1967). [Google Scholar]
  3. Widom B. Equation of State in the Neighborhood of the Critical Point. J. Chem. Phys. 43, 3898 (1965). [Google Scholar]
  4. Karube K. et al. Universality and critical behavior at the critical endpoint in the itinerant-electron metamagnet UCoAl. Phys. Rev. B 86, 024428 (2012). [Google Scholar]
  5. Khan N., Mandal P., Mydeen K. & Prabhakaran D. Magnetoelectronic phase separation in La1−xSrxCoO3 single crystals: Evidence from critical behavior. Phys. Rev. B 85, 214419 (2012). [Google Scholar]
  6. Zhou J. S. et al. Critical Behavior of the Ferromagnetic Perovskite BaRuO3. Phys. Rev. Lett. 101, 077206 (2008). [DOI] [PubMed] [Google Scholar]
  7. Lago J. et al. Critical behavior in the inhomogeneous ferromagnet SrFe0.80Co0.20O3.0. Phys. Rev. B 83, 104404 (2011). [Google Scholar]
  8. Boxberg O. & Westerholt K. Critical exponents at the ferromagnetic phase transition of Fe100-xPtx single crystals. Phys. Rev. B 50, 9331–9338 (1994). [DOI] [PubMed] [Google Scholar]
  9. Sokolov D., Aronson M., Gannon W. & Fisk Z. Critical Phenomena and the Quantum Critical Point of Ferromagnetic Zr1-xNbxZn2. Phys. Rev. Lett. 96, 116404 (2006). [DOI] [PubMed] [Google Scholar]
  10. Butch N. & Maple M. Evolution of Critical Scaling Behavior near a Ferromagnetic Quantum Phase Transition. Phys. Rev. Lett. 103, 076404 (2009). [DOI] [PubMed] [Google Scholar]
  11. Jiang W. J., Zhou X. Z., Williams G., Mukovskii Y. & Glazyrin K. Is a Griffiths Phase a Prerequisite for Colossal Magnetoresistance? Phys. Rev. Lett. 99, 177203 (2007). [DOI] [PubMed] [Google Scholar]
  12. Chamberlin R. V. Mean-field cluster model for the critical behaviour of ferromagnets. Nature 408, 337–339 (2000). [DOI] [PubMed] [Google Scholar]
  13. Salamon M., Lin P. & Chun S. Colossal Magnetoresistance is a Griffiths Singularity. Phys. Rev. Lett. 88, 197203 (2002). [DOI] [PubMed] [Google Scholar]
  14. Tong P. et al. Griffiths phase and thermomagnetic irreversibility behavior in slightly electron-doped manganites Sm1−xCaxMnO3 (0.80 ≤ x ≤ 0.92). Phys. Rev. B 77, 184432 (2008). [Google Scholar]
  15. Bray A. J. Nature of the Griffiths phase. Phys. Rev. Lett. 59, 586–589 (1987). [DOI] [PubMed] [Google Scholar]
  16. Deisenhofer J. et al. Observation of a Griffiths Phase in Paramagnetic La1-xSrxMnO3. Phys. Rev. Lett. 95, 257202 (2005). [DOI] [PubMed] [Google Scholar]
  17. He C. et al. Non-Griffiths-like clustered phase above the Curie temperature of the doped perovskite cobaltite La1−xSrxCoO3. Phys. Rev. B 76, 014401 (2007). [Google Scholar]
  18. DeTeresa J. M. et al. Evidence for magnetic polarons in the magnetoresistive perovskites. Nature 386, 256–259 (1997). [Google Scholar]
  19. Rivadulla F. Conduction-electron spin resonance and spin-density fluctuations of CoS2−xSex (x ≤ 0.1). Phys. Rev. B 84, 132406 (2011). [Google Scholar]
  20. Zhang L. et al. Critical properties of the 3D-Heisenberg ferromagnet CdCr2Se4. EPL (Europhysics Letters) 91, 57001 (2010). [Google Scholar]
  21. Zhou S. M., Guo Y. Q., Zhao J. Y., Zhao S. Y. & Shi L. Nature of short-range ferromagnetic ordered state above TC in double perovskite La2NiMnO6. Appl. Phys. Lett. 96, 262507 (2010). [Google Scholar]
  22. Tong P., Wang B. S. & Sun Y. P. Mn-based antiperovskite functional materials: Review of research. Chin. Phys. B 22, 067501 (2013). [Google Scholar]
  23. Takenaka K. et al. Magnetovolume effects in manganese nitrides with antiperovskite structure. Sci.Technol. Adv. Mater. 15, 015009 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Tong P. et al. Magnetic transition broadening and local lattice distortion in the negative thermal expansion antiperovskite Cu1−xSnxNMn3. Appl. Phys. Lett. 102, 041908 (2013). [Google Scholar]
  25. Wang C. et al. Tuning the range, magnitude, and sign of the thermal expansion in intermetallic Mn3(Zn, M)x N(M = Ag, Ge). Phys. Rev. B 85, 220103 (2012). [Google Scholar]
  26. Song X. Y. et al. Adjustable Zero Thermal Expansion in Antiperovskite Manganese Nitride. Adv. Mater. 23, 4690 (2011). [DOI] [PubMed] [Google Scholar]
  27. Huang R. J., Li L. F., Cai F. S., Xu X. D. & Qian L. H. Low-temperature negative thermal expansion of the antiperovskite manganese nitride Mn3CuN codoped with Ge and Si. Appl. Phys. Lett. 93, 081902 (2008). [Google Scholar]
  28. Takenaka K. & Takagi H. Giant negative thermal expansion in Ge-doped anti-perovskite manganese nitrides. Appl. Phys. Lett. 87, 261902 (2005). [Google Scholar]
  29. Takenaka K. et al. Extremely low temperature coefficient of resistance in antiperovskite Mn3Ag1-xCuxN. Appl. Phys. Lett. 98, 022103 (2011). [Google Scholar]
  30. Lin J. C. et al. Tunable temperature coefficient of resistivity in C- and Co-doped CuNMn3. Scr. Mater. 65, 452–455 (2011). [Google Scholar]
  31. Chi E. O., Kim W. S. & Hur N. H. Nearly zero temperature coefficient of resistivity in antiperovskite compound CuNMn3. Solid State Commun. 120, 307–310 (2001). [Google Scholar]
  32. Yan J. et al. Phase transitions and magnetocaloric effect in Mn3Cu0.89N0.96. Acta Mater. 74, 58–65 (2014). [Google Scholar]
  33. Asano K., Koyama K. & Takenaka K. Magnetostriction in Mn3CuN. Appl. Phys. Lett. 92, 161909 (2008). [Google Scholar]
  34. Takenaka K., Hamada T., Shibayama T. & Asano K. Ferromagnetic shape memory effects in tetragonally distorted antiperovskite manganese nitrides. J. Alloy. Compd. 577, S291–S295 (2013). [Google Scholar]
  35. Lin J. C. et al. The study of structure, magnetism, electricity, and their correlations at martensitic transition for magnetostriction system Cu1−xMnxNMn3 (0 ≤ x ≤ 0.5). J. Appl. Phys. 111, 113914 (2012). [Google Scholar]
  36. Kouvel J. S. & Fisher M. E. Detailed Magnetic Behavior of Nickel Near its Curie Point. Phys. Rev. 136, A1626–A1632 (1964). [Google Scholar]
  37. Zhang L. et al. Critical behavior in the antiperovskite ferromagnet AlCMn3. Phys. Rev. B 85, 104419 (2012). [Google Scholar]
  38. Yang J. et al. Structural, magnetic, and EPR studies of the Aurivillius phase Bi6Fe2Ti3O18 and Bi6FeCrTi3O18. Phys. Rev. B 86, 104410 (2012). [Google Scholar]
  39. Khan N. et al. Critical behavior in single-crystalline La0.67Sr0.33CoO3. Phys. Rev. B 82, 064422 (2010). [Google Scholar]
  40. Zhao Y. L., Chai Y. S., Pan L. Q. & Sun Y. Abnormal magnetic behaviors induced by the antisite phase boundary in La2NiMnO6. Chin. Phys. B 22, 087601 (2013). [Google Scholar]
  41. Tong W., Tang Y. J., Liu X. M. & Zhang Y. H. Charge-order melting and phase separation in La0.5Ca0.5Mn1-xTixO3. Phys. Rev. B 68, 134435 (2003). [Google Scholar]
  42. Ouyang Z., Nojiri H., Yoshii S., Rao G. & Wang Y. Correlation between electron spin resonance and magnetization in Gd5Ge4. Phys. Rev. B 80, 054401 (2009). [Google Scholar]
  43. Tovar M. et al. ESR and magnetization in Jahn-Teller-distorted LaMnO3+δ: Correlation with crystal structure. Phys. Rev. B 60, 10199–10205 (1999). [Google Scholar]
  44. Fisher M. E., Ma S.-k. & Nickel B. Critical Exponents for Long-Range Interactions. Phys. Rev. Lett. 29, 917 (1972). [Google Scholar]
  45. Munakata K., Geballe T. H. & Beasley M. R. Quenching of impurity spins at Cu/CuO interfaces: An antiferromagnetic proximity effect. Phys. Rev. B 84, 161405 (2011). [Google Scholar]
  46. Tahara D., Motome Y. & Imada M. Antiferromagnetic Ising Model on Inverse Perovskite Lattice. J. Phys. Soc. Jpn. 76, 013708 (2007). [Google Scholar]
  47. Fruchart D. & Bertaut E. F. Magnetic Studies of the Metallic Perovskite-Type Compounds of Manganese. J. Phys. Soc. Jpn. 44, 781 (1978). [Google Scholar]
  48. Lheritier P., Fruchart D., Madar R. & Fruchart R. [Alloys and Compounds of d-Elements with Main Group Elements (Part 2)]. Landolt-Börnstein: Numerical Data and Functional Relationships in Science and Technology - Group III Condensed Matter Vol. 19c [Wijn, H. P. J. et al. (eds.)] 186–253 (Springer-Verlag, Berlin, 1988). [Google Scholar]
  49. Takenaka K., Inagaki T. & Takagi H. Conversion of magnetic structure by slight dopants in geometrically frustrated antiperovskite Mn3GaN. Appl. Phys. Lett. 95, 132508 (2009). [Google Scholar]
  50. Iikubo S. et al. Local Lattice Distortion in the Giant Negative Thermal Expansion Material Mn3Cu1-xGexN. Phys. Rev. Lett. 101, 205901 (2008). [DOI] [PubMed] [Google Scholar]
  51. Sun Y. et al. Carbon-Induced Ferromagnetism in the Antiferromagnetic Metallic Host Material Mn3ZnN. Inorg. Chem. 52, 800–806 (2013). [DOI] [PubMed] [Google Scholar]
  52. Fruchart D., Givord D., Convert P., Lheritier P. & Senateur J. P. Non-Collinear Component in the Magnetic-Structure of Mn4N. J. Phys. F-Met. Phys. 9, 2431–2437 (1979). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary information

srep07933-s1.pdf (1.6MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES