A Multiple Splitting Approach to Linkage Analysis in Large Pedigrees Identifies a Linkage to Asthma on Chromosome 12

Abstract

Large genealogies are potentially very informative for linkage analysis. However, the software available for exact nonparametric multipoint linkage analysis is limited with respect to the complexity of the families it can handle. A solution is to split the large pedigrees into sub-families meeting complexity constraints. Different methods have been proposed to “best” split large genealogies. Here, we propose a new procedure in which linkage is performed on several carefully chosen sub-pedigree sets from the genealogy instead of using just a single sub-pedigree set. Our multiple splitting procedure capitalizes on the sensitivity of linkage results to family structure and has been designed to control computational feasibility and global type I error. We describe and apply this procedure to the extreme case of the highly complex Hutterite pedigree and use it to perform a genome-wide linkage analysis on asthma. The detection of a genome-wide significant linkage for asthma on chromosome 12q21 illustrates the potential of this multiple splitting approach.

INTRODUCTION

Performing linkage analysis in large and complex genealogies has long been a challenge for geneticists, especially in population isolates where individuals are connected through multiple lines of descent.

Computational demands for exact multipoint IBD estimations [Lander and Green, 1987] are such that analysis of the entire genealogy is prohibited. Reasoning that analysis of the pedigree as a whole is the most powerful approach if the mode of inheritance is homogeneous across the entire pedigree [Chapman and Wijsman, 2001], efforts have been undertaken to derive approximate inheritance computation. In particular, Monte Carlo [Dyer et al., 2001] and Markov Chain Monte Carlo [Chapman et al., 2001; Greenwood et al., 2001] procedures have been used. However, complexity may be such that, except for single-point analysis [Dyer et al., 2001] and at huge computation costs impossible to generalize for now, entire pedigrees may not be handled at once. Splitting the pedigree is thus necessary. If the number of ways to split a pedigree increases with the number of sub-units chosen, this number may be quite high even if small numbers of sub-units are considered when individuals are related through multiple lines of descent.

Linkage results are highly dependent on how sub-pedigrees are chosen [Chapman et al., 2001; Ciullo et al., 2006]. It has even been argued that the method used to simplify the pedigree may be more important than the method of analysis for linkage [Chapman and Wijsman, 2001]. In what follows, we will use the term “pedigree configuration” to designate a set of sub-pedigrees resulting from the breaking of a large genealogy. The identification of the best pedigree configuration for any particular genealogy or phenotype is not always apparent. The power attributed to a pedigree (we refer here to the power of the subsequent analysis) will depend on the true underlying genetic model as well as on the analytical approach that is used. While identification of deep sub-pedigrees connecting all members of a group to a single common ancestor may be important for mapping rare Mendelian diseases, maximizing the number of affected relative pairs and focusing on their relationship through their closest common ancestors are more suitable strategies for mapping complex traits with non-parametric affected-only linkage analyses. In this type of analysis, the power attributed to a given affected relative pair varies with both the frequency and the genotype relative risks of the variant [Falchi et al., 2004]. Consequently, there is no uniformly best way to split a large pedigree a priori when the characteristics of the variant are not precisely known.

In this paper, we propose a new procedure where linkage is systematically evaluated on multiple different pedigree configurations rather than on a single one. With such an approach of the problem, computation time, flexibility and systematisation of the linkage step are key components. This is why we only consider pedigree configurations that can be handled by software packages that perform fast exact multipoint linkage analyses.

Briefly, a variety of different pedigree configurations that meet pre-specified constraints on family complexity are first generated with an automated method for pedigree breaking (GREFFA, [Falchi et al., 2004]). To limit the cost both in terms of power and computational time, a limited number of pedigree configurations is then selected, favoring the most “a priori” interesting and non-redundant ones. Linkage analyses are then conducted independently on these selected configurations and significance is assessed with a simulation procedure to correct for multiple testing.

We apply this procedure to the extreme case of the highly complex Hutterite pedigree and use it to perform a genome-wide linkage analysis on asthma. The identification of a previously undetected genome-wide significant linkage on chromosome 12q21 in the Hutterites, a region reported by many studies [Barnes et al., 1999; Barnes et al., 1996; Blumenthal et al., 1998; Celedon et al., 2007; CSGA, 1997; Dizier et al., 2000; Nickel et al., 1997; Wjst et al., 1999; Yokouchi et al., 2000], suggests that the multiple splitting procedure is a new tool of interest for linkage analyses in large pedigrees.

In what follows, we start with a short description of the Hutterite data set followed by a brief presentation of GREFFA and its different parameters. Our procedure to generate a diversity of pedigree configurations and to select the most informative configurations that best represent this diversity, is explained and illustrated on the data. Finally, we describe the conditions of the linkage analysis, including the procedure to handle multiple testing, and the linkage results obtained on the data.

MATERIAL AND METHODS

Hutterite data

Various phenotypes have been evaluated in a sample of Hutterites from South Dakota, all related through a 3028-member pedigree. The study subjects here are 896 individuals, linked through a multiple 13-generation pedigree that includes 1840 individuals. The mean inbreeding coefficient in this sample is 0.035 (sd = 0.015), slightly greater than that of first cousins once-removed. The phenotype considered is based on the presence of self-reported asthma symptoms (at least two of the following three: cough, wheeze, or shortness of breath). 137 individuals are affected in the sample.

Genotyping was performed by the Mammalian Genotyping Service; 639 individuals were genotyped for both Marshfield sets 9 and 51 (658 autosomal microsatellites), 208 individuals for set 51 only (293 autosomal microsatellites) and 49 individuals for set 9 only (365 autosomal microsatellites). 6 affected individuals are genotyped for set 51 only and 4 for set 9 only.

Splitting the pedigree

GREFFA is an automatic two-step approach to pedigree splitting developed by Falchi et al [2004]. In the first step – the clustering step – subgroups of related individuals – or cliques – are created through a maximum clique partitioning algorithm. Using pairwise kinship values, cliques of maximum size are iteratively constructed so that a given individual may only be included in one clique. The user defines constraints on the minimum clique size (minCS) and on the minimum kinship level (minKin) between the individuals in the cliques. Maximum clique size (maxCS) and maximum kinship level (maxKin) are additional optional parameters. In the second step – the reconstruction step – an algorithm based on joining binary trees is used to reconstruct most of the genealogical links between all the individuals of each clique while keeping a small pedigree size.

In contrast to the clustering step that can be performed on a subgroup of individuals, the reconstruction step uses all the individuals in the genealogy who were included to compute the pairwise kinship coefficients used in the clustering step. After the reconstruction step, an individual may thus be a member of more than one sub-pedigree if he/she is required to link members of different cliques.

In complex genealogies, the partitioning can not always be entirely determined by fixing parameters only on clique size and kinship level. To overcome this limit, a Monte Carlo (MC) procedure has recently been implemented in GREFFA [Falchi and Fuchsberger, 2008] that browses the different partitions meeting the same clique characteristic parameters in order to identify the partitions that maximize either the number of individuals assigned to a clique or the number of pairwise relationships over all cliques. Each of these two criteria may be more or less powerful, depending on the analyses conducted after the splitting. In particular, maximizing the number of affected relative pairs should be more powerful for affected-only NPL analysis where relationships between affected are the units of information. In the large and highly complex Hutterite pedigree, we found that even with 5000 replicates, the outcome of the MC procedure can be sensitive to the simulation starting point. Consequently, we considered this starting point as an additional parameter, referred to as the seed in what follows.

The two-step structure of GREFFA is appropriate for linkage analysis as the clique definition can be concentrated on specific individuals of interest. In particular, we have shown that basing the clustering step only on affected individuals rather than on all genotyped individuals identifies pedigree configurations that are more powerful for affected-only NPL analysis [Ciullo et al., 2006]. However, a consequence of this two-step structure is the lack of direct control on the size of the final sub-pedigrees obtained after the reconstruction step. The optional user-defined parameters of GREFFA (maxCS and maxKin) only indirectly control the final sub-pedigree sizes. They are not simply correlated with the bit size (2n-f, with n the number of non-founders and f the number of founders), a measure of familial complexity directly relevant for software packages implementing multipoint NPL analysis [Abecasis et al., 2002; Gudbjartsson et al., 2000].

To combine the two requirements for NPL analysis – sub-pedigrees with a high number of affected relative pairs and a controlled bit size – while still allowing an automated splitting of the large pedigree, we favour the optional maxCS parameter over the other GREFFA parameters and choose to control the sub-pedigree bit size through this parameter. For fixed values of minCS, minKin and seed, we iteratively identify the largest value for maxCS that allows extracting subpedigrees with a bit size below a threshold C. In practice, we start by extracting sub-pedigrees without constraining maxCS. If the bit size of at least one sub-pedigree in the set is above the threshold C, we specify a maxCS. We begin with a large value for maxCS (in practice maxCS = 15) and decrease it iteratively until all sub-pedigrees have a bit size below the threshold C. Here, we use C = 23 for NPL analysis with Merlin [Abecasis et al., 2002] but this threshold may vary according to the analysis that will be performed. The maximum number of iterations used in the Huterrite data was 11, which suggests that this automated procedure is an efficient way to control family complexity in highly complex pedigrees such as the Hutterites. The procedure is summarized in Figure 1.

Figure 1.

Procedure to maximize the number of informative pairs in sub-families meeting bit size constraints C

Generating a diversity of pedigree configurations

The above procedure is applied for varying values of minCS, minKin and seed to generate pedigree configurations representing a range of possible configurations. In the Hutterites, we experimented minCS of [3-5] and minKin of [0.05, 0.0625, 0.07, 0.08, 0.09, 0.1] with three different seed values for each combination of minCS / minKin. Fifty-one of the 54 parameter sets provided a unique pedigree configuration, allowing us to explore a diversity of configurations. Table I presents the characteristics of 24 pedigree configurations, selected to represent the characteristics of the 51 different configurations obtained on the asthma Hutterite pedigree. The sensitivity of the configuration characteristics to the GREFFA parameters is critical in determining the number of affected relative pairs included, which varied between 191 and 366.

Table I.

Characteristics of 24 pedigree configurations extracted from the large Hutterite pedigree. Bold cells: linkage pedigree configurations selected for linkage analysis, numbered 1 to 16. Standard pedigree configurations selected for genome-wide linkage analysis in the case of 4 standard pedigree configuration selection are numbered 1 to 4. The 2 additional standard pedigree configurations selected for genome-wide linkage analysis in the case of 6 standard pedigree configuration selection are numbered 5 and 6.

	Minimum kinship (minKin) : 0.1			Minimum kinship (minKin) : 0.09
Seed	100			100000
Clique size [minCS - maxCS]	3-11	4-11	5-11	3-10	4-11	5-11
Number of families	20	10	6	22	15	10
Number of affected individuals	101	72	55	115	94	77
Number of affected relative pairs	267	240	214	301	288	266
Mean kinship between affected pairs (sd)	0.165 (0.074)	0.164 (0.073)	0.162 (0.073)	0.139 (0.082)	0.149 (0.078)	0.141 (0.077)
Mean information content	0.86	0.88	0.89	0.85	0.85	0.88
Pedigree configuration number				2	7

	Minimum kinship (minKin) : 0.08
Seed	100	10000	100000
Clique size [minCS - maxCS]	3-7	5-8	3-9	4-10	5-10
Number of families	22	14	21	15	13
Number of affected individuals	117	98	120	106	99
Number of affected relative pairs	279	284	331	343	330
Mean kinship between affected pairs (sd)	0.137 (0.079)	0.142 (0.077)	0.136 (0.08)	0.122 (0.082)	0.134 (0.079)
Mean information content	0.82	0.87	0.84	0.84	0.87
Pedigree configuration number	5	8	9	10	11

	Minimum kinship (minKin) : 0.07
Seed	100		10000	100000
Clique size [minCS - maxCS]	3-10	4-8	5-10	4-8	4-9	5-10
Number of families	21	18	14	18	19	14
Number of affected individuals	125	117	104	117	119	105
Number of affected relative pairs	366	336	339	329	343	344
Mean kinship between affected pairs (sd)	0.127 (0.082)	0.127 (0.082)	0.126 (0.083)	0.126 (0.081)	0.129 (0.082)	0.129 (0.084)
Mean information content	0.81	0.81	0.83	0.81	0.8	0.84
Pedigree configuration number	12	13	14	15	16	4

	Minimum kinship (minKin) : 0.0625				Minimum kinship (minKin) : 0.05
Seed	100	10000		100000	10000
Clique size [minCS - maxCS]	5-7	4-7	5-7	5-8	3-4	4-4	5-6
Number of families	16	20	18	15	34	32	21
Number of affected individuals	108	119	114	109	135	130	128
Number of affected relative pairs	299	310	299	337	196	191	312
Mean kinship between affected pairs (sd)	0.112 (0.086)	0.117 (0.085)	0.116 (0.087)	0.119 (0.084)	0.118 (0.096)	0.105 (0.091)	0.108 (0.091)
Mean information content	0.81	0.78	0.8	0.82	0.64	0.65	0.73
Pedigree configuration number	1		6	3

Among the different pedigree configurations created by this incremental procedure, some are inevitably very similar. To quantify the similarity between two configurations, we introduced a measure of concordance. Concordance is defined as the ratio of the number of affected relative pairs that two pedigree configurations have in common over the maximum number of affected relative pairs that they could possibly share. The denominator is thus the number of affected relative pairs in the pedigree configuration that has the smallest number of affected relative pairs. For example, if we note N_A and N_B the number of affected relative pairs in pedigree configurations A and B, and N_AB the number of pairs these two configurations share in common, the concordance conc(A,B) between A and B is defined as :

$$conc(A,B)=\frac{N_{AB}}{\min (N_A,N_B)}$$

Among the 51 different pedigree configurations obtained for the Hutterite asthma pedigree, the median concordance was 0.5 (range [0.19 – 1]). A concordance of one between two different configurations occurs when the affected relative pairs of one configuration are all included in the other. The concordance is particularly high among configurations with minKin of 0.1 (median concordance 0.86 [0.79 – 1]) and low among configurations with minKin of 0.0625 and 0.05 (median concordance 0.56 [0.46 – 0.7] and 0.38 [0.3 – 0.5] respectively). Indeed, a minKin of 0.1 is very restrictive, leading to a weak diversity of pedigree configurations meeting this criterion. On the contrary, a minKin of 0.0625 can create very different configurations, even with small variations of the other clique parameters. For example, using minKin = 0.0625, minCS = 5 and maxCS = 7 but two different seed values (100 and 10000) generates two pedigree configurations with a weak concordance of 0.57.

The parameter range choice is key to generate a diversity of pedigree configurations. It is sensitive to both the genealogy characteristics and the distribution of the individuals of interest (affected individuals in our case) in the genealogy, in part determined by the genetic model underlying the trait. Consequently, the parameter ranges used in the present work might not be an appropriate choice in other studies. Range choices must be guided by the diversity created, measured both in terms of number of pedigree configurations, concordance among them and relative informativity for linkage (see below).

Selecting pedigree configurations for the two-stage linkage analysis

Running a linkage analysis on all the pedigree configurations generated would not only be time-costly, but would also cost in terms of power because multiple testing would be increased. Consequently, we ran the linkage analyses on a sub-group of pedigree configurations chosen on the basis of high “power predictors”.

Selection of non redundant pedigree configurations for linkage analysis

As mentioned above, the number of affected relative pairs is important in determining the power of NPL analyses, but other factors affect power as well. As an illustration, consider a pedigree configuration A with 300 affected relative pairs clustered into 10 families and a pedigree configuration B with 300 affected relative pairs clustered into 20 families. In this case, the configuration B includes more affected individuals than the configuration A. Yet, the configuration A may be more powerful to detect linkage if there is a familial heterogeneity of the genetic variants involved in the disease, in which case, there may be more heterogeneity in configuration B.

In Table I, each pedigree configuration is described in terms of number of sub-families, number of affected individuals included in the analysis, number of affected relative pairs, as well as the mean kinship among the pairs and mean linkage information content (IC) [Kruglyak et al., 1996] computed for markers on chromosome 1. If a minKin of 0.05 can generate a pedigree configuration with a reasonably high number of affected relative pairs (up to 312 pairs), it is only at a cost in information content (IC = 0.73 vs IC ≥ 0.8 in many other configurations with more than 275 pairs). Indeed, sub-pedigrees connecting more distantly related affected individuals tend to include more non-genotyped ancestors in their genealogy, which may lead to smaller ICs and therefore decreased power. Thus both a high number of affected relative pairs (above a threshold NP) and a high information content (above a threshold IC) are used as “power predictors” to select pedigree configurations prior to the linkage analysis.

After this pedigree configuration screening on NP and IC, the pairwise concordances between all the remaining configurations are computed. We consequently identify the smallest sub-group of pedigree configurations with no concordance above a threshold CT. This is done with a systematic selection of configurations with maximum NP and IC when a choice is required. Thus, this two-step screening identifies a reduced number of pedigree configurations (referred to as linkage pedigree configurations) that represent the diversity of all possible configurations.

Applying this strategy to the Hutterite pedigree and using NP=275, IC=0.8 and CT=85%, 16 linkage pedigree configurations were identified (bold cells, Table I). The NP was chosen to include pedigree configurations with at least 75% of the maximum number of affected relative pairs (366) that could be included in a configuration. In the 16 selected linkage pedigree configurations, the number of affected relative pairs ranges from 279 to 366, the information content ranges from 0.8 to 0.87, and the mean kinship coefficients in affected pairs ranges from 0.112 to 0.149. Median concordance is 0.57 (range [0.39 – 0.84]). Seven pedigree configurations were removed due to excesses of concordance with other (retained) configurations at the second step of the configuration screening.

All 16 linkage pedigree configurations selected were generated with a minKin between 0.0625 and 0.09. The variation range chosen for the minKin values is thus large enough to generate a diversity of “interesting” configurations. More generally, the parameter values corresponding to the linkage pedigree configurations should be used to decide whether the different parameter ranges chosen are adapted to the genealogy under study.

Two-stage linkage analysis

Because the number of linkage pedigree configurations that were identified with this selection procedure is large, we performed a two-stage linkage analysis to limit multiple testing. First, only a fixed number (NSS) of pedigree configurations (referred to as the standard pedigree configurations) are analysed on the whole genome. When a suggestive linkage is detected, the linkage analysis on this chromosome only is then performed on all the other linkage pedigree configurations identified by our procedure. A linkage signal is considered suggestive if LODs above a threshold T are detected within a 15 cM region in at least half of the NSS standard pedigree configurations.

The NSS standard pedigree configurations are selected among the linkage sub-pedigree configurations to be as different as possible through an iterative procedure described in Appendix 1. The threshold T was assessed by simulations as explained in Appendix 2. We consider T = 1.6 to be suggestive in our analysis.

To assess the impact that the choice of the number NSS of standard pedigree configurations has on linkage results, we experimented our procedure with NSS = 4 and 6 in the Hutterite data. Selected standard pedigree configurations are given in Table I (the 4 standard configurations selected for NSS = 4 are numbered 1 to 4, the two additional standard configurations selected for NSS = 6 are numbered 5 and 6). Median concordance among standard pedigree configurations is 0.5 (range [0.39 – 0.55]) when NSS = 4 and 0.51 (range [0.39 – 0.6]) when NSS = 6.

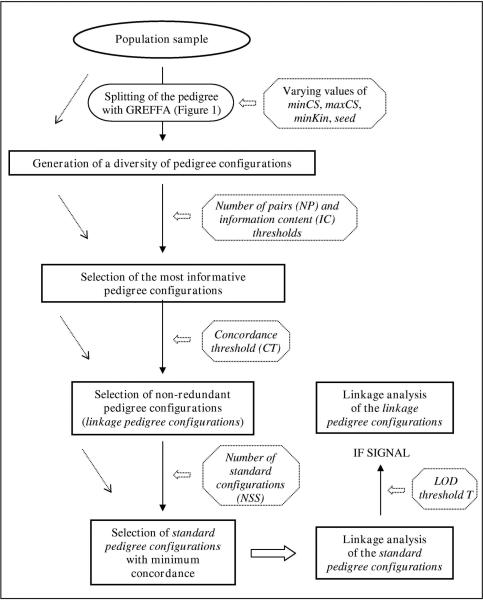
The multiple splitting procedure is summarized in Figure 2, where the different parameters whose values must be specified according to the population under study are highlighted. The GREFFA parameters should be specified so as to generate a diversity of pedigree configurations. Parameters NP (minimum number of pairs), IC (information content), CT (concordance threshold) and NSS should allow to reduce the number of configurations considered for linkage analysis while still allowing a diversity of pedigree configurations to be analysed.

Figure 2.

Multiple splitting procedure. Parameters likely to vary according to the population are in italics in dashed octagons.

Linkage analysis

Non parametric linkage analysis is performed with the LOD score based on Spairs with the exponential model [Kong and Cox, 1997] and multipoint IBD computation using Merlin [Abecasis et al., 2002].

In the splitting procedure implemented in GREFFA, a given individual may be present in several sub-pedigrees. Indeed, even though an affected individual is allocated to only one clique during the clustering step of the splitting, he/she can be used several times in the reconstruction step to join the individuals of other families. This problem is particularly important in a highly complex pedigree. To avoid the bias introduced by including the phenotypic information from the same affected individuals multiple times, we consider as missing the status of an affected individual in the families he/she joined during the reconstruction step, but we keep his genotypic information to clarify the inheritance pattern within the families.

Controlling multiple testing

Generating a correct genome-wide significance threshold for linkage results obtained after this multiple splitting procedure is a key issue. We designed a simulation scheme to assess the empirical type I error, based on the one proposed by Ciullo et al [2006]. This scheme takes into account the particular characteristics of the marker map used, the breaking of a large pedigree into sub-pedigrees and the analysis of several different pedigree configurations.

Briefly, genome-wide gene dropping simulations are conducted using the complete pedigree information, without respect to the phenotypes, using the Genedrop program of the MORGAN 2.6 package [Thompson, 2005]. Transmission of the alleles for all markers included in the analysis is simulated with ancestor alleles randomly drawn from the allele frequency distributions observed in the data. In each replicate, the statistic of interest (LOD) is computed on the whole genome for the NSS standard pedigree configurations, considering the real observed phenotypes. If a suggestive linkage is detected on a chromosome, all the other linkage pedigree configurations selected by our procedure are analysed for this chromosome (as mentioned above, a linkage signal is considered suggestive if LODs above a threshold T are detected within a 15 cM region in at least half of the NSS standard pedigree configurations). Finally, the maximum LOD score over the whole genome is identified for each replicate. The empirical distribution of these whole genome maximum LOD values is used to estimate empirical genome-wide significance thresholds and p-values of the maximum LOD observed in the data. The mean computation time for each replicate is four hours on a computer with a 3.6 GHz processor and 2 GB of RAM. Thus, only 1000 replicates were performed.

Different genome-wide significance thresholds computed in the Hutterite data are presented in Table II. The thresholds are not sensitive to the number NSS of standard pedigree configurations analysed in the first linkage analysis step. The increase of NSS (4 vs 6), and therefore the higher number of tests performed in the first linkage analysis step, is offset by a more stringent definition of a suggestive linkage signal under the null hypothesis (2 vs 3 pedigree configurations with a LOD higher than the threshold T) required prior to the analysis of all the other linkage pedigree configurations.

Table II.

Genome-wide significance thresholds of the maximum LOD score in the asthma Hutterite pedigree, for 2 different numbers of standard pedigree configurations (NSS) to control for 3 different global type I errors. Based on 1000 replicates.

	Significance threshold
Global type I error	NSS = 4	NSS = 6
1%	4.4	4.35
5%	3.85	3.85
10%	3.53	3.55

Linkage analysis results

After genome-wide linkage analysis of the NSS standard pedigree configurations, only chromosome 12 revealed linkage results that were considered suggestive according to our criteria, with either NSS = 4 or 6 (Table IIIA). The other linkage pedigree configurations were therefore analysed for this chromosome only.

Table III.

Linkage results on chromosome 12 and 14. Pedigree configuration numbers are those given in Table I

A)
Pedigree configuration number	Max LOD chr12 (position)	Max LOD chr14 (position)
1	4.03 (95.17)	1.01 (24.23)
2	1.19 (95.17)	1.31 (29.72)
3	3.75 (95.17)	0.91 (20.46)
4	1.41 (96.54)	1.89 (24.23)
5	2.48 (93.80)	1.08 (26.27)
6	1.67 (83.06)	0.89 (20.46)

B)
Pedigree configuration number	Max LOD chr12 (position)
7	2.65 (18.18)
8	1.78 (93.80)
9	1.60 (93.80)
10	2.20 (95.17)
11	2.57 (95.17)
12	1.41 (96.54)
13	2.90 (96.54)
14	1.75 (96.54)
15	3.67 (96.54)
16	3.44 (96.54)

After the second step of linkage analysis, the maximum LOD score among all the linkage pedigree configurations was 4.03 on chromosome 12q21 at 95.17 cM, which was obtained on a standard pedigree configuration. It reaches genome-wide significance (p-value = 0.029 considering NSS = 4 and p-value = 0.027 considering NSS = 6).

Maximum LOD scores on chromosome 12 are highly sensitive to the pedigree configurations but are most often detected at the same position. The maximum LOD score of only one of 16 configurations is not located near 95 cM (Table IIIA and B, Figure 3).

Figure 3.

LOD score curves on chromosome 12 for the 16 linkage pedigree configurations

The linkage on chromosome 12 is not sensitive to the standard pedigree configurations selected. Indeed, only four out of the 16 linkage pedigree configurations do not have a LOD above the defined threshold near 95 cM on chromosome 12. Among them, two pairs of configurations have a relatively high concordance (the concordance between the two configurations with minKin higher than 0.9 is 0.76 and the concordance between the two configurations with minKin higher than 0.07 – maxCS of 10 and minCS of 3 or 5 – is 0.77). Because the standard pedigree configurations are selected to be as different as possible, only two of these four configurations could have been selected all together as standard pedigree configurations, which would not hamper the linkage detection on chromosome 12.

The results of the first linkage step also seem robust to the threshold used. Indeed, the linkage signal on chromosome 12 would still have been considered suggestive in the first step with a threshold T as high as 3.75 for NSS = 4 and 2.48 for NSS = 6. In contrast, it would have been necessary to decrease the threshold T to 1.3 with NSS = 4 to detect one additional interesting linkage signal on chromosome 14 in the first linkage analysis step (Table IIIA).

On chromosome 12, eight pedigree configurations yielded a LOD higher than 2.0 near 95 cM and, among these, four had a LOD higher than 3.4. Among the 22000 chromosome scans performed under the null hypothesis (1000 replicates on 22 chromosomes), only five scans had at least four pedigree configurations with a LOD score higher than 3.4 in the same region, considering either NSS = 4 or 6. This result strengthens the significance of the linkage result on chromosome 12.

DISCUSSION

The perspective adopted to design the multiple splitting procedure presented in this paper is necessarily time consuming. Although completely tractable with standard computers, it prevents from performing power simulations. We believe that the successful detection of a chromosome 12q21 asthma locus is a first demonstration of the value of the approach. Indeed, evidence for linkage of asthma or asthma-related traits to chromosome 12q has been reported by many studies, several of them specifically on chromosome 12q21 [Barnes et al., 1999; Barnes et al., 1996; Blumenthal et al., 1998; Celedon et al., 2007; CSGA, 1997; Dizier et al., 2000; Nickel et al., 1997; Wjst et al., 1999; Yokouchi et al., 2000]. Although no genetic risk factor has yet been identified in this region, the number of studies localizing to this region suggests that it may harbour a true asthma gene. The fact that only modest evidence of linkage with this region had been reported by previous analyses based either on a single splitting of the pedigree in 20 families (Ober et al [2000], nominal p-value of likelihood ratio statistic p = 0.0159 at 81 cM with asthma symptoms) or on 3, 4 or 11 extended sub-pedigrees (Chapman et al [2001], maximum LOD score of 1.73 at 95 cM with asthma) and would not be detected in the present analysis if only the pedigree configuration maximizing the number of affected relative pairs was considered (maximum LOD score was 1.41 at 95.17 cM in this configuration 12 on Table 3), suggest that the multiple splitting procedure might be a valuable tool.

Time saving is in great part also underlying our decision to predefine parameter ranges in the pedigree configuration generation step and parameter values in the selection and linkage steps. Doing so, we reintroduce user-based decisions in the procedure. We have suggested guidelines and tools (concordance, “power predictors”) to help in the decision making. Still, we believe that the variety of human genealogies and disease models prevents from designing systematic rules.

The main interest of this procedure might lie in its greatest robustness to genetic heterogeneity. Indeed, as noted by Chapman and Wijsman [Chapman and Wijsman, 2001], there is some evidence of heterogeneity for the asthma phenotype even within the very well isolated Hutterite population. More generally, population isolates are expected to be a particularly interesting sampling scheme to detect rare variants, founder effect and genetic drift having a stronger impact on such variants [Pardo et al., 2005]. Models with rare variants contributing to complex diseases require multiple rare risk variants [Pritchard and Cox, 2002]. If such rare variants happen to be in the same gene, the power of linkage analysis in a single large genealogy is limited. In contrast, particular splitting of the genealogy may result in sub-pedigrees with only one segregating variant per sub-pedigree and different variants across the different sub-pedigrees.

Although developed in the context of exact multipoint non parametric affected only linkage analysis, the present procedure – where a diversity of pedigree configurations is generated before selecting the most a priori “interesting” and non-redundant configurations for linkage, followed by a two-stage approach to the linkage analysis and a simulation-based assessment of significance – is more generally applicable. In particular, a recent linkage analysis of quantitative traits in the less inbred isolated populations of Cilento was based on this procedure. Interestingly, this led to the detection and replication of a new locus for BMI on chromosome 1q24 [Ciullo et al., 2008]. Other usages, including implementing simulation-based linkage statistics on larger sub-pedigrees, might also be interesting to consider.

Table V.

Example of standard pedigree configuration selection among the seven configurations considered in Appendix 1 and in Table IV. conc(i,j) is the concordance between configurations i an j.

Pedigree configuration k	Median concordance with all other configurations	Maximum between conc(2,k) and conc(3,k)
1	65	76
2	57	/
3	65	/
4	68	65
5	71	72
6	71	74
7	72	66

Appendix 1: Selection of standard pedigree configurations

The NSS standard pedigree configurations are selected among the linkage pedigree configurations to be as different as possible through an iterative procedure. The pedigree configuration which minimizes the median concordance with all the other configurations is taken as the first standard pedigree configuration. Then, standard pedigree configurations are chosen iteratively by selecting at the step k the configuration that minimizes the maximum concordance with the k-1 standard pedigree configurations already defined. In case of equality, the configuration with higher NP and IC is systematically preferred.

Consider for example seven pedigree configurations, whose concordance matrix conc(i,j), with i = 1,..7, j = 1..,7, is given in Table IV. We want to select NSS = 3 standard pedigree configurations. For each of the seven pedigree configurations, we compute its median concordance with all the other configurations (Table V). The configuration 2 minimizes this median concordance and is thus taken as the first standard configuration. The second standard pedigree configuration is the number 3, since it is the one that shows the lowest concordance with the configuration 2:

$$\mathrm{conc}(2,3)=\min (\mathrm{conc}(2,\mathrm{k}),\mathrm{k}\ne 2)$$

Table IV.

Concordance matrix of the seven pedigree configurations for example in Appendix 1

	1	2	3	4	5	6	7
1		76	56	65	63	66	70
2	76		48	52	60	56	58
3	56	48		65	72	74	66
4	65	52	65		78	72	84
5	63	60	72	78		71	74
6	66	56	74	72	71		76
7	70	58	66	84	74	76

Next, we look for a third configuration that will minimize the concordance with the two first standard configurations. For that, we compute conc(k,2) and conc(k,3) for each of the five remaining configurations k and select the configuration for which the maximum of conc(k,2) and conc(k,3) is minimal. In our example, the fourth configuration is thus selected as the third standard pedigree configuration.

Appendix 2: Assessment of the suggestive linkage threshold T

Simulations under the null hypothesis similar to those described in the “Controlling multiple testing” paragraph were performed to globally evaluate the LOD threshold T above which a linkage signal should be considered as suggestive. In a replicate, the maximum LOD of each chromosome is retained for each of the NSS standard pedigree configurations (NSS = 4 or 6), resulting in 22 × NSS different LOD by replicate. With 100 replicates, the 95% quantile of the empirical distribution of these maximum LOD is 1.59 considering NSS = 4 (based on computation of 22 × 4 × 100 = 8800 LOD) and 1.6 considering NSS = 6 (based on computation of 22 × 6 × 100 = 13200 LOD). We thus consider T = 1.6 to be suggestive in our analysis.