ESTIMATING PERSON-CENTERED TREATMENT (PeT) EFFECTS USING INSTRUMENTAL VARIABLES: AN APPLICATION TO EVALUATING PROSTATE CANCER TREATMENTS

SUMMARY

This paper builds on the methods of local instrumental variables developed by Heckman and Vytlacil (1999, 2001, 2005) to estimate person-centered treatment (PeT) effects that are conditioned on the person’s observed characteristics and averaged over the potential conditional distribution of unobserved characteristics that lead them to their observed treatment choices. PeT effects are more individualized than conditional treatment effects from a randomized setting with the same observed characteristics. PeT effects can be easily aggregated to construct any of the mean treatment effect parameters and, more importantly, are well suited to comprehend individual-level treatment effect heterogeneity. The paper presents the theory behind PeT effects, and applies it to study the variation in individual-level comparative effects of prostate cancer treatments on overall survival and costs.

1. INTRODUCTION

Much of the literature on treatment effects has focused on estimating effect parameters that inform population-level or policy-level decisions. Even when distributional impacts of treatments and policies are studied, the impacts are viewed as informing a social decision maker to help choose across alternative options (Heckman, 2001). However, in the presence of heterogeneous treatment effects, it is natural to expect that individual choices of treatments may vary from the socially optimal treatment that is identified based on some average social welfare criterion. More importantly, treatment effect information that can help change future individual-level behavior on treatment choices would automatically influence social choice of treatments through positive self-selection. Hence estimating treatment effects that can inform individual-level decision making can be of great social value.

This conundrum manifests in its most acute form in the healthcare setting. In traditional clinical outcomes research, the focus has always been on finding average effects either through large clinical trials or observational datasets. Estimating treatment effect heterogeneity has mostly been relegated to post hoc analysis, rather than becoming the central goal of the analysis.¹ Yet the clinical setting is an obvious place where individual-level decision making is most relevant as a physician–patient dyad tries to decide on the best line of treatment for that patient. There is a growing recognition, based on fundamental theoretical principles, that more nuanced estimates of treatment effects between alternative medical interventions that can provide evidence on individualized treatments by possibly conditioning on a variety of risk factors can lead to increased welfare through more efficient use of medical technologies (Basu, 2009, 2011a). In contrast, failing to generate such individualized estimates and also producing results on population average effects without recognizing the underlying heterogeneity could lead to welfare losses including faster growth in healthcare expenditures (Basu et al., 2011; Basu, 2011a, 2011b).²

In this paper, we develop and present a new individualized treatment effect concept called person-centered treatment (PeT) effects, which can be estimated using local instrumental variable (LIV) methods (Heckman and Vytlacil, 1999). We begin in Section 2 with a motivating example from healthcare evaluation in patients diagnosed with prostate cancer (PCa) where the use of PeT effects will be valuable. In Section 3, we provide a brief background on the heterogeneous treatment effects literature. We then present a formal definition, identification and estimation of PeT effects. In Section 4, we apply the proposed methods to estimate PeT effects of surgery versus active surveillance on 7-year survival and costs among patients diagnosed with clinical localized PCa. Discussions follow in Section 5.

2. A MOTIVATING EXAMPLE

2.1. Prostate Cancer: Background

PCa is the most commonly detected non-cutaneous malignancy among American men, with an estimated 241,740 cases to be diagnosed in 2012 and more than 28,000 men dying from the disease. As the cohort of ‘baby boomers’ age, the incidence and prevalence of PCa will likely continue to increase as long as contemporary screening patterns continue. Elderly men (65+ years) account for over 60% of all diagnosed PCa; 80% of those diagnoses are for clinically localized cancer. Because prostate tumors are usually characterized by slow progression rates, active surveillance (AS) of PCa patients, where no invasive procedures are employed, is common in clinical practice. However, up to 60% of elderly PCa patients receive some form of aggressive therapy: either prostatectomy (PS) or a form of radiation therapy (RT). We focus on the questions of understanding the effects of PS over AS on overall and on total expenditures among elderly patients and the effect moderation by various patient-level factors.

2.2. Prior Evidence

Despite the high prevalence and burden of PCa among elderly American men, there is a considerable dearth of evidence on the comparative effectiveness of treatments for patients with PCa (Wilt et al., 2008). As the cohort of ‘baby boomers’ age, the incidence and prevalence of PCa will continue to increase and the value of such research would likely continue to grow.

Although it has been suggested that patients overestimate benefits of treatment and underestimate benefits of AS while making treatment choices (Mohan et al., 2009), it is not clear on what basis patients and physicians continue to form their expectations about survival benefits of RP over AS. An 18-year long Scandinavian trial was conducted prior to the era of common PSA screening, which compared PS versus AS (Bill-Axelon et al., 2009). Only a fraction of patients older than 65 years was enrolled in this trial, which found no significant difference in mean overall survival among elderly patients. Many factors render this RCT evidence to be obsolete. Besides the fact that this RCT was not powered to look at differences among the elderly group of patients, life expectancies for elderly individuals have dramatically improved over the last two decades. Between 1975 and 2005, 15-year survival probabilities for 65-year-old men have increased by 17 percentage points in the USA (Muening and Glied, 2010). This indicates that the survival gains from eliminating cancer are likely to be more than those 20 years ago, even when the underlying disease progression from diagnosis had remained the same. Moreover, with a more aggressive screening regimen implemented during the late 1980s and early 1990s, and especially with the advent of prostate-specific antigen (PSA) screening, distribution of PCa diagnosed among elderly men in the late 1990s was less advanced than in those diagnosed during the pre-PSA era. Last, but not least, the quality of surgery has risen over the past two decades, as evident from the declining morbidity from such procedures. Therefore, exploring the comparative effectiveness of alternative PCa treatments among elderly patients using recent data becomes important.

Precisely for the reasons stated above, a more recent randomized trial (PIVOT) was conducted that explored the comparative survival of PS versus AS for clinically localized PCa. It recruited most patients during 1995–2002 and followed them through January 2010 with a median follow-up time of 10 years (Wilt et al., 2012). This trial is of specific importance to us as our analyses will be conducted over a very similar time period, but using population-based registry data. PIVOT investigators found that among men with localized PCa detected during the early era of PSA testing radical prostatectomy did reduce, but not significantly, the all-cause and PCa mortality, as compared with observation, through at least 12 years of follow-up.

Many drawbacks remain in interpreting the results of this trial. Not only was the trial under-powered for its primary outcomes, as exemplified by its failure to meet its projected sample size (Thompson and Tangen, 2012), but the reported results were also based on an intention-to-treat analysis which does not accurately capture the comparative effectiveness of receipt of treatment. For example, about 20% of patients in the AS arm received curative treatment, whereas about 15% of men randomized to the PS arm did not receive the treatment. Moreover, the generalizability of results from such trials remains to be a contentious issue. Only 15% of the eligible patients agreed to enroll in the PIVOT trial (Wilt et al., 2009). Moreover, the investigators report that, compared to men who were PIVOT eligible but declined enrollment, PIVOT enrollees were slightly older, more likely to be African-American, had well-differentiated PCa and reported their health status as excellent or very good.

2.3. Evidence on Heterogeneity

Examinations of treatment effect heterogeneity within these trials have also been limited. Typically, post hoc analyses of broad subgroups are conducted to evaluate variation in effects – for example by stage or grade of the prostate tumor at diagnosis. Most often they are age adjusted but rarely age stratified (Bill-Axelson et al., 2009). Similarly, in the PIVOT trial, subgroups analyses were performed by age (<65 years vs. ≥65 years), race, Charlson comorbidity score, stage and grade. In most of these subgroups, surgery was found to be better than watchful waiting, but did not reach statistical significance. However, it is not clear whether the inefficiency is driven due to small sample sizes within a subgroup or the lack of specificity of these subgroups in identifying individuals who would truly benefit from surgery. For example, a secondary analysis of the Scandinavian trial data revealed substantial individual-level variability in treatment effects, especially across the dimensions of age and tumor characteristics when considered simultaneously (Vickers et al., 2012). The authors found that only a quarter of the patients had individual level benefits that lay within 50% of the average effect. This implies that broad subgroup analyses based on one risk factor cannot explain much of the individual-level variation in treatment effects. We plan to answer this question directly based on our methods.

3. PERSON-CENTERED TREATMENT EFFECTS

3.1. Econometrics of Treatment Effect Heterogeneity

In the evaluation literature, nuanced treatment effects are most popularly characterized by conditional average treatment effects (CATE) where an average treatment effect is estimated conditional on certain values of observed covariates over which treatment effects vary. For example, if age is the only observed risk factor, one can establish a conditional effect of surgery versus active surveillance on mortality for patients of age 60 years diagnosed with clinically localized PCa. This is an average effect for all 60-year-olds in this condition. However, does this estimate apply to all men with clinically localized PCa at age 60 years? Certainly not, as there may be many other factors that determine heterogeneity in treatment effects in this population. For example, clinical stage and grade of cancer not only determine overall survival but may also determine differential effects from alternative treatments. To the extent that all potential moderators of treatments effects are observed to the analyst of the data, a nuanced CATE can be established conditioning on values of all of these factors.

In most applied work, however, not all moderators of treatment effects are observed. One reason is that many of these moderators are yet to be discovered and hence remain unknown to scientific knowledge. They are typically represented by the pure stochastic error term in statistical analysis of data. However, there are some moderators that fall within the purview of scientific knowledge but remain unmeasured in the data at hand. This is usually the case for most randomized studies that rely on randomization to equate the distribution of all these factors across the randomization arms and forgo measurement of several factors in the interest of time and expenses.

In observational studies, these unmeasured moderators of treatment effects play a vital role in generating essential heterogeneity as often they are observed by individuals and acted upon by some while making treatment selection (Heckman, 1997; Heckman and Vytlacil, 1999).³ An entire genre of methods, including methods based on local instrumental variable (LIV) approaches, have been developed to estimate policy-relevant and structurally stable mean treatment effect parameters in the presence of essential heterogeneity (Heckman and Vytlacil, 1999, 2001, 2005). Basu et al. (2007, 2011) introduced these methods to the health economics literature. where essential heterogeneity is widespread and instrumental variable methods are gaining meteoric popularity.

More importantly, distributions of treatment effects are useful for policy makers who care about distributional effects of policies (Heckman and Robb, 1985). For individual decision makers, such distributional effects are of central importance. Although difficult to establish, the most useful metrics to study distributional impacts of policies and treatments are the full marginal and joint distributions of potential outcomes. Previous work by Imbens and Rubin (1997) and Abadie (2002, 2003) have developed estimators for the marginal distributions of potential outcomes under the local average treatment effect (LATE) framework, where the instrument corresponds to the specific policy question that is being studied. Carniero and Lee (2009) extends the LIV framework of Heckman ad Vytlacil (1999, 2001, 2005) to identify distributions of potential outcomes and to develop a semiparametric estimator for the entire marginal distribution of potential outcomes. However, when it comes to understanding individualized decision making, estimating the marginal distribution of potential outcomes is not enough. They carry no information to help identify the quantile of the marginal distribution of counterfactual outcomes where an individual may lie had he taken an alternative treatment (Carniero et al., 2001). One must have knowledge about the full joint distribution of potential outcomes, which can only be established under much stronger assumptions (Heckman and Honoré, 1990; Heckman et al., 1997).⁴

LIV methods can seamlessly explore treatment effect heterogeneity across both observable characteristics and unobserved confounders and also be used to establish CATE based on observed factors. In this paper, we develop and present a new individualized treatment effect concept called person-centered treatment (PeT) effects, which can also be estimated using LIV methods. This new treatment effect concept is more personalized than CATE as it takes into account individual treatment choices and the circumstances under which people are making those choices in an observational data setting in order to predict their individualized treatment effects. In our PCa example, suppose that we not only have data on age of the PCa patients but also the treatment they choose and the distances of their residence from the hospitals that offer surgical procedures. Assume that these distances impart a cost for accessing surgery and therefore influence treatment selection but do not affect the potential outcomes for these patients under either treatment, i.e. they are instrumental variables. Under such circumstances, 60-year-old patients, who live far from hospital and still choose surgery, are likely to have a different distribution of unobserved confounders than 60-year-old patients who live close to the hospital and choose surgery. Therefore, by taking into account treatment choices and the observed circumstances under which those choices were made, we can enrich CATE to form a PeT effect that provides a conditional treatment effect that is averaged over a personalized conditional distribution of unobserved confounders and not their marginal distribution as in CATE.

There are several intuitive aspects about the PeT effects:

1. They help to comprehend individual-level treatment effect heterogeneity better than CATEs.

2. They are better indicators for the degree of self-selection than CATE. Specifically, they are better predictors of true treatment effects at the individual level both in terms of the positive predictive value and the negative predictive value.

3. They can explain a larger fraction of the individual-level variability in treatment effects than CATEs. The marginal distribution of PeT effects is a better proxy for the true marginal distribution of individual effects than that of CATEs.

4. All mean treatment effect parameters can be easily computed from PeT effects without any further weighting. Thus they also form integral components for population-level decision making.

All of these features of PeT effects will be studied here.

3.2. Structural Models for Outcomes and Choices

We start by formally developing structural models of outcomes and treatment choice following Heckman and Vytlacil (1999, 2001, 2005). For the sake of simplicity we will restrict our discussion to two treatment states: the treated state denoted by j = 1 and the untreated state denoted by j = 0. The corresponding potential individual outcomes in these two states are denoted by Y₁ and Y₀. We assume

$$Y_1={\mu }_1(X_{\mathrm{O}},X_{\mathrm{U}}\vartheta )\text{and}{Y}_0={\mu }_0(X_{\mathrm{O}},X_{\mathrm{U}}\vartheta )$$ (1)

where X_O is a vector of observed random variables, X_U is a vector of unobserved random variables, which are also believed to influence treatment selection (they are the unobserved confounders), and ϑ is an unobserved random variable that captures all remaining unobserved random variables.

Assumption 1

(X_O, X_U)∐ϑ and X_O∐X_U, where ∐ denotes statistical independence.

We assume individuals choose to be in state 1 or 0 (prior to the realization of the outcome of interest) according to the following equation:

$$D=1\text{if}{\mu }_D(X_{\mathrm{O}},Z)-U_D>0$$ (2)

where Z is a (non-degenerate) vector of observed random variables (instruments) influencing the decision equation but not the potential outcome equations, μ_D is an unknown function of X_O and Z, and U_D is a random variable that captures X_U and all remaining unobserved random variables influencing choice. By definition, U_D∐ϑ, which also defines the distinction between X_U and ϑ in equation (1). Equations (1) and (2) represent the nonparametric models that conform to Imbens and Angrist’s (1994) independence and monotonicity assumptions needed to interpret instrumental variable estimates in a model of heterogeneous returns (Vytlacil, 2002). As in Heckman and Vytlacil (1999, 2001, 2005), we can rewrite equation (2) as

$$D=1\text{if}P(X_{\mathrm{O}},Z)>V$$ (3)

where V = F_UD|XO,Z[U_D|x_O, z], P(x_O,z) = F_UD|XO,Z[μ_D(x_O, z)]. Therefore, for any arbitrary distribution of U_D conditional on X_O and Z, by definition, V ~ Unif[0, 1] conditional on X_O and Z.

Assumption 2

Assume that (a) μ_D(x_O, Z) is a non-degenerate random variable conditional on X_O = x_O; (b) (X_U, ϑ, U_D) are independent of Z conditional on X_O = x_O; (c) The distribution of U_D conditional on (X_O, Z) and that of μ_D(x_O, Z) conditional on X_O = x_O are absolutely continuous with respect to the Lebesgue measure; (d) Y₁ and Y₀ have finite moments; and (e) Pr(D = 1) > 0.

An individual-level treatment effect is given as

$$\text{TE}=(Y_1-Y_0)$$ (4)

Obviously, we never observe both the potential outcomes for each individual. Our observed outcome Y is given as

$$Y=Y_1\text{if}D=1\text{and}Y=Y_0\text{if}D=0$$ (5)

Therefore, the goal of the analysis is to obtain estimates of Y₁ for subjects with D = 0 and of Y₀ for subjects with D = 1. These outcomes are known as counterfactual outcomes as they represent the potential outcomes had the subjects chosen a different treatment from the one they have in practice. Differences in the counterfactual outcomes across individual subjects will depend on X_O, X_U and ϑ. Several individual-level treatment effect parameters can be defined that reflect these variations.

3.3. Treatment Effect Definitions

3.3.1. Individualized Expected Treatment Effect (IETE)

Since ϑ is typically not only unmeasured but also unknown (as otherwise it would have been used for treatment selection), the most precise IETE that one can hope for in terms of predictions is given by

$$\begin{array}{l}\text{IETE}=\xi (x_{\mathrm{O}},x_{\mathrm{U}})=E_{Y_1-Y_{\mathrm{O}}\mid X_{\mathrm{O}},X_{\mathrm{U}}}(Y_1-Y_0\mid x_{\mathrm{O}},x_{\mathrm{U}})\\ =E_{\vartheta }({\mu }_1(x_O,x_U\vartheta )-{\mu }_0(x_O,x_U\vartheta ))(\text{based}\text{on}\text{Assumption}1)\end{array}$$ (6)

Throughout this paper, we will denote IETE by ξ(x_O, x_U) and it will serve as a reference to which our proposed individual treatment effect parameter and other parameters will be compared. The typical population-level mean treatment effect parameters—average treatment effect (ATE), effect on the treated (TT) and effect on the untreated (TUT)—can be derived by appropriate aggregation of ξ(x_O, x_U)over the relevant subgroups.

$$\text{ATE}=E_{X_{\mathrm{O}}}\{E_{X_{\mathrm{U}}\mid X_{\mathrm{O}}}\{\xi (X_{\mathrm{O}},X_{\mathrm{U}})\}\}=E_{X_{\mathrm{O}}}\{E_{X_{\mathrm{U}}\mid X_{\mathrm{O}}}\{\xi (X_{\mathrm{O}},X_{\mathrm{U}})\}\}(\text{by}\text{Assumption}1)$$

Similarly

$$\begin{array}{r}\text{TT}=E_{X_{\mathrm{O}}\mid D=1}\{E_{X_{\mathrm{U}}\mid D=1}\{\xi (X_{\mathrm{O}},X_{\mathrm{U}})\}\}\\ \text{TUT}=E_{X_{\mathrm{O}}\mid D=0}\{E_{X_{\mathrm{U}}\mid D=0}\{\xi (X_{\mathrm{O}},X_{\mathrm{U}})\}\}\end{array}$$ (7)

3.3.2. Conditional Average Treatment Effect (CATE)

Since X_O are the only observed variables from the outcomes equation, a CATE (Heckman, 1997) can be formed, which is the average treatment effect conditioned on levels of X_O only:

$$\text{CATE}(x_{\mathrm{O}})=E_{X_{\mathrm{U}}\mid X_{\mathrm{O}}}\{\xi (x_{\mathrm{O}},x_{\mathrm{U}})\}=E_{X_{\mathrm{U}}}\{\xi (x_{\mathrm{O}},X_{\mathrm{U}})\}$$ (8)

where the second equality follows from Assumption 1. We will denote CATE as ξ(x_O). This is the treatment effect parameter that an ideal experiment can give where only X_O are observed. Note that the outer expectation in CATE averages over the marginal distribution of X_U. Although ATE can be obtained by trivial aggregation of CATEs over all individuals (as in equation (7)), aggregation of CATE over the treated or untreated individuals does not produce the TT or the TUT parameters respectively.

3.3.3. Marginal Treatment Effect (MTE)

The MTE is perhaps the most nuanced or individualized estimable effect (Heckman, 1997; Heckman and Vytlacil, 1999, 2001). It identifies an effect for an individual who is at the margin of choice such that one’s levels of X_O and Z are just balanced by one’s level of V (which includes X_U), i.e. P(x_O, z) = v. MTE can be expressed as

$$\text{MTE}(x_{\mathrm{O}},v)=E_{X_{\mathrm{U}}\mid X_{\mathrm{O}},V=P(z)}\{\xi (x_{\mathrm{O}},X_{\mathrm{U}})\}$$ (9)

Note that, unlike CATE, the expectation in MTE averages over the conditional distribution of X_U conditioned on meeting the definition for marginal patients. Heckman and Vytlacil (1999, 2001) have provided the weights needed to aggregate MTEs to form the mean treatment effect parameters. These weights need to be calculated from the data at hand.

3.3.4. Person-Centered Treatment Effect

Despite the granularity of MTEs, it may be hard to use MTEs directly as a representation of individual treatment effects as they themselves lack individual identity. This is because it is hard (if not impossible) to pinpoint an individual to whom an MTE estimate can be applied. Instead, another treatment effect parameter, which we call the person-centered treatment (PeT) effect (denoted by Δ), can be written as

$$\mathrm{\Delta }=E_{X_{\mathrm{U}}\mid X_{\mathrm{O}},P(Z),D}\{\xi (x_{\mathrm{O}},X_{\mathrm{U}})\}$$ (10)

where the expectation of unobserved confounders is made conditional on person-specific estimates of X_O, P(Z) and D. Naturally, PeT effects are more nuanced than CATEs as the latter average ξ(x_O, X_U) over the entire marginal distribution of X_U. Note that the PeT parameter was originally defined by Heckman and Vytlacil (1999). However, they use this parameter as a stepping stone for defining structurally stable mean effects on treated parameter whose definition does not depend on data (Y, X, Z). The PeT effect in equation (10) would take on different values corresponding to two values of Z = (z, z′), z ≠ z′, with (Y, X, D) being constant. However, this is exactly the variation we are after when we are envisioning PeT effects. The fact that two otherwise observably similar persons choose the same treatment under two values of Z informs us that their personalized treatment effects may be different.

Conceptually, a PeT effect is also a weighted version of MTEs. This is because an MTE is the treatment effect of a hypothetical individual who is at the margin of choice because their propensity to choose treatment based on X and Z is balanced by the propensity to select the alternative based on V. As the value of V is changed from this point, this person would either choose the treatment or the alternative. The PeT effect for a real individual is then the average of MTE, with the same X and Z levels as those for this real individual, over those values of V that corresponds to the real individual’s own treatment choice. Therefore, for any given individual, the PeT effects identify the specific margins where that individual may belong given its individual values of X_O, P(Z) and D. It then averages the MTEs over those margins, but not all as in ATE. As we prove below, a PeT effect is basically the X–Z-conditional effect on the treated (x–z-CTT) for persons undergoing treatment and is the X–Z-conditional effect on the untreated (x–z-CTUT) for persons not undergoing treatment. Because conditioning is done based on identifiable individual-level characteristics, a PeT effect can be identified for each individual in the data.

3.4. Uses of PeT Effects

All mean treatment effect parameters can be easily computed from the PeT effects without any further weighting. For example:

$$\begin{array}{l}\text{ATE}=E_{X_{\mathrm{O}},P(Z),D}(\mathrm{\Delta })\\ \text{TT}=E_{X_{\mathrm{O}},P(Z)\mid D=1}(\mathrm{\Delta })\\ \text{TUT}=E_{X_{\mathrm{O}},P(Z)\mid D=0}(\mathrm{\Delta })\end{array}$$ (11)

In fact, any policy parameter that shifts a certain subgroup of individuals, characterized by shifting the distribution of X_O, to take up or give up treatment can be predicted. Therefore, these patient-centered treatment effects can form integral components for population-level decision making.

In the absence of identification of the joint distribution of potential outcomes, however, the marginal distribution of the PeT effect can be crucial for understanding individual-level decision making. The PeT effects can be used to more accurately comprehend individual-level treatment effect heterogeneity that CATEs fail to convey. First, they may be better predictors of true treatment effects at the individual level both in terms of the positive predictive value (Pr(ξ(x_O, x_U) ≥ 0|Δ ≥ 0)) and the negative predictive value (Pr(ξ(x_O, x_U) < 0|Δ < 0)) than the CATEs (we will study this using simulations). Second, PeT effects are more likely to explain a larger fraction of the individual-level variability in treatment effects than the CATEs. Both play a big role not only in identifying person characteristics to guide treatment allocations but also in guiding future research to focus on collection of relevant measures of X_O and X_U.

Naturally, in the absence of essential heterogeneity, the PeT effects converge to CATEs.

3.5. Identification of PeT Effects

Theorem 1

Consider the nonparametric selection and outcome models in equations (1) and (2). Under Assumptions 1 and 2:

$$\begin{array}{l}{E}_{X_{\mathrm{U}}\mid X_{\mathrm{O}},P(Z),D=1}{E}_{\vartheta }({\mu }_1(x_{\mathrm{O}},X_{\mathrm{U}}\vartheta )-{\mu }_0(x_{\mathrm{O}},X_{\mathrm{U}}\vartheta ))=P{(z)}^{-1}{\int }_0^{P(z)}\left({\frac{E(Y\mid x_{\mathrm{O}},P=p)}{\partial p}|}_{p=v}\right)\mathrm{d}v\\ E_{X_{\mathrm{U}}\mid X_{\mathrm{O}},P(Z),D=0}{E}_{\vartheta }({\mu }_1(x_{\mathrm{O}},X_{\mathrm{U}}\vartheta )-{\mu }_0(x_{\mathrm{O}},X_{\mathrm{U}}\vartheta ))={(1-P(z))}^{-1}{\int }_{P(z)}^1\left({\frac{E(Y\mid x_{\mathrm{O}},P=p)}{\partial p}|}_{p=v}\right)\mathrm{d}v\end{array}$$

provided that E(Y|X_O, P = p) is continuously differentiable with respect to p for almost every x_O.

Proof

The identification for PeT effects follows identification of MTEs (Heckman and Vytlacil, 1999, 2001, 2005) and is given in the Appendix.

However, while Heckman and Vytlacil (1999, 2001, 2005) are mainly concerned with average treatment effects in the population, we use their results to identify individualized expected treatment effects and their marginal distribution in the population.

The PeT effects can be trivially aggregated over observed distribution of (X_O, P(Z), D) in order to estimate mean treatment effect parameters such as the effect on the treated (TT), effect on the untreated (TUT) and the average treatment effect (ATE). These derivations are provided in Heckman and Vytlacil (1999).

3.6. Semiparametric Estimation

In order to avoid certain disadvantages of full nonparametric estimation of the models in equations (1) and (2), we propose a partially separable outcomes model as follows:

$$Y=\mu (X_{\mathrm{O}},X_{\mathrm{U}},D;\beta )+\vartheta$$ (12)

where μ(X_O, X_U, D) is an unknown nonlinear function of observable (X_O) and unobservable (X_U) characteristics and treatment indicator (D); ϑ is a purely random error term. Conditional on specific levels of X_O and X_U, idiosyncratic expected gains (or losses) from treatment over control is given by μ(x_O, x_U, D = 1; β) − μ(x_O, x_U, D = 0; β). These idiosyncratic gains or losses may vary either over observed characteristics X_O or over unobserved characteristics X_U or both, giving rise to treatment effect heterogeneity. The terms observable and unobservable pertain to the analyst’s perspective and these covariates enter the structural model symmetrically in determining potential outcomes (Mullahy, 1997). We will refer to this formulation of the symmetric structural nonlinear model as the pure nonlinear model. It encompasses the broad categories of all parametric and semiparametric generalized linear models (McCullagh and Nelder, 1989) that include models for limited dependent variables.

In addition to the assumption of X_O, X_U∐ ϑ, X_O∐ X_U and that of Assumption 1, we make the following additional assumptions.

Assumption 3

E(μ(X_O, X_UD, β)|P = p, Z) = ϖ(X_O, K(P); α) is continuously differentiable with respect to p, where K(P) is a nonlinear kernel for P.

Estimation of PeT effects proceeds in four steps:

1. An estimate P is constructed using a semiparametric regression of D on X_O and Z (Das et al., 2003).

2. α is estimated using local polynomial approximation of ϖ(X_O, K(P); α) over P (Robinson, 1988; Fan and Gijbels, 1996). Here, K(P) is represented by the polynomial approximation. Such approximation can be estimated using GMM estimators using the well-known quasi score equations (Wedderburn, 1974). For N individuals:

   $$G_{\alpha }=\sum _{i=1}^N{G}_{\alpha }^i=\sum _{i=1}^N(Y_i-{\mu }_i)V_i^{-1}(\partial {\mu }_i/\partial \alpha )=0$$ (13)
   where i denotes individuals. α is estimated by solving G_α = O, yielding estimator α̂_N. Under mild regularity conditions, α̂_N →^P α as N → ∞ and (α̂_N − α) is asymptotically normal with mean 0 and covariance matrix A_N given by

   $$A_N={[E(-\partial G_{\alpha }/\partial \alpha )]}^{-1}\frac{N}{(N-1)}\left(\sum _{i=1}^{N}E\left(G_{\alpha }^i{G}_{\alpha }^{iT}\right)\right){[E(-\partial G_{\alpha }/\partial \alpha )]}^{-T}$$ (14)

   Replacing α by â_N and $E(G_a^I{G}_a^{iT})$ with $E(G_a^i{G}_a^{iT})$ in equation (9) yields a sandwich estimator of the variance–covariance of â_N (Huber, 1972; Liang and Zeger, 1986).

• 1
  Obtain estimates for MTE following Assumption (2):

  $$\mathrm{M}\widehat{\mathrm{T}}\mathrm{E}(X_{\mathrm{O}},V=v)=\partial \varpi (X_{\mathrm{O}},K(P);\widehat{\alpha })/\partial p{\mid }_{p=v}$$ (15)
• 1Construct PeT effects for each individual as Δ̂(x_O, p, D) = I(D = 1) · E_V|D^*=1 (MT̂E(x_O, V)) + I(D = 0) · E_V|D^*=0 (MT̂E(x_O, V))
  where⁵

  $$D^{\ast }=D^{\ast }(p,v)=[{\mathrm{\Phi }}^{-1}(p)+{\mathrm{\Phi }}^{-1}(1-v)]>0$$ (16)

The proof follows directly realizing that V~Unif[0,1].

Variance estimates for PeT effects at the individual level can be readily obtained by bootstrap, which is in line with obtaining variance estimates of CATEs. For each replicate of the bootstrap with-replacement sample, the average effect for each person is saved. In any given replicate, only those persons who are sampled would have an estimate. However, multiple bootstrap replicates should be able to cover all individuals. The required total number of bootstrap replicates can be determined by monitoring the minimum number of times each individual is sampled across replicate datasets.

We used an extensive set of Monte Carlo simulations to demonstrate the consistency of the PeT estimators in finite samples, where we study the effects of a binary treatment variable on three different types of outcomes. First is a typical normally distributed outcome. Second is a binary outcome and the third is a count data outcome. These results are presented in an online Appendix as supporting information. The simulations present strong evidence that the PeT estimates can provide consistent and nuanced individual-level treatment effects in observational data.

4. DISTRIBUTIONAL IMPACTS OF PROSTATE CANCER TREATMENTS ON 7-YEAR COSTS AND SURVIVAL

4.1. Background

We study the distributional effects of alternative treatment modalities on health and economic outcomes in PCa patients using PeT effects. Note that although this empirical example is set to look at an evaluation in healthcare, the methods employed have broad applicability to a wide variety of evaluations across many different fields.

4.2. Data

Our data come from the 1995–2009 SEER–Medicare linked dataset. SEER is an epidemiologic surveillance system consisting of population-based tumor registries designed to track cancer incidence and survival in the USA. The SEER–Medicare data links claims for health services collected by Medicare for its beneficiaries to the SEER registry (Cooper et al., 2002; Viring et al., 2002). We extracted data for patients of age 66 years or older and who were diagnosed with PCa between 1995 and 2002. The data contain zip codes for patient residences which were used to link to hospital referral regions (HRR) identifiers and HRR–year-specific characteristics based on Dartmouth Atlas data.⁶ We used the linked claims data from these patients for up to December 2009 or their death if that occurred before December 2009. We have 7 years’ follow-up data for everyone in our sample. The key variables in our sample are categorized as (a) outcomes variables (Y); treatment (D); independent risk factors (X_O); instrumental variable (Z). These categories are common to any type of evaluation analysis:

• (a)Outcome variables. We look at two outcomes. On the benefits side we use a binary indicator for 7-year overall survival. On the costs side we use the total undiscounted 7-year expenditures on healthcare expressed in 2009 dollars. Expenditures accumulate over all types of medical costs reimbursed by Medicare or a third-party payer and patients’ out-of-pocket costs.
• (b)Treatment (D). Comparison is made between the use of surgery (without any form of radiation of hormone therapy) in the first 6 months of diagnosis versus active surveillance that is defined as no use of surgery, hormone therapy or radiation in the first 6 months of diagnosis, along with at least two PSA tests within the first year of diagnosis. Treatment indicator takes a value of one for surgery.

An indicator of surgery is likely to be endogenous for three reasons: True severity of cancer is unobserved as we only have data on the cross-sectional characteristics of the tumor at diagnosis, but not how the tumor is growing or prostate-specific antigen (PSA) levels (used to detect PCa) is rising. Higher severity may be positively correlated with surgery receipt and also negatively correlated with survival, but positively correlated with costs.⁷ These correlations render the naïve effects on surgery to be biased downward and that on costs to be biased upward. Second, general frailties of the patients are unobserved, which again would follow the same correlations as tumor severity.⁸ Third, the psychological anxiety of being diagnosed with cancer would be positively correlated with both surgery receipt and costs and utilizations. Its correlation with survival remains ambiguous.

• (c)Independent risk factors (X_O). These include clinical stage and grade of cancer for patients at diagnosis using standard definitions (Meltzer et al., 2001), demographics, indicator for metropolitan area, Elixhauser comorbidity indices based on hospitalization in year preceding diagnosis, year and state fixed effects, zip-code level area characteristics on racial makeup, density and education levels. We also adjust for HRR-level characteristics using logged versions of population size, and per 100,000 patients’ supply of hospital beds, physicians, specialists and urologists.
• (d)Instrumental variable (Z). We use HRR-specific rates of active surveillance in PCa patients in the year prior to the diagnosis of a patient. Such an instrument has been used in the past in the context of PCa (Hadley et al., 2010); however, concerns exist about the contamination in area-level variations that would violate the exclusion restriction for two reasons: first, such variations may be correlated with variations in case-mix of patients; second, contamination may exist due to productivity spillovers that make areas with more efficient deliveries of treatments correlated with higher rates of treatment (Chandra and Staiger, 2007). We try to address both of these concerns and mitigate the effect of such contaminations on the IV. In order to address the first concern, we control for many concurrent area-level fixed effects and variations, as mentioned above. Contamination due to productivity spillovers (Chandra and Staiger, 2007) are directly controlled by adjusting for the number of urologists per capita, as the urologists are the main specialists delivering surgery for PCa patients. We study the properties of our IV after controlling for these factors and believe that it meets the requirements for a valid and strong instrumental variable.

4.3. Methods

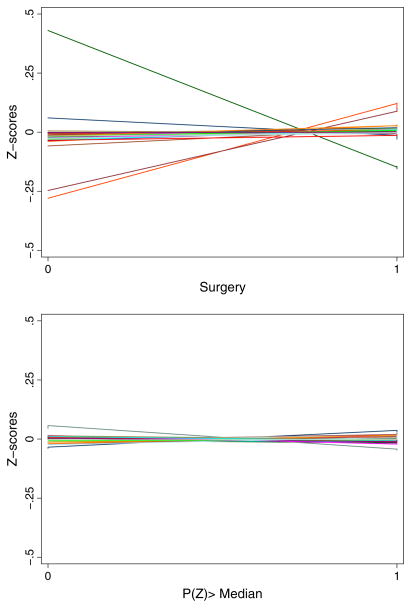
We study the strength of the IV in a logistic model for surgery along with all other independent risk factors. To explore plausible contamination in the IV due to patient-level characteristics, we run a separate logistic model for treatment with only the IV as a regressor. We then compare the imbalance in the patient-level independent risk factors across treatment categories with the imbalance in the same across the median of the IV-only predicted propensity to choose surgery. A valid IV would necessarily appear to reduce such imbalances. We explore these comparisons mainly for individual-level demographic and illness severity factors after converting them to their respective z-scores.

Next, MTEs and PeT effects are estimated using standard LIV methods described in our estimation and simulation sections. For the binary survival outcome we use a logistic regression. For the expenditure outcome, we use a semiparametric generalized linear model with log link and Gamma variance. Various goodness-of-fit tests were employed to ensure good model fit to these data. We study both the mean treatment effect parameters and also the joint distribution of PeT effects across survival and costs and the implications of such distributions for treatment choices.

4.4. Results and Discussion

Our final analytic sample consists of 13,495 patients, of whom 9913 (73.5%) received surgery. As is evident from the first-stage regression results in Table I, the likelihood of receiving surgery increases with ages younger and older than 74 years, T1 stage, advancing grade and increased number of hospitalization in previous year. The instrumental variable was found to be strongly predictive of surgery receipt conditional on other factors (F-statistic: 10.9, p < 0.0001).

Table I.

First-stage results from logistic regression on surgery indicator

Covariate	Logit coefficient (SE) [z-statistic]
IV
ivrate_activesurv	−1.496 (0.5) [−3.02]++
DEMOGRAPHICS
Age (centered at 74)	−0.176 (0.01) [−30.95]++
Age^2	0.0124 (0) [17.89]++
T1-stage (Ref: T2)	1.05 (0.05) [22.11]++
Grade – Well (Ref: Undetermined)	1.402 (0.14) [9.67]++
Grade – Moderate	1.424 (0.13) [11.04]++
Grade – Poor	2.261 (0.14) [16.14]++
White (Ref: Other)	−0.425 (0.15) [−2.76]++
Black	−0.347 (0.19) [−1.82]+
Hispanic	−0.089 (0.23) [−0.39]
Metropolitan area of residence	−0.052 (0.09) [−0.58]
ILLNESS SEVERITY
1 hospitalization last year (Ref: No hosp)	0.283 (0.09) [3.02]++
2 hospitalizations last year	0.288 (0.15) [1.87]+
>2 hospitalizations last year	0.545 (0.21) [2.6]++
Congestive heart failure	0.338 (0.21) [1.59]
Valvular disease	−0.113 (0.23) [−0.48]
Peripheral vascular disease	0.02 (0.21) [0.1]
Paralysis	0.638 (0.34) [1.89]+
Other neurological disorders	−0.22 (0.23) [−0.97]
Chronic lung disease	0.13 (0.14) [0.9]
Diabetes	0.05 (0.16) [0.32]
Diabetes with chronic complications	0.226 (0.36) [0.63]
Hypothyroidism	0.232 (0.26) [0.88]
Obesity	−0.03 (0.36) [−0.08]
Fluid and electrolyte disorders	0.136 (0.15) [0.88]
Deficiency anemias	0.258 (0.2) [1.28]
Alcohol abuse	0.116 (0.35) [0.34]
Depression	0.167 (0.31) [0.54]
Hypertension with complications	−0.053 (0.11) [−0.48]
ZIPCODE-LEVEL 2000 CENSUS XTICS	YES
YEAR FIXED EFFECTS	YES
STATE FIXED EFFECTS	YES
HRR-SPECIFIC XTICS	YES

⁺p-val. < 0.10;

⁺⁺p-val. < 0.05.

Figure 1 illustrates that the IV may be particularly suitable in reducing residual confounding in this application since it is able to reduce imbalance in observed factors considerably.⁹ The identified support of the IV-based predicted propensity score (PS) ranges from 0.07 to 0.995.

Figure 1.

Covariate imbalance across treatments versus across instrumental variable.

Polynomials of propensity scores were not found to be significant in either of the LIV models. The final models for either outcomes contained covariates, interaction of covariates with PS and PS.¹⁰ This indicates that essential heterogeneity is small for these outcomes.¹¹ This is presumably because we capture a very rich array of observed factors and estimate significant treatment effect heterogeneity across those factors. In essence, in this application PeT effects become similar to CATEs, where conditioning is done on the entire vector of observed factors. The mean treatment effect estimates are given in Table II. The average treatment effect was estimated to be −$30,056 and 7.4% points for costs and survival respectively, which were not significant. The average survival effects, although not significant, indicates the potential for substantial benefits of surgery over AS in this population, which are in stark contrast to the results from the largest and only randomized trial comparing these two treatments that was conducted on patients diagnosed with PCa about a quarter century ago (Holmberg et al., 2002).

Table II.

Mean treatment effects based on estimated PeT effects (surgery versus active surveillance)

Effect	7-year costs, 2009 $ Mean (95% CIa)	7-year surv. pr., %pt Mean (95% CIa)
Average treatment effect (ATE)	−30,056 (−115,807, 19,355)	7.4 (−17.7, 40.2)
Effect on the treated (TT)	−28,191 (−115,877, 20,451)	7.4 (−17.1, 43.2)
Effect on the UNTREATED (TUT)	−35,255 (−109,419, 16,543)	7.4 (−19.3, 30.8)
TT – TUT	7064 (−8,969, 15,340)	0.01 (−5.8, 13.3)
With perfect selection on survival PeTs
Average treatment effect	−30,641 (−119,640, 22,116)	12.6 (2.5, 37.0)
Effect on the treated	−28,332 (−119,927, 22,859)	12.7 (1.5, 40.5)
Effect on the untreated	−28,332 (−117,645, 17,882)	12.4 (5.1, 26.7)
Gains with perfect selection
ATE(Sel) – ATE	−585 (−14,394, 4,885)	5.2 (−3.4, 23.3)
TT(Sel) – TT	−141 (−14,035, 5,475)	5.3 (−3.0, 21.9)

Note: Bold face indicates exclusion of zero from 95% CI.

^a95% CI based on bias-corrected estimates from 1000 bootstrap replicates.

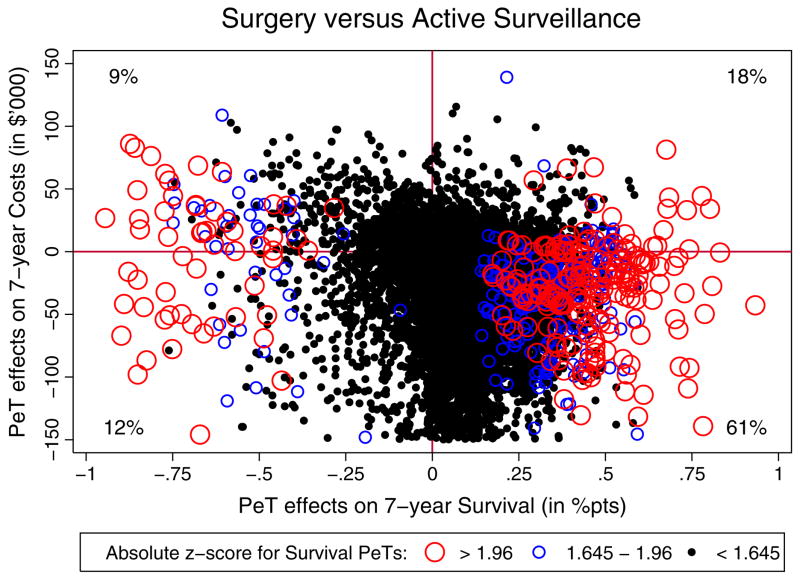
Figure 2 illustrates the joint distribution of PeT effects for 7-year survival and costs in an incremental cost-effectiveness plane where the x-axis represents PeT effects on survival and the y-axis the PeT effects on costs. Each dot on the plane represents a patient. The size of the treatment effect marker for each patient is driven by the z-score of their respective treatment effect. Patients with more significant effects have larger markers. The correlation between estimated PeT effects on costs and survival was small: 0.03 (95% CI: −0.20, 0.25). Only 21% of patients were found to have negative incremental survival from surgery. Surgery was found to be a dominant treatment in 61% of patients (southeast quadrant of graph) as it incurs lower costs and increased survival.

Figure 2.

Distribution of PeT effects on survival and costs, differentially illustrated by significance.

There is little evidence of positive self-selection in practice. Surgery rates were 74% among patients for whom surgery produces negative effects versus 73% among those who would benefit from surgery. This is reflected in the estimates for the effect on the treated (TT) and untreated (TUT) (Table II). Both TT and TUT are identical to ATE and neither reach statistical significance for costs or survival. This indicates that although allocation of surgery varied across various patient-level characteristics, patients receiving surgery are not benefiting more on average than if everyone were to receive surgery.

The heterogeneity of treatment effects illustrated in Figure 2, however, indicates that there may be much room for improvement. In a hypothetical world of perfect selection (Meltzer et al., 2003), where patients who would get hurt by surgery are removed from being eligible for comparing these two modalities of treatment, the ATE and TT of surgery would climb to 12.6% points (95% CI: 2.5, 37.0) and 12.7% pt (95% CI: 1.5, 40.5) respectively for 7-year survival (Table II). These estimates can also be used to establish the value of a more targeted approach to treatment allocation in terms of survival. However, compared to the ATE and TT estimates without selection, the ATE and TT estimates with perfect selection indicate only modest cost savings and better survival (Table II), which do not reach statistical significance.

Since survival outcomes are revealed several years after treatment, it is expected that any learning process would be slow. However, based on these data it is challenging to infer that choices are suboptimal or that clinicians are not learning from their experiences from treating multiple patients. This is because there may be other dimensions of outcomes, such as quality-of-life impacts of treatments on which treatment choices are being made that are not captured here but are important for evaluating PCa treatments.

5. CONCLUSIONS

This paper interprets a treatment effect parameter, originally defined by Heckman and Vytlacil (1999), to represent PeT effects. Heckman and Vytlacil (1999) use this parameter to establish the relationship between mean treatment effect parameters such as LATE, ATE, TT and TUT with the MTE parameter but do not use it further. A PeT effect is derived as an alternative weighting of MTEs and is shown to represent individualized treatment effects that not only condition on the individual’s observed characteristics but also average over a conditional distribution of unobserved characteristics (in contrast to their marginal distributions as in CATEs) that condition on treatment choice made by an individual and the circumstances under which that choice was made. The paper presents the theory behind PeT and proposes semiparametric estimators to estimate PeT effects using instrumental variables.

The introduction of PeT effects and its role in identifying treatment effect heterogeneity line up well with the political economy of healthcare evaluations. Despite the age-old practice of evaluating healthcare technologies using randomized trials and more recently with observational data that were used to estimate average treatment effects (and often local average effects), the Affordable Care Act of 2010 specifically asked for production of estimates at a more nuanced and individualized level. It created a Patient Centered Outcomes Research Institute (PCORI) as an independent, non-profit research organization to conduct research to provide information about the best available evidence to help patients and their healthcare providers make more informed decisions. Its mission is to help people make informed healthcare decisions – and to improve health care delivery and outcomes –by producing and promoting high-integrity, evidence-based information – that comes from research guided by patients, caregivers and the broader healthcare community (PCORI Mission Statement, 2011). PCORI is positioned to be one of the largest funders of outcomes research in the USA in the coming years and has so far asserted that one of the primary focus in patient-centered outcomes research (PCOR) should be answering the question for patients: ‘Given my personal characteristics, conditions and preferences, what should I expect will happen to me?’

While CATEs can provide answers to these questions, estimating CATEs directly based on multiple observed covariates can be tricky. In contrast, PeT effects can serve as outcomes that can be used to develop predictive algorithms for CATEs based on combinations of patient and other observed characteristics in the data. Such an approach would be most valuable for allocating category II and III treatments, as defined by Chandra and Skinner (2011), since uncertainties in their comparative effectiveness either precludes them from access in some settings or facilitates rapid adoption that leads to welfare loss. Furthermore, since PeT effects allow for estimating more nuanced individual treatment effects, understanding the difference in variance between PeT effects and CATEs can help establish the value of future research that can identify factors relevant for treatment effect heterogeneity that are not collected in the current databases (Basu and Meltzer, 2007).

Our application of these methods to evaluating PCa treatments revealed the empirical distribution of individual-level treatment effects on 7-year overall survival and costs. We are unaware of any clinical or social science study that has revealed such nuanced treatment effects for this population. Almost all of this research had focused on estimating average effects. Nevertheless, our previous discussions with PCa survivors reveal that there is a strong demand for information on the side effects of treatments and the impact of treatments on survival that are more suited to their own characteristics, since that would enable them to apply their own preferences to these outcomes and more accurately weigh the benefits and risks of alternative PCa treatments. We believe that this can be better achieved by using PeT effects rather than large subgroup-specific CATEs as are typically studied in clinical trials. Table III highlights the limitations of these CATEs and presents the estimated CATEs by averaging the PeT effects within specific subgroups. There appears to be some variability of CATEs across these broad subgroups but none reach statistical significance. These results, especially the effects on survival, align well with the CATEs reported in the recent PIVOT trial (Wilt et al., 2012).¹² However, the proportion of variance in PETs that is explained by each of these subgroup-specific CATEs is quite small, implying that it would be hard to achieve true individualization of care based on such broad subgroup analyses.

Table III.

Subgroup-specific CATEs

	7-year costs, 2009 $	% of PET variance explained	7-year surv. pr., %pt	% of PET variance explained
	Mean (95% CIa)		Mean (95% CIa)
Age
66–69 years	−12873 (35,572)		8.8 (16.0)
70–74 years	−25850 (35,589)		8.7 (14.8)
75–79 years	−43,728 (36,900)		7.1 (14.7)
80+ years	−52,643 (39,996)	15%	2.9 (16.2)	2%
Race
White	−32,325 (35,866)		8.6 (15.0)
Black	−10,707 (35,928)		−7.7 (15.8)
Other	−27,306 (45,487)	3%	13.1 (17.9)	10%
Stage
T1	−48,783 (49,120)		8.0 (17.0)
T2	−13,266 (24,383)	21%	6.8 (13.5)	0.1%
Grade
Well	−39,434 (41,627)		1.9 (16.4)
Moderate	−29,565 (34,120)		6.3 (14.0)
Poor	−24,563 (43,029)		12.4 (20.2)
Undetermined	−50,155 (45,959)	2%	20.5 (14.8)	6%
No. of comorbidities
0	−23,975 (33,157)		9.9 (15.0)
1	−25,738 (33,9998)		9.4 (15.0)
>1	−33,261 (36,847)	1%	6.1 (14.9)	1%

Note: Bold face indicates exclusion of zero from 95% CI.

^a95% CI based on bias-corrected estimates from 1000 bootstrap replicates.

The PeT effects can help in establishing algorithms that take into account multiple factors simultaneously in order to explore the dimensions (factors) along which treatment selections are efficient (i.e. they conform to gains) and where they are inefficient (i.e. they conform to losses). In our analyses, compared to patients for whom survival effects are significantly positive (at the 10% level), patients with significant negative survival effects with surgery had significantly higher rates of cancer with well grade, higher number of pre-period hospitalization and higher rates of every comorbidity listed in Table I except for peripheral vascular disease. Future work can refine and validate these prediction algorithms for treatment effects using split-sample analyses.

In summary, PeT effects can serve as a useful treatment concept for a variety of evaluations both at the policy and at the individual level.

APPENDIX

Theorem 2

Consider the nonparametric selection and outcome models in equations (1) and (2). Under Assumption 1 and 2:

$$\begin{array}{c}{E}_{X_{\mathrm{U}}\mid X_{\mathrm{O}},P(Z),D=1}{E}_{\vartheta }({\mu }_1(x_0,,X_U,\vartheta )-{\mu }_0(x_{\mathrm{O}},,X_{\mathrm{U}},\vartheta ))=P{(z)}^{-1}{\int }_0^{P(z)}\left({\frac{E_{Y\mid X_O,P}(Y\mid x_O,P=p)}{\partial p}|}_{p=v}\right)\mathrm{d}v\\ E_{X_{\mathrm{U}}\mid X_{\mathrm{O}},P(Z),D=0}{E}_{\vartheta }({\mu }_1(x_{\mathrm{O}},,X_{\mathrm{U}},\vartheta )-{\mu }_0(x_{\mathrm{O}},,X_{\mathrm{U}},\vartheta ))={(1-P(z))}^{-1}{\int }_{P(z)}^1\left({\frac{E_{Y\mid X_{\mathrm{O}},P}(Y\mid x_{\mathrm{O}},P=p)}{\partial p}|}_{p=v}\right)\mathrm{d}v\end{array}$$

provided that E_{Y|XO,P(Y|xOp)} is continuously differentiable with respect to p for almost every x_O.

Proof

The identification for PeT effects follows identification of MTEs. Assumptions 1(a) and (c) ensure that P is a nondegenerate, continuously distributed random variable conditional on X_O. Assumption 2(d) is needed to ensure that the expectations considered are finite. First, following Heckman and Vytlacil (1999, 2001, 2005), the marginal treatment effect is identified as

$$\begin{array}{l}{E}_{Y\mid X_{\mathrm{O}},P(Z)}(Y\mid x_{\mathrm{O}},p)=E_{Y\mid X_{\mathrm{O}},Z}(Y\mid x_{\mathrm{O}},z)=E_{Y\mid X_{\mathrm{O}},Z}({DY}_1+(1-D)Y_0\mid x_{\mathrm{O}},z)\\ =E_{Y_{\mathrm{O}}\mid X_{\mathrm{O}}}(Y_0\mid x_{\mathrm{O}})+E_{Y_1-Y_0\mid X_{\mathrm{O}},Z}(D(Y_1-Y_0)\mid x_{\mathrm{O}},z)(\text{by}\text{Assumption}2\mathrm{b})\\ =E_{Y_0\mid X_{\mathrm{O}}}(Y_0\mid x_{\mathrm{O}})+Pr(D=1\mid x_{\mathrm{O}},z)·E_{Y_1-Y_0\mid X_{\mathrm{O}},Z}((Y_1-Y_0)\mid x_{\mathrm{O}},V<P(z))\\ =E_{Y_0\mid X_{\mathrm{O}}}(Y_0\mid x_{\mathrm{O}})+{\int }_o^p{E}_{Y_1-Y_0\mid X_{\mathrm{O}},V}((Y_1-Y_0)\mid x_{\mathrm{O}},v)\mathrm{d}v\\ =E_{Y_0\mid X_{\mathrm{O}}}(Y_0\mid x_{\mathrm{O}})+{\int }_o^p{E}_{\vartheta }({\mu }_1(x_0,v,\vartheta )-{\mu }_0(x_{\mathrm{O}},v,\vartheta ))\mathrm{d}v\end{array}$$

where the second to last equality comes from the fact that V is uniformly distributed on [0,1] conditional on X_O and Z. Therefore, differentiating both sides with respect to p, we have

$$\frac{\partial E_{Y\mid X_{\mathrm{O}},P(Z)}(Y\mid x_{\mathrm{O}},p)}{\partial p}=E_{\vartheta }({\mu }_1(x_{\mathrm{O}},v,\vartheta )-{\mu }_0(x_{\mathrm{O}},v,\vartheta ))=\text{MTE}(x_{\mathrm{O}},v)$$ (17)

It then follows that

$$\begin{array}{l}{E}_{X_{\mathrm{U}}\mid X_{\mathrm{O}},P(Z),D=1}{E}_{\vartheta }({\mu }_1(x_{\mathrm{O}},,X_{\mathrm{U}},\vartheta )-{\mu }_0(x_{\mathrm{O}},,X_{\mathrm{U}},\vartheta ))\\ =E_{V\mid X_{\mathrm{O}},P(Z),D=1}{E}_{\vartheta }({\mu }_1(x_{\mathrm{O}},V,\vartheta )-{\mu }_0(x_{\mathrm{O}},V,\vartheta ))=P{(z)}^{-1}{\int }_0^{P(z)}\text{MTE}(x_{\mathrm{O}},v)\mathrm{d}v\end{array}$$ (18)

Similarly, the conditional effect on the untreated (CTUT) is obtained by integrating MTEs over values of V that are greater than p.