Abstract
A direct numerical simulation adopting an arbitrary Lagrangian-Eulerian based finite element method is employed to simulate the motion of a nanocarrier in a quiescent fluid contained in a cylindrical tube. The nanocarrier is treated as a solid sphere. Thermal fluctuations are implemented using two different approaches: (1) fluctuating hydrodynamics; (2) generalized Langevin dynamics (Mittag-Leffler noise). At thermal equilibrium, the numerical predictions for temperature of the nanoparticle, velocity distribution of the particle, decay of the velocity autocorrelation function, diffusivity of the particle and particle-wall interactions are evaluated and compared with analytical results, where available. For a neutrally buoyant nanoparticle of 200 nm radius, the comparisons between the results obtained from the fluctuating hydrodynamics and the generalized Langevin dynamics approaches are provided. Results for particle diffusivity predicted by the fluctuating hydrodynamics approach compare very well with analytical predictions. Ease of computation of the thermostat is obtained with the Langevin approach although the dynamics gets altered.
INTRODUCTION
The major motivation for the present study is the simulation of a nanoparticle thermal motion in a fluid flow that occurs in targeted drug delivery. Targeted drug delivery often uses nanocarries laden with drugs in blood vessels for transport. The binding interactions between the ligands on the nanocarrier and the receptors on the cell membrane at the involved sites define the efficacy of nanocarrier arrest by the targeted cell. In order to more broadly integrate this technology into medicine, a precise understanding of how to guide the nanoparticle to the target site is necessary. To achieve this goal, as a first step, it is necessary to accurately determine the motion of a nanocarrier (due to thermal and hydrodynamic effects) in a fluid medium.
Nanoparticles undergo thermal motion in a fluid which can be simulated either using the fluctuating hydrodynamics (FHD) or using the generalized Langevin dynamics (GLD). The fluctuating hydrodynamics method essentially consists of adding stochastic stresses to the stress tensor (random stress) in the momentum equation and stochastic fluxes to the heat flux where an energy equation is present in the formulation [1]. In generalized Langevin approach, the thermal fluctuations from the fluid are incorporated as random forces and torques in the particle equation of motion where the power spectrum for the variance of the random force and torque terms are in terms of a correlated or colored noise with a well defined characteristic memory time [2]. In this paper, we have considered both the procedures to evaluate the suitability and efficacy of any particular procedure for future comprehensive evaluations.
Over the years, numerical simulations based on these procedures have been carried out employing the finite volume method [3], lattice Boltzmann method (LBM) [4,5], stochastic immersed boundary method [6], smoothed profile method [7, 8] and the finite element method [1, 2]. In this paper, a direct numerical simulation adopting an arbitrary Lagrangian-Eulerian (ALE) based finite element method (FEM) is employed to simulate the Brownian motion of a nanoparticle in an incompressible Newtonian fluid contained in a horizontal micron sized circular tube. Both translational and rotational motions of a nanoparticle in a stationary fluid medium are investigated. The results for the attainment of thermal equilibrium between the particle and the surrounding medium, diffusivity for the particle in the medium, effect of the presence of the confining vessel wall on particle displacement and diffusivity are evaluated using both procedures and comparisons are summarized in the conclusions.
THEORETICAL FORMULATION
The Brownian motion of a nanoparticle in an incompressible Newtonian stationary fluid medium in a horizontal circular vessel is considered (Figure 1). The fluid and particle equations are formulated in an inertial frame of reference with the origin coinciding with the center of the vessel. The diameter, D, and the length, L, of the vessel (tube) are very large compared to the particle size, d, the diameter of the particle. Initially, a nanoparticle is introduced either at the vessel centerline or at suitably chosen locations away from the center line towards the bounding wall. Initially both the fluid and particle are at rest. No body force is considered either for the particle or for the fluid domain. Starting at time t = 0, the nanoparticle experiences Brownian motion. The motion of the nanoparticle is determined by the hydrodynamic forces and torques acting on the particle and subject to the wall interactions.
FIGURE 1.
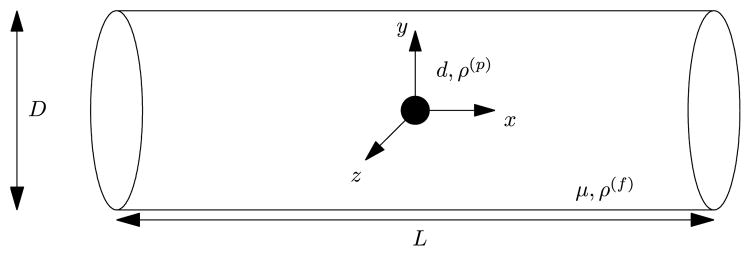
Schematic representation of a nanoparticle in a stationary fluid medium in a circular vessel (not to scale). Diameter of the vessel: D = 2R = 10 μm; Length of the vessel: L = 10 μm; Diameter of the nanoparticle: d = 2a = 400 nm; Viscosity of the fluid: μ = 10−3kg/ms; Density of the fluid and the nanoparticle: ρ(f) = ρ(p) = 103 kg/m3. Particle locations away from the center are not displayed in this figure.
The motion of an incompressible Newtonian fluid satisfies the conservation of mass and momentum given by
| (1) |
| (2) |
where u and ρ(f) are the velocity and density of the fluid, respectively, σ is the stress tensor, p is the pressure, J is the identity tensor, μ is the dynamic viscosity, D[u] is the rate of deformation tensor. The random stress tensor S is assumed to be zero (S = 0) for generalized Langevin method, and is assumed to be a Gaussian with
| (3) |
for fluctuating hydrodynamics (FHD) method. Here 〈 〉 is the ensemble average, kB is the Boltzmann constant, T is the absolute temperature, δij is the Kronecker delta, and the Dirac delta function δ(x −x′) denotes that the components of the random stress tensor are spatially uncorrelated (Markovian). The right hand side of equation (3) shows that the mean and variance of the thermal fluctuations are chosen to be consistent with the fluctuation-dissipation theorem [9–11] for an incompressible fluid.
For a rigid particle suspended in an incompressible Newtonian fluid, the translational and rotational motions of the particle satisfies
| (4) |
where m is the mass of the particle, I is its moment of inertia, and, U and ω are the translational and angular velocities of the particle, respectively. The hydrodynamic force F and torque T acting on the particle are given by
| (5) |
where X is the position of the centroid of the particle, (x − X) is a vector from the center of the particle to a point on its surface, ∂Σp denotes the particle surface, and n̂ is the unit normal vector on the surface of the particle pointing into the particle. The random force R and random torque Ω are assumed to be zero (R = 0; Ω = 0) for FHD and are assumed to be Gaussian with
| (6) |
| (7) |
for generalized Langevin dynamics (GLD). Here α and β are the dissipative memory kernels for force and torque, respectively. The equations (6) and (7) satisfy the fluctuation-dissipation theorem [12,13]. The right hand sides of equations (6) and (7) denote the mean and variance of the thermal fluctuations.
For a non-Markovian stochastic process, the random-noise depends on the memory effects considered through time-correlations. For a time correlated Mittag-Leffler noise (MLN) [2, 14, 15], the dissipative memory kernel for force and torque in equations (6) and (7) are given by
| (8) |
respectively, where τ is the characteristic memory time, λ is the exponent taken as 0 < λ < 2, α0(λ) (units of α0(λ) is sλ−2) and β0(λ) (units of β0(λ) is sλ−2) are the proportionality coefficient dependent on the exponent λ but independent of t or τ and Eλ (y) is the Mittag-Leffler function [16] defined through the series given by equation
| (9) |
When λ ≠ 1, the noise correlation function in equation (8) behaves as a stretched exponential for short times and as an inverse power-law in the long time limit [17].
The initial and boundary conditions for the problem are
| (10) |
| (11) |
| (12) |
where Σ0 is the domain occupied by the fluid and ∂Σi and ∂Σo are the inlet and outlet boundaries, respectively. The stochastic governing equations (1) – (5) along with the initial and boundary conditions (10) – (12) are solved numerically. It is assumed that there is no body torque acting at any point in the fluid and the viscous stress tensor, σ, is symmetric. A numerical simulation at a mesoscopic scale involving a particle in a fluid could be based on a discretization of the equations (1) – (12). However, the discrete forms have to satisfy the fluctuation-dissipation theorem [18]. The details of the finite-element spatial and temporal discretization, and, mesh movement algorithm are discussed in Uma et al. [1, 2].
RESULTS AND DISCUSSION
A solid spherical particle of radius a = 200 nm is initially placed at the center of a cylindrical tube (R = 5 μm) containing a stationary Newtonian fluid. From the particle location, the ends of the computational domain are at a distance of 20a at any instant of time [1]. The physical parameters chosen are: kB = 1.3806503 × 10−23 kg m2/s2 K; μ = 10−3 kg/m s; ρ(f) = ρ(p) = 103 kg/m3. The temperature of the fluid is initially set to Tp = 310K and the particle at zero degrees.
The time scale for the computation of the Brownian motion of the particle may be derived from evaluating the various time scales (macroscopic and mesoscopic) governing the problem. The different time scales involved in this study are: (i) hydrodynamic time scale, τν = a2/ν (the time scale for momentum to diffuse over a distance equal to the radius of the nanoparticle); Brownian time scales, (ii) τb = m/ζ(t) (Brownian relaxation time over which velocity correlations decay in the Langevin equation) and (iii) τd = a2ζ(t)/kBT (Brownian diffusion time over which the nanoparticle diffuses over a distance equal to its radius). Here, a is the radius of the nanoparticle, ν is the kinematic viscosity and ζ(t) = 6πμa is the Stokes dissipative friction force coefficient for a sphere.
It is noted that the time scales encountered in this problem are such that τb < τν < τd. For a nanoparticle of radius 200 nm, τb ≈ 8.8×10−9s, τν ≈ 4×10−8s and τd ≈ 3.5×10−2s. As a consequence, the relevant time scales for the Brownian motion of a nanoparticle in an incompressible fluid can span many orders of magnitude. It is required that the time step for the numerical simulation Δt be smaller than the smallest of all the physical time scales. The simulations presented in this study have been carried out for long enough durations to allow for the temperature of the particle to equilibrate - i.e., if N is the number of simulated time steps then N ·Δt = t ≫ τν. The number of time steps depends upon equilibration of particle temperature, or determination of velocity autocorrelation functions (VACFs) and mean square displacements (MSDs). In order to ensure the uniqueness of the realizations, different initial seeds are chosen for a Gaussian random number generator.
Figure 2 shows the minimum time step for the numerical simulation, Δt, required by the fluctuating hydrodynamics (FHD) and the generalized Langevin dynamics with Mittag-Leffler noise (GLD with MLN) procedures to achieve the convergence in the translational and rotational temperatures of the nanoparticle as a function of radius of the particle. Radius of the particle, a, and the time step for the numerical simulation, Δt, are non-dimensionalized with the radius of the cylindrical vessel, R, and the hydrodynamic time scale, τν, respectively. It is observed that the minimum time step required in FHD to obtain converged numerical results is about two orders of magnitude less compare to the GLD. The later procedure is therefore attractive for routine computations that may be required in modeling targeted drug delivery.
FIGURE 2.
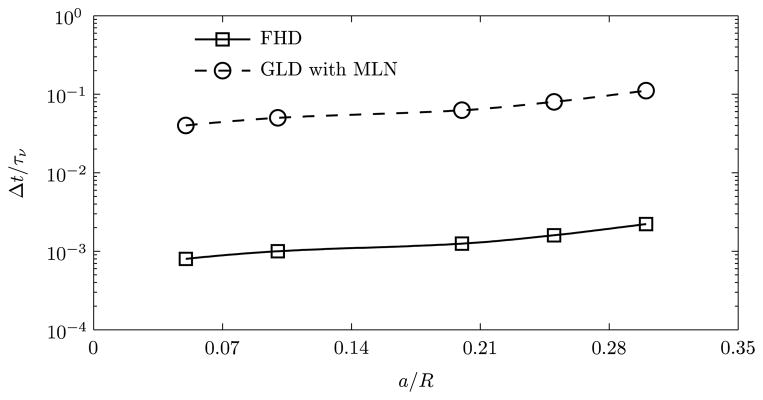
Minimum time step for the numerical simulation required by fluctuating hydrodynamics (FHD) and generalized Langevin dynamics with Mittag-Leffler noise (GLD with MLN) methods to achieve the convergence in the translational and rotational temperatures as a function of radius of the particle.
From the equipartition theorem, at thermal equilibrium, the translational and rotational temperatures of the nanoparticle are given by
| (13) |
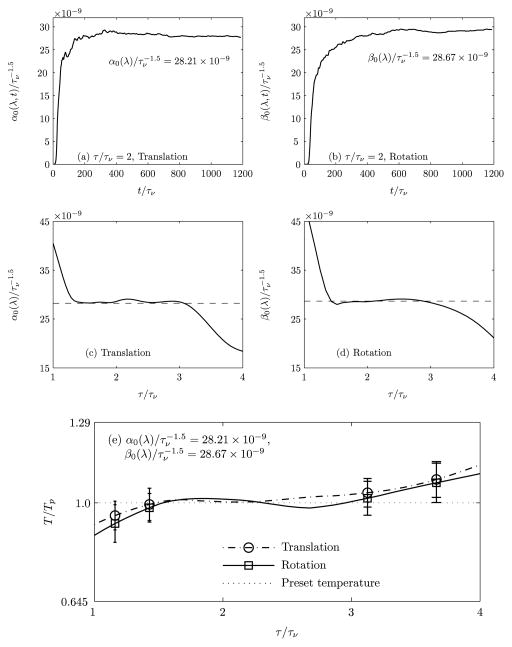
For GLD with MLN (λ = 0.5), the proportionality coefficients α0 and β0 are chosen such that the MLN satisfies the equipartition theorem. In our numerical simulations, initially α0 and β0 are dynamically optimized during the course of a trajectory according to the scheme described by Iwashita et al. [7] (for details, see [2]). Figures 3(a) and (b) show that for λ = 0.5 and τ/τν = 2, α0, β0 converge to constant values over an ensemble average of 15 different realizations. Each realization consists of N = 50,000 time steps. Thus, to optimize α0 and β0 as independent of t, we have employed 15 × 50,000 = 750,000 time steps. The proportionality coefficients α0 and β0 are non-dimensionalized using (for λ = 0.5).
FIGURE 3.
Convergence in the proportionality coefficient, (a) α0(λ), (b) β0(λ) for τ/τν = 2; characteristic memory time as a function of proportionality coefficient (c) α0(λ), (d) β0(λ) and (e) translational and rotational temperatures of the nanoparticle of radius a = 200 nm by using Mittag-Leffler noise (λ = 0.5). The proportionality coefficients α0 and β0 are non-dimensionalized using . For a given τ/τν, if α0(λ), β0(λ) are chosen from (c) and (d), respectively, then the thermostat satisfies the equipartition theorem within 3% error. When (a) and (b) are independent of τ, the thermostat satisfies the equipartition theorem in the plateau region given by (e). It is to be noted that in the same plateau region ((c) and (d)), α0 and β0 remain constant and agree with the values given in (a) and (b) respectively.
Figures 3(c) and (d) show α0 and β0 as functions of τ. For any given value of τ/τν, if α0 and β0 are chosen from Figures 3(c) and (d), respectively, then the evaluated temperature of the nanoparticle is noted to agree with the preset temperature of fluid within 3% error. As a result, the model serves as a general thermostat for a range of the characteristic memory time τ/τν.
It is interesting to note from Figures 3(c) and (d) that α0 and β0 remain constant (i.e., independent of τ) over a finite plateau region where the characteristic memory time τ is larger than the hydrodynamic time scale, τν. The significance of this numerical result is that when τ is sampled from the interval defined by the plateau region, the values of α0 and β0 for which the nanoparticle translational as well as rotational temperatures agree with the preset temperature (Figure 3(e)) are independent of τ and t. In order to adhere to the equipartition theorem within the statistical error, the characteristic memory time in the external noise has to be chosen consistent with the inherent time scale of the memory kernel, i.e., the hydrodynamic time scale. The error bars have been plotted from standard deviations of the temperatures obtained with 15 different realizations.
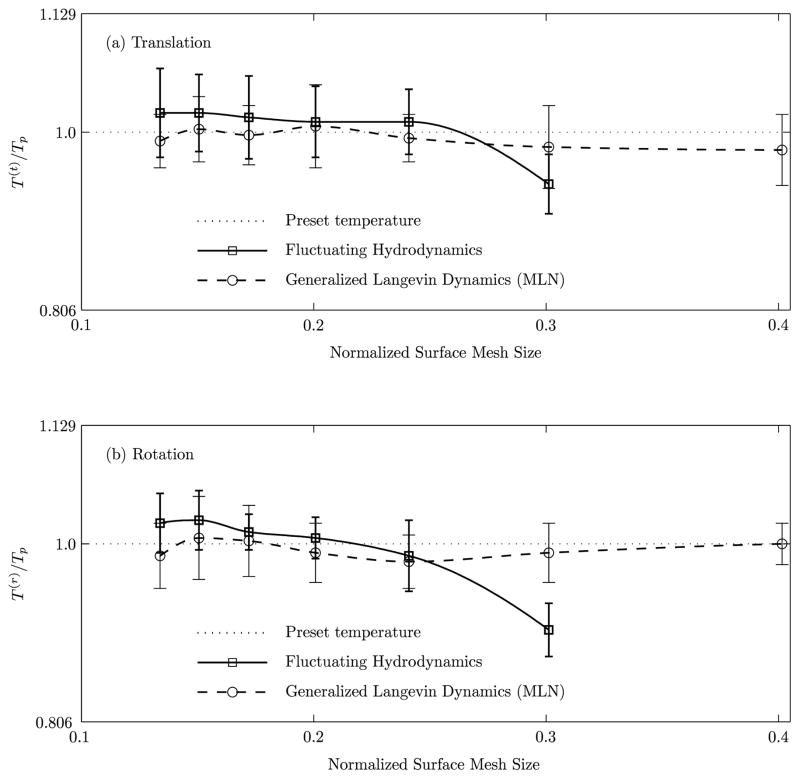
Figure 4 shows the translational and rotational temperatures of the particle in a stationary medium as a function of the normalized surface mesh length (mesh length divided by particle radius) using FHD and GLD with MLN. For GLD with MLN, λ = 0.5, τ/τν = 2, and . These are obtained from five different realizations in each coordinate direction. To account for compressibility effects in the FHD method, the particle mass m is augmented by an added mass m0/2, M = m + m0/2, where m0 is the mass of the displaced fluid [1, 19]. Each realization consists of N = 20,000 time steps. Thus, to evaluate the equilibration of the particle temperature with the preset fluid temperature, we have employed 3 × 5 × 20,000 = 300,000 time steps. The error bars have been plotted from standard deviations of the temperatures obtained with 15 different realizations (3 × 5 = 15). It is observed that translational and rotational temperatures of the nanoparticle agree with the preset temperature to within 5% error and the convergence is noted as the normalized mesh size is decreased. It is observed that compared to GLD, FHD requires finer mesh to achieve convergence for the temperature of the nanoparticle.
FIGURE 4.
Translational and rotational temperatures of the nanoparticle as a function of the normalized surface mesh length (mesh length divided by particle radius) in a stationary Newtonian fluid medium using FHD and GLD with MLN (λ = 0.5, τ/τν = 2, and ).
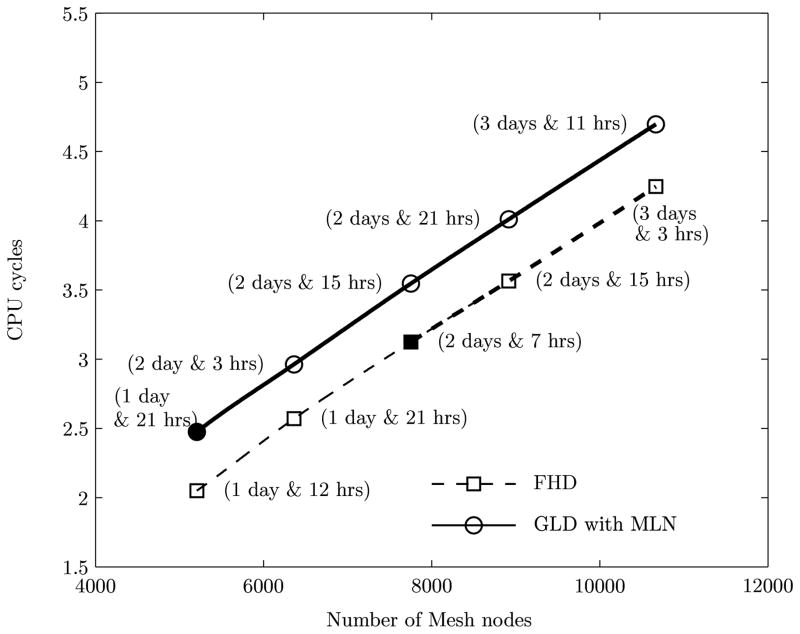
Figure 5 demonstrates the approximate number of CPU cycles required for the computation of a single time step for a particle of radius 200 nm in a cylindrical tube of radius 5 μm. All simulations are carried out on a 2.93 GHz processor. Each CPU cycle displayed on the figure corresponds to the average of 300 time steps, spread across three realizations. The number of mesh nodes are displayed on the horizontal axis. Number of days required to complete the simulations with 20,000 time steps using two different methods are specified inside the brackets and for 100,000 time steps this will be five times higher. It is observed from Figure 4 that for a given mesh size, the computational cost for both the methods are comparable. In order to obtain a converged numerical result, FHD requires finer mesh compare to GLD. Thick solid and dotted lines in Figure 5 correspond to the converged normalized surface mesh size in Figure 4. The mesh size chosen for the present numerical simulations are represented by filled circle and square for GLD and FHD, respectively.
FIGURE 5.
Computational cost for fluctuating hydrodynamics (FHD) and generalized Langevin Dynamics with Mittag-Leffler noise (GLD with MLN). Number of days required to complete the simulations with 20,000 time steps are specified inside the brackets. Thick solid and dotted lines correspond to the converged normalized surface mesh size in Figure 4. The mesh size chosen for the present numerical simulation is represented by filled circle and square for GLD and FHD, respectively.
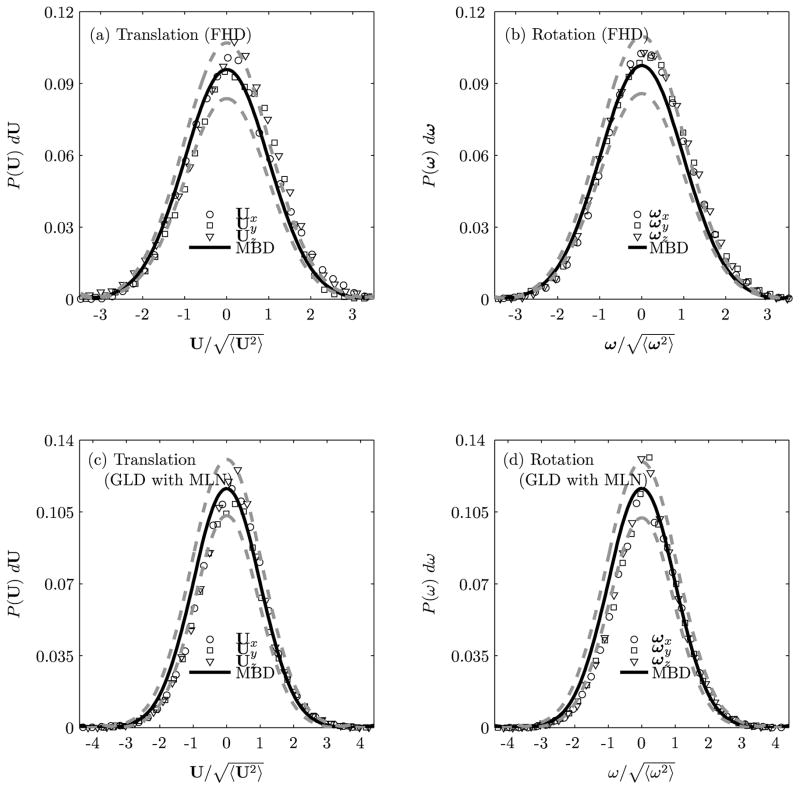
The apparent translational and rotational velocities of the nanoparticle are determined as U and ω. For determining the velocity distribution of the nanoparticle, 5 realizations in each coordinate direction consisting of 5 × 20,000 = 100,000 time steps have been computed. Thus, a total of 300,000 time steps have been computed. In Figure 6, the numerically simulated components of U (FLD: Figure 6(a) and GLD: Figure 6 (c)) and ω (FHD: Figure 6(b) and GLD: Figure 6(d)) (represented by three different symbols) of the nanoparticle with radius a = 200 nm are compared with the analytical Maxwell-Boltzmann distribution with a zero mean and variance of kBT/M and kBT/I, respectively. It is observed that each degree of freedom individually follows a Gaussian distribution. In particular, the mean and the variance calculated by using the FHD and GLD agrees within 5% error (see dotted line in Figure 6) with that of the analytical Maxwell-Boltzmann distribution.
FIGURE 6.
Equilibrium probability of the translational ((a) and (c)) and rotational ((b) and (d)) velocities of the nanoparticle (a = 200 nm) in a stationary fluid medium using FLD ((a) and (b)) and GLD ((c) and (d)).
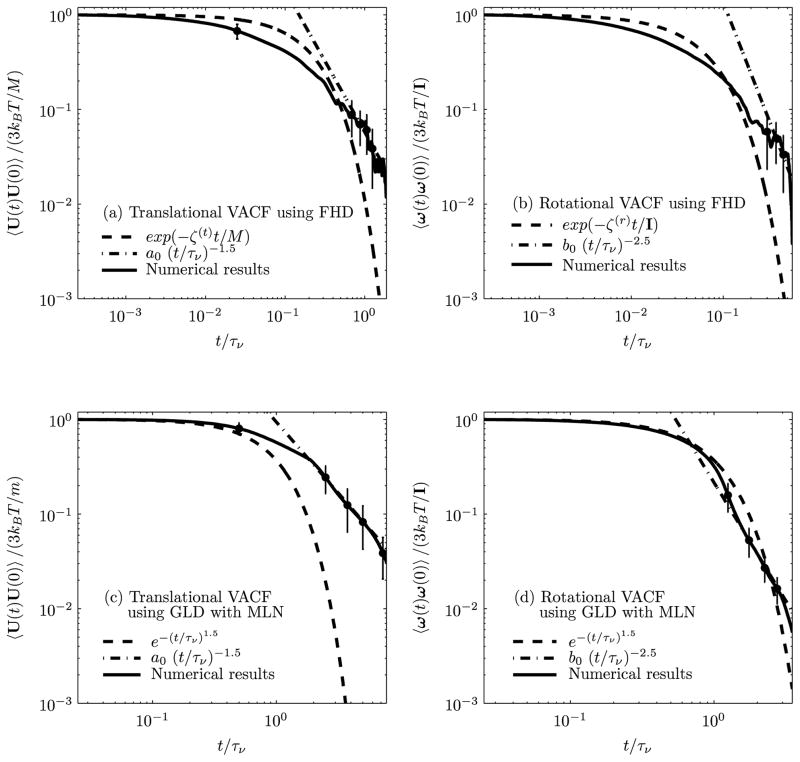
Figure 7 shows the VACF of the translational and rotational motions of a nanoparticle (a = 200 nm) in a quiescent fluid medium in a circular vessel as obtained from our numerical simulations. For determining the VACF of the nanoparticle, 45 (15 × 3 = 45) realizations have been employed with total computation of 45 × 100,000 = 4,500,000 time steps. It may be observed that the translational and rotational VACFs of the Brownian particle have power-law decays over long times that are ~t−3/2 and ~t−5/2, respectively. Hauge and Martin-Löf [10] have analytically shown that the decay of the translational and rotational VACFs at long time obeys a power-law:
| (14) |
| (15) |
where the values of constants a0 and b0 are provided in Table 1. It is observed from Figures 7(a) and (b) that at short times, the translational and rotational VACFs of the nanoparticle using FHD follow an exponential decay, exp(−ζ(t)t/M) and exp(−ζ(r)t/I)), respectively, while with GLD (Figures 7(c) and (d)) they follow a stretched exponential decay, exp{−(t/τν)3/2}. At long times, the translational and rotational VACFs follow a power-law decay, a0(t/τν)−3/2 and b0 (t/τν)−5/2, respectively, using both the FHD and the GLD with MLN. The error bars have been plotted from standard deviations of the decay at particular time instants obtained with 45 different realizations.
FIGURE 7.
Translational and rotational VACFs of a nanoparticle particle of radius a = 200 nm in a stationary fluid medium. The values of constants a0 and b0 are provided in Table 1.
TABLE 1.
Values of a0 (translational) and b0 (rotational) for long time decay of VACF.
| Method | a0 | b0 |
|---|---|---|
| FHD (Hauge and Martin-Löf [10]) | 0.094 | 0.014 |
| GLD with MLN | 0.943 | 0.215 |
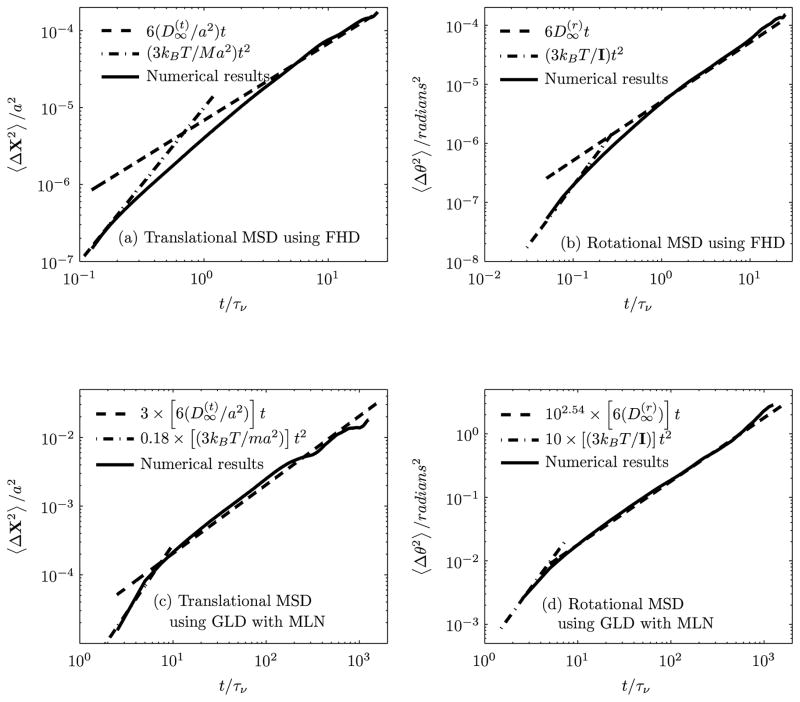
Figure 8 shows the numerically obtained translational and rotational MSDs of a neutrally buoyant nanoparticle (a = 200 nm) in a quiescent fluid medium, initially placed at the center of the vessel (R = 5 μm), for both short and long times. For determining the MSD of the nanoparticle, 45 (15 × 3 = 45) realizations have been employed with each realization computed up to 100,000 time steps. It is observed that in the regime where the particle’s motion is dominated by its own inertia (ballistic), the translational and rotational motions of the particle obtained using FHD follow (3kBT/Ma2)t2 (Figure 8(a)) and (3kBT/I)t2 (Figure 8(b)), respectively, whereas the translational and rotational motions of the particle obtained using GLD with MLN follow 0.18 × (3kBT/ma2)t2 (Figure 8(c)) and 10 × (3kBT/I)t2 (Figure 8(d)), respectively.
FIGURE 8.
Translational and rotational MSDs of a nanoparticle particle of radius a = 200 nm in a stationary fluid medium.
In the diffusive regime, the translational and rotational MSDs of the particle obtained using FHD increase linearly in time to follow (Figure 8(a); Stokes-Einstein relation [20]) and (Figure 8(b); Stokes-Einstein-Debye relation [21]), respectively, where , and are the translational and rotational self-diffusion coefficients. The translational and rotational MSDs of the particle obtained using GLD with MLN follow Stokes-Einstein and Stokes-Einstein-Debye relations, respectively, with scaling factors of 3 (Figure 8(c)) and 102.54 (Figure 8(d)), respectively.
The hydrodynamic wall effects on the particle diffusivity are important for a nanoparticle thermal motion in a fluid flow that occurs in TDD and similar microparticle flows. For a particle initially located at the center of the cylindrical vessel, the wall effects play a minimal role (≤ 3%, compared to an unbounded fluid domain) on the diffusion coefficient (in other words MSD) (see Figure 8) [22]. When a particle of radius a is initially placed at a distance h from the tube wall to the center of the particle, h < R, the particle-wall interactions modify the particle diffusivity. For a ≪ R, in a quiescent fluid, the Brownian motion near the vessel wall is similar to that of motion in the vicinity of a plane wall (curvature effects may be neglected) [22, 23]. For a particle initially located in the near vicinity of the wall, there is reduced space for the surrounding fluid to negotiate the particle, and the corresponding drag force in a direction parallel to the wall is higher. The diffusivity of the particle in the proximity of the wall may be estimated to be in x, y and z directions [24], while depends on the particular direction.
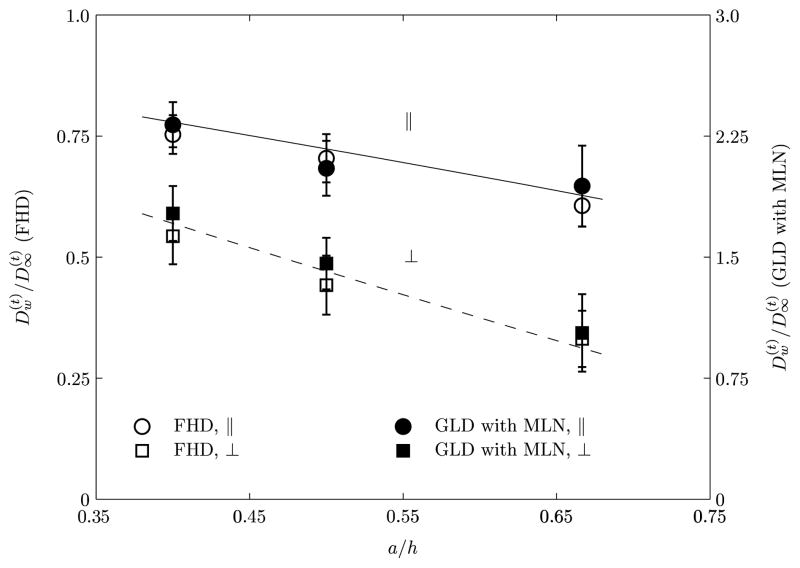
Figure 9 shows the numerically obtained parallel (x direction) and perpendicular (y direction) diffusion coefficients of a neutrally buoyant particle of radius, a = 200 nm, initially placed at various distances from the vessel wall, in a quiescent medium. As mentioned earlier, in the diffusive regime, the translational MSD of the particle increases linearly in time. We have numerically evaluated the gradient of the linear profile, normalized by the translational self-diffusion coefficient, , plotted as a function of a/h. The diffusivity of the particle obtained using (i) FHD (left hand side y-axis) agrees with the prediction of Happel and Brenner [22] (left hand side y-axis) and (ii) GLD with MLN (right hand side y-axis) agrees with the prediction of Happel and Brenner [22] with a scaling factor of 3. It is to be noted that for determining the translational MSD of a nanoparticle of radius, a = 200 nm, initially placed at various distances from the vessel wall, the scaling factor 3 remains unchanged.
FIGURE 9.
The translational diffusion coefficient of neutrally buoyant Brownian particle of radius a initially placed at different locations h from the wall of the circular vessel in a quiescent medium. Solid and dashed lines correspond to the perturbation solutions given in Happel and Brenner [22].
CONCLUSIONS
A direct numerical simulation adopting ALE based FEM is employed to simulate the Brownian motion of a nanoparticle in an incompressible Newtonian stationary fluid medium. The thermal fluctuations are incorporated using either of the following two methods:
Fluctuating hydrodynamics (FHD).
Generalized Langevin dynamics with Mittag-Leffler noise (GLD with MLN).
At thermal equilibrium, the numerical predictions are validated by comparing with analytical results. The comparison between the results obtained from FHD and GLD with MLN are summarized in the Tables 2 and 3.
TABLE 2.
Comparion between the FHD and the GLD with MLN methods. Abbreviations, CC: Computational cost.
| Comparison: FHD & GLD with MLN | |
|---|---|
|
| |
| Method | FHD: Thermal fluctuations from the fluid are added as random stress tensor in the fluid equation, that depends on the temperature and viscosity of the fluid. |
| GLD: Thermal fluctuations from the fluid are added as random force and torque in the particle equations of motion, that does not depends on position and shape of the particle. | |
|
| |
| Mesh, time step & CC | For a given mesh size, the computational cost for both the methods are comparable. In order to obtain a converged numerical result, FHD requires finer mesh and smaller time step compare to GLD. |
TABLE 3.
Comparion between the numerically predicted results by FHD and GLD with MLN methods. Abbreviations, EQT: Equipartition theorem; VACF: Velocity autocorrelation function; MSD: Mean square displacement.
| Comparison: FHD & GLD with MLN | |
|---|---|
|
| |
| EQT | FHD: Equipartition theorem is satisfied. The particle mass m is augmented by an added mass m0/2, to account for compressibility. |
| GLD: Equipartition theorem is satisfied. When the thermostat adheres to the equipartition theorem, the characteristic memory time in the noise is consistent with the inherent time scale of the memory kernel. | |
|
| |
| VACF | FHD: The translational and rotational VACFs of the particle follow an exponential decay, exp(−ζ(t)t/M) and exp(−ζ(r)t/I)), respectively, at short times, and a power-law decay, a0 (t/τν)−3/2 and b0 (t/τν)−5/2, respectively at long times. The value of a0 and b0 agrees with Hauge and Martin-Löf [10]. |
| GLD: The translational and rotational VACFs of the particle follow a stretched exponential decay, exp{−(t/τν)3/2}, at short times, and a power-law decay, a0 (t/τν)−3/2 and b0 (t/τν)−5/2, respectively, at long times. The value of a0 and b0 differs from those predicted by Hauge and Martin-Löf [10]. | |
|
| |
| MSD | FHD: In the diffusive regime, translational and rotational MSDs obey Stokes-Einstein and Stokes-Einstein-Debye relations, respectively. |
| GLD: In the diffusive regime, translational and rotational MSDs obey Stokes-Einstein and Stokes-Einstein-Debye relations, with scaling factors of 3 and 102.54, respectively. | |
Based on our observations presented in Tables 2 and 3, FHD approach captures the correct hydrodynamic correlations (algebraic decay) and normal diffusion, if compressibility effects are considered into account. A GLD thermostat based on the Mittag-Leffler noise captures hydrodynamic correlations and normal diffusion with a scaling factor with an altered dynamics. Our primary aim is to employ one of the approaches to evaluate the free energy landscapes of nanocarrier adhesion with surfaces in future applications. Either of the approaches can be employed for future computations of free energy landscapes of nanocarrier adhesion subject to hydrodynamic interactions.
Acknowledgments
This work was sponsored by National Institute of Health (NIH) Grant R01 EB006818 (D.M.E.); National Science Foundation (NSF) Grant CBET-0853389. Computational resources were provided in part by the National Partnership for Advanced Computational Infrastructure under Grant No. MCB060006.
Contributor Information
B. Uma, Email: umab@seas.upenn.edu, Department of Anesthesiology and Critical Care, University of Pennsylvania, Philadelphia, PA 19104
P.S. Ayyaswamy, Email: ayya@seas.upenn.edu, Department of Mechanical Engineering and Applied Mechanics, University of Pennsylvania, Philadelphia, PA 19104
R. Radhakrishnan, Email: rradhak@seas.upenn.edu, Department of Bioengineering, University of Pennsylvania, Philadelphia, PA 19104
D.M. Eckmann, Email: David.Eckmann@uphs.upenn.edu, Department of Anesthesiology and Critical Care, University of Pennsylvania, Philadelphia, PA 19104
References
- 1.Uma B, Swaminathan TN, Radhakrishnan R, Eckmann DM, Ayyaswamy PS. Nanoparticle Brownian motion and hydrodynamic interactions in the presence of flow fields. Phys Fluids. 2011;23:073602. doi: 10.1063/1.3611026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Uma B, Swaminathan TN, Ayyaswamy PS, Eckmann DM, Radhakrishnan R. Generalized Langevin dynamics of a nanoparticle using a finite element approach: Thermostating with correlated noise. The Journal of Chemical Physics. 2011;135:114104. doi: 10.1063/1.3635776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Sharma N, Patankar NA. Direct numerical simulation of the Brownian motion of particles by using fluctuating hydrodynamic equations. Journal of Computational Physics. 2004;201(2):466–486. [Google Scholar]
- 4.Ladd AJC. Numerical simulations of particulate suspensions via a discretized Boltzmann equation. part 2. numerical results. Journal of Fluid Mechanics. 1994;271:311–339. [Google Scholar]
- 5.Dünweg B, Ladd AJC. Lattice–Boltzmann simulations of soft matter systems. Advances in Polymer Science. 2008;221:89–166. [Google Scholar]
- 6.Atzberger PJ, Kramer PR, Peskin CS. A stochastic immersed boundary method for fluid-structure dynamics at microscopic length scales. Journal of Computational Physics. 2007;224(2):1255–1292. [Google Scholar]
- 7.Iwashita T, Nakayama Y, Yamamoto R. A numerical model for Brownian particles fluctuating in incompressible fluids. Journal of the Physical Society of Japan. 2008;77(7):074007. [Google Scholar]
- 8.Iwashita T, Yamamoto R. Short-time motion of Brownian particles in a shear flow. Phys Rev E. 2009 Mar;79(3):031401. doi: 10.1103/PhysRevE.79.031401. [DOI] [PubMed] [Google Scholar]
- 9.Landau LD, Lifshitz EM. Fluid Mechanics. Pergamon Press; London: 1959. [Google Scholar]
- 10.Hauge EH, Martin-Löf A. Fluctuating hydrodynamics and Brownian motion. Journal of Statistical Physics. 1973;7(3):259–281. [Google Scholar]
- 11.Grmela M, Öttinger H. Dynamics and thermodynamics of complex fluids. i. development of a general formalism. Phys Rev E. 1997;56(6):6620–6632. [Google Scholar]
- 12.Kubo R. The fluctuation-dissipation theorem. Reports on Progress in Physics. 1966;29(1):255–284. [Google Scholar]
- 13.Kubo R, Toda M, Hashitsume N. Nonequilibrium statistical mechanics. 2. II. Springer-Verlag; Berlin: 1991. [Google Scholar]
- 14.Viñales AD, Despósito MA. Anomalous diffusion induced by a mittag-leffler correlated noise. Phys Rev E. 2007 Apr;75(4):042102. doi: 10.1103/PhysRevE.75.042102. [DOI] [PubMed] [Google Scholar]
- 15.Viñales AD, Wang KG, Despósito MA. Anomalous diffusive behavior of a harmonic oscillator driven by a mittag-leffler noise. Phys Rev E. 2009;80:011101. doi: 10.1103/PhysRevE.80.011101. [DOI] [PubMed] [Google Scholar]
- 16.Erdélyi A, Magnus W, Oberhettinger F, Tricomi FG. Higher Transcendental Functions. Krieger; New York: 1981. Ch. 18 in Vol. 1. [Google Scholar]
- 17.Mainardi F, Gorenflo R. On mittag-leffler-type functions in fractional evolution processes. J Comput Appl Math. 2000;118(1–2):283–299. [Google Scholar]
- 18.Serrano M, Gianni D, Español P, Flekkøy E, Coveney P. Mesoscopic dynamics of voronoi fluid particles. Journal of Physics A: Mathematical and General. 2002;35(7):1605–1625. [Google Scholar]
- 19.Huang R, Chavez I, Taute K, Lukic B, Jeney S, Raizen M, Florin E. Direct observation of the full transition from ballistic to diffusive Brownian motion in a liquid. Nature Physics. 2011;7:576–580. [Google Scholar]
- 20.Zwanzig R. Nonequilibrium Statistical Mechanics. Oxford University Press; 2001. [Google Scholar]
- 21.Heyes DM, Nuevo MJ, Morales JJ, Branka AC. Translational and rotational diffusion of model nanocolloidal dispersions studied by molecular dynamics simulations. Journal of Physics: Condensed Matter. 1998;10(45):10159–10178. [Google Scholar]
- 22.Happel J, Brenner H. Low Reynolds number hydrodynamics. Martinus Nijhoff Publishers; The Hague, Netherlands: 1983. [Google Scholar]
- 23.Mavrovouniotis G, Brenner H. Hindered sedimentation, diffusion, and dispersion coefficients for Brownian spheres in circular cylindrical pores. Journal of Colloid and Interface Science. 1988;124(1):269–283. [Google Scholar]
- 24.Brenner H, Gaydos L. The constrained Brownian movement of spherical particles in cylindrical pores of comparable radius: Models of the diffusive and convective transport of solute molecules in membranes and porous media. Journal of Colloid and Interface Science. 1977;58(2):312–356. [Google Scholar]