Composite-180° Pulse-Based Symmetry Sequences to Recouple Proton Chemical Shift Anisotropy Tensors under Ultrafast MAS Solid-State NMR Spectroscopy

Abstract

There is considerable interest in the measurement of proton (¹H) chemical shift anisotropy (CSA) tensors to obtain deeper insights into H-bonding interactions which find numerous applications in chemical and biological systems. However, the presence of strong ¹H/¹H dipolar interaction makes it difficult to determine small size ¹H CSAs from the homogeneously broadened NMR spectra. Previously reported pulse sequences for ¹H CSA recoupling are prone to the effects of radio frequency field (B₁) inhomogeneity. In the present work we have carried out a systematic study using both numerical and experimental approaches to evaluate γ-encoded radio frequency (RF) pulse sequences based on R-symmetries that recouple ¹H CSA in the indirect dimension of a 2D ¹H/¹H anisotropic/isotropic chemical shift correlation experiment under ultrafast magic angle spinning (MAS) frequencies. The spectral resolution and sensitivity can be significantly improved in both frequency dimensions of the 2D ¹H/¹H correlation spectrum without decoupling ¹H/¹H dipolar couplings but by using ultrafast MAS rates up to 70 kHz. We successfully demonstrate that with a reasonable RF field requirement (< 200 kHz) a set of symmetry-based recoupling sequences, with a series of phase-alternating 270°₀-90°₁₈₀ composite-180° pulses, are more robust in combating B₁ inhomogeneity effects. In addition, our results show that the new pulse sequences render remarkable ¹H CSA recoupling efficiency and undistorted CSA lineshapes. Experimental results on citric acid and malonic acid comparing the efficiencies of these newly developed pulse sequences with that of previously reported CSA recoupling pulse sequences are also reported under ultrafast MAS conditions.

Introduction

Due to limited spectroscopic resolution and sensitivity originating from strong anisotropic interactions in solids, atomic-level characterization using solid-state nuclear magnetic resonance (NMR) spectroscopy technique has always been a challenging task. Over the past several years, detection of low abundant nuclei (¹³C, ¹⁵N) has been a routinely employed method for solids due to their large spread of chemical shift frequency.^1,2 On the other hand, methods based on direct detection of protons are still emerging. The main difficulty associated with these methods is the homogeneously broadened ¹H resonances resulting from strong ¹H/¹H dipolar interactions due to their high abundance and sensitivity. However, sample spinning at ultrafast (up to 110 kHz) magic angle spinning (MAS) frequencies - in combination with the application of high magnetic field strength (B₀ ≥ 14.1 T) can significantly improve the spectral resolution and sensitivity by completely suppressing the anisotropic interactions without any need for deuteration of the sample. This technique has opened up new avenues towards the development of proton detection-based experiments^3-8 on non-deuterated samples wherein full advantage of high sensitivity and natural abundance of protons can be taken into account. ^9-15 While the isotropic chemical shift values allow us to distinguish magnetically inequivalent nuclear spins in the system, various anisotropic interactions contain unique information about its structure and dynamics. The information about the local electronic environment and motions surrounding a nucleus is provided by chemical shift anisotropy (CSA) tensors which play a significant role in detailed structural and dynamics investigations of an enormous number of chemical and biological systems by both solution and solid-state NMR spectroscopy.^16-20 A variety of recoupling techniques have been developed in the past to reintroduce CSA and dipolar couplings to measure structural constraints that are otherwise averaged out due to MAS.^21-27 Particularly, it is important to have the knowledge of proton CSA tensors to get greater insights into both inter and intra molecular H-bonding interactions which provide structural stability to biomolecules, polymers and molecular self-assemblies.^28-33 In this regard it is important to have accurately determined ¹H CSA tensors and understand their variation in detail for structural and dynamics studies. Ab initio quantum chemical calculation is generally performed for the better interpretation of H-bonding interactions on the basis of ¹H CSA.³⁴ Subsequent development of this approach has generated a huge interest amongst researchers to utilize ¹H CSA in order to get piercing insights into structures in a range of chemical and biological systems. Nevertheless, the size of ¹H CSA is relatively small and consequently its extraction from homogeneously broadened NMR spectra becomes difficult due to the presence of strong ¹H/¹H dipolar couplings. In recent years, there has been a gradual progress in the development of methods to determine ¹H CSA tensors from multidimensional experiments.^35-39 Most of these experiments necessitate a combination of MAS and homonuclear decoupling to get well resolved proton resonances for different proton sites in a solid sample. In a previous study, ¹H CSA was reintroduced using a symmetry-based recoupling sequence in the indirect dimension and the individual proton sites were well resolved at their respective isotropic chemical shift values using homonuclear decoupling in the direct dimension of a 2D experiment.³⁵ However, the requirement of a strong RF field for homonuclear decoupling during acquisition and a relatively slow MAS for the symmetry sequence used in this study can be limiting factors of this approach. In another study, a 2D ¹H/¹H correlation experiment was performed at rotary resonance condition to reintroduce ¹H CSA in the indirect dimension in combination with fast MAS.³⁶ Again, this approach’s extreme sensitivity to radio frequency field (B₁) inhomogeneity can constrain the accurate determination of ¹H CSA tensors. In a recent report, CSA tensors for amide protons of U-¹³C, ¹⁵N-CAP-Gly domain of dynactin were determined by implementing symmetry-based sequence in 3D experiments wherein ¹H CSA was first recoupled in the indirect dimension with a subsequent magnetization transfer to a directly bonded heteronucleus.^37,38 In another study, ¹H CSA tensors for OH hydrogen-bonded protons in tyrosine.HCl and citric acid were determined using symmetry-based recoupling sequence $R{16}_3^2$.³⁹ Therein, 2D ¹H anisotropic-isotropic chemical shift correlation experiments were performed in combination with ultrafast MAS and high B₀ field, and without the application of homonuclear decoupling. Nevertheless, the existing symmetry-based ¹H CSA recoupling sequences are sensitive to RF field (B₁) inhomogeneity, resulting in lineshape distortion, poor signal-to-noise ratio (SNR) due to a strong center peak arising from non-oscillating components, and poor resolution and sensitivity. To overcome these difficulties, we have systematically carried out a study to find a set of more efficient symmetry-based CSA recoupling sequences as compared to earlier reported sequences based on R-symmetries through extensive numerical simulations in combination with experiments. Herein, we demonstrate that symmetry-based 2D ¹H CSA recoupling sequences with a series of phase-alternating 270°₀-90°₁₈₀ composite-180° pulses are more robust towards the presence of RF field (B₁) inhomogeneity as compared to the previously reported symmetry-based sequence with a series of phase-alternating 180° pulses under ultrafast MAS condition and high B₀ strength. The spectral resolution and sensitivity can be significantly improved both in the direct (isotropic chemical shift) and indirect (CSA) dimensions of a 2D ¹H/¹H correlation spectrum without the application of ¹H/¹H dipolar decoupling under ultrafast MAS rates. The use of ultrafast MAS rates (≥ 60 kHz), largely removes strong ¹H/¹H dipolar interactions, and high B₀ field strength (16.4 Tesla) is used to amplify small sized ¹H CSAs. We demonstrate the robustness of the new CSA recoupling sequences over the existing methods on powder samples of citric acid and malonic acid.

Selection of CSA recoupling pulse sequences

We have implemented γ-encoded rotor-synchronized pulse sequences of symmetry class $R{N}_n^{\nu }$ to recouple ¹H CSA through the first order average Hamiltonian as described in detail by Levitt and co-workers.^40-42 N,n and ν are integers and represent symmetry numbers associated with rotor-synchronized pulses wherein each rotational period nτ_r (τ_r: cycle time of sample spinning) is subdivided into N phase alternated inversion pulse elements such that each pulse has a length of nτ_r /N and a phase of ± πν /N. To begin with we performed a systematic selection of pulse sequences suitable for the present study from a list of possible γ-encoded symmetry-based sequences $R{N}_n^{\nu }$, given elsewhere.⁴⁰ The basic criteria for the selection of symmetry-based CSA recoupling pulse sequences suitable for the experimental data collection is fivefold: 1) ¹H CSA is recoupled through the first-order average Hamiltonian, 2) recoupling of ¹H/¹H dipolar interactions along with ¹H isotropic chemical shifts are avoided, 3) RF field amplitude, which is proportional to the MAS rate in symmetry-based sequence, is kept below 200 kHz at a MAS rate of 70 kHz to avoid any damage to the NMR probe, 4) a large scaling factor is desired as the span of ¹H CSA is small, and 5) the effect of RF field inhomogeneity is minimized.

The first two criteria are satisfied by a selection of {l, m, λ, μ} equal to {2, ±2, 1, ±1} or {2, ±2, 1, ∓ 1} terms where l and λ are space and spin rank with components m and μ, respectively. All inequivalent solutions for symmetry-based sequences $R{N}_n^{\nu }$ in the range N ≤ 20, n ≤ 10 and ν ≤ 10 can be found elsewhere.⁴⁰ Besides the choice of the symmetry numbers, the inversion pulse elements used in the symmetry-based sequences can significantly affect their practical performance. Consequently, in this study, we have implemented two different pulse sequences; a) a series of phase-alternating 180° pulses, and b) a series of phase-alternating 270°₀-90°₁₈₀ composite-180° pulses. It is to be noted that both CSA and heteronuclear dipolar interactions have the same symmetry with respect to sample and spin rotations; therefore ¹H CSA recoupling sequences simultaneously recouple heteronuclear (¹H-X) dipolar interactions as well. Nevertheless, heteronuclear dipolar interactions can be decoupled by applying a 180° pulse on the X-channel in the middle of the CSA recoupling pulses.³⁷ Since the X nuclei (or ¹³C/¹⁵N) are not abundant in the systems investigated in this study, all the experiments were carried without any application of 180° pulse on the X-channel. Out of 32 γ-encoded CSA recoupling symmetry sequences listed elsewhere,⁴⁰ we selected 24 sequences composed of a series of phase-alternating 180° pulses to satisfy the third criteria wherein the RF amplitude requirement was well within the limit under ultrafast MAS rates (in the range 60-70 kHz) (Figure 1A1). Obviously, the RF amplitude for the sequence with a series of phase-alternating 270°₀-90°₁₈₀ composite-180° pulses is two times higher than the RF amplitude associated with 180° pulses. This rules out some of the sequences and the number of symmetry sequences for this class reduces to 18 (Figure 1A2). To meet the fourth criteria we calculated scaling factor (κ_lmλμ) for these sequences (refer to Supporting Information for the values of scaling factor) and selected sequences with |κ_lmλμ| ≥ 0.13. The γ-encoded recoupling sequences result in amplitude modulated signal intensity which requires an application of real Fourier transform of FID; consequently, the sign of CSA cannot be determined. On the basis of the value of scaling factor, we chose symmetry sequences $R{14}_3^1$, $R{16}_3^2$, $R{14}_4^1$, $R{18}_4^1$ and $R{18}_5^1$ with a series of phase-alternating 180° pulses (Figure 1B1), and $R{12}_5^4$, $R{14}_5^3$, $R{14}_6^5$, $R{16}_7^6$, $R{18}_7^5$, $R{20}_7^4$, $R{14}_8^5$, $R{18}_8^7$, $R{16}_9^6$, $R{20}_9^8$ and $R{18}_{10}^7$ with a series of phase-alternating 270°₀-90°₁₈₀ composite-180° pulses (Figure 1B2). To select the sequences which are robust towards RF field inhomogeneity so as to fulfill the fifth criteria we carried out numerical simulations using SIMPSON^43,44 both in the absence and presence of RF field inhomogeneity (Figure 2) implementing ¹H CSA recoupling sequences with the scaling factor |κ_lmλμ| ≥ 0.13. We assumed a Gaussian shaped distribution of the RF field strengths centered at a nominal RF field strength with a standard deviation of 0.1. The presence of RF field inhomogeneity resulted in the center peak with varying intensity from these symmetry-based sequences in contrast to those observed in the absence of RF field inhomogeneity. Spectra obtained with many of these recoupling sequences exhibited a strong center peak, and hence a strong dependence on RF field inhomogeneity. It is essential to point out here that the presence of a strong center peak results in low SNR and hence poor resolution and sensitivity, and significant distortions in the recoupled powder lineshapes. To remove this center peak, DC balance (accomplished by subtracting the average of the final 1/8^th points in t₁ from total data points) is often applied prior to a real Fourier transform, but only at the cost of sensitivity of CSA powder lineshape which in turn makes it difficult to observe smaller CSAs due to their interference resulting from the strong center peak. All the symmetry-sequences with a series of phase-alternating 180° pulses and |κ_lmλμ| ≥ 0.13 were found to have strong dependence on RF field inhomogeneity leading to high center peak intensities with a distinct change in CSA lineshapes along with recoupling efficiencies in comparison to that observed in the absence of RF field inhomogeneity. Consequently, these sequences might lead to inaccurate ¹H CSA parameters and hence can be ruled out (Figure 1C1). On the other hand, except minor variations in center peak intensities, recoupled powder lineshapes as well as recoupling efficiency obtained from most of the above listed symmetry sequences with a series of 270°₀-90°₁₈₀ composite-180° pulses and |κ_lmλμ| ≥ 0.13 remained nearly unperturbed both in the presence and absence of RF field inhomogeneity and explain their robustness towards RF field inhomogeneity. On the basis of low center peak intensity we finally concluded that symmetry-based sequences $R{12}_5^4$, $R{14}_6^5$, $R{16}_7^6$, $R{14}_8^5$, $R{18}_8^7$, $R{16}_9^6$, $R{20}_9^8$ and $R{18}_{10}^7$ with a series of phase-alternating 270°₀-90°₁₈₀ composite-180° pulses (Figure 1C2) are the best set of sequences that can be implemented to extract ¹H CSAs under ultrafast MAS conditions. Out of the eight symmetry-based sequences mentioned above, $R{16}_7^6$, $R{18}_8^7$ and $R{20}_9^8$ are found to be almost identical in terms of CSA recoupling efficiency, scaling factor and center peak intensity while $R{12}_5^4$ and $R{14}_6^5$ resulted in a slightly higher center peak intensity and $R{14}_8^5$, $R{16}_9^6$ and $R{18}_{10}^7$ have relatively smaller scaling factor as compared to the other three sequences. It is worth mentioning that most of the γ-encoded symmetry-based sequences with the ratio of symmetry numbers N/2n < 2 shown in the present study are robust in combating the presence of RF field inhomogeneity. Nevertheless, there may be a few exceptions to this, as seen from Figure 2, wherein the ¹H CSA lineshape using symmetry-based sequence $R{18}_5^1(N/2n<2)$, with a series of phase-alternating 180° pulses, has a strong dependence on RF field inhomogeneity. To further substantiate the right selection of ¹H CSA recoupling sequences that are robust towards RF field inhomogeneity, we carried out numerical simulations by deliberately mis-setting the RF amplitudes of recoupling pulses from the theoretical value. It is evident from Figure 3 that mismatches of the RF amplitude by ±10% lead to strong center peaks as well as huge distortions in the CSA lineshapes when $R{16}_3^2(180°)$ is used, unlike $R{18}_8^7(270°90°)$ wherein an undistorted CSA lineshapes with relatively weak center peaks are observed. This observation clearly rationalizes our approach for the selection of robust ¹H CSA recoupling sequences towards RF field inhomogeneity on the basis of the center peak intensity. For a demonstration purpose in this study we have carried out experimental measurements using symmetry sequences $R{16}_3^2$ with a series of phase-alternating 180° pulses, and $R{18}_8^7$ and $R{20}_9^8$ with a series of phase-alternating 270°₀-90°₁₈₀ composite-180° pulses. Hereafter we will be using the notations $R{16}_3^2(180°)$, $R{18}_8^7(270°90°)$ and $R{20}_9^8(270°90°)$ to represent the symmetry-based sequences, $R{16}_3^2$, $R{18}_8^7$ and $R{20}_9^8$, respectively.

Figure 1.

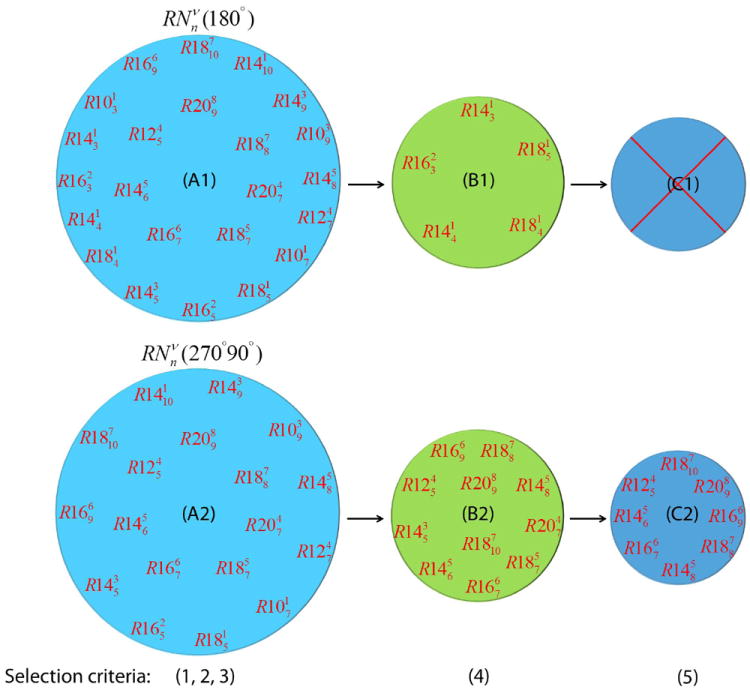
CSA recoupling sequences based on R symmetries with a series of phase-alternating (A1) 180° pulses, and (A2) composite-180° pulses that have RF field amplitude less than 200 kHz at a MAS rate of 70 kHz. (B1, B2) CSA recoupling sequences with a scaling factor |κ_lmλμ| ≥ 0.13 from A1 and A2, respectively. (C1, C2) All listed symmetry-based sequences showed relatively small center peak intensity in the presence of RF field inhomogeneity from numerical simulations using SIMPSON.

Figure 2.

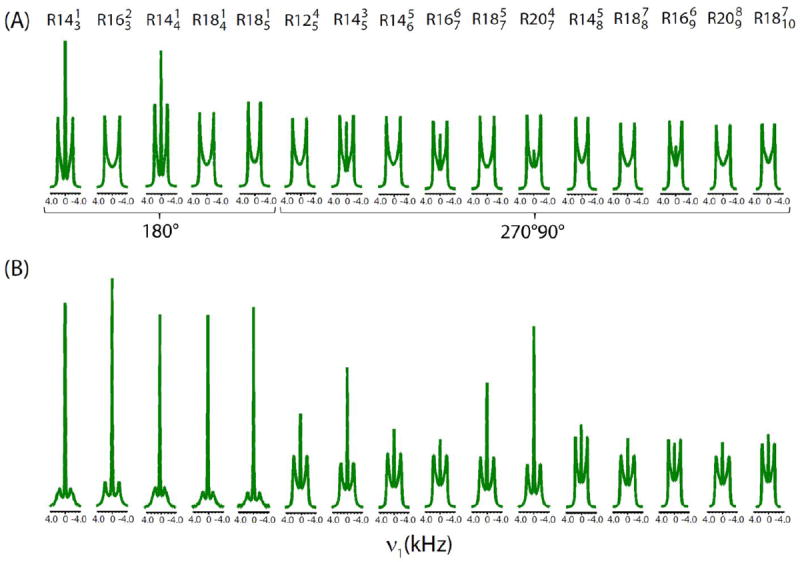
Recoupled ¹H CSA lineshapes generated from SIMPSON simulations using symmetry-based sequences $R{14}_3^1$, $R{16}_3^2$, $R{14}_4^1$, $R{18}_4^1$ and $R{18}_5^1$ with a series of phase-alternating 180° pulses and $R{12}_5^4$, $R{14}_5^3$, $R{14}_6^5$, $R{16}_7^6$, $R{18}_7^5$, $R{20}_7^4$, $R{14}_8^5$, $R{18}_8^7$, $R{16}_9^6$, $R{20}_9^8$ and $R{18}_{10}^7$ with a series of phase-alternating 270°₀-90°₁₈₀ composite-180° pulses having a scaling factor |κ_lmλμ| ≥ 0.13 in the absence (A) and presence (B) of RF field inhomogeneity. All simulations were carried out for a single ¹H spin at a Larmor frequency of 700 MHz and MAS rate of 70 kHz. Powder averaging was achieved using 678 (α, β) orientations and 26 γ angles with a fixed CSA value of 24 ppm and an asymmetry parameter (η) equals to zero.

Figure 3.

SIMPSON simulations of recoupled ¹H CSA lineshapes as a function of RF amplitude mismatch (±10%) from the theoretical value using symmetry-based sequences $R{16}_3^2$ employing a series of phase-alternating 180° pulses, and $R{18}_8^7$ with a series of phase-alternating 270°₀-90°₁₈₀ composite-180° pulses. All other simulation details are as mentioned in Figure 2 caption.

Experimental

All NMR experiments were performed on a 700 MHz solid-state NMR spectrometer (JEOL ECA700II) using a 1.0 mm double-resonance ultrafast MAS probe (JEOL RESONANCE Inc.) at spinning frequencies up to 70 kHz. One mg of citric acid or malonic acid was packed in a 1 mm zirconia rotor and all measurements were carried out at room temperature (~23°C). Two dimensional (2D) symmetry-based pulse sequences $R{16}_3^2(180°)$, $R{18}_8^7(270°90°)$ and $R{20}_9^8(270°90°)$ used in this study to record proton-detected 2D ¹H/¹H anisotropic/isotropic chemical shift correlation spectra under ultrafast MAS frequencies are shown in Figure 4. Each R block in $R{16}_3^2(180°)$ pulse sequence is composed of a 180° pulse whereas $R{18}_8^7(270°90°)$ and $R{20}_9^8(270°90°)$ are composed of 270° and 90° pulses. Table 1 gives the list of all parameters associated with symmetry-based sequences used in this study. All NMR data were acquired using an acquisition time of 10.24 ms with 1024 t₂ complex points. The amplitude modulated t₁ signal with 32 points and 3 scans per t₁ points was obtained at every Nτ_r for $R{18}_8^7(270°90°)$ and $R{20}_9^8(270°90°)$ and every 3Nτ_r for $R{16}_3^2(180°)$ to keep the spectral width in the indirect dimension at par with each other. A relaxation delay of 120 s was set prior to the application of symmetry-based recoupling pulses. All spectra were processed using Delta NMR software (JEOL RESONANCE Inc.). While the t₁ domain was Fourier transformed after zero filling, DC balance followed by zero filling was applied prior to real Fourier transformation in the t₂ domain. The isotropic and anisotropic chemical shifts, and the asymmetry parameter are defined as δ_iso = (δ_xx+δ_yy+δ_zz)/3, δ_ani = |δ_zz-δ_iso|, and η = (δ_yy -δ_xx)/δ_ani, respectively, wherein δ_xx, δ_yy and δ_zz are the principal components of chemical shift tensor such that |δ_zz - δ_iso| ≥ |δ_xx - δ_iso| ≥ |δ_yy - δ_iso|.

Figure 4.

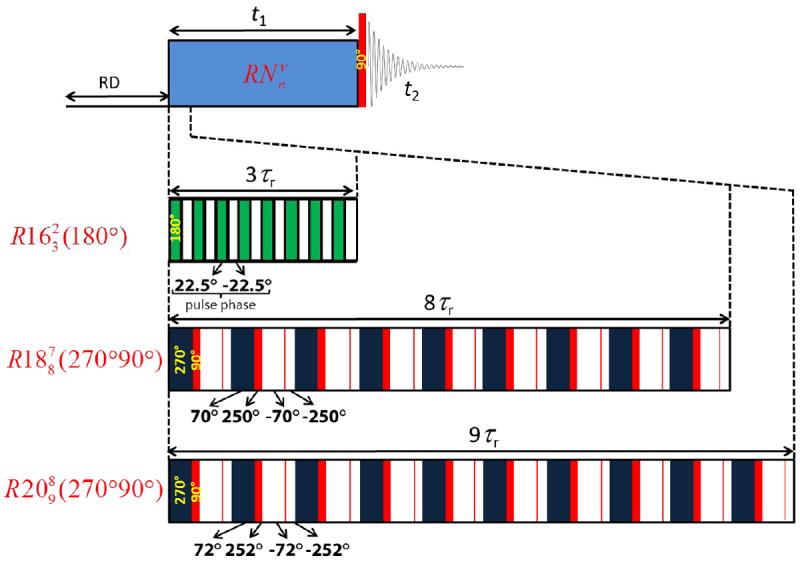
Symmetry-based pulse sequences $R{16}_3^2(180°)$, $R{18}_8^7(270°90°)$ and $R{20}_9^8(270°90°)$ to record proton-detected 2D ¹H/¹H anisotropic/isotropic chemical shift correlation spectra at ultrafast MAS frequencies. $R{16}_3^2(180°)$ is a series of 180° pulses with phases alternating between +22.5 (green rectangle) and -22.5 (unfilled/white rectangle). $R{18}_8^7(270°90°)$ is a series of (270°, 90°) pulses with phases alternating between (70°, 250°) (depicted as black and red rectangles) and (-70°, 250°) (depicted as unfilled/white rectangles). $R{20}_9^8(270°,90°)$ is a series of (270°, 90°) pulses with phases alternating between (72°, 252°) (depicted as black and red rectangles) and (-72°, -252°) (depicted as unfilled/white rectangles). More details can be found in Table 1. After the relaxation delay (RD), the thermal equilibrium longitudinal magnetization is allowed to evolve under the recoupled ¹H CSA interaction during the incrementable t₁ period following which a 90° pulse is applied to prepare the magnetization for detection. 2D spectra were collected without the application of homonuclear dipolar decoupling during the detection period t₂.

Table 1.

Parameters associated with γ-encoded symmetry-based sequences used in the present study at MAS rates (ν_r) of 70 and 60 kHz for powder samples of citric acid and malonic acid, respectively. The phase shift (ϕ) associated with pulses in each R element is calculated using the relation ± πν /N while the corresponding RF field strength is calculated using the equations Nν_r/2n for $R{16}_3^2(180°)$, and Nν_r /n for $R{18}_8^7(270°90°)$ and $R{20}_9^8(270°90°)$.

Symmetry sequence	N, n, ν	R	R’	Rϕ	$R_{\varphi }^{\prime }$	RF amplitude (kHz)
						νr
						70kHz	60kHz
$R{16}_3^2(180°)$	16, 3, 2	1800	1800	18022.5	180-22.5	186.7	160.0
$R{18}_8^7(270°90°)$	18, 8, 7	270090180	270090180	2707090250	270-7090-250	157.5	135.0
$R{20}_9^8(270°90°)$	20, 9, 8	270090180	270090180	2707290252	270-7290-252	155.6	133.3

Results and discussion

In this section the performances of a previously reported ¹H CSA recoupling symmetry sequence $R{16}_3^2(180°)$ and the new sequences $R{18}_8^7(270°90°)$ and $R{20}_9^8(270°90°)$ developed in this study are examined by carrying out 2D ¹H/¹H anisotropic/isotropic chemical shift correlation experiments under ultrafast MAS conditions on citric acid and malonic acid. A discussion on these results will be followed by demonstration of the role of ultrafast MAS to suppress strong ¹H/¹H homonuclear dipolar interactions to get undistorted recoupled ¹H CSA lineshapes.

¹H CSA recoupling experiments on citric acid and malonic acid

On the basis of results obtained from numerical simulations, we carried out ¹H CSA recoupling experiments using symmetry-based sequences $R{16}_3^2(180°)$, $R{18}_8^7(270°90°)$ and $R{20}_9^8(270°90°)$ on citric acid and malonic acid at ultrafast MAS rates of 70 and 60 kHz, respectively. 2D anisotropic/isotropic chemical shift correlation spectra recorded using the symmetry-based sequences described above are shown in Figure 5 (A) and (C) for citric acid and malonic acid, respectively. The ultrafast MAS spectra show well-resolved peaks both for citric acid and malonic acid in the isotropic dimension without application of ¹H/¹H homonuclear decoupling. It is worthwhile to mention here that narrow center peaks with high intensity were regularly observed from our experiments. Consequently, ¹H CSA lineshapes were largely affected by the wiggles/oscillations from these center peaks which affect the extraction of ¹H CSA. As suggested in earlier reports,^37,39 the origin of these center peaks is due to certain non-ideal conditions and one of them is believed to be the presence of RF field inhomogeneity. These conditions result in a slow decay and/or no decay of some longitudinal magnetization that leads to a DC offset in the time domain and hence the center peak in the indirect frequency dimension. As pointed out earlier, a DC balance was applied prior to the real Fourier transform in the indirect dimension to reduce the DC offset resulting from undecayed longitudinal magnetization. A comparison of ¹H CSA recoupling efficiency obtained from the spectral slices at isotropic ¹H chemical shifts using symmetry-based sequences $R{16}_3^2(180°)$, $R{18}_8^7(270°90°)$ and $R{20}_9^8(270°90°)$ in the direct dimension are shown in Figure 5 (B) and (D), respectively. It is obvious from the spectral slices obtained from 2D spectra that the sensitivity of recoupled ¹H CSA lineshapes can be significantly improved by implementing symmetry-based recoupling sequences $R{18}_8^7(270°90°)$ and $R{20}_9^8(270°90°)$ in comparison to the reported symmetry-based sequence $R{16}_3^2(180°)$ under the ultrafast MAS condition. This observation is completely in accordance with our results based on numerical simulations as described earlier. Furthermore, significant distortions in ¹H CSA lineshapes could also be seen using a symmetry-based sequence $R{16}_3^2(180°)$ which might lead to an error in the ¹H CSA values. It is noteworthy that in the case of malonic acid the effect of RF field inhomogeneity on the center peaks is more significant as compared to citric acid (Figure 5 (D)). This could probably be due to the slow MAS rate (60 kHz) used for 2D data collection and this effect can be minimized at MAS rates ≥ 70 kHz.

Figure 5.

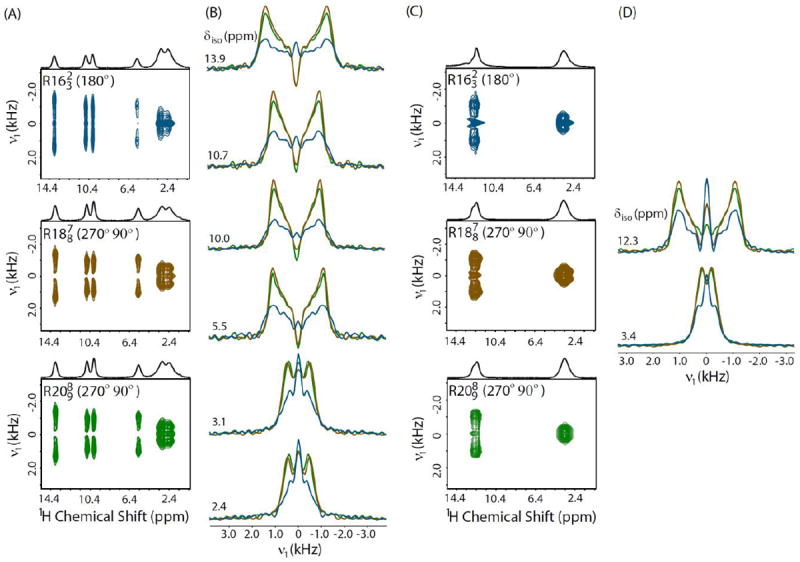
Two dimensional ¹H/¹H anisotropic/isotropic chemical shift correlation spectra of citric acid (A) and malonic acid (C) at 70 and 60 kHz MAS, respectively, recorded using symmetry-based $R{16}_3^2(180°)$ (blue), $R{18}_8^7(270°90°)$ (brown) and $R{20}_9^8(270°90°)$ (green) pulse sequences from a 700 MHz NMR spectrometer. Recoupled ¹H CSA lineshapes obtained from spectral slices parallel to the anisotropic dimension (ν₁) extracted at isotropic ¹H chemical shift values in the direct dimension for citric acid (B) and malonic acid (D), respectively.

Numerical simulations using SIMPSON were performed to extract ¹H CSA and asymmetry parameter values by fitting the experimental ¹H CSA lineshapes using symmetry-based pulse sequences $R{16}_3^2(180°)$, $R{18}_8^7(270°90°)$ and $R{20}_9^8(270°90°)$ for test samples citric acid and malonic acid as shown in Figure 6. All the simulations were carried out by taking a single spin system representative of a single quantum first-order average Hamiltonian using 678 (α, β) orientations and 26 γ angles for powder averaging at 700 MHz ¹H Larmor frequency in the absence of RF field inhomogeneity. The vertical scaling and line broadening of simulated ¹H CSA lineshapes were adjusted to fit the experimental lineshapes. The best fit parameters are listed in Table 2. ¹H CSA values obtained from the best fit from all the three recoupling experiments are generally in good agreement with earlier reported values both under ultrafast MAS³⁹ and slow MAS³⁵ rates for citric acid. Additionally, certain deviations from numerical simulations are observed in the zero-frequency region of the spectrum resulting mainly from RF field inhomogeneity that can contribute to the uncertainty in the determination of asymmetry parameter. While, we believe that the main contribution to center peak is from the presence of RF field inhomogeneity, other sources such as the amplitude and/or phase transient effects, and the deviation in rotor phase due to fluctuations in sample spinning may also contribute to the observed discrepancy. As pointed out earlier, $R{16}_3^2$ gives distorted CSA lineshapes both for small and large ¹H CSAs and can lead to errors in the extraction of CSA values from the data fitting. In particular, in the case where CSA is small, the symmetry sequence $R{16}_3^2(180°)$ leads to ¹H CSA lineshapes that differ significantly from the lineshapes obtained from symmetry sequences $R{18}_8^7(270°90°)$ and $R{20}_9^8(270°90°)$. This phenomenon can be attributed to the strong dependence of recoupling efficiency on RF field inhomogeneity for the symmetry sequence $R{16}_3^2(180°)$ which results in significant contribution to recoupled powder lineshapes for a small CSA while this imperfection is slightly reduced for a large CSA. There is a possibility that first-order single-quantum average Hamiltonian comprised of a single spin might not be sufficient to explain the spin dynamics in the case of symmetry sequence $R{16}_3^2$ and may require corrections to higher-order terms in the Hamiltonian to get the best fit. In contrast to this, CSA lineshapes using sequences $R{18}_8^7(270°90°)$ and $R{20}_9^8(270°90°)$ fit extremely well with the calculated lineshapes both for small as well as large CSAs and validates the robustness towards the presence of RF field inhomogeneity. We would like to mention here that the γ-encoded symmetry-based sequences, for e.g., $R{18}_8^7$ and $R{20}_9^8$ with a series of phase-alternating 180° pulses, can also be used for recoupling of ¹H CSAs at ultrafast MAS; however there can be certain limitations in implementing these sequences because of the small scaling factor (refer to Table S1 of Supporting Information for the values) and their behavior towards the presence of RF field inhomogeneity. It can be seen from Figure S1 of Supporting Information that the center frequency region of experimental ¹H CSA lineshape is affected most probably by the presence of RF field inhomogeneity for all ¹H resonances of citric acid, in contrast to ¹H CSA lineshapes obtained using the same symmetry-based sequences but with phase-alternating 270°₀-90°₁₈₀ composite-180° pulses (Figures 5 or 6). This effect is significant especially when recoupling small size CSAs - an observation which is similar to that for the use of $R{16}_3^2(180°)$.

Figure 6.

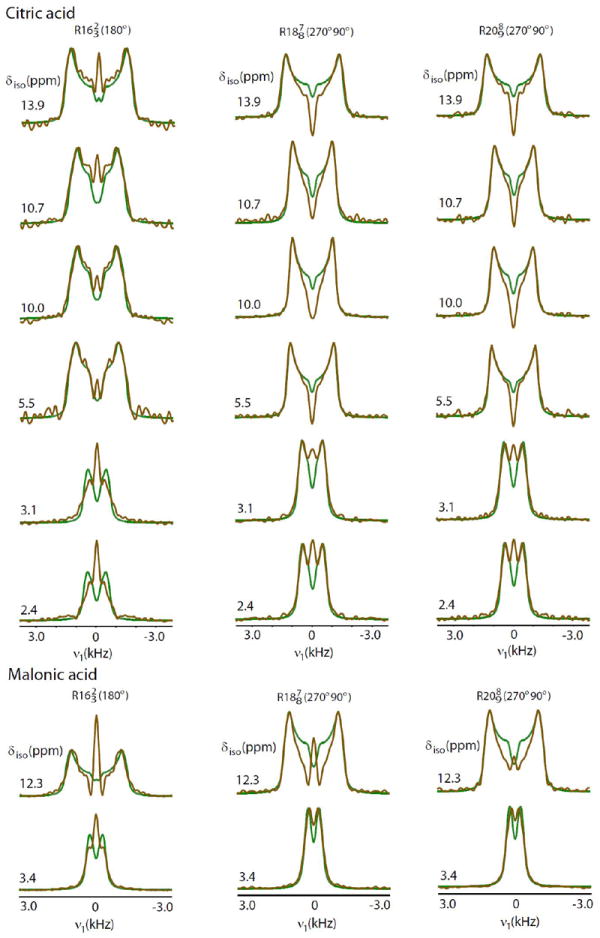
SIMPSON simulations (green lines) to extract chemical shift parameters from the best fit of experimentally measured spectral slices (brown lines) parallel to anisotropic dimension (ν₁) at isotropic ¹H chemical shift values for citric acid and malonic acid under 70 and 60 kHz MAS, respectively, by implementing symmetry-based sequences $R{16}_3^2(180°)$, $R{18}_8^7(270°90°)$ and $R{20}_9^8(270°90°)$ at 700 MHz spectrometer.

Table 2.

¹H CSA parameters obtained from fitting experimentally recoupled powder lineshapes for citric acid and malonic acid using symmetry-based sequences $R{16}_3^2(180°)$, $R{18}_8^7(270°90°)$ and $R{20}_9^8(270°90°)$.

	δiso (ppm)	δani (ppm)			η
Citric acid		$R{16}_3^2(180°)$	$R{18}_8^7(270°90°)$	$R{20}_9^8(270°90°)$	$R{16}_3^2(180°)$	$R{18}_8^7(270°90°)$	$R{20}_9^8(270°90°)$
-COOH	13.9	16.4	16.6	16.6	0.3	0.2	0.2
-COOH	10.7	12.7	12.5	12.5	0.5	0.3	0.3
-COOH	10.0	12.6	12.5	12.5	0.5	0.2	0.3
-OH	5.5	13.4	13.4	13.4	0.5	0.2	0.2
-CH2-	3.1	6.0	7.1	6.8	0.6	0.5	0.5
-CH2-	2.4	6.0	7.1	6.5	0.6	0.5	0.5
Malonic acid
-COOH	12.3	13.0	13.4	13.4	0.3	0.3	0.3
-CH2-	3.4	3.8	3.7	3.6	0.6	0.7	0.7

Suppression of strong ¹H/¹H homonuclear dipolar interactions using Ultrafast MAS

In this section we demonstrate the importance of ultrafast MAS to get undistorted ¹H CSA lineshapes using symmetry-based sequence. The γ-encoded CSA recoupling symmetry-sequences based on R-symmetries suppress isotropic chemical shift and homonuclear dipolar interaction resulting in the first-order average Hamiltonian comprised of a single spin. The use of moderate MAS rates (30-40 kHz) may not be sufficient to suppress ¹H/¹H dipolar interactions completely for strongly coupled systems. This can lead to distorted ¹H CSA lineshapes resulting from the second-order effects due to unsuppressed anisotropic interactions. Alternatively, the role of ultrafast MAS becomes important to suppress ¹H/¹H dipolar interactions completely in the strongly coupled spin systems. In order to show the necessity of ultrafast MAS so as to get undistorted CSA lineshapes originating from the second-order effects due to insufficient suppression of strong ¹H/¹H dipolar interactions we carried out numerical simulations on a five spin network representative of a −CH₂−CH−CH₂− system by changing MAS rates. All the simulations were performed using symmetry-based sequence $R{18}_8^7(270°90°)$ at MAS rates of 40, 60, 80 and 100 kHz. As shown earlier, this pulse sequence is more robust towards the presence of RF field inhomogeneity and leads to almost similar lineshape both in the absence and presence of RF filed inhomogeneity; therefore we avoided the inclusion of RF field inhomogeneity in simulations to reduce the simulation time. In the simulations CSA recoupling efficiency was calculated for −CH− proton which is surrounded by four strongly coupled −CH₂ protons and the initial density operator was taken as a sum of initial z-magnetization associated with each spin. As seen from Figure 7, distortion in the recoupled CSA lineshape is observed at a slow MAS rate of 40 kHz due to the presence of unsuppressed ¹H/¹H dipolar interactions. Moreover, these distortions could be significant for sequences like $R{16}_3^2(180°)$ and $R{14}_3^1(180°)$, which are more sensitive towards the presence of RF field inhomogeneity and can lead to error in the measurements of CSA parameters. Nevertheless, these distortions in the CSA lineshape can well be removed by spinning the sample at MAS rates greater than or equal to 60 kHz which results in a better suppression of ¹H/¹H dipolar interactions also seen from Figure 7. Furthermore, the choice of MAS rates can vary depending on the type of recoupling sequence used. As seen from Figure 7, a reduction in the center peak intensity with the increase in the spinning rate is observed which clearly recommends experiments to be performed under ultrafast MAS to minimize the contribution from multi-spins so as to suppress the center peak. Above all, the efficiency of the recoupled CSA lineshape can be improved under ultrafast MAS condition which is of huge importance for the case of CSA recoupling sequences with poor SNR. These observations obviously necessitate the use of ultrafast MAS to carryout ¹H CSA measurements. Moreover, ultrafast MAS provides wider spectral width 1 / nτ_r that allows the use of symmetry-based sequences with a large symmetry number n.

Figure 7.

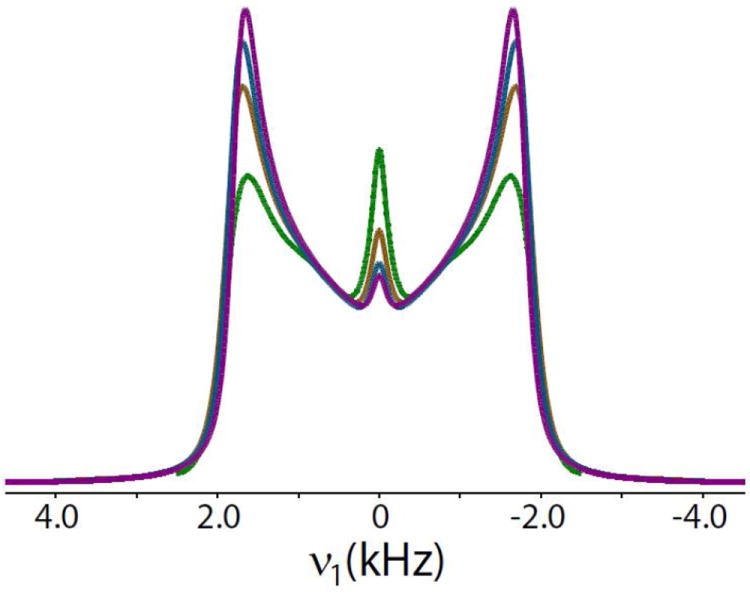
Recoupled ¹H CSA lineshapes of a five spin network representative of −CH₂−CH−CH₂− system generated from SIMPSON simulations using a symmetry-based sequence $R{18}_8^7(270°90°)$ at MAS rates of 40 kHz (green), 60 kHz (brown), 80 kHz (blue) and 100 kHz (magenta). The initial density operator was taken as a sum of initial z-magnetization associated with each spin while the recoupling efficiency was simulated for the −CH− proton. All simulations were carried out at a ¹H Larmor frequency of 600 MHz in the absence of RF field inhomogeneity while powder averaging was achieved using 678 (α, β) orientations and 26 γ angles with a fixed CSA (δ_ani) value of 24 ppm and an asymmetry parameter (η) equals to zero.

Conclusions

In this study, we have reported a systematic selection of γ-encoded symmetry-based sequences based on R-symmetries suitable for ¹H CSA recoupling under ultrafast MAS condition on the basis of symmetry numbers, RF field requirement, scaling factor and robustness towards RF field inhomogeneity using numerical simulations. We have shown that a set of γ-encoded symmetry-based sequences, with a series of phase-alternating 270°₀-90°₁₈₀ composite-180° pulses are found to be more robust towards the presence of RF field inhomogeneity in comparison to earlier reported sequences with a series of phase-alternating 180° pulses under ultrafast MAS condition. Our results from numerical simulations are cross-validated through 2D ¹H/¹H anisotropic/isotropic chemical shift correlation experiments carried out under ultrafast MAS conditions on citric acid and malonic acid. We have demonstrated that the previously reported ¹H CSA recoupling symmetry sequence $R{16}_3^2(180°)$, is extremely sensitive to RF field inhomogeneity that severely distorts the observed ¹H CSA lineshapes and significantly reduces the sensitivity. On the other hand the new sequences proposed in this study, $R{18}_8^7(270°90°)$ and $R{20}_9^8(270°90°)$ successfully suppress RF field inhomogeneity effects and result in undistorted recoupled ¹H CSA lineshapes with significantly improved sensitivity. We have determined ¹H CSA parameters by fitting the recoupled CSA lineshapes obtained from experiments for malonic acid and citric acid using numerical simulations. The recoupled ¹H CSA lineshapes correlate well with calculated lineshapes obtained from the first-order average Hamiltonian. Furthermore, we have also discussed the role of ultrafast MAS for better suppression of strong ¹H/¹H dipolar interactions through numerical simulations. We believe that the proposed symmetry-based recoupling pulse sequences in this study can be easily implemented in multidimensional ¹H CSA recoupling experiments under ultrafast MAS conditions both in the presence and absence of heteronuclei which will be a step forward to get better insights into the studies relying on ¹H CSA tensors.

Highlights.

R Symmetry-based sequences for ¹H CSA recoupling at ultrafast MAS are systematically evaluated.

¹H anisotropic / ¹H isotropic chemical shift 2D correlation spectra are obtained.

γ-encoded R sequences with composite-180 pulses are robust toward RF field inhomogeneity

Precise ¹H CSA determination is demonstrated.