Phenomapping for Novel Classification of Heart Failure with Preserved Ejection Fraction

Abstract

Introduction

Heart failure with preserved ejection fraction (HFpEF) is a heterogeneous clinical syndrome in need of improved phenotypic classification. We sought to evaluate whether unbiased clustering analysis using dense phenotypic data (“phenomapping”) could identify phenotypically distinct HFpEF categories.

Methods and Results

We prospectively studied 397 HFpEF patients and performed detailed clinical, laboratory, electrocardiographic, and echocardiographic phenotyping of the study participants. We used several statistical learning algorithms, including unbiased hierarchical cluster analysis of phenotypic data (67 continuous variables) and penalized model-based clustering to define and characterize mutually exclusive groups comprising a novel classification of HFpEF. All phenomapping analyses were performed blinded to clinical outcomes, and Cox regression was used to demonstrate the clinical validity of phenomapping. The mean age was 65±12 years, 62% were female, 39% were African-American, and comorbidities were common. Although all patients met published criteria for the diagnosis of HFpEF, phenomapping analysis classified study participants into 3 distinct groups that differed markedly in clinical characteristics, cardiac structure/function, invasive hemodynamics, and outcomes (e.g., pheno-group #3 had an increased risk of HF hospitalization [hazard ratio 4.2, 95% CI 2.0–9.1] even after adjustment for traditional risk factors [P<0.001]). The HFpEF pheno-group classification, including its ability to stratify risk, was successfully replicated in a prospective validation cohort (n=107).

Conclusions

Phenomapping results in novel classification of HFpEF. Statistical learning algorithms, applied to dense phenotypic data, may allow for improved classification of heterogeneous clinical syndromes, with the ultimate goal of defining therapeutically homogeneous patient subclasses.

INTRODUCTION

Heart failure (HF), regardless of underlying ejection fraction (EF), is a heterogeneous syndrome, the end result of one or more risk factors that ultimately lead to abnormal cardiac structure and function, which in turn causes reduced cardiac output and/or elevated cardiac filling pressures at rest or with exertion.¹ Despite its underlying heterogeneity, HF with reduced ejection fraction (HFrEF), particularly outpatient HFrEF, has proven to respond to a “one size fits all” approach, with several drugs and devices shown to improve outcomes in randomized clinical trials. Unlike in HFrEF, clinical trials of pharmacologic agents in HF with preserved ejection fraction (HFpEF) have been universally disappointing, and no treatments have improved outcomes in this group of patients.² In HFpEF, the underlying phenotypic heterogeneity is likely far greater than in HFrEF,^{3, 4} and may be a key reason for the poor track record of HFpEF clinical trials. Therefore, understanding the phenotypic heterogeneity of HFpEF, which includes the etiologic and pathophysiologic heterogeneity of the syndrome, may allow for more targeted (and more successful) HFpEF clinical trials. An ideal HFpEF classification system would group together pathophysiologically similar individuals who may respond in a more homogeneous, predictable way to treatment.

The problem of unresolved heterogeneity is not unique to medicine—and in fact appears routinely in such fields as document classification and image processing.⁵ Machine learning—the process of using data to learn relationships between objects—is ideally suited for this task.⁶ Machine learning approaches are typically subdivided into 2 categories: supervised and unsupervised. Supervised learning seeks to predict specified outputs or outcomes. The goal of unsupervised learning, on the other hand, is to try to learn the intrinsic structure within data—such as the analysis of genomic data to derive new subclasses of tumors. Although seemingly distinct, there is considerable overlap between these two categories of learning; unsupervised learning is increasingly seen as an invaluable initial strategy to derive robust set of features for novel classification of a disease or clinical syndrome, which can subsequently be used for supervised learning in a variety of settings.^{5, 7, 8}

With the advent of sophisticated phenotyping tools ranging from a multitude of biomarkers to comprehensive cardiovascular imaging modalities, the era of “deep phenotyping” is now available to improve characterization of heterogeneous syndromes like HFpEF. Prior studies in disease areas such as cancer and autoimmune disease have successfully coupled genomic characterization or protein expression with machine learning approaches,^7–9 although such strategies have typically relied on molecular profiling of the tissue of interest. Within the field of cardiovascular medicine, prior studies have utilized supervised learning algorithms such as neural networks and decision tree analysis as methods for assisting with diagnosis and clinical decision-making, respectively;^{10, 11} however, no prior study has used these techniques to better classify heterogeneous cardiovascular syndromes such as HFpEF. We hypothesized that applying statistical/machine learning algorithms to dense phenotyping alone would allow for the detection of novel patterns in dense, multi-dimensional data obtained from HFpEF patients. We further hypothesized that the identified “pheno-groups” of HFpEF patients would have unique pathophysiologic profiles and differential outcomes. We therefore prospectively investigated the utility of unbiased phenotype mapping (i.e., “phenomapping”) algorithms in a well-characterized HFpEF cohort.

METHODS

Study population

Between March 2008 and May 2011, 420 consecutive patients were prospectively enrolled from the outpatient clinic of the Northwestern University HFpEF Program as part of a systematic observational study of HFpEF (ClinicalTrials.gov identifier #NCT01030991). All patients were recruited after hospitalization for HF. Patients were initially identified by an automated daily query of the inpatient electronic medical record at Northwestern Memorial Hospital using the search criteria: (1) diagnosis of HF or the words “heart failure” in the hospital notes; or (2) B-type natriuretic peptide (BNP) >100 pg/ml; or (3) administration of 2 or more doses of intravenous diuretics. The list of patients generated was screened daily, and only those patients with an LV ejection fraction (LVEF) > 50% and who met Framingham criteria for HF¹² were offered post-discharge follow-up in a specialized HFpEF outpatient program. The HF diagnosis was confirmed in the post-hospitalization outpatient HFpEF clinic. Based on previously published criteria,¹³ besides the presence of symptomatic HF and LVEF > 50%, we required evidence of either significant diastolic dysfunction (grade 2 or 3) on echocardiography or evidence of elevated LV filling pressures on invasive hemodynamic testing or BNP > 100 pg/ml. Patients with greater than moderate valvular disease, prior cardiac transplantation, prior history of reduced LVEF < 40% (i.e., “recovered” EF), or diagnosis of constrictive pericarditis were excluded. All study participants gave written, informed consent, and the institutional review board at Northwestern University approved the study. Descriptions of the clinical characteristics collected on the study participants, definitions of comorbidities, and echocardiography, non-invasive pressure-volume analysis, and invasive hemodynamics methods are provided in the Supplementary Data section.

Phenotypic domains

Table 1 demonstrates the phenotype domains and individual continuous variables that served as phenotypic features for the phenomapping analysis. The phenotypic domains included clinical variables, physical characteristics, laboratory data, electrocardiographic parameters, and echocardiographic parameters.

Table 1.

Phenotype Domains and Individual Phenotypes

Phenotypic Domain	Phenotypes
Demographics	Age
Physical characteristics	Body-mass index, heart rate, systolic blood pressure, diastolic blood pressure, pulse pressure
Laboratory	Sodium, potassium, bicarbonate, blood urea nitrogen, creatinine, estimated GFR, fasting glucose, white blood cell count, hemoglobin, red cell distribution width, platelet count, B- type natriuretic peptide
Electrocardiography	PR interval, QRS duration, QTc interval, QRS axis, T wave axis, QRS-T angle
Echocardiography
• Left heart structure	LV end-diastolic volume, LV end-systolic volume, LV end-diastolic dimension, LV end-systolic dimension, septal wall thickness, posterior wall thickness, LV mass, left atrial volume
• LV systolic function	LV ejection fraction, tissue Doppler s’ velocity (septal and lateral), velocity of circumferential fiber shortening
• LV diastolic function	Mitral inflow characteristics (E velocity, A velocity, E/A ratio, E deceleration time, IVRT), tissue Doppler characteristics (septal e′ and lateral e′ velocities; septal a′ and lateral a′ velocities; septal E/e′ and lateral E/e′ ratios).
• Right heart structure	RV basal diameter, RV maximal diameter, RV length, RV wall thickness, RV end-diastolic area, RV end-systolic area, RV/LV maximal diameter ratio, right atrial area
• RV function	RV fractional area change, tricuspid annular plane systolic excursion
• Hemodynamics	Stroke volume, cardiac output, PA systolic pressure, RA pressure
• Pressure-volume analysis	Effective arterial elastance, end-systolic elastance, systolic blood pressure/end-systolic volume ratio, end-diastolic elastance, ventricular-arterial coupling, preload recruitable stroke work, pulse pressure/stroke volume ratio

Bolded phenotypes are those that were used in the model-based clustering analyses after filtering to remove correlated variables (R>0.6).

GFR = glomerular filtration rate; LV = left ventriular; RV = right ventricular; IVRT = isovolumic relaxation time; PA = pulmonary artery; RA = right atrial

Outcomes assessment

After enrollment, all study participants were evaluated in the Northwestern HFpEF Program as clinically indicated but at least every 6 months. At each visit, inter-current hospitalizations were documented, reviewed, and categorized as due to cardiovascular or non-cardiovascular causes. For cardiovascular hospitalizations, specific causes (e.g., HF, acute coronary syndrome, arrhythmia) were identified. Every 6 months, participants (or their proxy) were contacted to determine vital status with verification of deaths through query of the Social Security Death Index. Enrollment date was defined as the first visit to the outpatient HFpEF clinic. Date of last follow-up was defined as date of death or last HFpEF clinic visit. Follow-up was complete in all patients.

Exploration of the relationship between phenotypic variables

Prior to analysis, missing data (see Supplementary Figure S1) was imputed using the SVDimpute function within the impute package in R. Briefly, missing values were imputed using regression with eigenvectors as predictors. An iterative process was taken where all missing values are set to the row mean, eigenvectors are computed for the data matrix (using SVD) and a given number (5) of eigenvectors were used to impute missing values. The percentage of missing values for features ranged from 0% to 24% (for estimated pulmonary arterial systolic pressure). Hierarchical clustering was used to visualize redundancy among a total of 67 continuous phenotypic variables (Table 1). First, a correlation matrix of phenotypic variables was generated based on the absolute value of the Pearson correlation coefficient. Correlation profiles were used to eliminate redundant features. Variables that were correlated at a correlation coefficient of > 0.6 were filtered (keeping the variable that was most informative and had the least missingness), leaving 46 continuous variables for the final phenomapping analyses.

Biclustering of HFpEF subjects and phenotypic variables

Agglomerative hierarchical clustering, a commonly used unsupervised learning tool, was adapted for the purpose of grouping patients and phenotypic variables.⁶ The 46 continuous phenotypic variables identified after filtering were standardized to mean=0 and standard deviation=1. Hierarchical clustering was performed using the hclust function in R (3.0.1), with the dissimilarity matrix given by Euclidean distance and the average linkage score used to join similar clusters. Subsequent optimal leaf reordering was performed using the seriation package in R¹⁴ so that within a given branch, more similar rows/columns were grouped together. A visual representation of the resulting heatmap was generated using the hmap function. All clustering was performed blinded to clinical outcome data.

Penalized model-based clustering of participants

Although hierarchical clustering is effective as a means of visualization, it is problematic to use as a method for grouping patients into discrete clusters given the heuristic nature of the algorithm and the arbitrariness of defining height thresholds on the resulting dendrogram. To determine the optimal number of pheno-groups within the HFpEF cohort, we therefore used model-based clustering, which assumes a Gaussian distribution for values of phenotypic variables within a cluster, and achieves parameter fitting and patient assignment by minimizing a penalized likelihood.¹⁵ Specifically we used the mclust package in R and explored a full range of covariance structures, some of which relax the requirement for independence of features (i.e. non-diagonal covariance matrices). The Bayesian information criterion (BIC) was used to penalize increases in model complexity, such as a greater number of clusters or variability in standard deviation across variables and across clusters. As a result a parsimonious solution is reached. Such penalty functions serve as a means of “regularization” in machine learning, and improve generalizability to other data sets.⁶ In our implementation, we tried between 1 and 8 clusters.

Comparison of clinical characteristics and survival among pheno-groups

Once phenotype groups were defined, we compared differences in demographic, clinical, electrocardiographic, echocardiographic, and invasive hemodynamic characteristics among groups using Chi-squared tests (or Fisher exact tests when appropriate) for categorical variables and analysis of variance (or Kruskal-Wallis test, when appropriate) for continuous variables. For outcomes analyses, we used unadjusted and multivariable adjusted Cox proportional hazards models to determine the independent association between phenotype groups and outcomes. The proportionality assumption was tested and verified for all Cox regression models. We defined the primary outcome as cardiovascular hospitalization or death, and the secondary outcome as heart failure hospitalization. Covariates included in the multivariable model included variables known to be predictive of outcomes in HFpEF. We used the likelihood ratio test to determine whether the phenotype group variable was predictive of outcomes beyond BNP and the MAGGIC risk score¹⁶ (a recently developed mortality risk score for patients with HF, including HFpEF). Finally, we used receiver-operating characteristic (ROC), net reclassification improvement (NRI), and integrated discrimination improvement (IDI) analyses to determine the prognostic and discriminative utility of the pheno-group variable.

Statistical analyses for comparison of clinical data among groups, and for the association of phenotype groups with outcomes, were performed using Stata v.12 (StataCorp, College Station, TX).

Validation cohort

We performed an independent validation analysis in 107 additional HFpEF patients who were prospectively enrolled and followed for outcomes in the Northwestern HFpEF Program between January 2012 and February 2014. These additional study participants were identified in the same manner, and met the same inclusion and exclusion criteria, as the first 420 HFpEF study participants. Phenotypic data from the validation cohort was normalized entirely independently (thus avoiding any contamination from the training data [i.e., original cohort]), and patients were assigned to the original phenogroups using the predict function within mclust. We then looked to see whether there was again a difference in outcomes among the 3 groups, using the same outcomes analyses (Cox regression) as those used in the original cohort.

Supervised learning analyses for the prediction of disease outcomes

The unsupervised statistical learning analyses outlined above assume that there are naturally occurring subclasses within HFpEF that behave differently yet reproducibly across a number of populations and across varying scenarios (e.g. varying treatments, environments, etc.). Thus, the first part of our study emphasizes finding intrinsic structure within HFpEF patient phenotypic data, which can then be evaluated retrospectively and prospectively for predicting treatment outcomes and guiding clinical trial design.

One can also use the same set of phenotypic features simply to predict clinical outcome, without emphasizing any natural structure in the data (i.e., supervised learning analyses). We explored the use of support vector machines (SVM), a machine algorithm that identifies a separation boundary between classes of interest in a much higher dimensional feature space. SVM is a robust non-linear algorithm that can be used for classification or regression.¹⁷ We coded each of the cardiovascular outcomes (HF hospitalization, cardiovascular hospitalization, death, and the combined outcome of cardiovascular hospitalization or death) as binary outcomes (i.e., ignoring right-censoring), and used SVM with the 46 phenotypic predictors to predict outcome. We evaluated radial and sigmoid basis functions, tuning the values of the gamma and cost parameters using the derivation cohort, and evaluating performance on the validation cohort. Performance was evaluated using area under the receiver operating characteristic curve (AUROC), as well as mean sensitivity, mean specificity, and mean precision.

RESULTS

Characteristics of the HFpEF cohort

We prospectively enrolled 420 patients with HFpEF for our initial phenomapping analysis. Of the 420 patients, 23 had incomplete phenotypic data, including incomplete echocardiographic data. Thus, the final cohort consisted of 397 HFpEF patients. All enrolled patients were previously hospitalized for HF (though all patients were enrolled and studied in the outpatient HFpEF clinic). Similar to previous studies of HFpEF, patients were symptomatic based on NYHA functional class and had multiple comorbidities (Tables 2 and 3).^{18, 19} Several features corroborated the diagnosis of HFpEF in the study cohort: preserved LVEF, normal LV end-diastolic volume index, increased LA volume index, increased LV filling pressures (E/e′ ratio), a high frequency of moderate or greater diastolic dysfunction, and elevated BNP (Table 2).¹³ In the 216 patients who underwent invasive hemodynamic testing, mean pulmonary capillary wedge pressure was 23±9 mmHg at rest, confirming the presence of elevated LV filling pressures.

Table 2.

Objective Criteria for Heart Failure with Preserved Ejection Fraction Diagnosis in the Entire Study Cohort

Parameter	(Total N=397)
Prior hospitalization for symptomatic heart failure, n (%)	397(100)
New York Heart Association class III or IV, n(%)	190(48)
Left ventricular ejection fraction, %	61±7
Left ventricular end diastolic volume index, ml/m2	41±12
Grade 2 or 3 diastolic dysfunction, n(%)	297(75)
Left atrial volume index, ml/m2	34±14
E/e′ ratio	17±9
B-type natriuretic peptide, pg/ml*	234(86–530)
Invasive pulmonary capillary wedge pressure, mmHg (N=216)	23±9

Values expressed as mean±standard deviation unless otherwise specified

^*Median (25^th–75^th percentile)

Table 3.

Clinical and Laboratory Characteristics Stratified by Pheno-Group

Clinical characteristic	Group 1 (N=128)	Group 2 (N=120)	Group 3 (N=149)	P-value
Age, years	60.7±13.6	65.7±11.3	67.3±13.1	<0.001
Female, n(%)	86 (67)	81 (68)	82 (55)	0.049
Race, n(%)				0.32
White	72(56)	58(48)	77(52)
Black	42(33)	54(45)	56(37)
Other	14(11)	8(7)	16(11)
NYHA functional class, n(%)				0.17
I	25(20)	11(9)	13(9)
II	61(48)	40(33)	56(38)
III	38(30)	64(53)	78(52)
IV	3(2)	5(4)	2(1)
Comorbidities, n(%)
Coronary artery disease	54 (42)	58 (48)	75 (50)	0.38
Hypertension	84 (66)	108 (90)	112 (75)	<0.001
Hyperlipidemia	65 (51)	75 (62)	73 (49)	0.06
Diabetes mellitus	12 (9)	63 (52)	50 (34)	<0.001
Obesity	65 (51)	84 (70)	55 (37)	<0.001
Chronic kidney disease	8 (6)	41 (34)	79 (53)	<0.001
Atrial fibrillation	17 (13)	26 (22)	64 (43)	<0.001
Chronic obstructive pulmonary disease	43 (34)	46 (38)	56 (38)	0.70
Obstructive sleep apnea	35 (27)	60 (50)	46 (31)	<0.001
Vital signs and laboratory data
Heart rate, bpm	77.2±14.5	74.7±14.9	71.6±12.6	0.004
Systolic blood pressure, mmHg	122.4±16.6	129.2±19.0	123.0±22.7	0.011
Diastolic blood pressure, mmHg	73.3±10.2	70.1±10.2	67.3±13.6	<0.001
Pulse pressure, mmHg	49.1±12.4	59.2±16.9	55.7±19.6	<0.001
Body mass index, kg/m2	31.2±7.3	37.0±10.7	28.9±7.4	<0.001
Serum sodium, mEq/L	139.0±3.0	138.4±2.6	137.9±2.9	0.01
Blood urea nitrogen, mg/dl	13.7±4.5	24.4±11.8	33.6±19.9	<0.001
Serum creatinine, mg/dl	0.9±0.2	1.3±0.4	2.3±2.2	<0.001
Estimated GFR, ml/min/1.73m2	79.5±21.2	53.8±17.6	43.9±27.3	<0.001
Fasting glucose, mg/dl	98.4±15.6	153.2±85.2	111.5±29.2	<0.001
Hemoglobin, g/dl	12.5±1.7	11.8±1.8	11.4±1.9	<0.001
B-type natriuretic peptide, pg/ml	72(26–161)	188(83–300)	607(329–1138)	<0.001
Medications, n(%)
ACE-inhibitor or ARB	61 (48)	84 (70)	72 (48)	<0.001
β-blocker	67 (52)	89 (74)	112 (75)	<0.001
Calcium channel blocker	31 (24)	45 (38)	44 (30)	0.073
Nitrate	5 (4)	19 (16)	33 (22)	<0.001
Loop diuretic	40 (31)	82 (68)	109 (73)	<0.001
Thiazide diuretic	31 (24)	35 (29)	26 (17)	0.073
Statin	48 (38)	72 (60)	73 (49)	0.002
Aspirin	48 (38)	62 (52)	75 (50)	0.042
Heart failure duration, months	0.8 (0.4–4.3)	0.9 (0.4–16.3)	0.9 (0.4–11.7)	0.21
MAGGIC risk score	15.6±6.7	19.8±5.8	22.8±7.5	<0.001

Categorical variables are presented as counts and percentages, continuous variables are presented as mean±SD, and right skewed variables are presented as median (25^th–75^th percentile)

NYHA = New York Heart Association; GFR = glomerular filtration rate; ACE = angiotensin converting enzyme; ARB = angiotensin receptor blocker

Exploration of the continuous phenotypic variables

We first examined the phenotypes to determine the correlation among them and found that although some variables were correlated with each other, there were not tight correlations across large numbers of phenotypes. Nevertheless, as stated above, phenotypes that were correlated at r > 0.6 were filtered, leaving 46 minimally redundant phenotypes. These features were used for subsequent unsupervised and supervised learning analyses.

Heterogeneity of HFpEF

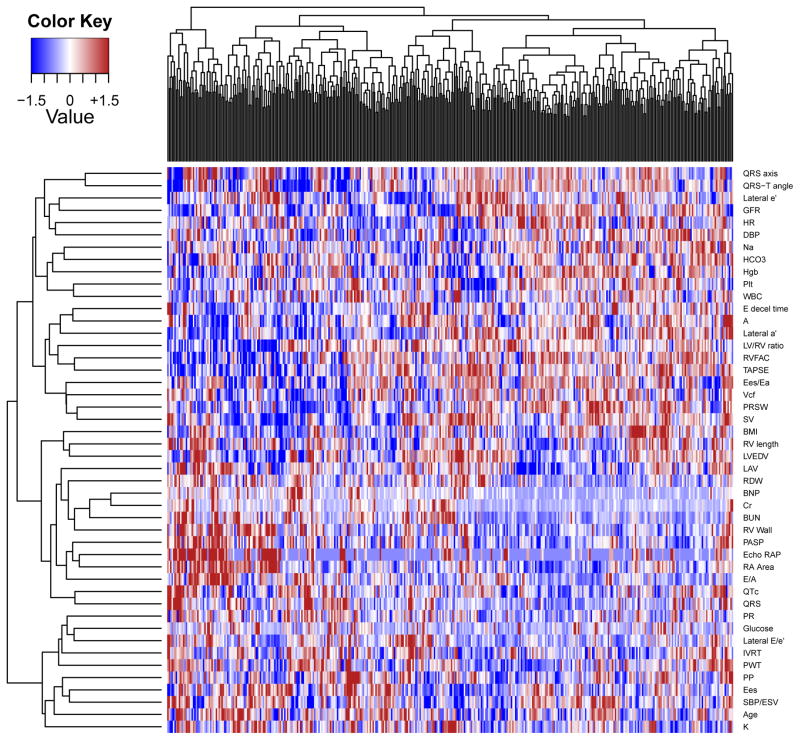
All study participants met common diagnostic criteria for HFpEF. Nonetheless, the phenotype heatmap created for HFpEF by hierarchical clustering (Figure 1) demonstrated substantial heterogeneity among study subjects. Within the heatmap, clusters of individuals with shared characteristics (“hotspots”) can be highlighted, corresponding in part to elevated activity of various pathophysiologic features such as increased right heart pressures and RV wall thickness, cardiac chamber enlargement, and elevated body size. However, these traits seemed to co-occur in varying patterns. For example, RV dilation seemed to occur in some individuals with poor renal function, in another subset with elevated right heart pressures, and in a third group with neither of the above. Unanticipated correlations between traits were also seen, such as between red cell distribution width and left atrial volume.

Figure 1.

Phenotype Heatmap (PhenoMap) of HFpEF. Columns represent individual study participants and rows represent individual phenotypes. Red = increased value of a phenotype; Blue = decreased value of a phenotype.

A parsimonious classification of HFpEF

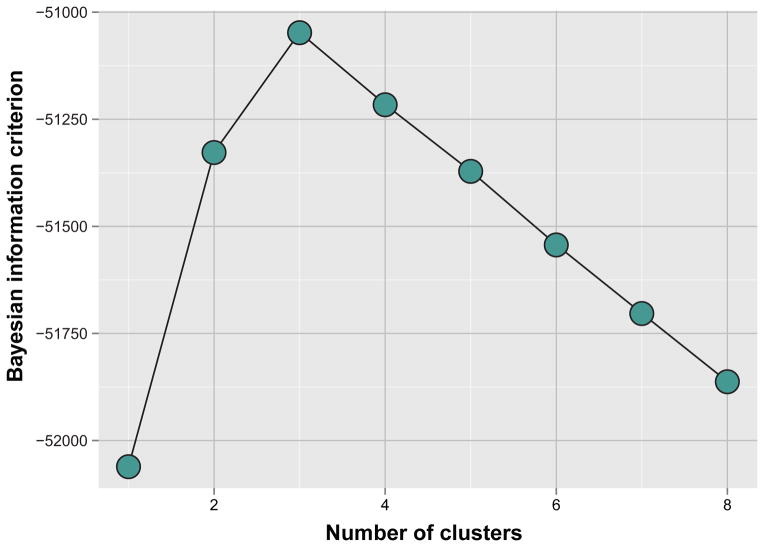
After examining the relationship between phenotypic features, our next goal was to group patients into a minimal group of clusters that accurately reflected the phenotypic variability. A variety of unsupervised learning methods can be used for this task. We elected to use model-based clustering, a method that attempts to define clusters of individuals by multivariate normal distributions of phenotypic variables.¹⁵ An important feature of this implementation of model-based clustering is the use of a penalty function to control the amount of complexity in the model – thus allowing a parsimonious description of the patients in the data set. Our analysis arrived at 3 as the optimal number of clusters (Figure 2), and allowed for some flexibility in the “shapes” of the multivariate normal distribution across clusters.

Figure 2.

Bayesian Information Criterion Analysis for the Identification of the Optimal Number of Pheno-Groups.

Comparison of clinical characteristics and laboratory, electrocardiographic, echocardiographic, and invasive hemodynamic data among pheno-groups

The 3 pheno-groups were significantly different from each other. As shown in Table 3, pheno-group #1 was younger and had lower BNP than participants in the other groups. Pheno-group #2 had the highest prevalence of obesity, diabetes, and obstructive sleep apnea and had the highest fasting glucose. Pheno-group #3 was the oldest, more likely to have chronic kidney disease (with the highest serum creatinine and lowest GFR), and had the highest BNP and MAGGIC risk score values. Table 4 displays the large variation in electrocardiographic characteristics, cardiac structure and function, and invasive hemodynamic data across the pheno-groups. Pheno-group #1 had the least electrical and myocardial remodeling and dysfunction, and the least hemodynamic derangement, although it should be noted that even within this group, 65% had at least grade 2 (moderate) diastolic dysfunction, mean PCWP was 20 mmHg, and the average invasive pulmonary artery systolic pressure was 42 mmHg. Pheno-group #2 had the worst LV relaxation (i.e., lowest e′ velocity), highest pulmonary capillary wedge pressure, and highest pulmonary vascular resistance. Finally, pheno-group #3 had the most severe electrical and myocardial remodeling with the longest QRS duration, largest QRS-T angle, highest relative wall thickness and LV mass index, highest E/e′ ratio, and worst RV function. Despite these differences between pheno-groups, HF duration was similar among the 3 groups (Table 3). On LV pressure-volume analysis, all 3 pheno-groups had similar end-systolic and end-diastolic elastances (Supplementary Table S1). However, in terms of stroke work and related phenotypes, pheno-groups #1 and #2 were similar, while pheno-group #3 was worst. Ventricular-arterial coupling was also most abnormal, and pulse pressure/stroke volume ratio highest, in pheno-group #3. In addition, despite similar end-systolic and end-diastolic elastance values among the 3 groups, RV remodeling and dysfunction were more prominent in pheno-group #3 (as shown in Table 4).

Table 4.

Electrocardiographic, Echocardiographic, and Invasive Hemodynamic Characteristics Stratified Pheno-Group

Parameter	Group 1 (N=128)	Group 2 (N=120)	Group 3 (N=149)	P-value
Electrocardiography
PR interval, ms	166.6±29.6	174.2±29.8	183.3±53.5	0.007
QRS duration, ms	93.8±21.0	91.3±13.6	112.7±33.3	<0.001
QTc interval, ms	450.6±35.2	449.8±34.0	464.6±48.9	0.005
QRS axis, degrees	10.7±39.0	20.4±38.4	−4.2±60.7	<0.001
QRS-T angle, degrees	42.6±41.7	53.4±44.0	86.6±54.0	<0.001
Echocardiography
LV end-diastolic volume, ml	81.2±23.4	84.2±24.0	84.6±32.3	0.56
LV end-systolic volume, ml	31.6±12.1	33.1±12.1	35.4±19.2	0.12
Relative wall thickness	0.47±0.11	0.49±0.09	0.56±0.20	<0.001
LV mass index, g/m2	89.1±22.6	96.4±26.3	122.0±47.3	<0.001
Left atrial volume index, ml/m2	29.1±11.1	31.5±10.6	40.9±16.7	<0.001
LV ejection fraction, %	61.8±5.6	61.2±6.5	60.0±7.1	0.05
Stroke volume, ml	84.8±22.9	88.6±32.0	80.7±31.3	0.09
Cardiac output, L/min/m2	6.5±2.0	6.6±2.5	5.8±2.6	0.006
Pulmonary artery systolic pressure, mmHg	35.3±9.7	43.5±14.6	51.2±16.3	<0.001
Right atrial pressure, mmHg	6.0±2.7	6.9±3.5	9.8±4.7	<0.001
E velocity, cm/s	93.2±28.6	103.2±34.5	118.2±40.9	<0.001
A velocity, cm/s	82.8±22.5	93.1±26.3	81.6±38.7	0.01
E/A ratio	1.2±0.5	1.1±0.4	1.7±1.0	<0.001
Tissue Doppler e′ velocity, cm/s	9.3±3.2	7.5±2.1	7.9±3.4	<0.001
E/e′ ratio	11.2±3.7	15.2±6.4	18.6±10.6	<0.001
Diastolic dysfunction grade, n (%)				<0.001
Normal diastolic function	21 (16)	9 (8)	2 (1)
Grade I (mild) diastolic dysfunction	15 (12)	16 (13)	12 (8)
Grade II (moderate) diastolic dysfunction	60 (47)	56 (47)	43 (29)
Grade III (severe) diastolic dysfunction	23 (18)	31 (26)	83 (56)
Indeterminate diastolic function	9 (7)	8 (7)	9 (6)
RV basal diameter, cm	3.6±0.6	3.8±0.5	4.2±0.8	<0.001
RV end-diastolic area index, cm/m2	12.4±2.1	12.7±2.4	16.2±4.7	<0.001
RV end-systolic area index, cm/m2	6.7±1.5	7.2±1.5	9.9±3.4	<0.001
RV wall thickness, cm	0.46±0.03	0.50±0.07	0.56±0.11	<0.001
RV fractional area change	0.46±0.06	0.43±0.05	0.40±0.08	<0.001
TAPSE, cm	2.2±0.6	2.1±0.6	1.7±0.6	<0.001
Invasive hemodynamics (N=216)
Right atrial pressure, mmHg	10.5±4.6	15.3±6.5	14.6±6.8	<0.001
Pulmonary artery systolic pressure, mmHg	42.4±12.0	55.9±15.4	56.7±19.7	<0.001
Pulmonary artery diastolic pressure, mmHg	21.7±6.3	28.2±7.7	26.5±9.1	<0.001
Mean pulmonary artery pressure, mmHg	28.8±7.7	35.9±9.9	36.6±11.7	<0.001
Pulmonary capillary wedge pressure, mmHg	19.9±6.3	24.6±8.3	23.7±9.7	0.002
Pulmonary vascular resistance, Wood units	1.2±2.5	2.8±4.6	2.3±3.7	0.043
Cardiac output, L/min	6.1±2.1	6.5±2.1	5.8±2.3	0.15

Continuous variables are presented as mean±SD; LV=left ventricular; RV=right ventricular; TAPSE = tricuspid annular plane systolic excursion

Association of pheno-groups with adverse outcomes

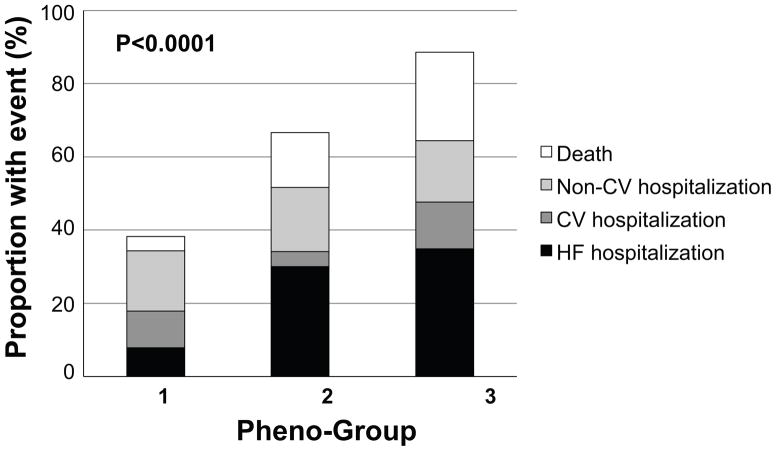
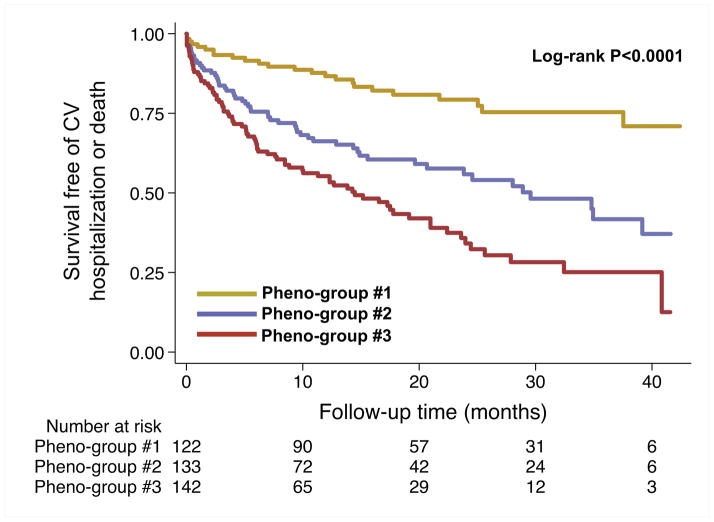
In order to provide external clinical validity of our phenomapping techniques, we studied the relationship between the pheno-groups and adverse outcomes. As shown in Table 5 and Figures 3 and 4, outcomes varied significantly by pheno-group, with a step-wise increase in risk profile going from lowest risk (pheno-group #1) to highest risk (pheno-group #3). Pheno-group #3 in particular represented a high-risk subset, independent of BNP (known to be one of the most potent risk markers in HF) and the MAGGIC HF risk score, which comprises 13 traditional clinical parameters. Table 6 shows that the phenomapping technique created pheno-groups with differential risk profiles that provided better discrimination compared to clinical parameters (i.e., the MAGGIC risk score) and BNP. Based on the IDI, NRI, and likelihood ratio tests, the pheno-group assignment provided prognostic information above and beyond traditional clinical variables. In addition, the association between pheno-group membership and outcomes persisted after adjustment for HF duration.

Table 5.

Association of Pheno-Groups with Adverse Outcomes on Cox Proportional Hazards Analysis

	Group 1 (N=128)	Group 2 (N=120)	Group 3 (N=149)	P-value
Outcome, n(%)
CV hospitalization	22 (17)	41 (34)	71 (48)	<0.001
HF hospitalization	10 (8)	36 (30)	52 (35)	<0.001
Death	5 (4)	18 (15)	36 (24)	<0.001
Combined endpoint	23 (18)	54 (45)	84 (56)	<0.001
Unadjusted, HR (95% CI)
CV hospitalization	1.0	2.4 (1.4–4.1)***	3.9 (2.4–6.3)***	—
HF hospitalization	1.0	4.8 (2.4–9.6)***	5.7 (2.9–11.3)***	—
Death	1.0	4.0 (1.5–10.9)**	6.5 (2.5–16.6)***	—
Combined endpoint	1.0	3.0 (1.9–5.0)***	4.4 (2.8–7.0)***	—
Model 1, HR (95% CI)
CV hospitalization	1.0	2.4 (1.4–4.2)***	4.0 (2.3–6.8)***	—
HF hospitalization	1.0	4.9 (2.3–10.1)	5.7 (2.7–11.8)**	—
Death	1.0	3.0 (1.1–8.4)*	4.0 (1.5–10.6)**	—
Combined endpoint	1.0	2.9 (1.7–4.8)***	4.1 (2.5–6.8)***	—
Model 2, HR (95% CI)
CV hospitalization	1.0	2.1 (1.2–3.6)**	2.9 (1.7–5.1)***	—
HF hospitalization	1.0	4.1 (1.9–8.6)***	4.2 (2.0–9.1)***	—
Death	1.0	2.2 (0.8–6.0)	1.7 (0.6–4.9)	—
Combined endpoint	1.0	2.4 (1.4–3.9)***	2.8 (1.6–4.8)***	—

^**≤0.01;

^***≤0.001

Model 1 = Pheno-groups + BNP; Model 2 = Pheno-groups + BNP + MAGGIC risk score

The MAGGIC risk score includes the following variables: age, ejection fraction, creatinine, diabetes, chronic obstructive pulmonary disease, systolic blood pressure, body-mass index, heart rate, New York Heart Association class, ACE-inhibitor use, beta-blocker use, heart failure duration, and current smoker.

Figure 3.

Outcomes by HFpEF Pheno-Group. Stacked bar graph of outcomes shows the step-wise increase in adverse events from pheno-group #1 to pheno-group #3.

Figure 4.

Survival Free of Cardiovascular Hospitalization or Death, Stratified by Pheno-Group. Kaplan-Meier curves for the combined outcome of heart failure hospitalization, cardiovascular hospitalization, or death, stratified by pheno-group. CV = cardiovascular.

Table 6.

Comparison of Risk Prediction Models With and Without Pheno-Groups for the Combined Outcome of Heart Failure Hospitalization, Cardiovascular Hospitalization, or Death in Heart Failure with Preserved Ejection Fraction

	HF hospitalization		CV hospitalization		HF hospitalization, CV hospitalization, or death
	Base model*	Base model+ Pheno-group variable	Base model*	Base model+ Pheno-group variable	Base model*	Base model+ Pheno-group variable
Discrimination
C-statistic	0.64	0.68	0.62	0.66	0.64	0.67
Absolute IDI (95% CI)	0.046 (0.026–0.066); P<0.001		0.038 (0.018–0.058); P<0.001		0.040 (0.020–0.060); P<0.001
Relative IDI	57%		100%		40%
Category-free NRI Index statistic (95% CI)	0.55 (0.37–0.73); P<0.001		0.31 (0.10–0.52); P=0.003		0.41 (0.22–0.61); P<0.001
Calibration
LR test, p-value	<0.001		<0.001		<0.001
Bayes information criterion	1022.54	1013.46	1357.50	1353.75	1564.94	1559.45

^*Base model = MAGGIC risk score + BNP (the MAGGIC risk score includes the following variables: age, ejection fraction, creatinine, diabetes, chronic obstructive pulmonary disease, systolic blood pressure, body-mass index, heart rate, New York Heart Association functional class, ACE-inhibitor use, beta-blocker use, heart failure duration, and current smoker)

IDI = integrated discrimination index; NRI = net reclassification improvement; BNP = B-type natriuretic peptide; MAGGIC = Meta-Analysis Global Group in Chronic heart failure risk score

Validation of the phenomapping analyses

In order to validate our phenomapping results, we prospectively enrolled an additional 107 patients in the HFpEF program. For the most part, these 107 new HFpEF participants had clinical, laboratory, and echocardiographic characteristics that were similar to the original HFpEF cohort (Supplementary Tables S2 and S3). There were less African Americans, less chronic obstructive pulmonary disease, less thiazide diuretic use, and worse RV fractional area change in the validation cohort; however, there were no differences in age, sex, NYHA functional class, LVEF, LV mass index, diastolic function grade, or E/e′ ratio between the original and validation cohorts. Using model-based clustering, each of the HFpEF validation cohort participants was successfully matched to 1 of the 3 previously defined pheno-groups (37/107 [34.6%] in pheno-group #1; 29/107 [27.1%] in pheno-group #2; and 41/107 [38.3%] in pheno-group #3).

Pheno-group membership in the validation cohort was independently associated with adverse outcomes, with a step-wise increase in risk profile going from lowest risk pheno-group (#1) to highest risk pheno-group (#3) (Supplementary Table S4). Pheno-group #3 in the validation cohort, as in the original cohort, was associated with adverse outcomes independent of BNP and the MAGGIC HF risk score with hazard ratios comparable to the training cohort (for the combined end-point of cardiovascular hospitalization, HF hospitalization, or death: unadjusted HR 3.6, 95% CI 1.6–8.4, P=0.003); adjusted HR 3.3, 95% CI 1.1–9.5, P=0.026).

Supervised learning analysis

After tuning SVM analyses to build optimal models for predicting a combined outcome of death and cardiovascular hospitalization (which includes HF hospitalization), and also for individual outcomes, we found that model performance was typically good, with AUROC values ranging from 0.70–0.76 in the validation cohort (Supplementary Table S5).

DISCUSSION

In a cohort of 397 patients with documented HFpEF, along with a validation cohort of 107 independent HFpEF patients, we have shown the feasibility and clinical validity of a novel classification technique for HFpEF, a heterogeneous clinical syndrome. Taking techniques commonly used for the analysis of gene expression data,²⁰ and applying these to dense phenotypic data, we were able to show the following: (1) HFpEF truly is a heterogeneous disorder; (2) despite the heterogeneity of HFpEF, phenomapping analysis of HFpEF patients produces mutually exclusive groups of individuals with related comorbidities and pathophysiologies; and (3) the identified pheno-groups have differential outcomes indicating differing risk profiles and clinical trajectories. To our knowledge, our study provides the first description of phenomapping for the novel classification of a cardiovascular disorder, and it is the first study that applies machine learning techniques to resolve heterogeneity in a cardiovascular syndrome using dense phenotypic data.

Using a variety of algorithms, we were able to take advantage of the deep phenotyping in our HFpEF cohort and find unique patterns of association among phenotypic variables, which allowed for a novel, unique grouping of study participants. Although all patients met established criteria for HFpEF, the PhenoMap (Figure 1) clearly demonstrates that HFpEF is a heterogeneous syndrome. Modern visualization methods provide a complete and striking depiction of the high variability of HFpEF that is clinically apparent when caring for these patients.

The robust assignment of group membership (i.e., clustering of HFpEF patients into categories) was possible due to our use of penalized machine learning techniques such as model-based clustering, which in turn are based on the solid foundation of parametric estimates of clustering individuals and regularization via the Bayesian information criterion (as shown in Figure 2). Thus, it appears that given this diverse collection of phenotypic variables, 3 mutually exclusive pheno-groups represents an optimal number for HFpEF.

Once the 3 pheno-groups were identified, the differences among them (as shown in Tables 3 and 4) were striking. Study participants within the 3 pheno-groups, despite having shared diagnostic features of HFpEF, differed markedly on almost every characteristic. From these analyses it became clear that the 3 pheno-groups represent 3 archetypes of HFpEF: (1) younger patients with moderate diastolic dysfunction who have relatively normal BNP; (2) obese, diabetic patients with a high prevalence of obstructive sleep apnea who have the worst LV relaxation; and (3) older patients with significant chronic kidney disease, electrical and myocardial remodeling, pulmonary hypertension, and RV dysfunction.

As an independent measure of the distinctness of our classification, we undertook clinical validation through the association of pheno-groups with adverse outcomes, which showed the robust ability of pheno-group membership (derived from unsupervised statistical learning analyses) as a method for risk stratification in HFpEF participants. In addition, we show that supervised learning analyses such as SVM can be applied to a rich dataset of quantitative phenotypic data for risk stratification in HFpEF. However, it is essential to note that while we were able to show that pheno-group membership was an important, independent predictor of differential outcomes, the aim of our study was not to create a new method for risk stratification. HFpEF risk prediction techniques, such as the MAGGIC risk score,¹⁶ are already available. Instead, the primary goal of our study was to show that using an unbiased approach allows for the clustering of patients into distinct, mutually exclusive groups that could be used to target specific therapies in the clinic and in clinical trials. It is for these same reasons that we chose to employ unsupervised machine learning algorithms (instead of supervised learning algorithms). Although methods such as neural networks and support vector machines,⁶ can be tremendously powerful for risk stratification, our emphasis was on highlighting distinct prototypes of HFpEF, which may be driven by fundamentally different underlying pathophysiologic mechanisms and thus have distinct responses in clinical trials. Moreover, the growing success of “deep learning” algorithms²¹ has demonstrated that pre-training with unsupervised learning approaches, as we have done, can be an effective means of higher order feature extraction and can markedly improve the performance of subsequent supervised approaches.⁵

Our study has several important ramifications for the study of HFpEF and the design of future HFpEF clinical trials. While epidemiologic studies and observational registries of HFpEF have enrolled a wide variety of patients with varying etiology and pathophysiology, detailed mechanistic studies of HFpEF often only enroll very specific subsets of patients with a “pure phenotype”, therefore limiting their generalizability to the larger population of HFpEF patients. For example, in a pathophysiologic study of HFpEF,²² Prasad and colleagues began with 1119 patients hospitalized for HF with EF > 50%. After applying their exclusion criteria, which included common HFpEF comorbidities such as atrial fibrillation, chronic kidney disease, myocardial infarction, and cognitive impairment, only 23 (2%) of patients remained eligible for their study.²² Thus, the pathophysiologic studies that have concluded that HFpEF is mainly a disease of diastolic dysfunction have been challenged,²³ and several studies have now shown that HFpEF is quite heterogeneous from both an etiologic and pathophysiologic standpoint.^{4, 24–26} Our study confirms the heterogeneity of HFpEF in an unselected group of high-risk, previously hospitalized HFpEF patients.

With the advent of sophisticated phenotyping tools ranging from a multitude of biomarkers to comprehensive cardiovascular imaging modalities to environmental characterization and activity monitoring, the era of “deep phenotyping” is now available to improve characterization of heterogeneous syndromes like HFpEF. Here we have shown that combined with machine learning algorithms to find patterns in dense, multi-dimensional data, novel phenotypic characterization of HFpEF is possible. Future clinical trials can harness these advances in phenotypic categorization by deep phenotyping of study participants using banked blood and cardiac imaging (such as comprehensive echocardiography), along with other tools (e.g., quality of life measures, exercise tests, etc.) as needed, which will allow for the development of phenotype heatmaps. These analyses can then be used in the clinical trial setting to determine whether certain groups of patients are more responsive to the investigational drug or device compared to other types of patients, thereby leading to improved future clinical trials and/or “theranostics”, a combined diagnostic and therapeutic treatment strategy.

Strengths and Limitations

Our study has several strengths, including the inclusion of a large, well-phenotyped HFpEF cohort; unselected, high-risk patients recruited and studied in the outpatient setting after hospitalization for HF; novel analytic techniques that utilized robust machine learning analyses with regularization; and validation of our findings in an independent HFpEF sample. Our study is also the first study to demonstrate the feasibility and utility of “phenomapping” for the unbiased categorization of a cardiovascular disorder. The prospective nature of our study, and the ascertainment of outcome data, allowed us to determine the clinical utility of the phenomapping technique in predicting differential risk of the study participants. Finally, although we enrolled a primarily urban population of patients who were previously hospitalized for HF, we enrolled a larger proportion of African Americans compared to other HFpEF studies, and the inclusion of patients previously hospitalized for HFpEF allowed us to study the highest risk patients and those most likely to be enrolled in clinical trials.

Although we were able to provide validation of the phenomapping technique via (1) demonstration of the prognostic utility of the pheno-grouping; and (2) successful validation of our findings in a separate, independent sample of HFpEF patients at Northwestern University, a potential limitation of our study is the lack of validation in a truly external cohort. Future studies that replicate our techniques in external HFpEF cohorts (i.e., in other institutions, hospitals, or multi-center studies) will be important to further demonstrate generalizability.

Conclusions

This is the first study to conduct high-density phenotypic classification (i.e., phenomapping) of a clinical cardiovascular syndrome. We have shown that unbiased cluster analysis of dense phenotypic data from multiple domains is feasible and can result in meaningful, clinically relevant categories of HFpEF patients, with significant differences in underlying etiology/pathophysiology and differential risk of adverse outcomes. Given the heterogeneous nature of HFpEF, phenomapping could be helpful for improved classification and categorization of HFpEF patients, and may lead to development of novel targeted therapies. Furthermore, phenomapping could help inform the design and conduct of future clinical trials and may be used to identify responders to therapies, thereby improving the unacceptably poor track record of HFpEF clinical trials.