Abstract
Cells moving collectively in tissues constitute a form of active matter, in which collective motion depends strongly on driven fluctuations at the single-cell scale. Fluctuations in cell area and number density are often seen in monolayers, yet their role in collective migration is not known. Here we study density fluctuations at the single- and multicell level, finding that single-cell volumes oscillate with a timescale of 4 h and an amplitude of 20%; the timescale and amplitude are found to depend on cytoskeletal activity. At the multicellular scale, density fluctuations violate the central limit theorem, highlighting the role of nonequilibrium driving forces in multicellular density fluctuations.
Main Text
Collective cell motion is essential to tissue development, health, disease, and repair (1–3). To explore the driving forces of cell motion in tissues, monolayers are often investigated (4–7). Motion in monolayers depends strongly on cell number density, and exhibits phase transitions as cell density rises (8–12). Theories of phase transitions and the statistical physics of active matter, including cells, have been investigated thoroughly, and often density fluctuations are strongly coupled to collective motion (13–15). A careful look at published snapshots and videos of cell monolayers reveals large variations in cell area and density fluctuations (6,7,16). However, these fluctuations in cell density and size have not been explored, limiting our understanding of the relationship between single-cell dynamics and collective cell motion.
Here we investigate fluctuations of cell size and spatial distribution in Madin Darby canine kidney (MDCK) cell monolayers. We find that cell volumes fluctuate by ±20%, oscillating with a timescale of 4 h. The cytoskeleton’s role is observed by inhibiting Myosin II with blebbistatin, which substantially reduces volume fluctuations and increases the oscillation time. We also observe large-scale density fluctuations that violate the central limit theorem, which has not yet been reported in monolayers of cells that form strong cell-cell junctions (17). Estimates of cell permeability show that cell volume fluctuations may involve fluid transport between cells through gap junctions or across the cell membrane. These results suggest that fluid transport associated with cell volume fluctuations may contribute to collective motion in monolayers and tissues.
Projected area fluctuations
We explore fluctuations in the projected area of MDCK cells with time-lapse microscopy. Monolayers are grown in standard culture conditions described in the Supporting Material. Imaging is performed with an incubation chamber mounted on an inverted microscope. Cell density is visibly heterogeneous in space and time; snapshots show large spatial variations in cell density and manual cell tracking shows large cell size fluctuations in time (Fig. 1, A–D).
Figure 1.
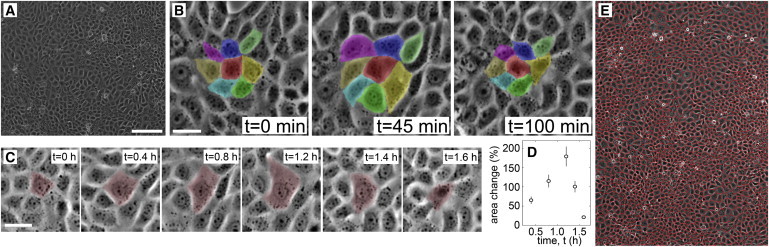
(A) Monolayers have large spatial variations in projected cell area; 150-μm scale bar. (B) Cell groups fluctuate together in time. Each color marks the same cell at different times; 30-μm scale bar. (C and D) Single cells can fluctuate by ∼200% relative to their minimum area; 30-μm scale bar. (E) Cell areas are measured with a Voronoi tessellation based on nucleus locations. To see this figure in color, go online.
To measure area fluctuations in large numbers, phase contrast images are thresholded to identify cell boundaries. The position and projected area of each cell is determined by its boundary, and cells are followed in time with tracking software (18). Large fluctuations can be directly seen in cell area traces over time and in time-lapse video (see Fig. S2 and Movie S1). The standard deviation in time of area fluctuations about the mean, averaged over all tracked cells, shows that the typical cell area fluctuates ±20.7% with a standard error of 0.4% (N = 323).
To check this result, the nuclei of MDCK cells expressing fluorescent histones are tracked, and a Voronoi tessellation is performed. Approximating each cell area with the area of its Voronoi cell, we find fluctuations of ±17.5% with a standard error of 0.2% (N = 1038). A reduced fluctuation is expected for Voronoi cells because Voronoi analysis cannot detect shape changes at cell boundaries. In both cases, treatment with 100 μM blebbistatin, a Myosin II inhibitor, reduces fluctuations by ∼50%; in phase-contrast analysis, the fluctuations are 10.1 ± 0.2% (N = 1015) and in Voronoi analysis, they are 9.4 ± 0.2% (N = 1014). Replacing blebbistatin with standard growth media yields a recovery of fluctuations within 2 h. These results suggest that the cytoskeleton drives cell area fluctuations, although other cytoskeletal treatments like Rac1 inhibition or actin depolymerization with cytochalasin will further reveal underlying mechanisms.
Thickness and tilt fluctuations
To test whether cells fluctuate in thickness, we perform confocal microscopy measurements, collecting stacks over time. Cells are fluorescently dyed with 5-chloromethyl-fluorescein diacetate, which permeates the cytosol. At each instant in time, the monolayer appears flat. We measure the monolayer thickness by fitting an error function to intensity profiles along the z axis. We use the midpoint of the intensity drop to identify the apical side of the cell, locally, at 1000 random XY locations over an area of 160 × 160 μm, covering ∼64 cells. The basal location is chosen to be the lowest focal plane in which cell cross-sections are observed, which is constant. We find that the layer is 7.1 ± 0.7 μm thick, averaged over space and time (mean ± standard deviation). To assess how local heights vary in time, we compute a temporal standard deviation of local height and average over all locations in space, yielding a mean fluctuation of 4.8% with a spatial variation of 2.0%. Thus, cell thickness fluctuates by ∼340 nm in time. The 95% confidence intervals of the intensity profile fits are ∼300 nm, so these fluctuations may be experimental uncertainty limited by sampling frequency along the z axis. We find the same instantaneous spatial variation in height, 4.7%, which varies in time by 1.1%. (Fig. 2, A–E).
Figure 2.
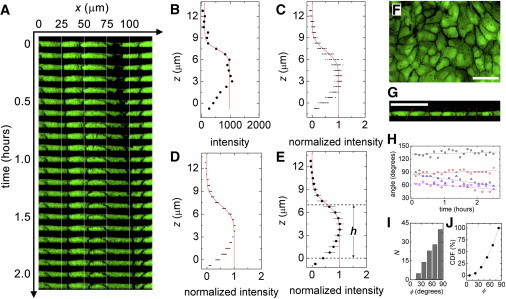
(A) XZ slices appear flat and boundary angles are steady during motion. (B) Intensity traces along the z axis are fit at 1000 locations over 2.4 h (one location and time shown; red line, fit). (C) The overlay of intensity at one location over time shows small variations. (D) The overlay of the space-averaged traces also shows small variations. (E) Layer thickness averaged over space and time is 7.1 ± 0.7 μm. (F) Z projections show clear boundaries. (G) Boundary angles are determined from XZ slices. (H) Boundaries maintain constant orientation (each dataset is for a different boundary). (I and J) Angle histogram and cumulative distribution function show that 73% of cell boundaries are oriented within 45° of vertical. (Scale bars = 50 μm; all XZ plots have the same scale along both directions.) To see this figure in color, go online.
The cell-cell interface is not perfectly vertical, so we explore interfacial orientation fluctuations. Z projections of confocal stacks show clear boundaries, suggesting that a substantial fraction of cell-cell interfaces is nearly vertical. We determine the orientation of interfaces from XZ slices, when clear boundaries are observed, using IMAGEJ software (N = 110; National Institutes of Health, Bethesda, MD). The histogram of angles is peaked at the vertical orientation, and the cumulative distribution function shows that >73% of interfaces are within 45° of vertical; 50% of cells are within 30° of vertical. We estimate the error in assuming vertical walls treating the real cell as a conical cross section, and the approximate cell as a cylinder with a radius equal to that of the midplane of the conical cell. The average cell is 7-μm thick with a diameter of ∼30 μm; assuming a 30° tilt, the error in volume is ∼2%. We also observe that the orientation of cell boundaries remains relatively constant in time (Fig. 2).
Volume fluctuations in time and space
For cells to conserve volume as they fluctuate in area, they would have to expand in height by 20%. Given the small height and tilt variations observed here, volume fluctuations may be approximated by area fluctuations, δV ≈ δA. Simultaneous measurements of cell volume, area, and thickness also support the validity of this approximation (see the Supporting Material). To characterize how cell volumes fluctuate in time, we compute a volume autocorrelation function, CδV-δV, correlating the approximate volume fluctuations, δV. We find that CδV-δV has a strong negative minimum at τ = 2 h, showing that cell volume oscillates about its mean with a timescale of 4 h. Reducing cytoskeletal contractions with blebbistatin shifts the peak in CδV-δV to 3 h, corresponding to a 6 h oscillation. The autospectral density function of volume fluctuations, S(ω), exhibits peaks corresponding to these oscillation times (Fig. 3 A).
Figure 3.
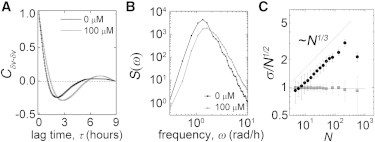
(A and B) Volume autocorrelation and autospectral density functions show that cell volume oscillates with a period sensitive to blebbistatin treatment. (C) Cell density fluctuations in monolayers violate the central limit theorem (solid circles, cells; shaded squares, random particle).
Cell volume fluctuations may be linked to the large-scale spatial variations in density seen in monolayers. Frequently seen in active matter systems, the central limit theorem (CLT) is violated (14,15,19). Randomly fluctuating equilibrium variables obey the CLT; in regions containing N particles on average, the number of particles fluctuates like σ ∼ N1/2, where σ is the standard deviation of particle number. The CLT is tested by dividing large systems into smaller subsystems, counting particles, and computing σ and N over the different subsystems. We test for a CLT violation by identifying all fluorescent nuclei within our field of view, as described above, averaging over 100 frames and roughly 2000 cells in each frame. A plot of σ/N1/2 demonstrates that cell density fluctuations violate the CLT, with σ ∼ N5/6. To ensure that this result is not due to small sample size, we repeat the calculation on 2000 randomly distributed particles 100 different times, finding no CLT violation.
Conclusions
The volume fluctuations observed here require water transport in and out of the cell. Isolated cells under isotonic conditions maintain a constant volume by regulating their osmotic pressure with ion pumps (20). However, volume regulation in monolayers may differ from the single-cell case, and long timescale reversals of ion transport could drive water in and out of the cell, generating volume changes under isotonic conditions. Typical timescales of volume recovery in response to osmotic pressure, combined with estimates of the hydraulic permeability of single cells, suggest that this mechanism could drive the volume fluctuations observed here (see the Supporting Material).
Another way that cells may change volume is by exchanging fluid with their neighbors through gap junctions. We estimate a cell-cell permeability based on the size and number of gap junctions in MDCK cells, and find that a cell could expel 20% of its own volume in 2 h by generating 1.1 kPa of excess pressure, relative to its neighbors. Comparable levels of spatial variability in cytoskeleton-generated normal stress have been measured in epithelial, endothelial, and cancer cell layers (7). Thus, it is possible that cell volume fluctuations involve cytoskeleton-driven fluid transport though gap junctions. Further estimates of potential permeability limitations of the cytoskeleton itself suggest that the cytoskeletal mesh may not inhibit this very slow flow (see the Supporting Material).
In future work we will manipulate gap junctions and ion channels to explore their relative roles in water transport-associated cell volume fluctuations. Further studies on the relationship between single-cell volume fluctuations and multicellular CLT violations will elucidate the microscopic origins of collective cell migration patterns. Studies of the interplay between contractile cell-generated tension and stress relaxation associated with cell motion or cell division are at the forefront of our growing understanding of collective cell motion. Further exploration of cell volume fluctuations may help to inform discovery in this developing area of research.
Acknowledgments
This project was funded by National Science Foundation grant No. CMMI-1161967.
Supporting Material
Supporting Citations
References (21–39) appear in the Supporting Material.
References
- 1.Friedl P., Gilmour D. Collective cell migration in morphogenesis, regeneration and cancer. Nat. Rev. Mol. Cell Biol. 2009;10:445–457. doi: 10.1038/nrm2720. [DOI] [PubMed] [Google Scholar]
- 2.Rørth P. Collective cell migration. Annu. Rev. Cell Dev. Biol. 2009;25:407–429. doi: 10.1146/annurev.cellbio.042308.113231. [DOI] [PubMed] [Google Scholar]
- 3.Ranft J., Basan M., Jülicher F. Fluidization of tissues by cell division and apoptosis. Proc. Natl. Acad. Sci. USA. 2010;107:20863–20868. doi: 10.1073/pnas.1011086107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Trepat X., Wasserman M.R., Fredberg J.J. Physical forces during collective cell migration. Nat. Phys. 2009;5:426–430. [Google Scholar]
- 5.Poujade M., Grasland-Mongrain E., Silberzan P. Collective migration of an epithelial monolayer in response to a model wound. Proc. Natl. Acad. Sci. USA. 2007;104:15988–15993. doi: 10.1073/pnas.0705062104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Puliafito A., Hufnagel L., Shraiman B.I. Collective and single cell behavior in epithelial contact inhibition. Proc. Natl. Acad. Sci. USA. 2012;109:739–744. doi: 10.1073/pnas.1007809109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tambe D.T., Hardin C.C., Trepat X. Collective cell guidance by cooperative intercellular forces. Nat. Mater. 2011;10:469–475. doi: 10.1038/nmat3025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Vedula S.R.K., Leong M.C., Ladoux B. Emerging modes of collective cell migration induced by geometrical constraints. Proc. Natl. Acad. Sci. USA. 2012;109:12974–12979. doi: 10.1073/pnas.1119313109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Szabó B., Szöllösi G.J., Vicsek T. Phase transition in the collective migration of tissue cells: experiment and model. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2006;74:061908. doi: 10.1103/PhysRevE.74.061908. [DOI] [PubMed] [Google Scholar]
- 10.Szabó A., Ünnep R., Czirók A. Collective cell motion in endothelial monolayers. Phys. Biol. 2010;7:046007. doi: 10.1088/1478-3975/7/4/046007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Angelini T.E., Hannezo E., Weitz D.A. Glass-like dynamics of collective cell migration. Proc. Natl. Acad. Sci. USA. 2011;108:4714–4719. doi: 10.1073/pnas.1010059108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Vedel S., Tay S., Quake S.R. Migration of cells in a social context. Proc. Natl. Acad. Sci. USA. 2013;110:129–134. doi: 10.1073/pnas.1204291110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Toner J., Tu Y., Ramaswamy S. Hydrodynamics and phases of flocks. Ann. Phys. 2005;318:170–244. [Google Scholar]
- 14.Ramaswamy S. The mechanics and statistics of active matter. Annu. Rev. Condens. Matter Phys. 2010;1:323–345. [Google Scholar]
- 15.Marchetti M., Joanny J., Simha R.A. Hydrodynamics of soft active matter. Rev. Mod. Phys. 2013;85:1143. [Google Scholar]
- 16.Serra-Picamal X., Conte V., Trepat X. Mechanical waves during tissue expansion. Nat. Phys. 2012;8:628–634. [Google Scholar]
- 17.Duclos G., Garcia S., Silberzan P. Perfect nematic order in confined monolayers of spindle-shaped cells. Soft Matter. 2014;10:2346–2353. doi: 10.1039/c3sm52323c. [DOI] [PubMed] [Google Scholar]
- 18.Crocker J.C., Grier D.G. Methods of digital video microscopy for colloidal studies. J. Colloid Interface Sci. 1996;179:298–310. [Google Scholar]
- 19.Narayan V., Ramaswamy S., Menon N. Long-lived giant number fluctuations in a swarming granular nematic. Science. 2007;317:105–108. doi: 10.1126/science.1140414. [DOI] [PubMed] [Google Scholar]
- 20.Hoffmann E.K., Simonsen L.O. Membrane mechanisms in volume and pH regulation in vertebrate cells. Physiol. Rev. 1989;69:315–382. doi: 10.1152/physrev.1989.69.2.315. [DOI] [PubMed] [Google Scholar]
- 21.Henkes S., Fily Y., Marchetti M.C. Active jamming: self-propelled soft particles at high density. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2011;84:040301. doi: 10.1103/PhysRevE.84.040301. [DOI] [PubMed] [Google Scholar]
- 22.Deforet M., Parrini M.C., Silberzan P. Automated velocity mapping of migrating cell populations (AVeMap) Nat. Methods. 2012;9:1081–1083. doi: 10.1038/nmeth.2209. [DOI] [PubMed] [Google Scholar]
- 23.Schaller V., Bausch A.R. Topological defects and density fluctuations in collectively moving systems. Proc. Natl. Acad. Sci. USA. 2013;110:4488–4493. [Google Scholar]
- 24.Dermietzel R., Spray D.C. Gap junctions in the brain: where, what type, how many and why? Trends Neurosci. 1993;16:186–192. doi: 10.1016/0166-2236(93)90151-b. [DOI] [PubMed] [Google Scholar]
- 25.Evans W.H., Martin P.E. Gap junctions: structure and function (Review) Mol. Membr. Biol. 2002;19:121–136. doi: 10.1080/09687680210139839. [DOI] [PubMed] [Google Scholar]
- 26.Meyer D.J., Yancey S.B., Revel J.P. Intercellular communication in normal and regenerating rat liver: a quantitative analysis. J. Cell Biol. 1981;91:505–523. doi: 10.1083/jcb.91.2.505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Caspar D.L.D., Goodenough D.A., Phillips W.C. Gap junction structures. I. Correlated electron microscopy and x-ray diffraction. J. Cell Biol. 1977;74:605–628. doi: 10.1083/jcb.74.2.605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bennett M.V., Verselis V.K. Biophysics of gap junctions. Semin. Cell Biol. 1992;3:29–47. doi: 10.1016/s1043-4682(10)80006-6. [DOI] [PubMed] [Google Scholar]
- 29.Giaume C., Sahuquillo C., Korn H. Evidence for ionic coupling between MDCK cells at non-confluent and confluent stages of culture. Biol. Cell. 1986;57:33–38. doi: 10.1111/j.1768-322x.1986.tb00462.x. [DOI] [PubMed] [Google Scholar]
- 30.Discher D.E., Janmey P., Wang Y.L. Tissue cells feel and respond to the stiffness of their substrate. Science. 2005;310:1139–1143. doi: 10.1126/science.1116995. [DOI] [PubMed] [Google Scholar]
- 31.Larsen W.J. Structural diversity of gap junctions. A review. Tissue Cell. 1977;9:373–394. doi: 10.1016/0040-8166(77)90001-5. [DOI] [PubMed] [Google Scholar]
- 32.Dullien F.A. Academic Press; New York: 1991. Porous Media: Fluid Transport and Pore Structure. [Google Scholar]
- 33.Howard J. Sinauer; Sunderland, MA: 2001. Mechanics of Motor Proteins and the Cytoskeleton. [Google Scholar]
- 34.Satcher R.L., Jr., Dewey C.F., Jr. Theoretical estimates of mechanical properties of the endothelial cell cytoskeleton. Biophys. J. 1996;71:109–118. doi: 10.1016/S0006-3495(96)79206-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Medalia O., Weber I., Baumeister W. Macromolecular architecture in eukaryotic cells visualized by cryoelectron tomography. Science. 2002;298:1209–1213. doi: 10.1126/science.1076184. [DOI] [PubMed] [Google Scholar]
- 36.Charras G.T., Yarrow J.C., Mitchison T.J. Non-equilibration of hydrostatic pressure in blebbing cells. Nature. 2005;435:365–369. doi: 10.1038/nature03550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Bursac P., Lenormand G., Fredberg J.J. Cytoskeletal remodeling and slow dynamics in the living cell. Nat. Mater. 2005;4:557–561. doi: 10.1038/nmat1404. [DOI] [PubMed] [Google Scholar]
- 38.Timbs M.M., Spring K.R. Hydraulic properties of MDCK cell epithelium. J. Membr. Biol. 1996;153:1–11. doi: 10.1007/s002329900104. [DOI] [PubMed] [Google Scholar]
- 39.Pierce S.K., Politis A.D. Ca2+-activated cell volume recovery mechanisms. Annu. Rev. Physiol. 1990;52:27–42. doi: 10.1146/annurev.ph.52.030190.000331. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


