Abstract
The kinetics of malate dehydrogenase (MDH) catalyzed oxidation/reduction of L-malate/oxaloacetate is pH-dependent due to the proton generated/taken up during the reaction. Previous kinetic studies on the mitochondrial MDH did not yield a consensus kinetic model that explains both substrate and pH dependency of the initial velocity. In this study, we propose, to our knowledge, a new kinetic mechanism to explain kinetic data acquired over a range of pH and substrate concentrations. Progress curves in the forward and reverse reaction directions were obtained under a variety of reactant concentrations to identify associated kinetic parameters. Experiments were conducted at physiologically relevant ionic strength of 0.17 M, pH ranging between 6.5 and 9.0, and at 25°C. The developed model was built on the prior observation of proton uptake upon binding of NADH to MDH, and that the MDH-catalyzed oxidation of NADH may follow an ordered bi-bi mechanism with NADH/NAD binding to the enzyme first, followed by the binding of oxaloacetate/L-malate. This basic mechanism was expanded to account for additional ionic states to explain the pH dependency of the kinetic behavior, resulting in what we believe to be the first kinetic model explaining both substrate and pH dependency of the reaction velocity.
Introduction
Malate dehydrogenase (MDH, EC: 1.1.1.37) reversibly catalyzes the oxidation of L-malate (MAL) to oxaloacetate (OAA), reducing NAD to NADH in the process. In eukaryotes this enzyme is expressed as mitochondrial (mMDH) and the cytosolic (cMDH) isoforms. To date, no unambiguous complete picture of the kinetics of catalysis of this reaction has been elucidated for either isoform. Both MDH isoenzymes exist in physiological conditions as dimers with identical subunits (1–4) with two equivalent binding sites. The mMDH dimer has a molecular mass of ∼70 kDa (5–7). The dimer form dissociates to monomer at low enzyme concentration, and at low pH (4,8), and is active only in dimer form (9). This enzyme is allosterically regulated by citrate (10–12), inhibited by 2-thenoyltrifluoroacetone (13), ATP, ADP, AMP, fumarate, citrate, and aspartate (14,15), and high OAA concentrations (16,17). The activity of mMDH may be further sensitive to ionic strength (18,19).
Prior studies have concluded that the MDH-catalyzed oxidation of MAL is a sequential mechanism with coenzyme (NAD/NADH) binding first followed the binding of the substrate (MAL/OAA) (20–23). Binding of NADH to the enzyme induces conformational changes and results in a proton release (24). As is the case for many enzymes involved in central energy metabolism, the literature reports several competing models (along with associated data sets and parameter estimates) for the catalytic mechanism of mMDH isoforms such as the Theorell-Chance mechanism (25), the reciprocating compulsory ordered mechanism (26,27), a compulsory ordered bi-bi mechanism with no dead-end (abortive) complex formed at some pH values with a dead-end E.NADH.MAL complex formed at other pH values (28), and an ordered bi-bi mechanism with several dead-end complexes formed (14). These kinetic studies have been performed at enzyme concentrations that are low enough to potentially be associated with partial reversion to the monomeric form (20,25,29), affecting the function of the enzyme.
Although a proton is released/taken up by the overall mMDH-catalyzed reaction, the pH effects on the reaction kinetics have been ignored in most prior studies. The exception is the study of Raval and Wolfe (29), which reported kinetic effects of pH on mMDH isoforms and proposed a pH-dependent kinetic model.
The primary aim of this study is to develop a catalytic mechanism that can explain the pH effects over a range of substrate concentrations at physiologically relevant ionic strength. In addition, this study represents a member in a series of studies reporting mechanistic models of the mitochondrial enzymes (30–34) and transporters (35–39) needed to simulate the integrated metabolic function of the organelle. Finally, along with a companion study of the cytoplasmic isoform (Dasika et al. (40)), this study facilitates a comparative analysis of kinetic control of this reaction in the cytosolic versus mitochondrial compartment.
To realize these goals, kinetics of the mMDH reaction were assayed at physiological ionic strength of 0.17 M and pH range between 6.5 and 9.0 and at various initial substrate and product concentrations. Rather than conducting experiments specifically designed to inform a model of a specified mechanism, testing competing models and identifying the catalytic mechanism requires a data set that probes reaction kinetics over a wide range of substrate and product concentrations and pH. Thus we collected and analyzed progress curves, which are more informative than initial velocity (initial slopes of progress curves) data alone (32,41). We did not study the effects of various allosteric regulators in this study. Although no previously established consensus mechanism for the catalytic mechanism exists, previously suggested models provide a set of trial models to be evaluated against data that are rich enough to allow us to discriminate among the competing hypotheses. Specifically, the models in Fig. 1 and those presented in Fig. S1 of the Supporting Material are evaluated to rule out those that cannot match the data and to estimate kinetic parameters of a model that can. Via this procedure, the model of Fig. 1 F is shown to capture the observed pH and reactant concentration dependencies of the enzyme-catalyzed reaction.
Figure 1.
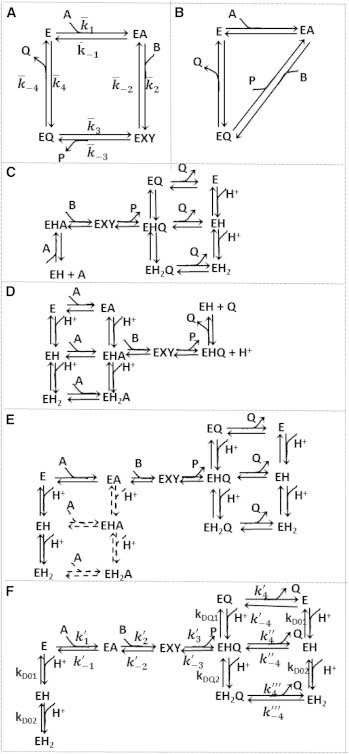
Schematics. (A) Simple ordered bi-bi model; the values represent the apparent rate constants. (B) Theorell-Chance mechanism. (C) pH dependency of NADH oxidation proposed by Raval and Wolfe (29). (D) pH dependency of NAD reduction proposed by Raval and Wolfe (29). (E) Proposed pH model that assumes NAD/NADH binding to all enzyme-protonated states. (Dashed lines) Steps for which parameters are not identifiable. (F) Schematic of the proposed model, including multiple pH-dependent ionic states. In each of these schemes, A, B, P, and Q represent NAD, MAL, OAA, and NADH, respectively, and the substrate binding or product release is represented by the direction of the arrow. The diagram uses the convention of explicitly showing association steps for binding of forward-reaction substrates A and B, and dissociation steps for unbinding of products P and Q. In the reverse operation, for example in the step from EA to E in panel A, the reactant A dissociates, even though dissociation of A is not explicitly illustrated in the figure.
Materials and Methods
Experimental materials
All reagents and enzyme (M2634) were purchased from Sigma-Aldrich (St. Louis, MO) and used without further purification. Experiments were conducted with porcine heart mMDH in both forward (NADH production) and reverse (NADH consumption) directions at several pH values between 6.5 and 9.0, physiological ionic strength of 0.17 M, and at 25°C. Experiments with pH values 6.5–7.5 were performed with 100 mM MOPS (pK = 7.2 at 25°C) while experiments with pH values 8.0–9.0 were performed with 100 mM TRIS (pK = 8.1 at 25°C). Temperature was maintained at 25°C using a circulating water bath. Ionic strength was adjusted by adding appropriate amount of KCl, calculated based on the initial substrate concentrations. Approximately 550 μL and 330 μL 3 M KCL was added for the reverse and forward directions, respectively, to adjust the ionic strength to 0.17 M. Experiments were performed in the forward direction with initial concentrations of 1 mM NAD and 10 mM or 20 mM MAL at pH 6.5, 1 mM NAD and 5 mM or 10 mM MAL at pH values 7.0 and 7.5, 1 mM NAD and 1 mM or 2 mM MAL at pH values 8.0 and 8.5, and 1 mM NAD and 0.5 mM or 1 mM NAL at pH 9.0. The initial concentrations in the forward direction were chosen such that the final [NADH] would be in the range 4–30 μM. Experiments were conducted in the reverse direction with 300 μM NADH and 50 μM OAA, and 300 μM NADH and 100 μM OAA initial concentrations for each pH. Product inhibition experiments were conducted in the reverse direction with initial 1 mM and 2 mM NAD and MAL for each pH.
For experiments using OAA in the initial reaction buffer, OAA stock was prepared fresh after every 4 h and stored on ice.
Approximately 4 μL of the enzyme stock solution (5000 IU, manufacturer’s specification) of the enzyme was reconstituted to prepare the 500 μL of 100 IU/mL enzyme solution. For forward-direction experiments, reactions were initiated by adding 3 μL of the reconstituted enzyme solution (0.3 IU/mL protein solution) to a 24-well plate well containing 1 mL of substrate solution consisting of appropriate concentrations of MAL and NAD. NADH concentration was assayed by fluorescence measurement at 470 nm with excitation at 340 nm in a Varioskan Flash multimode plate reader (Thermo Fisher Scientific, Waltham, MA). The data recording started 4 s after the enzyme solution was mixed to the substrate solution. In the reverse direction, reactions were initiated by adding 6 μL of 100 U/mL reconstituted enzyme solution (0.3 IU/mL enzyme concentration) to a cuvette containing 2 mL of appropriate concentrations of NADH and OAA, and NADH concentration was assayed by optical absorbance measured between 339 and 341 nm using a Jaz modular spectrophotometer (Ocean Optics, Dunedin, FL). The enzyme solution was reconstituted after every hour to avoid any variability in enzyme activity due to monomerization of the enzyme.
Reaction flux was also measured in the reverse direction with initial concentrations [NADH] = 10 μM and [OAA] = 10 μM with 50 mM of buffer (TRIS for pH range 8–9, MOPS for pH range 6.5–7.5), at 25°C. Experiments were initiated by adding 3 μL of 10 IU/mL (low enzyme concentration) or 100 U/mL (high enzyme concentration) of mMDH stock solution to a 24-well plate well containing the substrate solution 10 μM NADH and 10 μM OAA, and the progress of NADH oxidation was recorded in a Varioskan Flash multimode plate reader (Thermo Fisher Scientific) by fluorescence measurement at 470 nm with excitation at 340 nm. Experiments were repeated four times at each pH and enzyme concentration.
Mathematical model
Malate dehydrogenase catalyzes the biochemical reaction
| (1) |
Here, the ionic charges on the species NAD− and NADH2− indicate that the chemical reaction is expressed in terms of deprotonated reference species (42).
The thermodynamic equilibrium constant at a given temperature, T, is estimated (42) as
| (2) |
where ΔrG0 is the Gibbs free energy of the reaction, and R is the universal gas constant (8.314 × 10−3 kJ/mol K). The Gibbs free energy is computed as
| (3) |
where ΔrGi0 is the Gibbs standard free energy of formation of species i. The effects of temperature and ionic strength over the temperature range of 273–313 K on the Gibbs free energy for species i can be approximated as (42,43)
| (4) |
where I is the ionic strength; γi is the activity of species i; T1 and T are reference and desired temperatures, respectively; β = 1.6 M−1/2; and ∝(T) = 1.107 – 1.545 × 10−3T + 5.956 × 10−6 T2 (42,43). Under conditions of 298 K, pH 8.0, and ionic strength of 0.17 M, ΔrG0 = 71.09 kJ/mol (43). Over the temperature range of T = 273–313 K, the effect of ionic strength I on γi can be computed as
where zi is the valance of species i (42).
The apparent equilibrium constant K′eq is computed as
| (5) |
The kinetic model used to analyze data on this reaction is based on the ordered bi-bi mechanism illustrated in Fig. 1 A. Specifically, it is assumed that at a given pH, the reaction follows quasi-steady rate law for the ordered bi-bi mechanism, and can be computed as (44)
| (6) |
where the denominator term is
| (7) |
In this equation, E0 is the total enzyme concentration; [A], [B], [P], and [Q] represent the concentrations of species NAD−, MAL2−, NADH2−, and OAA−, respectively; and represents apparent rate constants. The concentrations of species malate and oxaloacetate depend on pH, and are expressed using binding polynomials, defined as
| (8) |
| (9) |
where h represents the hydrogen ion activity computed as h = 10−pH, and kH,OAA = 10−pK,OAA, and KH,MAL = 10−pK,MAL, pK,OAA = 3.9, pK,MAL = 4.715 (43). Because the concentrations of species NAD and NADH do not depend on the pH, we used the total NAD and NADH concentrations in this study. Using these binding polynomials, the concentrations of species MAL2− and OAA− are computed as
| (10) |
| (11) |
where [MAL] and [OAA] are the total concentrations of malate and oxaloacetate.
The effects of pH on reaction kinetics are simulated using the pH-dependent mechanism illustrated in Fig. 1 F. We assumed that NADH potentially binds to all protonated states of enzyme while NAD is assumed to only bind to the unprotonated enzyme state. The model is developed based on the structural studies on the enzyme complexes, which will be discussed in the following text. The model assumes rapid equilibrium between protonated enzyme states. Under these assumptions, the rate constants , , , and are independent of pH.
Based on the pH-dependent mechanism of Fig. 1 F, the apparent rate constants are computed as (45)
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
where p01 and pQ are defined as
and
In Eqs. 12–18, the activities are multiplied to the rate constants to take into account the charge of the enzyme complex. The parameters ki′ are not independent, and are bound by the following thermodynamic constraints:
| (19) |
| (20) |
Given the above definitions for the apparent rate constants, the quasi-steady reaction rate is computed according to Eqs. 6 and 7.
The K′eq, estimated from Li et al. (43), is I = 0.17 M, and T = 25°C is 8.3 × 10−5. Using Eq. 2 for the ordered bi-bi mechanism, apparent rate constants are constrained by the apparent equilibrium constant K′eq:
| (21) |
This model invokes a total of 13 parameters adjustable parameters, which are listed in Table 1 and identified based on experimental data as detailed below. Confidence intervals for parameter estimates are computed following the procedure of Landaw and DiStefano (46). Parameter estimation and other calculations were performed using the “fmincon” routine in the software MATLAB (The MathWorks, Cambridge, MA).
Table 1.
Estimated parameters values along with confidence intervals computed representing 95% confidence
| Parameters | Value | Unit |
|---|---|---|
| k1′0 | (1.800 ± 0.024) × 106 | mM−1 Min−1 |
| k−1′0 | (2.800 ± 0.026) × 106 | Min−1 |
| k2′0 | (4.700 ± 0.046) × 105 | mM−1 Min−1 |
| k−2′0 | (2.600 ± 0.0005) × 104 | Min−1 |
| k3′0 | (1.900 ± 0.002) × 104 | Min−1 |
| k4′0 | (1.300 ± 0.002) × 105 | Min−1 |
| k−4′0 | (7.500 ± 0.007) × 105 | mM−1 Min−1 |
| k−4″0 | 1.100 ± 68.000 | mM−1 Min−1 |
| k−4″′0 | (1.000 ± 0.001) × 107 | mM−1 Min−1 |
| pK01 | 7.320 ± 0.010 | Unitless |
| pK02 | 5.710 ± 0.010 | Unitless |
| pKQ1 | 9.100 ± 0.009 | Unitless |
| pKQ2 | 3.049 ± 1.660 | Unitless |
Results
The time course data at each fixed pH were fit to several competing mechanisms, including ordered bi-bi (Fig. 1 A), Theorell-Chance (Fig. 1 B), and ping-pong mechanisms. We found that of these alternatives only the ordered bi-bi mechanism was able to match the observed data at any given fixed pH value (see the Supporting Material). The previously proposed Theorell-Chance mechanism (25) was not able to match the data at any pH. These results mean that an appropriate pH-dependent model is expected to reduce to an ordered bi-bi mechanism at constant pH, and that the mMDH-catalyzed reaction can be represented as an ordered bi-bi mechanism with coenzyme binding to enzyme first, followed by the substrate. However, a single parameterization of a simple ordered bi-bi mechanism (Fig. 1 A) cannot fit the data with all pH values. The inability of competing models to fit the data using physically reasonable parameter values is illustrated in the Supporting Material.
The time-course data of the reaction were fit to the several pH-value models including the models proposed by Raval and Wolfe (29) (Fig. 1, C–F). Although the models proposed by Raval and Wolfe (Fig. 1, C and D) (29) represent the framework from which we constructed new trial models, the original Raval and Wolfe models could not fit the time-course data. The model of Fig. 1 E does effectively match the data. However, given the data available, not all parameters in this model can be identified with acceptable confidence. The reduced model of Fig. 1 F, which represents the effective compromise between ability to fit the data and identifiability of parameter values, is the model used for the data fits illustrated in Figs. 2, 3, 4, 5, 6, and 7. These figures show measured progress curves for the forward and reverse reactions measured under a variety of conditions with various pH values.
Figure 2.
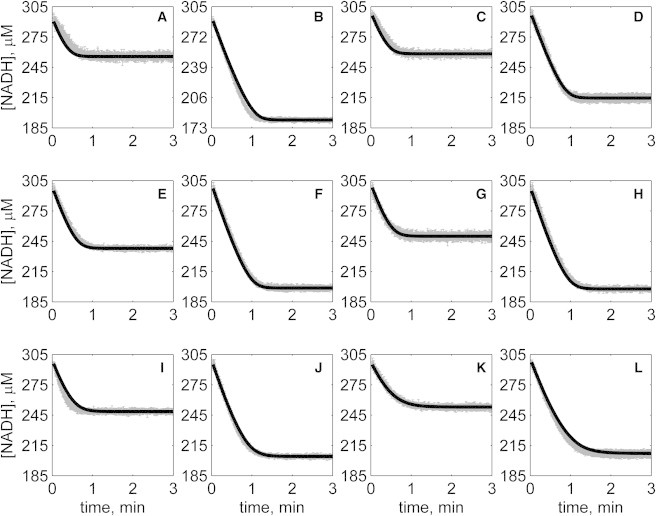
Progress curves of [NADH] versus time for reverse reaction (direction of NADH oxidation) at various pH values without product inhibitors present in initial buffer. Initial conditions are [NADH]0 = 300 μM and (A) [OAA]0 = 50 μM, pH 6.5; (B) [OAA]0 = 100 μM, pH 6.5; (C) [OAA]0 = 50 μM, pH 7.0; (D) [OAA]0 = 100 μM, pH 7.0; (E) [OAA]0 = 50 μM, pH 7.5; (F) [OAA]0 = 100 μM, pH 7.5; (G) [OAA]0 = 50 μM, pH 8.0; (H) [OAA]0 = 100 μM, pH 8.0; (I) [OAA]0 = 50 μM, pH 8.5; (J) [OAA]0 = 100 μM pH 8.5; (K) [OAA]0 = 50 μM, pH 9.0; and (L) [OAA]0 = 100 μM, pH 9.0. (In each plot the shaded lines and solid lines, respectively, represent mean with standard deviation of experimentally measured [NADH], and [NADH] obtained from fitting data to ordered bi-bi mechanism.)
Figure 3.
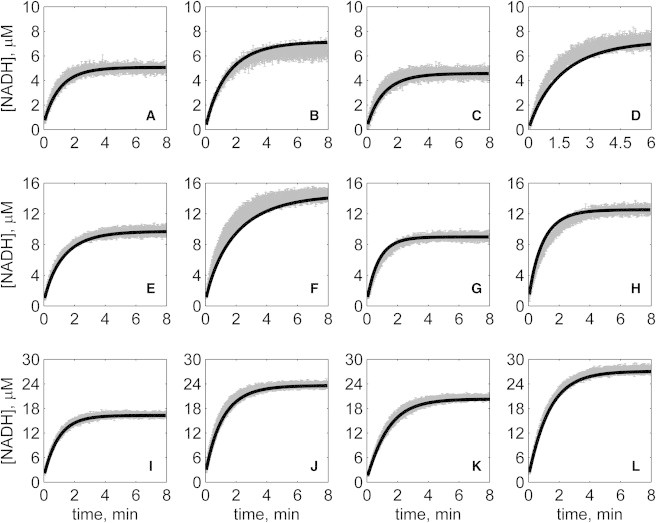
Progress curves of [NADH] versus time for forward reaction (direction of NAD reduction) at various pH values without product inhibitors present in initial buffer. Initial conditions are [NAD]0 = 1 mM and (A) [MAL]0 = 10 mM, pH 6.5; (B) [MAL]0 = 20 mM, pH 6.5; (C) [MAL]0 = 5 mM, pH 7.0; (D) [MAL]0 = 10 mM, pH 7.0; (E) [MAL]0 = 5 mM, pH 7.5; (F) [MAL]0 = 10 mM, pH 7.5; (G) [MAL]0 = 1 mM, pH 8.0; (H) [MAL]0 = 2 mM, pH 8.0; (I) [MAL]0 = 1 mM, pH 8.5; (J) [MAL]0 = 2 mM, pH 8.5; (K) [MAL]0 = 0.5 mM, pH 9.0; and (L) [MAL]0 = 1 mM, pH 9.0. (In each plot the shaded lines and solid lines, respectively, represent mean with standard deviation of experimentally measured [NADH], and [NADH] obtained from fitting data to ordered bi-bi mechanism.)
Figure 4.
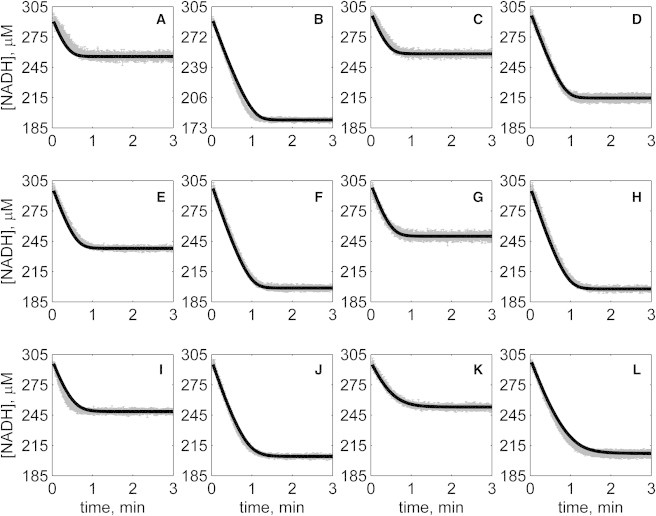
Progress curves of [NADH] versus time for reverse reaction (direction of NADH oxidation) at various pH values with 1 mM NAD as product inhibitor present in initial buffer. Initial conditions are [NADH]0 = 300 μM and (A) [OAA]0 = 50 μM, pH 6.5; (B) [OAA]0 = 100 μM, pH 6.5; (C) [OAA]0 = 50 μM, pH 7.0; (D) [OAA]0 = 100 μM, pH 7.0; (E) [OAA]0 = 50 μM, pH 7.5; (F) [OAA]0 = 100 μM, pH 7.5; (G) [OAA]0 = 50 μM, pH 8.0; (H) [OAA]0 = 100 μM, pH 8.0; (I) [OAA]0 = 50 μM, pH 8.5; (J) [OAA]0 = 100 μM, pH 8.5; (K) [OAA]0 = 50 μM, pH 9.0; and (L) [OAA]0 = 100 μM, pH 9.0. (In each plot the shaded lines and solid lines, respectively, represent mean with standard deviation of experimentally measured [NADH], and [NADH] obtained from fitting data to ordered bi-bi mechanism.)
Figure 5.
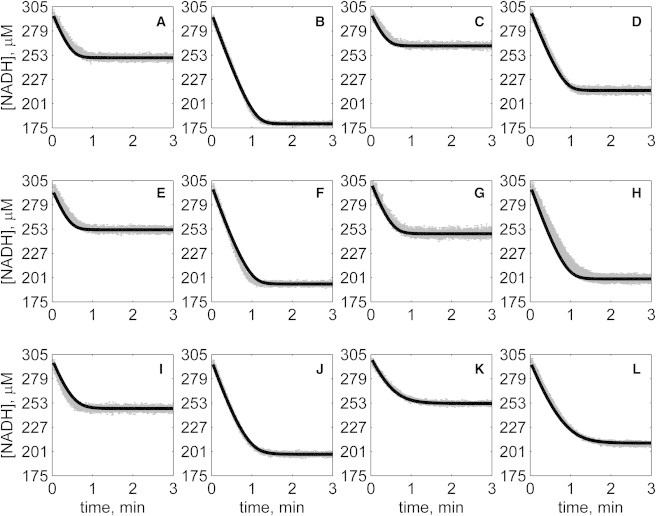
Progress curves of [NADH] versus time for reverse reaction (direction of NADH oxidation) at various pH values with 2 mM NAD as product inhibitor present in initial buffer. Initial conditions are [NADH]0 = 300 μM and (A) [OAA]0 = 50 μM, pH 6.5; (B) [OAA]0 = 100 μM, pH 6.5; (C) [OAA]0 = 50 μM, pH 7.0; (D) [OAA]0 = 100 μM, pH 7.0; (E) [OAA]0 = 50 μM, pH 7.5; (F) [OAA]0 = 100 μM, pH 7.5; (G) [OAA]0 = 50 μM, pH 8.0; (H) [OAA]0 = 100 μM, pH 8.0; (I) [OAA]0 = 50 μM, pH 8.5; (J) [OAA]0 = 100 μM, pH 8.5; (K) [OAA]0 = 50 μM, pH 9.0; and (L) [OAA]0 = 100 μM, pH 9.0. (In each plot the shaded lines and solid lines, respectively, represent mean with standard deviation of experimentally measured [NADH], and [NADH] obtained from fitting data to ordered bi-bi mechanism.)
Figure 6.
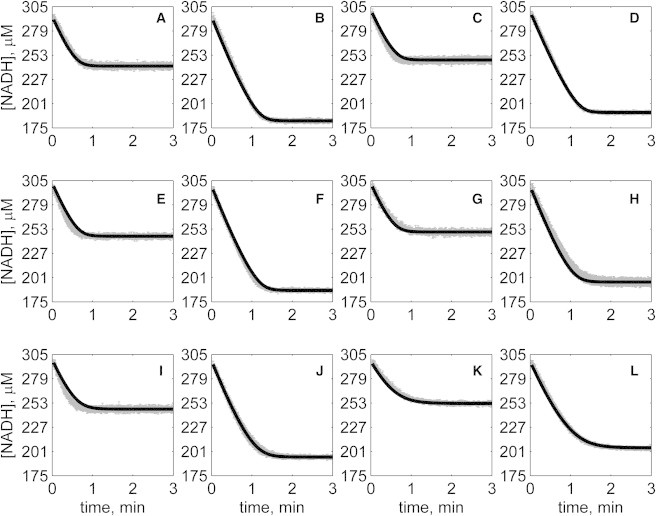
Progress curves of [NADH] versus time for reverse reaction (direction of NADH oxidation) at various pH values with 1 mM MAL as product inhibitor present in initial buffer. Initial conditions are [NADH]0 = 300 μM and (A) [OAA]0 = 50 μM, pH 6.5; (B) [OAA]0 = 100 μM, pH 6.5; (C) [OAA]0 = 50 μM, pH 7.0; (D) [OAA]0 = 100 μM, pH 7.0; (E) [OAA]0 = 50 μM, pH 7.5; (F) [OAA]0 = 100 μM, pH 7.5; (G) [OAA]0 = 50 μM, pH 8.0; (H) [OAA]0 = 100 μM, pH 8.0; (I) [OAA]0 = 50 μM, pH 8.5; (J) [OAA]0 = 100 μM, pH 8.5; (K) [OAA]0 = 50 μM, pH 9.0; and (L) [OAA]0 = 100 μM, pH 9.0. (In each plot the shaded lines and solid lines, respectively, represent mean with standard deviation of experimentally measured [NADH], and [NADH] obtained from fitting data to ordered bi-bi mechanism.)
Figure 7.
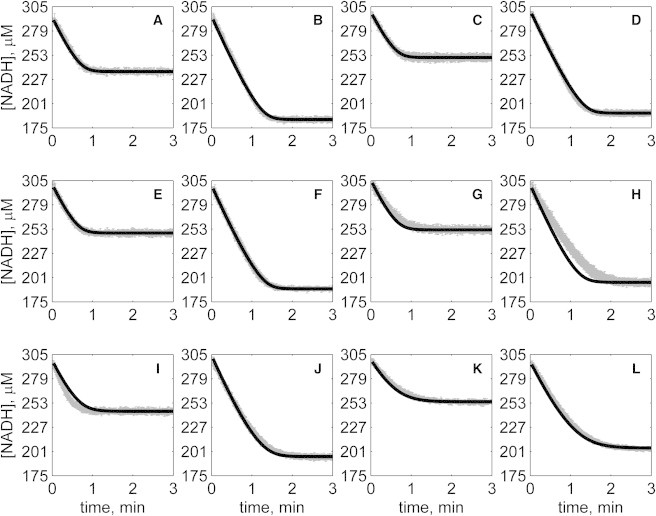
Progress curves of [NADH] versus time for reverse reaction (direction of NADH oxidation) at various pH values with 2 mM MAL as product inhibitor present in initial buffer. Initial conditions are [NADH]0 = 300 μM and (A) [OAA]0 = 50 μM, pH 6.5; (B) [OAA]0 = 100 μM, pH 6.5; (C) [OAA]0 = 50 μM, pH 7.0; (D) [OAA]0 = 100 μM, pH 7.0; (E) [OAA]0 = 50 μM, pH 7.5; (F) [OAA]0 = 100 μM, pH 7.5; (G) [OAA]0 = 50 μM, pH 8.0; (H) [OAA]0 = 100 μM, pH 8.0; (I) [OAA]0 = 50 μM, pH 8.5; (J) [OAA]0 = 100 μM, pH 8.5; (K) [OAA]0 = 50 μM, pH 9.0; and (L) [OAA]0 = 100 μM, pH 9.0. (In each plot the shaded lines and solid lines, respectively, represent mean with standard deviation of experimentally measured [NADH], and [NADH] obtained from fitting data to ordered bi-bi mechanism.)
Specifically, Fig. 2 shows reverse direction progress curves with no product present in the initial media. Fig. 3 shows progress curves for the forward direction without any product initially present. Figs. 4, 5, 6, and 7 show reverse direction progress curves with 1 mM NAD (Fig. 4), 2 mM NAD (Fig. 5), 1 mM MAL (Fig. 6), and 2 mM MAL (Fig. 7) present in the initial media as product inhibitor. The data of Figs. 2, 3, 4, 5, 6, and 7 represent 72 progress curves that were compared to model simulations to estimate the 13 adjustable parameters in Table 1. The model is able to effectively match the observed data with relatively sensitive estimates of all parameters, as indicated by the model fits in these figures. In all cases the model accurately fits the initial part (initial velocity) of the data. Model fits deviate from experimental data before reaching equilibrium in some cases (Figs. 2 B, 4, B and I, 5 F, 6 C, and 7, H and I). However, differences between model and data are always within 20% of the observed data, and can be attributed to variability in experimental conditions such as experiments conducted on different days, resulting in slightly different stock solution concentrations, the activity of the reconstituted enzyme, and variability arising from pipetting.
The confidence intervals indicated in Table 1 represent the 95% confidence interval. For all parameters, the uncertainty range is <12% of the mean parameter estimate. Attempts to improve the fits with additional pH-dependent states and additional dead-end complexes did not yield any significant improvement.
The final equilibrium concentrations attained under the conditions illustrated in Figs. 2, 3, 4, 5, 6, and 7provide estimates of the apparent equilibrium constant K′eq defined in Eq. 5. Measured values of K′eq under different experimental conditions are listed in Table 2. These values of K′eq as a function of pH are consistent with an estimate of Keq = 7.5 × 10−13 M−1 for the chemical reaction at I = 0.17 M, T = 25°C, which is within 10% of the value estimated from the database of Li et al. (43), yielding an estimate of Keq = 8.3 × 10−13 M−1. The variability in the K′eq may be attributed to the day-to-day variability in experimental conditions such as preparation of substrate solutions and pipetting uncertainties. The time-course data fits with all pH values in both directions were slightly better with Keq = 8.3 × 10−13 M−1 (value from the database) compared to Keq = 7.5 × 10−13 M−1. Hence the database value of Keq was used for the fits illustrated in Figs. 2, 3, 4, 5, 6, and 7.
Table 2.
Apparent equilibrium constant for various pH values and initial conditions from experiments and database; experimental values are close to the values from database
| pH | [MAL]0, mM | K′eq, experimental | K′eq, database |
|---|---|---|---|
| 6.5 | 10 | (2.52 ± 0.12) × 10−6 | 2.62 × 10−6 |
| 6.5 | 20 | (2.14 ± 0.31) × 10−6 | 2.62 × 10−6 |
| 7 | 5 | (4.26 ± 0.49) × 10−6 | 8.30 × 10−6 |
| 7 | 10 | (5.35 ± 0.40) × 10−6 | 8.30 × 10−6 |
| 7.5 | 5 | (1.91 ± 0.17) × 10−5 | 2.62 × 10−5 |
| 7.5 | 10 | (2.12 ± 0.15) × 10−5 | 2.62 × 10−5 |
| 8 | 1 | (8.28 ± 0.64) × 10−5 | 8.30 × 10−5 |
| 8 | 2 | (7.99 ± 0.47) × 10−5 | 8.30 × 10−5 |
| 8.5 | 1 | (2.79 ± 0.13) × 10−4 | 2.62 × 10−4 |
| 8.5 | 2 | (2.92 ± 0.15) × 10−4 | 2.62 × 10−4 |
| 9 | 0.5 | (9.14 ± 0.28) × 10−4 | 8.30 × 10−4 |
| 9 | 1 | (7.98 ± 0.40) × 10−4 | 8.30 × 10−4 |
Raval and Wolfe (29) reported initial reaction flux as a function of pH with initial concentrations [NADH] = 10 μM and [OAA] = 10 μM and enzyme concentration of 0.03 U/mL. Fig. 8 shows the plots of activity, defined as the ratio of initial velocity to the enzyme concentration, as a function of pH. Our model predictions using the model in Fig. 1 F (solid lines) are compared to the data of Raval and Wolfe (29) (open triangles) in Fig. 8. Predictions of the model (Fig. 1 F), identified based on the kinetic data detailed above, deviate from the data for pH values <7. To investigate this discrepancy, we repeated the experiment from Raval and Wolfe (29), yielding results (plotted as open circles in Fig. 8) that agree closely with Raval and Wolfe (29). In fact, it was determined that the model cannot simultaneously (with a single parameter set) capture both the behavior measured in the progress curves of Figs. 2, 3, 4, 5, 6, and 7, and the initial flux data illustrated in Fig. 8.
Figure 8.
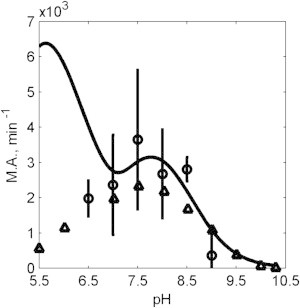
Molecular activity as a function of pH. Experimental data from this study (open circles) are plotted along with experimental data from Raval and Wolfe (29) (open triangles) obtained under identical experimental conditions: [NADH] = 10 μM and [OAA] = 10 μM. Model predictions (Fig. 1F) are plotted (solid line). The model predicts a peak at low pH (pH ∼6), contradicting the experimental data observations.
We hypothesized two alternative explanations for this discrepancy. One, the model is inadequate. Two, the enzyme behaves differently under the conditions of 0.3 U/mL for experiments of Figs. 2, 3, 4, 5, 6, and 7, and 0.03 U/mL for Fig. 8. To test the second hypothesis, we conducted progress-curve experiments for both enzymes concentrations with initial concentrations of [NADH] = 10 μM and [OAA] = 10 μM, corresponding to experiments summarized in Fig. 8. Fig. 9 shows progress curves at pH 6.5–9 for these conditions. The results are plotted on two different time axes for each pH, so that if the enzymes kinetics were not concentration-dependent, then the results at both enzyme concentrations would be identical. However, it is apparent from these results that at the lower enzyme concentration (shaded lines), progress is relatively slower (measured in flux per unit enzyme) than at higher concentration (solid lines). We can see that, particularly at the lowest pH assayed, the specific activity at low enzyme concentration is much lower than at high enzyme concentration.
Figure 9.
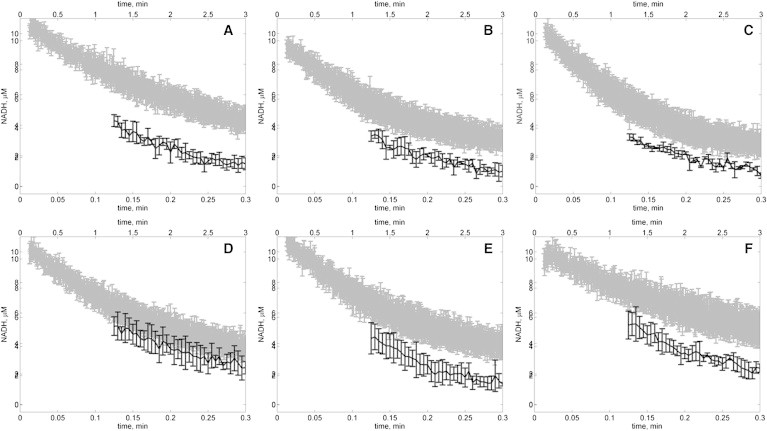
Progress of NADH oxidation for initial conditions [NADH] = 10 μM and [OAA] = 10 μM with high (100 IU/mL stock solution) and low (10 IU/mL stock solution) enzyme concentration for pH: (A) 6.5, (B) 7.0, (C) 7.5, (D) 8.0, (E) 8.5, and (F) 9.0 (shaded lines represents data with low enzyme concentration (∼0.6 nM); solid lines represent data with high enzyme concentration (∼6 nM)). The time axis for the low enzyme concentration is indicated on the bottom of each plot; the time axis for the high enzyme concentration is indicated on the top of each plot.
We speculate that this mismatch may arise from concentration- and pH-dependent monomerization and inactivation of the enzyme (4,8). Whether or not this is the explanation, it is clear that the kinetics rates are different at different enzyme concentrations. Investigation of the basis for this phenomenon is beyond the scope of this study. Analysis and estimation of parameter values in Table 1 are associated with the high-activity/high-concentration state of the enzyme. Thus, if the deactivation observed at low concentration is due to monomerization, then the model developed here represents the behavior of the enzyme in the active dimer form.
Discussion
Equilibrium constant
The K′eq from our study at pH 8.0 and ionic strength of 0.17 M was slightly different than that obtained by Raval and Wolfe (20,25) (1.03 × 10−4 at pH 8.0), and Heyde and Ainsworth (21) (8 × 10−4 at pH 8.0). However, in those cases K′eq was computed based on the parameters obtained by fitting initial velocity data rather than the parameters based on the observed equilibrium mass-action ratio. The K′eq estimates from our experimental data at pH 7.0 and 7.5 were lower compared to the value expected from a database (43). As a result, the Keq from our experimental data was lower than the value from the database (43). The global fits, which includes data with all pH values in both the forward and reverse directions, were slightly better when the database Keq value was used compared to the value from our estimates. Because, to within measurement detection, all of the OAA is consumed in the reverse direction, our reverse-direction data do not facilitate direct estimates of K′eq. However, the equilibrium Haldane constraint affects the fits to the data in both the forward and reverse directions.
Initial velocity measurements
Analysis of progress kinetic data based on the model of Fig. 1 A reveals that a compulsory ordered bi-bi mechanism modified to account for the specific pH dependency of Fig. 1 F is able to explain the kinetics of the mMDH-catalyzed reaction. The analysis did not require invoking any change in the basic kinetic mechanism with pH as suggested by Silverstein and Sulebele (28). Nor were we able to match the observed data based on previously suggested models, such as the Theorell-Chance mechanism, or the proposed pH-dependent model of Raval and Wolfe (29). The conclusions from prior studies that were based on initial velocity measurements and double reciprocal plots may be flawed because those approaches require precise estimation of initial velocities from progress curves, and small uncertainty in initial velocity has a large effect on the parameters estimated (34,40,47,48). Comparing time-course model predictions to progress curves allows us to extract much more information from a given experiment than a single initial velocity measurement. The observation of the strong dependence of specific activity on enzyme concentration and pH confounds any analysis that combines results obtained at different enzyme concentrations.
Kinetic mechanism
In the proposed model (Fig. 1 F), we assumed that NADH binds to all charged states of the enzyme. However, OAA binds to the EH.NADH complex while E.NADH and EH2.NADH are the abortive complexes that do not participate in the reaction. Our proposed model (Fig. 1 F) is based on the studies on pH-dependent proton uptake upon binding of NADH to the enzyme (49). These authors observed that mMDH exhibits proton uptake upon binding to NADH for pH values >6.0, and suggested the histidine residue to be the cause of proton uptake. We did not come across similar studies regarding pH effects on NAD binding to mMDH. However, Whitaker et al. (50) conducted similar studies on the proton uptake upon binding of NAD/NADH to lactate dehydrogenase (LDH), and observed that while a proton is consumed upon binding of NADH to LDH, no proton uptake was observed upon binding of NAD to LDH.
Bernstein and Everse (51) studied the mMDH complex formation and suggested that MAL binds to a nonprotonated enzyme complex. Based on these findings, we speculate that a proton is released into the solvent during MAL oxidation, and a proton is taken up during OAA reduction. The only other study of pH effects on mMDH kinetics was by Raval and Wolfe (29). However, they proposed a model in which the NADH binding to mMDH is not affected by pH. Using their model and parameters (29), and subsequently trying to optimize the parameters of their model, did not improve the fits. The kinetic scheme shown in Fig. 1 F is able to match the experimental data, and thus represents an effective model of the catalytic mechanism for mMDH-mediated oxidation of MAL.
Conclusions
The kinetic mechanism of mitochondrial MDH is effectively captured by the model illustrated in Fig. 1 F. The model, which is based on the pervious observations of enzyme complex formation as well as proton uptake studies up on NADH binding to the enzyme, explains the kinetic data represented by 72 progress curves for the forward and reverse reaction directions obtained over the pH range from 6.5 to 9. Observed K′eq for various pH values and various initial conditions match well with the K′eq values from the database (43) predictions. While the model predictions qualitatively deviate from initial velocity measurements attained at low enzyme concentrations, it is concluded that enzyme function at low concentration are not consistent with function at high concentration. The model identified here is matched to data obtained at the higher enzyme concentrations, under conditions where the active dimer form is expected to be dominant. The methods employed in this study could be utilized to understand the kinetics for other enzymes for which several competing mechanisms have been proposed.
Acknowledgments
This work was supported by the Virtual Physiological Rat Project funded through National Institutes of Health grant No. P50-GM094503.
Supporting Material
References
- 1.Holbrook J.J., Wolfe R.G. Malate dehydrogenase. X. Fluorescence microtitration studies of D-malate, hydroxymalonate, nicotinamide dinucleotide, and dihydronicotinamide-adenine dinucleotide binding by mitochondrial and supernatant porcine heart enzymes. Biochemistry. 1972;11:2499–2502. doi: 10.1021/bi00763a018. [DOI] [PubMed] [Google Scholar]
- 2.Roderick S.L., Banaszak L.J. The conformation of mitochondrial malate dehydrogenase derived from an electron density map at 5.3-Å resolution. J. Biol. Chem. 1983;258:11636–11642. [PubMed] [Google Scholar]
- 3.Roderick S.L., Banaszak L.J. The three-dimensional structure of porcine heart mitochondrial malate dehydrogenase at 3.0-Å resolution. J. Biol. Chem. 1986;261:9461–9464. [PubMed] [Google Scholar]
- 4.Gleason W.B., Fu Z., Banaszak L. Refined crystal structure of mitochondrial malate dehydrogenase from porcine heart and the consensus structure for dicarboxylic acid oxidoreductases. Biochemistry. 1994;33:2078–2088. doi: 10.1021/bi00174a014. [DOI] [PubMed] [Google Scholar]
- 5.Murphey W.H., Kitto G.B., Kaplan N. Malate dehydrogenases. I. A survey of molecular size measured by gel filtration. Biochemistry. 1967;6:603–610. doi: 10.1021/bi00854a031. [DOI] [PubMed] [Google Scholar]
- 6.Noyes B.E., Glatthaar B.E., Bradshaw R.A. Structural and functional similarities between mitochondrial malate dehydrogenase and L-3-hydroxyacyl CoA dehydrogenase. Proc. Natl. Acad. Sci. USA. 1974;71:1334–1338. doi: 10.1073/pnas.71.4.1334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Shore J.D., Chakrabarti S.K. Subunit dissociation of mitochondrial malate dehydrogenase. Biochemistry. 1976;15:875–879. doi: 10.1021/bi00649a023. [DOI] [PubMed] [Google Scholar]
- 8.Bleile D.M., Schulz R.A., Gregory E.M. Investigation of the subunit interactions in malate dehydrogenase. J. Biol. Chem. 1977;252:755–758. [PubMed] [Google Scholar]
- 9.Breiter D.R., Resnik E., Banaszak L.J. Engineering the quaternary structure of an enzyme: construction and analysis of a monomeric form of malate dehydrogenase from Escherichia coli. Protein Sci. 1994;3:2023–2032. doi: 10.1002/pro.5560031115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mullinax T.R., Mock J.N., Harrison J.H. Regulation of mitochondrial malate dehydrogenase. Evidence for an allosteric citrate-binding site. J. Biol. Chem. 1982;257:13233–13239. [PubMed] [Google Scholar]
- 11.McEvily A.J., Mullinax T.R., Harrison J.H. Regulation of mitochondrial malate dehydrogenase: kinetic modulation independent of subunit interaction. Arch. Biochem. Biophys. 1985;238:229–236. doi: 10.1016/0003-9861(85)90160-2. [DOI] [PubMed] [Google Scholar]
- 12.Gelpí J.L., Dordal A., Cortés A. Kinetic studies of the regulation of mitochondrial malate dehydrogenase by citrate. Biochem. J. 1992;283:289–297. doi: 10.1042/bj2830289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Gutman M., Hartstein E. Inhibition of mitochondrial malate dehydrogenase by 2-thenoyltrifluoroacetone. FEBS Lett. 1974;49:170–173. doi: 10.1016/0014-5793(74)80504-1. [DOI] [PubMed] [Google Scholar]
- 14.Casadó F., Cortés A., Bozal J. Extraction and kinetic characteristics of chicken liver mitochondrial malate dehydrogenase. Int. J. Biochem. 1980;11:437–447. doi: 10.1016/0020-711x(80)90315-8. [DOI] [PubMed] [Google Scholar]
- 15.Oza N.B., Shore J.D. The effects of adenine nucleotides on NADH binding to mitochondrial malate dehydrogenase. Arch. Biochem. Biophys. 1973;154:360–365. doi: 10.1016/0003-9861(73)90068-4. [DOI] [PubMed] [Google Scholar]
- 16.Raval D.N., Wolfe R.G. Malic dehydrogenase. V. Kinetic studies of substrate inhibition by oxalacetate. Biochemistry. 1963;2:220–224. doi: 10.1021/bi00902a003. [DOI] [PubMed] [Google Scholar]
- 17.DuVal G., Swaisgood H.E., Horton H.R. Some kinetic characteristics of immobilized protomers and native dimers of mitochondrial malate dehydrogenase: an examination of the enzyme mechanism. Biochemistry. 1985;24:2067–2072. doi: 10.1021/bi00329a039. [DOI] [PubMed] [Google Scholar]
- 18.Kun E., Eanes R.Z., Volfin P. Selective modification of mitochondrial malate dehydrogenase activity by changes in ionic strength. Nature. 1967;214:1328–1330. doi: 10.1038/2141328a0. [DOI] [PubMed] [Google Scholar]
- 19.Place G.A., Beynon R.J. The effect of ionic environment on pig heart mitochondrial malate dehydrogenase. Int. J. Biochem. 1982;14:305–309. doi: 10.1016/0020-711x(82)90091-x. [DOI] [PubMed] [Google Scholar]
- 20.Raval D.N., Wolfe R. Malic dehydrogenase. III. Kinetic studies of the reaction mechanism by product inhibition. Biochemistry. 1962;1:1112–1117. doi: 10.1021/bi00908a012. [DOI] [PubMed] [Google Scholar]
- 21.Heyde E., Ainsworth S. Kinetic studies on the mechanism of the malate dehydrogenase reaction. J. Biol. Chem. 1968;243:2413–2423. [PubMed] [Google Scholar]
- 22.Dupourque D., Kun E. Malate dehydrogenases of ox kidney. 2. Two substrate kinetic and inhibition analyses. Eur. J. Biochem. 1969;7:247–252. doi: 10.1111/j.1432-1033.1969.tb19599.x. [DOI] [PubMed] [Google Scholar]
- 23.Wiseman M.S., McKay D., Hardman M.J. Rat liver mitochondrial malate dehydrogenase: purification, kinetic properties, and role in ethanol metabolism. Arch. Biochem. Biophys. 1991;290:191–196. doi: 10.1016/0003-9861(91)90607-k. [DOI] [PubMed] [Google Scholar]
- 24.Wood D.C., Hodges C.T., Harrison J.H. The n-ethylmaleimide-sensitive cysteine residue in the pH-dependent subunit interactions of malate dehydrogenase. J. Biol. Chem. 1981;256:9895–9900. [PubMed] [Google Scholar]
- 25.Raval D.N., Wolfe R.G. Malic dehydrogenase. II. Kinetic studies of the reaction mechanism. Biochemistry. 1962;1:263–269. doi: 10.1021/bi00908a012. [DOI] [PubMed] [Google Scholar]
- 26.Harada K., Wolfe R.G. Malic dehydrogenase. VI. A kinetic study of hydroxymalonate inhibition. J. Biol. Chem. 1968;243:4123–4130. [PubMed] [Google Scholar]
- 27.Harada K., Wolfe R.G. Malic dehydrogenase. VII. The catalytic mechanism and possible role of identical protein subunits. J. Biol. Chem. 1968;243:4131–4137. [PubMed] [Google Scholar]
- 28.Silverstein E., Sulebele G. Equilibrium kinetic study of the mechanism of mitochondrial and supernatant malate dehydrogenases of bovine heart. Biochim. Biophys. Acta. 1969;185:297–304. doi: 10.1016/0005-2744(69)90422-7. [DOI] [PubMed] [Google Scholar]
- 29.Raval D.N., Wolfe R.G. Malic dehydrogenase. IV. pH dependence of the kinetic parameters. Biochemistry. 1962;1:1118–1123. doi: 10.1021/bi00912a024. [DOI] [PubMed] [Google Scholar]
- 30.Li X., Wu F., Beard D.A. Identification of the kinetic mechanism of succinyl-CoA synthetase. Biosci. Rep. 2013;33:145–163. doi: 10.1042/BSR20120069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Qi F., Pradhan R.K., Beard D.A. Detailed kinetics and regulation of mammalian 2-oxoglutarate dehydrogenase. BMC Biochem. 2011;12:53. doi: 10.1186/1471-2091-12-53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mescam M., Vinnakota K.C., Beard D.A. Identification of the catalytic mechanism and estimation of kinetic parameters for fumarase. J. Biol. Chem. 2011;286:21100–21109. doi: 10.1074/jbc.M110.214452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Qi F., Chen X., Beard D.A. Detailed kinetics and regulation of mammalian NAD-linked isocitrate dehydrogenase. Biochim. Biophys. Acta. 2008;1784:1641–1651. doi: 10.1016/j.bbapap.2008.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Beard D.A., Vinnakota K.C., Wu F. Detailed enzyme kinetics in terms of biochemical species: study of citrate synthase. PLoS One. 2008;3:e1825. doi: 10.1371/journal.pone.0001825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Chen X., Qi F., Beard D.A. Kinetics and regulation of mammalian NADH-ubiquinone oxidoreductase (Complex I) Biophys. J. 2010;99:1426–1436. doi: 10.1016/j.bpj.2010.06.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Bazil J.N., Vinnakota K.C., Beard D.A. Analysis of the kinetics and bistability of ubiquinol:cytochrome c oxidoreductase. Biophys. J. 2013;105:343–355. doi: 10.1016/j.bpj.2013.05.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Tewari S.G., Dash R.K., Bazil J.N. A biophysical model of the mitochondrial ATP-Mg/Pi carrier. Biophys. J. 2012;103:1616–1625. doi: 10.1016/j.bpj.2012.08.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Dash R.K., Qi F., Beard D.A. A biophysically based mathematical model for the kinetics of mitochondrial calcium uniporter. Biophys. J. 2009;96:1318–1332. doi: 10.1016/j.bpj.2008.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Vinnakota K.C., Beard D.A. Kinetic analysis and design of experiments to identify the catalytic mechanism of the monocarboxylate transporter isoforms 4 and 1. Biophys. J. 2011;100:369–380. doi: 10.1016/j.bpj.2010.11.079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Dasika S.K., Vinnakota K.C., Beard D.A. Characterization of the kinetics of cardiac cytosolic malate dehydrogenase and comparative analysis of cytosolic and mitochondrial isoforms. Biophys. J. 2015;108:420–430. doi: 10.1016/j.bpj.2014.11.3466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Johnson K.A. A century of enzyme kinetic analysis, 1913 to 2013. FEBS Lett. 2013;587:2753–2766. doi: 10.1016/j.febslet.2013.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Alberty R.A. Wiley; New York: 2005. Thermodynamics of Biochemical Reactions. [Google Scholar]
- 43.Li X., Dash R.K., Beard D.A. A database of thermodynamic quantities for the reactions of glycolysis and the tricarboxylic acid cycle. J. Phys. Chem. B. 2010;114:16068–16082. doi: 10.1021/jp911381p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Cleland W. The kinetics of enzyme-catalyzed reactions with two or more substrates or products: I. Nomenclature and rate equations. Biochim. Biophys. Acta. 1963;67:104–137. doi: 10.1016/0006-3002(63)91800-6. [DOI] [PubMed] [Google Scholar]
- 45.Segel I.H. Wiley; New York: 1993. Enzyme Kinetics. [Google Scholar]
- 46.Landaw E.M., DiStefano J.J., 3rd Multiexponential, multicompartmental, and noncompartmental modeling. II. Data analysis and statistical considerations. Am. J. Physiol. 1984;246:R665–R677. doi: 10.1152/ajpregu.1984.246.5.R665. [DOI] [PubMed] [Google Scholar]
- 47.Eisenthal R., Cornish-Bowden A. The direct linear plot. A new graphical procedure for estimating enzyme kinetic parameters. Biochem. J. 1974;139:715–720. doi: 10.1042/bj1390715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Cornish-Bowden A. The use of the direct linear plot for determining initial velocities. Biochem. J. 1975;149:305–312. doi: 10.1042/bj1490305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Hodges C.T., Jurgensen S.R., Harrison J.H. Investigation of the pH dependence of proton uptake by porcine heart mitochondrial malate dehydrogenase upon binding of NADH. Arch. Biochem. Biophys. 1980;203:580–586. doi: 10.1016/0003-9861(80)90215-5. [DOI] [PubMed] [Google Scholar]
- 50.Whitaker J.R., Yates D.W., Gutfreund H. The identification of intermediates in the reaction of pig heart lactate dehydrogenase with its substrates. Biochem. J. 1974;139:677–697. doi: 10.1042/bj1390677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Bernstein L.H., Everse J. Studies on the mechanism of the malate dehydrogenase reaction. J. Biol. Chem. 1978;253:8702–8707. [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


