Characterization of the Kinetics of Cardiac Cytosolic Malate Dehydrogenase and Comparative Analysis of Cytosolic and Mitochondrial Isoforms

Abstract

Because the mitochondrial inner membrane is impermeable to pyridine nucleotides, transport of reducing equivalents between the mitochondrial matrix and the cytoplasm relies on shuttle mechanisms, including the malate-aspartate shuttle and the glycerol-3-phosphate shuttle. These shuttles are needed for reducing equivalents generated by metabolic reactions in the cytosol to be oxidized via aerobic metabolism. Two isoenzymes of malate dehydrogenase (MDH) operate as components of the malate-aspartate shuttle, in which a reducing equivalent is transported via malate, which when oxidized to oxaloacetate, transfers an electron pair to reduce NAD to NADH. Several competing mechanisms have been proposed for the MDH-catalyzed reaction. This study aims to identify the pH-dependent kinetic mechanism for cytoplasmic MDH (cMDH) catalyzed oxidation/reduction of MAL/OAA. Experiments were conducted assaying the forward and reverse directions with products initially present, varying pH between 6.5 and 9.0. By fitting time-course data to various mechanisms, it is determined that an ordered bi-bi mechanism with coenzyme binding first followed by the binding of substrate is able to explain the kinetic data. The proposed mechanism is similar to, but not identical to, the mechanism recently determined for the mitochondrial isoform, mMDH. cMDH and mMDH mechanisms are also shown to both be reduced versions of a common, more complex mechanism that can explain the kinetic data for both isoforms. Comparing the simulated activity (ratio of initial velocity to the enzyme concentration) under physiological conditions, the mitochondrial MDH (mMDH) activity is predicted to be higher than cMDH activity under mitochondrial matrix conditions while the cMDH activity is higher than mMDH activity under cytoplasmic conditions, suggesting that the functions of the isoforms are kinetically tuned to their individual physiological roles.

Introduction

Malate dehydrogenase (MDH) (EC:1.1.1.37) utilizes NAD/NADH as coenzyme to reversibly catalyze the oxidation/reduction of the malate/oxaloacetate. The mitochondrial isoenzyme (mMDH) catalyzes the oxidation of malate (MAL), and is the last step of the citric acid cycle, while the cytoplasmic isoenzyme (cMDH) primarily reduces oxaloacetate (OAA) in the cytoplasm. Together, these two isoenzymes participate in the malate-aspartate shuttle to transport the reducing equivalents between the cytoplasm and the mitochondrial matrix. The cytosolic enzyme cMDH tends to be highly expressed in tissues with high ATP demand, such as the heart, in which the malate-aspartate shuttle is particularly active (1,2). One of the functions of the malate-aspartate shuttle is to clear NADH generated by cytosolic substrate oxidation, to allow those processes to remain thermodynamically favorable. Thus, the extent to which the mMDH and cMDH isoforms are sensitive to NAD and NADH is an important factor in determining how the shuttle system is able to regulate cytoplasmic redox state.

Both the isoenzymes are homodimers with molecular mass of ∼70 kDa per dimer (3). Despite low structural similarity between the two isoenzymes, the key residues in the catalytic loop are conserved (3). The cMDH is more polar and acidic compared to mMDH due to the presence of more acidic residues in cMDH compared to mMDH (3). The mMDH dissociates to monomer at pH of ∼5 (4) while, perhaps related to its acidic nature, the cMDH remains dimerized even at low pH values (3).

The kinetic mechanisms of both isoforms have been extensively investigated. It has been generally accepted that, for both isoforms, the reaction follows an ordered bi-bi mechanism with coenzyme (NAD/NADH) binding to the enzyme followed first by the substrate (5–7). Using structural studies on enzyme complexes with 1,4,5,6-tetrahydronicotinamide and α- ketomalonate as substitutes for NADH and MAL, respectively, Chapman et al. (8) concluded that the MAL/OAA are specific substrates to MDH and that conformational changes occur only after the proton is transferred from NADH to OAA. This suggests that the enzyme-catalyzed reaction is an ordered reaction with coenzyme (NAD/NADH) binding first, followed by substrate (MAL/OAA) binding, after which confirmation changes occur (8). Because the reaction involves the reversible exchange of protons, the reaction progress is affected by the pH and ionic strength of the solvent (9). However, different groups, based on their kinetic data, proposed several competing mechanisms for the pH-dependent effects, including a partial random-ordered bi-bi mechanism (10), abortive complexes being formed at higher pH values (11), a reciprocating compulsory ordered mechanism (12), and an ordered bi-bi mechanism with several abortive complexes formed (13,14).

To identify the underlying kinetic mechanism for cMDH and develop a kinetic model for cMDH-catalyzed oxidation of MAL to explain pH-dependent effects, reaction progress was assayed in the forward (NAD reduction) and reverse (NADH oxidation) directions with NAD and MAL as product inhibitors at various pH values. The time-course data were fitted to various schemes to identify the cMDH-catalyzed reaction mechanism. Specifically, the alternative models illustrated in Fig. 1 as well as the models described in the Supporting Material were evaluated to determine those that cannot match the data and to estimate kinetic parameters of a model that can explain the data at all pH values. Finally, the identified mechanism for cMDH is compared to that reported from a recent similar study of mMDH (15).

Figure 1.

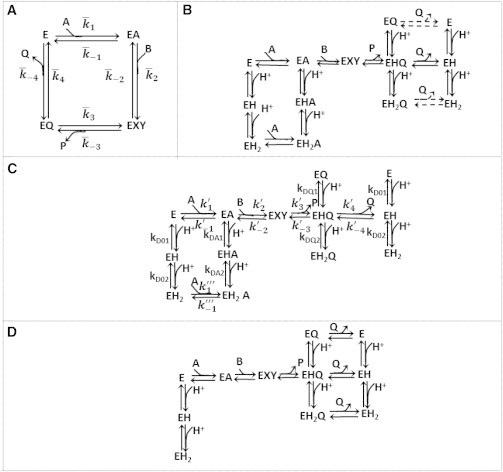
Schematic of the models employed. (A) An ordered bi-bi mechanism without any pH dependency; ${\overline{k}}_i$ denotes the apparent rate constants. (B) Ordered bi-bi mechanism with proposed pH mechanism; it is assumed that the coenzymes bind to all charged states. (Dashed lines) Reaction steps for which the rate constants are not identifiable for cMDH-catalyzed reaction. (C) Proposed model for cMDH. NAD binds to unprotonated and di-protonated enzyme states, while NADH binds to the uniprotonated enzyme state. (D) Proposed mechanism for pH dependency for mMDH (15). (Arrows) Binding/dissociation of coenzyme/substrate. In each of these schematics, A, B, P, and Q represent NAD, MAL, OAA, and NADH, respectively. In these schematics, EXY denotes the rapid conversion of EAB to EPQ.

Materials and Methods

Experimental materials

All reagents, including cMDH enzyme from porcine heart in ammonium sulfate suspension, were purchased from Sigma (Sigma-Aldrich, St. Louis, MO) and used without further purification. Approximately 5 μL of the enzyme stock solution (5 k IU, manufacturer’s specification) of the enzyme was diluted to prepare the 500 μL of 100 IU enzyme solution. All other aspects of experimental protocols were identical to the protocols reported for mMDH (15). Briefly, experiments were performed at a physiological ionic strength of 0.17 M; 25°C temperature; enzyme concentration of ∼0.3 IU/mL (according to manufacturer’s specification) in the cuvette; pH varying between 6.5 and 9.0; and in the forward (NAD reduction) and reverse (NADH oxidation) directions, both with and without products initially present. The time-course data for the reaction to reach steady state was collected by measuring NADH absorbance/fluorescence, as detailed in Dasika et al. (15). Experiments with each initial condition were repeated four times for reproducibility.

Mathematical model

Malate dehydrogenase catalyzes the following chemical reaction:

$${\text{NAD}}^{-}+{\text{MAL}}^{2-}\rightleftarrows {\text{NADH}}^{2-}+{\text{OAA}}^{2-}+{\text{H}}^{+}.$$ (1)

The thermodynamic equilibrium constant at a given temperature, T, is computed (16) as

$$K_{\text{eq}}=\text{exp}\left(-\frac{{\text{Δ}}_r{G}^0}{RT}\right),$$ (2)

where Δ_rG⁰ is the standard Gibbs free energy of the reaction, and R is the universal gas constant (8.314 × 10⁻³ kJ/mol K). The standard Gibbs free energy of the reaction can be expressed as (16,17)

$${\text{Δ}}_r{G}^0={\text{Δ}}_f{G}_{\text{NADH}}^0+{\text{Δ}}_f{G}_{\text{OAA}}^{\text{0}}-{\text{Δ}}_f{G}_{\text{NAD}}^{\text{0}}-{\text{Δ}}_f{G}_{\text{MAL}}^{\text{0}},$$ (3)

where ${\text{Δ}}_f{G}_{\text{NADH}}^{\text{0}}$, ${\text{Δ}}_f{G}_{\text{OAA}}^{\text{0}}$, ${\text{Δ}}_f{G}_{\text{NAD}}^{\text{0}}$, and ${\text{Δ}}_f{G}_{\text{MAL}}^{\text{0}}$ are the standard formation free energies for the chemical species in the reaction. The effects of temperature and ionic strength over the temperature range of 273–313 K on the Gibbs free energy for species i can be approximated as (16,17)

$${\text{Δ}}_f{G}_i^0\left(I,T\right)=\frac{T}{T_1}{\text{Δ}}_f{G}_i^0\left(0,T_1\right)-RT\propto \left(T\right){\gamma }_i,$$ (4)

where I is the ionic strength; γ_i is the activity of species i; T₁ and T are the reference and desired temperatures, respectively; β = 1.6 M^−1/2; and ∝ (T) = 1.107 – 1.545 × 10⁻³ T + 5.95 × 10⁻⁶ T² (16,17). Over the temperature range of T = 273–313 K, the effect of ionic strength I on γ_i is estimated as

$${\gamma }_i=\frac{I^{1/2}}{\left(1+\beta I^{1/2}\right)}{z}_i^2,$$

where z_i is the valance of species i (16). Under conditions of 298 K and ionic strength of 0.17 M, Δ_rG⁰ = 71.09 kJ/mol (17) for the reaction of Eq. 1.

We define the equilibrium mass action ratio as

$${\left(\frac{\left[{\text{NADH}}^{2-}\right]\left[{\text{OAA}}^{2-}\right]}{\left[{\text{NAD}}^{-}\right]\left[{\text{MAL}}^{2-}\right]}\right)}_{\text{eq}}=K_{\text{eq}}^{\prime }=K_{\text{eq}}\frac{1}{h},$$ (5)

where h represents the hydrogen ion activity computed as h = 10^−pH. The K′_eq, estimated from Li et al. (17) at I = 0.17 M and T = 25°C, is 8.3 × 10⁻¹³ M⁻¹.

The kinetic model used to analyze data on this reaction is based on the ordered bi-bi mechanism illustrated in Fig. 1 A. Specifically, it is assumed that at a given pH, the reaction follows a quasi-steady rate law for the ordered bi-bi mechanism that can be computed as (18)

$$\frac{dP}{dt}=\frac{dQ}{dt}=-\frac{dA}{dt}=-\frac{dB}{dt}=\frac{E_0\left({\overline{k}}_1{\overline{k}}_2{\overline{k}}_3{\overline{k}}_4\left[A\right]\left[B\right]-{\overline{k}}_{-1}{\overline{k}}_{-2}{\overline{k}}_{-3}{\overline{k}}_{-4}\left[P\right]\left[Q\right]\right)}{\text{den}},$$ (6)

where the denominator term is

$${\overline{k}}_{-1}{\overline{k}}_4\left({\overline{k}}_{-2}+{\overline{k}}_3\right)+{\overline{k}}_1{\overline{k}}_4\left({\overline{k}}_{-2}+{\overline{k}}_3\right)\left[A\right]+{\overline{k}}_2{\overline{k}}_3{\overline{k}}_4\left[B\right]+{\overline{k}}_{-1}{\overline{k}}_{-2}{\overline{k}}_{-3}\left[P\right]+{\overline{k}}_1{\overline{k}}_{-4}\left({\overline{k}}_{-2}+{\overline{k}}_3\right)\left[Q\right]+{\overline{k}}_1{\overline{k}}_2\left({\overline{k}}_3+{\overline{k}}_4\right)\left[A\right]\left[B\right]+{\overline{k}}_1{\overline{k}}_{-2}{\overline{k}}_{-3}\left[A\right]\left[P\right]+{\overline{k}}_2{\overline{k}}_3{\overline{k}}_{-4}\left[B\right]\left[Q\right]+{\overline{k}}_{-3}{\overline{k}}_{-4}\left({\overline{k}}_{-1}+{\overline{k}}_{-2}\right)\left[P\right]\left[Q\right]+{\overline{k}}_1{\overline{k}}_2{\overline{k}}_{-3}\left[A\right]\left[B\right]\left[Q\right]+{\overline{k}}_2{\overline{k}}_{-3}{\overline{k}}_{-4}\left[B\right]\left[P\right]\left[Q\right].$$ (7)

In this equation, E₀ is the enzyme concentration; [A], [B], [P], and [Q] represent concentration of species NAD⁻, MAL²⁻, NADH²⁻, and OAA²⁻, respectively; and the ${\overline{k}}_i$ represent apparent rate constants. The concentrations of species malate and oxaloacetate depend on pH and are expressed using binding polynomials, defined as

$$\begin{array}{l}{P}_{\text{MAL}}=\left(1+\frac{h}{K_{H,\text{MAL}}}\right),\\ P_{\text{OAA}}=\left(1+\frac{h}{K_{H,\text{OAA}}}\right),\end{array}$$ (8)

where $K_{H,\text{OAA}}={10}^{-pK,\text{OAA}}$, $K_{H,\text{MAL}}={10}^{-pK,\text{MAL}}$, $pK,\text{OAA}=3.9$, and $pK,\text{MAL}=4.715$ (17). Using these binding polynomials, the concentrations of species MAL²⁻ and OAA⁻ are computed as

$$\begin{array}{l}\left[{\text{MAL}}^{2-}\right]=\frac{\left[\text{MAL}\right]}{P_{\text{MAL}}},\\ \left[{\text{OAA}}^{2-}\right]=\frac{\left[\text{OAA}\right]}{P_{\text{OAA}}},\end{array}$$ (9)

where [MAL] and [OAA] are the total concentrations of malate and oxaloacetate. The reactants NAD and NADH are assumed to not significantly bind protons or other cations in the reaction buffers used (17).

Thermodynamic aspects of the model and the application of the ordered bi-bi mechanism are identical to those detailed in Dasika et al. (15). Thus, Eqs. 1–9, which are reproduced here for completeness, are identical to Eqs. 1–9 in Dasika et al. (15).

The effects of pH on reaction kinetics are simulated using the pH-dependent mechanisms illustrated in Fig. 1, B–D, which assume that the enzyme exists in three protonated states. Fig. 1 D illustrates the mechanism of minimal complexity determined to fit the kinetic data from the mMDH isoform (15), while Fig. 1 C illustrates the proposed mechanism determined to fit the data reported here on the cMDH isoform. (The consensus mechanism of Fig. 1 B combines the minimal models for the mMDH and cMDH into a common global mechanism.)

Here, the kinetic equations for the proposed cMDH mechanism (Fig. 1 C) are presented in detail. Similar equations for the mMDH model are presented in Dasika et al. (15). The mMDH model was found to be inadequate to fit the data presented below for the cMDH isozyme. It is assumed that NAD potentially binds to unprotonated and diprotonated state while NADH is assumed to bind only to a uniprotonated state. The model assumes rapid equilibrium between protonated enzyme states. Under these assumptions, the effective rate constants, ${\overline{k}}_{-2}$, and ${\overline{k}}_3$ are independent of pH.

Based on the mechanism of Fig. 1 C, the apparent rate constants ${\overline{k}}_i$ are computed as (19)

$$\begin{array}{l}{\overline{k}}_1=\frac{\left(k_1^{\prime }+k_1^{\prime \prime \prime }\frac{h}{k_{D01}}\frac{h}{k_{D02}}\right)}{p_{01}},\\ {\overline{k}}_{-1}=\frac{\left(k_{-1}^{\prime }+k_{-1}^{\prime \prime \prime }\frac{h}{k_{DA1}}\frac{h}{k_{DA2}}\right)}{p_A},\\ {\overline{k}}_{-2}=k_{-2}^{\prime },\\ {\overline{k}}_3=k_3^{\prime },\\ {\overline{k}}_{-3}=\frac{\left(k_{-3}^{\prime }\frac{h}{k_{DQ1}}\right)}{p_Q},\\ {\overline{k}}_4=\frac{\left(k_4^{\prime }\frac{h}{k_{DQ1}}\right)}{p_Q},\\ {\overline{k}}_{-4}=\frac{\left(k_{-4}^{\prime }\frac{h}{k_{D01}}\right)}{p_{01}},\end{array}$$ (10)

where p₀₁, p_A1, and P_Q are defined as

$$p_{01}=1+\frac{h}{k_{D01}}+\frac{h}{k_{D01}}\frac{h}{k_{D02}},$$

$$p_{A1}=1+\frac{h}{k_{DA1}}+\frac{h}{k_{DA1}}\frac{h}{k_{DA2}},\text{and}$$

$$p_Q=1+\frac{h}{k_{DQ1}}+\frac{h}{k_{DQ1}}\frac{h}{k_{DQ2}},k_{Di}={10}^{-p{K}_i}.$$

In Eq. 10, the activities are lumped into the rate constants to take into account the charge of the enzyme complex. The parameters k_i^′ are not independent, and are bound by the following thermodynamic constraint:

$$\frac{k_1^{\prime }}{k_{-1}^{\prime }}=\frac{k_1^{\prime \prime \prime }}{k_{-1}^{\prime \prime \prime }}\frac{k_{DA1}}{k_{D01}}\frac{k_{DA2}}{k_{D02}}.$$ (11)

Given the above definitions for the apparent rate constants, the quasi-steady reaction rate is computed according to Eqs. 6 and 7.

This model invokes a total of 14 adjustable parameters, which are listed in Table 1 and identified based on experimental data detailed below. The criterion used to discriminate between the models was the cost function, defined as the sum of squares of error between the model output and experimental data normalized by the standard deviation in the data. Confidence intervals for parameter estimates are computed following the procedure of Landaw and DiStefano (20). Parameter estimation and other calculations were obtained using the software MATLAB (The MathWorks, Cambridge, MA).

Table 1.

Values for various models with confidence intervals

Parameter	Value	Unit
k1′	2.57 × 104 ± 5.13 × 102	mM−1 min−1
k1″′	5.37 × 103 ± 3.54 × 102	mM−1 min−1
k−1′	8.16 × 104 ± 5.78 × 102	Min−1
k−2′	1.00 × 107 ± 3.06 × 106	Min−1
k3′	4.98 × 106 ± 1.82 × 106	Min−1
k−3′	1.50 × 106 ± 2.70 × 105	mM−1 min−1
k4′	1.73 × 104 ± 2.94 × 102	Min−1
k−4′	3.61 × 106 ± 1.02 × 105	mM−1 min−1
pK01	7.80 ± 0.01	Unitless
pK02	6.22 ± 0.04	Unitless
pKA1	7.42 ± 0.01	Unitless
pKA2	5.27 ± 0.19	Unitless
pKQ1	8.68 ± 0.01	Unitless
pKQ2	5.00 ± 0.15	Unitless

Results

Figs. 2, 3, 4, 5, 6, and 7 illustrate time-course measurements of reaction progress, measured by appearance or disappearance of NADH, under a variety of conditions representing forward and reverse reaction kinetics. Fig. 2 shows forward-direction progress curves assayed under pH values of 6.5, 7, 7.5, 8, 8.5, and 9, with initial [MAL] ranging from 0.5 to 20 mM, and with initial [NAD] of 1 mM for all cases. Fig. 3 shows reverse-direction progress curves assayed at the same pH values, using initial [NADH] of 300 μM and varying initial [OAA] of 50 and 100 μM. Progress curves in Figs. 2 and 3 were obtained with no reaction product initially present in the reaction buffers. Figs. 4, 5, 6, and 7 show reverse-direction progress curves assayed under the same conditions as the experiments of Fig. 3, with the addition of varying amounts of initial products (NAD and MAL) present in the reaction buffer, as indicated in figure legends.

Figure 2.

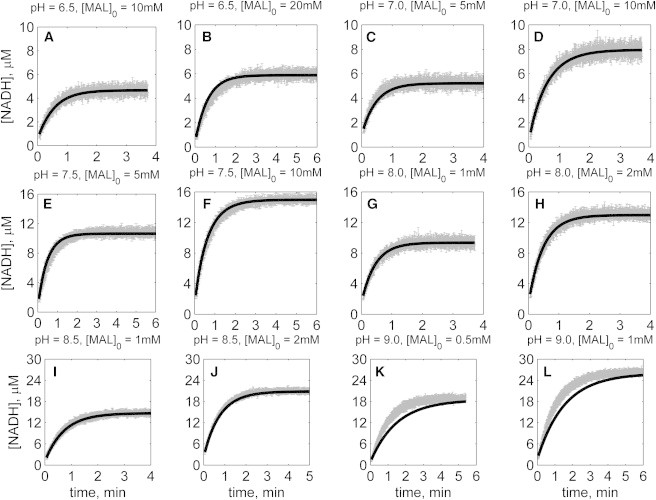
Time-course data in the forward direction (NAD reduction) at various pH values (A–L) without product inhibitors present in the initial buffer. Initial conditions are [NAD]₀ = 1 mM, and pH and [MAL]₀ represented in the individual plot (in each plot, shaded lines and solid lines, respectively, represent mean with standard deviation of experimentally measured [NADH], and [NADH] obtained from fitting data to ordered bi-bi mechanism; Fig. 1C).

Figure 3.

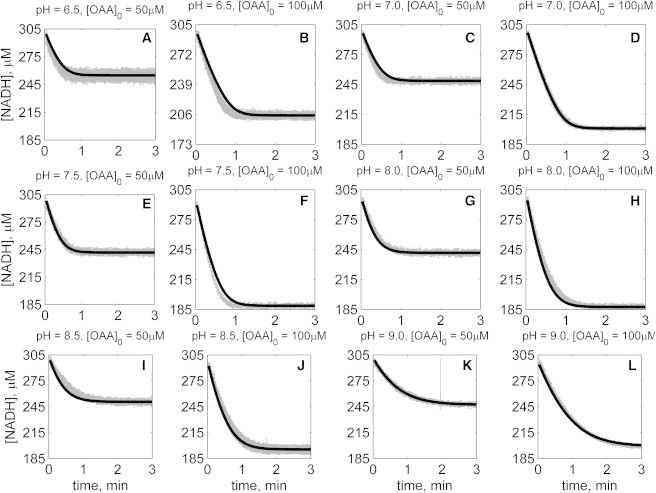
Time-course data in the reverse direction (NADH oxidation) at various pH values (A–L) without product inhibitors present in the initial buffer. Initial conditions are [NADH]₀ = 300 μM, and pH and [OAA]₀ represented in the individual plot (in each plot, shaded lines and solid lines, respectively, represent mean with standard deviation of experimentally measured [NADH], and [NADH] obtained from fitting data to ordered bi-bi mechanism; Fig. 1C).

Figure 4.

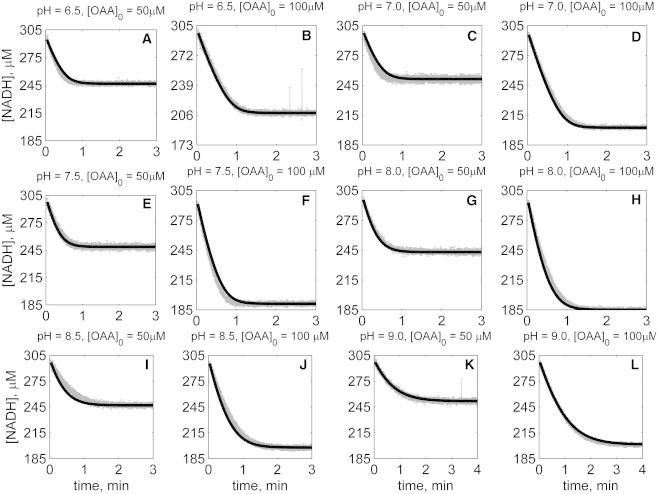
Time-course data in the reverse direction (NADH oxidation) at various pH values (A–L) with 1 mM NAD as product inhibitor present in the initial buffer. Initial conditions are [NADH]₀ = 300 μM, [NAD]₀ = 1 mM, and pH and [OAA]₀ represented in the individual plot (in each plot, shaded lines and solid lines, respectively, represent mean with standard deviation of experimentally measured [NADH], and [NADH] obtained from fitting data to ordered bi-bi mechanism; Fig. 1C).

Figure 5.

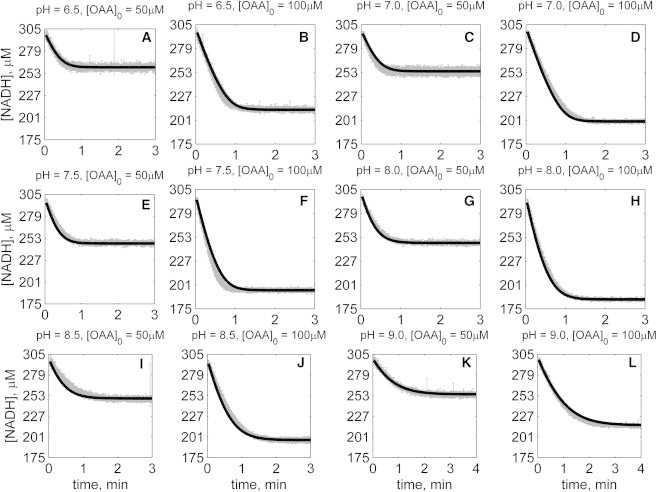
Time-course data in the reverse direction (NADH oxidation) at various pH values (A–L) with 2 mM NAD as product inhibitor present in the initial buffer. Initial conditions are [NADH]₀ = 300 μM, [NAD]₀ = 2 mM, and pH and [OAA]₀ represented in the individual plot (in each plot, shaded lines and solid lines, respectively, represent mean with standard deviation of experimentally measured [NADH], and [NADH] obtained from fitting data to ordered bi-bi mechanism; Fig. 1C).

Figure 6.

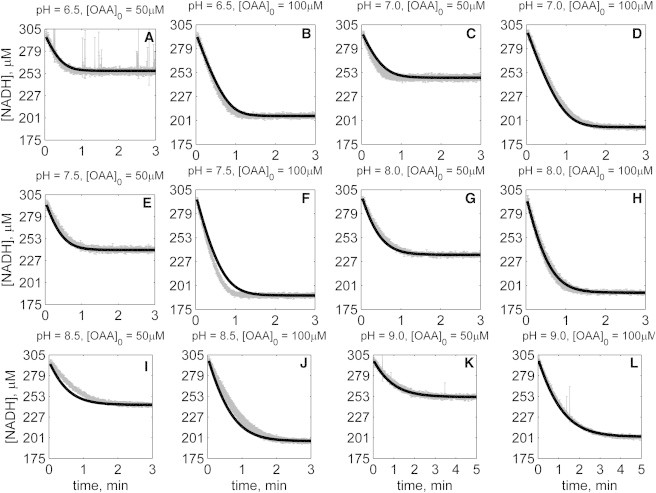
Time-course data in the reverse direction (NADH oxidation) at various pH values (A–L) with 1 mM MAL as product inhibitor present in the initial buffer. Initial conditions are: [NADH]₀ = 300 μM, [MAL]₀ = 1 mM, and pH and [OAA]₀ represented in the individual plot (in each plot, shaded lines and solid lines, respectively, represent mean with standard deviation of experimentally measured [NADH], and [NADH] obtained from fitting data to ordered bi-bi mechanism; Fig. 1C).

Figure 7.

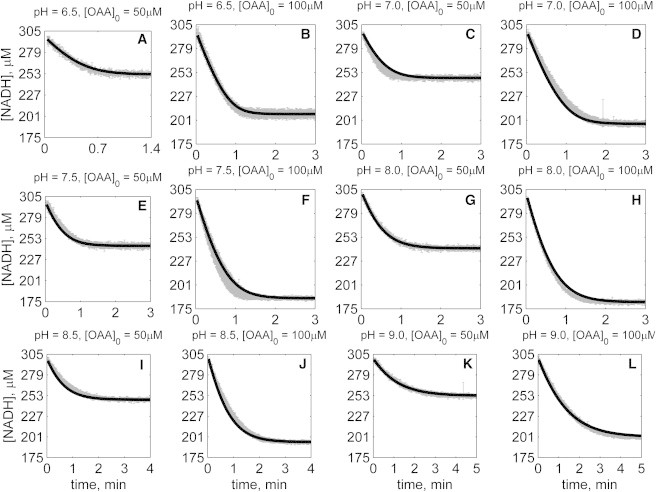
Time-course data in the reverse direction (NADH oxidation) at various pH values (A–L) with 2 mM MAL as product inhibitor present in the initial buffer. Initial conditions are [NADH]₀ = 300 μM, [MAL]₀ = 2 mM, and pH and [OAA]₀ represented in the individual plot (in each plot, shaded lines and solid lines, respectively, represent mean with standard deviation of experimentally measured [NADH], and [NADH] obtained from fitting data to ordered bi-bi mechanism; Fig. 1C).

In sum, the 72 progress curves illustrated in Figs. 2, 3, 4, 5, 6, and 7 represent a rich data set for model identification. It was determined that at each fixed pH value an ordered bi-bi mechanism can effectively fit the time-course data while the Theorell-Chance mechanism cannot, regardless of the value of the kinetic parameters. (For details, see the Supporting Material.) Thus, the mechanisms illustrated in Fig. 1, B–D, which reduce to an ordered bi-bi mechanism at constant pH, represent viable alternative mechanisms to test against the global data set.

Model fits described below are associated with the mechanism of Fig. 1 C, which is able to effectively capture the observed kinetics for the cMDH-catalyzed reaction. The mechanism in Fig. 1 B represents a general mechanism capturing all of the steps in the mechanisms given in Fig. 1, C and D. The mechanism of Fig. 1 B is able to explain both the data set reported here for cMDH and that for mMDH reported by Dasika et al. (15), albeit with different parameter values. The global model of Fig. 1 B resulted in the lowest cost function of the three pH-dependent mechanisms tested. However, some of the parameters were unidentifiable for this model. By systematically eliminating the steps in the mechanism of Fig. 1 B that are associated with the parameters least sensitive to the time-course data, we arrived at the proposed kinetic mechanism of Fig. 1 C, for which the best-fit to the data is associated with an error that is only 2% greater than that of the model of Fig. 1 B. This mechanism is the least complex (in terms of number of adjustable parameters) viable model cMDH-catalyzed oxidation of MAL that we were able to find. The best fits to the time-course kinetic data associated with Fig. 1 C are similar to those obtained based on the more complex model of Fig. 1 B.

The mechanism of Fig. 1 D, which explains the data from the mMDH isozyme (15), proved unable to match the data reported here for the cMDH isoform, particularly in the forward direction. (Equations for the Fig. 1 D mechanism are detailed in Dasika et al. (15). The inability of this model to fit the kinetic data is illustrated in the Supporting Material.)

The solid lines in Figs. 2, 3, 4, 5, 6, and 7 represent best-fit model simulations, using the parameter values tabulated in Table 1. These 14 adjustable parameters are identified with mean values and reported 95% confidence intervals based on fitting the model predictions to the 72 progress curves. In all cases the model accurately fits the initial part (initial velocity) of the data. Model fits deviate from experimental data before reaching equilibrium in some cases (Figs. 2, K and L, 4, F and I, 6, I and J, and 7, H and I). However, differences between model and data are always within 25% of the observed data and can be attributed to variability in experimental conditions such as enzyme reconstitution. For all parameters, the uncertainty range is <18% of the mean parameter estimate. Attempts to improve the fits with additional pH-dependent states and additional dead-end complexes did not yield any significant improvement.

The final equilibrium concentrations attained under the conditions illustrated in Figs. 2, 3, 4, 5, 6, and 7 provide estimates of the apparent equilibrium constant K′_eq at the different pH values studied. The measured values of K′_eq as a function of pH are listed in Table 2, and the thermodynamic equilibrium constant K_eq was computed from Eq. 5. These values of K′_eq as a function of pH are consistent with an estimate of K_eq = 7.5 × 10⁻¹³ M⁻¹ for the chemical reaction at I = 0.17 M, T = 25°C, which is within 10% of the value estimated from the database of Li et al. (17), which yields an estimate of K_eq = 8.3 × 10⁻¹³ M⁻¹. Note that the predicted equilibrium [NADH] value attained in the forward experiments varies with the square-root of K_eq. Consequently, the value of K_eq = 8.3 × 10⁻¹³ M⁻¹ would result in an equilibrium [NADH] that is 5% greater than the value K_eq = 7.5 × 10⁻¹³ M⁻¹, for a given experiment. This difference is not distinguishable within the noise of the data. However, the kinetic time course for all experiments in the forward and reverse directions depends on K_eq. Because we observed that the time-course data fits with all pH values in both forward and reverse directions yielded a lower error with K_eq = 8.3 × 10⁻¹³ M⁻¹ (value from the database) compared to K_eq = 7.5 × 10⁻¹³ M⁻¹ (value estimated above), we used the K_eq = 8.3 × 10⁻¹³ M⁻¹ in the model fits.

Table 2.

Apparent equilibrium constant for various pH values and initial conditions from the experiments and the database; experimental values are close to the values from the database

pH	[MAL]0, mM	K′eq, experiment	K′eq, database
6.5	10	2.21 × 10−6 ± 9.27 × 10−8	2.62 × 10−6
6.5	20	1.77 × 10−6 ± 1.12 × 10−7	2.62 × 10−6
7	5	5.50 × 10−6 ± 4.90 × 10−7	8.30 × 10−6
7	10	6.46 × 10−6 ± 6.64 × 10−7	8.30 × 10−6
7.5	5	2.29 × 10−5 ± 1.98 × 10−6	2.62 × 10−5
7.5	10	2.29 × 10−5 ± 4.28 × 10−7	2.62 × 10−5
8	1	9.00 × 10−5 ± 5.49 × 10−6	8.30 × 10−5
8	2	8.67 × 10−5 ± 3.18 × 10−6	8.30 × 10−5
8.5	1	2.27 × 10−4 ± 1.48 × 10−5	2.62 × 10−4
8.5	2	2.27 × 10−4 ± 8.54 × 10−6	2.62 × 10−4
9	0.5	7.52 × 10−4 ± 4.31 × 10−5	8.30 × 10−4
9	1	7.35 × 10−4 ± 3.17 × 10−5	8.30 × 10−4

Discussion

Kinetic mechanism

Our observation that an ordered bi-bi mechanism can fit kinetic time-course data on the cMDH-catalyzed reaction is consistent with previous studies, including structural studies performed by Chapman et al. (8), where they observed the active loop on cMDH closing after sequential binding of NADH binding to the enzyme followed by the substrate. The identified pH-dependent mechanism for cMDH (Fig. 1 C) differs from that identified for mMDH (Fig. 1 D). Specifically, in the proposed model for cMDH it is assumed the NAD binds to E⁰ and E²⁻ enzyme charged states whereas NADH binds to the E⁻ charged state alone. This is in contrast with the mMDH model of Dasika et al. (15), where NADH binds to all protonated states of the enzyme while NAD binds to E⁰ state alone. Combining the mechanisms of Fig. 1, C and D, results in the common global mechanism represented by Fig. 1 B.

The kinetic behaviors of the two isoenzymes can be compared by simulating the identified models for mMDH and cMDH under identical conditions. Fig. 8 shows the plots of activity of both enzymes in the forward direction (NAD reduction) as functions of pH. Simulations were performed at T = 25°C, I = 0.17 M, with pH values varying from 6.5 to 9.0 in the forward direction with [NAD] varying from 5 μM to 1.5 mM, and [MAL] varying from 0.5 to 10 mM, with no product present. The cMDH activity (solid gray lines) is similar to that of mMDH for low [MAL] (Fig. 8, A, D, and G) while the mMDH activity (solid black lines) is higher than cMDH for all other concentrations of NAD and MAL. Also, the cMDH activity exhibits a peak at pH 8 while the mMDH activity increases with pH for all concentrations of NAD and MAL (Fig. 8, E, F, H, and I), suggesting that cMDH becomes sensitive to pH at high NAD and MAL concentrations while the mMDH is relatively insensitive to pH for all NAD and MAL concentrations. At high NAD and MAL concentrations (Figs. 8, H and I), the cMDH activity is higher than mMDH for pH <8, while the mMDH activity is higher than cMDH for pH >8.

Figure 8.

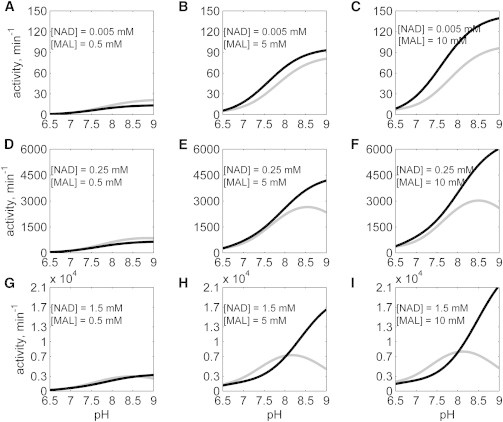
Simulated data comparison between cMDH and mMDH in the forward direction with no products present (A–I): NAD and MAL concentrations were as indicated in the individual plots; the activity (defined as the ratio of initial velocity to the enzyme concentration) of mMDH (represented by solid black line) is higher compared to cMDH (represented by solid gray line).

To compare function in the reverse direction (NADH oxidation, Fig. 9), simulations were performed with [NADH] varying from 5 μM to 2.5 mM, and [OAA] varying from 1 to 10 μM, with no NAD or MAL present. The activities of both isoenzymes increase with increasing [NADH]. In this reaction direction, cMDH activity is higher than mMDH for low [NADH] (5 μM) (Fig. 9, A–C) whereas the mMDH activity is higher than cMDH activity for higher [NADH] (Fig. 9, D–I). The sensitivity of mMDH activity to pH decreases with increase in [NADH], with the mMDH activity decreasing for higher pH values (Fig. 9, A–C). The cMDH mechanism is predicted to be much more sensitive to [NADH] than the mMDH mechanism under these conditions.

Figure 9.

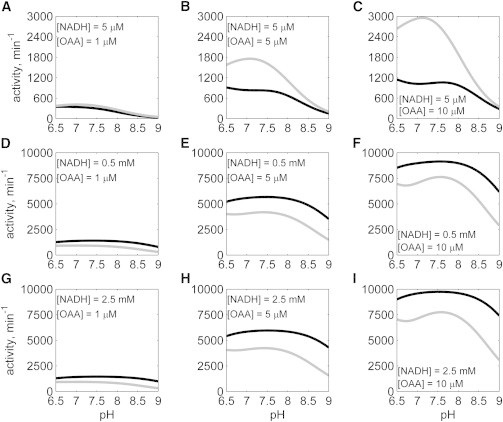
Simulated data comparison between cMDH and mMDH in the reverse direction with no products present (A–I): NADH and OAA concentrations were as indicated in the individual plots; the activity of mMDH (represented by solid black line) is lower compared to cMDH (represented by solid gray line) for low [OAA], whereas the mMDH activity is higher compared to cMDH for higher [OAA].

These predicted activity differences are further probed by comparing predicted activity under approximate physiological conditions in Fig. 10. These calculations were conducted with physiological ionic strength of 0.17 M and pH varying from 6 to 8. For Fig. 10 A (mimicking the mitochondrial matrix conditions), reactant conditions are [NADH] = 0.8 mM and [NAD] = 5.8 mM (21), [MAL] = 5 mM, and [OAA] = 0.3 μM (22). For Fig. 10 B (mimicking cytosolic conditions), reactant concentrations are [NADH] = 0.01 mM, [NAD] = 0.99 mM (21), [MAL] = 0.5 mM, and [OAA]₀ = 5 μM (22). Under mitochondrial conditions, mMDH activity (solid black lines) is higher than cMDH activity (solid gray lines, Fig. 10 A), while cMDH activity is higher than mMDH activity under cytoplasmic conditions (Fig. 10 B). Thus, the model identified here for cMDH and that identified by Dasika et al. (15) for mMDH suggest that each of these enzymes operates ideally (in terms of having higher activity) in its respective cellular compartment.

Figure 10.

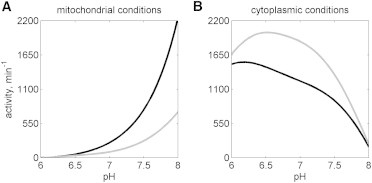
Activity comparison between both isoenzymes under the following physiological conditions: (A) [NADH] = 0.8 mM, [OAA] = 0.3 μM, [NAD] = 5.8 mM, [MAL] = 5 mM; and (B) [NADH] = 0.01 mM, [OAA] = 5 μM, [NAD] = 0.99 mM, [MAL] = 0.5 mM. The mMDH activity (solid black lines) is higher than cMDH (solid gray lines) under mitochondrial conditions, whereas the cMDH activity is higher than the mMDH activity under cytoplasmic conditions, suggesting these enzymes are efficient under their physiological concentrations.

Equilibrium constant

The apparent equilibrium constant has been computed for each pH value in the forward direction (Table 2). The K′_eq from our experiments at pH 8.5 (2.3 × 10⁻⁴) is in agreement with the value obtained from Cassman and Englard (2.5 × 10⁻⁴) (10), similar to the value found by Dasika et al. (15) (2.7 × 10⁻⁴), and close to the value predicted from the database (2.6 × 10⁻⁴) (17), while K′_eq at pH 8.0 (8.6 × 10⁻⁵) is in agreement with that of Dupourque and Kun (8.5 × 10⁻⁵) (23). The thermodynamic equilibrium obtained at each pH varied between 6 × 10⁻¹³ M⁻¹ and 8.9 × 10⁻¹³ M⁻¹ with an average of 7.5 × 10⁻¹³ M⁻¹. To avoid any variability in the results, we employed the K_eq value of 8.3 × 10⁻¹³ M⁻¹ from the database (17).

Conclusions

A kinetic model for cMDH-catalyzed reaction has been developed and identified based on an extensive set of reaction progress curves. It is concluded that the cMDH-catalyzed reaction is an ordered mechanism with coenzyme binding first followed by the substrate binding. The detailed pH-dependent mechanism is illustrated in Fig. 1 C. Comparing the activity with mMDH under physiological conditions, the mMDH activity is predicted to be higher than cMDH activity under mitochondrial conditions while the cMDH activity is predicted to be higher than mMDH activity under cytoplasmic conditions.