SLAM: Cross-Species Gene Finding and Alignment with a Generalized Pair Hidden Markov Model

Abstract

Comparative-based gene recognition is driven by the principle that conserved regions between related organisms are more likely than divergent regions to be coding. We describe a probabilistic framework for gene structure and alignment that can be used to simultaneously find both the gene structure and alignment of two syntenic genomic regions. A key feature of the method is the ability to enhance gene predictions by finding the best alignment between two syntenic sequences, while at the same time finding biologically meaningful alignments that preserve the correspondence between coding exons. Our probabilistic framework is the generalized pair hidden Markov model, a hybrid of (1) generalized hidden Markov models, which have been used previously for gene finding, and (2) pair hidden Markov models, which have applications to sequence alignment. We have built a gene finding and alignment program called SLAM, which aligns and identifies complete exon/intron structures of genes in two related but unannotated sequences of DNA. SLAM is able to reliably predict gene structures for any suitably related pair of organisms, most notably with fewer false-positive predictions compared to previous methods (examples are provided for Homo sapiens/Mus musculus and Plasmodium falciparum/Plasmodium vivax comparisons). Accuracy is obtained by distinguishing conserved noncoding sequence (CNS) from conserved coding sequence. CNS annotation is a novel feature of SLAM and may be useful for the annotation of UTRs, regulatory elements, and other noncoding features.

The idea of comparing organisms in order to further the understanding of their biology has been a central theme in biology, arguably originating with the work of Darwin, who formalized the theory of evolution by observing the similarities and differences between related organisms. The comparative method itself has evolved, advancing much in recent years with the ability to compare the genomic sequences of organisms. These comparisons have yielded many new results, often leading directly to important biological discoveries (for a recent example, see Penacchio et al. 2001). Indeed, motivated by the success of comparative genomics in identifying regulatory elements, Hardison et al. (1997) suggested sequencing the mouse genome for the purpose of annotating the human genome.

Comparative gene finding with such large volumes of data requires formalization and automation of methods. This process began with the ROSETTA program (Batzoglou et al. 2000), the first automated program for annotating human genes using syntenic unannotated mouse genomic DNA. The comparative approach was subsequently adopted by several groups, resulting in the CEM program (Bafna and Huson 2000), TWINSCAN (Korf et al. 2001; http://genes.cs.wustl.edu), SGP-1 (Wiehe et al. 2001; http://www1.imim.es/datasets/humanmouse), and SGP-2 (R. Guigó, pers. comm.). These programs differ from the homology-based gene finders such as PROCRUSTES (Gelfand et al. 1996), GENOMESCAN (Yeh et al. 2001), and GENEWISE2 (Birney and Durbin 2000) in that rather than using protein homologs or confirming EST evidence to help in coding exon prediction, they compare two identical types of sequences (genomic DNA). This distinction is subtle but important; comparative-based gene finders can use extra information such as gene structure and splice site conservation, introducing complications different from the issues arising in other homology-based approaches.

At the same time that gene finding was moving toward the comparative approach, a similar development was taking place in the alignment community. Alignment programs such as BLAST (Altschul et al. 1990) had traditionally been based on pure sequence comparison. In both BLAST and other methods there had been no attempt to incorporate the annotation of the sequences being aligned into the alignment program. Because biological sequences do not display random patterns of conservation, the consideration of biological features during alignment can greatly improve performance. An excellent example of this is WABA (Wobble Aware Bulk Aligner, Kent and Zahler 2000), which takes advantage of the third base wobble in coding exons to improve alignment and was successfully applied towards the problem of aligning the Caenorhabditis elegans and C. briggsae genomes.

In this paper we describe a program that places the annotation and alignment problems on an equal footing. Our probabilistic model is a generalized pair hidden Markov model (GPHMM). Generalized hidden Markov models (GHMMs) have been applied successfully in gene finding programs such as GENSCAN (Burge and Karlin 1997; http://genes.mit.edu/GENSCAN.html) and GENIE (Reese et al. 2000). Pair hidden Markov models (PHMMs) have been used for alignment, and can be shown to be equivalent to the Needleman-Wunsch (Needleman and Wunsch 1970) alignment method (Durbin et al. 1998; Holmes 1998). The GPHMM we have developed directly generalizes both of these types of HMMs. As a special case, by appropriately altering model parameters, our method can be made equivalent to GHMM-based single-organism gene finders like GENSCAN and GENIE, or to comparative gene finders such as ROSETTA (which separates the steps of alignment and gene finding). We have built a program called SLAM which implements these ideas and can be used to annotate syntenic sequences by finding coding exons and conserved noncoding sequences, or as a global alignment program which takes advantage of the biological features of the sequences to improve the accuracy of the alignments.

RESULTS

The SLAM program was tested on the ROSETTA test set (Batzoglou et al. 2000) of 117 single-gene sequences as well as on the multigene HoxA cluster (220 Kb; L. Elnitski, pers. comm.), and the Elastin gene region (390 Kb, accession nos. NT_025776 and NT_014920). SLAM was compared to the following programs:

1. GENSCAN (Burge and Karlin 1997): makes gene predictions in genomic DNA from a single organism.

2. ROSETTA (Batzoglou et al. 2000): uses syntenic DNA pairs to make gene predictions in one sequence.

3. SGP-1 (Wiehe et al. 2001): uses syntenic DNA pairs to make gene predictions in both sequences.

4. SGP-2 (R. Guigó, pers. comm.): predicts genes in one sequence, incorporating as evidence matches to a collection of informant sequences.

5. TWINSCAN (Korf et al. 2001): predicts genes in one sequence, incorporating as evidence matches to a collection of informant sequences.

Note that the TWINSCAN web-server allows for the specification of a custom informant sequence to be used instead of the default informant sequence database. By supplying the syntenic mouse DNA as a custom informant sequence for a human region, it is therefore possible to run TWINSCAN on syntenic DNA pairs—we use the modifier TWINSCAN.p to label runs of this type. The most direct comparison is then between ROSETTA, SGP-1, SLAM, and TWINSCAN.p, because all run on a syntenic pair of genomic DNA sequences.TWINSCAN and SGP-2 fall into their own category, each incorporating matches against a database of mouse sequences to predict genes in human, and GENSCAN serves as a benchmark, making gene predictions using only one sequence.

Results for GENSCAN and TWINSCAN were obtained by submitting the test sets to their servers, and the results of SGP-1 on the ROSETTA set were retrieved from (Wiehe 2001). SGP-2 results for HoxA and Elastin were obtained from (R. Guigó, pers. comm.). The programs were compared using standard performance measures (Burset and Guigó 1996; Burge and Karlin 1997). The results of the programs on the test sets are summarized in Table 1. The table presents the sensitivity (SN) and the specificity (SP) at both the nucleotide and exon levels, the approximate correlation (AC), and rates for missed (ME) and wrong (WE) exons (false positives not overlapping any true exons).

Table 1.

Results on the Test Sets

Test set	Nucleotide level			Exon level
	SN	SP	AC	SN	SP	(SN+SP)/2	ME	WE
The ROSETTA set
ROSETTA	0.935	0.978	0.949	0.833	0.829	0.831	0.048	0.047
SGP-1	0.940	0.960	0.940	0.700	0.760	0.730	0.120	0.040
SLAM	0.951	0.981	0.960	0.783	0.755	0.769	0.038	0.057
TWINSCAN.p	0.960	0.941	0.940	0.855	0.824	0.840	0.045	0.081
TWINSCAN	0.984	0.889	0.923	0.839	0.767	0.803	0.034	0.118
GENSCAN	0.975	0.908	0.929	0.817	0.770	0.793	0.057	0.107
HoxA
SLAM	0.852	0.896	0.864	0.727	0.533	0.630	0.000	0.333
TWINSCAN.p	0.976	0.829	0.896	0.773	0.531	0.652	0.000	0.312
TWINSCAN	0.949	0.511	0.704	0.591	0.173	0.382	0.000	0.707
SGP-2	0.640	0.637	0.619	0.409	0.173	0.291	0.091	0.596
GENSCAN	0.932	0.687	0.796	0.545	0.235	0.390	0.000	0.569
Elastin
SLAM	0.876	0.981	0.926	0.802	0.859	0.831	0.121	0.059
TWINSCAN.p	0.942	0.950	0.945	0.879	0.889	0.884	0.066	0.056
TWINSCAN	0.933	0.877	0.903	0.835	0.826	0.831	0.110	0.120
SGP-2	0.755	0.998	0.873	0.593	0.900	0.291	0.352	0.017
GENSCAN	0.947	0.766	0.852	0.835	0.731	0.783	0.121	0.231

The measures of sensitivity SN = TP/TP + FN and specificity SP = TP/TP + FP (where TP = true positives, TN = true negatives, FP = false positives and FN = false negatives) are shown at both the nucleotide and exon level. ME is entirely missed exons, WE is wrong exons, and the approximate correlation AC = 1/2 (TP/TP + FN + TP/TP + FP + TN/TN + FP + TN/TN + FN) − 1 summarizes the overall nucleotide sensitivity and specificity by one number. Within each of the three data sets the methods are divided into three classes: those operating on a syntenic DNA pair, those operating on a human sequence using as evidence matches against a database of mouse sequences, and a single-organism gene finder (GENSCAN).

Perhaps the most striking aspect of the results shown in Table 1 is the difference in performance between the class of programs operating on syntenic pairs (ROSETTA, SGP-1, SLAM, and TWINSCAN.p) and the class of programs operating on human sequence using matches against a mouse database (SGP-2, TWINSCAN). This is not unexpected—when homology against a large database of sequences is used to boost exon scores, this will naturally include more false-positive alignments, leading to a degradation in specificity (the difference is particularly large in the case of HoxA, where the sensitivity achieved is even lower than that of a single-organism gene finder). At the same time, the increase in sensitivity when using homology against a large database is negligible. It is clear that whenever possible, it is better to operate on a syntenic DNA pair (though of course in practice the finished genomic data may not be available).

Analysis of the programs operating on syntenic pairs on the ROSETTA test set shows that although SLAM nucleotide sensitivity is slightly lower than that for TWINSCAN.p, the specificity is significantly higher, with half as many nucleotides being incorrectly predicted as coding. At the exon level, ROSETTA and TWINSCAN.p perform better. SLAM's high nucleotide scores in conjunction with the low wrong and missed exon rates suggest that it is getting exon boundaries slightly wrong rather than missing them entirely. The current model used for a human-mouse splice-site pair treats the splice-site sequences as independent in each organism. Clearly, modeling the significant conservation in splice-site pairs will improve exon-level performance. Examination of the longer HoxA and Elastin regions shows that SLAM's specificity is consistently higher. The lower sensitivity rates for SLAM on these regions is due in part to inaccurate approximate alignments (a preprocessing step done with AVID [Bray et al. 2003; http://bio.math.berkeley.edu/avid] to reduce the computational complexity of the GPHMM); this problem, which arises with longer (more difficult to align) regions, should be fixed with the forthcoming implementation of more sophisticated approximate alignment methods.

There are a number of reasons why we believe SLAM should be highly specific. A notable property shared by SLAM and SGP-1 is that the gene prediction is performed symmetrically in both sequences. In addition to requiring good alignment between exons, this has the effect of requiring conservation of exon-order and frame consistency in both sequences.

Another important and novel feature of SLAM is the prediction of conserved noncoding sequence (CNS). The annotation of CNSs allows for the distinction between conserved coding and conserved noncoding sequence in a probabilistic manner.

It has been observed (Makalowski et al. 1996; Burge and Karlin 1997) that in the case of human/mouse comparisons there is much noncoding conservation to be found, including UTR-, regulatory element-, and other biologically related conservation, and also nonfunctional background conservation. The CNS state significantly lowers the false-positive rate by eliminating the consideration of noncoding conserved regions as exons. To test the effectiveness of the CNS state, we examined the performance of SLAM on the ROSETTA test set with and without the CNS state. With the CNS state, SLAM predicted 548 CNSs with an average length of 103.2 bp and 78.9% identity. Running SLAM without the CNS state resulted in a drop in nucleotide specificity from 98.1% to 95.4%, and in exon specificity from 75.5% to 69.1%. One might expect the CNS state to increase the rate of false-negatives (missed exons) due to the fact that some true exons might be mistaken for CNS, but the exon sensitivity increased, from 76.9% without the CNS state to 78.3% with the state. This can almost certainly be attributed to the protein space exon scoring, which effectively distinguishes the type of conservation. Thus, it seems that comparative gene finding requires both an exon recognition component (based on protein alignment) and a conserved noncoding comparison (based on DNA alignment) to be effective.

Another example demonstrating the importance of the CNS state is the HoxA cluster in human and mouse. The region contains 11 HoxA genes (according to RefSeq annotations), each consisting of two exons. What makes this region particularly difficult for comparative gene finders is the remarkably high level of conservation in both coding and noncoding sequence. The intron and intergenic regions are 69% identical at the DNA level as opposed to the ∼36% that has been observed on average for human and mouse (Makalowski et al. 1996). This makes the overprediction of exons more likely, particularly for TWINSCAN and SGP-2, which boost exon scores on the basis of local alignments against a large database. The poor performance is due to the number of false-positive exons: 29 for GENSCAN, 53 for TWINSCAN, and 31 for SGP-2, as opposed to 10 for SLAM and 10 for TWINSCAN.p.

Figure 1 shows the region of the HoxA2 and HoxA3 genes in human (accession numbers NM_006735 and NM_030661, respectively), where there is a high level of conservation.The TBLASTX hits represent matches between this region and a database of mouse genomic sequence. SLAM and TWINSCAN.p do a good job of distinguishing between exons and CNSs, whereas SGP and TWINSCAN are led to some false positives by the high rate of TBLASTX hits against the mouse genome.

Figure 1.

Fourteen thousand bp from the HoxA cluster showing the HoxA2 and HoxA3 genes. The top half of the figure consists of predictions and annotations for the 5′ → 3′ strand and the bottom half for the 3′ → 5′ strand. The tracks shown are: RefSeq annotations, GENSCAN, TWINSCAN, SGP-2, and SLAM predictions, Repeats masked by RepeatMasker (A. Smit and P. Green, unpubl.), TBLASTX alignments, and SLAM and VISTA CNS annotations. The figure was created using gff2ps by J.F. Abril and R. Guigó, available at http://www1.imim.es/software/gfftools/GFF2PS.html.

In addition to being a necessary component to reduce false-positive predictions, we found that the CNS state enabled the identification of biologically important noncoding features. For instance, we have observed many cases where the SLAM CNS predictions agree excellently with UTR regions (we currently do not report quantitative results for UTR predictions due to the lack of reliable UTR annotations in our data sets).

The model used by SLAM is useful for organism pairs other than human and mouse. It has been retrained for use in comparisons between the malaria parasites Plasmodium falciparum and Plasmodium vivax. There are very few sequenced orthologous pairs currently available, but we were interested in these organisms because of the importance of the malaria genome and the major sequencing efforts underway. Because of the lack of data we were not able to undertake a performance analysis such as in Table 1 but as an example, we tested on the chloroquin resistance transporter syntenic gene pair (accessions AF030694 and AF314649). SLAM correctly found nine of the exon pairs, there being 13 exons in P. falciparum and 14 in P. vivax. The performance is good when one considers that the third exon in P. falciparum has an intron inserted in P. vivax, leading to a differing number of exons and violating the model assumptions. Moreover, the first two exon pairs were not included in the approximate alignment determined by AVID because of weak sequence homology, and so were not even considered. Also, the smaller size of this example allowed us to test the program with larger approximate alignments, thus moving us closer to simultaneous alignment and gene prediction, and these approximate alignments did not result in any extra false positives.

DISCUSSION

SLAM is the first implementation of a GPHMM, which simultaneously aligns and predicts genes in two orthologous sequences. Moreover, the requirement of valid gene structures in both sequences improves the accuracy of the program, most notably reducing the false-positive rate. The novel components of the program, such as a CNS state and paired exon scoring in protein space to distinguish coding from noncoding conservation, make SLAM a powerful tool that can be used for gene prediction as well as for alignment.

SLAM compares favorably to other gene finders, particularly with regard to the false-positive rate, which has been the Achilles' heel of many gene finding programs. It should be noted that the numbers quoted in our comparisons should be examined qualitatively to determine the relative strengths and weaknesses of the programs, rather than to obtain quantitative measures of their (expected) performance. In the tests performed it was impossible to ensure that the programs were trained and tested on the same sequences, partly due to the fact that there is not a lot of publicly available, well annotated orthologous sequence. Furthermore, different programs were optimized for different inputs. For instance, most of the gene finders (including SLAM) were optimized for larger genomic regions (or even for draft sequence) rather than single-gene sequences such as in the ROSETTA set. To account for this we also tested on two long regions, the HoxA cluster and the Elastin region. An extensive and quantitative comparison similar to the single-organism gene finding comparison in (Guigó et al. 2000) is a worthwhile endeavor to pursue in the future, as more data become available.

Nevertheless, we believe that the results obtained shed light on some of the relative strengths and weaknesses of the programs tested, and are valuable in that regard. For example, it is a well known fact that single-organism GHMM-based gene finders such as GENSCAN and GENIE have high false-positive rates (Guigó et al. 2000), and it has been universally accepted that “adding” homology information can reduce this problem. However, merely adding alignment information by boosting the scores of highly conserved potential exons is not enough. In shorter, single-gene regions, such as in the ROSETTA set, the difference between GENSCAN and TWINSCAN is negligible. On the other hand, longer, highly conserved regions such as the HoxA cluster demonstrate the difficulty faced by an approach that does not explicitly address the problem of distinguishing the type of conservation (the TWINSCAN program does leverage the third base pair wobble in determining whether to boost an exon score, but it does not distinguish coding from noncoding conservation). The introduction of a CNS state turned out to be crucial for bringing down the false-positive rate, and we included it in the model only after we discovered that it was impossible to remove false-positive predictions of UTRs that were highly conserved, and happened to contain open reading frames.

Examining CNS predictions by eye, we already noticed that they should be valuable for the detection of noncoding features, such as regulatory regions and UTRs. Indeed, it appears that predictions of CNSs will be an important application of human/mouse comparative studies, and it remains an open problem to establish the precise criteria for what a CNS is. The CNS model described in this paper can be extended and enhanced to take advantage of more complex conservation patterns when these are revealed through biological studies.

On the ROSETTA set, the SLAM performance is somewhat lower at the exon level. However, the high nucleotide sensitivity and specificity in conjunction with a low rate of missed exons indicate that most exons not predicted correctly have a significant overlap with true exons, the exon boundaries being slightly off. Future developments to the SLAM program will include the introduction of a paired splice-site model. The development of a good theoretical model for scoring splice sites in pairs remains an interesting, unsolved problem. The structure of the underlying Markovian-state space in SLAM models genes in both organisms, and includes the assumption that there the genes have the same number of exons (in the same order) in each organism. As mentioned above, this assumption allows for an increase in specificity by imposing additional constraints that are almost always valid. However, these assumptions are violated (albeit less than 1% of the time in human–mouse; Pachter 1999) and some orthologous genes have different numbers of exons, and/or frameshifts (related exons which have lengths that do not differ by a multiple of 3). These difficulties can be addressed by suitably modifying the GPHMM used.

A more serious obstacle to practically using the SLAM GPHMM method, is that in a naive implementation, the memory usage and the computational complexity scale as the order of the product of the lengths of the input sequences. One way of mitigating this problem is to preprocess the data, producing an approximate alignment as described in the Methods section, such that the computational task grows linearly in the length of one of the input sequences. This already helps immensely, but the pressing need for high-throughput algorithms requires even more sophisticated methods to reduce the memory and computational demands. Producing lean approximate alignments is an interesting problem in its own right, and we have been exploring different strategies, one of which is in development (Pachter et al. 2002).

The prospect of investigating the utility of SLAM CNS predictions, as well as the application of SLAM to finding alternatively spliced transcripts (by looking, for example, for suboptimal parses) is particularly exciting in light of the many successes that have been obtained by application of the comparative method.

A SLAM server, including datasets and additional information, is available at http://bio.math.berkeley.edu/slam/. The Web site also contains results of a SLAM human–mouse whole-genome analysis.

METHODS

Pairs of sequences and their associated gene structures and alignment were modeled using a GPHMM (Pachter et al. 2001). The input to SLAM consists of two sequences and an approximate alignment (Pachter et al. 2001). Approximate alignments are used to reduce the search space for the Viterbi algorithm, and allow for improvements in speed and reductions in memory usage. The main components in the SLAM GPHMM are currently a splice-site detector, an intron/intergene (I-state) model, an exon pair scoring model, and a conserved noncoding sequence (CNS) model. The state space and structure of the SLAM GPHMM are described below, followed by details of the various new components we have introduced.

The SLAM GPHMM

There are two types of HMMs relevant to our problem: pair HMMs and generalized HMMs. Whereas HMMs generate one single output in each step, a PHMM generates output in pairs, and GHMMs can generate output of different lengths (determined from a distribution) in each hidden state. The SLAM GPHMM is a combination of a PHMM and a GHMM. Details can be found in (Pachter et al. 2001).

The main difference between the SLAM GPHMM model and previous HMM-based gene finders is the interpretation of the outputs of the states. The SLAM model is a PHMM, and so the outputs in every state are aligned pairs of DNA bases. It is also a GHMM, meaning that there is a duration distribution associated with each of the generalized states (the exon states in this case). The result of combining the two HMMs is that the generalized states now generate two sets of durations (or lengths) for the exons, one for each of the sequences.

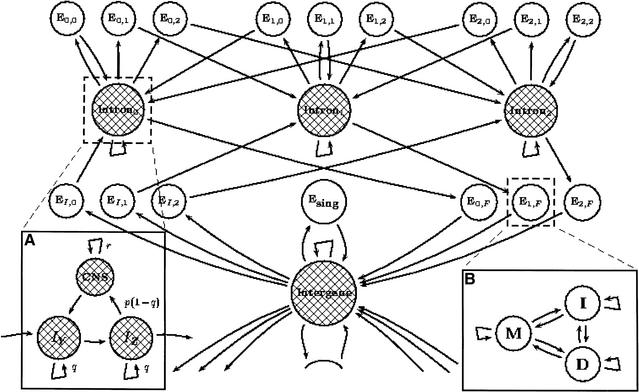
The state space of the SLAM GPHMM is outlined in Figure 2 (the model also contains a mirror-image to the unidirectional model, which allows for finding genes on both the forward and reverse strands). The generalized states (unshaded) have been distinguished from states, which allow self-transitions (shaded) to highlight the resulting partitioning of the state space. This partition results in the property that every unshaded state must be followed by a shaded one. This feature allows for a simplification of the HMM algorithms; in particular, it is only necessary to compute the various HMM variables for shaded states (leading to a reduction in memory requirements).

Figure 2.

A GPHMM for alignment and prediction of exons using genomic DNA from two different organisms. The shaded states are the typically less-conserved intergene and intron states, each producing either a single base or a gap in each organism. The use of self-transitions models their state durations as geometric. The unshaded states (all of which are exons) will all have duration 1, as they have no self-transitions; however, they are generalized and produce exon pairs according to some predetermined joint distribution. (A) In order to avoid the prediction of coding exons in all conserved regions, it was necessary to introduce conserved noncoding states (CNS). Each intron and intergene state consist of two parts: an I-state for modeling long unrelated noncoding regions, and a CNS state for modeling interspersed conserved domains. (B) The modeling of coding exon states in pairs required the construction of a specialized PHMM, consisting of match/mismatch (M), insertion (I), and deletion states (D), which was used to assign probabilities to exon pairs based on alignments in protein space using an appropriate evolutionary model.

A key component of the model was the introduction of paired exon states that allow for the computation of exon probabilities based on the alignment in protein space. This is described in more detail below. CNS states were also added, allowing us to model the difference between DNA conservation in introns and intergenes, and protein conservation in coding exons. Splice sites were modeled independently using organism-specific, nonstationary variable-length Markov models (VLMMs) as described (Cawley 2000).

Exon Model

A natural probabilistic model for a pair of exons is a PHMM at the amino-acid level. However, there are two difficulties with such a model in the context of a gene finding GPHMM: First, the state outputs must consist of pairs of DNA bases (not amino acids), and second, it is necessary to assign probabilities to exon pairs.

We assigned probabilities to exon pairs by computing the probability of codon pairs under different possible alignments. The codon pairs were assigned probabilities from a 61 × 61 codon-based PAM matrix, which was constructed using a PAM20 matrix and factoring in codon usage probabilities in the appropriate manner. The dependency on previous sequence in the codon usage table was modeled with a fifth-order Markov model (corresponding to codon pair correlations).

Intron and Intergenic Models

Simple PHMMs, such as the one shown in Figure 2B, have the inherent property that any combination of parameters results in a correlation between the lengths of the output sequences. This restrictive property, coupled with the empirical observation that in pairs of orthologous sequences, noncoding regions appear to consist of unrelated, nonconserved regions interspersed by highly conserved regions, led us to develop a more refined PHMM for the intron and intergenic states.

The model, shown in Figure 2A, is formed of two components: The first component, consisting of states l_Y and l_Z, generates a pair of independent intron or intergenic (I-state) sequences, and the second component, a CNS state for generating related, conserved, noncoding sequence. The l_Y and l_Z states were each modeled as a single-state second-order Markov model, leading to the generation of independent I-state sequences with geometrically distributed lengths. In addition, the self-transition probabilities for l_Y and l_Z were set to be equal; this was found to be reasonable for human/mouse comparisons. A standard PHMM was used for the CNS state, having the advantage of creating Needleman-Wunsch-type DNA alignments for the CNS pairs.

Computational Complexity

A naive implementation of the GPHMM described has the drawback that the Viterbi algorithm has a running time on the order of D⁴N²TU, where D is the maximum allowable length for an exon (on the order of thousands), N is the number of states, and T and U are the two sequence lengths. The memory requirements are on the order of NTU, which also scales as the product of the sequence lengths—ideally we would like the problem to grow linearly in the length of the larger of the observation sequences. Because most alignments in the space of all possible alignments are very unlikely to be real, we adopted the approach of preprocessing to restrict the alignment search space to a set of more likely, or reasonable alignments. We call a set of possible alignments an approximate alignment (details in Pachter et al. 2001); this is similar to the concept of the envelope of an alignment (Holmes 1998).

Our strategy was to first align the two input sequences using the AVID global alignment tool (Bray et al. 2003). AVID is a recursive anchor-based alignment algorithm that generalizes and extends GLASS (Pachter 1999; Batzoglou et al. 2000) and MUMmer (Delcher et al. 1999). The AVID global alignment was “relaxed” in two steps, first by extending the base-to-base alignments to an interval or window of bases surrounding each matching base. We used a window size of three bases. Larger window sizes slow the program down and require more memory, but increase the chance that the Viterbi algorithm will find the best (in the sense that orthologous exons will be properly aligned) alignment between the sequences. A window size of 1 would be equivalent to separating the alignment and gene finding steps, as is done in the ROSETTA program (Batzoglou et al. 2000). In the second step, the potential state boundaries (e.g., boundaries separating exons and introns) were localized and the approximate alignment was expanded around them.

Parameters

The SLAM GPHMM parameters can be divided into two categories: those parameters that are organism-specific, and parameters that depend on the evolutionary distance of the two input organisms. It is interesting to note that in the current implementation of SLAM, only the CNS and exon-pair parameters are in the latter category. The exon states require the selection of an appropriate PAM matrix, and the CNS states require a similar paired output distribution on the DNA level. We selected these parameters by using aligned sequences of the organism pairs in which we were interested.

Initial and transition probabilities, splice-site VLMMs, state duration distributions, and output probabilities were all obtained from appropriate training sets. Parameters were stratified by GC content as described (Burge and Karlin 1997). Parameter sets for different pairs of organisms can be obtained easily with the SLAM parameter toolbox, which parses GenBank files containing annotated sequences, generating all the required parameters.

The training sets used for obtaining the results presented here consisted of the GENIE human set (Reese et al. 2000). The same parameters were used for both human and mouse sequences. The parameters were stratified according to GC content into four bins: bin1 = [0,43], bin2 = [43,51], bin3 = [51,57], and bin4 = [57,100]. CNS parameters were set to be consistent with Bergman and Kreitman 2001.

Finally, the output distribution in the CNS state was set such that each pair of bases was independently generated from a joint distribution over {A,C,G,T} × {A,C,G,T} where the probability of a match was set to 0.5, the distribution being otherwise uniform.

WEB SITE REFERENCES

http://bio.math.berkeley.edu/slam/; SLAM web server.

http://www1.imim.es/software/gfftools/GFF2PS.html; GFF to PS conversion.

http://bio.math.berkeley.edu/avid/; AVID web server.

http://genes.cs.wustl.edu/; Twinscan web server.

http://www1.imim.es/datasets/humanmouse/; SGP information.

http://genes.mit.edu/GENSCAN.html; Genscan web server.