SUMMARY
The rehabilitation of edentulous patients is today a challenge for the clinicians. The healthy of the hard and soft issue may be considered a fundamental element for having long-term results. The dental implant progresses about the predictable and safe results made this technique chosen from a large group of practitioners. However some problems related intra-operative and postoperative conditions may create discomfort on the patients and consequently to the clinician. The unfavourable results are often related to the bone tissue quality but sometime the dental implant shape and the prosthesis framework may undergo to technical difficulties. The purpose of this work is, through the use of appropriate FEM models, to analyse the effect of all these parameters in the construction of a prosthesis type “Toronto”, evaluating all the surgical and prosthetic components in order to direct the choices made by the surgeon and to optimize the distribution of loads reducing the patient’s discomfort and having a long term clinical success.
Keywords: FEM analysis, bone tissue, load, dental implant
Introduction
The dental implant first application is related with the treatment of edentulous jaw. This surgical technique allows a permanent solution for replacing missing teeth, and for rehabilitating either partial or total-edentulous jaws. Today, the use of dental implants for supporting and anchoring the dental prosthesis has become a predictable and safe procedure. In Italy it has been positioned a number of 360,000 implants per year of different companies and the 7% of these patients choice for a full arch prosthesis. Even if it is founded on scientific and clinical bases, the practice of implant dentistry is closely dependent on empirical factors related to biological and morphological characteristics of the individual patient. This involves in a considerable inconvenience to the operator, often forced to offer quick solutions in a short time without any feedback from dental implant design and structure related to the clinical condition of the patient bone and soft tissues. The problem of positioning dental implant accordingly with the next prosthesis may be a problem, considering the long term esthetical and functional results expected from the patients. For this reason, during these years the research has been very attentive to this problem and it has gone from a pioneering stage and craft, where the personal opinions mattered above all to a scientific research supported by targeted and rigorous methods and results. The finite element analysis offers a valid contribution in this sense. Considering the whole different variables (material characteristics, type of loads, bio- subjectivity) FEM study is support in the dental field for modern understanding of some particular phenomena like stress distribution and geometry evaluation (1–4). The knowledge of the distribution of stress and strain, in the mandibular bone and in the osseointegrated implants is fundamental for an adequate long-term stability of the implant itself. In the recent literature, there are numerous studies devoted to the problem of the characterization of the efforts on the bone and on the dental implant (5). Those investigations using a finite element environment have the purpose of directing the choices of the surgeon about all those biomechanical factors such as positioning, inclination, and type of the implant (6, 7). However, an adequate simplification of process is requested for approaching a not so easy research (8, 9).
Aim of the study, depending on the experience gained by the authors in this field, is to show how the application of the methodology FEM in dentistry can be useful for preventing possible errors due to incorrect operation of the system. Therefore the study results may justify appropriate choices of industrial construction companies about the dental implants surface features and geometric shape (2, 5).
Materials and methods
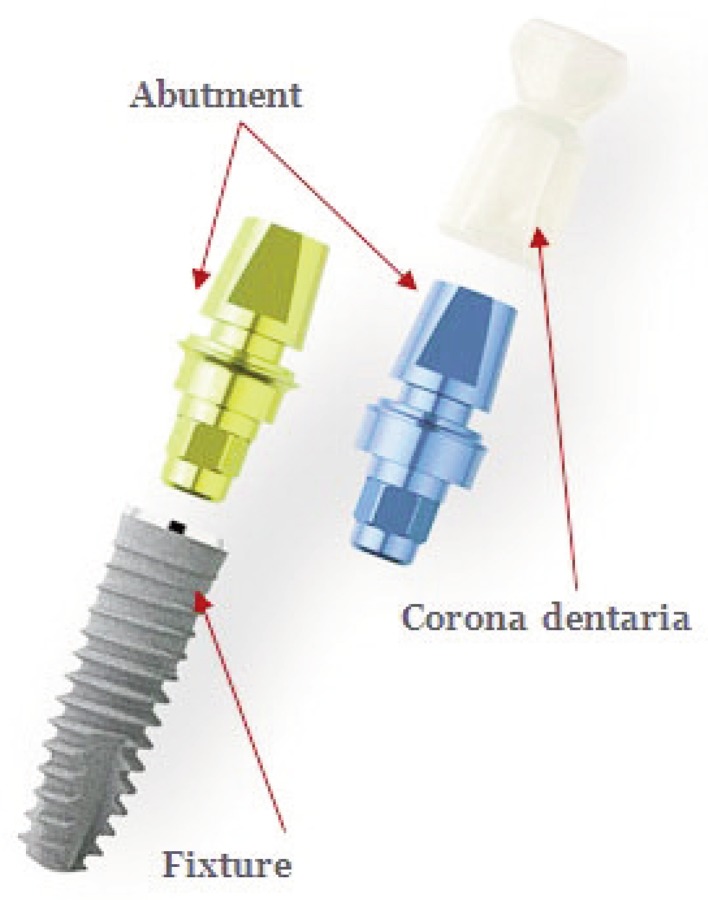
Implants with different shapes and mechanical features have been proposed and used over the recent years. In general, a common dental implant (Fig. 1) consists of several separate elements, which are assembled to form a final prosthetic system:
Fixture: those are defined like structures mainly made of titanium alloy (usually grade 4 or 5) attached to the inside of the jawbone. It is possible having different geometries and sizes;
Abutment: those are defined like components also made of titanium alloy on which is fixed the dental crown, usually made of resin material that constitutes of the replacement of the dental system (10);
Screw connection: screw made of titanium alloy used to connect the abutment to the fixture.
Figure 1.
Sample of the dental implant-abutment system.
The separation of the fixture from the rest of the system has the purpose of facilitating the surgical operation of installation and at the same time it allows to firmly maintain the non-biological element during the healing phase of the bone tissue, facilitating the proper osseointegration in the fabric. The manufacturers of dental prostheses have developed, over the years, processing techniques to improve the resistance of the fixture and osseointegration.
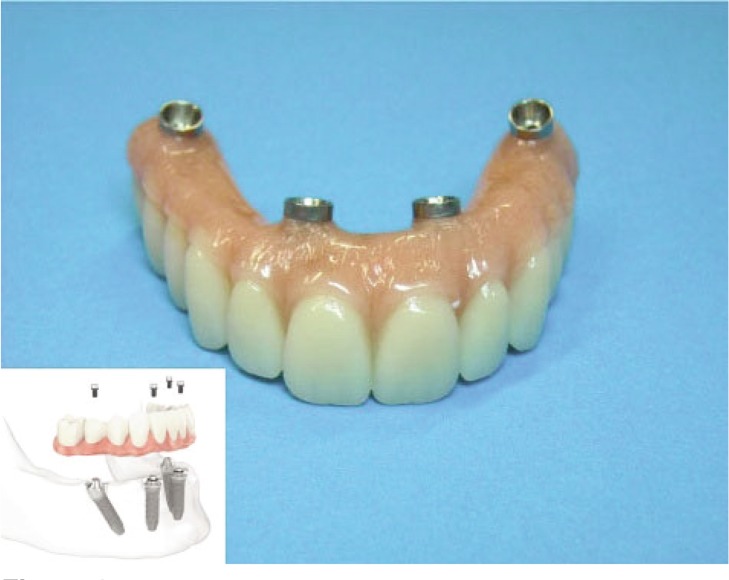
The dental implants have been intended to replace a single tooth (or a small group of them) until the Conference on osseointegration of Toronto were called the basic features of an osseointegrated implant for edentulous cases thereby giving the name of prosthesis Toronto (7). It consists of fixtures installed on a mandible (jaw) edentulous and connected together by a frame made of titanium alloy above which the dental prosthesis is installed in resinous material (Fig. 2).
Figure 2.
Sample of Toronto screwed prosthesis.
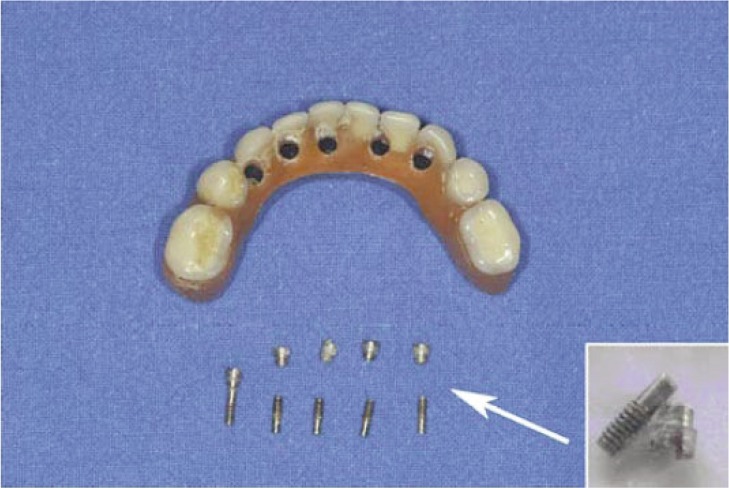
The set of the frame and of structure of the abutments have the purpose of supporting the prosthesis and transferring the load in from the fixture and to the surrounding bone tissue (5). The dental implant shape should be designed for a proper distribution of the stress in order to avoid problems at the first stage of osseointegration. The connection screw between abutment and dental implant is generally considered as a simple connector for the prosthetic part and the osseointegrated component but it really represents a fundamental component. The functionality of the connector means that this is subjected to stress during the loading phase (dynamic or static), but unlike the other elements even during the resting phase. The passant screw serves to keep firmly anchored the two elements that constitute the “system”. The connection screws are the smaller elements of the system and for this reason; they are subject to higher voltages and stresses. Moreover it is the weak link of the system, and often it is also the cause of non-effectiveness of the system. A single implant is designed to withstand axial predominantly sedges (not necessarily perpendicular) in compression (10). The life of connection and then, in addition to having a preload for keeping closed the two parts (fixture and abutment), is not designed to withstand high tensile sedges. Unfortunately, the increasingly frequent use by clinicians of Toronto prosthesis for edentulous cases with the aid of prosthetics “single concept”, has given rise to several cases of sudden failure of the entire prosthesis (Fig. 3).
Figure 3.
The passant screws broken after the masticatory cycle.
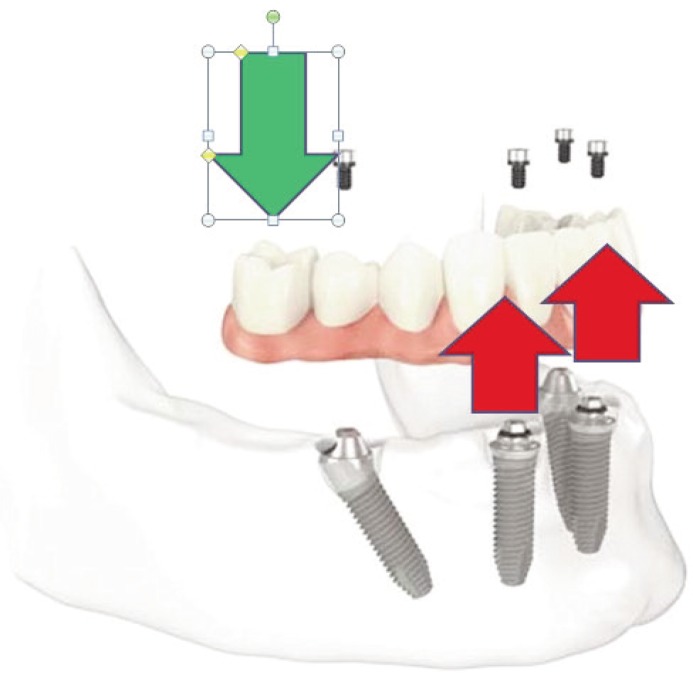
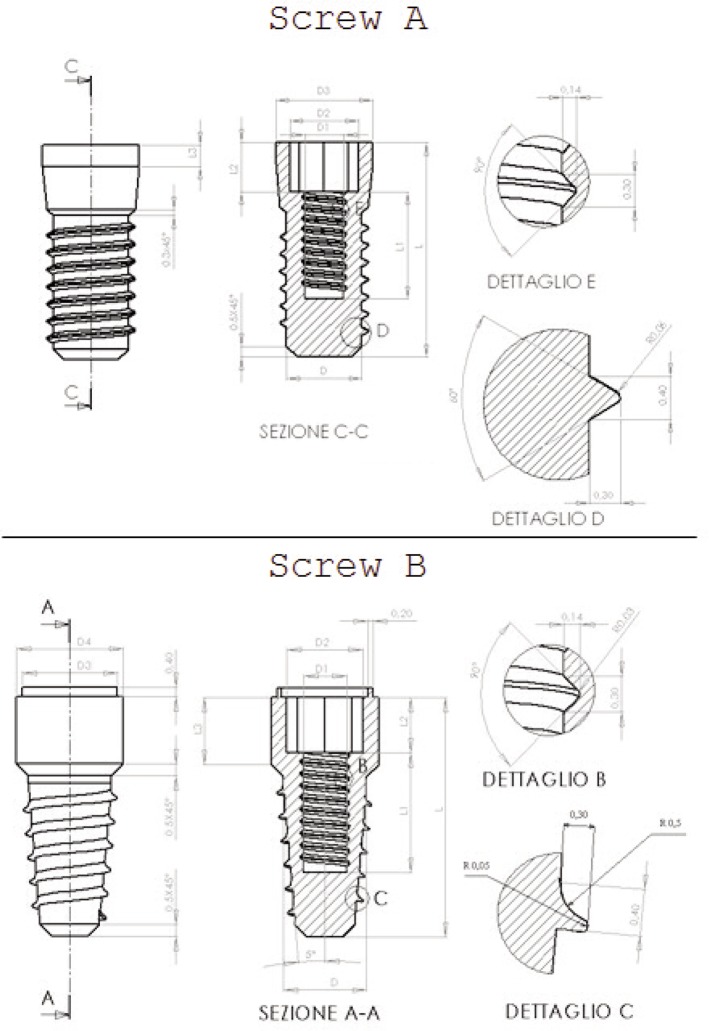
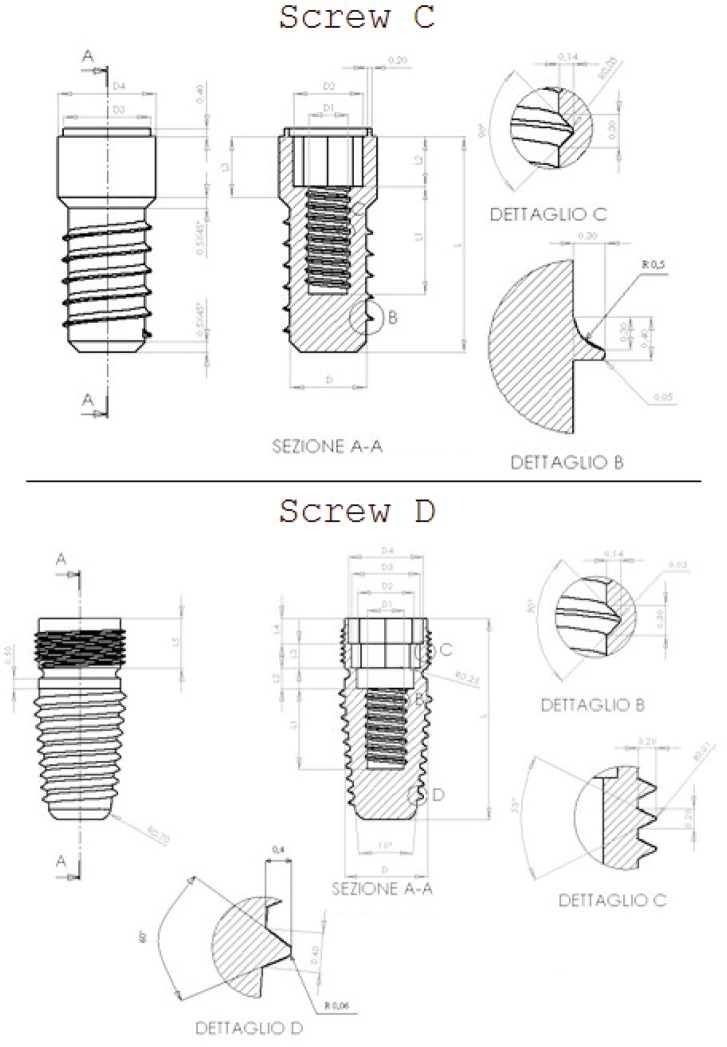
In fact, compressive loads in the premolar or molar region (arrow in green in Fig. 4), for a simple “leverage effect”, tensile stress in the single prosthesis and especially the screw connection have been recorded (red arrows in Fig. 4). It is clear that a break of these systems is mainly due to fatigue phenomena and not related to a simple static breakage. It is of interest, therefore, to understand what is the follow-up of prosthesis Toronto made with screws designed initially to use a diametrically different one as the replacement of a single (or torque at maximum) tooth. Taking into account the above, the authors have focused their attention on four different fixture of the Italian firm: A, B, C and D (Figs. 5 and 6). As it possible to see from the reported CAD, all of the threads have special and different prosthesis. Actually, there is a different surgical procedure to provide a first milling of the mandible (or maxilla) with specific machine tools and then the insertion of self-tapping fixture. It is evident how even if it is precise, this operation creates stress concentration on the bone that is on the prosthesis itself.
Figure 4.
Direction of the vertical load over dental prosthesis and dental implants.
Figure 5.
Dental Implants with different threads shape and design model A and B.
Figure 6.
Dental Implants with different threads shape and design model C and D.
A difference from the first three models, the D one presents a micro-threaded part on the neck of the implant. The manufacturer claims, in fact, that this allows a greater primary stability and prevents the natural bone resorption. Interesting it becomes, therefore, the evaluation of the benefits of the threaded neck of the D model compared to other implants lacking a similar feature. Authors have realized the FEM analysis in ANSYS® environment for evaluation of the D Model too.
In general, for each type of implant, there are differences for diameter and length. In order to make a comparative assessment between the systems, the authors analysed comparable sizes (Tab. 1). The implants were made of titanium alloy (grade 4) with a Young’s modulus equal to 110,000 MPa and a Poisson’s ratio of 0.33.
Table 1.
Evaluation of the load distributed on the screw.
| Screw | A | B | C | D |
|---|---|---|---|---|
| D[mm] | 3,8 | 3,5 | 3,5 | 3,85 |
|
| ||||
| L[mm] | 10 | 10 | 10 | 10 |
|
| ||||
| D1[mm] | 1,8 | 1,8 | 1,8 | 1,8 |
| D2[mm] | 2,5 | 3,2 | 3,2 | 3,2 |
| D3[mm] | 3,2 | 4,5 | 4 | 4 |
| D4[mm] | 3,5 | - | 4,5 | 4,5 |
|
| ||||
| L1[mm] | L/2–L2 | (4L/5)-L2 | L/2 | L/2 |
| L2[mm] | 1 | 2,3 | 2,3 | 2,3 |
| L3[mm] | 1,25 | 0,75 | 2,8 | 2,8 |
| L4[mm] | 1,25 | - | - | - |
| L5[mm] | 2,5 | - | - | - |
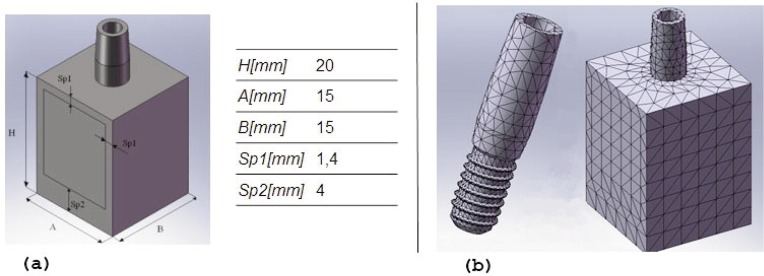
For doing a comparative analysis, it was created a cube consisting of cortical and cancellous bone. The dimensions of the two types of bone have been taken accordingly with the dimensions shown in a jawbone of a normal type (9) (Fig. 7a). The characteristics of the bone were considered according to the indications of current literature on bone biology and bioengineering models (11–14) (Tab. 2).
Figure 7.
FEM investigation of the dental implants and the bone accordingly with the material characteristics.
Table 2.
Cortical and spongious value considered in the study.
| Corticale Bone | |
|
| |
| E11 | 19400 MPa |
| E22 | 10800 MPa |
| E33 | 13300 MPa |
| G12 | 4120 MPa |
| G23 | 3810 MPa |
| G31 | 4630 MPa |
| ʋ12 | 0,31 |
| ʋ23 | 0,21 |
| ʋ31 | 0,16 |
| Density | 1,74 g/cm3 |
|
| |
| Spongious Bone | |
|
| |
| Elstic Modulus | 1870 MPa |
| Poisson Ratio | 0,12 |
| Density | 0,9 g/cm3 |
By applying the Boolean subtraction in the CAD environment, each implant was placed inside the cube to preserve the geometry and shape of the fillet. The FEM analyses have been performed by tetrahedral elements (SOLID 187 library ANSYS®) to discretize both the bone and the implant. In this case, the geometric model is very complex and for this reason, particular care has been devoted to the definition of the mesh parameters. Evidence of the discretization highlighted the difficulties in finding solutions with very low value of the items and models. For this reason, small values of the size of the elements only in the areas of most interest (threads) have been used. The model approximation was achieved by imposing for the mesh the size around 0.5 mm. In the Figure 7b it is possible to underline how the size of the elements is greatly reduced in the vicinity of the thread while it is maintaining a regular distribution of the elements themselves. The FEM model has a total of approximately 500.000 elements. The contact between the implant and the abutment was simulated with no interpenetration. The screw connection has been processed by the FEM analysis too. In the present model, the assuming a total osseointegration between the thread of the implant and the bone (cortical and cancellous), authors imposed a direct contact without penetration, and this has greatly burdened the work of processing by the CPU. Finally, based on the cube a constraint joint has been imposed.
Calculations and results
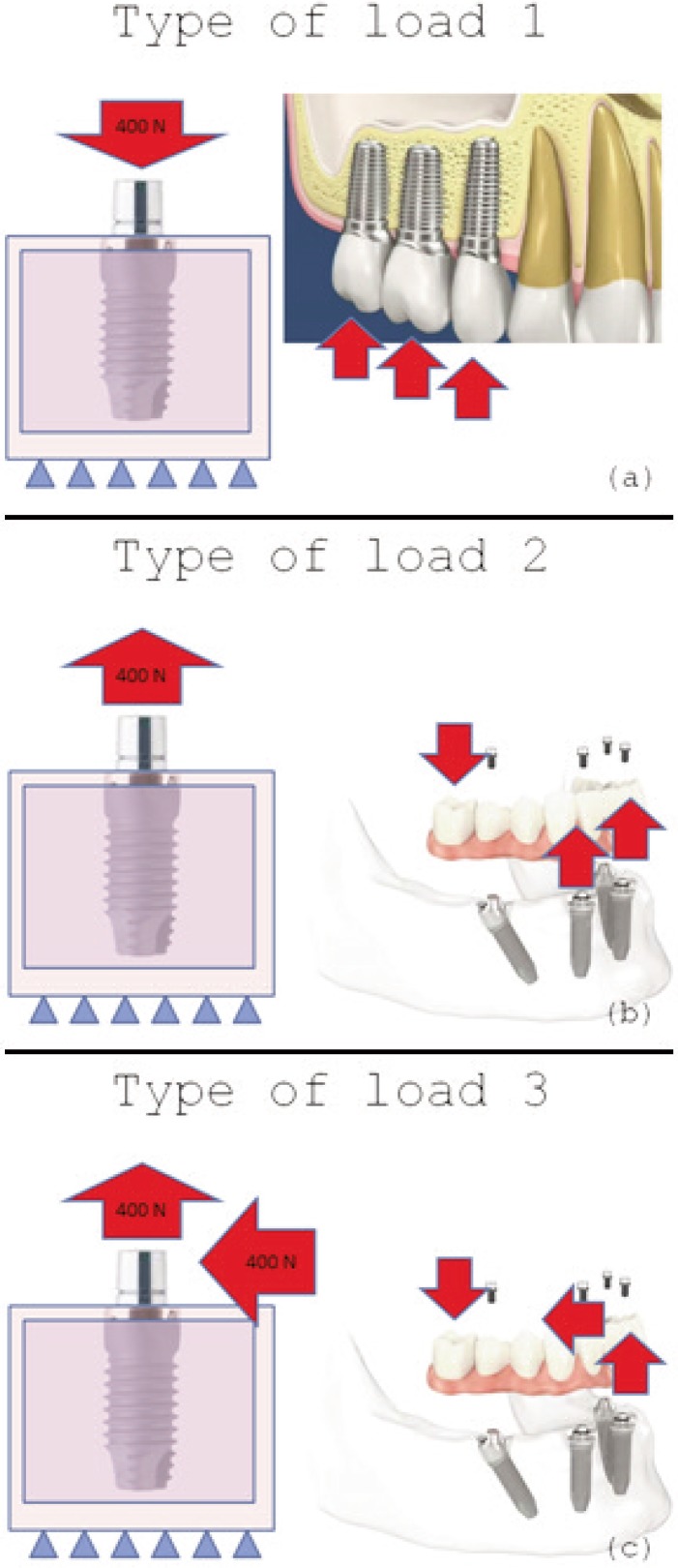
The FEM analysis for each dental implant was performed with three different types of static load:
compression load (type 1);
tensile load (type 2);
tensile load and bending moment (type 3).
In the literature, the value of the load is highly variable. Authors suggested a compressive load of 400 N equal to what was said by Craig in 1980 (12). As mentioned earlier, the type of load 1 is one for which the implant has been designed (Fig. 8 a). The type of load 2 is of considered “pure traction load” (Fig. 8 b). The type of load 3 also provides the bending moment due to the rigid rotation of the frame of the Toronto screwed prosthesis (Fig. 8 c).
Figure 8.
Occlusal and paraxial load over dental implant and prosthesis framework. (a, b) occlusal and vertical load; (c) occlusal lateral load.
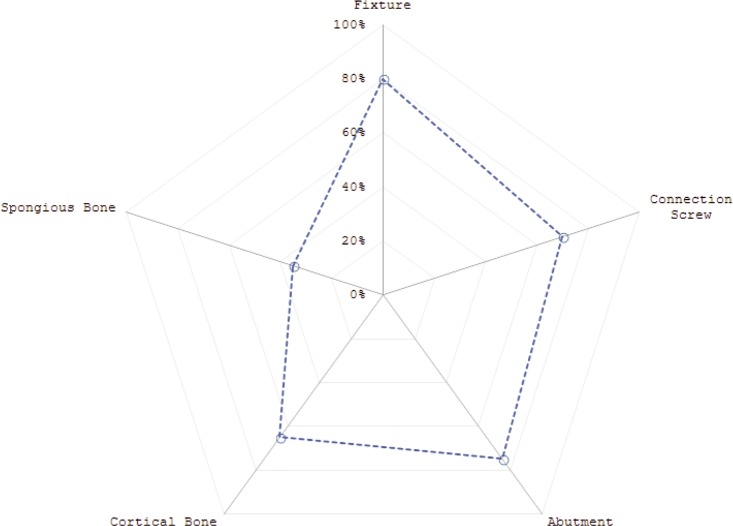
The post-processing data for each component of the system has been calculated through the Von Mises stress media. The same thing was done to the cortical and cancellous bone. By way of example, Figure 9 shows the results for the load mode 1.
Figure 9.
Graph about the stress distributions.
Discussion
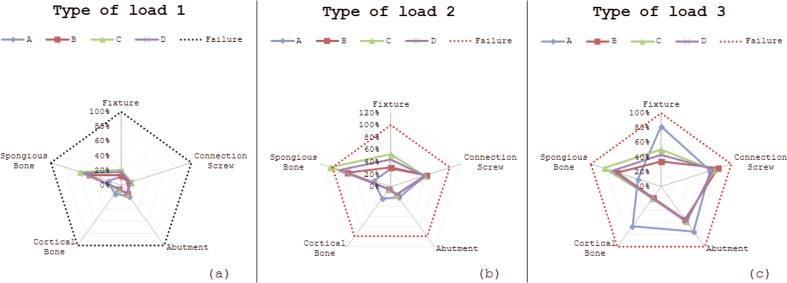
The FEM analysis and the relative phases of post-processing, as seen in the previous paragraph, have been realized for each type of load and then evaluated by a pentagonal graph (Fig. 10 a–b). The leaders represented the five elements of the system under investigation (fixture and abutment screw connection for the implant; cancellous and cortical bone). Taking in-to consideration the limitations of the materials, we calculated the percentages of all elements survival (17, 20–22). It was considered as the yield strength of the titanium alloy grade 4 a value of 550 MPa. Furthermore, regarding the type of load 1, the system was constituted by a cortical bone with a value breaking stress of 205 MPa and a cancellous bone of the elastic with a stress limit equal to 22 MPa; regarding the function of the type of load 2 and 3, the cortical bone breaking stress was about 135 MPa and the cancellous bone with an elastic strain limit of 17 MPa. The dashed line in red represents the border area for the static failure of the prosthesis. None of the three types of static load leads to failure of the prosthesis (if one excludes the fixture C for overcoming the elastic limit stress of cancellous bone). It is interesting to note how under the stress of load 3, [simulates in a more real use conditions (static) of the prosthesis Toronto], the D dental implant loses significantly the advantages compared to the other fixture that had so evident for type 1 and 2. This behaviour is related to own micro-threaded neck (Fig. 11) that seems create a conditions in flexion- traction (type 3) that makes the tensions splashing from the fixture to the cortical bone in contact. This seems due to be related with excessive values when compared to the other prosthesis (Fig. 10 c).
Figure 10.
Comparison of the three different kind of load. (a, b) occlusal and vertical load; (c) occlusal lateral load.
Figure 11.
Von Mises analysis over the dental implant frameworks.
It is then evident that the possible failures of the prosthesis Toronto (Fig. 3) are dynamic in nature. Indeed, doing the ratio between the average voltage of Von Mises derived from FE analysis by type of load 3 and the fatigue limit (R = −1) of the titanium alloy grade 4 (358 MPa), it is underlined from the study data how that all three the components of the D exceed the value “limit” of the load 1 (Tab. 3). As well as other types of dental implants, the screw connection seems to be the actual weak link in the chain, resulting in values related with fatigue and consequent failure of the prosthesis (6, 17, 23). The notation that stands out, however, is how the D dental implant characterized by the presence of the micro-threaded neck has a significantly different behaviour if compared with the other model (15–19). Even its geometry and shape should ensure the primary stability (which is impossible for the high values of the cortical bone), the study results underline how the fixture and the abutment of this model have values of the average Von Mises voltage significantly above the fatigue limit of the material. This justifies, in part, the decision of Brand Production of replacing this model after a few years since the introduction in the market with a new “D model” concerned with a neck design completely different shape (24–26).
Table 3.
Comparison of the load between fixture, connection screw and abutment.
| A | B | C | D | |
|---|---|---|---|---|
| Load Ratio σi/σ0 | ||||
| Fixture | 1,25 | 0,52 | 0,77 | 0,67 |
|
| ||||
| Connection Screw | 1,07 | 1,24 | 1,14 | 1,15 |
|
| ||||
| Abutment | 1,16 | 0,85 | 0,89 | 0,9 |
Conclusions
During the last years, research in the field of dentistry has been very careful to approach problems of implant related prosthesis. Scientific investigation passed from a pioneering stage to a scientific one; the FEM analysis gave a good qualitative contribution in this sense being many variables in play. The knowledge of the distribution of stress and strain, in the mandibular and osseointegrated implants, is fundamental for the evaluation of an adequate stability of the dental implant itself.
The authors’ aim is to show how the application of the methodology FEM in dentistry may point out possible errors in the incorrect operation of the system, and even justify appropriate choices of industrial construction companies.
This research have focused on four different fixtures of an Italian firm (A, B, C, D), characterized by different threads shape and designs. Unlike the other three, the D one presents a micro-threaded part on the neck of the implant. The manufacturer argued that this would allow a greater primary stability and prevented from the natural bone resorption. Interesting was the evaluation of the advantages and disadvantages of the threaded neck of the D compared to other installations not fitted with a similar feature via a numerical approach altogether.
As expected, the failure of the prosthesis is never static load. It is interesting, however, to note how in the flexion-strength loading condition (typical of the prosthesis Toronto voltages) on the fixture and over cortical bone the D model results to be stressed by excessive strength contact if compared with the other models. Moreover, unlike the other types of systems, which have average voltages of Von Mises higher fatigue limit (R = −1) only for the screw connection, the D one has Von Mises tensions higher than the fatigue limit of the material even for the fixture and for the abutment. The FEM-analysis, although depending on many variables and uncertainties as the characteristics of the material, type of cargo and bio-subjectivity, as well as indicate which bad results involving improper handling of the system, the decision of the manufacturer to replace, after just a few years, the D one with a dental implant having a different geometry of the neck.
References
- 1.De Cos Juez FJ, Sánchez Lasheras F, García Nieto PJ, Álvarez-Arenal A. Non-linear numerical analysis of a double-threaded titanium alloy dental implant by FEM. Applied Mathematics and Computation. 2008;206:952–967. [Google Scholar]
- 2.Bozkaya D, Muftu S. Mechanics of the tapered interference fit in dental implants. Journal of Biomechanics. 2003;36:1649–1658. doi: 10.1016/s0021-9290(03)00177-5. [DOI] [PubMed] [Google Scholar]
- 3.Pietrabissa R, Contro R, Quaglini V, Soncini M, Gionso L, Simion M. Experimental and computational approach for the evaluation of the biomechanical effects of dental bridge misfit. Journal of Biomechanics. 2000;33:1498–1495. doi: 10.1016/s0021-9290(00)00089-0. [DOI] [PubMed] [Google Scholar]
- 4.De Vico G, Bonino M, Spinelli D, Schiavetti R, Sannino G, Pozzi A, Ottria L. Rationale for tilted implants: FEA considerations and clinical reports. Oral Implantol (Rome) 2011 Jul;4(3–4):23–33. [PMC free article] [PubMed] [Google Scholar]
- 5.Sannino G, Marra G, Feo L, Vairo G, Barlattani A. 3D finite element non linear analysis on the stress state at bone-implant interface in dental osteointegrated implants. Oral Implantol (Rome) 2010 Jul;3(3):26–37. [PMC free article] [PubMed] [Google Scholar]
- 6.Sannino G, Barlattani A. Mechanical evaluation of an implant-abutment self-locking taper connection: finite element analysis and experimental tests. Int J Oral Maxillofac Implants. 2013 Jan-Feb;28(1):e17–26. doi: 10.11607/jomi.2058. [DOI] [PubMed] [Google Scholar]
- 7.Sannino G. All-on-four concept: a three-dimensional finite element analysis. J Oral Implantol. 2013 Apr 5; doi: 10.1563/AAID-JOI-D-12-00312. [DOI] [PubMed] [Google Scholar]
- 8.Risitano G, Cicciù M, Dini R, Franceschini G, Maiorana C.Evaluation of Strength in the Toronto Osseous-Prosthesis System ICEM14 ConferencePoitiers, France20104–9July(EPJ volume 6, 2010) [Google Scholar]
- 9.Bono B, Girello A, Gerarci D. Indagine numerica e sperimentale sullo stato di sollecitazione indotte nel per impianto dentario. AIAS XXXII Convegno Nazionale; Salerno. 2003. [Google Scholar]
- 10.Sannino G, Gloria F, Ottria L, Barlattani A. Influence of finish line in the distribution of stress trough an all ceramic implant-supported crown. A 3d finite element analysis. Oral Implantol (Rome) 2009 Apr;2(2):14–27. Epub 2010 Mar 4. [PMC free article] [PubMed] [Google Scholar]
- 11.Armentani E, Cali C, Caputo F, Citarella R, Infante M, Lavorgna G. Modello agli elementi di contorno per l’analisi tensionale dell’articolazione temporo-mandibolare. AIAS XXXI Convegno Nazionale; Parma. 2002. [Google Scholar]
- 12.Craig RG. Restorative dental material. 6th ed. St. Louis: C. V. Mosby; 1980. [Google Scholar]
- 13.Michailidis N, Karabinas G, Tsouknidas A, Maliaris G, Tsipas D, Koidis P. A FEM based endosteal implant simulation to determine the effect of peri-implant bone resorption on stress induced implant failure. Biomed Mater Eng. 2013;23(5):317–27. doi: 10.3233/BME-130756. [DOI] [PubMed] [Google Scholar]
- 14.Covani U, Ricci M, Tonelli P, Barone A. An evaluation of new designs in implant-abutment connections: a finite element method assessment. Implant Dent. 2013 Jun;22(3):263–7. doi: 10.1097/ID.0b013e318292625f. [DOI] [PubMed] [Google Scholar]
- 15.Roychowdhury A, Pal S. A 3-D FEM analysis of single and multiple screw-root dental implant fixed in a mandible. Crit Rev Biomed Eng. 2000;28(3–4):405–10. doi: 10.1615/critrevbiomedeng.v28.i34.100. [DOI] [PubMed] [Google Scholar]
- 16.Moon HJ, Lee JH, Choi K, Choi JB, Koh CS. Homogenized stress analysis in a dental implant system. J Med Eng Technol. 1997 Nov-Dec;21(6):233–40. doi: 10.3109/03091909709070014. [DOI] [PubMed] [Google Scholar]
- 17.Sano M, Ikebe K, Yang TC, Maeda Y. Biomechanical rationale for six splinted implants in bilateral canine, premolar, and molar regions in an edentulous maxilla. Implant Dent. 2012 Jun;21(3):220–4. doi: 10.1097/ID.0b013e31825023f5. [DOI] [PubMed] [Google Scholar]
- 18.Lan TH, Huang HL, Wu JH, Lee HE, Wang CH. Stress analysis of different angulations of implant installation: the finite element method. Kaohsiung J Med Sci. 2008 Mar;24(3):138–43. doi: 10.1016/S1607-551X(08)70141-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bergkvist G, Simonsson K, Rydberg K, Johansson F, Dérand T. A finite element analysis of stress distribution in bone tissue surrounding uncoupled or splinted dental implants. Clin Implant Dent Relat Res. 2008 Mar;10(1):40–6. doi: 10.1111/j.1708-8208.2007.00059.x. [DOI] [PubMed] [Google Scholar]
- 20.Van Staden RC, Guan H, Johnson NW, Loo YC, Meredith N. Step-wise analysis of the dental implant insertion process using the finite element technique. Clin Oral Implants Res. 2008 Mar;19(3):303–13. doi: 10.1111/j.1600-0501.2007.01427.x. Epub 2007 Dec 13. [DOI] [PubMed] [Google Scholar]
- 21.Van Staden RC, Guan H, Loo YC. Application of the finite element method in dental implant research. Comput Methods Biomech Biomed Engin. 2006 Aug;9(4):257–70. doi: 10.1080/10255840600837074. [DOI] [PubMed] [Google Scholar]
- 22.Al-Sukhun J, Lindqvist C, Helenius M. Development of a three-dimensional finite element model of a human mandible containing endosseous dental implants. II. Variables affecting the predictive behavior of a finite element model of a human mandible. J Biomed Mater Res A. 2007 Jan;80(1):247–56. doi: 10.1002/jbm.a.30881. [DOI] [PubMed] [Google Scholar]
- 23.Cicciù M, Risitano G, Maiorana C, Franceschini G. Parametric analysis of the strength in the “Toronto” osseous-prosthesis system. Minerva Stomatol. 2009 Jan-Feb;58(1–2):9–23. [PubMed] [Google Scholar]
- 24.Boschian Pest L, Guidotti S, Pietrabissa R, Gagliani M. Stress distribution in a post-restored tooth using the three-dimensional finite element method. J Oral Rehabil. 2006 Sep;33(9):690–7. doi: 10.1111/j.1365-2842.2006.01538.x. [DOI] [PubMed] [Google Scholar]
- 25.Kitagawa T, Tanimoto Y, Odaki M, Nemoto K, Aida M. Influence of implant/abutment joint designs on abutment screw loosening in a dental implant system. J Biomed Mater Res B Appl Biomater. 2005 Nov;75(2):457–63. doi: 10.1002/jbm.b.30328. [DOI] [PubMed] [Google Scholar]
- 26.Roychowdhury A, Pal S, Saha S. Stress analysis of an artificial temporal mandibular joint. Crit Rev Biomed Eng. 2000;28(3–4):411–20. doi: 10.1615/critrevbiomedeng.v28.i34.110. [DOI] [PubMed] [Google Scholar]