Modeling and Validation of Microwave Ablations with Internal Vaporization

Abstract

Numerical simulation is increasingly being utilized for computer-aided design of treatment devices, analysis of ablation growth, and clinical treatment planning. Simulation models to date have incorporated electromagnetic wave propagation and heat conduction, but not other relevant physics such as water vaporization and mass transfer. Such physical changes are particularly noteworthy during the intense heat generation associated with microwave heating. In this work, a numerical model was created that integrates microwave heating with water vapor generation and transport by using porous media assumptions in the tissue domain. The heating physics of the water vapor model was validated through temperature measurements taken at locations 5, 10 and 20 mm away from the heating zone of the microwave antenna in homogenized ex vivo bovine liver setup. Cross-sectional area of water vapor transport was validated through intra-procedural computed tomography (CT) during microwave ablations in homogenized ex vivo bovine liver. Iso-density contours from CT images were compared to vapor concentration contours from the numerical model at intermittent time points using the Jaccard Index. In general, there was an improving correlation in ablation size dimensions as the ablation procedure proceeded, with a Jaccard Index of 0.27, 0.49, 0.61, 0.67 and 0.69 at 1, 2, 3, 4, and 5 minutes. This study demonstrates the feasibility and validity of incorporating water vapor concentration into thermal ablation simulations and validating such models experimentally.

I. Introduction

Tumor ablation is an emerging treatment for early-stage solid tumors that are not amenable to surgical resection or which have failed chemotherapy or radiotherapy [1], [2]. Thermal ablation is typically performed using applicators that have a thin, needle-like profile that can be inserted into the target zone under imaging guidance. Once positioned, energy is applied from the distal tip of the applicator to elevate the temperature of the adjacent tissue to cytotoxic temperatures (above 50–60°C) over the course of several minutes.

The most widely utilized ablation modality to date is radiofrequency (RF) ablation, which generates heat using RF electrical current applied directly to the tumor [2]. However, at cytotoxic temperatures, the electrical impedance of the tissue quickly rises due to dehydration and water vaporization, limiting the application of additional RF current. There is now increased interest in the application of microwave energy, which is not limited by the presence of charred or desiccated tissue. Microwave systems are capable of creating larger and more homogenous ablation zones compared to those made with predicate RF ablation systems, even around heat-siphoning vasculature – leading to more complete treatment and a potentially decreased risk for tumor recurrence [3].

Numerical simulation of thermal ablations is an area of active research, leveraging computer-aided design to optimize ablation systems and treatment planning. However, numerical techniques used previously to simulate RF ablations cannot be fully applied to microwave ablations. Microwave ablation systems are capable of heating tissues to well above 100°C and maintaining those temperatures for several minutes, vaporizing tissue water and driving vapor away from the antenna. Vapor diffuses through the tissue and re-condenses within peripheral tissue or blood vessels [4]–[6]. Thus physically accurate models must account for the energy required to vaporize water, and the associated heat and mass transport.

While water vaporization and transport have been incorporated into numerical models of food preparation by using a porous media approach, those models have not been applied to an interstitial energy source such as a microwave ablation antenna, nor have they been used to evaluate heating in other biological tissues such as the liver, kidney or bone [7]–[10]. The purpose of this study was to evaluate the porous media approach for simulating water vaporization in liver tissue during microwave ablation, and experimentally validate the simulation outputs such as tissue temperature and moisture content.

II. Methods

A. Numerical Technique

Hepatocytes and blood vessels may be regarded as a porous skeleton, with water being the major constituent bound within it. As liver tissue is being heated from microwave energy, tissue water undergoes a phase change to gas and can be transported through the porous matrix. Therefore, a numerical description of microwave ablation may be developed using established techniques for heat and mass transport in porous media [9].

1) Geometric Model

An axially-symmetric geometric model was developed for homogenized tissue in a cylindrical glass container (80 mm radius × 90 mm height) and a clinical microwave ablation antenna inserted into the liver model as shown in Fig. 1.

Fig. 1.

A) The two-dimensional, axially-symmetric geometry of a clinical microwave antenna inserted within ex vivo, homogenized bovine liver tissue. The dashed centerline denotes the symmetry axis. B) A cross-section of the experimental setup as seen under computed tomography (CT) imaging.

2) Governing Equations

Heat and water mass transfer during microwave ablation heating were simulated using the finite-element method (FEM) in commercial software (COMSOL Inc, Burlington, MA). Electromagnetic field vectors were calculated by solving Maxwell’s equations (not shown for brevity) at 2.45 GHz. Electromagnetic power dissipation density, Q was determined through the equation:

$$Q=\frac{1}{2}\mathrm{\sigma }{|\mathrm{E}|}^2(\mathrm{W}/{\mathrm{m}}^3)$$ (1)

where σ was the electrical conductivity (S/m) and E was the electric field intensity magnitude (V/m). Energy conservation included convection, diffusion, conduction, phase change of water and microwave heating source, which were described using the heat transfer equation in porous media:

$$\frac{\partial }{\partial \mathrm{t}}\left(\sum _{i=s,w,v}{\mathrm{\rho }}_{\mathrm{i}}{\mathrm{C}}_{\mathrm{p},\mathrm{i}}\mathrm{T}\right)+\nabla (\sum _{i=w,v}{\mathrm{\rho }}_{\mathrm{i}}{\mathrm{C}}_{\mathrm{p},\mathrm{i}}{\mathrm{u}}_{\mathrm{i}}\mathrm{T})=\nabla ({\mathrm{k}}_{\text{eff}}·\nabla \mathrm{T})-\mathrm{\lambda }\mathrm{İ}+\mathrm{Q}$$ (2)

where ρ_i was the density (kg/m³), C_p was the specific heat (kJ/kg∙K), T was the temperature (K), λ was the latent heat of water vaporization (2,435 kJ/kg), k_eff was the effective thermal conductivity calculated as a weighted mean of thermal conductivities of constituent species, solid (s), liquid water (w) and water vapor (v).

The governing equation for water and vapor saturation within the tissue was given by a conservation of mass relation:

$$\frac{\partial {\mathrm{c}}_{\mathrm{i}}}{\partial \mathrm{t}}+\nabla ·(-{\mathrm{D}}_{\mathrm{i}}\nabla {\mathrm{c}}_{\mathrm{i}})+{\mathit{u}}_{\mathit{i}}·\nabla {\mathrm{c}}_{\mathrm{i}}=\frac{\mathrm{İ}}{{\mathrm{M}}_{\mathrm{w}}}$$ (3)

where c_i (mol/m³) was the concentration of species (water or vapor), D_i (m²/s) was the diffusivity and u_i was the convective (Darcy’s) velocity of fluid. The right-hand side of (3), with units (mol/m³·s) represents the reaction term describing water vaporization or condensation, where M_w (18 g/mol) was the water molecular weight and İ (kg/s∙ m³) is the water vaporization rate. Darcy’s law was used to describe the convective flows of liquid water and water vapor caused by pressure gradients within the tissue:

$${\mathit{u}}_{\mathit{i}}=-\frac{{\mathrm{k}}_{in,i}·k_{r,i}}{{\mathrm{\mu }}_i}\nabla \mathrm{p}(\mathrm{m}/\mathrm{s})$$ (4)

where k_in,i (m²) is the intrinsic permeability, k_r,i is the relative permeability, μ_i(Pa·s) is the viscosity, p (Pa) is the vapor pressure.

Darcy’s Law was combined with the continuity equation to solve for the pressure and velocity of the water vapor:

$$\frac{\partial }{\partial \mathrm{t}}(\mathrm{\rho }\varnothing )+\nabla ·(\mathrm{\rho }{\mathrm{u}}_{\mathrm{i}})=\mathrm{İ}$$ (5)

where ϕ was porosity, defined as the fraction of the domain occupied by pores (zero for pure solid regions to unity for domains of free flow).

3) Evaporation Rate Determination

In tissue, the liquid and vapor phases of water were assumed to in equilibrium. The equilibrium vapor pressure (P_v,eq,Pa) at a particular moisture content and temperature was described by the moisture isotherm [11],

$$\text{ln}\frac{P_{v,\mathit{\text{eq}}}}{P_{\mathit{\text{sat}}}(T)}=-0.0267M^{-1.65}+0.01e^{1.287M}{M}^{1.5}\text{ln}[P_{\mathit{\text{sat}}}(T)]$$ (6)

where, P_sat(Pa) was the saturated vapor pressure of pure water, and M was the moisture content on dry basis. The phase change of water (vaporization) was described using non-equilibrium evaporation method [12]:

$$\mathrm{İ}=\mathrm{\tau }\frac{{\mathrm{P}}_{\mathrm{v},\text{eq}}-{\mathrm{P}}_{\mathrm{v}}}{\mathrm{R}\mathrm{T}}(\mathrm{k}\mathrm{g}/\mathrm{s}·{\mathrm{m}}^3)$$ (7)

where P_v was the vapor density (kg/m³), τ was a parameter signifying the rate constant of vaporization, which was of the order of one for hygroscopic material estimated in previous literature [12].

4) Boundary Conditions

For solving Maxwell’s equations, a scattering boundary condition was imposed at the outer surface of the homogenized liver sample. Water vapor in the tissue was transported by both diffusion and convection. At the tissue-air boundary

$$n_{v,\mathit{\text{sur}}}=c_v·v_{n,v}+D_v·\nabla c_v(\mathrm{k}\mathrm{g}·{\mathrm{m}}^{-2}·{\mathrm{s}}^{-1})$$ (8)

where n_{v, sur} was the total mass flux through the surface of the tissue, c_v was the vapor concentration on tissue boundaries, v_n,v was effective vapor velocity on tissue boundaries and D_v was vapor diffusivity in air. Along with the mass transport of species, the tissue boundaries also lose heat q_n because of the vapor loss, as well as cooling by ambient air

$$q_n=n_{v,\mathit{\text{sur}}}·C_{p,v}T+h·(T_{\mathit{\text{air}}}-T)(\mathrm{W}·{\mathrm{m}}^{-2})$$ (9)

where C_p,v was the specific heat of water vapor (kJ/kg∙K) and h was the convective heat transfer coefficient of vapor at the surface (W/m²·K). The pressure at the domain boundaries was set to be atmospheric to mimic experimental conditions. These boundary conditions were set to mimic our experimental setup, as opposed to a clinical case.

Table 1 shows the key input variables and their values. Several of these parameters in the model were adopted from previous studies focused on microwave heating in porous media [7], [8], [12]–[18].

Table 1.

Input Parameters Used In Numerical Model

Parameter	Unit	Solid Liver	Water	Vapor
Specific Heat Capacity	J/kg·K	1650	4178	1006
Thermal Conductivity	W/m·K	0.21	0.57	0.03
Density	kg/m3	1430	998	ideal gas
Viscosity	Pa·s	------	9.88E-4	1.80E-5
Diffusivity	m2/s	------	1.00E-7	2.60E-6
Intrinsic Permeability	m2	------	5.00E-14	10.0E-14
Relative Permeability		$\{\begin{array}{cc}{\left(\frac{S_w-0.08}{0.92}\right)}^3\hfill & S_w>0.09\hfill \\ 0\hfill & S_w<0.09\hfill \end{array}$		$\{\begin{array}{cc}1-1.1S_w\hfill & \hfill S_w<\frac{1}{1.1}\hfill \\ 0\hfill & \hfill S_w>\frac{1}{1.1}\hfill \end{array}$

5) Model Assumptions

Some simplifying assumptions were made to facilitate simulation of the microwave ablation process.

1. Initial uniform water content of 80%, which also accounted for residual fat content [19].

2. The liver architecture was set to 80% porous structure, as estimated from foodstuff literature [20].

3. No consideration of tissue contraction in the heating zone was given [21].

6) Simulation Strategy and Comparison

The electromagnetic power dissipation rate (1) was solved using time-harmonic Maxwell’s equations and the remaining heat (2), mass (3) and continuity (4,5) transfer equations were solved using a transient solver. The electromagnetic power dissipation was updated continuously with temperature-dependent relative permittivity and effective conductivity [22]. Segregated solvers were used for calculating temperature, water/ vapor velocities, and water/vapor concentrations. For rapid convergence, a boundary layer mesh was created at the antenna-tissue interface. The antenna input power of 50 W was applied for 300 seconds.

The new model was compared to a thermal conduction-only model, using the same initial electromagnetic model in the microwave ablation as the heat source. Temperature outputs at 5, 10 and 20 mm away from the emission point of the antenna in both models were compared against each other in 10 second intervals throughout the ablation period.

B. Experimental Setup

Samples of fresh ex-vivo bovine liver tissue (n=5) were obtained from a local abattoir and brought to room temperature (20°C). The samples (n=5) were homogenized in order to eliminate the influence of larger hepatic vessels on water vapor transport. A clinical microwave ablation antenna (Neuwave Medical Inc, Madison, WI) was placed near the center of the homogenized liver sample at a depth of 6 cm. Ablations were created using a generator output of 90 W at 2.45 GHz for 300 s, which corresponded to a power deposition of approximately 50 W in tissue after accounting for cable and generator losses. Temperatures were measured 5, 10 and 20 mm from the microwave antenna, flush with the plane of maximal heating in another cohort of samples (n=5) (Fig 2). Mean temperatures at each location were averaged across samples (n=5) and used as a comparison against the numerical models.

Fig. 2.

Experimental setup for the homogenized liver model. A) Fiber-optic temperature probes were placed 5, 10 and 20 mm away from the microwave antenna. Ablations were created at 90 W for 5 minutes. B) Post-ablation visualization of the homogenized liver. The heating zone near the antenna has desiccated and collapsed upon the microwave antenna and temperature probes.

A microwave antenna was also placed in intact liver samples (n=5) in an open environment. Temperature probes were placed 5, 10 and 20 mm away from the antenna and ablations were created with the same parameters used in the homogenized liver sample. Temperature comparisons between the homogenized liver samples and the intact liver samples were made against the numerical simulations to evaluate the role of anatomical liver structures.

During the ablation of the homogenized liver solution, computed tomography (CT) data were acquired over the entire tissue volume every 15 seconds (120 kVp, 200 mA, 512 × by 512, 1:1 helical pitch, 0.625 mm slice thickness; Discovery 750 HD, GE Healthcare, Milwaukee, WI). CT volumes were co-registered using rigid assumptions and the antenna tip as a fiducial marker. CT data were then averaged over all experimental samples at each time point to produce a single composite dataset for comparison to the numerical modeling results.

C. Parametric Study and Model Comparison

A preliminary study was performed to find a simulated vapor concentration that mapped well to experimental attenuation found in the CT images. The area enclosed within simulated vapor concentrations of 1%, 5%, 10% and 50% were compared against CT images thresholded at −200, −400, −600 and −800 Hounsfield Units (HU). Similarity between the simulated and experimental image masks, A and B, respectively, was calculated using the Jaccard index, J [23]:

$$\mathrm{J}(\mathrm{A},\mathrm{B})=\frac{A\cap B}{A\cup B}$$ (10)

where greater Jaccard indices (from 0 to 1) implied greater overlap between the simulated and experimental data. The vapor concentration and CT threshold pair that yielded the greatest Jaccard index was used to compare simulated and experimental data in later analyses.

Temperatures and Jaccard index from each sample group in experimental studies were averaged across samples to obtain a representative data point. All data presented in graphs are displayed as the mean with the error bars representing standard deviation.

III. Results

A. Numerical Simulations and Validation

Simulation of the fully coupled computational model for 47,635 triangular elements required 30 minutes on a 2.4 GHz Xeon processor work station with 24 GB RAM.

Qualitatively, the numerical model predicted an elongated pattern of vapor movement along the shaft of the antenna for the first two minutes, followed by a movement predominantly outward from the antenna until the end of the ablation procedure. The simulated rate of radial and longitudinal ablation zone growth was greatest at the beginning of the heating cycle, then decreased over time as noted in previous experimental studies [24]–[26].

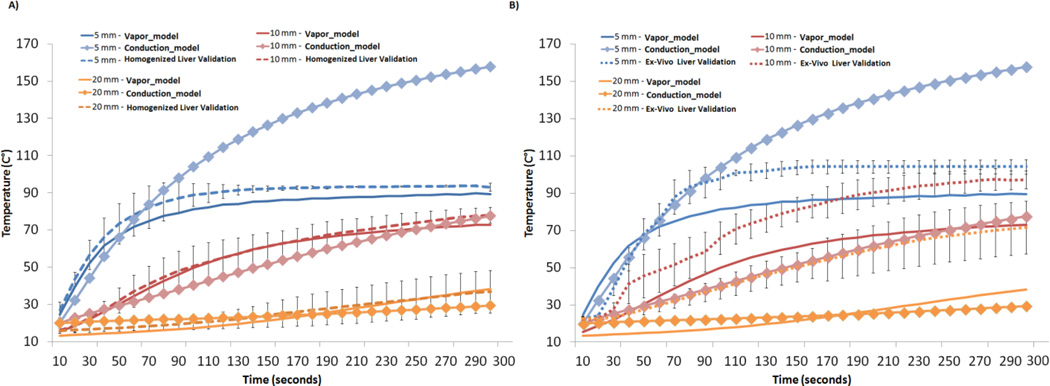
The temperature output from the numerical model at discrete points 5–20 mm away from the microwave antenna and its comparison to the homogenized liver experiment is summarized in Fig. 3A. The water vapor model 5 mm away from the microwave antenna exceeded 80 C° within the first two minutes of the ablation before leveling off at 90–100 C°. This plateau-effect is consistent with energy being absorbed during the phase transformation from water to vapor [4]. Temperatures simulated at more peripheral locations exhibited a much slower increase to lower levels, as expected. The experimental model matched that of the water vapor model, but demonstrated a plateau at a slightly higher temperature that was closer to 100 °C. Experimental temperature comparisons at distances of 10 mm and 20 mm, where the water remained in liquid form, were measured to be within a standard deviation of the water vapor model at corresponding locations.

Fig. 3.

A) Temperature comparisons between the water vapor model, the thermal conduction model and the experimental validation at positions 5 mm, 10 mm and 20 mm away from the microwave antenna. The greatest discrepancy between the thermal conduction model and vapor model occurred in the 5 mm position, where temperatures exceeded 100 °C in the thermal conduction model. The experimental validation demonstrated temperatures peaking at close to 100 °C, showing good correlation to the water vapor model. B) Temperature comparisons between the intact ex-vivo liver tissue model and the numerical mode. The intact ex-vivo liver model maintained the anatomical structure and vasculature that characterizes liver tissue. Microwave ablations created in the intact ex-vivo tissue exhibited temperature much higher than that predicted in the numerical model at all distances. This can be attributed to the fact that the numerical model utilized a homogenous porous media system and assumed isotropic thermal and electrical properties throughout the tissue. There was also higher variability in the ex vivo tissue compared to the homogenized liver, limiting its use for validation studies of numerical models.

Temperature elevation in the homogenized liver model did not match the intact liver as well. After 1 minute of heating, the temperature at the 10 mm and 20 mm locations was approximately 20 C° higher in the ex vivo intact liver compared to the homogenized liver samples. This difference was also seen in the 5 mm location but was minimized as the temperature peaked as the temperature approached 100 °C (Fig. 3B). Standard deviation of the homogenized liver solution ranged from 1.50–7.31°C while that of the ex vivo liver tissue ranged from 1.63–15.44 °C.

B. CT Imaging Study

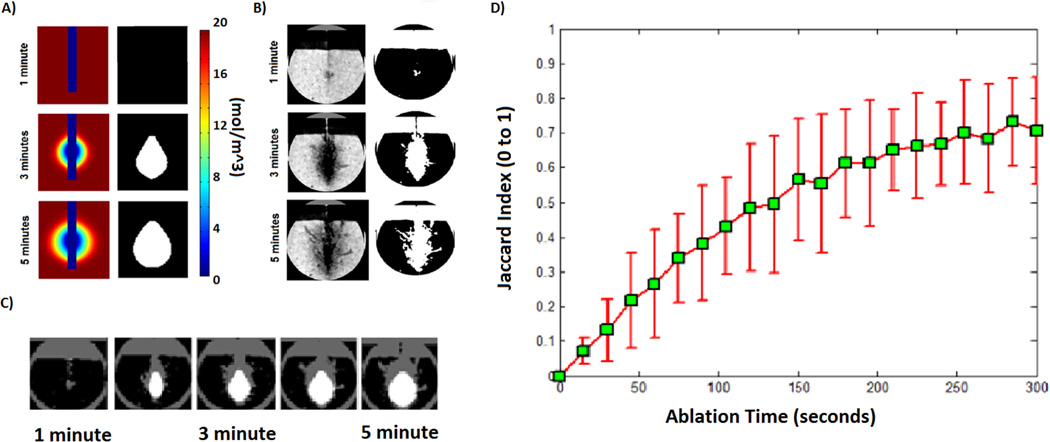
CT-imaging in homogenized liver showed trends in water vaporization formation similar to simulation results. Water vapor appeared as a gradient from complete liquid water in normal tissue (0 HU) to pure water vapor (−1000 HU), with some variation in the baseline liver tissue. Very little vapor was observed in the sample periphery, as indicated by the lack of change seen in the radio density for liver tissue (50 HU). Significant water vapor generated near the antenna reduced attenuation to levels associated with highly aerated tissue (−800 HU). Towards the end of the heating period, pockets of water vapor were observed migrating to discrete positions away from the ablation zone. These vapor-filled pockets collapsed after the microwave energy was turned off, marking an almost immediate phase change from water vapor to liquid in the absence of a microwave energy input. This rapid phase change is expected due to the continuous heating rate necessary to overcome the enthalpy of vaporization of liquid water (40.65 kJ/mol).

C. Parametric Study and Model Comparison

The preliminary study showed the highest Jaccard Index value of 0.613 between the 1% water vapor threshold in simulations and the −200 HU threshold in the CT images. These values were used to define the boundaries on simulated and experimental vapor concentration maps.

Experimental water vapor profiles were somewhat larger than those of simulations, especially toward the proximal portion of the heating zone. In contrast, the distal portion of the ablation zone exhibited excellent correlation to the modeling data. The 1% vapor contour diameter reached 2.40 cm, 3.20 cm, 3.80 cm, 4.20 cm and 4.60 cm at 1, 2, 3, 4 and 5 minutes respectively (Fig. 4A). These measurements compared favorably with the corresponding −200 HU threshold diameter: 2.56 cm, 3.41 cm, 4.00 cm, 4.29 cm, and 4.45 cm at 1, 2, 3, 4 and 5 minutes respectively (Fig. 4B). Similarity between the simulated and experimental vapor maps was relatively low for early ablation times (Jaccard index: 0.071 ± 0.039 at 15 s) but increased to a good correspondence at later time points (Jaccard index: 0.73 ± 0.130 at 300 s; Fig. 4C and 4D).

Fig. 4.

A) Computational model of a water vapor map during microwave ablation heating was created and thresholded at 1% vapor to find the outer boundaries of the ablation zone B) CT imaging was used to visualize the boundaries of the water vapor map using the −200 HU threshold. C) Boundaries of simulated and experimental vapor maps were compared to each other at multiple time points. D) A similarity measure using the Jaccard Index was calculated across each time point in order to validate water vapor model.

IV. Discussions

This study demonstrated the feasibility of adding water vaporization and transport to the simulation of microwave tissue heating. The water vapor model showed improved agreement against experimental temperature validations over the thermal-conduction model, particularly in areas of intense heating near the center of the ablation zone. Simulation of temperature changes where vaporization was occurring leveled off near 100 °C, a phenomenon not previously observed with the thermal-conduction model. Lastly, the study demonstrated the utility of CT imaging technique to validate the numerical predictions of water vapor movement in a cross-sectional area with high spatial and temporal resolution.

Accounting for water vaporization and transport allows for more flexible tissue property definition in future numerical studies. To date, models that describe physical properties of tissue have been mostly limited to temperature as an input variable [21], [22], [27]. The ability to predict when and where water vaporization occurs would permit the use of tissue models that decouple temperature and water content dependencies, leading to more physically accurate simulations. Improved model accuracy could improve the design of ablation devices and energy delivery techniques. Validating water vaporization and transport may also facilitate more thorough analysis of heat transfer from the various thermal ablation modalities.

The CT imaging and analysis technique used to observe vaporization and transport add another tool to characterize thermal ablations. In previous studies, tissue water content could only be analyzed from excised samples after an ablation zone was created. Thus the water content measurements were limited to the final ablation zone and the time evolution of dehydration could not be ascertained [19]. While water vapor content was not explicitly quantified, CT imaging provided a direct and temporally-sensitive method of validating the model vapor map boundaries of the ablation zone. This novel technique augments the previous strategies of temperature measurement and comparison to final ablation zone dimensions.

Ablations in the ex vivo liver model heated tissue at a fasterrate and to higher temperatures compared to the homogenized liver model. This could be explained by the intact anatomical structures in the liver, which offered resistance against free water vapor movement. The water vapor remained localized in the tissue and was able to absorb more energy. The intact liver anatomy, which included micro- and macro-vasculature and lobular geometry, also disrupted the heat transfer process and led to greater variability in temperatures between samples. The ex vivo liver model also heated tissue at a faster rate compared to that seen in the numerical model. This was an expected result as the numerical model was based on a homogenous porous media environment, conditions much closer to that of the homogenized liver model than that in an intact liver model. Thus, the homogenized liver experimental setup provided more reliable temperature measurements for the numerical model validation.

Simulated and measured temperatures showed trends consistent with previous work, but with improved consistency in the homogenized liver solution [22], [27], [28]. In studies that did not account for water vaporization, simulated temperatures tended to exceed measured values [27]. Such discrepancies were more obvious over 100 °C, since the latent heat of vaporization was not considered. Other work has also shown that incorporating the effects of water vaporization into temperature-dependent dielectric models can improve simulation-experiment correlation [22]. With the prediction of water content realized in the present study, a numerical model of properties based on temperature and water content would likely improve the generality of simulations. In turn this would increase the applicability of simulations to a wider range of clinical goals.

Experimental vapor contours were consistently larger than simulations, which may be due to assumptions made in constructing the numerical model. Permeability and porosity assumptions related to the homogenized liver solution were estimated from foodstuff data, as these properties were not readily available for liver tissue. Assumed values may also have changed during homogenization. Tissue contraction was not calculated, which could potentially affect porosity and diffusion constants associated with water vapor [21]. In addition, the tendency for low-density water vapor to rise upward toward a lower-pressure environment was neglected in the numerical model. Additional refinements to the numerical model inputs may improve correspondence with experimental data.

V. Conclusion

This study demonstrated the potential of incorporating water and water vaporization and transport physics into the simulation of microwave thermal ablations. CT imaging was used as a real-time tool to monitor water vapor boundaries during experimental studies, and could therefore be applied to validate the simulation model. The new model may help to improve the accuracy of microwave ablation simulations, allow more general analysis of ablation inputs, and facilitate the analysis of heat and mass transfer contributing to thermal ablation growth.