Probing Substrate Interactions in the Active Tunnel of a Catalytically Deficient Cellobiohydrolase (Cel7)

Background: Substrate interactions in the long tunnel of processive cellulases govern both their catalytic activity and stepwise movement along a cellulose strand.

Results: The energetics of enzyme-substrate interactions at different depths of the tunnel are reported.

Conclusion: The affinity for the substrate varies strongly through the tunnel.

Significance: Quantitative information on interactions is required to understand the complex processive mechanism.

Abstract

Cellobiohydrolases break down cellulose sequentially by sliding along the crystal surface with a single cellulose strand threaded through the catalytic tunnel of the enzyme. This so-called processive mechanism relies on a complex pattern of enzyme-substrate interactions, which need to be addressed in molecular descriptions of processivity and its driving forces. Here, we have used titration calorimetry to study interactions of cellooligosaccharides (COS) and a catalytically deficient variant (E212Q) of the enzyme Cel7A from Trichoderma reesei. This enzyme has ∼10 glucopyranose subsites in the catalytic tunnel, and using COS ligands with a degree of polymerization (DP) from 2 to 8, different regions of the tunnel could be probed. For COS ligands with a DP of 2–3 the binding constants were around 10⁵ m⁻¹, and for longer ligands (DP 5–8) this value was ∼10⁷ m⁻¹. Within each of these groups we did not find increased affinity as the ligands got longer and potentially filled more subsites. On the contrary, we found a small but consistent affinity loss as DP rose from 6 to 8, particularly at the higher investigated temperatures. Other thermodynamic functions (ΔH, ΔS, and ΔC_p) decreased monotonously with both temperature and DP. Combined interpretation of these thermodynamic results and previously published structural data allowed assessment of an affinity profile along the length axis of the active tunnel.

Introduction

Finely tuned interactions with substrate, transition state, and product are crucially important in any enzymatic process. One intriguing example of such fine-tuning is seen for cellobiohydolases (CBHs),² which make up the main part of mixtures secreted by some fungi and bacteria that degrade plant material. Cellobiohydrolases attack the end of a cellulose molecule and subsequently cleave off soluble sugars as it slides along the cellulose surface with a single polysaccharide strand threaded through the active tunnel. This so-called processive mechanism relies on a complex array of interactions between the substrate and different domains of the enzyme. Some aspects of this were recently discussed by Payne et al. (1), who among other things emphasized that enzyme-cellulose interactions must be strong enough to outweigh the intra- and intermolecular forces that stabilize crystalline cellulose. If this was not the case, the free energy gradient required to transfer a part of the strand from the crystal to the active site would be absent, and the Michaelis complex would only form slowly if at all. As crystalline cellulose is stabilized by a tight network of hydrogen bonding (2, 3), it will clearly require quite strong interactions in the active site to establish the free energy gradient, discussed by Payne et al. (1). On the other hand, different factors suggest that too strong interactions could be detrimental to the catalytic action of CBHs. One of these is the fundamental premise for enzyme catalysis (independent of the processive mechanism) that very strong interactions with the substrate ground state will favor this with respect to the transition state and hence oppose catalysis. In addition, the special sliding movement of the CBH could be compromised by strong binding and a concomitant high activation barrier between processive steps. In light of this, it appears that fine-tuning of the forces of attraction that underlie catalysis may be particularly decisive for processive enzymes such as CBHs acting on crystalline substrates and hence that a better description of such interactions will be essential for a molecular understanding of this industrially important class of enzymes.

The most studied CBH is Cel7A from the filamentous fungus Trichoderma reesei (an anamorph of Hypocrea jecorina). For this enzyme (henceforth abbreviated TrCel7A) and several other fungal CBHs, it appears that the strict requirements to substrate interactions outlined above have been met by a design that combines a small carbohydrate binding module (CBM) with a flat cellulose interaction plane (4) and a catalytic domain with a long tunnel-shaped active site. For TrCel7A this tunnel is 50 Å long and contains ∼10 subsites for binding of glucopyranose moieties (5). Seven of these subsites (named site −1 through −7) are upstream with respect to the scissile glycosidic bond, whereas two or three subsites (site +1 through +3) constitute the expulsion site where the soluble product is transiently located after hydrolysis (5, 6) (cf. Fig. 6). TrCel7A is a retaining cellulase with a catalytic triad, Glu-212–Asp-214–Glu-217, flanking the scissile bond between subsite +1 and −1. Specific roles of these three residues were studied by Ståhlberg et al. (7), who concluded that Glu-212 was the (anionic) nucleophile responsible for the initial attack of the glycosidic bond, whereas Glu-217 was the proton donor in the second step of a double displacement reaction mechanism. Accordingly, Ståhlberg et al. (7) found that the single-point variants E212Q and E217Q, which cannot perform acid/base reactions, were severely deficient in catalytic activity. These two variants are isosteric with the wild type and perhaps for that reason it was found that the active site structures of E212Q and E217Q were essentially identical to wild type TrCel7A (7). The same workers (5) have also provided high resolution structures of complexes between these variants and cellooligosaccharides with a degree of polymerization (DP) of 4, 5, and 6 (i.e. cellotetraose, cellopentaose, and cellohexaose). More recently, the structure of E217Q in complex with a longer oligosaccharide that fills the whole active site (6) has also been published. All in all this makes the E212Q and E217Q variants attractive candidates for quantitative studies of Cel7A-substrate interactions. Thus, if the catalytic activity is negligibly small and the enzyme structure is mainly conserved so that interactions will resemble those in the wild type, thermodynamic measurements may provide useful quantitative information on the interactions; particularly so if cellooligosaccharides with different DP and known complex structure are compared. In the current work we pursue this idea by calorimetric measurements of the interaction of cellooligosaccharides with DP ranging from 2 to 8 and the E212Q mutant of TrCel7A, which was found by Ståhlberg et al. (7) to have the lowest residual activity.

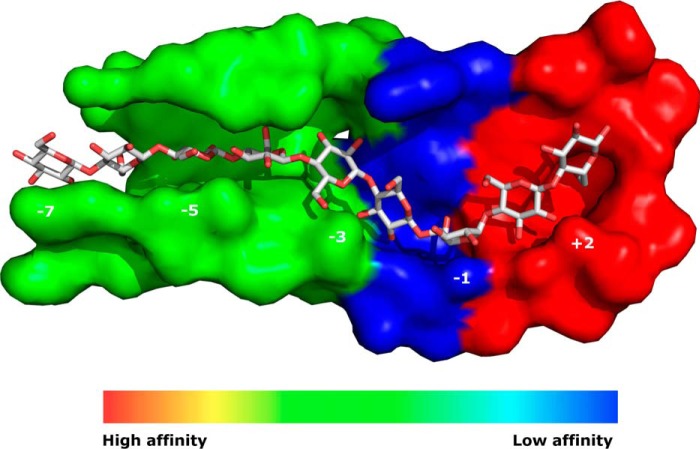
FIGURE 6.

Combined interpretation of the current thermodynamic results and earlier structural data showing regions of high and low substrate affinity along the active tunnel. Numbers identify glycopyranose subsites.

EXPERIMENTAL PROCEDURES

Enzymes

TrCel7A (UniProt G0RVK1) was expressed in Aspergillus oryzae as previously described (8). Site-directed mutagenesis on the wild type gene was done to create the E212Q variant gene by PCR using partially overlapping primers E212Q forward (GGCCATGGCTCCTGTTGTTCGCAGATGGATATCTGGGAGGCC) and E212Q reverse (CGAACAACAGGAGCCATGGCCTCCAATGCCGG). Expression of TrCel7A E212Q was done as the wild type. Both wild type and variant were purified as previously described (8).

The concentration of purified enzyme stocks was measured by amino acid analysis. Protein samples were dried and hydrolyzed in 18.5% HCl + 0.1% phenol at 110 °C for 16 h. Amino acid analyses were performed by precolumn derivatization using the Waters AccQ-Tag Ultra Method. In short, amino acids were derivatized by the AccQ-Tag Ultra Reagent and separated with reversed-phase UPLC (Waters Corp., Milford, MA), and the derivatives were quantitated based on UV absorbance. Stock concentrations were also measured by conventional UV absorption in a Shimadzu 4600 instrument. We used a theoretical extinction coefficient (9) at 280 nm of 84.8 mm⁻¹cm⁻¹. No systematic differences between these two methods were detected. Enzyme concentrations in diluted samples used in the calorimetric measurements were routinely checked by UV adsorption measurements.

Cellooligosaccharides

In the following we use the notation COSX for cellooligosaccharides, where X is the DP. COS2 (cellobiose) was purchased from Sigma (>98%), COS3-COS6 (94–95%) was from Megazyme (Wicklow, Ireland), and COS7 and COS8 was from Elicityl (Crolles, France). The purities stated by the manufacturer of COS7 and COS8 were 80 and 70%, respectively. Chromatographic analysis (high performance anion exchange chromatography with pulsed electrochemical detection (HPAEC-PAD; see below) identified some contamination by longer and particularly shorter COS, and a somewhat higher purity (85–90%) for COS7 and COS8. This either means that the delivered product was a bit more pure than the stated value or that a part of the impurities could not be detected in our protocol. For COS3-COS6, HPAEC-PAD suggested purities around or slightly below the stated values (90–95%). Again, the main detected impurity was smaller COSs. All solutions used in the experimental work were made in a standard 50 mm acetate buffer, pH 5.0.

Calorimetry

COS binding was studied by isothermal titration calorimetry (ITC) using either the VP-ITC- or the ITC200 instrument (both from Microcal, Malvern Instruments, Worcestershire, UK). Both calorimeters were first calibrated by the build-in heater, and this calibration (and the injection system) was subsequently tested by a so-called chemical calibration using the reaction of dilute HNO₃ and Tris base as described by Baranauskiene et al. (10). If necessary, a post experiment correction factor was applied on the basis of the chemical calibration. The quality of ITC binding isotherms depends on the so-called c-value, c = K_B[r_cell] (11), where K_B is the binding constant, and [r_cell] is the initial concentration of the reactant in the calorimetric cell. Optimal values are approximately in the 10–100 range. This limitation together with solubility considerations necessitated that experiments were conducted in two different ways. For experiments with the smaller, more soluble COSs (COS2-COS4) we loaded the calorimetric cell with enzyme solution (between 35 and 50 μm) and titrated with 2.0 mm COS until the ITC peaks became essentially undetectable at a COS:enzyme molar ratio of ∼10. The longer COS ligands were sparsely soluble, and the concentration in the syringe required for the above procedure could not be reached. Thus, for COS5-COS8 the experiment was reversed so that the enzyme was in the syringe and the ligand in the cell. Specifically, a COS solution (4–8 μm) was loaded into the calorimeter cell and titrated with the enzyme (100–140 μm). No systematic differences between binding parameters obtained by these two protocols were observed for either COS5-E212Q or COS6-E212Q, which were studied in both ways.

Activity

E212Q is not completely inactive against soluble substrates (7), and residual COS activity was tested as a function of both temperature and ligand DP. To this end a number of 1-ml aliquots with 10 μm COS solution in Eppendorf tubes were equilibrated at the desired temperature in an Eppendorf Thermomixer Comfort. The reaction was started by the addition of E212Q to a final concentration of 0.5 μm and quenched at appropriate time-points through the addition of 100 μl of 1.0 m NaOH. The concentrations of the tested COS ligand and possible hydrolysis products in these samples were measured and compared with two types of controls. One control was made in the same way as the reaction samples except that the quencher was added to the Eppendorf before the E212Q variant, hence preventing the reaction. The other control was a 10 μm COS solutions without any enzyme. COS concentrations were measured by HPAEC-PAD. The instrument was a Dionex ICS-5000 ion chromatograph equipped with a CarboPac PA-10 column (Thermo Fisher Scientific, Waltham, MA), and the procedures have been described elsewhere (12). Results were expressed as the specific enzyme activity (in min⁻¹), A_spec = ΔC_COS/(tE₀), where E₀ is the concentration of E212Q, and t is the contact time. ΔC_COS is the reduction in the concentration of the investigated COS determined from the chromatographic peaks of the reaction sample and the control that was quenched before adding enzyme.

Adsorption

Binding of respectively wild type TrCel7A and the E212Q variant to bacterial cellulose was tested using preparation methods and adsorption protocols described previously (13).

RESULTS

Hydrolytic Activity and Adsorption

To mimic the conditions of the calorimetric experiments, several activity measurements were conducted for COS4-COS8 at contact times between 10 and 100 min. At 10 °C, no statistically significant reduction in COS concentration could be detected by HPAEC-PAD. The standard deviation of the chromatographic response for triplicate measurements ranged from 2 to 5%, and based on this we conclude that the specific activity, A_spec, of E212Q against a 10 μm COS solution at 10 °C was <0.01 min⁻¹. At higher temperatures the activity of E212Q became detectable, and at 30 °C we found A_spec = 0.03, 0.06, 0.07, 0.09, and 0.09 min⁻¹ for COS4, COS5, COS6, COS7, and COS8, respectively. The Michaelis-Menten constants, K_m, at 30 °C for the longer COSs are in the 2–4 μm range for the wild type enzyme (14), and this suggests that the current A_spec values (measured at a substrate concentration of 10 μm) will be close to the maximal rate. At 50 °C the analogous values for A_spec were 0.07, 0.09, 0.16, 0.15, and 0.21 min⁻¹. In the current context, these measurements primarily serve as controls for the interpretation of the calorimetric data (see below). We note, however, that that at 30 °C A_spec values for E212Q are ∼5000 times lower than published maximal rates for wild type TrCel7A (14). Interestingly, a similar reduction in activity was found by Ståhlberg et al. (7) using the soluble substrate analog 2-chloro-4-nitrophenyl β-lactoside.

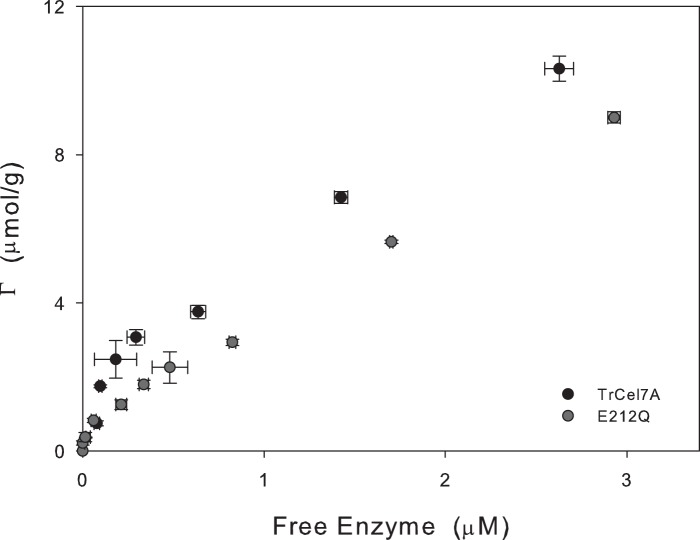
We also compared the adsorption properties of the E212Q variant and the wild type enzyme on bacterial cellulose. Binding isotherms in Fig. 1 suggested that the mutation slightly reduced both the affinity and binding capacity. This may be illustrated by the so-called partitioning coefficient, K_p, defined as the initial slope of the isotherms. We found K_p values of 14 and 11 liters/g for TrCel7A and E212Q, respectively. This value for the wild type enzyme was in accord with earlier measurements (15–17).

FIGURE 1.

Adsorption isotherms for TrCel7A wild type and the E212Q variant. The substrate was bacterial cellulose and the experimental temperature was 25 °C.

Calorimetry

We first studied ligand binding at 10 °C, where the activity measurements had shown very low hydrolytic activity (we will return to possible interference from hydrolysis below; cf. Fig. 3). The integral of each injection peak was plotted as a function of the injectant concentration in a so-called enthalpogram, as exemplified for COS2, COS4, and COS6 in Fig. 2.

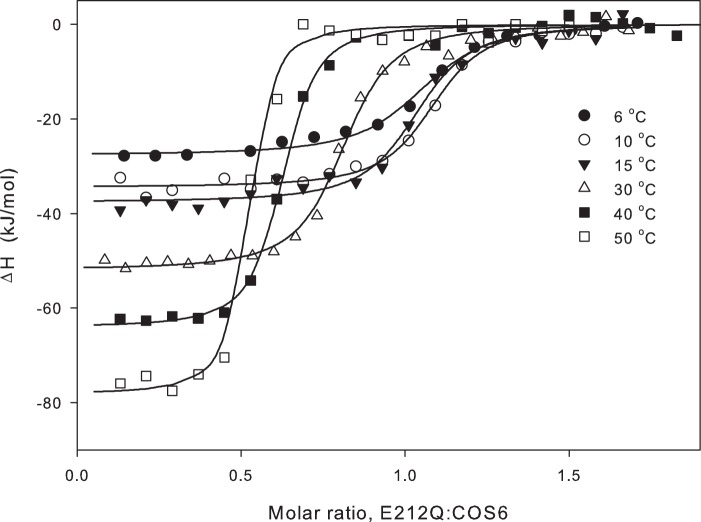
FIGURE 3.

Temperature series for the binding of COS6 to the E212Q variant. The enthalpy change upon injecting E212Q into a COS6 solution in the calorimetric cell is plotted against the E212Q:COS6 molar ratio. Lines represent best fits of the binding model discussed under “Results.”

FIGURE 2.

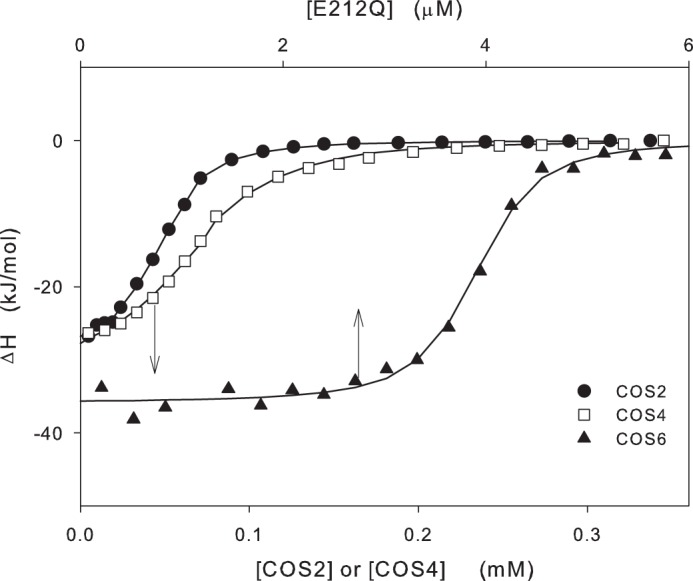
Examples of raw data from the calorimetric measurements at 10 °C. Areas of injection peaks were normalized with respect to the amount of injectant delivered to get the enthalpy change in kJ/(mol injectant) and plotted as a function of the concentration of the injectant. In the experiments with COS2 and COS4 (lower abscissa), 42 μm enzyme (E212Q) in the calorimetric cell was titrated with doses of 2 mm COS ligand. For COS6 (upper abscissa), the experiment was conducted in the opposite way with the COS ligand (4 μm) in the calorimetric and 132 μm E212Q solution in the syringe. This difference in the procedure for, respectively, short and long COS ligands was dictated by solubility limitations (see “Experimental Procedures”). The lines show the best fits of a simple binding model based on one set of equal and independent binding sites.

All data at 10 °C were initially analyzed with respect to a simple binding model (11), which stipulates a number (n) of independent and thermodynamically identical binding sites on each enzyme molecule. We emphasize that although we changed between using enzyme and COS as the injectant (see “Experimental Procedures”) n values in Table 1 were consistently defined in this way (i.e. number of COS sites per enzyme molecule). We used the nonlinear regression routine provided by the instrument manufacturer (Microcal), and examples of model fits are included in Fig. 2. Maximum likelihood values for the three regression parameters, stoichiometry (n), enthalpy change (ΔH), and binding constant (K_B), for all investigated systems at 10 °C are listed in Table 1. Errors in the Table 1 are S.D. for 2–4 independent experiments. We also assessed confidence intervals from separate regressions and found that n and ΔH were consistently quite well identified with confidence intervals <5% of the parameter value. Identifiability of K_B was poorer with confidence intervals of 15–40% of the parameter value. Table 1 shows that the COS ligands may be coarsely divided into two groups. Thus, the shorter ligands (COS2-COS4) showed binding constants around 10⁵ m⁻¹ (i.e. dissociation constants, K_D = 1/K_B, of ∼10 μm) and n > 1. The latter suggested that more than one ligand associated with the enzyme over the concentration range studied here, and we will return to this observation below. For the longer COS ligands (COS5-COS8) we found stoichiometries close to 1 and binding constants around 10⁷ m⁻¹ (K_D ∼ 100 nm). The strongest affinity was for COS6, with K_B = 3.6 × 10⁷ m⁻¹ (K_D ∼ 30 nm). One noticeable trend in Table 1 is that the binding strength does not simply increase as the COS ligand gets longer and potentially fills more subsites in the active tunnel. Rather, within the group of small ligands the simple model suggested slightly stronger binding for COS2 compared with COS3. Analogously, the affinity did not increase with ligand size through the COS5-COS8 series. In this latter group, K_B was independent of DP to within the experimental scatter for COS5-COS7 and slightly lower (slightly weaker binding) for COS8. The enthalpy changes at 10 °C were quite similar for all ligands (-34 ± 2 kJ/mol) with the noticeable exception of COS3 that was more exothermic (−47 kJ/mol).

TABLE 1.

Results from non-linear regression analysis of the calorimetric data at 10 °C

A model based on one set of independent, thermodynamically equal binding sites was fitted to the experimental data to get maximum likelihood parameters for the binding enthalpy (ΔH), stoichiometry (n), and binding constant (K_B). Binding to the E212Q variant was measured for cello oligosaccharides with a DP from 2 to 8. The interaction of cellobiose (DP = 2) and the wild type TrCel7A enzyme (WT) was also measured. Errors are S.D. for 2–4 separate measurements.

DP	Enzyme	ΔH	n	KB
		kJ/mol		m−1
2	WT	35.8 ± 0.3	1.39 ± 0.04	(1.3 ± 0.08) × 105
2	E212Q	30.5 ± 0.3	1.41 ± 0.04	(1.8 ± 0.04) × 105
3	E212Q	47.3 ± 1.8	1.55 ± 0.13	(7.2 ± 0.6) × 104
4	E212Q	33.0 ± 1.2	2,01 ± 0.03	(8.7 ± 1.3) × 104
5	E212Q	34.1 ± 4.2	1.02 ± 0.11	(1.4 ± 0.7) × 107
6	E212Q	35.2 ± 1.7	0.89 ± 0.19	(3.6 ± 2.2) × 107
7	E212Q	33.9 ± 2.6	0.79 ± 0.12	(2.6 ± 1.4) × 107
8	E212Q	36.1 ± 2.4	0.97 ± 0.14	(5.3 ± 1.1) × 106

Returning to the stoichiometry we note that n = 2 for COS4 (Table 1). This implies that two sites on E212Q get saturated with COS4 in the concentration range (0–0.3 mm) studied here. To test this further we analyzed the data for COS4 with a model based on two sets of binding sites (18, 19). Direct fitting of this more complex model, which has a total of six parameters (separate n, ΔH, and K_B for each of the two types of sites), was unsuccessful inasmuch as the parameter dependence was unacceptably high (some correlation coefficients >0.98). If, however, this model was applied with a fixed value of n = 1 for both sites (in accordance with the observation n = 2 for the simple model), the remaining 4 parameters could be determined with correlation coefficients in the 0.65–0.85 range. Analysis of duplicate COS4 measurements suggested a high affinity site with K_B = (7.3 ± 3.6) × 10⁵ m⁻¹ and ΔH = −26.7 ± 0.2 kJ/mol and a low affinity site with the parameters K_B = (3.6 ± 0.1) × 10⁴ m⁻¹ and ΔH = 39.4 ± 0.8 kJ/mol. For the two smallest ligands, COS2 and COS3, the simple model found intermediate stoichiometries (n ∼ 1.5). This probably reflects one strong binding site in addition to other interaction points with weaker affinity, which do not reach high occupancy in the investigated concentration range. This interpretation is supported by structural studies on related GH7 enzymes, which has documented binding of more than one small COS ligand to the same molecule under some conditions (20–22) (also seen in unpublished PDB structures 3PFZ and 3PL3). All attempts to apply the two-site model for COS2 and COS3 and hence single out the parameters for the high affinity site remained unsuccessful due to high parameter dependence.

We conclude that at 10 °C, the thermodynamics of COS binding to the E212Q variant (and cellobiose binding to the enzyme wild type) could be elucidated by conventional ITC procedures. For the smallest ligands (COS2 and COS3) a binding stoichiometry around 1.5 suggested interference between a primary site and weaker interactions. It follows that the thermodynamic parameters in Table 1 can only be considered approximate for these two ligands. For COS4 we could single out two sites with dissociation constants of ∼1 and 30 μm, respectively. For still larger ligands (COS5-COS8) we found n values close to 1 and dissociation constants and enthalpy changes of ∼0.1 μm and −35 kJ/mol, respectively. Interestingly, these latter values at 10 °C were almost independent of DP within this group of ligands (COS5-COS8).

The previous results were all at 10 °C, and at this temperature the activity of cellulases is generally quite low. Most cellulase research, therefore, focuses on higher temperatures particularly around 50 °C, where CBHs are applied industrially. In an attempt to assess ligand binding over a broader temperature range we conducted ITC measurements between 10 and 50 °C. As the temperature was increased, some hydrolysis of the ligand occurred on the time scale of the calorimetric experiment, and this obviously complicates subsequent data analysis. Hence, the hydrolytic reaction will reduce ligand concentration and generate heat, and both of these effects could obscure analysis of the calorimetric data. We found that the hydrolytic heat flow arising from the severely impeded enzyme reaction was negligibly small,³ and we will henceforth ignore this problem. Changes in ligand concentration during the calorimetric measurement, on the other hand, turned out to be a major problem above room temperature (Fig. 3), and we tested different strategies to account for this in the data analysis. For the smaller ligands (COS3-COS4) all such attempts proved unsuccessful primarily due to the comparably low binding affinity and the existence of multiple, interfering binding sites. Hence, these ligands were only analyzed at 10 °C. For the larger COSs, on the other hand, we found that one of the parameters, the interaction enthalpy, ΔH(T), could be determined as a function of temperature between ∼5 and 50 °C. This was because strong binding in these systems gave rise to a flat plateau in the enthalpograms before the sigmoidal course when the binding approaches saturation (see Fig. 3). This plateau provides a direct (model-free) measure of ΔH, because it reflects a situation where essentially all added injectant binds and ΔH is simply the measured heat normalized with respect to the amount of injectant.

Fig. 3 shows an example (for COS6) of a temperature series, and it appears that two main changes occurred in the enthalpograms as the temperature increased; the inflection point gradually shifted to the left and the plateau level decreased (from −26 kJ/mol at 6 °C to −78 kJ/mol at 50 °C in the example in Fig. 3). The molar ratio (E212Q/COS6) at the inflection point fell from ∼1 in the experiments at 6, 10, and 15 °C to 0.67 at 30 °C and 0.45 at 50 °C. Similar shifts with increasing temperature were found for all larger ligands (COS5-COS8). In the light of the activity data derived from the HPAEC-PAD measurements we interpret this shift as the result of partial ligand hydrolysis, which becomes significant above room temperature. Thus, if a fraction of the ligand in the calorimetric cell is lost due to hydrolysis during the measurement, the inflection point will occur at a lowered E212Q/COS ratio. This means that model parameters derived from the fits in Fig. 3 are without physical meaning. As mentioned above, however, one parameter, ΔH, can be assessed directly without residing to any model in cases with a well defined plateau region. We read off the initial plateau levels in Fig. 3 and similar plots for the other ligands and plotted ΔH for COS5-COS8 as a function of temperature in Fig. 4. The results showed that ΔH scaled linearly with T for all four ligands, and this implies that binding is associated with a change in heat capacity, ΔC_p = dΔH/dT, which is independent of temperature. Linear fits to ΔH(T) in Fig. 4 suggested that ΔC_p was, respectively, −0.79 ± 0.08 kJ/(mol K), −1.10 ± 0.09 kJ/(mol K), −1.52 ± 0.09 kJ/(mol K), and -1.78 ± 0.08 kJ/(mol K) for COS5, COS6, COS7, and COS8.

FIGURE 4.

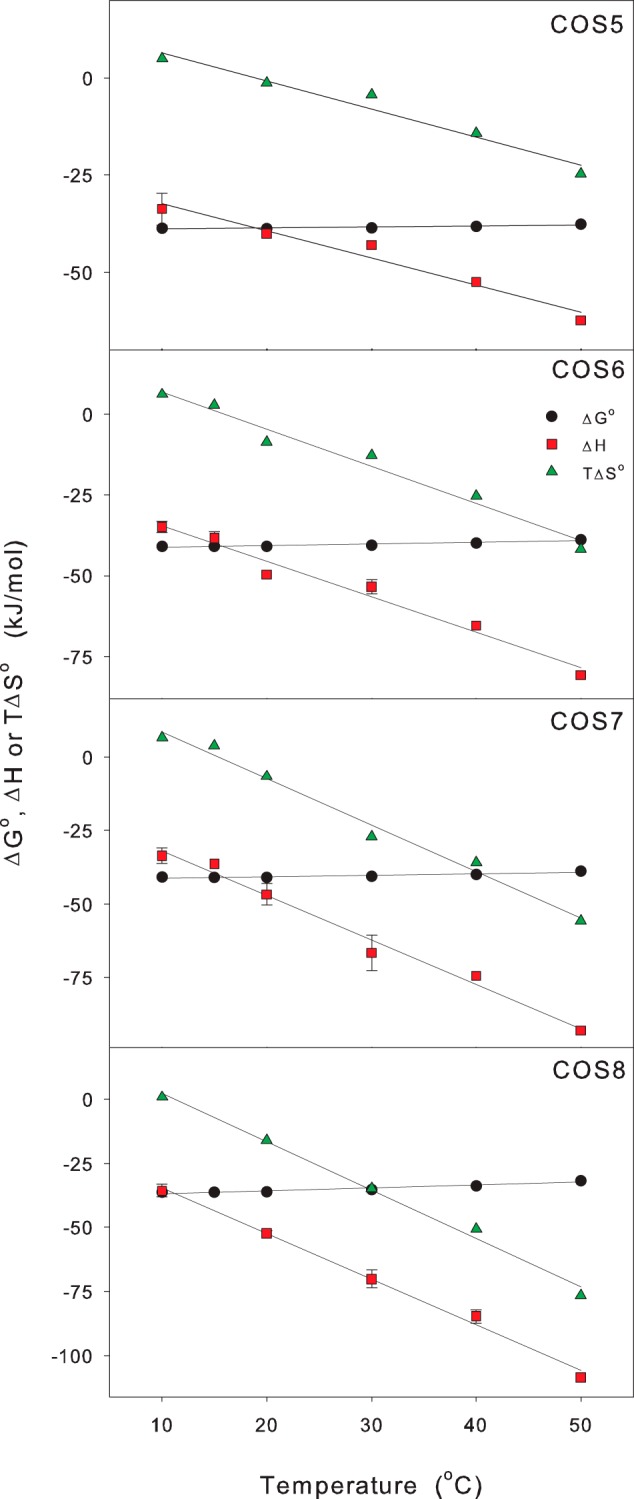
Effect of temperature and DP on the thermodynamics of E212Q-COS interactions. Binding enthalpies were found from plateau levels in the raw ITC data as exemplified in Fig. 3. Subsequently, the heat capacity change, ΔC_p, was determined as the slope of a linear fit to ΔH(T). Insertion of ΔC_p and thermodynamic data at 10 °C (Table 1) into Equation 1 gave K_B(T), and hence the standard free energy change (ΔG⁰(T) = −RT ln[K_B(T)]) and standard entropy change (TΔS⁰(T) = ΔH(T) − ΔG⁰(T)). The error bars for ΔH represent two S.D. for 2–4 independent titrations. We did not have enough enzyme variant to conduct multiple replicates for all temperatures and COS lengths, and instead we made selected reproducibility tests for ∼one third of the cases (including all measurements at 10 °C). In addition to random scatter, a small systematic error in ΔH arises from COS impurities (see “Experimental Procedures”). For COS8 (the most impure ligand) we used the HPAEC-PAD results and the enthalpy data in this figure to estimate that ΔH could be between 0.5 kJ/mol (25 °C) and 3 kJ/mol (50 °C) more exothermic that the values reported here. These shifts are smaller than the random scatter in the measurement of ΔH (the effect is limited because the impurities are related COS ligands with similar binding enthalpies).

These results together with the binding constants at 10 °C (Table 1) allows calculation of binding constants at other temperatures by the Van't Hoff equation, d ln[K_b(T)]/dT = ΔH⁰(T)/RT². In the current case, where ΔH changes with temperature and ΔC_p is constant, the differential Van't Hoff equation solves to

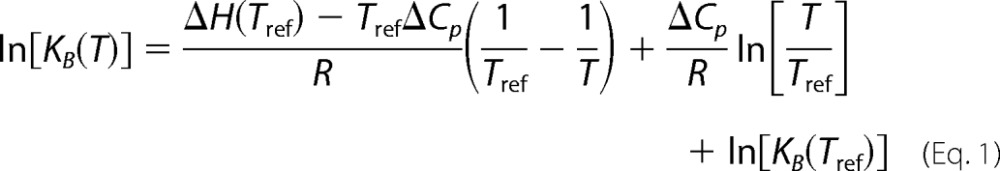where T_ref is a reference temperature at which both K_B and ΔH is known (in this case 10 °C) (23, 24). We used Equation 1 to calculate K_B at the temperatures where ΔH had been measured and determined the corresponding standard free energy changes, ΔG⁰ = −RTlnK_B. This function (ΔG⁰) together with the entropic contribution to the binding,⁴ TΔS⁰ = ΔS − ΔG⁰, are also plotted against temperature in Fig. 4.

One interesting result in Fig. 4 was that the thermodynamic functions at higher temperatures (particularly ΔH and TΔS⁰) varied quite distinctively with the size of the COS. To illustrate this more directly, we plotted the thermodynamic functions against ligand size at 25 °C and 50 °C in Fig. 5. This figure shows that at room temperature (and above), the functions ΔH, TΔS⁰, and ΔC_p all decreased linearly with DP. The increment per glucopyranose unit at 50 °C was ∼−15 kJ/mol for ΔH, −17 kJ/mol for TΔS⁰, and −0.37 kJ/(mol K) for ΔC_p (the latter was temperature-independent).

FIGURE 5.

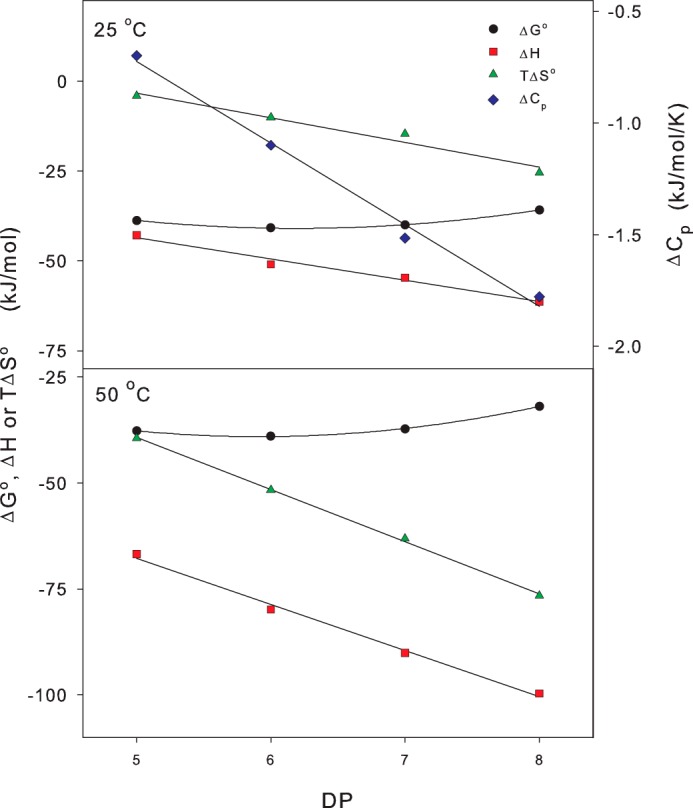
Thermodynamic data from Fig. 4 at 25 °C and 50 °C, respectively, plotted as a function of the ligand size (DP). The heat capacity change, ΔC_p, was independent of temperature and is only plotted in the (25 °C).

An important result in Figs. 4 and 5 is the illustration of reduced net affinity (increased ΔG⁰) upon heating. Lowered affinity at higher temperature is inevitable for an exothermic reaction (according to Le Chatelier's principle), but it is interesting to note its extent and dependence of COS size. If we consider COS8, ΔG⁰ changes from −37 kJ/mol at 10 °C to −32 kJ/mol at 50 °C. This corresponds to a 40-fold reduction in binding constant from K_B(10 °C) = 5.3 × 10⁶ m⁻¹ to K_B(50 °C) = 1.4 × 10⁵ m⁻¹, and this shows that site occupancy changes significantly with temperature. As an example, we may consider a solution that is 1 μm with respect to total concentrations of both COS8 and E212Q. Neglecting any interference from hydrolysis, insertion into the law of mass action shows that 65% of the enzyme will carry a COS8 ligand in this solution at 10 °C and that heating to 50 °C will reduce occupancy to 11%. For COS5 the analogous values are 76 and 43%, and this illustrates how temperature-induced weakening of E212Q-COS complexes becomes more pronounced the longer the ligand.

DISCUSSION

Cellobiohydrolases are currently under intense study due to their application in upcoming industries producing ethanol and other chemicals from lignocellulosic feedstock (25–27). Improvements of CBH performance are highly desirable, but rational approaches through e.g. protein engineering or modifications of reaction conditions are often hampered by insufficient understanding of fundamental molecular mechanisms (28, 29). These mechanisms have proven intricate, and current descriptions of processive catalysis by CBHs consider a complex scheme of intermediate states that interconvert on different time scales (30–34). Progress in the area will require isolated analyses of the central reaction steps, and the current work has zoomed in on one such aspect, namely the strength of substrate interactions. We used the E212Q variant of TrCel7A because earlier work suggested that this variant had a near-native structure and a strongly reduced catalytic activity (7). At 30 °C we found that the residual activity of E212Q against soluble COS was ∼0.02% that of previously reported values for the wild type (14), and this reduction was in line with earlier studies of E212Q activity against a soluble substrate analog (7). This coincidence supports the interpretation that residual activity relies on limited catalysis exerted by the variant rather than artifacts such as contamination of the variant sample by wild type enzyme (cf. Ref. 7). On a practical level, this degree of residual activity meant that titration calorimetric experiments around 10 °C could be conducted with minimal interference from ligand hydrolysis and analyzed in the conventional way by a mass action model. Around and above room temperature, on the other hand, an increasing fraction of the COS ligand was hydrolyzed during the experiment, and this prevented model analysis of the calorimetric data. For the longer ligands (COS5-COS8) this problem could be partially circumvented as the enthalpy of interaction, ΔH (but not the binding constant, K_B) could be estimated directly from the enthalpograms (Fig. 3) without the application of any model. Once ΔH and its temperature derivative, ΔC_p, had been established up to 50 °C, other thermodynamic parameters could be calculated by the Van't Hoff equation.

The E212Q variant used here was the intact enzyme including both the (mutated) catalytic domain and the CBM. This raises the question of whether interactions of both of these domains could be reflected in the calorimetric results. To this end we note that the CBM of TrCel7A previously has been shown not to interact with small COS ligands (COS2 and COS3) (35). The same study also found that K_B at 5 °C for the CBM-COS6 interaction was around 2900 m⁻¹, and this translates into a negligible (∼1%) site occupancy on the CBM in the COS concentration range (4–8 μm) studied here. A more recent work (36) reported slightly stronger binding of COS6, but again this was negligible compared with the affinity observed here. We conclude that the ITC saturation behavior illustrated in Figs. 2 and 3 reflects interactions with the catalytic domain; i.e. the mode of interaction that has previously been described in detail with respect to structure (5–7). This interpretation implies that the binding constant for COS6 association with the catalytic domain is ∼4 orders of magnitude larger than for binding to the CBM (35, 36).

It has previously been shown that the active site structure of TrCel7A is essentially unchanged by the E212Q mutation (7), and this is in line with the observation that cellobiose bound with similar thermodynamic parameters to, respectively, wild type and variant (Table 1). It is also in accord with the comparable partitioning coefficients found for the adsorption on bacterial cellulose (Fig. 1). The slight (∼15%) reduction in the partitioning coefficient of the variant could reflect structural changes, but it could also rely on contributions from the covalent bond, which is transiently formed between Glu-212 and the cellulose strand in the glycosyl-enzyme intermediate (6). Obviously, this interaction is absent for E212Q. All this considered, we suggest that E212Q is a useful model for thermodynamic characterization of TrCel7A-COS interactions. Hence, although further mutations could provide a fully inactive (experimentally convenient) mutant, such variants are not yet structurally characterized and the risk of introducing changes in the active site, which would lessen the relevance of the results, appears evident. The residual activity of E212Q is obviously a limitation, and it dictates an indirect approach (Equation 1) to the thermodynamic functions except at low temperatures. However, as ΔH(T) could be measured with acceptable reproducibility (Fig. 4), this was a manageable problem, and E212Q appears a reasonable compromise for binding studies.

For COS2-COS4 the simple model suggested binding constants ∼10⁵ m⁻¹ (ΔG⁰ ∼ −27 kJ/mol at 10 °C), and this is in reasonable accord with an earlier measurements of TrCel7A-COS2 interactions, which reported K_B = 5.4 × 10⁴ m⁻¹ (37). It also parallels affinity assessments based on COS2 inhibition of the hydrolysis of soluble substrate analogs by TrCel7A (K_i ∼ 20 μm corresponding to K_B∼ 5 × 10⁴ m⁻¹) (37, 38). A recent computational study suggested stronger binding of COS2 with ΔG⁰ ∼−50 kJ/mol (39). Structural studies (7) have shown that COS2 primarily accumulates in the expulsion site (subsites +1 and +2), and it, therefore, appears likely that thermodynamic parameters for COS2 in Table 1 represents binding to this locus. We emphasize, however, that the intermediate stoichiometry found for COS2 and COS3 (n ∼ 1.5 in Table 1) may reflect interference from weaker interactions with other subsites, which could make the parameters for COS2 and COS3 imprecise (because the simple model is based on equal and independent sites). For COS4 the calorimetric results suggested two discernable binding modes; one strong site with K_B = 7 × 10⁵ m⁻¹ and a moderate binding enthalpy (ΔH = −27 kJ/mol) and a weaker site with K_B = 4 × 10⁴ m⁻¹ and a more exothermic binding (ΔH = −39 kJ/mol). Structural studies (5) of the same system also found two bound COS4 molecules, and they were positioned in subsites −7 to −4 and −2 to +2 (cf. Fig. 6). These two locations correspond to, respectively, the first part of the catalytic tunnel, where the longer COS ligands also bind (see below), and the expulsion site plus the region around catalytic triad. An unambiguous assignment cannot be made on the basis of the current data, but the high density of cellulose-enzyme hydrogen bonding in the −2 to +2 region (5, 6, 40) combined with an unfavorable contribution to ΔG⁰ from subsite −1 found here (see Fig. 6) would be in accord with a strongly exothermic binding with moderate net affinity. Hence, it appears most likely that COS4 binding to the −2 to +2 location has a K_B = 4 × 10⁴ m⁻¹ and ΔH 39 kJ/mol, whereas the stronger, less exothermic binding (K_B = 7 × 10⁵ m⁻¹ and ΔH = −27 kJ/mol) occurs at subsites −7 to −4.

Longer ligands (COS5-COS8) bound with higher affinity, K_B ∼ 10⁷ m⁻¹, corresponding to ΔG⁰ ∼ −40 kJ/mol and an enthalpy change of ∼−35 kJ/mol (at 10 °C). Structural studies of E212Q complexes with (some of) these ligands have shown that they bind in the first part of the active tunnel from subsite −6 to −2 (COS5) or subsite −7 to −2 (COS6) (5). The most interesting thermodynamic observation for the longer COS ligands was that the affinity for E212Q did not increase with increasing DP beyond DP = 6. In fact, at the higher temperatures, we found a small but systematic loss of affinity through the sequence COS6, COS7, COS8 (Fig. 5). Structural data for COS7 and COS8 are not available, but the structure of E217Q in complex with COS9 has recently been published (6). This work followed the trend found for COS5 and COS6 and suggested that COS9 penetrated further into the tunnel essentially filling all subsites. We could not perform calorimetric measurements for COS9 so we cannot compare directly, but it appears reasonable to infer that COS7 and COS8 are positioned analogously to COS5, COS6, and COS9 and hence, respectively, occupy subsites −7 to −1 (COS7) and −7 to +1 (COS8). If indeed so, the results suggest that interactions near the scissile bond do not contribute to the net affinity. This may reflect the strong twist of the cellulose strand in this region (5, 40) or pyranose ring distortion in subsite −1 (34). These conformations promote catalysis, but they may be associated with strain penalties that could balance out favorable contributions to ΔG⁰ that arise from subsite contacts. Such penalties can be quite sizable. For example, the suggested change from a stable chair conformation to a half-chair (34) of the pyranose ring in subsite −1 is associated with an in vacuo free energy change of +35 kJ/mol (41); i.e. a value almost corresponding to the whole standard binding free energy (Fig. 4). In the active tunnel this in vacuo value is obviously compensated by protein-cellulose interactions (42), but we suggest that the slightly unfavorable contributions to the net affinity from the leading pyranose units of COS7 and COS8 observed here rely on such twisting or distortion effects. A similar suggestion was put forward already in early mechanistic studies of glycoside hydrolases (43), and this interpretation is also in line with a comment recently made by Knott et al. (6). After considering many related complexes these workers noted that structures with an occupied −1 subsite are rare, and this corroborates the idea of unfavorable interactions in this region. In this respect it is also interesting to compare the current COS data with binding studies for xylo oligosaccharides of similar DP. These ligands bind to TrCel7A at the same loci and with the same directionality as COS (44), although the binding constant for the same DP is 2–3 orders of magnitude lower for the xylo oligosaccharide ligands (45). Interestingly, the xylo oligosaccharide ligands, which have a different binding mode compared with COS in the vicinity of the catalytic center (44), showed the more intuitive behavior of a gradually increasing affinity with increasing DP until the size of the ligand approximately matched the catalytic tunnel (45). This difference could reflect a strain penalty, which occurs for the substrate but not for xylose-based ligands.

We are not aware of other experimental studies on the binding affinity of these ligands, but the results may be compared with the kinetic measurements by Nidetzky et al. (14), who studied the hydrolysis of COSs by the TrCel7A wild type. These workers found that the Michaelis constant, K_m, decreased slightly through the series COS4-COS6 but remained constant (2–3 μm) for longer substrates up to COS8. To the extent that K_m can be interpreted as a gauge of substrate affinity, these results are in line with the current observation of nearly constant affinity through the series COS6-COS8. Recent computational work (1) analyzed the interaction of COS7 and TrCel7A. As in the case of COS2 (discussed above) the theoretical affinity (ΔG⁰∼−70 kJ/mol) for COS7 binding was much higher than the value found here (ΔG⁰∼−38 kJ/mol). This difference may reflect that the simulations investigate one specific COS position, whereas experiments sample a range of binding conformations. In this connection it is relevant to notice that the small difference in ΔG⁰ for different COS lengths (Table 1 and Fig. 4) suggests that a range of binding positions may be populated. Differences may also arise from ambiguities relating the standard state of the unbound ligand (46).

An alternative interpretation of the nearly constant ΔG⁰ for the longer ligands could be that COS7 and COS8 bound without filling subsides +1 and −1 at all but, rather, left 1 or 2 glucopyranose units outside the tunnel. This interpretation is in contrast to structural data for COS9, which filled the whole tunnel (6) but differences could occur because COS9 was long enough to simultaneously exploit favorable contacts with subsites near the tunnel entrance and the expulsion site (cf. Fig. 6). Although a final interpretation of the complex structure for COS7 and COS8 awaits crystallographic investigations, we note that the thermodynamic picture presented here speaks against the idea of these ligands sticking out of the active tunnel (leaving corresponding subsites unfilled). This is because the parameters, ΔH, ΔS°, and ΔC_p, all change linearly with DP (Fig. 5). In aqueous solutions these functions generally respond strongly to even subtle changes in molecular interactions, whereas changes in ΔG⁰ are disguised by enthalpy/entropy compensation (47). Hence, the steady increments of ΔH, ΔS°, and ΔC_p seen in Fig. 5 strongly suggest a gradually increasing interacting surface as DP gets higher. In particular, the negative changes in entropy and heat capacity are considered hallmarks of dehydration of hydrophobic surface (48). Some studies have taken this idea one step further and suggested proportionality between ΔC_p and the change in nonpolar, water-accessible surface area, ΔASA_NP. If such proportionality indeed occurs, the change in the hydrated area can obviously be estimated from experimental values of ΔC_p. Earlier studies on this have varied somewhat with respect to the proportionality coefficient that links ΔASA_NP and ΔC_p, and different types of binding and transfer processes suggested values between −1.7 and −2.2 J/(mol K) for the dehydration of 1 Ų of hydrophobic area (48–52). We found an increment in ΔC_p of ∼−370 J/(mol K) per glucopyranose unit, and using the above numbers, this would correspond to the dehydration of 160–220 Ų of hydrophobic area per glucopyranose unit bound in the active tunnel. To put this into perspective we note that the hydrophobic surface area of a glucopyranose moiety in an oligosaccharide is ∼70 Ų (53) and hence that the above values would correspond to full dehydration of the nonpolar surface of the COS ligand and a concomitant dehydration of similar or slightly larger nonpolar area of the enzyme. The observation of a large negative ΔC_p for this type of interaction is not unprecedented. Creagh et al. (54) studied binding of the family II CBM from a Cellulomonas fimi exoglucanase to crystalline cellulose and reported heat capacity changes between −1.5 to −2.5 kJ/(mol K) depending on substrate coverage. This C. fimi CBM binds a cellulose strand in a 37 Å-long groove that is lined with three tryptophan residues (55) and accommodates ∼7 pyranose units. Interestingly, the ΔC_p value reported by Creagh et al. (54) is similar to ΔC_p for COS7 found here (−1.52 ± 0.09 kJ/(mol K).

In conclusion we have found binding constants at 10 °C ∼10⁵ m⁻¹ for small COS ligands (COS 2 and COS3), which most likely bind in the expulsion site of TrCel7A. For larger ligands (COS5-COS8), which bind in the active tunnel between the entry and the catalytic region, we found binding constants around 10⁷ m⁻¹, with little dependence of the COS length. The binding enthalpy for COS5-COS8 became more exothermic with both DP and temperature and reached a sizable level of ∼−100 kJ/mol for COS8 at 50 °C. Conversely, extrapolation of ΔH(T) data in Fig. 4 toward lower temperatures suggested that binding would become essentially athermal (ΔH∼0) and thus solely driven by a positive entropy change at temperatures close to 0 °C. On the basis of this, we suggest that the binding enthalpy is dominated by two contributions. One is polar interactions that generate a negative (exothermic) and fairly temperature-independent (56) contribution. Structural analyses have identified 2–4 enzyme-COS hydrogen bonds in each subsite (5, 6), and this appears to be a likely origin of the exothermic contribution. The second dominant contribution to ΔH is hydrophobic interactions. This is associated with the (endothermic) release of structured water from nonpolar surfaces of both cellulose and enzyme as the complex is formed. The hydrophobic enthalpy contribution shows pronounced temperature dependence and hence dominates the ΔC_p function. The low ΔH around 0 °C reflects near equality of the two opposing contributions to ΔH, whereas strongly exothermic binding at higher temperatures results from dominance of hydrogen bonding. The increasingly favorable enthalpy change at higher temperatures was outweighed by a negative (unfavorable) trend in TΔS so that the net affinity decreased with temperature. This change in net affinity was pronounced for the longer the COS ligands, which may show significantly decreased site occupancy in the investigated temperature range.

In has previously been reported (7, 39) that the strongest interaction is in the expulsion site (subsite +1 and +2), and combining this and the current data for COS2 suggest that these subsites each contribute ∼−14 kJ/mol to the net affinity (ΔG⁰). A second location that appears important for the affinity is the first part of the catalytic tunnel (subsite −7 to ∼-3). The data in Table 1 suggested a contribution to ΔG⁰ of ∼−7 to −8 kJ/mol per subsite in this region. Finally, we found that filling the subsites around the catalytic area had no or (particularly at higher temperatures) a slightly unfavorable impact on the net affinity. These subsites are rich in enzyme-ligand hydrogen bonding (5), and we suggest that the absence of a contribution to the net affinity may reflect associated, unfavorable effects including twisting of the cellulose strand or pyranose ring distortion. This overall interpretation is illustrated in the “heat-map” in Fig. 6, which corroborates the statement by von Ossowski et al. (38) that “tight binding on both sides of the catalytic center seems to be required.” Binding before the catalytic region involves many contacts of moderate affinity, whereas affinity near the exit relies on fewer and stronger interactions. This balance of forces was also discussed by Knott et al. (34) who concluded that the weaker interactions in the tunnel were optimized for processive sliding, whereas the strong binding to the expulsion site provided the driving force for the forward movement. It should certainly be kept in mind that the region with low affinity in Fig. 6 is exactly where the E212Q mutation is located, and this could influence the results for the enzyme variant. Nevertheless, it appears relevant to consider the affinity gradient suggested in Fig. 6 in future studies of the complex processive mechanism.