The Psychometric Latent Agreement Model (PLAM) for Discrete Latent Variables Measured by Multiple Items

Abstract

The Psychometric Latent Agreement Model (PLAM) is proposed for estimating the subpopulation membership of individuals (e.g., satisfactory performers vs. unsatisfactory performers) at discrete levels of multiple latent trait variables. A binary latent Type variable is introduced to take account of the possibility that, for a given set of observed variables, the latent group memberships of some individuals are indeterminate. The latent Type variable allows for separating individuals who can reliably be assigned to satisfactory versus unsatisfactory performers classes from those individuals whose ratings do not contain the necessary information to make the class assignment possible for a particular set of rating items. Agreements among discrete latent trait variables are also estimated. The PLAM was illustrated with two examples using real data on behavioral rating measures. One example involved ratings of two behavioral constructs by a single rater type, whereas the other involved ratings of one construct by three rater types. Implications were presented for using behavioral ratings to determine the subpopulation membership, such as qualified versus unqualified groupings in hiring decisions and pass versus fail groupings in performance evaluations.

Since the seminal paper by Charles Spearman (1904) more than a century ago, the latent variable conceptualization of behavioral attributes has been widely used in a variety of measurement contexts. A latent variable is conceptualized as having a continuous distribution in traditional measurement models (i.e., models originating from factor analysis [FA] and item-response theory [IRT]). Continuously distributed latent variables have been found useful in conceptualizing attitudes, personality, achievement, attainment, intelligence, and many other behavioral and organizational attributes, where the purpose of testing is to determine the location of individuals on a latent continuum. In addition to locating individuals on latent continua, rating scales are sometimes used to make categorical judgments about individuals. The purpose of this study was to propose a model-based approach, that is, the Psychometric Latent Agreement Model (PLAM), for estimating group membership of individuals at the latent variable level while taking account of the possibility that some individuals’ observed responses fail to distinguish between the categories of discrete latent trait variables.

Traditionally, supervisors rate employees’ performance on one or more dimensions during the evaluation process (e.g., Funderburgh & Levy, 1997). For each dimension, supervisory ratings are used to locate employees on a performance continuum as accurately as possible. This practice has limitations. First, supervisory ratings are often motivated to make categorical judgments about employees such as promotion, continuation, or termination of employment. Yet there is no one-to-one correspondence between the performance measurement on a continuum and performance categories. Setting cut scores on a continuum is often the method of choice to achieve this goal. Despite their widespread use and intuitive appeal, however, cut scores may cause more problems than they resolve. First, test scores obtained from traditional measurement models assume that individuals represent a sample drawn from a single population (i.e., homogeneity assumption), yet cut scores assume population heterogeneity. It seems contradictory to assume that the same population is simultaneously homogeneous and heterogeneous. Second, group assignments based on a cut score imply categorical certainty (e.g., unsatisfactory performance below the cut score and satisfactory performance above it). It may be more realistic to assume that employees whose score close to the cut point are less likely to belong in either of these categories than those who score farther away from the cut score. Third, equally well-designed procedures (e.g., consensus among experts, agreement with an external criterion) may not necessarily yield the same cut scores. Evidence supporting a particular cut score does not necessarily invalidate all other possible cut scores. Finally, the cut score is not a part of the measurement model that is used to estimate the continuous performance scores. Consequently, inferences (i.e., test score interpretations) made from the cut score are not justified by the measurement model. Most recently, Rupp, Templin, and Henson (2010) advocate the model-based approaches involving discrete latent variables as an alternative to the cut score method.

The second limitation of traditional supervisory performance ratings of employees is that it provides only a one-sided view of employees’ performance (Campbell & Fiske, 1959; Lawler, 1967). To overcome this limitation, the multirater approach, also known as the 360° feedback, has been widely adopted in organizational research and practice (Brett & Atwater, 2001). The 360° feedback system involves ratings from individuals at different levels of organizational hierarchy including employees, coworkers, supervisors, and subordinates (Funderburgh & Levy, 1997). Edwards and Ewen (1996) reported that the vast majority of Fortune 500 companies has adopted a form of the 360° feedback system. The transition from the traditional supervisory rating to the 360° feedback system effectively overcomes the shortsighted view of employee performance (Maylett, 2009) but, at the same time, it exaggerates the problem associated with making categorical performance judgments from the commonly employed continuously distributed rating scores. The discrete latent variable framework is well suited to address this issue. In this study, we illustrate the extension of traditional latent class analysis involving one discrete latent variable to latent class models with two or more discrete latent variables, each of which represents the rater-specific classes of individuals.

The 360° feedback system highlights the issue of agreement among raters. For example, Brett and Atwater (2001) reported that self, boss, peer, and direct report rating correlations are low to moderate (range: .04–.48). Subsequent hypothesis testing of relationships between the rating level and the accuracy and reactions to ratings further revealed that the predictive relationships are rater-specific. The use of cut scores further complicates the issue of rater agreement in this multirater context. For example, equally plausible cut scores would not necessarily yield the same magnitude of agreement. Because true group memberships are unknown, use of sensitivity/specificity analyses and chance-corrected agreement to validate cut scores is of limited value without an error-free external criterion that can serve as a gold standard (Glarus & Kline, 1988; Guggenmoos-Holzmann & Vonk, 1998; Rindskopf & Rindskopf, 1986).

In organizational research, recent advances in testing the rater agreement for multi-item scales are illustrated within the continuous observed variable framework by Cohen, Doveh, and Nahum-Shani (2010). Pasisz and Hurtz (2010) discuss the between-group differences in within-rater agreement. Most recently, Cheung (2010) proposed a latent congruence model to estimate rater agreement within the confirmatory factor analytic framework with predictors and outcomes of congruence. Several probability models have also been proposed to study rater agreement within the discrete latent variable framework (e.g., Agresti & Lang, 1993; Bergan, Schwarz, & Reddy, 1999; Flaherty, 2002; Guggenmoos-Holzmann & Vonk, 1998; Rindskopf & Rindskopf, 1986; Uebersax & Grove, 1990). By extending Aickin’s (1990) model, Schuster and Smith (2002) proposed the target-type approach to rater agreement within the discrete latent variable framework and showed its conceptual and parametric relations with previously proposed latent agreement models originating from the target-type approach (e.g., Agresti, 1989; Guggenmoos-Holzmann, 1996). The response-error approach has also been widely used to study rater agreements under the discrete latent variable framework (Agresti, 1988; Becker, 1989; Darroch & McCloud, 1986; Dayton & Macready, 1976, 1980; Dillon & Mulani, 1984; Macready & Dayton, 1977; Tanner & Young, 1985). By extending Goodman’s (1979) model, Schuster and Von Eye (2001) proposed a latent agreement model and showed its relations with previously proposed latent agreement models using the response-error approach. Schuster (2006) has provided an overview of response-error and target-type approaches to modeling rater agreement, as well as their strengths and weaknesses.

The one-discrete-observed-variable was the dominant paradigm in modeling agreement under the discrete latent variable framework. In this paradigm, raters were asked to independently assign each of N individuals (or objects, targets) into exhaustive and mutually exclusive categories of one observed variable. Observed cross-classification tables between raters then contained the information needed to estimate the parameters of a particular latent agreement model. In contrast, the multiple-discrete-observed-variable paradigm was dominant in traditional psychometric models, particularly in measuring employee performance, job satisfaction, and a host of behavioral constructs using binary or ordinal (i.e., Likert-type) items, where latent variables are conceptualized as continuously distributed. The modeling approaches adopted in the current study involve a hybrid of the multiple-discrete-observed-variable paradigm drawn from the traditional psychometric models and the discrete latent variable paradigm drawn from the rater agreement models.

Although differing in their parameterizations, two kinds of discrete latent variables have been considered in the past. The first kind, labeled as “discrete latent trait,” represents the subpopulation status of individuals. Examples of discrete latent traits include job performance with unsatisfactory, adequate, and excellent categories and job satisfaction with unsatisfied and satisfied categories. The second kind of discrete latent variable, labeled as “Type,” represents whether the subpopulation status of individuals is determined by a systematic process (Type = informative) or by a random process (Type = uninformative). For example, a particular group of employees might rate their own performance by responding to a set of items haphazardly for one reason or another, for example, they may think that the self ratings cannot possibly be taken seriously by anyone to make judgments about their job performance. Thus, item responses from this group of employees do not tell us (or are uninformative) about their job performance. The introduction of latent Type variable allows for testing the presence/absence of such a group of employees in organizational settings. The discrete latent trait and Type variables would be classified as latent class variables by Bartholomew and Knott (1999) because both variables have discrete distributions.

In the past, systematic processes have been used to define a subpopulation of individuals whose observed response patterns conform to Guttman’s scaling (i.e., intrinsically scalable type; Goodman, 1975), a latent class model (i.e., obvious type; Schuster & Smith, 2002), and an item-response model (IRT; Gitomer & Yamamoto, 1991). It may be unreasonable to assume that all responses follow a particular stochastic process. Random processes have, therefore, been used to define a subpopulation of individuals whose observed response patterns are inconsistent with systematic processes, such as the intrinsically unscalable type proposed by Goodman (1975), the ambiguous type proposed by Schuster and Smith (2002), and the types of individuals whose responses do not follow an IRT model as proposed by Gitomer and Yamamoto (1991). Despite conceptual similarities among models involving one discrete latent trait variable and one latent Type variable, these models are not parametrically equivalent.

Traditionally, models with a latent Type variable have had one discrete latent trait variable. This article introduces the PLAM in which the systematic process is defined in terms of two or more discrete latent traits (i.e., a latent class model with two or more latent class variables), whereas the random process is defined in terms of a binary latent Type variable. The development of the PLAM is introduced with a traditional latent class model involving one discrete latent variable with and without a latent Type variable followed by a model involving multiple discrete latent trait variables with and without a latent Type variable. Prior to the parametric introduction of these models, examples from the 360° feedback system are used to illustrate possible applications of discrete latent variable modeling in organizational research. Examples using empirical data, however, come from a substantive field outside the mainstream organizational research: adolescent problem behavior. Specifically, the PLAM is illustrated with two data sets, one data set involving teachers’ ratings of attention-deficit hyperactivity (ADH) and the other data set involving mother, teacher, and self ratings of oppositional defiant (OD) to estimate latent subtypes of problem behavior.

Modeling One Discrete Latent Trait Variable

Employees’ self ratings of job satisfaction are sometimes used to identify individuals dissatisfied with their current jobs. Instead of conceptualizing the job satisfaction as a unidimensional trait, it may be best suited to treat job satisfaction as a discrete latent variable with satisfied, tolerable, and unsatisfied categories in this example. Consider three manifest categorical variables, y1, y2, and y3 with I = 1…I, j = 1…J, and k = 1…K categories, respectively. The dependencies among the observed categorical variables are explained by a discrete latent trait variable, denoted as R, with p = 1…P categories. Let ${\mathrm{\pi }}_{\mathit{ijk}}^{y1y2y3}$ represent the probability of observing a response pattern for the manifest variables, that is, P(y1 = i, y2 = j, y3 = k). The latent class model can then be expressed in terms of marginal probabilities of the joint distribution of y1, y2, y3, and R as:

$${\mathrm{\pi }}_{\mathit{ijk}}^{y1y2y3}=\sum _{p=1}^P{\mathrm{\pi }}_{\mathit{ijkp}}^{y1y2y3R}.$$ (1)

Under the assumption of local independence, that is, the independence of the manifest variables conditional on the discrete latent trait variable, the joint probabilities can be expressed as a function of conditional and unconditional probabilities (Lazarsfeld & Henry, 1968):

$${\mathrm{\pi }}_{\mathit{ijkp}}^{y1y2y3R}={\mathrm{\pi }}_p^R{\mathrm{\pi }}_{ip}^{y1\mid R}{\mathrm{\pi }}_{jp}^{y2\mid R}{\mathrm{\pi }}_{kp}^{y3\mid R},$$ (2)

where the unconditional probability of ${\mathrm{\pi }}_p^R$ is P(R = p) and the conditional probabilities of ${\mathrm{\pi }}_{ip}^{y1\mid R}=\mathrm{P}(y1=i\mid R=p);{\mathrm{\pi }}_{jp}^{y2\mid R}=\mathrm{P}(y2=j\mid R=p)$; and ${\mathrm{\pi }}_{kp}^{y3\mid R}=\mathrm{P}(y3=k\mid R=p)$.

The latent class model for one discrete latent trait variable is obtained by inserting equation 2 into equation 1:

$${\mathrm{\pi }}_{\mathit{ijk}}^{y1y2y3}=\sum _{p=1}^P{\mathrm{\pi }}_p^R{\mathrm{\pi }}_{ip}^{y1\mid R}{\mathrm{\pi }}_{jp}^{y2\mid R}{\mathrm{\pi }}_{kp}^{y3\mid R}.$$ (3)

Analogous to the factor score estimates in FA and ability estimates in item-response theory models, posterior probabilities can be estimated from the discrete latent variable models by model fitting. Posterior probability estimates are informative of class separation.

Modeling One Discrete Latent Trait Variable and the Latent Type Variable

Ideally, equation 3 holds for each and every member of the population. Yet, it is possible that, for a particular group of individuals, the observed variables y1, y2, and y3 do not contain the necessary information to distinguish P categories of the discrete latent variable R. In employees’ self rating of job satisfaction, for example, a particular group of individuals may fill out the rating scales without paying close attention to items by thinking that their ratings will be inconsequential. Similarly, it is not uncommon to observe a small group of individuals with low ability responding to difficult items correctly or vice versa in ability testing. The latent Type variable, denoted as T with x = 1 (informative) and x = 2 (uninformative) categories, is introduced to take account of the possibility that equation 3 may not hold for a group of individuals. Specifically, equation 3 holds for x = 1, whereas it holds for x = 2 with the following restrictions on the conditional probabilities:

$${\mathrm{\pi }}_{ip}^{y1\mid R}={\mathrm{\pi }}_i^{y1},{\mathrm{\pi }}_{jp}^{y2\mid R}={\mathrm{\pi }}_j^{y2},{\mathrm{\pi }}_{kp}^{y3\mid R}={\mathrm{\pi }}_k^{y3},\forall i,j,k,p.$$

These restrictions imply that the probability of responding to a category of an observed variable remains the same across the levels of the discrete latent trait variable for individuals in the uninformative category of the latent Type variable. Therefore, item responses are simply “uninformative” regarding the latent trait status of individuals in this subpopulation. The T enters into equation 1 as a discrete latent variable as:

$${\mathrm{\pi }}_{\mathit{ijk}}^{y1y2y3}=\sum _{p=1}^P\sum _{x=1}^2{\mathrm{\pi }}_{\mathit{ijkpx}}^{y1y2y3RT}.$$ (4)

With the restrictions on the conditional probabilities for x = 2 and under the assumption of local independence, the observed response patterns are modeled as:

$${\mathrm{\pi }}_{\mathit{ijk}}^{y1y2y3}=\sum _{p=1}^P\sum _{x=1}^2{\mathrm{\pi }}_{px}^{RT}{\mathrm{\pi }}_{\mathit{ipx}}^{y1\mid RT}{\mathrm{\pi }}_{\mathit{jpx}}^{y2\mid RT}{\mathrm{\pi }}_{\mathit{kpx}}^{y3\mid RT}.$$ (5)

Modeling Two Discrete Latent Trait Variables

In addition to the self-reported ratings of job satisfaction, organizational researchers may be interested in the self-reported job performance, which is also conceptualized as a discrete latent variable with unsatisfactory, satisfactory, excellent categories. It may also be of interest to estimate the agreement between job satisfaction and job performance at the latent variable level. Another example of latent agreement would be between the self and supervisory ratings of employees’ job satisfaction. Therefore, in addition to the discrete latent trait variable R, consider a second discrete latent trait variable S with q = 1…Q categories that underlies the dependencies among three manifest categorical variables y4, y5, and y6 with l = 1…L, m = 1…M, and n = 1…N categories, respectively. The model for two discrete latent trait variables can be expressed in terms of the marginal joint probability distribution of y1,…y6, R, and S:

$${\mathrm{\pi }}_{i\dots n}^{y1\dots y6}=\sum _{p=1}^P\sum _{q=1}^Q{\mathrm{\pi }}_{i\dots \mathit{npq}}^{y1\dots y6RS}.$$ (6)

Under the assumption of local independence:

$${\mathrm{\pi }}_{i\dots \mathit{npq}}^{y1\dots y6RS}={\mathrm{\pi }}_{pq}^{RS}{\mathrm{\pi }}_{ip}^{y1\mid R}{\mathrm{\pi }}_{jp}^{y2\mid R}{\mathrm{\pi }}_{kp}^{y3\mid R}{\mathrm{\pi }}_{lq}^{y4\mid S}{\mathrm{\pi }}_{mq}^{y5\mid S}{\mathrm{\pi }}_{nq}^{y6\mid S}.$$ (7)

Note that R influences y1, y2, and y3, whereas S influences y4, y5, and y6. Inserting equation 7 into equation 6 gives the latent class model for two discrete latent trait variables (e.g., Croon, 2002):

$${\mathrm{\pi }}_{i\dots n}^{y1\dots y6}=\sum _{p=1}^P\sum _{q=1}^Q{\mathrm{\pi }}_{pq}^{RS}{\mathrm{\pi }}_{ip}^{y1\mid R}{\mathrm{\pi }}_{jp}^{y2\mid R}{\mathrm{\pi }}_{kp}^{y3\mid R}{\mathrm{\pi }}_{lq}^{y4\mid S}{\mathrm{\pi }}_{mq}^{y5\mid S}{\mathrm{\pi }}_{nq}^{y6\mid S}.$$ (8)

It is of interest to examine the association (i.e., agreement) between the discrete latent trait variables R and S, analogous to a factor correlation matrix for continuously distributed latent trait variables. To ease the presentation, consider a simple case of two binary latent trait variables (i.e., p = q = 2). The cross-classification of R and S appears in Table 1. Analogous to Cohen’s kappa (κ) for chance-corrected agreement between two observed variables, the chance-corrected agreement between two binary latent trait variables, denoted as κ_l(R,S), is given by:

$${\mathrm{\kappa }}_{l(R,S)}=\frac{({\mathrm{\pi }}_{11}^{RS}+{\mathrm{\pi }}_{22}^{RS})-({\mathrm{\pi }}_1^R{\mathrm{\pi }}_1^S+{\mathrm{\pi }}_2^R{\mathrm{\pi }}_2^S)}{1-({\mathrm{\pi }}_1^R{\mathrm{\pi }}_1^S+{\mathrm{\pi }}_2^R{\mathrm{\pi }}_2^S)}.$$ (9)

Table 1.

Cross-tabulation of two binary latent variables designated as R and S

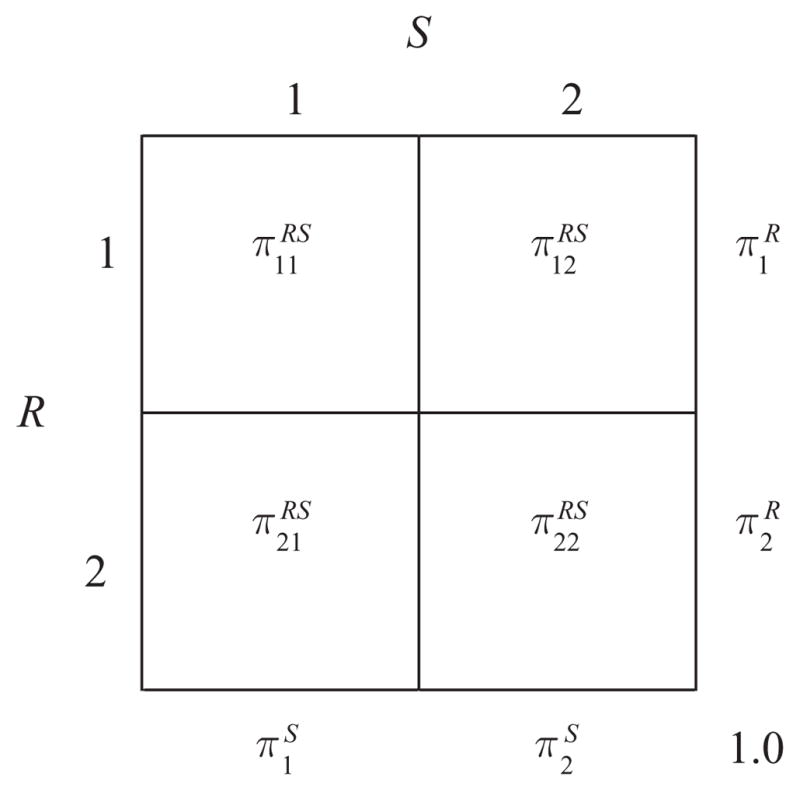
From Table 1, ${\mathrm{\pi }}_1^R,{\mathrm{\pi }}_2^R,{\mathrm{\pi }}_1^S$, and ${\mathrm{\pi }}_2^S$ represent the marginal distributions of discrete latent trait variables, for example, ${\mathrm{\pi }}_1^R={\mathrm{\pi }}_{11}^{RS}+{\mathrm{\pi }}_{12}^{RS}$. Similar to Cohen’s unweighted κ for three observed variables (Von Eye & Mun, 2005), the latent agreement for three variables is given by:

$${\mathrm{\kappa }}_{l(R,S,Z)}=\frac{({\mathrm{\pi }}_{111}^{\mathit{RSZ}}+{\mathrm{\pi }}_{222}^{\mathit{RSZ}})-({\mathrm{\pi }}_1^R{\mathrm{\pi }}_1^S{\mathrm{\pi }}_1^Z+{\mathrm{\pi }}_2^R{\mathrm{\pi }}_2^S{\mathrm{\pi }}_2^Z)}{1-({\mathrm{\pi }}_1^R{\mathrm{\pi }}_1^S{\mathrm{\pi }}_1^Z+{\mathrm{\pi }}_2^R{\mathrm{\pi }}_2^S{\mathrm{\pi }}_2^Z)},$$ (10)

where Z is a binary latent trait variable.

The PLAM

In the examples of both the self ratings of job satisfaction and job performance (two discrete traits with one rater type) and the self and supervisory ratings of employees’ job satisfaction (one discrete trait with two rater types), it may be of interest to test the presence of a subpopulation whose ratings are uninformative to make inferences about the discrete latent traits. The PLAM is defined as a latent class model for two or more discrete latent trait variables, plus a binary latent Type variable. Each latent trait variable explains associations among a unique set of categorical observed variables. The binary latent Type variable distinguishes individuals whose response patterns are consistent with the multiple discrete latent trait model from those whose responses are uninformative about the discrete latent trait variables. The PLAM with two discrete latent trait variables R and S and the binary latent Type variable of T is given by:

$${\mathrm{\pi }}_{i\dots n}^{y1\dots y6}=\sum _{p=1}^P\sum _{q=1}^Q\sum _{x=1}^2{\mathrm{\pi }}_{i\dots \mathit{npqx}}^{y1\dots y6\mathit{RST}},$$ (11)

with the following restrictions on the conditional probabilities:

$${\mathrm{\pi }}_{ip2}^{y1\mid RT}={\mathrm{\pi }}_{i2}^{y1\mid T},{\mathrm{\pi }}_{jp2}^{y2\mid RT}={\mathrm{\pi }}_{j2}^{y2\mid T},\dots ,{\mathrm{\pi }}_{nq2}^{y6\mid ST}={\mathrm{\pi }}_{n2}^{y6\mid T},\forall i,\dots n,p,q.$$

The joint probability distribution of discrete observed and latent variables can be rewritten as:

$${\mathrm{\pi }}_{i\dots \mathit{npqx}}^{y1\dots y6\mathit{RST}}=({\mathrm{\pi }}_{pq1}^{\mathit{RST}}{\mathrm{\pi }}_{ip1}^{y1\mid RT}{\mathrm{\pi }}_{jp1}^{y2\mid RT}{\mathrm{\pi }}_{kp1}^{y3\mid RT}{\mathrm{\pi }}_{lq1}^{y4\mid ST}{\mathrm{\pi }}_{mq1}^{y5\mid ST}{\mathrm{\pi }}_{nq1}^{y6ST})+({\mathrm{\pi }}_{pq2}^{\mathit{RST}}{\mathrm{\pi }}_{i2}^{y1\mid T}{\mathrm{\pi }}_{j2}^{y2\mid T}{\mathrm{\pi }}_{k2}^{y3\mid T}{\mathrm{\pi }}_{l2}^{y4\mid T}{\mathrm{\pi }}_{m2}^{y5\mid T}{\mathrm{\pi }}_{n2}^{y6\mid T}),$$ (12)

hence,

$${\mathrm{\pi }}_{i\dots n}^{y1\dots y6}=\sum _{p=1}^P\sum _{q=1}^Q({\mathrm{\pi }}_{pq1}^{\mathit{RST}}{\mathrm{\pi }}_{ip1}^{y1\mid RT}{\mathrm{\pi }}_{jp1}^{y2\mid RT}{\mathrm{\pi }}_{kp1}^{y3\mid RT}{\mathrm{\pi }}_{lq1}^{y4\mid ST}{\mathrm{\pi }}_{mq1}^{y5\mid ST}{\mathrm{\pi }}_{nq1}^{y6\mid ST})+({\mathrm{\pi }}_{pq2}^{\mathit{RST}}{\mathrm{\pi }}_{i2}^{y1\mid T}{\mathrm{\pi }}_{j2}^{y2\mid T}{\mathrm{\pi }}_{k2}^{y3\mid T}{\mathrm{\pi }}_{l2}^{y4\mid T}{\mathrm{\pi }}_{m2}^{y5\mid T}{\mathrm{\pi }}_{n2}^{y6\mid T}).$$ (13)

For Type = informative, κ_l provides the chance-corrected agreement between the two binary latent trait variables R and S because this subpopulation follows Equation 8. For Type = uninformative, however, the restrictions on the conditional probabilities imply:

$${\mathrm{\pi }}_{112}^{\mathit{RST}}={\mathrm{\pi }}_{122}^{\mathit{RST}}={\mathrm{\pi }}_{212}^{\mathit{RST}}={\mathrm{\pi }}_{222}^{\mathit{RST}},$$

hence, κ_{l (R,S)} = 0 for this subpopulation. Intuitively, the agreement between two discrete latent trait variables is due solely to chance when the categories of these variables are indistinguishable.

In the sections that follow, the PLAM is illustrated with two data examples. The first example involves teachers’ ratings of five inattentive (Ina) and seven hyperactivity-impulsivity (H-I) items (similar to the self ratings of job satisfaction and job performance example), whereas the second example involves ratings of four OD items by mother, teacher, and self (similar to the 360° feedback system where the job performance ratings are obtained from employees, supervisors, and subordinates). Each example is presented with a rationale, data characteristics, graphical display of the PLAM, model selection strategies, and interpretation of parameter estimates. For pedagogical purposes, analogies are drawn between the PLAM and the traditional measurement models originating from FA and IRT, where the latent trait variables are conceptualized as continuously distributed.

PLAM Example I: Attention Deficit/Hyperactivity (ADH)

Rationale

The Diagnostic and Statistical Manual of Mental Disorders (DSM) typology of ADH disorder classifies children into five categories: (a) children without the disorder; (b) children with predominantly Ina type; (c) children with predominantly H-I type; (d) children with both Ina and H-I (i.e., the combined type), and (e) children with the disorder not-otherwise-specified (NOS) type. The ADH types cannot be observed directly. Each component (i.e., Ina and H-I) is best represented as a latent trait variable with two categories: case versus noncase. Therefore, the ADH types can be grouped into 2 × 2 tables representing the cross-classification of two binary latent trait variables Ina and H-I. Because there is no error-free observed variable to determine the true ADH types, multiple items are needed to represent the latent diagnostic status.

Data Characteristics

The Teacher’s Report Form (TRF; Achenbach, 1991; Achenbach & Rescorla, 2001) was completed by the teachers of 2,619 students who were representative of the U.S. population (49.1% female). The students were 6–18 years old with a mean age of 12.0 years (SD = 3.4). The mean SES was 5.7 (SD = 2.1; range: 1–9) on Hollingshead’s (1975) 9-step scale for parents’ occupations. The students were 72.6% Caucasian, 13.2% African American, 6.9% Latino/Latina, and 7.3% mixed or other. In the preceding 12 months, 4.7% of children had been referred for mental health or special education services for a wide range of psychological and educational problems.

The TRF is a standardized instrument for obtaining teacher reports of academic and adaptive functioning and behavioral/emotional problems. The ADH example focused on 5 Ina and 7 H-I items scored from the TRF. The Ina items were i4. Fails to finish things he/she starts, i8. Can’t concentrate, can’t pay attention for long, i22. Difficulty following directions, i78. Inattentive or easily distracted, and i100. Fails to carry out assigned tasks. The H-I items were h10. Can’t sit still, restless, or hyperactive, h15. Fidgets, h24. Disturbs other pupils, h41. Impulsive or acts without thinking, h53. Talks out of turn, h67. Disrupts class discipline, and h93. Talks too much. These items were used to score the TRF DSM-oriented Inattention and Hyperactivity-Impulsivity scales. Based on the preceding 2 months, teachers rated items on a 3-point Likert-type scale as 0 = not true (as far as you know); 1 = somewhat or sometimes true; and 2 = very true or often true.

Model Specification

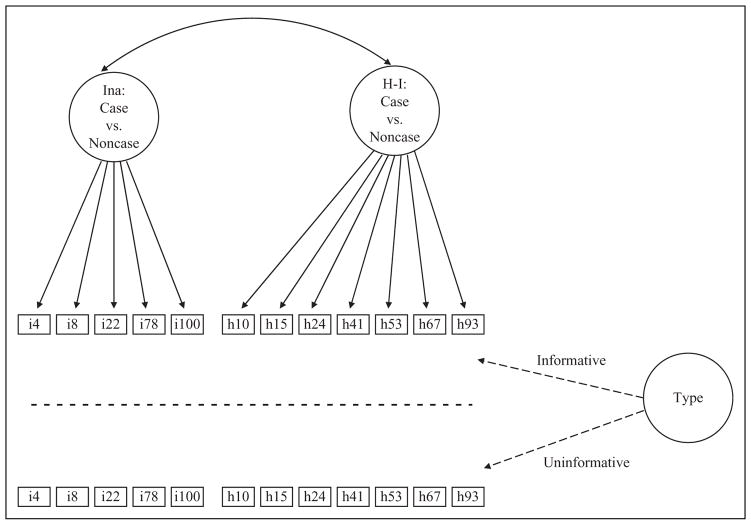
The PLAM for ADH appears in Figure 1. Five items were used to measure the binary latent trait variable of Ina and 7 items were used to measure the binary latent trait variable of H-I. The one-way arrows leading from the Ina and H-I latent trait variables to the items represent conditional probabilities, for example, the probability of obtaining teachers’ ratings of 2 from i22. Difficulty following directions given that the student had Ina problems (i.e., Ina = case). The two-sided arrow is used to represent a two-way contingency table between the latent Ina and H-I variables. Each cell in this contingency table defines the latent subpopulations of ADH: (a) no ADH (Ina = noncase and H-I = noncase), (b) Inattentive type (Ina = case and H-I = noncase), (c) Hyperactive-Impulsive type (Ina = noncase and H-I = case), and (d) combined type (Ina = case and H-I = case). Two categories of the latent Type variable refer to two different models that were separated by the dotted line in Figure 1. The binary latent Type variable defines two sets of four ADH types: informative versus uninformative. When Type = informative, conditional probabilities are expected to be larger when the Ina and H-I variables take the value of case than noncase. For Type = uninformative, the conditional probabilities are defined as equal whether Ina or H-I takes the value of case or noncase.

Figure 1.

The PLAM for ADH: Graphical representation. Note. PLAM = Psychometric Latent Agreement Model; ADH = attention-deficit hyperactivity.

Model Selection

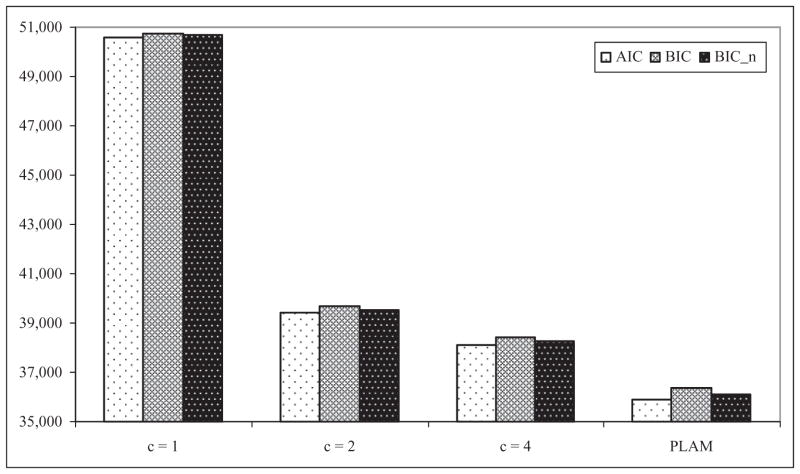
The PLAM specification may well be more complex than it should be in this example. To evaluate this possibility, three competing models were specified a priori by placing restrictions on the PLAM. First, a model with two binary latent trait variables (see equation 8) was obtained by eliminating the latent Type variable from the PLAM. The comparison between the two-binary-latent-trait model (c = 4, where c represents the total number of classes in a discrete latent variable model) and the PLAM indicates whether the informative versus uninformative distinction is supported by the teachers’ ratings. Second, the one-binary-latent-trait model (c = 2) was obtained by using all 12 variables as indicators of a binary ADH latent trait variable with case and noncase categories. The comparison between one- and two-binary-latent-trait models indicates whether the Ina versus H-I distinction is supported by the teachers’ ratings. Third, the independence model (c = 1) was obtained by eliminating the binary ADH latent variable in the one-binary-latent-trait model. The independence model states that there is no association among the 12 observed variables. Three indices of fit were used to compare the models: The Akaike information criterion (AIC; Akaike, 1987), the Bayesian information criterion (BIC; Schwarz, 1978), and the sample-size adjusted BIC by a factor of (n + 2)/24 (BIC_n; Sclove, 1987). All three indices penalize model complexity. The model with the smallest fit value is regarded as the optimal model. Mplus (v.4.1; Muthén & Muthén, 1998–2006) was used to estimate the models. Mplus input files are provided in the appendix.

The AIC, BIC, and BIC_n values appear in Figure 2. Of the four competing models, the PLAM had the smallest values for all three fit indices, indicating that it was the optimal model. The PLAM had a loglikelihood value of −17,868.38 with 78 free parameters.

Figure 2.

The PLAM for ADH: Model comparison. Note. PLAM = Psychometric Latent Agreement Model; ADH = attention-deficit hyperactivity.

Parameter Estimates

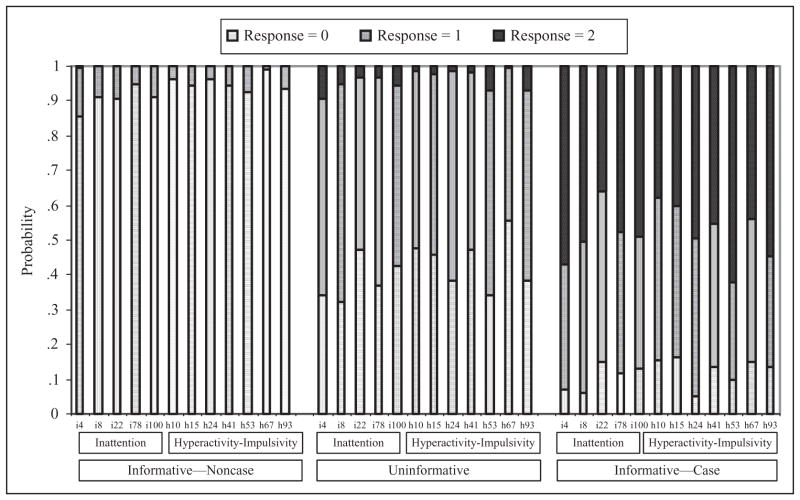
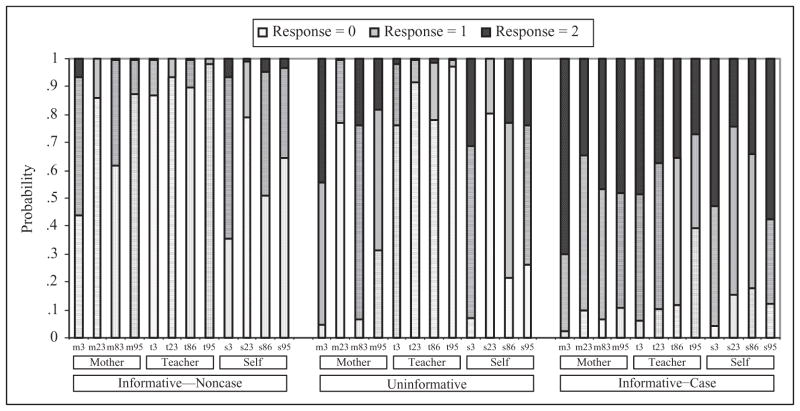
Three sets of conditional probability estimates appear in Figure 3. The first set (first 12 bars in Figure 3) describes the probability of rating an item 0, 1, or 2 when Type = informative and Ina/H-I = noncase. For example, i22. difficulty following directions had a .907 probability of being rated 0, .091 probability of being rated 1, and .002 probability of being rated 2 when Type = informative and the latent Ina variable takes the value of noncase. When Type = informative and the latent Ina variable takes the value of case, the conditional probability of obtaining 0, 1, and 2 ratings for this item were .473, .495, and .032, respectively. There is only one set of unconditional probabilities for Type = uninformative because these probabilities are the same whether the binary latent trait variables (i.e., Ina and H-I) take the value of case or noncase. For Type = uninformative, the 0, 1, and 2 response probabilities for i22 were .474, .495, and .032, respectively. Under the condition of Informative–Noncase in Figure 3, all items were strong indicators of the absence of Ina and H-I reported by teachers because the probability of a rating of 0 was approximately .90 for all 12 variables. When Type = informative and the binary latent trait variables take the value of case, the probability of observing a rating of 0 was low (i.e., .10 to .20).

Figure 3.

The PLAM for ADH: Conditional probability estimates. Note. PLAM = Psychometric Latent Agreement Model; ADH = attention-deficit hyperactivity.

The unconditional probabilities represent the estimated class sizes. The PLAM classified 79.7% of the 2,619 students as belonging in the informative category of the latent Type variable (T = 1) with the following classification for ADH: (a) 57.0% were classified as having neither Ina nor H-I (Type = informative; Ina = noncase; H-I = noncase); (b) 13.1% as having both Ina and H-I, that is, the combined type (Type = informative; Ina = case; H-I = case); (c) 7.9% as having Ina only (Type = informative; Ina = case; H-I = noncase); and 1.7% as having H-I only (Type = informative; Ina = noncase; H-I = case). For Type = informative, κ_{l (Ina, H-I)} = .80. The remaining 20.3% of students comprised the uninformative category of the latent Type variable (T = 2). That is, teachers’ ratings of 12 items are uninformative about Ina and H-I status for one fifth of the students; κ_{l(Ina, H-I)} = 0 in this subpopulation, by definition.

Posterior probability estimates for five selected students appear in Table 2. In the PLAM, individuals belong to the levels of latent variables probabilistically. Therefore, the probabilities of a person belonging to each of the latent subpopulations add up to unity. Student A in Table 2, for instance, belongs to the informative–combined type with a probability of .998, whereas Student A’s probability of belonging to the uninformative category of latent Type variable was .002. Student B had a response pattern with a probability of belonging to the informative–Ina type of .992. The response pattern for Student C indicates a .886 chance of belonging to the informative H-I type and Student D had a .914 chance of belonging to the informative–noncase type. The highest posterior probability of the response patterns exhibited by Student E was Type = uninformative, meaning that Student E could not be reliably assigned into one of four ADH types.

Table 2.

The PLAM for ADH: Posterior Probability Estimates for 5 Selected Students

	Latent Variable Type	Informative				Uninformative
	Ina	Case		Noncase
Case	H-I	Case	Noncase	Case	Noncase
Student A		.998	.000	.000	.000	.002
Student B		.000	.992	.000	.000	.008
Student C		.102	.000	.886	.000	.012
Student D		.000	.062	.000	.914	.024
Student E		.000	.001	.009	.214	.785

Note. Observed response patterns of 5 Ina and 7 H-I items are (22111, 1212101) for Student A, (21112, 0100000) for Student B, (10001, 1022211) for Student C, (10101, 0000000) for Student D, and (11000, 00010100) for Student E. PLAM = Psychometric Latent Agreement Model; ADH = attention-deficit hyperactivity; Ina = inattentive; H-I = hyperactivity-impulsivity.

PLAM Example II: Mother, Teacher, and Self Ratings of OD

Rationale

The OD can be conceptualized as a latent variable with two categories: OD versus no OD (i.e., case vs. noncase). Mother, teacher, and self ratings provide data from a wide range of contexts in which youths might exhibit OD. Directly asking an informant whether a youth has OD may not be an optimal procedure for determining the youth’s diagnostic status. Consistent with the psychometric literature multiple indicators of OD may be expected to provide more reliable assessment than a response to one item (i.e., whether the youth has OD). It should also be recognized that stochastic measurement models are simplified versions of complex processes. Models should therefore take account of the possibility that some youths may not be reliably classified into OD versus no OD groupings.

Data Characteristics

Data consisted of mother, teacher, and self ratings for 2,030 youths from two U.S. national general population samples (N = 1,245; 50.1% female) and from a clinical sample (N = 785; 28.7% female). The youths were 11 to 18 years old, with a mean age of 13.8 years (SD = 2.1). The mean SES was 5.7 (SD = 2.1; range 1–9) on Hollingshead’s (1975) 9-step scale for parents’ occupations. The youths were 82.9% Caucasian, 8.1% African American, 4.4% Latino/Latina, and 4.6% mixed or other. The general population samples were obtained in home interview surveys conducted in 1989 and 1999 (Achenbach, 1991; Achenbach & Rescorla, 2001). The samples were representative of the 48 contiguous states, with a 90% completion rate in 1989 and 93% in 1999. Of the 1,245 youths in the general population samples, 174 had been referred to mental health services in the preceding 12 months. The reasons for referral included a wide variety of emotional, social, and behavioral problems. The clinical sample included youths from 27 mental health and special education settings (Achenbach & Rescorla, 2001).

The assessment instruments were the Child Behavior Checklist (CBCL), TRF, and Youth Self-Report (YSR; Achenbach, 1991; Achenbach & Rescorla, 2001), which are standardized forms for obtaining parent, teacher, and self reports of academic and adaptive functioning and behavioral/emotional problems. PLAM example II focuses on 4 OD items rated by mothers, teachers, and youths themselves: 3. Argues a lot, 23. Disobedient at school, 86. Stubborn, sullen, or irritable, and 95. Temper tantrums or hot temper. Items were rated on the following 3-point scale: 0 = not true (as far as you know); 1 = somewhat or sometimes true; and 2 = very true or often true. These items were included in the DSM-oriented OD Problems scale from the CBCL, TRF, and YSR.

Model Specification

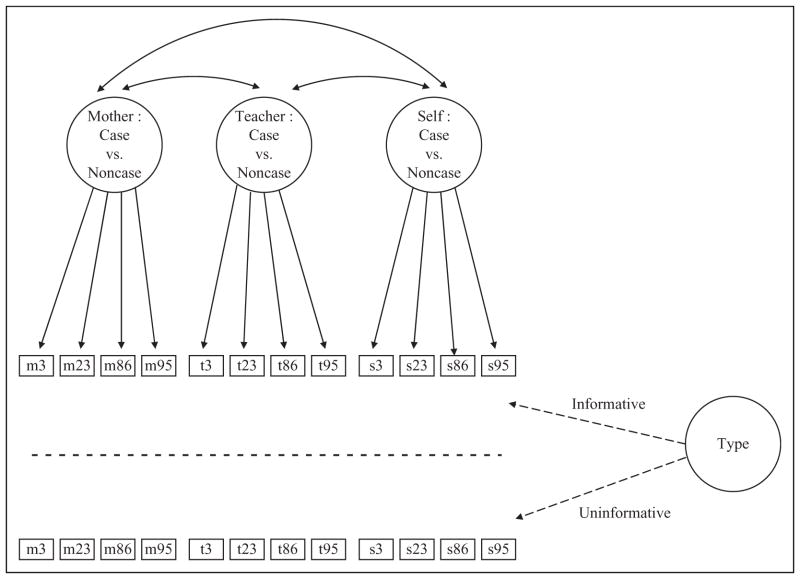
The graphical representation of the PLAM appears in Figure 4. The PLAM specifies two sets of discrete latent variables to characterize the population of interest. Each group of raters (or simply each rater) is represented as a discrete latent trait variable with case and noncase categories in the first set. For the OD example, three binary latent trait variables are used to characterize the diagnostic status of youths from the perspective of three groups of raters: mother (M), teacher (T), and self (S). Ratings on four items (i.e., observed variables) are used to measure the diagnostic status of youths in the first set of latent trait variables. The arrows from the first set of latent trait variables to the OD items represent the measurement relations (i.e., conditional probabilities). The two-sided arrows are used to represent a three-way contingency table among the first set of binary latent trait variables. Each cell in this three-way contingency table represents the diagnostic status of individuals. Two of these eight cells are called complete agreement classes when all three raters agree on the diagnostic status at the latent variable level, that is, the complete agreement class of cases (M+T+S+) and the complete agreement class of noncases (M+T+S+). The remaining six cells (2³ − 2 = 6) represent partial agreement classes because the latent diagnostic status according to one rater disagrees with the remaining two raters, i.e., M+T+S−, M+T−S+, M+T−S−, M−T+S−, M−T−S+, and M−T+S+.

Figure 4.

The PLAM for OD: Graphical representation. Note. PLAM = Psychometric Latent Agreement Model; OD = oppositional defiant.

The second set consists of one latent variable, labeled as Type, which takes two values: informative or uninformative. The latent Type variable generates two sets of three-way contingency tables among the three binary latent trait variables. The first set of three-way contingency tables classifies individuals into their informative diagnostic groups (i.e., Type = informative). However, the second set of three-way contingency tables cannot tell us anything about the youths’ true diagnostic status (i.e., Type = uninformative). The difference between informative and uninformative categories is defined in terms of conditional probabilities such that, when Type = uninformative, the probabilities of item responses do not change as a function of the value the discrete latent trait variable takes (i.e., case vs. noncase). When Type = informative, however, the response probabilities are conditioned on the discrete latent trait variable.

Model Selection

The rule of parsimony dictates that simpler models should be preferred to complex ones. Therefore, in addition to the PLAM, three models with decreasing complexity were tested: (a) the PLAM without the latent Type variable (c = 8); (b) one binary-latent-trait-variable of OD with case and noncase categories (c = 2); and (c) the independence model (c = 1). The AIC, BIC, and BIC_n were used to compare the models. Models with smaller values indicate better fit than models with larger values for all three indices.

Relative fit indices appear in Figure 5. Of the four models, the PLAM was the optimal model according to all three fit indices (i.e., the smallest AIC, BIC, and BIC_n values). The difference in fit between the PLAM and the PLAM without the latent Type variable (c = 8) indicated that not all individuals could be reliably assigned to case or noncase categories of the three latent trait variables. The difference in fit between the PLAM without the latent Type variable and the latent OD variable with case and noncase categories (c = 2) indicated that the two complete agreement classes are insufficient to classify individuals and that the partial agreement classes are needed. Of the four competing models, the independence model had the largest fit values indicating the worst. The PLAM had a loglikelihood value of −19,266.70, with 82 free parameters.

Figure 5.

The PLAM for OD: Model comparison. Note. PLAM = Psychometric Latent Agreement Model; OD = oppositional defiant.

Parameter Estimates

Three sets of parameter estimates are of special interest in the PLAM: (a) conditional probabilities, (b) unconditional probabilities, and (c) posterior probabilities. The conditional probability estimates appear in Figure 6. The conditional probabilities are analogous to the discrimination parameters in IRT models and the factor loadings in FA. Similar to item-response functions in IRT models, Figure 6 plots the probability of rating an Item 0, 1, or 2 as a function of latent variables. For Type = informative, for example, the probability of mothers’ rating item 95. Temper tantrums or hot temper as 0, 1, or 2 was .87, .12, and .01, respectively, for M = noncase and .11, .41, and .48 for M = case. For Type = uninformative, the conditional probabilities were .31, .51, and .18 for both case and noncase categories of the latent Mother variable because the conditional probabilities did not change across the levels of latent trait variables when Type = uninformative. Therefore, youths in the latent subpopulation of Type = uninformative cannot be reliably classified into case or noncase categories. In IRT terms, Type = uninformative is analogous to a measurement model with zero discrimination (i.e., a flat item-response curve). Similarly in factor-analytic terms, Type = uninformative corresponds to FA with factor loadings equaling zero. As expected from the PLAM parameterization, the probability of rating an item zero is largest when the latent trait variables take the value of noncase. The probability of rating an item zero is smallest when the latent trait variable takes the value of case for Type = informative. For Type = uninformative, the unconditional probabilities take intermediate values between informative–noncase and informative–case probabilities (see Figure 6).

Figure 6.

The PLAM for OD: Conditional probability estimates. Note. PLAM = Psychometric Latent Agreement Model; OD = oppositional defiant.

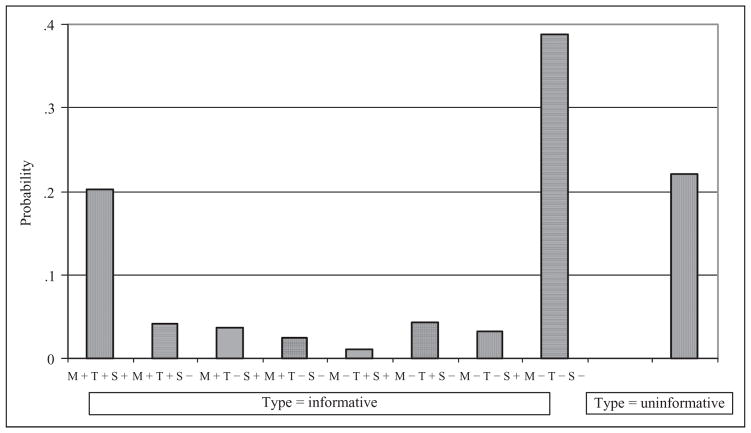
Unconditional probability estimates appear in Figure 7. Unconditional probabilities indicate the size of subpopulations. The latent Type variable divides individuals into informative (78%) and uninformative (22%) categories. Results indicated that 22% of youths cannot be reliably assigned into case or noncase categories of the latent trait variables. For Type = informative, the complete agreement class of cases (i.e., true complete agreement class of cases or M+T+S+) and noncases (i.e., true complete agreement class of noncases or M−T−S−) encompassed 20% and 39% of the youths, respectively. The six true partial agreement classes encompassed 19% of the youths ranging from 1% (M−T+S+) to 4% (M+T+S− and M−T+S−). This is consistent with the finding that the c = 8 model fit better than the c = 2 model (see Figure 5).

Figure 7.

The PLAM for OD: Unconditional probability estimates. Note. PLAM = Psychometric Latent Agreement Model; OD = oppositional defiant.

For Type = uninformative, κ_{l (M,T,S)} = κ_{l (M,T)} = κ_{l (M,S)} = κ_{l (T,S)} = 0, by definition. For Type = informative, κ_{l (M,T,S)} = .66 (see equation 10). From equation 9, κ_{l (M,T)} = .76, κ_{l (M,S)} = .77, and κ_{l (T,S)} = .67. The κ_l values between pairs of discrete latent trait variables were obtained by collapsing the unconditional probabilities over the levels of the third discrete latent trait variable.

Posterior probability estimates for four selected youths appear in Table 3. For a given response pattern, the posterior probabilities indicate the degree of subpopulation membership. For example, Youth A has a .819 chance of belonging to the true complete agreement class of noncase (M−T−S−; Type = informative, M = noncase, T = noncase, and S = noncase), .156 chance of belonging to the true partial agreement class of M−T−S+ (Type = informative, M = noncase, T = noncase, and S = case), and .025 chance of belonging to the uninformative category of the latent Type variable. Youth A may thus be assigned to the true complete agreement class of noncase as the most likely category. This assignment, however, comes with the risk of incorrectly classifying Youth A with the probability of .181 (i.e., 1−.819). A visual inspection of the response patterns and the probability of being in either informative or uninformative categories of the latent Type variable reveals that within-rater inconsistency across the four OD items increases the probability of belonging to the uninformative subpopulation.

Table 3.

The PLAM for OD: Posterior Probability Estimates for Four Selected Youths

Subject	Latent Variable Type	Informative								Uninformative
	Mother	Case				Noncase
	Teacher	Case		Noncase		Case		Noncase
	Youth	Case	Noncase	Case	Noncase	Case	Noncase	Case	Noncase
Youth A		.000	.000	.000	.000	.000	.000	.156	.819	.025
Youth B		.000	.000	.000	.000	.000	.000	.013	.155	.832
Youth C		.933	.000	.009	.000	.008	.000	.000	.000	.050
Youth D		.282	.005	.000	.000	.058	.020	.000	.000	.634

Note. Observed response patterns of mothers, teachers, and youths for items 3, 23, 86, and 95 are (1000, 0000, 1111) for Youth A, (1010, 0010, 1021) for Youth B, (2110, 2010, 1122) for Youth C, and (1011, 2002, 2021) for Youth D, respectively. OD = oppositional defiant.

Conclusions

A variety of tests are used to classify individuals into discrete groups. Examples include use of rating scales by organizations to classify prospective and current employees to make employment and placement decisions (e.g., hire vs. not hire, entry-level vs. mid-level managerial assignments), use of standardized English proficiency tests by universities to determine the readiness of applicants for educational programs (e.g., qualified vs. unqualified), and use of test scores by state agencies to award licenses for professional practice (e.g., accountants, builders). Continuous latent trait conceptualization of constructs embedded in traditional psychometric models may not be an optimal strategy for grouping individuals. Ideally, applied organizational researchers would make an informed decision about the latent trait distribution based on substantive theory and the kinds of inferences that they wish to make from item responses. As an extension of latent class models, the PLAM provides a probabilistic formulation of observed responses as a function of discrete latent variables.

The PLAM is especially useful when (a) attributes cannot be observed directly (e.g., job satisfaction), (b) attributes are believed to consist of a relatively small number of categories (e.g., satisfied vs. unsatisfied), (c) multiple items are available to make inferences on discrete latent traits (e.g., rating scales), (d) agreement between discrete latent trait variables is of interest, and (e) given the subjectivity of item responses (e.g., ratings of attitude, personality, and satisfaction), there may be individuals whose responses do not distinguish between categories of discrete latent trait variables.

The PLAM combines multiple discrete latent variables with a particular latent Type variable. Latent class models involving multiple discrete latent trait variables are not new (e.g., Croon, 2002). The concept of nonfitting individuals has also been used in a variety of measurement models including IRT, Guttman scaling, and latent class models (Gitomer & Yamamoto, 1991; Goodman, 1975; Schuster & Smith, 2002). The PLAM definition of the latent Type variable is similar to the ones used in these models in that it specifies a probability distribution for both fitting and nonfitting groups. Alternatively, an unspecified probability distribution may be assumed for the nonfitting group (Dayton, 2006). In this case, the purpose becomes finding the maximum number of individuals whose responses are consistent with a specified probability distribution. Consequently, no distributional assumption is necessary for the remaining group of individuals whose responses are inconsistent with the specified probability distribution.

Despite conceptual similarities, the intended meaning and formal parameterizations of the latent Type variable were different in these models. One unique contribution of the PLAM to the measurement literature lies in the definition and integration of the latent Type variable into the multiple discrete latent trait models. For Type = informative, the underlying model is simply the multiple discrete latent trait model. For Type = uninformative, however, the multiple discrete latent trait model is modified by setting up the categories of discrete latent variables to be indistinguishable from one another. This is achieved by fixing the conditional probabilities to be equal across the levels of discrete latent trait variables. This definition of the latent Type variable is unique to the PLAM. The uninformative category of the PLAM is defined in reference to the discrete latent traits with indistinguishable categories, rather than in reference to a group of individuals whose responses are simply inconsistent with the multiple discrete latent trait model. It is this specific definition that results in κ_l = 0 for Type = uninformative.

Within the rater agreement literature, the PLAM is the first to represent each rater type as a discrete latent trait (Dumenci, 2005). Consequently, the PLAM distinguishes true partial agreement (e.g., Type = informative, M = case, T = case, S = noncase) from chance partial agreement (e.g., Type = uninformative, M = case, T = case, S = noncase), as illustrated with the OD example. The idea behind the true partial agreement is that rater disagreements may not necessarily reflect the characteristics of raters. Rather, rater disagreements may reflect individual difference characteristics of the people being rated (e.g., Achenbach, McConaughy, & Howell, 1987). The PLAM incorporates the concept of true partial agreement into psychometric modeling. The overall size of the true partial agreement classes was found to approximate the size of the true complete agreement class of cases in the OD example. That is, the model would be misspecified without the true partial agreement classes in this example. The true partial agreement classes can be evaluated statistically, as illustrated in the model selection strategies.

The PLAM is appropriate for models involving ratings of multiple observed variables (i.e., items) in a traditional psychometric sense. Existing latent agreement models deal only with the rater facet of measurement design. By contrast, the PLAM may be used to model latent agreements for additional facets of measurement designs, such as traits. As illustrated in the ADH example, the combined ADH type was the most prevalent (13.1%), the H-I type was the least prevalent (1.7%), and the Ina type was moderately prevalent (7.9%). These estimates are comparable to those reported in general population surveys (e.g., Pinada, Lopera, Palacio, Ramirez, & Henao, 2003).

General latent class agreement models provided by Schuster and Von Eye (2001) and Schuster and Smith (2002) should be consulted first when the design characteristics call for each rater assigning each of N subjects into one category of one observed variable. Schuster and colleagues showed how their models can be reparameterized to obtain previously proposed latent class agreement models. Conceptual and parametric similarities and differences between their models and existing models of latent agreement have been well documented (Schuster, 2006; Schuster & Smith, 2002; Schuster & Von Eye, 2001).

Continuously distributed latent variable conceptualization of behavioral attributes serves well in most measurement contexts where the PLAM is not useful. Despite the fact that choices among distributions of latent variables are restricted in practice, a particular choice of latent variable distribution should ideally be justified over its alternatives on theoretical, empirical, and practical grounds, whether it is continuous, discrete, or both (i.e., factor mixture model). It becomes questionable to use a particular set of items to assign individuals to the categories of discrete latent traits when the unconditional probability estimate of Type = uninformative (i.e., ${\mathrm{\pi }}_2^T$) is relatively large. The question of “how large is large” needs to be answered by substantive researchers. Yet, researchers may be well advised to reconsider their selection of items when ${\mathrm{\pi }}_2^T\ge 1/3$. Although several features of the PLAM can be evaluated statistically (e.g., one vs. multiple discrete latent traits, the need for the latent Type variable), the optimal model among alternatives may not necessarily achieve close fit. The PLAM thus shares the limitations of absolute fit indices with other latent class models. Visual inspections of the response patterns that have the largest contributions to the loglikelihood values may reveal clues to detect some of the weaknesses of the model. In model fitting context, statistical evidence is not sufficient to claim the superiority of the PLAM. It is highly likely that there are many models (not tested here) that would fit the data better than the PLAM. However, the PLAM offers a logically consistent, practically useful, and statistically parsimonious interpretation.¹

Another limitation that the PLAM shares with other latent class models is that, given a fixed N, the sparseness of the contingency table due to an increase in the number of items and item-response categories will eventually lead to model identification problems (Collins & Wugalter, 1992). When this occurs, researchers might consider reducing the number of parameter estimates to achieve identification by imposing parameter constraints, for example, equality of unconditional probabilities across some or all facets of measurement designs (e.g., traits, raters). Eid, Langeheine, and Diener (2003) have provided an overview of such parameter constraints within the context of measurement invariance for discrete latent traits.

The PLAM opens the door for two exciting lines of research: The PLAM with continuous observed variables and with covariates. The PLAM is developed for discrete observed variables as an extension of latent class analysis. Whereas the latent profile analysis involves the estimation of discrete latent variables from continuous observed variables (Bartholomew & Knott, 1999), it is possible to further develop the latent profile analysis to include certain characteristics of the PLAM including discrete latent variable representations of raters and traits, as well as the latent Type variable. Another possible extension of the PLAM includes the introduction of covariates into the model. This is an important extension as applied researchers are interested in investigating the background characteristics of individuals that the test items work as intended from characteristics of those individuals that the test items do not work. The PLAM with covariates can be used, for example, to test the hypothesis that employees with low levels of organizational cohesion are more likely to belong to the uninformative subpopulation than those employees with high levels of organizational cohesion when rating scales are used to classify employees into latent job satisfaction categories. In fact, Muthén (2003) showed that the latent mixture models with covariates perform better when covariates are included. A drawback of addition of covariates to the PLAM is that it increases the model complexity which, in turn, may decrease the likelihood of obtaining an admissible solution.

Finally, the chance-corrected agreement statistic (i.e., κ_l) presented in equations 9 and 10 is simply one way to assess agreement. The extensive literature on agreement statistics estimated from observed cross-classification tables is beyond the scope of this study (for a comprehensive treatment, see Agresti, 2002; Shoukri, 2004; and Von Eye & Mun, 2005). It may suffice to note that the cross-classification of discrete latent variables for Type = informative (e.g., Table 1) provides the necessary information to estimate agreement, however defined, originally developed for discrete observed variables.

In conclusion, the PLAM is useful for modeling discrete item responses when tests are administered to determine the group membership of individuals in situations where the group memberships are not directly observable (e.g., pass/fail, qualified/unqualified). Examples include licensure, certification, and qualification examinations, as well as employment and performance tests. Loosely speaking, the PLAM is analogous to confirmatory factor analytic models for continuously distributed latent variables. It is confirmatory in the sense that latent variables and their relations with each other, as well as with observed discrete variables, are specified a priori. In the search for a parsimonious model, alternative models specified a priori should be estimated and contrasted with the full specification of PLAM. Alternative specifications may include the PLAM without the latent Type variable and the traditional one-latent class variable model. Information-based relative fit indices that take account of model complexity may be used to compare alternative models. Visual inspection of discrepancies between observed and model-implied response patterns may be used heuristically to detect shortcomings of the PLAM specification.

Biography

Levent Dumenci is an associate professor of Social and Behavioral Health at Virginia Commonwealth University. His research focuses on psychometric models and related statistical methods including continuous and discrete latent variable modeling, analysis of multitrait-multimethod matrix using structural equation modeling parameterizations, and measurement models for behavioral change.

APPENDIX. Mplus Input Files

I. MPLUS input file used to estimate the PLAM in example 1: ADH

TITLE: ADH - PLAM
DATA:
FILE IS odd.dat;
FORMAT IS FREE;
VARIABLE:
NAMES ARE t4 t8 t22 t78 t100 t10 t15 t24 t41 t53 t67 t93;
CATEGORICAL ARE t4 t8 t22 t78 t100 t10 t15 t24 t41 t53 t67 t93;
CLASSES = t (2) i (2) h (2);
ANALYSIS:
TYPE IS MIXTURE;
   PARAMETERIZATION = LOGLINEAR;
   LOGHIGH = +15;
   LOGLOW = –15;
   UCELLSIZE = 0.01;
   ESTIMATOR IS MLR;
   LOGCRITERION = 0.0000001;
   ITERATIONS = 1000;
   CONVERGENCE = 0.000001;
   MITERATIONS = 1000;
   MCONVERGENCE = 0.000001;
   MIXC = ITERATIONS;
   MCITERATIONS = 2;
   MIXU = ITERATIONS;
   MUITERATIONS = 2;
MODEL:
   %OVERALL%
   [i#1 h#1];
   i#1 with t#1;
   h#1 with t#1;
MODEL T:
   %t#1%
   i#1 with h#1@0;
   %t#2%
   i#1 with h#1;
MODEL T.I:
   %t#1.i#1%
   [t4$1] (1);  [t8$1] (2);  [t22$1] (3);  [t78$1] (4);  [t100$1] (5);
   [t4$2] (6);  [t8$2] (7);  [t22$2] (8);  [t78$2] (9);  [t100$2] (10);
   %t#1.i#2%
   [t4$1] (1);  [t8$1] (2);  [t22$1] (3);  [t78$1] (4);  [t100$1] (5);
   [t4$2] (6);  [t8$2] (7);  [t22$2] (8);  [t78$2] (9);  [t100$2] (10);
   %t#2.i#1%
   [t4$1*3]; [t8$1*3];  [t22$1*3];  [t78$1*3];  [t100$1*3];  [t4$2*5];
   [t8$2*5]; [t22$2*5];  [t78$2*5];  [t100$2*5];
   %t#2.i#2%
   [t4$1*–5];  [t8$1*–5];  [t22$1*–5];  [t78$1*–5];  [t100$1*–5]; [t4$2*–3];
   [t8$2*–3];  [t22$2*–3];  [t78$2*–3];  [t100$2*–3];
MODEL T.H:
   %t#1.h#1%
   [t10$1] (11);  [t15$1] (12);  [t24$1] (13); [t41$1] (14);  [t53$1] (15);
   [t67$1] (16);  [t93$1] (17);  [t10$2] (18); [t15$2] (19);  [t24$2] (20);
   [t41$2] (21);  [t53$2] (22);  [t67$2] (23); [t93$2] (24);
   %t#1.h#2%
   [t10$1] (11);  [t15$1] (12);  [t24$1] (13); [t41$1] (14);  [t53$1] (15);
   [t67$1] (16);  [t93$1] (17);  [t10$2] (18); [t15$2] (19);  [t24$2] (20);
   [t41$2] (21);  [t53$2] (22);  [t67$2] (23); [t93$2] (24);
   %t#2.h#1%
   [t10$1*3];  [t15$1*3];  [t24$1*3];  [t41$1*3];  [t53$1*3];  [t67$1*3];
   [t93$1*3];  [t10$2*5];  [t15$2*5];  [t24$2*5];  [t41$2*5];  [t53$2*5];
   [t67$2*5];  [t93$2*5];
   %t#2.h#2%
   [t10$1*–5];  [t15$1*–5];   [t24$1*–5];  [t41$1*–5];  [t53$1*–5];  [t67$1*–5];
   [t93$1*–5];  [t10$2*–3];   [t15$2*–3];  [t24$2*–3];  [t41$2*–3];  [t53$2*–3];
   [t67$2*–3];  [t93$2*–3];
SAVEDATA:
   FILE IS adhplam.dat;  save = cprob;
OUTPUT:  TECH10;

II. MPLUS input file used to estimate the plam in example 2: ODD

TITLE: ODD - PLAM
DATA:
   FILE IS odd1.dat;
FORMAT IS FREE;
VARIABLE:
   NAMES ARE m3 m23 m86 m95 t3 t23 t86 t95 s3 s23 s86 s95;
   CATEGORICAL ARE m3 m23 m86 m95 t3 t23 t86 t95 s3 s23 s86 s95;
    CLASSES = c (2) m (2) t (2) s (2);
ANALYSIS:
   TYPE IS MIXTURE;
   PARAMETERIZATION = LOGLINEAR;
   LOGHIGH = +15;
   LOGLOW = –15;
   UCELLSIZE = 0.01;
   ESTIMATOR IS MLR;
   LOGCRITERION = 0.0000001;
   ITERATIONS = 1000;
   CONVERGENCE = 0.000001;
   MITERATIONS = 1000;
   MCONVERGENCE = 0.000001;
   MIXC = ITERATIONS;
   MCITERATIONS = 2;
   MIXU = ITERATIONS;
   MUITERATIONS = 2;
MODEL:
   %OVERALL%
   [m#1 t#1 s#1];
   m#1 with c#1;
   t#1 with c#1;
   s#1 with c#1;
MODEL C:
   %c#1%
   s#1 with m#1@0;
   s#1 with t#1@0;
   t#1 with m#1@0;
   %c#2%
   s#1 with m#1;
   s#1 with t#1;
   t#1 with m#1;
MODEL C.M:
   %c#1.m#1%
   [m3$1] (1);  [m23$1] (2);  [m86$1] (3);  [m95$1] (4);
   [m3$2] (5);  [m23$2] (6);  [m86$2] (7);  [m95$2] (8);
   %c#1.m#2%
   [m3$1] (1);  [m23$1] (2);  [m86$1] (3);  [m95$1] (4);
   [m3$2] (5);  [m23$2] (6);  [m86$2] (7);  [m95$2] (8);
   %c#2.m#1%
   [m3$1*+3];  [m23$1*+3];  [m86$1*+3];  [m95$1*+3];
   [m3$2*+5];  [m23$2*+5];  [m86$2*+5];  [m95$2*+5];
   %c#2.m#2%
   [m3$1*–5];  [m23$1*–5];  [m86$1*–5];  [m95$1*–5];
   [m3$2*–3];  [m23$2*–3];  [m86$2*–3];  [m95$2*–3];
MODEL C.T:
   %c#1.t#1%
   [t3$1] (9);  [t23$1] (10); [t86$1] (11);  [t95$1] (12);
   [t3$2] (13);  [t23$2] (14); [t86$2] (15);  [t95$2] (16);
   %c#1.t#2%
   [t3$1] (9);  [t23$1] (10); [t86$1] (11);  [t95$1] (12);
   [t3$2] (13);  [t23$2] (14); [t86$2] (15);  [t95$2] (16);
   %c#2.t#1%
   [t3$1*+3];   [t23$1*+3]; [t86$1*+3];  [t95$1*+3];
   [t3$2*+5];   [t23$2*+5]; [t86$2*+5];  [t95$2*+5];
   %c#2.t#2%
   [t3$1*–5];   [t23$1*–5]; [t86$1*–5];   [t95$1*–5];
   [t3$2*–3];   [t23$2*–3]; [t86$2*–3]; t95$2*–3];
MODEL C.S:
   %c#1.s#1%
   [s3$1] (17);  [s23$1] (18); [s86$1] (19);  [s95$1] (20);
   [s3$2] (21);  [s23$2] (22); [s86$2] (23);  [s95$2] (24);
   %c#1.s#2%
   [s3$1] (17);  [s23$1] (18); [s86$1] (19);  [s95$1] (20);
   [s3$2] (21);  [s23$2] (22); [s86$2] (23);  [s95$2] (24);
   %c#2.s#1%
   [s3$1*+3];  [s23$1*+3]; [s86$1*+3];  [s95$1*+3];
   [s3$2*+5];  [s23$2*+5]; [s86$2*+5];  [s95$2*+5];
   %c#2.s#2%
   [s3$1*–5];  [s23$1*–5]; [s86$1*–5];   [s95$1*–5];
   [s3$2*–3];  [s23$2*–3]; [s86$2*–3];   [s95$2*–3];
SAVEDATA:
   FILE IS oddplam.dat;  save = cprob;
OUTPUT:  TECH10;