Abstract
What do inferring what a person is thinking or feeling, deciding to report a symptom to your doctor, judging a defendant’s guilt, and navigating a dimly lit room have in common? They involve perceptual uncertainty (e.g., a scowling face might indicate anger or concentration, which engender different appropriate responses), and behavioral risk (e.g., a cost to making the wrong response). Signal detection theory describes these types of decisions. In this tutorial we show how, by incorporating the economic concept of utility, signal detection theory serves as a model of optimal decision making, beyond its common use as an analytic method. This utility approach to signal detection theory highlights potentially enigmatic influences of perceptual uncertainty on measures of decision-making performance (accuracy and optimality) and on behavior (a functional relationship between bias and sensitivity). A “utilized” signal detection theory offers the possibility of expanding the phenomena that can be understood within a decision-making framework.
Keywords: Signal detection theory, utility, perception, decision making
INTRODUCTION
The goal of this tutorial is to familiarize readers with less well known aspects of signal detection theory (SDT; Green & Swets, 1966; Macmillan & Creelman, 1991) that stem from using it a model of optimal decision making. SDT characterizes how perceivers separate meaningful information from “noise.” SDT is widely used to measure performance on perception, memory, and categorization tasks. In the realm of social perception, for example, when interacting with someone, it is advantageous to know whether the person is angry (and likely means you harm) or not. SDT is particularly useful when the alternative options are perceptually similar to one another (e.g., a scowling facial expression sometimes means that the person is angry and sometimes means that the person is merely concentrating), called uncertainty, and when misclassification carries some relative cost (e.g., when failing to correctly identify someone as angry incurs punishment that would otherwise have been avoided), called risk1.
Overview of SDT
SDT’s power as an analytic tool comes from separating a perceiver’s behavior into two underlying components, sensitivity and bias (see Précis of Signal Detection Theory in Supplemental Material available online). Sensitivity is the perceiver’s ability to discriminate alternatives: targets (e.g., a person who is angry) vs. foils (e.g., a person who is not angry). Bias is the perceiver’s propensity to categorize stimuli as targets vs. foils and is described as liberal, neutral, or conservative. For example, if failing to correctly identify threat is relatively costly (resulting in, say, psychological or physical punishment), or if targets are common relative to foils, then a perceiver might treat equivocal stimuli as threatening targets rather than safe foils (resulting in liberal bias, in which even mildly scowling faces are treated as angry). If, instead, incorrectly identifying a stimulus as a threat is relatively costly (resulting in, say, embarrassment arising from a misperceived need to apologize), or if targets are uncommon relative to foils, then a perceiver might treat equivocal stimuli as safe (resulting in conservative bias, in which only strongly scowling faces are treated as angry).
SDT is applicable across a spectrum of perceptual to conceptual domains. In fact, a diverse array of non-psychophysical “perceptions” have been treated as issues of signal detection, including eyewitness lineups (Clark, 2012), child foster home placement (Ruscio, 1998), memory (Wixted & Stretch, 2004), cancer detection (Abbey, Eckstein, & Boone, 2009), statistical hypothesis testing (Green & Swets, 1966), and diagnostic decisions more generally (Swets, Dawes, & Monahan, 2000). In Supplemental Material, we use examples across the perceptual-conceptual spectrum to illustrate the points made in the main text with our social threat detection example, including interoception, social perception, jury deliberation, and travel speed.
Despite SDT’s breadth of application, it is largely used in a descriptive way to compare sensitivity and bias across study conditions or people. For example, current depression has been associated with decreased sensitivity for emotion perception and remitted depression with increased sensitivity and more neutral response bias for emotion perception, relative to control (Anderson et al., 2011). Yet, SDT has much more to offer as a generative model of decision making. Combining SDT’s treatment of perceptual uncertainty with the behavioral economic concept of utility (the net benefit expected to accrue from a series of decisions) highlights important aspects of decision making overlooked both by typical applications of SDT and by traditional models of decision making that focus on utility alone.
THE UTILITY OF PERCEPTION
According to the utility-based approach to SDT, three parameters characterize the uncertainty and risk within a specific decision environment.
Payoff. Every decision has its consequences. The payoff parameter describes the value of each of four possible decision outcomes: correct detections, missed detections, false alarms, and correction rejections (see Précis of Signal Detection Theory in Supplemental Material). False alarms and missed detections incur relative costs, whereas correct rejections and correct detections each impart relative benefits to the perceiver. In social threat detection, for example, false alarms might lead to unnecessary apologetic disruptions of the social interaction or to unnecessary social avoidance, whereas missed detections might lead to punishment or other aversive outcomes.
Base rate. The base rate parameter describes the perceiver’s probability of encountering targets (e.g., a person who is angry) relative to foils (e.g., a person who is not angry).
Similarity. Target and foil categories can be somewhat similar to one another, the source of perceptual uncertainty. The similarity parameter models this uncertainty by describing what targets and foils “look like.” For example, the physical similarity of facial expressions associated with two emotion categories can be modeled as Gaussian distributions over a continuous perceptual domain of facial expression intensity. There are two sources of perceptual uncertainty. Intrinsic sources are internal to the perceiver. Intrinsic sources may include, for example, sensory processing “noise” (e.g., Osborne, Lisberger, & Bialek, 2005), poorly learned discrimination (e.g., Lynn, 2005), and at an abstract level, perhaps even confusion about the difference between more conceptual categories. Extrinsic sources are external to the perceiver, arising from the environment or the signaler. Extrinsic sources may include, for example, environmental noise (e.g., Wollerman & Wiley, 2002) or signal attenuation (e.g., Naguib, 2003), and variation in signaler expressivity (e.g., in emotional expressivity, Zaki, Bolger, & Ochsner, 2009). Research in psychophysics often emphasizes intrinsic uncertainty. Research in applied decision making (e.g., medical diagnostics) and behavioral ecology often emphasizes extrinsic uncertainty.
It is well known that payoffs and base rate influence bias (Green & Swets, 1966; Macmillan & Creelman, 1991). Rare targets or costly false alarms each promote a conservative bias (i.e., a higher threshold, or criterion, for judging that a target is present) whereas common targets or costly misses each promote a liberal bias (i.e., a lower criterion for judging that a target is present; e.g., Quigley & Barrett, 1999). The perceptual similarity between targets and foils influences sensitivity (i.e., perceivers have greater sensitivity when targets and foils are less perceptually similar to one another; Green & Swets, 1966; Macmillan & Creelman, 1991). However, it is the utility-based approach to SDT (combining uncertainty with behavioral economics) that quantifies and predicts these relationships between environmental parameters and behavior.
Establishing the optimal criterion location
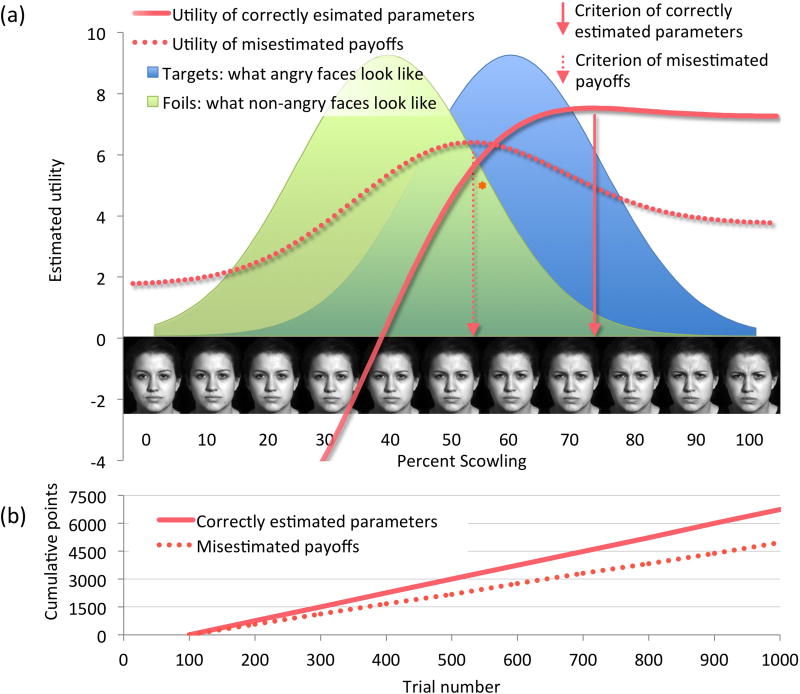
When in the presence of perceptual uncertainty, mistakes cannot be avoided. A liberal criterion (leftward in Fig. 1a) minimizes missed detections but increases exposure to false alarms. A conservative criterion (rightward in Fig. 1a) minimizes false alarms but increases exposure to missed detections. Therefore, perceivers should seek to optimize their criterion location–to adopt a criterion that maximizes expected utility, producing the optimal blend of missed detections and false alarms in light of the environmental parameters.
Fig. 1.
In a social threat detection scenario, facial expressions are evaluated by one person (the perceiver or decision maker) to gauge another person’s (the sender or signaler) threat to the perceiver. (a) The payoff, base rate, and similarity parameters can be combined to derive a utility function for the decision environment that they characterize. The location on the stimulus domain (x-axis) with the highest utility is the decision criterion location (solid drop-line) that will maximize benefit over a series of decisions. A simulated perceiver who underestimates the base rate (dotted utility function), adopts a suboptimally neutral criterion (dotted drop-line). The perceiver’s expected utility is dictated by where the criterion meets the utility function derived from correctly estimated parameters, denoted by an asterisk. (b) That the misestimate is suboptimal is shown by a shallower rate of utility gain
The SDT utility function uses the three parameters to calculate the expected value (to the perceiver) of placing a decision criterion at any location on the perceptual domain (see The Signal Utility Estimator and Receiver Operating Characteristics, in Supplemental Material). For example, it is possible to compute the expected utility of placing a decision criterion at each facial expression along the continuum in Fig. 1a. The criterion location with the highest expected utility will maximize net benefit over a series of decisions. By modeling the environmental parameters that underlie bias and sensitivity, we can mathematically predict and empirically compare perceivers’ optimality within and between environments or experimental conditions of a study.
To implement these ideas in a laboratory setting, it is possible to create different decision environments defined within an experiment by assigning values to the three parameters (see Lynn, Cnaani, & Papaj, 2005, for an example with non-humans; see Lynn, Zhang, & Barrett, 2012, for an example with humans). Payoffs can be implemented behaviorally. For example, participants earn points or lose points depending on the outcome of each trial. In this way it is possible to set unequal payoff outcomes (e.g., a missed detection of anger might have a different cost than a false alarm in a particular context). Outside the laboratory, payoffs may not be known or easily quantified, of course. In such cases a ratio of payoffs might be used. For example, Clark (2012) explored the utility of eye-witness police line-up reforms using a 10:1 ratio of the cost of missed detections (the perpetrator goes free) to false alarms (the wrong person is identified as the perpetrator). Base rate can be implemented as the proportion of target vs. foil trials shown. Base rate can model, e.g., that some people with whom a perceiver interacts may be angry more often than other people. The similarity parameter can be implemented with targets and foils randomly drawn from their respective distributions imposed on a continuum of stimuli.
Because criterion location is a function of the three environmental parameters, suboptimal bias or sensitivity in a perceiver can be understood as a perceiver “misestimate” of one or more parameters (Fig. 1b). Individual differences, alone or in interaction with the decision environment, may influence parameter estimates (Fig. S3 in Supplemental Material; Lynn et al., 2012).
The application of utility to SDT is not new—it was part of the theory’s initial development in psychophysics (Tanner & Swets, 1954; Green & Swets, 1966). Nonetheless, a “utilized” SDT–the notion that perceivers attempt to maximize net benefit while operating under perceptual uncertainty2–generates a number of unexpected but important theoretical observations that have yet to be widely explored in the psychological literature. One surprising observation is that there are contexts in which maximizing accuracy conflicts with maximizing utility, so that there are common situations in which accuracy should be sacrificed to achieve effective decision making. This conflict has implications for the use of accuracy as a measure of performance. A second surprising observation is a functional relationship between bias and sensitivity—within a perceiver, optimal criterion location is not independent of sensitivity. Probably the most widely appreciated insight of SDT is its separation of sensitivity and bias as factors explaining behavior (Swets, Tanner, & Birdsall, 1961), and many users believe that the two are orthogonal or independent of one another. This relationship between sensitivity and bias has implications for interpreting differences in sensitivity and bias among perceivers or different contexts.
MEASURING BEHAVIOR: OPTIMAL IS BETTER THAN ACCURATE
One clear tenant of SDT is that estimates of accuracy (i.e., proportion of trials garnering correct response) should be abandoned in favor of estimates of bias and sensitivity as measures of performance when feasible (Macmillan & Creelman, 1991). There are two reasons to avoid accuracy. First, accuracy does not account for two aspects of decision making under uncertainty and risk that are important for a full understanding of the perceiver’s behavior. Accuracy confounds the effects of sensitivity and bias on performance, and this is true whether one applies a utility framework to SDT or not. Second, the inadequacy of accuracy is compounded under economic risk, when payoffs should optimally bias behavior, because accuracy simply tallies correct and incorrect decisions without regard to their actual benefits and costs.
Accuracy confounds sensitivity and bias
Accuracy not a good indicator of what people are doing–it does not describe their behavior. This is because accuracy is blind to the separate contributions of sensitivity and bias to decision making. While this fact is well-known, it is less appreciated that multiple combinations of sensitivity and bias values produce the same accuracy (Fig. 2). The overt differences in behaviors that yield a given accuracy level may encompass dramatic extremes of liberal and conservative bias. Consequently, the researcher analyzing accuracy rather than optimality will pool participants who are potentially behaving quite differently from one another (Lynn, Hoge, Fischer, Barrett, & Simon, In press).
Fig. 2.
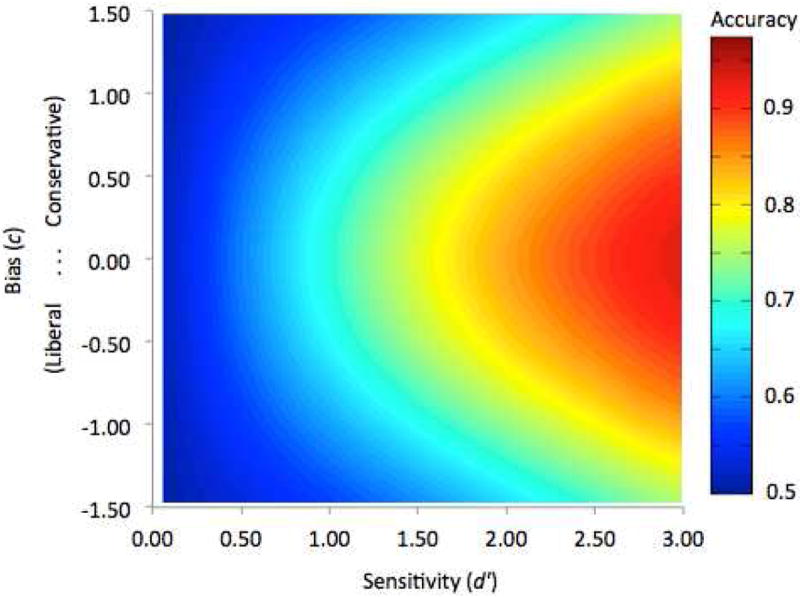
Iso-accuracy gradients (regions of the same color) show that multiple combinations of sensitivity and bias produce the same accuracy. For example, at moderate sensitivity (d′=2), both liberal bias (c=-0.5) and conservative bias (c=0.5) can produce accuracy near 0.8 in this simulated neutral-bias environment (parameter values provided in Supplemental Material).
Accuracy ignores payoffs but not base rate
When benefits and costs differ, accuracy is not a good indicator of how well people are doing – it is an inadequate measure their performance. Accuracy is blind to the influences of benefits and costs on decision making (Egan, 1975; Maddox & Bohil, 2005) because it is determined without regard to the value accrued to the perceiver for those decisions. This means that maximizing accuracy and maximizing utility can be at odds with one another in environments in which bias is due to payoffs. However, accuracy is derived from the proportions of correct and incorrect responses. It is therefore congruent with utility in environments in which bias is due to base rate.
A comparison of simulated environments with different sources of bias exemplifies these points. When payoffs alone bias behavior (Table 1, Payoff environment, in which false alarms are relatively costly but base rate is balanced at 0.5), accuracy is highest for bias=0 (neutral bias). Nevertheless, utility is maximized at bias=0.4 (somewhat conservative). Utility at the criterion that maximizes accuracy is 7.1 points, less than the maximum utility possible, 7.5 points. Accuracy at the criterion that maximizes utility is 0.82, less than the maximum accuracy possible, 0.84. Perceivers with bias=0 will achieve lower maximum utility over a series of decisions than those with bias=0.4, despite exhibiting higher accuracy. When base rate alone biases behavior (Table 1, Base Rate environment, in which benefits and costs cancel each other out but base rate=0.3) the amount of bias that maximizes accuracy also maximizes utility (again at bias=0.4). When benefits and costs differ, then, optimally biased decision making will yield lower accuracy than unbiased decision making, in spite of its greater utility. Consequently, accuracy cannot properly describe performance in environments in which there is risk due to payoffs.
Table 1.
Comparison of four simulated decision environments shows that the criterion location and amount of bias that maximize accuracy do not maximize utility when payoffs cause bias, but do maximize utility when base rate causes bias.
| Expected value | Type of Decision Environmenta
|
|||
|---|---|---|---|---|
| Neutral | Base Rate | Base rate & Payoff | Payoff | |
| Maximum accuracy for environment | 0.84 | 0.86 | 0.86 | 0.84 |
| Criterion location (% of range) that maximizes accuracy | 50.0 | 50.4 | 50.4 | 50.0 |
| Bias (c) that maximizes accuracy | 0.0 | 0.4 | 0.4 | 0.0 |
| Utility (points) at criterion location that maximizes accuracy | 6.8 | 7.2 | 7.7 | 7.1 |
|
| ||||
| Maximum utility for environment | 6.8 | 7.2 | 8.0 | 7.5 |
| Criterion location (% of range) that maximizes utility | 50.0 | 50.4 | 50.8 | 50.4 |
| Bias (c) that maximizes utility | 0.0 | 0.4 | 0.8 | 0.4 |
| Accuracy at criterion location that maximizes utility | 0.84 | 0.86 | 0.85 | 0.82 |
Expected accuracy, criterion location, bias, and utility values for each environment were derived by applying each environment’s parameters to the SDT utility function. Neutral environment parameter values: correct detections and correct rejections=10 points, missed detections and false alarms=-10 points; base rate=0.5; and similarity mean target and foil at 60% and 40%, respectively, with standard deviation=10% for both distributions. The Base Rate environment is identical to the Neutral environment except that base rate is reduced to 0.3. The Payoff environment is identical to the Neutral environment except that false alarms are more costly (-15 points) and missed detections less costly (-1 point). The Base Rate & Payoff environment combines the base rate and payoffs from the Base Rate and Payoff environments, respectively, with similarity parameter values as in the Neutral environment.
Accuracy sometimes reflects optimal decision making and sometimes not, depending on the environment. For example, participants engaged in an emotion perception experiment, of the sort described in Fig. 1a, attempted to maximize points earned over 178 trials (see Lynn et al., 2012 for methodological details). Additional analysis of data from Lynn et al. (2012) shows that, as illustrated in Table 1, accuracy did not reflect optimal decision making when bias was caused by payoffs. For participants in a condition that implemented a liberal bias via relatively costly missed detections (all else being equal), more liberal bias (c) was associated with lower accuracy (one-tailed partial correlation controlling for sensitivity, d′: ρ=0.50, p<0.001, n=67). Additionally, more liberal bias was associated with more points earned (ρ=-0.82, p<0.001) while higher accuracy was marginally associated with fewer points earned (ρ=-0.17. p>0.086). These results show that when bias is caused by payoffs, accuracy is not a useful measure of performance.
Also as illustrated in Table 1, accuracy did reflect optimal decision making when bias was caused by the base rate of targets (targets less common than foils). For participants in a condition that implemented a conservative bias via relatively low base rate, more conservative bias was associated with higher accuracy (ρ=0.91, p<0.001, n=75). Additionally, more conservative bias and higher accuracy were associated with higher points earned (bias: ρ=0.50, p<0.001; accuracy: ρ=0.58, p<0.001). These results show that when bias is caused by base rate, accuracy is congruent with utility.
Humans appear to more easily adapt their response bias to base rate than to payoffs (Bohil & Maddox, 2001). This discrepancy leads to an observed response bias that maximizes accuracy at the expense of optimality (Maddox & Bohil, 2005). When payoffs matter, perceivers maximizing accuracy over optimality will accrue less benefit than could otherwise be the case.
By ignoring the differences between benefits and costs, such perceivers will be unable to tune their bias to balance those differences. Moreover, when the payoff matrix and base rate demand opposing liberal- vs. conservative-going bias, perceivers who neglect payoffs could exhibit bias in the wrong direction relative to what is optimal for the environment.
Many studies are blind to the difference between optimality and accuracy as a consequence of not assigning separate payoff values to correct detections vs. correct rejections, or false alarms vs. missed detections. Emphasizing accuracy instead of optimality corresponds to misalignment of behavior with the contingencies of the decision because those contingencies are ignored. In social threat perception, for example, emphasizing accuracy over a series of judgments could correspond to considering the costs of false alarm and missed detection to be of equal value, and the benefits of correct detection and correct rejection to be of equal value. While an assumption of balanced payoffs may be true in most laboratory experiments of emotion perception, that assumption seems unlikely to be the case outside the laboratory, reducing ecological validity. Outside the laboratory, decisions involve benefits and costs, and maximizing net benefit, not accuracy, is what matters. Testing perceivers under conditions that demand a non-neutral bias and measuring performance as accumulated payoff or optimality of bias, rather than accuracy, better reflects decisions made outside the laboratory.
INTERACTION OF UNCERTAINTY AND RISK: THE RELATIONSHIP BETWEEN BIAS AND SENSITIVITY
Perceivers maximizing utility experience a functional relationship between bias and sensitivity predicted by the SDT utility function. This relationship dictates that, given some non-neutral response bias required by the environment (determined by base rate and/or payoffs), to maximize their utility, perceivers with low sensitivity should be more biased than a perceivers with high sensitivity.
To get an intuitive feel for this relationship, consider walking through an obstacle-strewn room as a signal detection issue (this example is further developed in Supplemental Material). Why do people navigate space more cautiously in conditions of poor visibility than good visibility? A missed detection (say, stepping barefoot on an object) is costly (it is painful to the perceiver and may break the object). When the room is well lit, a person can walk quickly through the room. When the room is dimly lit, the person walks more cautiously, reducing the frequency of missed detections that would otherwise occur: a change in bias. What about the environment has changed to cause this change in bias? The benefits and costs of correct vs. incorrect judgment about the presence or absence of obstacles in the person’s path have not changed, nor has the base rate of encountering obstacles. Only the perceptual similarity between targets and foils has changed–obstacles and clear space look more similar in the dark, reducing the person’s sensitivity to discriminate obstacles against the background. Here, a decrease in sensitivity has led to a more liberal bias, which produces a change in response (decreased walking speed): fewer missed detections and more false alarms than if walking speed had not changed.
In short, decreased sensitivity makes errors more likely. Perceivers can mitigate this increased risk to some extent by adopting a more extreme bias. For perceivers, the consequence of this functional relationship is more extreme behavior associated with greater uncertainty (modeled in Fig. 3; see also discussion of the receiver operating characteristic in Supplemental Material).
Fig. 3.
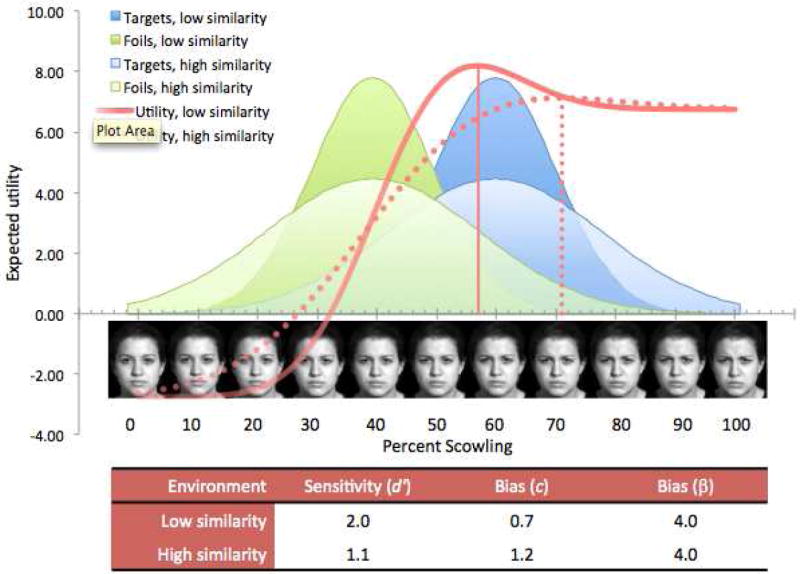
To optimize their performance in a biased environment, perceivers with low sensitivity must adopt a more extreme bias than those with high sensitivity. Comparison of two optimal models that differ in similarity of targets vs. foils illustrates that, to offset the decrement in performance caused by low sensitivity, perceivers with low sensitivity should adopt a more extreme bias (depicted by the rightward shift of the criterion for the “high similarity” utility function; see inset table). Note that bias as measured by beta does not explicitly reflect the difference in behavior. Parameter values provided in Supplemental Material.
The Line of Optimal Response
A Line of Optimal Response (LOR, Fig. 4; Lynn et al., 2012) depicts the functional relationship between bias and sensitivity. Any unique set of environmental base rate and payoff values has a unique LOR. The LOR can be derived from the equation relating the likelihood ratio of the signal distributions (a measure of bias called beta, β; see Précis of Signal Detection Theory in Supplemental Material) to the “criterion” or “center” bias measure, c, and sensitivity, measured as d′ (Macmillan & Creelman, 1991, Equation 2.10):
| (1) |
Fig. 4.
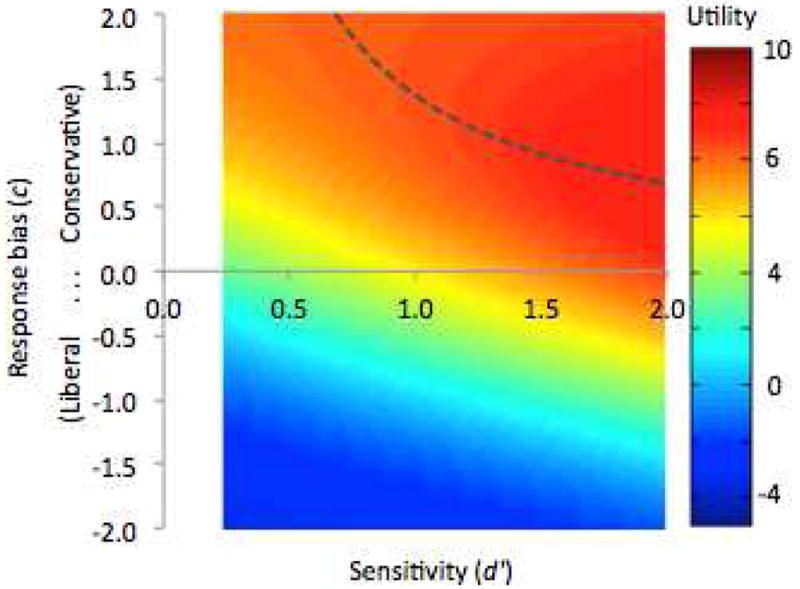
The utility approach to signal detection theory indicates a relationship between bias and sensitivity that functions to maximize the utility of perceptual decisions. Mathematical modeling shows that a perceiver’s sensitivity and bias should be inversely related. A “line of optimal response” (LOR; dashed line) is defined by the bias that yields maximum utility for any given level of sensitivity, for constant base rate and payoff values. Curvature of the LOR indicates that the decrease in utility that results from reduced sensitivity can be mitigated by increased magnitude of bias (here, more conservative-going). Parameter values provided in Supplemental Material.
Providing the environment’s optimal beta value and solving for c=log(β)/d′ over a range of d′ values yields the LOR. The environment’s optimal beta value can be calculated from the base rate and payoffs (Tanner & Swets, 1954, Equation 2; see also Wiley, 1994):
| (2) |
where α=base rate; j, a, h, and m=payoffs for correct rejections, false alarms, correct detections, and missed detections respectively (see The Signal Utility Estimator in Supplemental Material).
βoptimal is constant for all sensitivity values; it is set by the environmental payoffs and base rate, and not a function of sensitivity. By Equation 1, defining beta in terms of c and d′, c must change with sensitivity if beta is constant. While there is a literature examining beta (e.g., Wood, 1976; Snodgrass & Corwin, 1988), we have chosen to focus on how c changes with sensitivity (Stretch & Wixted, 1998). Focusing on the lability of c, rather than the stability of beta, emphasizes how perceivers’ behavior—which stimuli they categorize as “target” and which as “foil”—must differ between environments that differ in target/foil similarity or among individuals that differ in sensitivity (e.g., compare beta and c values for the high and low similarity environments of Fig. 3, inset table).
We interpret the distance from the point defined by a perceiver’s observed sensitivity and bias (d′, c) to the LOR as a measure of how well the perceiver is able to adjust his or her bias to optimally accommodate his or her level of sensitivity. We have elected to measure each participant’s distance to the LOR (which we call do, distance-sub-optimal), as Euclidian distance rather than vertical distance, as a means of accounting for the unknown bivariate error distribution in the estimates of sensitivity and bias (Lynn et al., 2012).
Sensitivity as a source of bias
Surprisingly, this functional relationship means that low sensitivity can prompt extreme bias, just like the payoff and base rate parameters. As a consequence, bias can change solely from a difference in the perceived similarity of targets and foils, without changes in the parameters commonly understood to drive bias, base rate and payoffs3. In studies where response bias (c) has been found to be inversely associated with perceptual sensitivity (d′), the associations have sometimes been explained as methodological or measurement artifact (e.g., Snodgrass & Corwin, 1988; See, Warm, Dember, & Howe, 1997). However, when sensitivity and bias (measured as either c or absolute criterion location on the perceptual domain) vary inversely between conditions, low sensitivity should be considered as a possible explanation for high bias.
Recognizing a functional relationship between sensitivity and bias is critical because it has the potential to reverse researchers’ conclusions about differences in bias that are observed whenever signal detection issues occur (i.e., decisions involving category uncertainty and costly mis-categorization). For example, under the assumption that bias is functionally independent of sensitivity, perceivers exhibiting poor sensitivity combined with high bias (relative to a control group) would be considered to exhibit two separate impairments in decision making: poor sensitivity and high bias. To optimize decision making, however, bias should vary inversely with sensitivity, particularly at low sensitivity. On the utility-based account, therefore, more extreme bias may not reflect an impairment but a normal adaptive mechanism, offsetting the single impairment, poor sensitivity. Conversely, under the independence assumption, perceivers exhibiting poor sensitivity with no difference in bias (relative to more sensitive individuals) would be considered to exhibit a single impairment, in sensitivity. In fact, such individuals may have a dual impairment: failure to calibrate their bias to their poor sensitivity.
Additional analysis of data from Lynn et al. (2012) shows that perceivers exhibited wide variation in their ability to optimally adjust their bias to their sensitivity, but that an inverse relationship between bias and sensitivity did function to maximize utility (Fig. 5). As predicted by the utility approach to SDT, perceivers with poor sensitivity (d′) exhibited a more extreme bias (c) than did perceivers with better sensitivity (in an environment using payoffs to induce a liberal bias: r=0.26, p<0.023, n=67; in an environment using base rate to induce a conservative bias: r=-0.48, p<0.001, n=75). Furthermore, as predicted, perceivers with more optimal bias (shorter distance from LOR, do) earned more points over the series of trials (liberal payoff environment, one-tailed partial regression controlling for sensitivity, ρ=-0.81, p<0.001; conservative base rate environment, ρ=-0.50, p<0.001) indicating that perceivers who adopted a more extreme bias that reflected their reduced sensitivity—following the LOR—made more optimal perceptual decisions.
Fig. 5.

An inverse relationship between bias and sensitivity functions to optimize decision making. Participants in a liberally or conservatively biased decision environment showed inverse relationships between bias and sensitivity as predicted by the Line of Optimal Response (LOR, dashed lines) for the environment’s parameter value set. Perceivers closer to their environment’s LOR earned significantly more points than those farther away, indicating that the inverse relationship is driven by utility maximization. Data from Lynn et al. (2012).
CONCLUSIONS
SDT is a well-established analytic tool for describing decision-making performance in a wide variety of perceptual to conceptual phenomena. A “utilized” SDT goes farther – it provides a theoretical framework to predict or explain behavior. The SDT utility function (Swets et al., 1961) makes SDT a predictive tool by modeling the perceptual uncertainty and behavioral risk that are inherent to many decisions both inside and outside the laboratory. The model can be used to pose novel experimental questions about computational processes underlying bias and sensitivity and functional decision making (e.g., see Affective Calibration in Mental Illness, in Supplemental Material).
Understanding decision making and criterion placement as dependent on perceivers’ subjective estimates of parameters that characterize the environment has exciting ramifications. First, designing experiments to manipulate the payoff, base rate, and similarity parameters, and measuring optimality of decision making, will provide a more mechanistic approach to understanding the factors that underlie perceiver bias and sensitivity. Examining how perceivers make decisions in biased conditions will better reflect decision making in more realistic environments than is typically the case in cognitive and perceptual experiments, where payoffs are unspecified and base rate is balanced across alternatives.
Second, adopting SDT as a theoretical model of decision making offers a path by which behavioral economic and neuroeconomic studies of judgment and decision making can investigate the influence of uncertainty. Examining perceivers operating under uncertainty would reflect decision making in more realistic environments than typically employed in judgment and decision-making tasks that manipulate economic risk—the variation in payoffs—but ignore “signal-borne” risk—the variation in what options look like.
Sensitivity to the three signal parameters is taxonomically wide-spread, exhibited by vertebrates and arthropods (e.g., Lynn, 2010). Model-driven approaches to the study of choice making (Glimcher & Rustichini, 2004; Redish, 2004; Gold & Shadlen, 2007; Redish, Jensen, & Johnson, 2008) that systematically manipulate SDT’s three parameters may thus permit a broadly comparative investigation of how decision making is accomplished across levels of biological organization and complexity.
Supplementary Material
Acknowledgments
We thank Eric Anderson, Jennifer Fugate, and David Levari, for helpful feedback during the development of the manuscript. Preparation of this manuscript was supported by the National Institutes of Health (R01MH093394 to SKL, DP1OD003312 to LFB) and the U.S. Army Research Institute for the Behavioral and Social Sciences (contract W5J9CQ-12-C-0028 to SKL, W91WAW-08-C-0018 to LFB). The views, opinions, and/or findings contained in this paper are those of the authors and shall not be construed as an official National Institutes of Health or Department of the Army position, policy, or decision, unless so designated by other documents.
Footnotes
These definitions of uncertainty and risk differ somewhat from those used in strictly economic decision making, where commonly risk is defined as knowable variation in the value (payoff) of a decision’s outcome and uncertainty as unknowable variation (reviewed by, e.g., Volz & Gigerenzer, 2012).
It is perceptual uncertainty, modeled by the similarity parameter, that distinguishes SDT from other models of decision making. Other models of decision making attempt to account for how decisions are influenced by variability in benefits and costs accrued from correct or incorrect decisions, variability in the probability of alternative choices or events, and/or variability in factors internal to the decision maker that affect risk sensitivity (e.g., reviews in Krebs & Kacelnik, 1991; McNamara, Houston, & Collins, 2001). Game theoretic approaches to decision making additionally account for the effect of others’ responses on the decision maker’s own behavior (e.g., Grafen, 1991). Yet, ignored by the these models is that a perceiver’s expectation of the payoff to be accrued, the encounter rates, the responses of others, and even his or her own body state (e.g., homeostatic and metabolic response), are based on signals emitted by the resources, game partners, body, etc. SDT posits that these signals themselves have variation.
Bias and sensitivity independently characterize decision making: a perceiver’s ability to distinguish targets from foils is a separate consideration from his or her estimate of payoffs and base rate. Additionally, the measures d′ and c are estimated with statistical independence from one another (Dusoir, 1975; Snodgrass & Corwin, 1988; Macmillan & Creelman, 1990; See et al., 1997). Nonetheless, these notions of conceptual and statistical independence have inadvertently influenced assumptions about functional independence, such that there exists a misconception that a perceiver’s observed bias should be independent of his or her observed sensitivity. The utility approach to SDT shows instead that a perceiver’s observed bias and sensitivity are functionally related by the maximization of utility.
AUTHOR CONTRIBUTIONS
S.K. Lynn developed the tutorial material and drafted the manuscript. L. F. Barrett provided critical revisions. Both authors approved the final version of the manuscript for submission.
References
- Abbey CK, Eckstein MP, Boone JM. An equivalent relative utility metric for evaluating screening mammography. Medical Decision Making. 2009;30:113–122. doi: 10.1177/0272989X09341753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson IM, Shippen C, Juhasz G, Chase D, Thomas E, Downey D, Deakin JFW, et al. State-dependent alteration in face emotion recognition in depression. British Journal of Psychiatry. 2011;198:302–308. doi: 10.1192/bjp.bp.110.078139. [DOI] [PubMed] [Google Scholar]
- Bohil C, Maddox W. Category discriminability, base-rate, and payoff effects in perceptual categorization. Attention, Perception, & Psychophysics. 2001;63:361–376. doi: 10.3758/bf03194476. [DOI] [PubMed] [Google Scholar]
- Clark SE. Costs and benefits of eyewitness identification reform: Psychological science and public policy. Perspectives on Psychological Science. 2012;7:238–259. doi: 10.1177/1745691612439584. [DOI] [PubMed] [Google Scholar]
- Dusoir A. Treatments of bias in detection and recognition models: A review. Perception & Psychophysics. 1975;17:167–178. [Google Scholar]
- Egan JP. Signal Detection Theory and ROC Analysis. New York, NY: Academic Press; 1975. [Google Scholar]
- Glimcher PW, Rustichini A. Neuroeconomics: The consilience of brain and decision. Science. 2004;306:447–452. doi: 10.1126/science.1102566. [DOI] [PubMed] [Google Scholar]
- Gold JI, Shadlen MN. The neural basis of decision making. Annual Review of Neuroscience. 2007;30:535–574. doi: 10.1146/annurev.neuro.29.051605.113038. [DOI] [PubMed] [Google Scholar]
- Grafen A. Modelling in behavioural ecology. In: Krebs JR, Davies NB, editors. Behavioural Ecology An Evolutionary Approach. 3. Oxford: Blackwell Scientific; 1991. pp. 5–31. [Google Scholar]
- Green DM, Swets JA. Signal Detection Theory and Psychophysics. New York: Wiley; 1966. [Google Scholar]
- Krebs JR, Kacelnik A. Decision-making. In: Krebs JR, Davies NB, editors. Behavioural Ecology An Evolutionary Approach. 3. Oxford: Blackwell Scientific; 1991. pp. 105–136. [Google Scholar]
- Lynn SK. Learning to avoid aposematic prey. Animal Behaviour. 2005;70:1221–1226. [Google Scholar]
- Lynn SK. Decision-making and learning: The peak shift behavioral response. In: Breed M, Moore J, editors. Encyclopedia of Animal Behavior. Vol. 1. Oxford: Academic Press; 2010. pp. 470–475. [Google Scholar]
- Lynn SK, Cnaani J, Papaj DR. Peak shift discrimination learning as a mechanism of signal evolution. Evolution. 2005;59:1300–1305. [PubMed] [Google Scholar]
- Lynn SK, Hoge EA, Fischer LE, Barrett LF, Simon NM. Gender differences in oxytocin-associated disruption of decision bias during emotion perception. Psychiatry Research. doi: 10.1016/j.psychres.2014.04.031. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynn SK, Zhang X, Barrett LF. Affective state influences perception by affecting decision parameters underlying bias and sensitivity. Emotion. 2012;12:726–736. doi: 10.1037/a0026765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macmillan NA, Creelman CD. Response bias: Characteristics of detection theory, threshold theory, and “nonparametric” indexes. Psychological Bulletin. 1990;107:401–413. [Google Scholar]
- Macmillan NA, Creelman CD. Detection Theory: A User’s Guide. New York: Cambridge University Press; 1991. [Google Scholar]
- Maddox WT, Bohil C. Optimal classifier feedback improves cost-benefit but not base-rate decision criterion learning in perceptual categorization. Memory & Cognition. 2005;33:303–319. doi: 10.3758/bf03195319. [DOI] [PubMed] [Google Scholar]
- McNamara JM, Houston AI, Collins EJ. Optimality models in behavioral biology. SIAM Review. 2001;43:413–466. [Google Scholar]
- Naguib M. Reverberation of rapid and slow trills: Implications for signal adaptations to long-range communication. The Journal of the Acoustical Society of America. 2003;113:1749–1756. doi: 10.1121/1.1539050. [DOI] [PubMed] [Google Scholar]
- Osborne LC, Lisberger SG, Bialek W. A sensory source for motor variation. 2005;437:412–416. doi: 10.1038/nature03961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quigley KS, Barrett LF. Emotional learning and mechanisms of intentional psychological change. In: Brandtstadter J, Lerner RM, editors. Action and Development: Origins and Functions of Intentional Self-development. Thousand Oaks, CA; Sage: 1999. pp. 435–464. [Google Scholar]
- Redish AD. Addiction as a computational process gone awry. Science. 2004;306:1944–1947. doi: 10.1126/science.1102384. [DOI] [PubMed] [Google Scholar]
- Redish AD, Jensen S, Johnson A. A unified framework for addiction: Vulnerabilities in the decision process. Behavioral and Brain Sciences. 2008;31:415–437. doi: 10.1017/S0140525X0800472X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruscio J. Information integration in child welfare cases: An introduction to statistical decision making. Child Maltreatment. 1998;3:143–156. [Google Scholar]
- See JE, Warm JS, Dember WN, Howe SR. Vigilance and signal detection theory: An empirical evaluation of five measures of response bias. Human Factors: The Journal of the Human Factors and Ergonomics Society. 1997;39:14–29. [Google Scholar]
- Snodgrass JG, Corwin J. Pragmatics of measuring recognition memory: Applications to dementia and amnesia. Journal of Experimental Psychology: General. 1988;117:34–50. doi: 10.1037//0096-3445.117.1.34. [DOI] [PubMed] [Google Scholar]
- Stretch V, Wixted JT. Decision rules for recognition memory confidence judgments. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1998;24:1397–1410. doi: 10.1037//0278-7393.24.6.1397. [DOI] [PubMed] [Google Scholar]
- Swets JA, Dawes RM, Monahan J. Psychological science can improve diagnostic decisions. Psychological Science in the Public Interest. 2000;1:1–26. doi: 10.1111/1529-1006.001. [DOI] [PubMed] [Google Scholar]
- Swets JA, Tanner WP, Jr, Birdsall TG. Decision processes in perception. Psychological Review. 1961;68:301–340. [PubMed] [Google Scholar]
- Tanner WP, Jr, Swets JA. A decision-making theory of visual detection. Psychological Review. 1954;61:401–409. doi: 10.1037/h0058700. [DOI] [PubMed] [Google Scholar]
- Volz KG, Gigerenzer G. Cognitive processes in decisions under risk are not the same as in decisions under uncertainty. Frontiers in Neuroscience. 2012;6 doi: 10.3389/fnins.2012.00105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiley RH. Errors, exaggeration, and deception in animal communication. In: Real LA, editor. Behavioral Mechanisms in Evolutionary Ecology. Chicago: University of Chicago Press; 1994. pp. 157–189. [Google Scholar]
- Wixted J, Stretch V. In defense of the signal detection interpretation of remember/know judgments. Psychonomic Bulletin & Review. 2004;11:616–641. doi: 10.3758/bf03196616. [DOI] [PubMed] [Google Scholar]
- Wollerman L, Wiley RH. Background noise from a natural chorus alters female discrimination of male calls in a Neotropical frog. Animal Behaviour. 2002;63:15–22. [Google Scholar]
- Wood CC. Discriminability, response bias, and phoneme categories in discrimination of voice onset time. Journal of the Acoustical Society of America. 1976;60:1381–1389. doi: 10.1121/1.381231. [DOI] [PubMed] [Google Scholar]
- Zaki J, Bolger N, Ochsner K. Unpacking the informational bases of empathic accuracy. Emotion. 2009;9:478–487. doi: 10.1037/a0016551. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.