A new finite element approach for near real‐time simulation of light propagation in locally advanced head and neck tumors

Abstract

Background and Objectives

Several clinical studies suggest that interstitial photodynamic therapy (I‐PDT) may benefit patients with locally advanced head and neck cancer (LAHNC). For I‐PDT, the therapeutic light is delivered through optical fibers inserted into the target tumor. The complex anatomy of the head and neck requires careful planning of fiber insertions. Often the fibers' location and tumor optical properties may vary from the original plan therefore pretreatment planning needs near real‐time updating to account for any changes. The purpose of this work was to develop a finite element analysis (FEA) approach for near real‐time simulation of light propagation in LAHNC.

Methods

Our previously developed FEA for modeling light propagation in skin tissue was modified to simulate light propagation from interstitial optical fibers. The modified model was validated by comparing the calculations with measurements in a phantom mimicking tumor optical properties. We investigated the impact of mesh element size and growth rate on the computation time, and defined optimal settings for the FEA. We demonstrated how the optimized FEA can be used for simulating light propagation in two cases of LAHNC amenable to I‐PDT, as proof‐of‐concept.

Results

The modified FEA was in agreement with the measurements (P = 0.0271). The optimal maximum mesh size and growth rate were 0.005–0.02 m and 2–2.5 m/m, respectively. Using these settings the computation time for simulating light propagation in LAHNC was reduced from 25.9 to 3.7 minutes in one case, and 10.1 to 4 minutes in another case. There were minor differences (1.62%, 1.13%) between the radiant exposures calculated with either mesh in both cases.

Conclusions

Our FEA approach can be used to model light propagation from diffused optical fibers in complex heterogeneous geometries representing LAHNC. There is a range of maximum element size (MES) and maximum element growth rate (MEGR) that can be used to minimize the computation time of the FEA to 4 minutes. Lasers Surg. Med. 47:60–67, 2015. © 2015 The Authors. Lasers in Surgery and Medicine Published by Wiley Periodicals, Inc.

INTRODUCTION

Presently, there is no effective treatment for patients with locally advanced head‐and‐neck cancers (LAHNC) 1, 2. These tumors fail to respond or recur subsequent to standard therapy. Palliative chemotherapy, the most common treatment option for these patients, yields objective response rates of 10–36% with median survival of approximately 6 months and low quality of life (QoL) 3, 4, 5. Re‐irradiation is still considered experimental by many, and feasible only in a limited patient population 6, 7. Salvage surgery, the only standard treatment, often requires extended hospital stay and results in poor long‐term survival rate 2. In general, these patients have poor QoL with distressing symptoms including pain, bleeding and dysphagia 8.

Photodynamic therapy (PDT) is approved for the treatment of esophageal and early stage lung cancer 9. In PDT, systemic administration of a light sensitive drug (i.e., photosensitizer, PS) is followed by illumination of the target tumor with visible light. This leads to the generation of reactive oxygen species, notably singlet oxygen, 10 and results in the destruction of the tumor by a combination of direct cellular and secondary vascular effects 11. While the response to PDT is a function of PS level, tissue oxygenation and immune response, it is well accepted that adequate light delivery is a key to successful application of PDT 9.

PDT of small, accessible tumors uses external beam illumination, while bulky tumors (as in LAHNC) require interstitial light delivery, via optical fibers, for effective illumination. Several studies and our experience suggest that interstitial photodynamic therapy (I‐PDT) is a promising therapeutic approach for these patients 12, 13, 14. While these results are encouraging, there is a need for an algorithm that can be used to plan the treatment of I‐PDT. This tool is essential to decide on the number and location of optical fibers inserted into the tumor. The treatment planning is also needed to estimate the light propagation within the entire tumor, so that the target tumor receives the prescribed light dose while adjacent normal tissue is spared.

In I‐PDT, the laser light is delivered from the diffuse tip of the optical fiber. The volume of the affected zone is defined by the length of the diffused tip of the optical fiber and the light propagation in tissue. Larger lesions in surgically inaccessible sites can be treated with interstitial therapy using multiple optical fibers inserted directly into tumors or through optically transparent catheters 13, 15.

Several studies have shown that light propagation in human tissue can be simulated by solving the diffusion equation with finite elements analysis (FEA) 16, 17, 18, 19, 20, 21, 22, 23, 24. FEA has been used for pretreatment planning of light delivery for I‐PDT in homogenous structures such as the human prostate 16, 17, 18, 25, 26. This technique yields a quantitative map of the light transport within the tumor, which can be used to calculate the distribution of the irradiance and radiant exposure. Our group developed a FEA code with commercial software (Comsol Inc., Burlington, MA) to model and study laser‐tissue interaction for the treatment of heterogeneous superficial benign lesions with sub‐millimeter spatial resolution 19, 20, 21, 22, 23, 24. These were 2‐D models representing skin cross sectional structure. The complex anatomy of head and neck patients with LAHNC requires FEA in 3D. In these cases, the size of the computer model (a few GB) requires the use of high‐end hardware, and the computation time becomes an issue, in particular for I‐PDT when the planning may need to change according to the optical properties of the tumor and the actual location of the laser fibers. In this circumstance, a rerun of the simulation must be completed within minutes while the patient is under general anesthesia being prepared for I‐PDT.

In this paper, we report how our custom code of FEA has been modified to simulate light propagation in LAHNC in near real‐time. We took a three‐step approach. In the first step, we tested the validity of the modified model in a phantom that mimics the optical properties of human tumors. In the second step, we investigated methods to optimize the FEA settings for minimizing the computation time. In the third step, we demonstrated how the optimized FEA settings are used to simulate light propagation in geometries that accurately replicate LAHNC in patients that are amenable for I‐PDT.

MATERIALS AND METHODS

Mathematical Model

A detailed description of the mathematical model and basic assumptions is given in Shafirstein et al. 20. In this approach, the time‐dependent diffusion equation is derived from the equation for radiative transfer, 27, 28 and is given by:

$$\frac{1}{{\mathit{c}}_{\mathit{n}}}\left(\frac{\mathit{\partial }}{\mathit{\partial }\mathit{t}}\mathrm{\Phi }(\mathit{x}\mathit{,}\mathit{y}\mathit{,}\mathit{z}\mathit{,}\mathit{t})-\nabla \left({\mathit{\alpha }}^{\mathit{n}}\nabla \mathrm{\Phi }(\mathit{x}\mathit{,}\mathit{y}\mathit{,}\mathit{z}\mathit{,}\mathit{t})\right)\right)=-{\mathit{\mu }}_{\mathit{\alpha }}^{\mathit{n}}\mathrm{\Phi }(\mathit{x}\mathit{,}\mathit{y}\mathit{,}\mathit{z}\mathit{,}\mathit{t})$$ (1)

where

$${\mathit{\alpha }}^{\mathit{n}}={\mathit{c}}_{\mathit{n}}·{\left[3({\mathit{\mu }}_{\mathit{\alpha }}^{\mathit{n}}+(1-\mathit{g}){\mathit{\mu }}_{\mathit{s}}^{\mathit{n}})\right]}^{-1}$$

$\mathrm{\Phi }(\mathit{x}\mathit{,}\mathit{y}\mathit{,}\mathit{z}\mathit{,}\mathit{t})$ is the photon flux (Pn/m²/s), where P _n is the number of photons, α ⁿ is the optical diffusion coefficient (m²/s) of tissue n, ${\mathit{\mu }}_{\mathit{\alpha }}^{\mathit{n}}$ and ${\mathit{\mu }}_{\mathit{s}}^{\mathit{n}}$ are the linear absorption and scattering coefficients (1/m) of tissue n, g is the optical anisotropy factor, and c_n is the speed of light in tissue n. The right‐hand side of equation 1 represents the rate that the photons are absorbed in a unit volume (Pn/m³/second). The laser light is delivered from a diffuse tip of an optical fiber that is placed within a closed‐end catheter. Therefore, Neumann boundary conditions can be used for a flux of diffused photons emitted from the inside surface of the catheter, and is given by:

$$\frac{{\mathit{P}}_{\mathit{l}\mathit{a}\mathit{s}\mathit{e}\mathit{r}}{\mathit{c}}_{\mathit{o}}}{\left({\mathit{h}}_{\mathit{p}}{\mathit{v}}_{\mathit{l}}\right)}=-{\mathit{\alpha }}^{\mathit{n}}\nabla \mathrm{\Phi }(\mathit{x},\mathit{y},\mathit{z},\mathit{t})$$ (2)

P _laser is the laser irradiance (W/m²), c ₀ is the speed of light in a vacuum, 3 × 10⁸ m/second, and h_p is Planck's constant (6.6260957 × 10⁻³⁴ J/second). v_l is the laser light frequency (1/second) defined as c ₀ divided by λ (the wavelength of the laser light). The boundary condition for the absorption and scattering at the most outer surface of the FE model is given by:

$${\mathit{c}}_{\mathit{n}}\mathrm{\Phi }(\mathit{x},\mathit{y},\mathit{z},\mathit{t})=-{\mathit{\alpha }}^{\mathit{n}}\nabla \mathrm{\Phi }(\mathit{x},\mathit{y},\mathit{z},\mathit{t})$$ (3)

The initial condition is:

$$\mathrm{\Phi }(\mathit{x},\mathit{y},\mathit{z},\mathit{t})=\frac{{\mathit{p}}_{\mathit{b}\mathit{g}}}{{\mathit{h}}_{\mathit{p}}{\mathit{v}}_{\mathit{l}}}$$ (4)

P_bg, W/m², is the irradiance of the background light radiation (e.g., daylight). It is assumed that the initial distribution of photons in the tissue results from visible daylight. The optical properties, P_bg, and laser parameters are detailed in Table 1. The FEAs were conducted with Comsol 4.4 (Comsol Inc., Burlington, MA). A high performance desktop computer (HPC, TwrX, Silicon Mechanics, Bothell, WA) was used to run all the simulations.

Table 1.

Parameters for Computing Light Propagation in Phantom

Input	Description
λ = 630 (nm)	Free‐space wavelength
µa = 4.07 (1/m)	Linear absorption coefficient
µs = 2500 (1/m)	Linear scattering coefficient
g = 0.8	Optical anisotropy factor
n = 1.37	Tissue refractive index
Pbg = 10‐6 (W/m2)	Background irradiance
Psource = 100 (mW/cm)	Laser fiber irradiance per cm length of diffuser

Mesh Optimization

The objective of this part of the study was to define mesh settings that would minimize computation time while preserving the accuracy of the computed results. A mesh with small elements (fine mesh) not only increases the accuracy of the FEA, but also increases the number of elements (mesh size) and computation time. Two factors that affect the mesh size are the maximum element growth rate (MEGR) and maximum element size (MES). The MEGR (in units of length/length) determines the characteristic length of a mesh transition from small to larger elements. The MES represents the largest edge length of the elements in the mesh. For both MES and MEGR, a small value leads to a finer mesh, which results in a longer computation time. A parametric study was conducted to investigate the relationship of MEGR and MES with mesh size, computation time and accuracy. Eighteen values in the range of 1.5–3.0 were selected for the MEGR while twelve values in the range of 0.00246–0.0211 m were selected for the MES. The Comsol mesh generator was used to create a tetrahedral mesh with the various MES and MEGR settings. The test geometry (shown in Fig. 1) was identical for all of these simulations. This geometry represents the phantom study described in the section below. In each simulation, the computation time was calculated by using the computer internal clock. The computed radiant exposure was compared with measurements that were done in a phantom, as described below.

Figure 1.

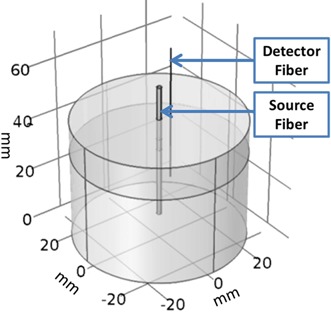
The 3‐D model created in COMSOL used for finite element analysis of the phantom experiment. The source optical fiber (0.98 mm diameter) is at the center, and the detection fiber (0.2 mm in diameter) is off the center.

Phantom Study

The phantom was made from a 100 ml liquid of distilled water with 2.5 uM of ferrous stabilized hemoglobin A₀ (Sigma–Aldrich Co LLC, St. Louis, MO) and 0.195% by volume of 1‐μm nominal size Polybead polystyrene microspheres (Polysciences, Inc., Warrington, PA). This composition results in a phantom with a linear absorption coefficient of 4.07 m⁻¹ and a reduced scattering coefficient of 500–m⁻¹ at a wavelength of 630 nm. The phantom was placed in a well that is made of black Delrin (Fig. 2). The dimensions of the well were: 6.35 cm diameter and 4.5 cm deep. The top of the well was covered with an opaque template that includes a grid of channels through which catheters can be inserted. In one catheter, we placed a 0.98 mm diameter optical fiber with a 3 cm cylindrical light diffuser (RD30, Medlight S.A., Ecublens, Switzerland). This optical fiber was connected to a tunable Argon laser pumping a dye laser system (Spectra Physics 2080‐BR will pump a Coherent 599 Dye laser system manufactured by Coherent Inc., 1335 Terra Bella Avenue, Mountain View, CA). The laser was tuned to emit 630 ± 3 nm light wavelength. In the other catheter, we placed a cleaved and polished 0.2 mm diameter optical fiber. This fiber was used as a detector, and was connected to a calibrated spectrometer (USB 2000 + , Ocean Optics, Dunedin, FL). The paired detection fiber and spectrometer were calibrated with an integrating sphere and light source (Labsphere Inc., North Sutton, NH). We used this calibration procedure to generate a scaling factor that converts the photon flux into irradiance (mW/cm²). The detection fiber measured the transmitted light at distances of 10–25 mm from the laser fiber. A correction factor was applied to account for differences of the index of refraction between the measurements in the medium and the calibration in air, following the method described in Marijnissen and Star, 1996 29.

Figure 2.

The phantom experimental set‐up includes a Delrin well and tempelete. The diameter of the well is 6.35 cm and its height is 4.5 cm. The template includes channels that are spaced at 5 mm apart.

The light propagation was computed by solving equation 1 with the appropriate initial and boundary conditions (equations 2 to 4) for a geometry that represents the phantom experiment (Fig. 1). The absorbed irradiance was computed by multiplying the rate of photons absorption (right‐hand side of equation 1) with the energy of each photon. The laser settings and optical properties of the phantom are given in Table 1.

Modeling Light Propagation in Head and Neck Tumors

De‐identified computed tomography (CT) scans of LAHNC of two patients amenable to I‐PDT were used to model light propagation in head and neck tumors. This was a proof‐of‐concept evaluation of the computational methods developed in this study. The human research ethics committee at Roswell Park Cancer Institute (RPCI) approved the use of these clinical data. Typically, patients who undergo I‐PDT of head and neck cancer have locally advanced tumors that failed to respond to other forms of therapy such as chemotherapy or radiation therapy. The patients whose tumor geometries were modeled in this paper, failed to respond to standard therapies. The first patient had a recurrent locally advanced base of tongue SCC, and the second patient had a recurrent locally advanced SCC of the larynx. These patients fit the criteria for I‐PDT, due to the size and the location of their tumors. We selected a series of images of CT scans that include the head and neck region. An image visualization and analysis software package (Simpleware, Exeter, UK) was used to segment tumor, bones, adjacent normal tissues, blood vessels and other important anatomical features. The treating physician, Dr. Hassan Arshad, marked the boundaries of each tumor and margins and critical structures. The segmented scans were reconstructed to create a 3‐D model, and converted into CAD files that were imported into the FEA software. In Comsol, catheters were virtually placed into the tumor to represent the laser treatment fibers. The spacing between adjacent catheters was between 10 and 15 mm, which is typical for I‐PDT. The location and number of the catheters were based on the size and location of the target tumor. The entire geometry was meshed using fine and optimized meshes. The light propagation was computed by solving equation 1 with the appropriate initial and boundary conditions (equations 2 to 4). The laser settings and optical properties of the solid tumor are given in Table 2.

Table 2.

Parameters for Computing Light Propagation in LAHNC Tumor Models

Input Data	Description
µa = 20 (1/m)	Tissue linear absorption coefficient
µs = 2777.8 (1/m)	Tissue linear scattering coefficient
g = 0.82	Optical anisotropy factor
Psource = 400 (mW/cm)	Laser fiber irradiance per cm length of diffuser

RESULTS

Mesh Optimization and Validation in a Phantom

Figure 3A shows that the mesh size rapidly decreases as the MEGR increases from 1.3 to 2.25 m/m. Figure 3B shows that the computation time decreases as the MEGR increases from 1.3 to 2.0 m/m. The effect of the MES on the mesh size and the computation time is shown in Figure 3C and 3D, respectively. The computation time remains constant for MES in the range of 0.005–0.02 m, a modest decrease in the computation time is accomplished when the MES increases to >0.005 m. Figure 3E shows the effect of MEGR and MES on the computation time. This data suggest that the computation time can be minimized by using MES of 0.005–0.02 m and MEGR of 2.0–2.5 m/m to generate a mesh. The computed irradiance (mW/cm²) when the MES ranged from 0.005 to 0.02 m and the MEGR ranged from 2.0 to 2.5 m/m remained fairly constant with a mean of 9.23 ± 0.48 mW/cm².

Figure 3.

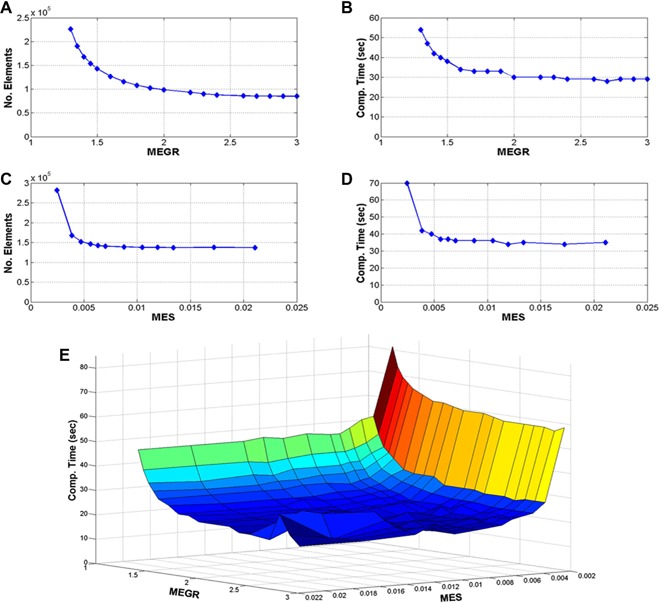
(A) The number of mesh elements as a function of maximum element growth rate (MEGR), (B) computation time as a function of MEGR, (C) number of mesh elements as a function of maximum element size (MES), (D) computation time as a function of MES, and (E) computation time as a function of MEGR and MES.

Table 3 shows a comparison between the results obtain from a fine and optimized mesh. These data show that there was no significant difference between the irradiance calculated with a fine mesh and an optimized mesh. However, the computation time was reduced from 45 to 26 seconds by increasing the MEGR from 1.4 to 2.0 m/m and the MES from 0.00387 to 0.00703 m (see Table 3). Noteworthy, these short computation times were possible because the model representing the phantom is relatively small. Importantly, these results demonstrate that by selecting an optimal MES and MEGR (shown in Fig. 3E) we can reduce the computation time by a factor of approximately two.

Table 3.

The MEGR and MES Affects Mesh Size and Computation Time

	Mesh 1 (fine mesh)	Mesh 2 (optimized mesh)
Total number of elements	164109	66151
Maximum element growth rate (MEGR)	1.4	2.0
Maximum element size (MES) for Phantom solution, m	0.00387	0.00703
Maximum element size for fibers	0.00387	0.00387
Computation time, s	45	26
Results:
Irradiance (mW/cm2) at 10 mm spacing	19.57	19.03
Irradiance (mW/cm2) at 15 mm spacing	10.02	9.48
Irradiance (mW/cm2) at 20 mm spacing	5.69	5.73
Irradiance (mW/cm2) at 25 mm spacing	3.58	3.38

Table 4 shows the calculated and measured irradiances, for 10–25 mm spacing between the source and detector. A two‐tailed heteroscedastic t‐test indicates that there was no significant difference (P = 0.0271) between the calculated and measured irradiances.

Table 4.

Calculated Versus Measured Irradiance in Phantom Irradiated With 630 nm Light

Detector – Light source spacing (mm)	Calculated irradiance (mW/cm2)	Measured irradiance (mW/cm2)
10	19.03	18.49 ± 0.011
15	9.48	10.64 ± 0.006
20	5.73	5.83 ± 0.003
25	3.38	3.34 ± 0.002

FEA of Light Propagation in LAHNC

Two geometries representing different LAHNCs are shown in Figures 4 and 5. The first tumor model includes a base of tongue SCC (Fig. 4A). The FEA suggests that eight catheters are required to illuminate the entire tumor. Optimal MES and MEGR, defined and verified in the phantom studies were used to generate the mesh shown in Figure 4B. The size of the optimized mesh was about a fifth of the fine mesh, 629,737 versus 3,186,132 elements (Table 5). The computation time with the optimized mesh was 14.3% of the time needed to simulate light propagation with a fine mesh, 3.7 minutes versus 25.9 minutes (see Table 5). There was a minor difference (1.62%) between the radiant exposures calculated with either mesh.

Figure 4.

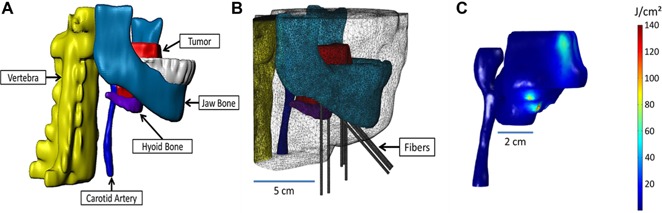
(A) The 3‐D model created using the 3‐D image data visualization, analysis, and model generation software, Simpleware. (B) The mesh created in COMSOL from the 3‐D model, including eight catheters. (C) The radiant exposure (J/cm²) calculated within the tumor and the carotid artery, for a treatment time of 250 seconds.

Figure 5.

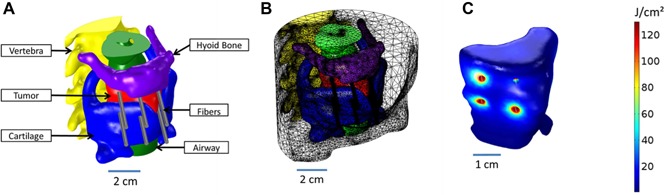
(A) The 3‐D model created using the 3‐D image data visualization, analysis, and model generation software, Simpleware. (B) The mesh created in COMSOL from the 3‐D model, including six catheters. (C) The radiant exposure (J/cm²) calculated within the tumor, for a treatment time of 250 seconds.

Table 5.

The Impact of MEGR and MES on Mesh Size and Computation Time on the Radiant Exposure Computed for Two Tumor Models of LAHNC

	Fine mesh	Optimized mesh
Tumor model 1:
Number of mesh elements	3,186,132	629,737
MEGR	1.4	2.0
MES of patient geometry	0.00716	0.01
MES of fibers	0.00716	0.00716
Computation time (minute)	25.9	3.65
Calculated radiant exposure (J)	92.5	91
Tumor model 2:
Number of mesh elements	1,505,024	602,613
MEGR	1.4	2.0
MES of patient geometry	0.00806	0.00806
MES of fibers	0.00443	0.00443
Computation time (minute)	10.1	4.0
Calculated radiant exposure (J)	44.25	43.75

The radiant exposure distribution within the target tumor and carotid artery is shown in Figure 4C. A maximum of 140 J/cm² was calculated at the surface of the catheters, for a treatment time of 250 seconds. This simulation suggests that 26% of the tumor volume received at least 48.6 J/cm², while the maximum radiant exposure absorbed in the carotid artery is no more than 0.033 J/cm².

The second tumor model represents a locally advanced laryngeal SCC (Fig. 5A). The FEA suggests that six catheters are required to illuminate this tumor. The size of the optimized mesh was just under half of the fine mesh, 602,613 versus 1,505,024 elements (Table 5). The computation time with the optimized mesh was 39.6% of the time needed to simulate light propagation with a fine mesh, 4.0 minutes versus 10.1 minutes. There was a minor difference (1.13%) between the radiant exposures calculated with either mesh.

The radiant exposure distribution is shown in Figure 5C. A maximum of 130 J/cm² was calculated at the surface of the catheters. This simulation suggests that 37.75% of this tumor received at least 50 J/cm².

DISCUSSION

In this work we demonstrated that our original FEA approach can be used to model light propagation in tumors in a complex head and neck geometry, within minutes, while providing excellent clarity for presenting fibers’ positions and light distribution in the treated region (Figs. 4 and 5). The accuracy of the modeling was validated by comparing the simulations results with experimental measurements in phantoms. The relatively simple model of the phantom was successfully used to define optimal mesh settings for the FEA to minimize the computation time.

We presented the notion of using FEA with Comsol to model light propagation in heterogeneous tissue structures several years ago 23. In that original work, we used this approach to simulate selective photothermolysis. That model was validated with animal studies and has been used to define optimal laser settings for the treatment of skin lesions 19, 20, 21, 22, 23, 24. The major new contribution reported in this paper is the optimization of FEA to complete the simulations within 4 minutes and allow clear presentation of the results in 3D.

Ultrasound or CT is used to place the interstitial fibers in LAHNC to provide precise treatment delivery of PS‐activating light. However, in practice, some optical fibers may have to be inserted proximate to the originally planned positions and, rarely, some optical fibers may be displaced prior to light delivery, leading to erroneous light delivery and under‐dosage and over‐dosage. As such, it will be necessary to rerun the FEA to simulate the light distribution in the treating tumor. In past years, it took several hours to run FEA with Comsol for such a large geometry. The use of HPC reduced the simulation time to 30–10 minutes, but that is still a long time, while the patient is in the operating room (OR) under general anesthesia. Since the mesh is the primary parameter that defines the FEA size and computation time, we investigated how MES and MEGR can be modified to reduce mesh size and computation time. Our results showed that there is a range of MEGR and MES that can be used to minimize the computation time, while maintaining the accuracy of the simulations. Our results also showed that the optimized mesh will reduce the computation time to 4 minutes, when simulating light propagation in LAHNC. Although 3–4 minutes is still not real‐time, this time maybe short enough to rerun the FEA immediately after the actual location of the fibers has been measured in the OR. The mesh size is largely dependent on the complexity of the model geometry and the number of fibers inserted into the tumor volume. Our experience suggests that the computation time will increase linearly with the number of fibers. If a specific computation time is required, the optimal range of values for MES or MEGR may need to be reevaluated.

We note that the accuracy of the FEA also depends on the actual optical properties of the target tumor and surrounding tissue. In the pretreatment planning, we use literature data. However, we may need to update the model and rerun the simulations using the actual optical properties. We can achieve that goal with using the optimized mesh as described above. We can measure the optical properties of the tumor with the use of new commercial real time optical spectroscopy device (Zenascope, Zenalux Biomedical, Durham, NC), within seconds. We have this device in our laboratory, and are testing its use for I‐PDT. Our Zenascope has been modified to measure PS concentration in real time, in collaboration with Zenalux. The results of this ongoing work are beyond the scope of this paper, and thus not reported here. It is mentioned in this discussion to highlight the potential obstacle and present a solution to accurately model light propagation in LAHNC.

It is also important to stress that accurate modelling of light distribution in I‐PDT solves only part of the problem, as the efficacy of PDT depends on PS levels, tumor oxygenation and immune response, which were not addressed here. In addition, it is essential to measure the delivered radiant exposure within the tumor with a real time light dosimetry system. We have developed and tested such a system, which was used to measure the radiant exposure in the phantom study. A detailed description of that system is also outside the scope of this paper.

CONCLUSIONS

Our FEA approach can be used to model light propagation from diffused laser fibers for I‐PDT in complex heterogeneous geometries representing LAHNC. There is a range of MES and MEGR that can be used to minimize the computation time of the FEA to less than 4 minutes. The FEA can be used to clearly present fiber locations and light distribution in 3D of LAHNC.