The US hospital standardised mortality ratio: Retrospective database study of Massachusetts hospitals

Summary

Objectives

To present a case-mix adjustment model that can be used to calculate Massachusetts hospital standardised mortality ratios and can be further adapted for other state-wide data-sets.

Design

We used binary logistic regression models to predict the probability of death and to calculate the hospital standardised mortality ratios. Independent variables were patient sociodemographic characteristics (such as age, gender) and healthcare details (such as admission source). Statistical performance was evaluated using c statistics, Brier score and the Hosmer–Lemeshow test.

Setting

Massachusetts hospitals providing care to patients over financial years 2005/6 to 2007/8.

Patients

1,073,122 patients admitted to Massachusetts hospitals corresponding to 36 hospital standardised mortality ratio diagnosis groups that account for 80% of in-hospital deaths nationally.

Main outcome measures

Adjusted in-hospital mortality rates and hospital standardised mortality ratios.

Results

The significant factors determining in-hospital mortality included age, admission type, primary diagnosis, the Charlson index and do-not-resuscitate status. The Massachusetts hospital standardised mortality ratios for acute (non-specialist) hospitals ranged from 60.3 (95% confidence limits 52.7–68.6) to 130.3 (116.1–145.8). The reference standard hospital standardised mortality ratio is 100 with the values below and above 100 suggesting either random or special cause variation. The model was characterised by excellent discrimination (c statistic 0.87), high accuracy (Brier statistics 0.03) and close agreement between predicted and observed mortality rates.

Conclusions

We have developed a case-mix model to give insight into mortality rates for patients served by hospitals in Massachusetts. Our analysis indicates that this technique would be applicable and relevant to Massachusetts hospital care as well as to other US hospitals.

Introduction

The hospital standardised mortality ratio (HSMR) is an indicator derived from administrative databases and used to assess adjusted in-hospital mortality.¹ Since 2001, in England, HSMRs have been published annually by Imperial College and Dr Foster Intelligence and on the NHS Choices website^2,3 since April 2009. They have also been published in Denmark, Canada, Scotland and Wales. In England a simplified methodology, i.e. the standardised hospital mortality indicator, has been developed by a group of experts to help hospitals understand the trends associated with patient deaths.⁴ Although subject to debate,^4,5 in UK the HSMRs have correctly indicated real and major quality of care issues.^5,6 For some years the HSMR has been calculated for the USA, the Netherlands, Canada, Sweden, Australia (New South Wales), France, Japan, Hong Kong, Wales and Singapore. While the HSMR calculation relies on a clearly defined approach, the overall methodology varies to some extent from country to country taking into account factors such as the structure of the healthcare delivery or the availability of information within the administrative hospital databases. Within this article we describe the methodology used for Massachusetts and we refer to this as Massachusetts HSMR. The paper makes use of a state database as a practical example for the calculation. The HSMR is equal to the ratio of actual deaths to expected deaths multiplied by 100, for the diagnoses leading to 80% of all in-hospital deaths nationally.¹ The reference standard HSMR is 100 with the values below and above 100 suggesting either random or special cause variation. Issues with its construction such as choice of numerator and denominator are discussed in more detail elsewhere.⁷

Patient level admission data provided by the Agency for Healthcare Research and Quality and Centers for Medicare and Medicaid Services have been used by Professor Jarman since 2001 in the USA working in conjunction with the Institute for Healthcare Improvement Boston and, for some years, in the UK by Imperial College.⁸ HSMRs are currently calculated monthly for 263 US hospitals. The development of the US HSMRs, carried out in a manner similar to that used in England, has been used by hospitals as a tool to understand their organisational performance with regard to adjusted hospital death rates.^8,9

One important feature of the US healthcare system is the variation of adjusted hospital death rates.¹⁰ In the context of monitoring standards of clinical care, the concept of US hospital mortality data integrated into reports made publicly available has drawn interest from the Massachusetts Health Care Quality and Cost Council.¹¹ The aim of this article is to present a risk adjustment model that can be used to calculate Massachusetts HSMRs and could be further adapted for other less-rich state-wide data-sets. The paper describes the Massachusetts HSMR model and its statistical performance, as well as the variation of HSMRs throughout Massachusetts.

Methods

We used an administrative data-set provided by the Division of Health Care Finance and Policy, Boston, Massachusetts. The data-set covers records for 2,529,268 patients discharged from all 81 Massachusetts hospitals between 1 October 2005 and 30 September 2008 and includes patient demographic and clinical characteristics (e.g. age, gender, discharge diagnoses (ICD-9)) as well as healthcare details (e.g. type of admission, payer type, surgical procedure codes).¹²

The primary diagnosis codes were allocated to the Agency for Healthcare Research and Quality’s 259 Clinical Classification Software groups and corresponding subgroups using a look-up file.¹³ From these Clinical Classifications Software groups we used only the top 36 diagnostic groups that led to 80% of in-hospital deaths nationally (national estimates based on the Agency for Healthcare Research and Quality 2004 data-set). In England we have compared HSMRs based on admissions leading to 80% of hospital deaths with those based on all admissions and found excellent agreement at hospital level, correlation coefficient r = 0.98. The secondary diagnosis codes were used to derive the Charlson index of co-morbidity using the ‘enhanced ICD9-CM’ version.^14,15 Two deprivation deciles were derived and attached to each patient via their zip code: proportion earning less than $10,000 and the median household income¹⁶ and the analyses were done with and without these variables. We excluded from the analysis patients with unknown or missing information for age or gender (overall <0.01% of records).

The dependent variable was defined as death in hospital at any time during a patient’s stay in hospital. The independent variables considered for inclusion in the models have been selected using factors available in the state database, based on clinical expertise and statistical modelling. Patient characteristics of age (five-year bands), sex, race (White, Black, Asian, other), deprivation, veteran status, do-not-resuscitate (DNR) status, admission source (e.g. emergency room transfer, direct physician referral), admission type (e.g. emergency, urgent and elective), payer type (e.g. self-pay, Medicaid, Medicare), Charlson co-morbidity index, Clinical Classifications Software subgroup, month and year of discharge have been made appropriately categorical and included in the regression.

We applied SAS’s inbuilt backwards elimination procedure for variable selection for each Clinical Classifications Software group model separately and we used a cut-off of p < 0.1 to minimise the risk of excluding potentially important variables that might have been significant with a larger sample.

The binary logistic regression models across the Clinical Classifications Software groups give an expected probability of death for each patient. The sum of the actual deaths was compared with the sum of expected deaths by taking the ratio observed/expected deaths and multiplying by 100 to give the HSMR. The HSMR values were plotted against the expected deaths for each hospital within a control chart. Upper and lower 99.8% control limits were superimposed to form the ‘funnel’ around the benchmark (by definition 100) and to determine outliers.¹⁷ We calculated three measures of model performance: area under the receiver operating characteristics curve or c statistic, Brier score and Hosmer–Lemeshow test.^18–20 C statistics show how well the model can discriminate between those who die and those who survive; a c-statistic of 0.5 indicates that the model is useless in predicting deaths and a value of 1.0 suggests perfect discrimination. We calibrated the model by plotting the total observed and predicted number of deaths by deciles of risk. The Hosmer–Lemeshow test is often used for this.²¹ Brier scores have been calculated as a measure of both calibration and goodness of fit. Brier scores vary between 0 and 1, a lower score indicating higher accuracy. For the overall model when summed across all included Clinical Classifications Software groups, we calculated an overall c statistic and Brier score. Data manipulation and analysis were performed using SAS (v9.1).

Results

The database selected for the Massachusetts HSMR calculation comprised 36 Clinical Classifications Software groups representing 42.4% of the total admissions and 81.4% of the total deaths for the three years combined. The database included 42,536 deaths from 1,073,122 admissions (a case fatality rate of 3.96%) reported by 73 (out of 81) Massachusetts hospitals. The study population was heterogeneous with respect to sociodemographic and healthcare details. Selected characteristics include average age 52.3 years (standard deviation 32.6), 50.1% male, 79.4% white ethnic background and 53.0% emergency admissions. The Charlson co-morbidity index was 0 for 47.4% of the patients. Almost 40% of the patients were admitted through emergency room transfer; Medicare patients represented half of the total number of admissions. The average length of stay was 5.1 days (standard deviation 6.8). Major diagnosis groups were liveborn (21.6%), pneumonia, except that caused by tuberculosis or sexually transmitted diseases (7.4%) and congestive heart failure, non-hypertensive (6.7%).

Table 1 presents the number of admissions and deaths by Clinical Classifications Software group used in calculating the Massachusetts HSMRs. The data show that observed in-hospital mortality per Clinical Classifications Software group ranges between 47.2% for cardiac arrest and ventricular fibrillation to 0.25% for the liveborn group. Table 1 also shows that the number of retained variables varies from 14 (i.e. all variables included in the model) for septicaemia to a minimum of 4 for pulmonary heart disease. Of note, the most commonly included variables were do-not-resuscitate status (always included), age and the Charlson index (both included in all but the liveborn group) and the source of admission (included 33 times). Adjustment was less commonly made (under one-third of the models) for the deprivation variables (data not shown). The c statistics of the Massachusetts HSMRs range across the Clinical Classifications Software groups from 0.678 to 0.86 (the overall c statistic was 0.87). The Brier statistics range across Clinical Classifications Software groups from 0.004 to 0.21 (the overall Brier statistic was 0.03).

Table 1.

Descriptive statistics of mortality by Clinical Classifications Software group; number of relevant variables and performance metrics for the prediction models, Massachusetts financial years 2005–2007.

CCS no	CCS group name	Deaths	Admissions	Observed in-hospital mortality %	Number of variables selected in the model	Model performance
						C statistics	Brier score
2	Septicaemia (except in labour)	6312	27,241	23.17	14	0.728	0.157
5	HIV infection	228	4198	5.43	5	0.735	0.046
14	Cancer of colon	303	7816	3.88	8	0.825	0.033
17	Cancer of pancreas	321	2899	11.07	8	0.748	0.090
19	Cancer of bronchus, lung	1395	12,336	11.31	10	0.789	0.088
38	Non-Hodgkin’s lymphoma	356	3709	9.60	8	0.747	0.078
39	Leukaemia	487	3235	15.05	6	0.706	0.119
42	Secondary malignancies	2152	22,380	9.62	11	0.743	0.080
50	Diabetes mellitus with complications	222	26,808	0.83	6	0.835	0.008
55	Fluid and electrolyte disorders	567	38,110	1.49	10	0.825	0.014
99	Hypertension with complications and secondary hypertension	224	9292	2.41	10	0.825	0.021
100	Acute myocardial infarction	2956	47,782	6.19	9	0.736	0.055
101	Coronary atherosclerosis and other heart disease	239	55,147	0.43	6	0.76	0.004
103	Pulmonary heart disease	480	10,549	4.55	4	0.735	0.041
106	Cardiac dysrhythmias	489	50,537	0.97	9	0.823	0.009
107	Cardiac arrest and ventricular fibrillation	539	1141	47.24	6	0.726	0.210
108	Congestive heart failure, non-hypertensive	2625	71,953	3.65	11	0.704	0.034
109	Acute cerebrovascular disease	3634	32,554	11.16	12	0.77	0.088
114	Peripheral and visceral atherosclerosis	651	15,179	4.29	11	0.855	0.036
115	Aortic, peripheral and visceral artery aneurysms	560	6892	8.13	11	0.864	0.057
122	Pneumonia (except that caused by tuberculosis or STDs)	3226	79,890	4.04	11	0.766	0.037
127	Chronic obstructive pulmonary disease and bronchiectasis	706	39,807	1.77	12	0.741	0.016
129	Aspiration pneumonitis, food/vomitus	2280	16,688	13.66	9	0.676	0.111
131	Respiratory failure, insufficiency,  arrest (adult)	3590	17,047	21.06	11	0.719	0.149
145	Intestinal obstruction without hernia	514	20,617	2.49	9	0.827	0.022
150	Liver disease, alcohol related	466	5418	8.60	8	0.767	0.071
151	Other liver diseases	632	8651	7.31	9	0.752	0.062
153	Gastrointestinal haemorrhage	634	22,170	2.86	7	0.764	0.026
157	Acute and unspecified renal failure	1730	27,070	6.39	11	0.733	0.056
159	Urinary tract infections	358	36,486	0.98	9	0.791	0.009
218	Liveborn	593	232,659	0.25	8	0.7	0.002
226	Fracture of neck of femur (hip)	630	20,455	3.08	7	0.749	0.028
233	Intracranial injury	1050	11,465	9.16	9	0.749	0.076
234	Crushing injury or internal injury	190	6353	2.99	7	0.755	0.028
237	Complication of device, implant or graft	738	42,692	1.73	10	0.804	0.016
238	Complications of surgical procedures or medical care	459	35,896	1.28	9	0.823	0.012

CCS: Clinical Classifications Software.

Figure 1 graphically displays calibration. The Hosmer–Lemeshow test demonstrates close agreement between predicted and observed mortality rates across deciles of risk subgroups with a tendency to overestimate the risk in the lowest and highest groups.

Figure 1.

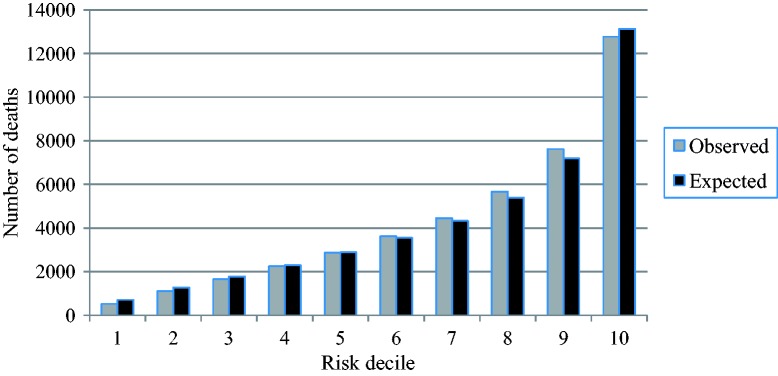
The hospital standardised mortality ratio model calibration: observed and expected deaths across 10 risk interval.

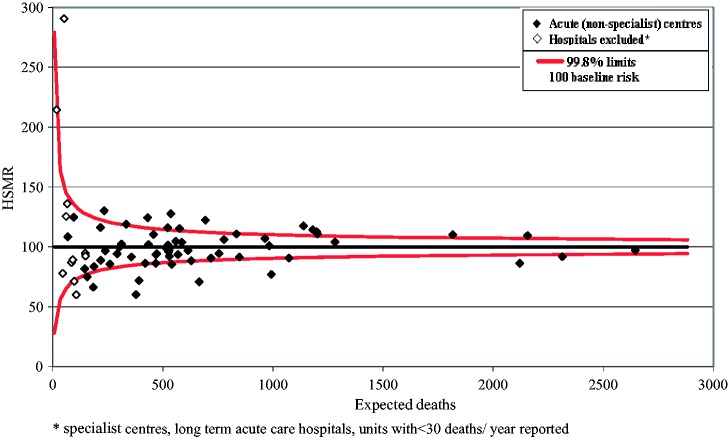
Figure 2 presents the Massachusetts HSMRs for the whole three-year period, 2005–2008. Of the 73 hospitals, two hospitals – with just one reported death overall – have been excluded from the comparison of HSMRs. Of the 71 remaining hospitals in the data-set, all but two hospitals had HSMRs between 50 and 150. The funnel plot shows that the majority of HSMRs were ‘in control’, i.e. within 99.8% control limits. Figure 2 differentiates the HSMRs for the 60 acute, non-specialist hospitals compared with the other 13 reporting hospitals, i.e. specialist or long-term acute care hospitals and units reporting less than 30 deaths per year on average. The HSMRs for acute (non-specialist) units range between 60.3 (95% control limits 52.7–68.6) and 130.3 (116.1–145.8).

Figure 2.

The hospital standardised mortality ratio with 99.8% control limits, Massachusetts financial years 2005–2007.

Discussion

The paper presents Massachusetts HSMRs calculated in a manner similar to that used in England and other countries. A total of 36 Clinical Classifications Software groups accounted for 80% of in-hospital deaths nationally and 81% in this data-set. The significant factors determining in-hospital mortality included do-not-resuscitate status, age, the Charlson index as well as year and the payer type. Previous research undertaken on US hospital discharge data showed the top factors explaining variation in HSMRs include, apart from the characteristics of admitted patients, also factors such as the percentage of Medicare deaths occurring in hospitals and the percentage of discharges to short-term hospitals, skilled nursing facilities or intermediate care facilities.⁹ In this study, due to time and logistical constraints (i.e. analysis undertaken at the request of the Massachusetts Division of Health Care Finance & Policy, within a limited three-week time frame) we decided not to adjust for contextual factors. Furthermore, within any further analysis we would consider adjustment for hospital and environmental factors that are significantly correlated with the outcome and outside of the control of the hospital, using multilevel modelling if appropriate.²²

We have used the conventional binary logistic regression modelling to calculate Massachusetts HSMRs, an approach that ignores clustering of patients within hospitals. The clustering may be handled using generalised estimated equations or multilevel models. However, since we compare performance between hospitals, use of these models will remove most of the variation between hospitals and therefore might not be useful to performance comparison. In our experience with hospital data, multilevel modelling generally has very little effect on the coefficients (i.e. the correlation coefficient of observed per expected death ratios obtained from logistic and multilevel modelling was r = 0.992).²²

The Massachusetts model has demonstrated good statistical performance. The overall c statistic was 0.87 suggesting excellent discrimination. Similar values have been shown in other countries, for example for the Dutch HSMR over 2005–2007 the value was 0.91.²³ Of note, the paper presenting Dutch HSMR corrects mortality for length of stay also, a factor sometimes considered to lead to overadjustment and consequently to increase model performance: addition of the length of stay in our model would increase the overall c statistic to 0.89. The overall Brier statistic was 0.03, i.e. high accuracy of predicted probabilities. Although there was some slight overestimation of risk for patients at the lowest and the highest groups, which is perhaps to be expected with administrative data, there appears to be close agreement between observed and predicted numbers, and therefore good fit.

Within the category of acute (non-specialist) centres, there was some variation between Massachusetts hospitals as expressed by the HSMRs for the whole three-year period. After adjusting for the independent variables, the highest HSMR was 2.2 times the lowest HSMR. The results from Massachusetts show similar levels of variation in in-hospital mortality to those in England.^1,24 Moreover, research using Dutch hospital data shows a 1.8/2.3 times higher HSMR between highest and lowest hospital scores, using data from 2003–2005/2005–2007 time period.²³ In this context, it is noteworthy the HSMRs are published in the UK and Canada for acute non-specialist hospitals only.^2,25 HSMRs are not appropriate for publication for specialist and community hospitals, although they may still be useful to a hospital, for instance for information on trends of hospital adjusted death rates. Moreover, hospitals reporting less than 30 deaths per year are also likely to be subject to random variation. We also decided to present HSMRs by hospital type, i.e. acute, non-specialist centres and the other hospitals, the results from the latter two being interpreted with extreme caution. The latter hospitals had the largest proportions of large deviance residuals from the regression models, suggesting that our model did not predict risk as well for these hospitals as for the others. We would recommend that any published US HSMRs include only acute non-specialist hospitals reporting over 30 deaths per year for the HSMR diagnoses.

We included as covariates socioeconomic variables, payer type and race as a proxy for different risk profiles not directly available within the data, i.e. different socioeconomic groups have different risk profiles in terms of smoking, obesity and other lifestyle factors. Previous work with US data (Agency for Healthcare Research and Quality data) has found death rates varied significantly by these variables. It has been argued that risk adjustment for these factors is inappropriate, i.e. adjusting out disparities and limiting the initiative of health plans to implement disparity-reducing programmes.²⁶ Nevertheless, acknowledging the potential for overadjustment, it could be argued that the adjustment is justified by the lack of any lifestyle data on individual patients. However, because the case-mix of patients already reflects to some extent sociodemographic characteristics, socioeconomic status had only a very small additional effect on the model: the correlation between HSMR with and without socioeconomic factors was 0.998.

We included the do-not-resuscitate covariate as a powerful predictor of mortality. However, it became clear following our analysis that some hospitals make little use of this variable, and that patients could potentially be labelled with a do-not-resuscitate flag as a consequence of adverse events or poor quality care. Until this variable is more consistently recorded, we would suggest that it is not appropriate for future models. It was our decision to keep all palliative care patients although coding issues are well known to be associated with this factor.²⁶ In the United Kingdom we do include palliative care as one of the variables in the standardised mortality ratio. However, the country context is different in the US, and with any further analysis we would recommend further sensitivity analyses, and a refinement of the definition of palliative care so that patients inappropriately coded as palliative care are excluded and only patients admitted with a prior intention to treat palliatively are included.²⁷

To calculate the co-morbidity variable we used Charlson index ‘enhanced ICD9-CM’ version¹⁵ partially justified by the fact that this index covers a ‘conservative’ list of codes, being designed for databases without present-on-admission flags. Present-on-admission is an indicator intended to distinguish between conditions present at the time the order for inpatient admission occurs (co-morbidity) and those developing during the hospitalisation (complication). Within the Massachusetts database, the completeness of the present-on-admission variable was poor and therefore we did not use the flags. However, we do not exclude the possibility that, given an improved quality of this variable, other coding algorithms for defining co-morbidity may perform better.²⁸

Finally, some other methodological considerations are important regarding the Massachusetts HSMR calculation. Firstly, we used all admissions rather than just one per patient in a year for two principal reasons: in surveillance context of continuous monitoring the record linkage required is cumbersome and each admission represents an opportunity for the patient’s life to be saved. Secondly, within this study, as we were not supplied with information on out-of-hospital deaths, we were not able to account for these. Our experience with calculating 30-day HSMRs in the UK shows that they differ little from the inpatient HSMRs (r = 0.92 Scottish hospital data 2000/1 to 2002/3).²⁹ However, the greater use of different forms of intermediate care (between home and hospital) in the US may mean that 30-day mortalities differ from the in-hospital mortalities more than in the UK. Consequently, we recommend use of the 30-day mortality data as an additional analysis for any further calculations of Massachusetts HSMRs if the record linkage information is available. Thirdly, with regard to the standard practice that involves model fitting of dividing the data-sets into a ‘training’ and a ‘testing’ part, within a previous analysis we have found almost identical model performance in the two parts and did not do this here.³⁰

Conclusions

The paper presents a methodology to measure standardised mortality for in-hospital deaths in the Massachusetts hospital discharge database. The case-mix models have been further developed to incorporate local variables, and were individually tailored for each diagnosis group, allowing easy analysis of the component diagnosis making up the HSMR. Our analysis indicates that this technique would be applicable and relevant to the Massachusetts hospital discharge data as well as to other similar US state-wide inpatient data that have the variables used for the Massachusetts analysis.

Declarations

Competing interests

None declared

Funding

The authors are funded by research grants from the Rx Foundation, Boston, Massachusetts and from Dr Foster Intelligence. The Dr Foster Unit at Imperial is largely funded by a research grant from Dr Foster Intelligence (an independent health service research organisation) and is affiliated with the Centre for Patient Safety and Service Quality at Imperial College Healthcare NHS Trust, funded by the National Institute for Health Research. We are grateful for support from the NIHR Biomedical Research Centre funding scheme.

Ethical approval

We have permission from the NIGB under Section 251 of the NHS Act 2006 (formerly Section 60 approval from the Patient Information Advisory Group) to hold confidential data and analyse them for research purposes. We have approval to use them for research and measuring quality of delivery of healthcare, from the South East Ethics Research Committee.

Guarantor

PA

Contributorship

All authors have been involved in the study design, analysis and manuscript revision. All authors contributed with final writing and editing.

Acknowledgements

The authors wish to thank the support of the Dr Foster Intelligence (an independent health service research organisation) and Rx Foundation of Cambridge, Massachusetts, USA for the financial support of this project through research grants. The Dr Foster Unit at Imperial is affiliated with the Centre for Patient Safety and Service Quality at Imperial College Healthcare NHS Trust which is funded by the National Institute for Health Research.

Provenance

Not commissioned; peer-reviewed by Omar Bouamra