Phaseguide-assisted blood separation microfluidic device for point-of-care applications

Abstract

We propose a blood separation microfluidic device suitable for point-of-care (POC) applications. By utilizing the high gas permeability of polydimethylsiloxane (PDMS) and phaseguide structures, a simple blood separation device is presented. The device consists of two main parts. A separation chamber with the phaseguide structures, where a sample inlet, a tape-sealed outlet, and a dead-end ring channel are connected, and pneumatic chambers, in which manually operating syringes are plugged. The separation chamber and pneumatic chambers are isolated by a thin PDMS wall. By manually pulling out the plunger of the syringe, a negative pressure is instantaneously generated inside the pneumatic chamber. Due to the gas diffusion from the separation chamber to the neighboring pneumatic chamber through the thin permeable PDMS wall, low pressure can be generated, and then the whole blood at the sample inlets starts to be drawn into the separation chamber and separated through the phaseguide structures. Reversely, after removing the tape at the outlet and manually pushing in the plunger of the syringe, a positive pressure will be created which will cause the air to diffuse back into the ring channel, and therefore allow the separated plasma to be recovered at the outlet on demand. In this paper, we focused on the study of the plasma separation and associated design parameters, such as the PDMS wall thickness, the air permeable overlap area between the separation and pneumatic chambers, and the geometry of the phaseguides. The device required only 2 μl of whole blood but yielding approximately 0.38 μl of separated plasma within 12 min. Without any of the requirements of sophisticated equipment or dilution techniques, we can not only separate the plasma from the whole blood for on-chip analysis but also can push out only the separated plasma to the outlet for off-chip analysis.

I. INTRODUCTION

Blood tests have been one of the most widely used clinical test methods¹ because blood, being composed of blood cells and plasma, provides key information about the human body. But at present, most blood tests are performed using plasma or blood serum, as blood cells may provide a great level of noise, even falsifying the results of a biochemical tests.² Therefore, the separation of plasma from whole blood is always the first step for further blood analysis. However, by traditional methods, not only does it require a large volume of the blood sample, but it also takes a long time and the separation process may result in the breaking of the blood cells and in return introducing unnecessary noise in the system.^1–4

Meanwhile, the advent of microfluidic devices provides a promising way to overcome these limitations.⁵ One approach is to employ active separation forces such as centrifugation,^6–8 magnetophoresis,⁹ dielectrophoresis (DEP),¹⁰ and acoustic standing waves¹¹ to selectively separate blood cells from plasma. For these kinds of methods, the blood samples usually need to be diluted either off chip or on chip. Moreover, the active separation forces can damage the blood cells. Also in order to apply the separating force, complicated mechanisms and an external power supply are often needed, which are usually not suitable for point-of-care (POC) applications. Another approach adopts methods without active separation forces and instead uses the inertia force or filtering system. In order to realize all the benefits of the inertia force, as in the Zweifach-Fung effect^12–14 or pinch flow effect,¹⁵ the microfluidic channel usually needs to be long, narrow and have a high flow rate. For filtering, a filtration unit such as membranes,^14,16 microparicles,¹⁷ and/or micropillars^14,16,18 are required. Oftentimes, these filtration units will cause clogging of the blood cells resulting in a high percentage of damaged cells. Thus, this approach is also not very suitable for POC applications. Similarly, microfluidic devices based on spiral inertial mechanism for blood separation are able to separate plasma in a continuous fashion with high throughput. Since this kind of methods usually needs diluted blood and syringe pumps, it may not be suitable for the point-of-care applications.¹⁹

In order to realize a blood separation device capable for POC applications, two issues need to be addressed: The first one is pumping without sophisticated equipment, or in other words, how to make the blood sample flow passively; the second one is separation, or how to separate plasma from blood cells passively. One of the most commonly used methods for blood separation is through the capillary effect. Recently, Lee and Ahn²⁰ proposed a new approach to blood separation by employing asymmetric capillary forces. By coating the whole channel surface with multiple layers of nanoparticles, they make it hydrophilic with the exception of the middle part of the channel, which is still hydrophobic. By adjusting the length of the uncoated part of the channel, they successfully separated up to 100 nl of plasma from 3 μl of whole blood. The main disadvantages of this method is that it requires partially changing the property of the channel surface and also that the percentage of plasma separated from whole blood is relatively small and limited. However, even with these disadvantages, this method is quite suitable for point-of-care applications. Similar limitations are applicable to the paper-based devices.²¹ Recently, a microfluidic device employing contactless positive DEP force (cDEP) was proposed to separate plasma from whole blood.²² By applying an AC voltage (1 v, 1 MHz) to the top electrode of the channel, 69.8% of plasma with a purity of 89.4% was separated from whole blood in around 30 min. Here, the plasma separation efficiency was defined as the ratio between the actual percentage of plasma separated in the device and the initial plasma percentage (1- Hct, where Hct stands for haematocrit of the whole blood sample, which was detected in the lab by a conventional method). Because low voltage was employed, hemolysis could be avoided. But AC voltage of high frequency is needed, which may need extra components and external power source. Another approach is pumping by the use of degassed polydimethylsiloxane (PDMS) and plasma extraction using sedimentation in trenches. By exploring the degassed PDMS^23,24 and the sedimentation,^2,25 Lee et al.²⁶ showed a vacuum-packaged microfluidic device that can be used for blood separation. However, in order to utilize the sedimentation in microfluidic devices, they need to fabricate a large trench hole to trap the blood cell, which will waste a lot of blood samples in order to fill the trench. Once the degassed PDMS is exposed to air, its pumping ability will decay quickly with time, which may cause separation failure if the blood sample is not timely loaded. Also, due to the design of dead-end channels, no methods are available to retrieve the extracted plasma from the device for additional off-chip analysis.

Herein, we propose a novel blood separation microfluidic device to meet the requirements of POC applications but avoiding the disadvantages mentioned above (Fig. 1(a)). In terms of the pumping technique, we employed a syringe-assisted micropumping method based on our previous work.²⁷ This pumping method is extremely suitable for POC applications because it is only assisted by manual syringes, without pre-evacuating the whole PDMS device in a bulky vacuum chamber. The manual operation of the hand-held syringes allowed air to diffuse through the air permeable thin PDMS wall from or into the dead-end channel, in order to drive the fluid in the dead-end channel. This pumping method was bidirectional, recurrent, tuneable, and on-demand, compared with that of the degassed PDMS or the capillary effect. In terms of blood separation, we have adopted the sediment separation method which only requires a gravity field. Moreover, in our approach, instead of using a large trench hole, we demonstrated that with the help of a modified phaseguide-structure, we could extract around 0.38 μl of plasma from only 2 μl of whole blood. Due to the phaseguides, we can not only separate plasma from the whole blood but also collect the separated plasma at outlets for further off-chip analysis. Phaseguides were initially introduced by Vulto et al.²⁸ to manipulate the filling process of liquids without air bubbles by the pinning effect. Through studying different geometries of the phaseguides, we have designed a new type of phaseguide structures specifically for blood separation purposes. Different parameters, such as a PDMS wall thickness, an air permeable overlap area, and geometry of the phaseguides, influencing the blood separation efficiencies were also studied in this paper.

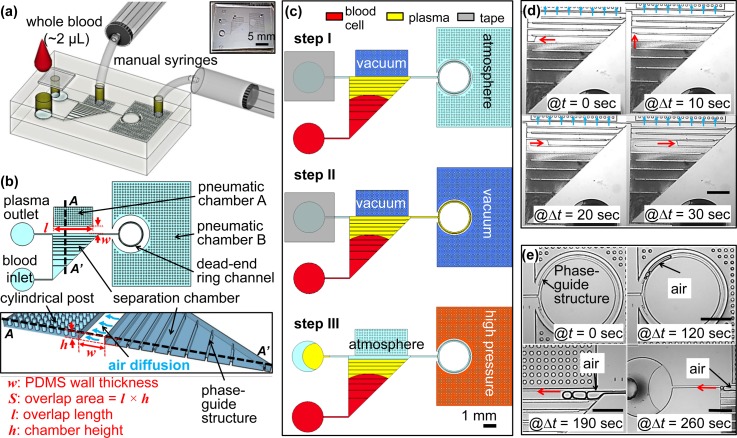
FIG. 1.

Schematics of the proposed device. (a) Overview of the experimental setup with the proposed device. The top layer is a PDMS cover with an inlet, a tape-sealed outlet and is bonded irreversibly with a bottom fluidic layer. (b) Top view and cross-section view. The separation chamber is divided into ten segments with equal volume by nine phaseguides at the bottom. Cylindrical posts are used to prevent the collapsing of the pneumatic chamber when it is vacuumed by the manual syringes. w and S stand for the PDMS wall thickness and the overlap area between the pneumatic chamber A and the separation chamber, respectively. The overlap area (S), where the flux of air diffuses, is calculated by the overlap length (l) multiplied by the chamber height (h). Drawings are not to scale. (c) Experimental steps. Step I: Apply vacuum at the pneumatic chamber A by pulling the syringe to 2 ml and add 2 μl of whole blood at the inlet (see Movie S1). Step II: after the separation chamber is filled with sample, the pneumatic chamber B is vacuumed in a similar way to the step I, which will withdraw the separated plasma into the dead-end ring channel. In this step, the separated plasma can be analysed with on-chip sensors, which is not a focus of this paper (see Movie S2). Step III: unseal the tape and apply high pressure at the pneumatic chamber B to push out the separated plasma to the plasma outlet by the help of the last phaseguide for further off-chip applications, which is an optional step (see Movie S3). (d) Image sequences taken from the filling process during the Step I. (e) Image sequences taken from the recovery process during the Step III. Red arrows in (d) and (e) indicate the flow directions, which shows the plasma/air interface flows along the phaseguides. Scale bars in (d) and (e) is 1 mm.

II. WORKING PRINCIPLE

As illustrated in Figs. 1(a) and 1(b), two pneumatic chambers (A and B) were neighbouring with the separation chamber and the dead-end ring channel, disconnected through the air permeable thin PDMS wall. By pulling or pushing the plunger of the manual syringe, a vacuum or a high pressure will be generated inside the pneumatic chambers to indirectly withdraw or push the blood sample in or out of the separation chamber, respectively. Cylindrical posts were embedded to prevent the shrinkage or expansion of the pneumatic chambers when they are vacuumed or pressurized. From our previous study,²⁷ through employing a triangular-shape separation chamber and a pneumatic chamber at its side, a high flow rate as well as a constant flow can be generated most of the time during the filling and separation process. Only at the end of the filling process, the flow rate will be reduced for a short time.

To withdraw the blood sample into the separation chamber, the pneumatic chamber A will be vacuumed first by pulling the syringe. After the blood sample is loaded at the inlet, the air trapped inside the separation chamber will start to diffuse through the gas permeable PDMS wall into the pneumatic chamber A. This will generate a pressure difference between the inlet and the separation chamber, withdrawing the blood sample into the separation chamber. By tuning the thickness and surface area of the PDMS wall,²⁷ the flow rate of the blood sample can be well controlled. Meanwhile due to gravity, blood cells will sediment toward the bottom of the separation chamber, perpendicular to the flow direction. Therefore, plasma extraction will take place during the filling process in the separation chamber (Fig. 1(c): step I and Fig. 1(d)). No special skills were required because only two hand-held syringes are employed and whole blood from the finger tips without any treatment ise needed. The volume of the surrounding pneumatic chamber is around 2 μl, and we pull the syringe more than 2 ml. Therefore, after pulling the syringe, the pressure level inside the pneumatic chamber will change from 1 atm to 10⁻³atm, resulting in sufficient vacuum inside the pneumatic chamber. Also because PDMS has low gas diffusion coefficient (3.4 × 10⁻⁹ m² s⁻¹),²⁷ the vacuum level inside the pneumatic chamber can be held for more than 30 min without significant change, which was verified by the observation from experiments. Once the syringes were pulled more than 2 ml and the plungers' positions were hold by a spacer, the proposed device would be ready for the blood separation. Minimization of the perturbation of the blood flow in the separation chamber is a key for successful plasma extraction using sedimentation.

As mentioned in the introduction, the plasma separation efficiency can be defined as the ratio between the percentage of separated plasma in the device and the initial percentage of plasma in the whole blood sample (1-Hct).²² But, in our case, only 2 μl of whole blood was used, so it is hard to measure the Hct level from the same drop of blood used for the separation tests. Instead, the RBC counts of the whole blood obtained from the same drop of blood used for the separation tests were measured three times using an automated haematology analyser (Z1 D/T, Beckman Coulter, Fullerton, CA), and the value is ranging from around 4.4 × 10⁶/μl–6.1 × 10⁶/μl. Here, instead of calculating the plasma separation efficiency, plasma separation ratio was employed and defined as the area ratio between the area of clear plasma compared with the total area of the separation chamber. For the calculation of the area ratio of the clear plasma and the whole area of the separation chamber, microscope images (15 times magnification) were analysed by Matlab. If the intensity of the pixel inside the separation chamber was lower than a critical value, it was considered as clear plasma. Then the total pixel number of the clear plasma was divided by the total pixel number of the separation chamber. The result was considered as the plasma separation ratio (α). In order to check the purity of the separated plasma, absorption spectra of the separated plasma and whole blood were measured (See Ref. 49 for Fig. S1). The test result showed that our separated plasma has similar purity to the one separated by the centrifuge method.²⁹

Note here that phaseguides structures are added at the bottom of the separation chamber mainly for two purposes: (1) to make sure that no air bubble is trapped in the dead end separation chamber and (2) to increase the plasma separation ratio. Through adding phaseguides at the bottom of the separation chamber, the height of the separation chamber would be reduced at the locations where phaseguides are added. Therefore, less sedimentation time is required and plasma separation ratio is expected to be increased.

Once the separation chamber is filled with the blood sample, the flow will stop automatically because the wall surface at the separation chamber—where air diffusion occurs—is curtained by the blood sample. In a similar way, the pneumatic chamber B can be vacuumed to further withdraw the separated plasma into the dead-end ring channel (Fig. 1(c): step II and Fig. 1(e)). Note here that phaseguides are also employed in the ring channel to guide the filling or pushing out of the sample liquids without trapped air bubbles.

One of the advantages of using our pumping method is that the withdrawn liquid can be recovered from the dead-end channel, unlike the conventional degassing method. Application of a high pressure to the pneumatic chamber will make the air to diffuse back into the dead-end channel. In our approach, to retrieve the separated plasma to the plasma outlet, the tape is unsealed. Then, we push the plunger of the manual syringe in order to apply a high pressure to the pneumatic chamber B. This time the air will diffuse from the pneumatic chamber B back into the ring channel reversely. The air bubbles will grow in the ring channel. Therefore, the plasma will be pushed away from the dead-end ring channel to the plasma outlet. By the help of the last phaseguide in the separation chamber, the plasma/air interface will flow out to the outlet without disturbing the blood cell sediment (Fig. 1(c): step III and Fig. 1(e)). In addition to the blood separation step (step I), steps II and III can be optionally used for further on-chip or off-chip applications.

III. MATERIALS AND METHODS

The proposed device was fabricated using soft lithography to form microfluidic channels by PDMS.³⁰ First, a layer of negative photoresist (MicroChem, SU-8 2050) was spin-coated and patterned on a silicon wafer, which defines the base layer. Before developing the first layer of SU-8 photoresist, a second layer of negative photoresist (MicroChem, SU-8 2015) was spin-coated and patterned to form the phaseguides. After developing the UV-exposed double-layered photoresist, a mould with different thickness was formed. Then, the PDMS mixture (Dow Corning, SYLGARD 184) was poured over the mould, followed by curing at 80 °C for 1 h. Then PDMS replica was peeled off from the master mould. A PDMS cover was punched to form ports correspondingly. Followed by air plasma treatment, the PDMS cover and the PDMS replica were aligned and bonded together irreversibly. Finally, the whole device was placed on a hot plate for 3 days at 70 °C to make sure the channel surface was hydrophobic and stable. However, from other report,^31,32 3 days is too long to restore the stable surface property of PDMS. In our case, the extra time is employed to make sure that the surface is stable, but further optimization is needed in the future to reduce the time consumption.

2 μl of whole blood samples were collected by micropipette directly from healthy male donors after a finger prick at the same depth and similar positions using a lancing device (Microlet^® 2 Lancing Device, Bayer) according to the manufacturer's protocols. Then the whole blood samples were added to the inlet of the test device within one minute without any treatment. The volume of the separation chamber is ranging from 1 μl to 1.3 μl in our experiments. Therefore, around 0.7 μl to 1 μl of whole blood sample remained in the inlet port. The extra amount of whole blood sample is needed to make sure that the inlet port is totally filled with whole blood. Normal red blood cell (RBC) counts with venous blood range from 4.5 × 10⁶/μl to 5.9 × 10⁶/μl (or hematocrit levels from 41% to 53%) for men.³³ It is well known that blood test results obtained from capillary sampling via a fingertip puncture may be different from those taken from venous samples, possibly owing to the mechanical and chemical effects during the sampling process.^34,35 However, the reported differences between capillary and venous RBC counts were not significant (≲±5%),^35–37 although other authors have found no such a difference.^38,39 Because only 2 μl of whole blood from finger tips is used directly in our devices for point-of-care purpose, the variations of the plasma separation ratio are relatively large. In our experiment, the RBC counts of the whole blood obtained from capillary sampling via a fingertip puncture were measured separately for several times using an automated hematology analyzer (Z1 D/T, Beckman Coulter, Fullerton, CA), and the value is ranging from around 4.4 × 10⁶/μl to 6.1 × 10⁶/μl. Two glass syringes (5 ml) were connected to pneumatic chambers A and B, respectively, through air-tight plastic tube (Fig. 1(a)). To apply a vacuum, the syringe was pulled from zero to 2 ml, and to apply a high pressure, the syringe was pushed from 0.5 ml to zero. As described in our previous paper,²⁷ pulling the syringe to 2 ml was enough to maintain the pneumatic chamber vacuumed for more than 1 h. If pushing the syringe much more than 0.5 ml, the thin PDMS wall between the separation chamber and the pneumatic chamber was sometimes damaged.

IV. RESULTS AND DISCUSSION

In order to study the effects of different designs of phaseguides and flow rates on the blood plasma separation ratio (α), two sets of experiments were performed. In the first set (case I), flow rates (Q) were kept same by fixing the wall thickness (w) and the overlap area (S) between the pneumatic chamber A and the separation chamber; meanwhile, test devices with different phaseguides were designed (Table I). The overlap area (S), where the flux of air diffuses, is calculated by the overlap length (l) multiplied by the chamber height (h) as illustrated in Fig. 1(b). In the second set (case II), flow rates were tuned among test devices by changing the wall thickness (w) and the overlap area (S) between the pneumatic chamber A and the separation chamber (Table II), meanwhile the phaseguide design was kept the same. In all of the designs, the width and length of the separation chamber and the ring channel were kept the same. The PDMS wall thickness (w_B) and overlap area (S_B) between the pneumatic chamber B and the ring channel were also the same for all the devices (w_B = 100 μm and S_B = 670 000 μm²).

TABLE I.

Geometries of the different designs of the phaseguide structures in case I.

Device	Phaseguide height Hph (μm)	Chamber height Hch (μm)	Ratio Hph/Hch	Neck length Lneck (μm)	Graph
A	0	80	0	NA	Fig. 3(c)
B	60	83	0.72	0	Fig. 3(b)
C	60	83	0.72	100	Fig. 3(b)
D	60	83	0.72	200	Fig. 3(b)
					Fig. 3(c)
E	24	82	0.29	200	Fig. 3(c)
F	52	74	0.70	200	Fig. 3(c)
G	60	74	0.81	200	Fig. 3(c)

TABLE II.

Geometries of the different devices in case II.

Device	PDMS wall thickness w (μm)	Overlap area S (μm2)	Ratio Hph/Hch	Graph
H	100	120 000	0.3	Fig. 4
I	200	240 000	0.3	Fig. 4
J	100	240 000	0.3	Fig. 4

A. Case I: Same flow rates, different designs of phaseguides

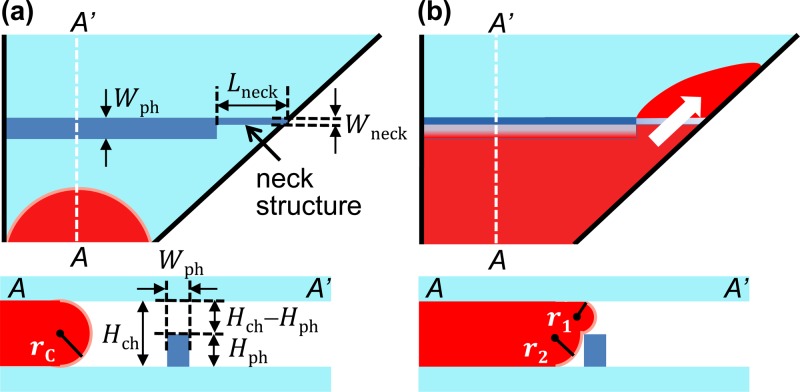
In this set of experiments, flow rates were kept same (Q ≈ 2.5 nl/s) by fixing the wall thickness (w_A = 100 μm) and the overlap area (S_A = 320 000 μm²) between the pneumatic chamber A and the separation chamber, and seven test devices (A, B, C, D, E, F, and G) with different phaseguides were designed. Table I provides the detail geometries of the test devices with different shapes of phaseguides. As shown in Fig. 1, we divided the separation chamber into ten segments with equal volume by nine phaseguides. Note here that except device A (no phaseguides) and B (no neck structure), the width of phaseguides for the other five devices is not uniform. There is a narrow part, or a neck structure, at one side of each phaseguide (Fig. 2).

FIG. 2.

Schematics of filling process in the separation chamber. (a) Overview and cross-section view of the device before blood reached the phaseguides. (b) Overview and cross-section view of the device when blood is going to pass the phaseguides.

1. Blood sedimentation

As in whole blood, more than 90% of the blood cells are erythrocytes, or red blood cells (RBCs). Thus, in this paper, we mainly focused on the movement of RBCs. The sedimentation velocity (v_⊥) of one single red blood cell in whole blood, perpendicular to the flow direction could be calculated by

$$v_{\perp }=\frac{2 \Delta \rho g {a_{\mathrm{g}}}^3}{9 \mu a_{\mathrm{d}}},$$ (1)

through force balancing between the buoyancy-corrected gravitational sedimentation force

$$F_{\mathrm{g}}=\frac{4}{3}\pi {a_{\mathrm{g}}}^3 \Delta \rho g$$ (2)

and the drag force due to viscosity^25,36,40

$$F_{\mathrm{d}}=6\hspace{0.17em}\pi \hspace{0.17em}{a}_{\mathrm{d}} \hspace{0.17em}\eta \hspace{0.17em}{v}_{\perp }.$$ (3)

Here, a_g and a_d are the equivalent particle radii used for the calculation of the buoyancy-corrected gravitational sedimentation force and the drag force due to viscosity, respectively. For the calculation of buoyancy-corrected gravitational sedimentation force, the shapes of RBCs are considered as spheres; therefore, the equivalent particle radius (a_g) is rangine from 2.67 μm to 2.88 μm for a single blood cell.⁴¹ But, for the calculation of drag force due to viscosity, the shapes of RBCs cannot be considered as spheres. Different orientations of the RBCs should be considered. Therefore, the equivalent particle radius (a_d) is ranging from 1 μm to 4.1 μm.⁴² Δρ is the density difference between RBCs and plasma (∼97 kg/m³ for one red blood cell),⁴³ g is the gravitational acceleration, and η is the viscosity of the whole blood at normal conditions (3–4 mPa·s for whole blood at 37 °C).⁴³ Thus, the theoretical sedimentation rate for a single red blood cell would be ∼0.25–1.68 μm/s. The order of theoretical sedimentation rate agrees with that from other clinical reports. ^5,44,45

In our design, the height of the separation chamber (H_ch) is around 80 μm, which will take roughly 100 s for all the RBCs to settle down near the bottom of the separation chamber (t_s ≈ 100 s). The flow rate of all the devices in case I was kept the same (Q ≈ 2.5 nl/s), and the volume of the separation chamber (V_s) is around 10⁹μm³. Therefore, the total filling time (t_f = V_s/Q) of the separation chamber will be around 7 min, which matches with our experiment results.

2. Without phaseguides

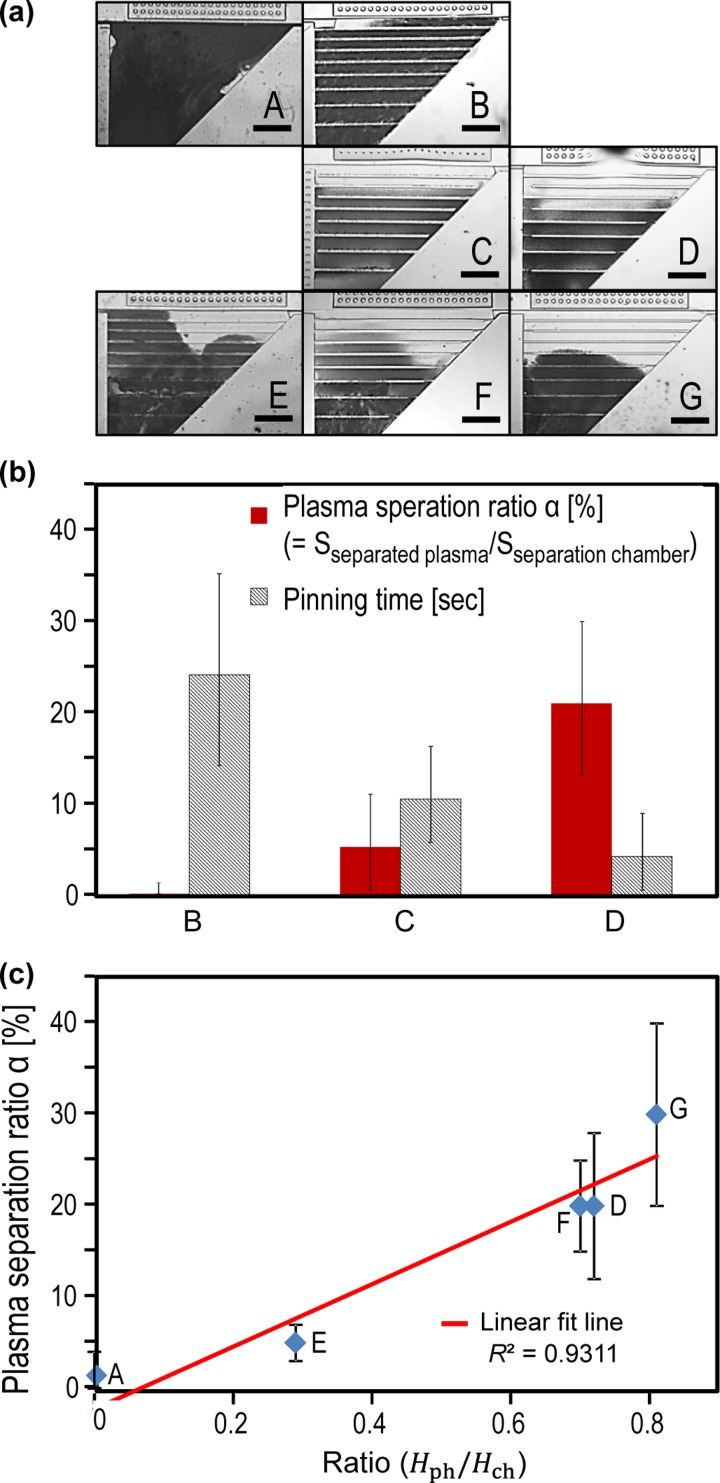
As the filling time is much longer compared with the sedimentation time (t_f ≫ t_s), we expected the separation of plasma from the whole blood would happen inside the separation chamber. However, as shown in Fig. 3(a), device A (without phaseguides) could not separate plasma from the whole blood during the filling process. The reason is that even the RBCs are settled down near the bottom of the separation chamber, they are still sliding forward along the direction of the flow.²⁵ Moreover, without phaseguides, air bubbles are occasionally trapped inside the separation chamber.

FIG. 3.

Experimental results of the devices in case I. (a) Device A, B, C, D, E, F, and G after the filling process in the separation chamber. (b) Effect of the pinning time on the blood plasma separation ratio (α) based on device B, C, and D. (b) Effect of the ratio between the height of phaseguides and the separation chamber on the blood plasma separation ratio (α) based on device A, D, E, F, and G. The linear fit line is plotted in red colour. Blue diamonds (⋄) stand for the experimental data. The error bar represents the standard deviation based on three tests. Scale bar is 1 mm.

3. With phaseguides

Thus, phaseguides with a uniform width of W_ph = 100 μm were introduced in device B (without a neck structure). However, as shown in Fig. 3(a), almost no separation was observed during the filling process. Because the pinning effect of the phaseguides is too strong, a burst flow will happen when the sample flow overcomes the phaseguide. This perturbation increases the entrainments of blood cells over the phaseguides.

As illustrated in Fig. 2(a), before the flow reaches the phaseguides, the initial Laplace pressure^46,47 (p_i) within the blood sample is

$$p_{\mathrm{i}}=\gamma \frac{2}{r_{\mathrm{C}}}.$$ (4)

Here, γ is the surface tension between the blood sample and air. r_C is the principle radii of curvature of the blood sample, which equals to half of the height of the separation chamber by assuming that the contact angle between the blood sample and PDMS is 180 degrees (r_C = 0.5 H_ch). When the blood sample reaches the phaseguide as shown in Fig. 2(b), due to the restriction of the phaseguide, the new Laplace pressure (p_new) becomes

$$p_{\text{new}}=\gamma \left(\frac{1}{r_1}+\frac{1}{r_2}\right).$$ (5)

Similarly, here, r₁ and r₂ are the principle radius of curvature of the blood sample, which roughly equal the height of the phaseguide (r₁ = H_ph) and half of the opening between the phaseguide and the chamber ceiling (r_C = 0.5(H_ch − H_ph)), respectively. From Eqs. (4) and (5), the change of the Laplace pressure is

$$\Delta p=p_{\mathrm{i}}-p_{\text{new}}=\gamma \frac{{H_{\text{ch}}}^2-H_{\text{ch}}{H}_{\text{ph}}+{H_{\text{ph}}}^2}{H_{\text{ch}}{H}_{\text{ph}}(H_{\text{ch}}-H_{\text{ph}})}>0\hspace{0.17em}.$$ (6)

Also, the hydraulic flow resistance (R_H) will increase at the phaseguide due to the restriction of the phaseguide.⁴⁸ Because of the increase of Laplace pressure (Δp) and the hydraulic flow resistance (R_H), the sample flow rate will drop sharply at the phaseguide or the flow is pinned at the phaseguide structure.

Meanwhile, negative pressure will be built up in the separation chamber because the trapped air keeps diffusing from the separation chamber to the pneumatic chamber A, which is dictated by

$$\frac{\mathit{d}\mathit{p}}{\mathit{d}\mathit{t}}=\frac{R_{\mathrm{g}} T}{V}\frac{\mathit{d}\mathit{n}}{\mathit{d}\mathit{t}}-\frac{R_{\mathrm{g}} T n}{V^2}\frac{\mathit{d}\mathit{V}}{\mathit{d}\mathit{t}},$$ (7)

where p is pressure inside the separation chamber, R_g is the gas constant, T is the absolute temperature, n is the amount of trapped air inside the separation chamber, and dn/dt equals the air flux (F) times the overlap area (S), which are both fixed by the geometry design as discussed in our previous paper.²⁵ V is the volume of the trapped air, which is roughly constant because the sample flow is pinning at the phaseguide, therefore dV/dt ≈ 0. So, Eq. (7) can be written as

$$\frac{\mathit{d}\mathit{p}}{\mathit{d}\mathit{t}}=\frac{R_{\mathrm{g}} T}{V}F S\Rightarrow \Delta p=\frac{R_{\mathrm{g}} T F S}{V}\Delta t.$$ (8)

Equation (8) predicts that the longer the pinning time is, the higher the built up pressure will be, causing unbalanced pressure between the surface tension of the sample and the vacuum pressure inside the separation chamber. Thus, a burst can be observed once the unbalanced pressure is large enough to let the sample flow overcome the restriction of the phaseguide. Then, the flow will be slowed down and be constant again until it meets the next phaseguide. Besides that, we observed that the burst flow happens at random point along the phaseguides.

4. Modified phaseguides

In order to reduce the effect of entrainments of blood cells when the whole blood passes over the phaseguides, we reduced the width of the phaseguide to W_ph = 25 μm. But, for this case, the pinning effect was too weak that blood flow will not follow the guiding of phaseguides resulting lots of trapped air bubble as in this case the phaseguides actually helped the trapping of air bubble. In our design, instead of having a phaseguide with the uniform width, a neck structure was added at one end of the phaseguide. Here, we fixed the width of the phaseguides (W_ph) and neck structure (W_neck) to be 100 μm and 25 μm, respectively, (Fig. 2(a)). Due to the reduced width, the hydraulic resistance at the neck structure will be lower compared with that at the phaseguides. Therefore, the breakpoint can be controlled to be at the neck structure (Figs. 1(d) and 2(b)).

Furthermore, we can manipulate the pinning time by controlling the length of the neck structure (L_neck), as shown in Fig. 3(b). As expected, by decreasing the pinning time, blood plasma separation ratio (α) was increased due to the reduced burst flow at the neck structure. Note that if the length of neck structure is too long (i.e., L_neck ≫ 200 μm), similar to the case that when the width of the phaseguides is 25 μm, air bubble can be trapped inside the separation chamber.

Moreover, when we keep the same design of neck structures while changing the ratio between the height of phaseguide structures and that of the separation chamber (Table I), blood plasma separation ratio (α) will also increase with the increase in the ratio between the height of phaseguide structures and that of the separation chamber (Fig. 3(c)). As mentioned before, the reason is that the higher the phaseguide compared to the height of the separation chamber, the blood cells will need less sediment time (t_s) to be low enough to be blocked by the phaseguides. Note here that the position of the neck structure, or whether it is at the left or the right end of the phaseguides, would not affect the test results.

B. Case II: Different flow rates, same design of phaseguides

In the previous experiment (case I), we maintained the flow rate to be same and devices with different designs of phaseguides were studied. For the following experiment (case II), we fixed geometries of the phaseguides, neck structures, and separation chamber (W_ph = 100 μm, W_neck = 25 μm, L_neck = 200 μm, H_ch = 83 μm, H_ph = 23 μm, and H_ph/H_ch = 0.3, same design as case E in Fig. 3(a)); meanwhile, we varied the flow rates by designing three devices (H, I and J) with different PDMS wall thickness (w) and overlap area (S) between the pneumatic chamber A and the separation chamber, as shown in Table II. Note here that we did not decrease the flow rate further below 1 nl/s to get better plasma separation ratio. When the flow rate is very slow, it takes too long to fill the separation chamber, and blood at the inlet is totally dried out before enough blood sample goes into the separation chamber. Instead, air is pushed into the separation chamber. Also, the long filling time is not beneficial for the POC applications. That is also why—in case I—we fixed volumetric flow rate Q to ∼2.5 nl/s (which is close to the highest flow rate that we can get utilizing our current design and vacuum-assisted micropumping) and varied the phaseguide structures to get higher plasma separation ratio.

Fig. 4 shows the test results of case II. As expected, slow flow rate gives higher blood plasma separation ratio (α). The reason is that when the flow rate is slow, filling time (t_f) of the whole separation chamber will be longer. Because the sediment time (t_s) is unchanged, increased filling time will increase the chance that more blood cells are settled down and blocked by the phaseguides earlier, giving a higher blood plasma separation ratio (α). However, slow flow rate will take a long time to extract plasma in the separation chamber. For example, with 1 nl/s (device H), it takes about 20 min, and with 2.5 nl/s (case I), it could take about 7 min. Therefore, as you expect from the results shown in Fig. 3(c), if we want to reduce the separation time, the better design would be the one with the higher ratio between the height of phaseguides and the separation chamber (i.e., H_ph/H_ch = 0.81 for device G).

FIG. 4.

Experimental results of the devices in case II. (a) Device H, I, and J after the filling process in the separation chamber. (b) Effect of average flow rate on the blood plasma separation ratio (α) based on device H, I, and J. The linear fit line is plotted in red colour. Blue diamonds (⋄) stand for the experimental data. The error bar represents the standard deviation based on three tests. Scale bar is 1 mm. Distortion in the images are due to the insertion of the tubes.

Note here that for all the devices in case I and II, once the plasma is extracted from the whole blood, steps II and III can be realized as mentioned in working principle in a similar way (see Ref. 49 for Movie S1 for step I, Movie S2 for step II, and Movie S3 for step III). For step III, due to the phaseguide, only the plasma in the last segment can be pushed out to the plasma outlet; meanwhile, the sample in other nine segments will be pushed to the inlet. For current design, the amount of plasma that can be pushed out is around 10% of the total volume of the separation chamber.

V. CONCLUSIONS

We have demonstrated a novel blood separation device with high plasma separation ratio for POC applications. This was accomplished by employing the modified phaseguides and syringe-assisted pumping by utilizing the gas permeability of PDMS. Key parameters influencing the plasma separation ratio, such as flow rates and geometries of the phaseguides, were also analysed. The experimental results demonstrated that the proposed device can efficiently separate plasma from whole blood in a simple way that is suitable for POC applications. Moreover, the proposed device has the potential to perform blood analysis either on chip or off chip. Therefore, the present device is expected to be an effective tool for blood separation and analysing, especially for POC applications.