Abstract
This work is directed toward the development of a computer-aided diagnosis (CAD) system to detect abnormalities or suspicious areas in digital mammograms and classify them as malignant or nonmalignant. Original mammogram is preprocessed to separate the breast region from its background. To work on the suspicious area of the breast, region of interest (ROI) patches of a fixed size of 128×128 are extracted from the original large-sized digital mammograms. For training, patches are extracted manually from a preprocessed mammogram. For testing, patches are extracted from a highly dense area identified by clustering technique. For all extracted patches corresponding to a mammogram, Zernike moments of different orders are computed and stored as a feature vector. A support vector machine (SVM) is used to classify extracted ROI patches. The experimental study shows that the use of Zernike moments with order 20 and SVM classifier gives better results among other studies. The proposed system is tested on Image Retrieval In Medical Application (IRMA) reference dataset and Digital Database for Screening Mammography (DDSM) mammogram database. On IRMA reference dataset, it attains 99 % sensitivity and 99 % specificity, and on DDSM mammogram database, it obtained 97 % sensitivity and 96 % specificity. To verify the applicability of Zernike moments as a fitting texture descriptor, the performance of the proposed CAD system is compared with the other well-known texture descriptors namely gray-level co-occurrence matrix (GLCM) and discrete cosine transform (DCT).
Keywords: Computer-aided diagnosis (CAD), Mammograms, Preprocessing, Segmentation, Zernike moments, Support vector machine (SVM)
Introduction
Breast cancer has become one of the significant and frequent forms of cancer for women all over the world. Presently, risk factors of breast cancer cannot be avoided, and the survival rate of the patient is only related to early detection. A mammogram is an x-ray image of the breast tissue which allows better visualization of internal structure of the breast. Computer-aided techniques for detecting, classifying, and annotating diagnostic features on the mammogram images is a reliable tool for screening and early detection of breast cancer. The sensitivity of screening mammography is affected by image quality and the radiologist’s level of expertise. It is difficult for the radiologists to provide both accurate and uniform evaluation for the huge number of mammograms generated in widespread screening. Lesions often occur in dense breast tissue areas in a number of different shapes such as circumscribed, speculate, lobulated, or ill-defined. Microcalcifications are deposited tiny calcium which accumulates in breast tissue [13]. It is shown that 90 % of impalpable ductal carcinomas in situ and 70 % of impalpable minimal carcinomas were visible as microcalcification alone [7]. Advance image processing can improve the odds of mammograms in detecting breast cancer early [28]. On an average, mammography detection rate of the breast cancer is 80–90 % [19]. High-resolution mammographic images can be used to detect the signs of breast cancer such as microcalcifications and masses. A fast and an efficient computer-aided diagnosis (CAD) system to detect the presence of microcalcifications and masses from the breast mammogram images is the need of the hour. It would be of great help to humanity especially for people living in those places where human expertise is not so easily available.
This work proposes a CAD system to classify malignant and nonmalignant mammogram patches. The study is focused on two different types of available datasets. One is a complete mammogram dataset, Digital Database for Screening Mammography (DDSM), and another is of mammogram patches (Image Retrieval In Medical Application (IRMA) reference). The rest of the paper is organized as follows. The “Literature Survey” section gives a brief review on mammogram-based CAD systems. The “Overview of the Proposed CAD System” section gives an overview of the proposed CAD system. Preprocessing steps for enhancement of mammogram image are described in the “Preprocessing” section. Region of interest (ROI) extraction technique is described in the “ROI Patch Extraction” section. The “Feature Extraction and Classification” section explains Zernike moments used as features along with support vector machine (SVM) used for mammogram classification. Experimental setup and results are summarized in the “Experimental Setup and Results” section. Finally, the “Conclusion” section concludes the work.
Literature Survey
CAD for mammography began in the 1990s, and the first mammography CAD unit was approved in 1998 as a second reader [18, 27]. It has been shown that the performance of radiologists can be increased by providing them the results of a CAD system [3, 39]. Mammogram-based CAD systems were designed with the aim of increasing the effectiveness and efficiency of screening procedures. With the use of computer, diagnostic accuracy is improved by reducing the numbers of false-positive diagnoses of varying lesions in an objective manner. As shown in Fig. 1, four basic modules are required to develop a CAD system for breast cancer detection. In order to get a better diagnostic system, automatic segmentation, feature extraction, suspicious area detection, and classification techniques can be improved.
Fig. 1.

Four main stages of a CAD system for breast cancer detection
Preprocessing steps are very important to limit the search for abnormalities without undue influence from background of the mammogram. Preprocessing involves removal of artifacts and unwanted parts from the background of the mammogram. Breast border contour extraction, pectoral muscle extraction, and nipple identification are also performed at this stage. Segmentation of breast mass plays an important role in the quantitative and qualitative analysis of mammograms. It has a direct impact on subsequent analysis and processing. The goal of segmentation is to isolate the ROI from the preprocessed image. Mammograms are rich with the presence of texture and shape. Hence, extraction of appropriate textural and shape features from extracted ROI is one of the necessary steps. Performance of the developed CAD system is measured by matching the features of query mammogram with the extracted stored features of the mammogram database.
Méndez et al. [32] developed a fully automatic technique to detect the border of the breast and the nipple. An algorithm that computes the gradient of gray levels is used to detect the breast border. To detect the nipple, three algorithms, maximum height of the breast border, maximum gradient, and maximum second derivative of the gray levels across the median top section of the breast, were used and compared. Yu and Guan [51] developed a CAD system that automatically detects the clustered microcalcifications in digitized mammograms. Wavelet and gray-level statistical features were used to categorize potential microcalcification objects according to their spatial connectivity. Table 1 summarizes most of the mammogram-based CAD systems developed in the last one and a half decades.
Table 1.
Summary of some mammogram based CAD systems
| Methods | Feature Vectors | Classifier | Database |
|---|---|---|---|
| Yu and Guan [51], 2000 | Statistical features | MLFFNN | Nijmegen |
| Database | |||
| Verma and Zakos [47], 2001 | Entropy, standard deviation | BPNN | Nijmegen |
| and number of pixels | Database | ||
| Bagui et al. [4], 2003 | Radius, texture, perimeter, | k-NN | WDBC, WBC |
| area, smoothness, compactness, | |||
| concavity, concave points, | |||
| symmetry, fractal dimensions | |||
| Fu et al. [17], 2005 | Texture, spatial and | SVM | Nijmegen |
| spectral domain | Database | ||
| Hwang and Kim [23], 2006 | Zernike moments | – | – |
| Oliver et al. [35], 2007 | Local binary patterns (LBP) | SVM | DDSM |
| Jasmine et al. [24], 2007 | 2D Wavelet transform | – | MIAS |
| Xu et al. [50], 2007 | DWT | MLP | Private |
| Zhang et al. [52], 2008 | Contrast, energy, entropy, | BPNN | |
| standard deviation, skew, | |||
| difference, average bound gray, | |||
| average gray level, | |||
| no. of pixels, and | |||
| average histogram | |||
| Rabottino et al. [38], 2008 | Shape and texture features | Fuzzy classifier | DDSM |
| Mencattini [31], 2009 | Shape features | – | DDSM |
| Wang et al. [48], 2009 | Zernike moment-mode | – | – |
| shape descriptor | |||
| Rejani and Selvi [40], (2009) | Shape feature | SVM | MIAS |
| Alofe et al. [1], (2009) | Wavelet, first and second | SVM | MIAS |
| order statistics, shape and | |||
| fractal dimensional features | |||
| Mazurowski et al. [30], 2011 | Histogram | DDSM, DBT | |
| Zhang et al. [53], 2011 | Shape features | k-NN | MIAS, DDSM |
| Xu et al. [49], 2011 | Statistical and shape features | – | DDSM |
| Tahmasbi et al. [43], 2011 | Shape features | MLP | MIAS |
| Oliveira et al. [33], 2011 | Texture features | SVM | IRMA |
| Balakumaran and Vennila [5], 2011 | Skewness, kurtosis and | – | DDSM |
| wavelet transform | |||
| Deserno et al. [11], 2012 | 2DPCA | SVM | IRMA |
| Dheeba and Tamil [12], 2010 | Gabor features | RBFNN | MIAS |
| Oliver [35], 2012 | Local features based | Gentle boost | MIAS |
| on morphology | Classifier | ||
| Kabbadj et al. [25], 2012 | Statistical and geometric features | SVM | MIAS |
| Shanthi and Bhaskaran [41], 2012 | Mean, standard deviation, | Self-adaptive resource | MIAS |
| skewness, kurtosis, entropy | Allocation network | ||
| Cabrera et al. [20], 2012 | Texture features | – | DDSM |
Verma and Zakos [47] presented a system for detection and classification of microcalcification in digital mammograms. They investigated and analyzed 14 feature extraction techniques with neural network classification. Bagui et al. [4] proposed a new generalization of the rank nearest neighbor (RNN) rule for the diagnosis of breast cancer from multivariate data. Cheng et al. [9] summarized enhancement and segmentation algorithms, mammographic features, and classifiers used in various stages of the CAD and compared their performances. They discussed and compared approaches for automatic mass detection and classification in mammograms. Ferrari et al. [15] proposed a segmentation technique for the fibro-glandular disc in mammograms using the Gaussian mixture modeling. The results were assessed by the radiologists using original and segmented image with referencing to a ranking table categorizing the segmentation result as excellent, good, average, poor, and complete failure. Ferrari et al. [16] presented a method for the identification of the pectoral muscle in MLO mammograms using Gabor filters based on a multiresolution technique. A method for breast boundary identification in mammograms using active contour models is developed by Ferrari et al. [14] that can be used for the preprocessing of mammogram. Fu et al. [17] proposed a two-stage procedure to detect microcalcifications.
Rangayyan et al. [39] gave an overview of techniques for detection and analysis of calcifications, masses, tumors, bilateral asymmetry, and architectural distortion. Xu et al. [50] gave a new algorithm based on two artificial neural networks (ANNs). Rabottino et al. [38] proposed a region growing segmentation algorithm for mass contour extraction. Zhang et al. [52] developed a fully automated CAD system with the help of back propagation neural network (BPNN) technique. Alofe et al. [1] proposed a CAD system based on SVM and linear discriminant analysis classification (LDA). Jasmine et al. [24] combined wavelet analysis of the image with ANNs for building the classifiers. Mencattini et al. [31] also introduced region growing tumoral mass segmentation and characterization algorithms by implementing uncertainty propagation through blocks. SVM has been a widely used classifier in medical diagnosis of mammography images [40]. Tang et al. [44] presented an overview of CAD systems and related techniques developed in the recent years such as radiological imaging. Dheeba and Tamil [12] developed a method with the help of Gabor features for detecting tumors in mammograms using RBFNN.
Balakumaran and Vennila [5] presented a multiresolution-based foveal algorithm for microcalcification detection. Mammograms were decomposed through wavelet transform without a sampling operator into different sub-bands, suppressing the coarsest approximation sub-band, and finally reconstructing the mammogram from the sub-bands containing only significant detailed information. Mazurowski et al. [30] developed a CAD system that uses mutual information-based template matching scheme with intelligently selected templates for diagnosing the mammographic masses. Tahmasbi et al. [43] developed a CADx system by utilizing Zernike moments as descriptors of shape and margin characteristics. Xu et al. [49] used traditional watershed transformation to obtain a boundary in the belt between the internal and external markers. The rough region of the lesion is identified by template matching and thresholding. Zhang et al. [53] applied a marker-controlled watershed algorithm on mammograms as an initial segmentation. Then, the contour line obtained by watershed is regarded as the initial curve, and a level set evolution without re-initialization is utilized for further segmentation.
It is well known that the best prevention method is early detection, but primary prevention in early stages of the disease becomes complex as the causes remain almost unknown. Nevertheless, some typical signatures of this disease can be targeted such as masses and microcalcifications appearing on mammograms, which can be used to improve early diagnostic techniques. As a result, most of the techniques focus on two types of breast cancer: microcalcifications and masses [20]. Oliver et al. [35] presented a knowledge-based approach for automatic detection of microcalcifications and clusters in mammographic images by using local features extracted from a bank of filters to obtain a local description of the microcalcifications morphology. Kabbadj et al. [25] also presented a novel approach to detect microcalcifications on digitized mammograms using shape features, fuzzy logic, and SVM. Deserno et al. [11] proposed a CAD system which classifies the suspicious tissue pattern based on the SVM. Shanthi and Bhaskaran [41] proposed an integrated methodology of intuitionistic fuzzy C-means clustering, discrete wavelet feature extraction technique, and a self-adaptive resource allocation network classifier for automatic detection and classification of breast cancer in mammogram images. Oliveira et al. [35] developed content-based image retrieval (CBIR) system in support with the classification of breast tissue density which can be used in the processing chain for lesion segmentation and classification.
Maitra et al. [29] enhanced the contrast of mammogram by using the contrast-limited adaptive histogram equalization (CLAHE) technique initially. Then a rectangle is defined to isolate the pectoral muscle from the ROI, and finally, the pectoral muscle was suppressed by using the modified seeded region growing (SRG) algorithm. The algorithm separates background region and removes the pectoral muscle to accentuate the breast profile region.
Overview of the Proposed CAD System
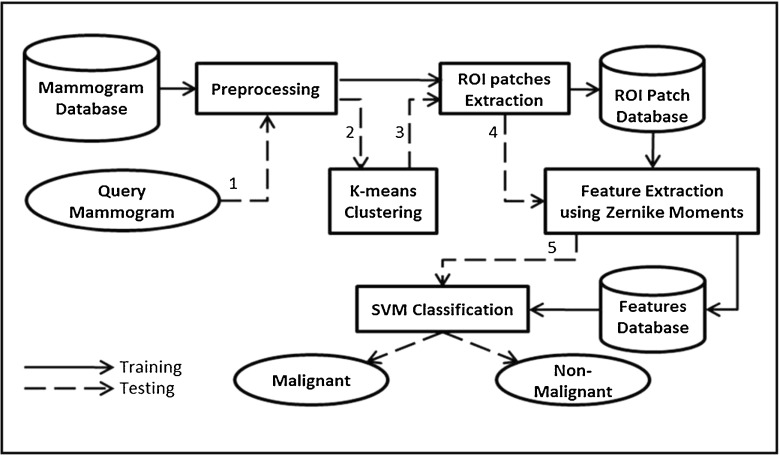
Figure 2 gives the block diagram of the proposed CAD system for large-sized full mammogram images. An image may contain several regions to examine, and the efficiency of the system depends on the successful identification of these ROI patches. These ROI patches are analyzed for the presence of malignancy.
Fig. 2.
Block diagram of the proposed CAD system
The system works through several consecutive steps, which are visualized in Fig. 2. Here, solid lines are representing the steps followed for training of the system and dashed lines are representing the steps for testing. The four basic modules, preprocessing, ROI patches extraction, feature extraction, and classification, are discussed in detail in the following subsections.
Preprocessing
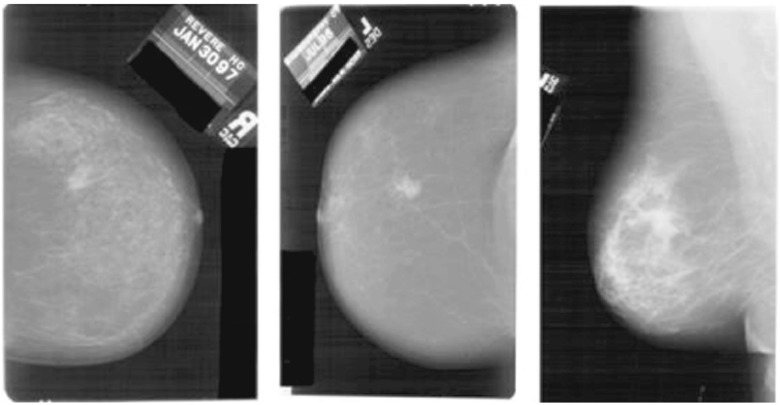
The presence of a lot of irrelevant and futile information can be noticed in the mammogram images shown in Fig. 3. The objective of preprocessing is to improve the quality of image in order to limit the search for abnormalities by removing artifacts and unwanted parts without having undue influence on the background of mammograms [37]. Preprocessing aims to enlarge the intensity difference between objects and background to produce reliable representation of breast tissue structures. Preprocessing not only removes the noise but also finds the orientation of the mammogram [29]. Preprocessing also helps in the standardization of the mammogram image along with the reduction of its size without losing the useful information required for any CAD system.
Fig. 3.
Original mammograms containing noise and useless information [22]
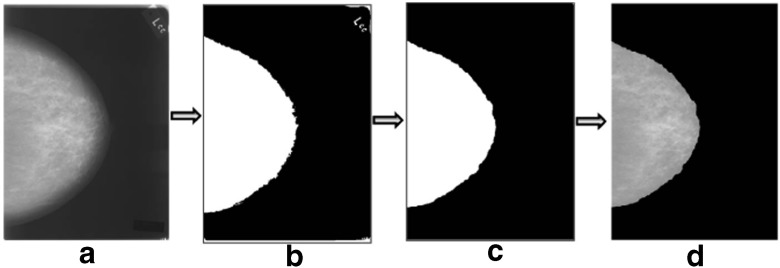
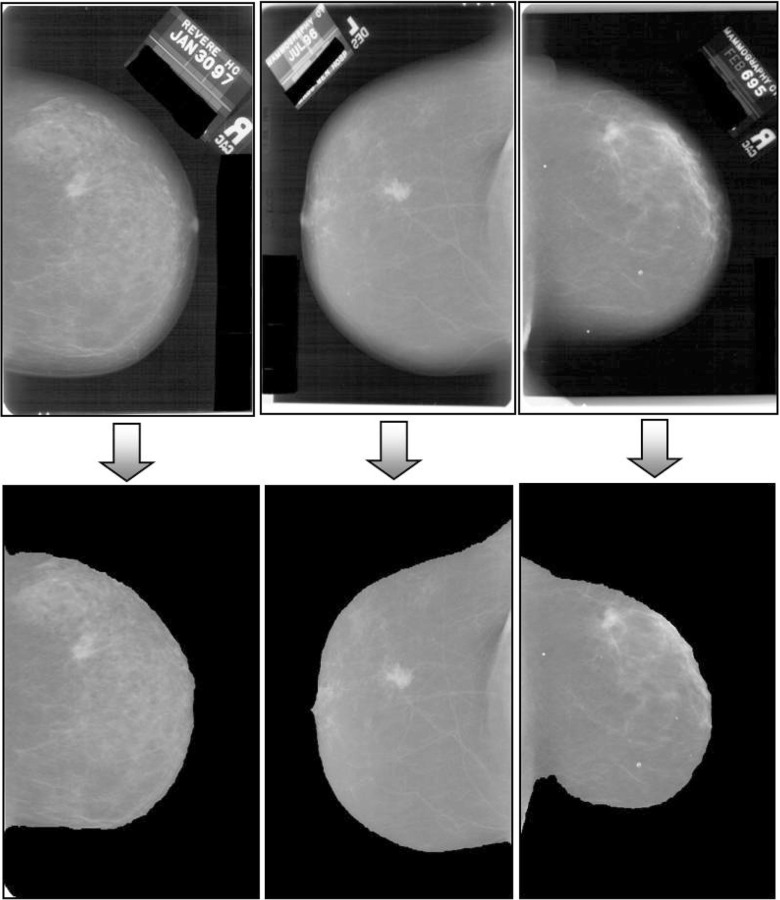
Preprocessing steps consist of scaling, binarization, erosion, and region identification. The effect of each step on a mammogram image is shown in Fig. 4. Due to their large size, mammograms are rescaled for further analysis. Original mammograms from the DDSM dataset are of 4,000×3,000 pixel resolution, which is scaled down to 1,024×1,024 pixels using the nearest-neighbor interpolation method. Binary erosion is applied to remove the “small” objects present in the binary image for cleaning the background texture. A disk-type structuring element is used here. Even after applying binary erosion, sometimes the binary image may contain some small-sized irrelevant components. In the binarized image, the large foreground area is of the breast that contains the useful information. Therefore, in the eroded binary image, connected components (of white color) are identified as regions, and the region with the maximum area is considered as a final mask image. Exterior boundary of the region is traced using a mask image and is plotted on the original image using the same pixel coordinate values. This mask image is superimposed on the original image to get clear boundary of the breast area in the image. Some of the results obtained with this preprocessing method are shown in Fig. 5.
Fig. 4.
Results of intermediate stages of preprocessing a scaled mammogram, b binarization, c binary eroded image with an identified region, and d preprocessed image
Fig. 5.
Original and preprocessed mammograms. The first row shows the original mammograms, and the second row shows preprocessed mammograms of the corresponding images
ROI Patch Extraction
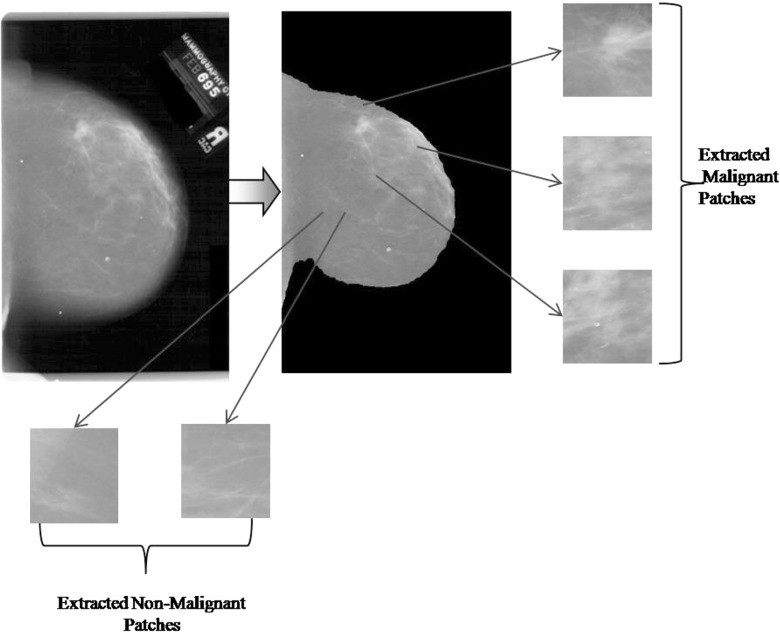
A mammogram image is very large in size consisting of both useful and nonuseful information. Instead of processing a complete mammogram, focus is enlightened only on the area containing some abnormality (intensity variations). The ROI is an abnormal region on the mammogram, segmented on the basis of visual textural information. ROI patches of 128×128 pixels are extracted from the segmented region and are used for training and testing purposes. A mammogram may contain many such patches. Extracting patches from the segmented regions also limits the processing time and speed of the system. Figure 6 shows ROI patches extracted from the preprocessed mammogram image. Patches are extracted in two different ways for training and testing separately. In training, the patches are extracted by selecting abnormal regions manually; while for testing, patches are extracted manually from the dense areas of the mammograms which are identified by k-means clustering automatically. Manual selection is a time-consuming task but promises a better result. Patches belonging to the respective classes are stored separately to facilitate training of the system.
Fig. 6.
From left to right: original mammogram, preprocessed mammogram, and extracted patches from the preprocessed mammogram
Dense Area Identification in Test Mammogram
The present work uses image enhancement followed by k-means algorithm to cluster pixels. Further, the concept of entropy is used to identify dense clusters. ROI patches of size 128×128 pixels are extracted from these dense areas and are further classified as malignant/nonmalignant. The process of cluster identification for ROI patch extraction is shown in Fig. 7.
Fig. 7.
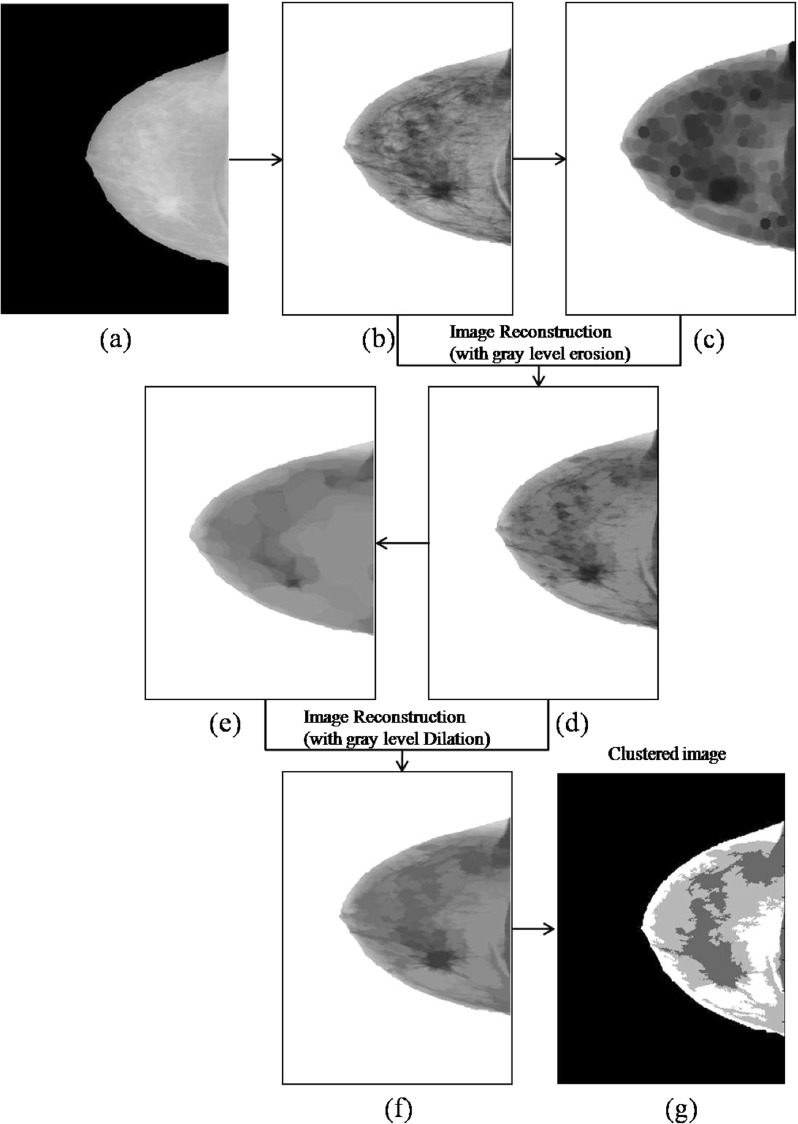
Cluster identification for ROI patch extraction
The preprocessed image is further enhanced through histogram equalization to emphasize certain interesting features of the image and restraining indifferent characteristics. Gray-scale erosion applied on the enhanced image shrinks the area of the foreground pixels and enlarges the holes within that area. The resultant eroded image is used for image reconstruction to remove the fine lines, or noncancerous parts, and enhances the visibility of malignant mass. Let enhanced image be represented as Ie and its eroded image be represented by Ier. Morphological reconstruction (MR) of the image component from the eroded image is defined as follows:
| 1 |
In reconstruction, Ier is used as a marker image and Ie as a mask image [6]. Figure 7(d) shows the enhanced image after reconstruction. This is a smooth image as compared to the image given in Fig. 7(b).
Although it has been observed that many similar and adjacent components are still unconnected, gray-scale dilation is applied to connect these components. Morphological reconstruction (MR) of the image component from the dilated image is done in a similar way as given in Eq. 1. Figure 7(f) is the resultant image.
Three types of components with different shades of gray are identified from the image shown in Fig. 7(f), i.e., light gray, gray, and dark gray. These components, regions of masses, normal, and dense tissues are required to be separated and checked for the malignancy. k-means clustering is applied to form clusters of these components. k-means algorithm is an unsupervised clustering algorithm that is used in this work to cluster gray levels of input image. The algorithm assumes that gray levels of input 2D image form 1D vector space and tries to find natural clustering in them [45]. The gray values of image are clustered around mean gray value of cluster ci ∀i=1,2,…k which are obtained by minimizing the objective function:
| 2 |
This method can be applied for the clustering of the same type of components present in the mammogram image in the following way:
Initialize k-clusters si(i=1,2,…k) with a random mean gray value (c1,c2,…ck).
Each pixel of the image is assigned to its closed cluster based on the distance between its gray value from mean gray value of the cluster.
- Compute the new mean gray value of each cluster.
where xi is gray values of set of pixels which belong to cluster si.3 Repeat steps 2 and 3 until the cluster labels do not change anymore.
Entropy is the measure of randomness present in the image. Entropy of these clusters is calculated from the distribution of gray-level intensities of corresponding pixel clusters in preprocessed query mammogram (Fig. 8).
| 4 |
A cluster having a maximum entropy represents the presence of more texture information. The patches obtained from this cluster are required to be tested for malignancy. The centroid of this cluster is taken as a reference point, and patches of size 128×128 are extracted from preprocessed mammogram as shown in Fig. 8.
Fig. 8.
ROI patch extraction for testing (a) clustered image, (b) preprocessed mammogram, (c) segmented image, and (d) extracted patches
Feature Extraction and Classification
This work utilizes the properties of Zernike moments to analyze texture properties of ROI patches. Zernike moments are rotation invariant, nonredundant, robust to noise and shape, and have a multilevel representation [21, 23, 43, 48]. An image can be better described by a small set of its Zernike moments than any other types of moments such as geometric moments, Legendre moments, rotational moments, and complex moments in terms of mean-square error.
Zernike Moments
Mapping of an image onto a set of complex Zernike polynomials are Zernike moments. Zernike polynomials are orthogonal to each other in nature, and therefore, they can represent the properties of an image with no redundancy or overlap of information between the moments [43, 48]. The procedure for obtaining Zernike moments from an input image begins with the computation of Zernike radial polynomials. It consists of three steps:
computation of radial polynomials
computation of Zernike basis functions
computation of Zernike moments by projecting the image on to the basis functions
The real-valued 1D radial polynomial is defined as
| 5 |
where p is a nonnegative integer representing the order of the radial polynomial, and q is a positive or negative integer satisfying that p≥0, 0≤q≤p, and p−|q| are even. Complex-valued 2D Zernike basis functions within a unit circle using the radial polynomial are defined as
| 6 |
Zernike basis function satisfies orthogonality condition as
| 7 |
Complex Zernike moments of order p with repetition q are finally defined as
| 8 |
where f(r,𝜃) is polar form of f(x,y) image function, and ∗ denotes the complex conjugate. To compute Zernike moments from a digital image, the integrals in Eq. 8 are replaced by summations and the coordinates of the image must be normalized by a mapping transform. The discrete form of Zernike moments for an image of size N×N is expressed as follows:
| 9 |
| 10 |
where 0≤rxy≤1, and normalization factor λN must be the number of pixels located in the unit circle π in the continuous domain. The transform distance rxy, and the phase 𝜃xy, at the pixel (x,y) are calculated as
| 11 |
| 12 |
Zernike moments are extremely dependent on the scale factor and translation of objects. Their magnitude is independent of the angle of rotation [26]. Therefore, the magnitude of the Zernike moment can be used as a descriptor to describe the characteristics of texture regardless of the rotation of the mass. Rotating the object around the Z-axis does not influence the magnitude response of the Zernike moments but influences only the phase response of Zernike moments [26]. It can also be explained as Eq. 13:
| 13 |
where and Zpq are moments extracted from the rotated object with an angle α and from the original object, respectively. Thus, the magnitudes of Zernike moments are proposed as features in this work.
Support Vector Machine
In the field of medical sciences, SVM has proved to be a good classifier in the diagnosis of mammograms [5]. SVM is a supervised learning algorithm based on the concept of hyperplane that aims to separate a set of objects with maximum margin. SVM determines some support vectors from the feature space which are helpful to determine the optimal hyperplane [10].
Let X {x1,x2...xN} be a training set containing N feature vectors in d-dimensional feature space and associated with two class labels zi∈{−1,+1}. For this work, two classes, malignant and nonmalignant, are labeled as (+1) and (−1), respectively. Two-class linear separable task is accomplished by defining a hyperplane that separates these feature vectors as follows:
| 14 |
| 15 |
These equations can be expressed in the general form as
| 16 |
The distance between two hyperplanes is . To get a better separation between the classes, this distance should be maximized by minimizing ||ω|| by using the Lagrangian function. Application of the Lagrangian function as given in Eq. 17 gives the most suitable optimal hyperplane.
| 17 |
where αi is the Lagrange multiplier of a dual optimization problem that describes the separating hyperplane wi(xi.x) and b is the threshold parameter of the hyperplane. If f(x)≥0, then x is classified as a member of the class +1; otherwise, it would be classified as a member of the second class (−1) [10]. This discrimination function will not work for linearly nonseparable dataset. Therefore, the kernel function is applied to get the optimal hyperplane in nonseparable datasets. SVM uses kernel function to map nonseparable data into kernel space. The resulting discrimination function is formally the same, except that everydot product used earlier is replaced by a nonlinear kernel function as follows:
| 18 |
As this is a linear nonseparable problem, the radial basis function (RBF) kernel given in Eq. 19 is used here to map the dataset into linear separable feature space.
| 19 |
Experimental Setup and Results
Mammogram Datasets
The proposed CAD system is validated by performing experiments on the following two datasets of mammograms.
IRMA reference database (DDSM mammographic patches)
Out of 800 patches taken from classes 1 and 5, 534 belong to class 5 and the remaining 266 belong to class 1. The data for training and testing has been separated into a ratio of 1:2. The system is trained with 178 malignant patches and 88 normal patches. The remaining 360 malignant and 174 normal patches are taken for testing.
DDSM mammogram database
A total of 200 mammograms (80 from class 1 and 120 from class 5) are taken. From these 200 mammograms, 1,264 patches are extracted, out of which 407 belongs to class 1 and the remaining to class 5. For this database also, the training-testing ratio is maintained to 1:2. Accordingly, 135 normal and 285 malignant patches are used to train the system. Testing is then performed on the remaining 272 and 572 patches from normal (class 1) and malignant (class 5) categories, respectively. This distribution of mammograms is tabulated in Table 2.
Table 2.
Summary of the databases used for experimentation
| Databases | Number of | Number of | Training cases | Testing cases | ||
|---|---|---|---|---|---|---|
| mammograms | patches | Malignant | Nonmalignant | malignant | Nonmalignant | |
| IRMA reference | – | 800 | 178 | 88 | 360 | 174 |
| (DDSMpatches) | ||||||
| DDSM | 200 | 1,264 | 285 | 135 | 572 | 272 |
Performance Measures
Performance of the proposed CAD system is evaluated in terms of sensitivity and specificity. Sensitivity measures the proportion of actual positives which are correctly identified as malignant, and specificity measures the proportion of actual negative which are correctly identified as nonmalignant negative. These are calculated as follows:
| 20 |
| 21 |
where, TP, FP, TN, and FN denote true positive, false positive, true negative, and false negative, respectively.
Experiment Results
Features are generated with different orders of Zernike moments. The aim is to achieve a higher sensitivity rate with as small feature size as possible. It has been observed that with k-NN classifier sensitivity of the proposed CAD system was low with low-order moments (below 20), but it increases with increasing order of moments. With SVM classifier sensitivity increases up to moments of order 20, but decreases with high-order moments. Table 3 compares the classification rates of both the classifiers with different orders of Zernike moments on the two datasets. All results of k-NN classifier are generated with k=10. RBF kernel function is used for SVM classifier.
Table 3.
Sensitivity and specificity achieved with the proposed CAD system
| Dataset | Order of Zernike moments | k-NN | SVM | ||
|---|---|---|---|---|---|
| Sensitivity | Specificity | Sensitivity | Specificity | ||
| IRMA reference DDSM | 20 | 0.83 | 0.77 | 0.99 | 0.99 |
| 25 | 0.94 | 0.90 | 0.97 | 0.96 | |
| 30 | 0.95 | 0.91 | 0.94 | 0.94 | |
| 35 | 0.97 | 0.92 | 0.91 | 0.91 | |
| DDSM | 20 | 0.89 | 0.88 | 0.96 | 0.96 |
| 25 | 0.90 | 0.89 | 0.92 | 0.90 | |
| 30 | 0.92 | 0.90 | 0.91 | 0.90 | |
| 35 | 0.94 | 0.93 | 0.89 | 0.90 | |
It is evident from Table 3 that SVM classifier performs better as compared to k-NN classifier. It gives a better classification rate at a small feature size. In general, a method is accurate if the percentage of both sensitivity and specificity is greater than 95 %. The system achieves 99 % TP rate for IRMA reference dataset (DDSM patches) with Zernike moments of order 20 and SVM classifier. It also gives 96 % TP rate for DDSM mammogram images. Achieving more than 96 % sensitivity and specificity at the moments of order 20 shows that the system is computationally efficient.
Table 4 compares features obtained with the Zernike moment sensitivity with two other well-known texture features: gray-level co-occurrence matrix (GLCM) and discrete cosine transform (DCT) for IRMA reference dataset (DDSM patches). GLCM gives 90 % sensitivity with SVM classifier, while the proposed system with Zernike moment gives 99 % sensitivity for the same dataset. The performance of the system with DCT features is only 78 %, which is not up to the mark. This shows that the proposed system performs well with Zernike moments used as features.
Table 4.
Results obtained with different texture features on IRMA reference dataset (DDSM patches)
| Feature vector | k-NN | SVM | ||
|---|---|---|---|---|
| Sensitivity | Specificity | Sensitivity | Specificity | |
| GLCM | 0.67 | 0.72 | 0.90 | 0.93 |
| DCT | 0.54 | 0.61 | 0.78 | 0.78 |
| Zernike | 0.83 | 0.87 | 0.99 | 0.99 |
Objective comparison of the performance of different CAD methods is difficult due to the use of different datasets, feature sets, and classification methods [8]. Even if a common dataset is used to test different methods, different preprocessing steps used by various researchers lead to development of CAD systems with varied accuracy. In most of the works, the size of feature vector is not mentioned, which is an important aspect in case the system is to be deployed for real-time applications. Moreover, different performance measures are used by researchers, and hence, a direct comparison of approaches is not possible. In order to compare different CAD systems, Table 5 summarizes the performance of the proposed system along with other existing methods in this field. Although various classifiers are used in these works, it is clearly visible that most of the existing methods rely on the SVM classifier. The results achieved by the proposed system are quite promising.
Table 5.
Comparison with other techniques
| Methods | Features | Classifier | Dataset | Results |
|---|---|---|---|---|
| Proposed method | Zernike | SVM | IRMA | 99 % Sensitivity |
| (texture descriptor) | reference | 99 % specificity | ||
| DDSM | ||||
| Proposed method | Zernike | SVM | DDSM | 96 % Sensitivity |
| (texture descriptor) | 96 % specificity | |||
| Tahmasbi et al. [43] | Zernike | MLP | MIAS | 97.6 % Area under |
| (shape descriptor) | curve | |||
| Deserno et al. [11] | 2DPCA | SVM | IRMA reference DDSM | 80.07 % Accuracy |
| Alolfe et al. [2] | Texture and shape | k-NN | DDSM | 71.93 % Sensitivity |
| 75 % specificity | ||||
| Oliver et al. [35] | Local morphological | Gentle boost | MIAS, DDSM | 80 %Area |
| classifier | under curve | |||
| Oliver et al. [34] | Local binary | SVM | DDSM | 90 % Value index |
| pattern (LBP) | curve | |||
| Subashini et al. [42] | Statistical | SVM | MIAS | 94 % Accuracy |
| Varela et al. [46] | Gray level, | BPN | Private | 94 % Sensitivity |
| contour-related, | ||||
| and morphological | ||||
| Polakowski et al. [36] | Size, shape, | MLP | Private | 92 % TPR/FPR |
| and texture |
Conclusion
This work proposes a CAD system to classify malignant and nonmalignant mammogram patches. Suitable methods are suggested for preprocessing, which not only removes the artifacts, unwanted components, and extracts the breast region from its background but also helps to extract abnormal regions from mammograms. To avoid processing of whole mammogram, methods to extract fix-sized ROI patches are also proposed. The Zernike moments-based texture feature extraction technique is used to recognize the pattern of malignancy/nonmalignancy in the mammogram patches. The variations in the results are observed by experimenting with the low- and high-order Zernike moments. Experiments are performed with other well-known texture descriptors GLCM and DCT, and it is observed that the proposed CAD system works well with Zernike moments. SVM with RBF kernel attains the highest sensitivity and specificity values at lower orders of Zernike moments. The proposed CAD system improves the accuracy of diagnosis and promises to perform a second-reader role.
Contributor Information
Shubhi Sharma, Email: shubhi.sharma@iiitdmj.ac.in.
Pritee Khanna, Email: pkhanna@iiitdmj.ac.in.
References
- 1.Alolfe MA, Mohamed WA, Youssef A, Mohamed AS, Kadah YM: Computer aided diagnosis in digital mammography using combined support vector machine and linear discriminant analysis classification. In: 16th IEEE International Conference on Image Processing (ICIP). IEEE, 2009, pp 2609–2612
- 2.Alolfe MA, Youssef A, Kadah YM, Mohamed AS: Development of a computer-aided classification system for cancer detection from digital mammograms. In: Radio Science Conference, NRSC 2008. National, IEEE, 2008, pp 1–8
- 3.Astley S, Hutt I, Miller P, Rose P, Taylor C, Boggis C, Adamson S, Valentine T, Davies J, Armstrong J: Automation in mammography: computer vision and human perception. Int J Pattern Recognit Artif Intell 7(06):1313–1338, 1993
- 4.Bagui SC, Bagui S, Pal K, Pal NR: Breast cancer detection using rank nearest neighbor classification rules. Pattern Recognit 36(1):–34, 2003
- 5.Balakumaran T, Vennila I: Detection of microcalcification clusters in digital mammograms using multiresolution based foveal algorithm. In: World Congress on Information and Communication Technologies (WICT). IEEE, 2011, pp 657–660
- 6.Bovik AC: Handbook of image and video processing. Access Online via Elsevier, 2010
- 7.Chan HP, Doi K, VYBRONY CJ, Schmidt RA, Metz CE, Lam KL, Ogura T, Wu Y, MacMahon H: Improvement in radiologists’ detection of clustered microcalcifications on mammograms: the potential of computer-aided diagnosis. Investig Radiol 25(10):1102–1110, 1990 [DOI] [PubMed]
- 8.Cheng H, Shi X, Min R, Hu L, Cai X, Du H: Approaches for automated detection and classification of masses in mammograms. Pattern Recognit 39(4):646–668, 2006
- 9.Cheng HD, Cai X, Chen X, Hu L, Lou X: Computer-aided detection and classification of microcalcifications in mammograms: a survey. Pattern Recognit 36(12):2967–2991, 2003
- 10.Cortes C, Vapnik V: Support vector machine. Mach Learn 20(3):273–297, 1995
- 11.Deserno TM, Soiron M, de Oliveira JE, Araújo AdA: Computer-aided diagnostics of screening mammography using content-based image retrieval. In: SPIE Medical Imaging. International Society for Optics and Photonics, 2012, pp 831, 527–831,527
- 12.Dheeba J, Tamil Selvi S: Screening mammogram images for abnormalities using radial basis function neural network. In: IEEE International Conference on Communication Control and Computing Technologies (ICCCCT). IEEE, 2010, pp 554–559
- 13.Feig SA, Galkin B: Breast microcalcifications: early warning for cancer. Diagn Imag November. 1990, pp 132–138
- 14.Ferrari R, Frere A, Rangayyan R, Desautels J, Borges R: Identification of the breast boundary in mammograms using active contour models. Med Biol Eng Comput 42(2):201– 208, 2004 [DOI] [PubMed]
- 15.Ferrari R, Rangayyan PR, Borges R, Frere A: Segmentation of the fibro-glandular disc in mammograms using gaussian mixture modelling. Med Biol Eng Comput 42(3):378–387, 2004 [DOI] [PubMed]
- 16.Ferrari R, Rangayyan R, Desautels J, Borges R, Frere A: Automatic identification of the pectoral muscle in mammograms. Trans Med Imaging IEEE 23(2):232–245, 2004 [DOI] [PubMed]
- 17.Fu J, Lee SK, Wong ST, Yeh JY, Wang AH, Wu H: Image segmentation feature selection and pattern classification for mammographic microcalcifications. Comput Med Imaging Graph 29(6):419–429, 2005 [DOI] [PubMed]
- 18.Giger ML: Computer-aided diagnosis in radiology. Acad Radiol 9(1):1–3, 2002 [DOI] [PubMed]
- 19.Gulsrud TO, Husoy JH: Optimal filter-based detection of microcalcifications. IEEE Trans Biomed Eng 48(11):1272–1281, 2001 [DOI] [PubMed]
- 20.Guzmán-Cabrera R, Guzmán-Sepúlveda J, Torres-Cisneros M, May-Arrioja D, Ruiz-Pinales J, Ibarra-Manzano O, Aviña-Cervantes G, Parada AG: Digital image processing technique for breast cancer detection: Int J Thermophys 34:1519–15311, 2012
- 21.Haddadnia J, Ahmadi M, Faez K: An efficient feature extraction method with pseudo-Zernike moment in RBF neural network-based human face recognition system. EURASIP J Appl Signal Process 2003:890–901, 2003
- 22.Heath M, Bowyer K, Kopans D, Moore R, Kegelmeyer P:The digital database for screening mammography. In: Proceedings of the 5th International Workshop on Digital Mammography. 2000, pp 212–218
- 23.Hwang SK, Kim WY: A novel approach to the fast computation of Zernike moments. Pattern Recognit 39(11):2065–2076, 2006
- 24.Jasmine JL, Govardhan A, Baskaran S: Microcalcification detection in digital mammograms based on wavelet analysis and neural networks. In: International Conference on Control, Automation, Communication and Energy Conservation(INCACEC). IEEE, 2009, pp 1–6
- 25.Kabbadj Y, Regragui F, Himmi MM: Microcalcification detection using a fuzzy inference system and support vector machines. In: International Conference on Multimedia Computing and Systems (ICMCS). IEEE, 2012, pp 312–315
- 26.Khotanzad A, Hong YH: Invariant image recognition by Zernike moments. IEEE Trans Pattern Anal Mach Intell 12(5):489–497, 1990
- 27.Ko JP, Naidich DP: Computer-aided diagnosis and the evaluation of lung disease. J Thorac Imaging 19(3):136–155, 2004 [DOI] [PubMed]
- 28.Lee SK, Lo CS, Wang CM, Chung PC, Chang CI, Yang CW, Hsu PC: A computer-aided design mammography screening system for detection and classification of microcalcifications. Int J Med Inform 60(1):29–57, 2000 [DOI] [PubMed]
- 29.Maitra IK, Nag S, Bandyopadhyay SK: Technique for preprocessing of digital mammogram. Comput Methods Prog Biomed 107(2):175–188, 2012 [DOI] [PubMed]
- 30.Mazurowski MA, Lo JY, Harrawood BP, Tourassi GD: Mutual information-based template matching scheme for detection of breast masses: From mammography to digital breast tomosynthesis. J Biomed Inform 44(5):815–823, 2011 [DOI] [PMC free article] [PubMed]
- 31.Mencattini A, Rabottino G, Salmeri M, Salicone S. Uncertainty propagation for the assessment of tumoral masses segmentation. In: IEEE International Workshop on Advanced Methods for Uncertainty Estimation in Measurement (AMUEM). IEEE, 2009, pp 39–43
- 32.Méndez AJ, Tahoces PG, Lado MJ, Souto M, Correa J, Vidal JJ: Automatic detection of breast border and nipple in digital mammograms. Comput Methods Programs Biomed 49(3):253–262, 1996 [DOI] [PubMed]
- 33.de Oliveira JEE, de Albuquerque Araújo A, Deserno TM: Content-based image retrieval applied to bi-rads tissue classification in screening mammography. World J Radiol 3(1):24, 2011 [DOI] [PMC free article] [PubMed]
- 34.Oliver A, Lladó X, Freixenet J, Martí J: False positive reduction in mammographic mass detection using local binary patterns. In: Medical Image Computing and Computer-Assisted Intervention–MICCAI. Springer, 2007, pp 286–293 [DOI] [PubMed]
- 35.Oliver A, Torrent A, Lladó X, Tortajada M, Tortajada L, Sentís M, Freixenet J, Zwiggelaar R: Automatic microcalcification and cluster detection for digital and digitised mammograms. Knowl-Based Syst 28:68–75, 2012
- 36.Polakowski WE, Cournoyer DA, Rogers SK, DeSimio MP, Ruck DW, Hoffmeister JW, Raines RA: Computer-aided breast cancer detection and diagnosis of masses using difference of Gaussians and derivative-based feature saliency. IEEE Trans Med Imaging 16(6):811–819, 1997 [DOI] [PubMed]
- 37.Ponraj DN, Jenifer ME, Poongodi P, Manoharan JS: A survey on the preprocessing techniques of mammogram for the detection of breast cancer. J Emerg Trends Comput Inf Sci 2(12):656–664, 2011
- 38.Rabottino G, Mencattini A, Salmeri M, Caselli F, Lojacono R: Mass contour extraction in mammographic images for breast cancer identification. 16th IMEKO TC4 Symposium, Exploring New Frontiers of Instrumentation and Methods for Electrical and Electronic Measurements, Florence, Italy. 2008
- 39.Rangayyan RM, Ayres FJ, Leo Desautels J: A review of computer-aided diagnosis of breast cancer: Toward the detection of subtle signs. J Frankl Inst 344(3):312–348, 2007
- 40.Rejani Y, Selvi ST: Early detection of breast cancer using SVM classifier technique. 2009, arXiv preprint arXiv:0912.2314
- 41.Shanthi S, Bhaskaran VM: Computer aided detection and classification of mammogram using self-adaptive resource allocation network classifier. In: International Conference on Pattern Recognition, Informatics and Medical Engineering (PRIME). IEEE, 2012, pp 284–289
- 42.Subashini T, Ramalingam V, Palanivel S: Automated assessment of breast tissue density in digital mammograms. Comp Vision Image Underst 114(1):33–43, 2010
- 43.Tahmasbi A, Saki F, Shokouhi SB: Classification of benign and malignant masses based on Zernike moments. Comput Biol Med 41(8):726–735, 2011 [DOI] [PubMed]
- 44.Tang J, Rangayyan RM, Xu J, El Naqa I, Yang Y: Computer-aided detection and diagnosis of breast cancer with mammography: recent advances. IEEE Trans Inf Technol Biomed 13(2):236–251, 2009 [DOI] [PubMed]
- 45.Tatiraju S, Mehta A: Image segmentation using k-means clustering, em and normalized cuts. University Of California Irvine, 2008
- 46.Varela C, Tahoces PG, Méndez AJ, Souto M, Vidal JJ: Computerized detection of breast masses in digitized mammograms. Comput Biol Med 37(2):214–226, 2007 [DOI] [PubMed]
- 47.Verma B, Zakos J: A computer-aided diagnosis system for digital mammograms based on fuzzy-neural and feature extraction techniques. IEEE Trans Inf Technol Biomed 5(1):46– 54, 2001 [DOI] [PubMed]
- 48.Wang W, Mottershead JE, Mares C: Mode-shape recognition and finite element model updating using the Zernike moment descriptor. Mech Syst Signal Process 23(7):2088– 2112, 2009
- 49.Xu S, Liu H, Song E: Marker-controlled watershed for lesion segmentation in mammograms. J Digit Imaging 24(5):754–763, 2011 [DOI] [PMC free article] [PubMed]
- 50.Xu W, Li L, Xu P: A new ann-based detection algorithm of the masses in digital mammograms. In: IEEE International Conference on Integration Technology (ICIT). IEEE, 2007, pp 26–30
- 51.Yu S, Guan L: A cad system for the automatic detection of clustered microcalcifications in digitized mammogram films. IEEE Trans Med Imaging 19(2):115–126, 2000 [DOI] [PubMed]
- 52.Zhang G, Yan P, Zhao H, Zhang X: A computer aided diagnosis system in mammography using artificial neural networks. In: International Conference on BioMedical Engineering and Informatics (BMEI). IEEE, 2008 vol 2, pp 823– 826
- 53.Zhang M, Chai Y, Wang J: An integrated method for breast mass segmentation in digitized mammograms. In: 3rd International Conference on Advanced Computer Control (ICACC). IEEE, 2011, pp 214–218