Computational Fluid Dynamics Investigation of Human Aspiration in Low Velocity Air: Orientation Effects on Nose-Breathing Simulations

Abstract

An understanding of how particles are inhaled into the human nose is important for developing samplers that measure biologically relevant estimates of exposure in the workplace. While previous computational mouth-breathing investigations of particle aspiration have been conducted in slow moving air, nose breathing still required exploration. Computational fluid dynamics was used to estimate nasal aspiration efficiency for an inhaling humanoid form in low velocity wind speeds (0.1–0.4 m s⁻¹). Breathing was simplified as continuous inhalation through the nose. Fluid flow and particle trajectories were simulated over seven discrete orientations relative to the oncoming wind (0, 15, 30, 60, 90, 135, 180°). Sensitivities of the model simplification and methods were assessed, particularly the placement of the recessed nostril surface and the size of the nose. Simulations identified higher aspiration (13% on average) when compared to published experimental wind tunnel data. Significant differences in aspiration were identified between nose geometry, with the smaller nose aspirating an average of 8.6% more than the larger nose. Differences in fluid flow solution methods accounted for 2% average differences, on the order of methodological uncertainty. Similar trends to mouth-breathing simulations were observed including increasing aspiration efficiency with decreasing freestream velocity and decreasing aspiration with increasing rotation away from the oncoming wind. These models indicate nasal aspiration in slow moving air occurs only for particles <100 µm.

INTRODUCTION

The ACGIH inhalable particulate mass (IPM) sampling criterion defines the desired collection efficiency of aerosol samplers when assessing exposures that represent what enters the nose and mouth of a breathing person. This criterion has been globally adopted by the ACGIH, CEN, and ISO and is given as:

$$\text{IPM = 0.5(1 + }{e}^{-\text{0.06}{d}_{ae}})$$ (1)

where d _ae is the aerodynamic diameter (1–100 µm) of a particle being sampled. In practical terms, human aspiration efficiency for a given particle size is defined as the ratio of particle concentration entering the nose/mouth to the concentration of particles in the worker’s environment. Ogden and Birkett (1977) were the first to present the idea of the human head as a blunt sampler. Original studies (Ogden and Birkett, 1977; Armbruster and Breuer, 1982; Vincent and Mark, 1982; and others) that formed the basis for the inhalable curve were conducted in wind tunnels with wind speeds ranging from 1 to 9 m s⁻¹, where mannequins inhaled particles. Concentrations aspirated by these mannequins were compared to uniform concentrations generated upstream of the mannequin to compute the aspiration efficiency of the human head. However, it is now known that the wind speeds investigated in these early studies were higher than the average wind speeds found in indoor workplaces. To determine whether human aspiration efficiency changes at these lower velocities, recent research has focused on defining inhalability at low velocity wind speeds (0.1–0.4 m s⁻¹), more typical for indoor workplaces (Baldwin and Maynard, 1998). At these low velocities, however, it becomes experimentally difficult to maintain uniform concentrations of large particles in wind tunnels large enough to contain a human mannequin, as gravitational settling of large particles couples with convective transport of particles travelling through the wind tunnel. However, Hinds et al. (1998) and Kennedy and Hinds (2002) examined aspiration in wind tunnels at 0.4 m s⁻¹, and Sleeth and Vincent (2009) developed an aerosol system to examine aspiration using mannequins in wind tunnels with 0.1 m s⁻¹ freestream.

To examine the effect of breathing pattern (oral versus nasal) on aspiration, mannequin studies have incorporated mechanisms to allow both oral and nasal breathing. It has been hypothesized that fewer particles would enter the respiratory system during nasal breathing compared to mouth breathing because particles with significant gravitational settling must change their path by as much as 150° to move upwards into the nostrils to be aspirated (Kennedy and Hinds, 2002). Hinds et al. (1998) investigated both facing-the-wind and orientation-averaged aspiration using a full-sized mannequin in wind tunnel experiments at 0.4, 1.0, and 1.6 m s⁻¹ freestream velocities and cyclical breathing with minute volumes of 14.2, 20.8, and 37.3 l and found oral aspiration to be larger than nasal aspiration, supporting this theory. They reported that nasal inhalability followed the ACGIH IPM curve for particles up to 30 µm, but beyond that, inhalability dropped quickly to <10% at 60 µm.

Calm air studies, however, found different trends. Aitken et al. (1999) found no difference between oral and nasal aspiration in a calm air chamber using a full-sized mannequin breathing at tidal volumes of 0.5 and 2 l at 1–40 breaths per minute in a sinusoidal pattern, while Hsu and Swift (1999) found much lower aspiration for nasal breathing compared to oral breathing in their mannequin study. Others examined calm air aspiration using human participants. Breysse and Swift (1990) used radiolabeled pollen (18–30.5 µm) and wood dust [geometric mean (GM) = 24.5 µm, geometric standard deviation (GSD) = 1.92] and controlled breathing frequency to 15 breaths per minute, while Dai et al. (2006) used cotton wads inserted in the nostrils flush with the bottom of the nose surface to collect and quantify inhaled near-monodisperse aluminum oxide particles (13–135 µm), while participants inhaled through the nose and exhaled through the mouth, with a metronome setting the participants’ breathing pace. Breysse and Swift (1990) reported a sharp decrease in aspiration with increasing particle size, with aspiration at 30% for 30.5-µm particles, projecting a drop to 0% at 40 µm by fitting the data to a nasal aspiration efficiency curve of the form 1–0.00066d ². Ménache et al. (1995) fit a logistic function to Breysse and Swift’s (1990) calm air experimental data to describe nasal inhalability, fitting a more complicated form, and extrapolated the curve above 40 µm to identify the upper bound of nasal aspiration at 110 µm. Dai et al. (2006) found similar trends, with nasal aspiration decreasing rapidly with particles 40 µm and larger for both at-rest and moderate breathing rates in calm air conditions, with nearly negligible aspiration efficiencies (<5%) at particle sizes 80–135 µm. Dai et al. found good agreement with Breysse and Swift (1990) and Kennedy and Hinds (2002) studies, but the mannequin results of Hsu and Swift (1999) were reported to under-aspirated relative to their in vivo data, with significant differences for most particle sizes for both at-rest and moderate breathing. Dai et al. (2006) attributes larger tidal volume and faster breathing rate by Aitken et al. (1999) to their higher aspiration compared to that of Hsu and Swift. Disagreement in the upper limit of the human nose’s ability to aspirate large particles in calm air, let alone in slowly moving air, is still unresolved.

More recently, Sleeth and Vincent (2009) examined both mouth and nasal aspiration in an ultralow velocity wind tunnel at wind speeds ranging from 0.1 to 0.4 m s⁻¹ using a full-sized rotated mannequin truncated at hip height and particles up to 90 µm. Nose-breathing aspiration was less than the IPM criterion for particles at 60 µm, but they reported an increased aspiration for larger particle sizes. However, the experimental uncertainties increased with increasing particle size and decreasing air velocity. They reported no significant differences in nasal aspiration between cyclical breathing flow rates of 6 l min⁻¹ and 20 l min⁻¹. Although significant differences in aspiration were seen between mouth and nose breathing at 6 l min⁻¹, no significant differences were seen at the higher 20 l min⁻¹ breathing rate. This work suggested markedly different aspiration efficiency compared to most calm air studies, with the exception of Aitken et al. (1999).

Conducting wind tunnel experiments at these low freestream velocities has inherent difficulties and limitations. Low velocity wind tunnel studies have difficulty maintaining a uniform concentration of particles due to gravitational settling, particularly as particle size increases, which introduces uncertainty in determining the reference concentration for aspiration calculations. Computational fluid dynamics (CFD) modeling has been used as an alternative to overcome this limitation (Anthony, 2010; King Se et al., 2010). CFD modeling allows the researcher to generate a uniform freestream velocity and particle concentration upstream of the inhaling mannequin. Use of computational modeling has been limited, however, by computational resources and model complexity, which limits the investigation of time-dependent breathing and omnidirectional orientation relative to the oncoming air. Previous research has used CFD to investigate orientation-averaged mouth-breathing inhalability in the range of low velocities (Anthony and Anderson, 2013). King Se et al. (2010) used CFD modeling to investigate nasal breathing, however their study was limited to facing-the-wind orientation. There have been numerous studies modeling particle deposition within the nasal cavity and thoracic region (Yu et al., 1998; Zhang et al., 2005; Shi et al., 2006; Zamankhan et al., 2006; Tian et al., 2007; Shanley et al., 2008; Wang et al., 2009; Schroeter et al., 2011; Li et al., 2012; among others); however, those studies generally ignore how particles enter the nose and focus only on the interior structure of the nose and head region and are of limited use to understanding how particles get into the nose from a work environment.

This study used CFD to provide additional insights into understanding how inhalable particles are aspirated into the nose when breathing as a worker’s orientation changes relative to oncoming, slow moving air. CFD simulations generated estimates of the airflow field around a simulated inhaling human (hereafter referenced as ‘humanoid’) and generated particle trajectory simulations to compute orientation-specific and orientation-averaged estimates of nasal aspiration efficiency. Resulting aspiration estimates were compared to reported wind tunnel study estimates, both facing the oncoming wind and omnidirectional. Variables examined in these aspiration estimates include freestream velocity, breathing rate, facial feature dimensions, and orientation relative to oncoming wind. This work also examined simplifications in the physical geometry of the nose used to represent an inhaling human (required geometry to accurately simulate the nostril) and the effect of numerical methods (turbulence model and wall functions) on estimates of aspiration to provide guidance for future model development.

METHODS

CFD modeling used Ansys Software (Ansys Inc., Lebanon, NH, USA) to generate the geometry and mesh and Fluent (Ansys Inc.) to solve fluid flow and particle trajectory equations. To examine orientation-averaged aspiration estimates, a series of simulations at seven discrete orientations relative to oncoming wind were performed. Aspiration efficiency was computed from particle trajectory simulations that identified the critical area, defined as the upstream area where all particles that travel through it would terminate in the nose of the inhaling humanoid. Specifics of each of these steps are detailed in the following. Table 1 summarizes the factors examined in this study.

Table 1.

Simulation variables examined in this work

			VelocityFreestream (m s−1)	Flow rateBreathing (l min−1)	Turbulence		# of Fluid simulations
Facial geometry	Nostril plane	Orientationa			k-epsilon Model	Wall functions
Small nose–small lips	Surface	0–180	0.1, 0.2, 0.4	7.5, 20.8	Standard	Standard	42
Small nose–small lips	Interior	0–90	0.2, 0.4	7.5, 20.8	Standard	Standard	20
Small nose–small lips	Surface	0–180	0.2	20.8	Realizable	Standard	7
Large nose–large lips	Surface	0–180	0.1	20.8	Standard	Enhanced	14
Large nose–large lips	Surface	0–180	0.4	7.5	Standard	Enhanced	14

^aSeven specific orientations, relative to oncoming wind, were: 0 (facing the wind), 15, 30, 60, 90, 135, 180°.

Geometry and mesh

A humanoid geometry with realistic facial features matching the 50th percentile female-US anthropometric dimensions with a simplified truncated torso was generated (Fig. 1). Previous studies have shown that truncation of the humanoid model will cause differences in the location of the critical area positions compared to a realistic anatomically correct model but not significantly impact aspiration efficiency estimates (Anderson and Anthony, 2013). Two facial geometries were investigated: small nose–small lip and large nose–large lip to determine how much the nose size affected aspiration efficiency estimates. The facial dimensions, neck, and truncated torso dimensions matched those from the models described in Anthony (2010). For clarity, the key dimensions are provided here. The head height was 0.216 m and width 0.1424 m; a cylindrical torso 0.1725 m deep and 0.2325 m wide represented the simplified torso; the small nose extended 0.009858 m in front of subnasale, while the large nose extended 0.022901 m; the furthest position of the lip relative to the mouth orifice extended 0.009615 m for small lips and 0.01256 m for large lips. Both the left and right sides of the humanoid were modeled, as the assumption of lateral symmetry was inappropriate at orientations other than facing the wind and back to the wind.

1.

Computational domain. Truncated torso positioned facing the wind.

Elliptical nostril openings were generated (Fig. 2). For the small nose–small lip geometry, the combined nostril surfaces had an area of 0.0001045 m². The area of the combined nostril surfaces for the large nose–large lips increased to 0.000189 m². For limited orientations (0–90°) and velocities (0.2 and 0.4 m s⁻¹, and at-rest and moderate breathing), two nasal opening configurations were investigated to examine the effect of the simplified velocity profile at the nasal opening plane. Using the small nose–small lip geometry, a simplified inhalation surface was located at the plane of the nose opening (referenced as ‘surface nostril plane’), and the more realistic simulations located the inhalation surface inside of the nose, on an elliptical cylinder that extended 10mm within the nose (‘interior nostril plane’). The increased nostril depth allowed for a more realistic fully developed velocity profile at the nasal entrance. Examination of the two nasal inlet geometries allowed the determination of model complexity necessary to investigate large particle aspiration.

2.

Humanoid head with small nose–small lip geometry (left) and large nose–large lip geometry (right). Arrows indicate the nostril plane surfaces where uniform velocities were specified for the surface and internal inlet plane simulations.

The center of the mouth opening was positioned at the origin (0, 0, 0) with a simulated wind tunnel positioned around the humanoid form. The wind tunnel extended 1.85 m upstream and 1.80 m downstream (X) of the mouth center and laterally (Y) to the walls by 1.14 m. The top of the wind tunnel was 0.875 m above the mouth center. The floor was positioned 0.375 m below the mouth center, at hip height. The dimensions of the wind tunnel were chosen to ensure no acceleration thorough the wind tunnel exit, that the entrance of the wind tunnel was far enough upstream for uniform velocity development, and that the blockage ratio was small (~11%).

Seven discrete orientation geometries of the humanoid model were investigated: 0, 15, 30, 60, 90, 135, and 180°. The humanoid geometry was rotated about the mouth center (0, 0, 0) to the humanoid’s left, which caused the right side of the face to project upstream as the form was rotated. This caused the bluff body centerline to shift from (0, 0, 0) for the facing-the-wind orientation to the +Y direction as rotation progressed through 90°. For the large nose–large lip geometry, the humanoid form was rotated to the right, which caused the bluff body centerline to shift in the opposite direction (−Y) as rotation progressed through 90°.

A paved meshing scheme (DesignModeler, Ansys, Inc.) was applied to the volume within the simulated wind tunnel, which used triangular surface and tetrahedral volume elements. Node counts on all surfaces were increased by a factor of 1.2 to generate three-mesh densities for convergence assessment. The node spacing was more refined around the nostrils (average node spacing = 0.3mm around the nasal openings) compared to the rest of the domain. The most refined mesh contained ~1.8 million nodes, at which the equations of fluid flow were solved. Additional details of the mesh densities for each geometry are provided in the Supplementary materials, available at Annals of Occupational Hygiene online.

Fluid simulations

Fluent software (V12.1 and V13.0; Ansys, Inc.) was used to solve equations of fluid flow. Fluid flow simulations were performed on 64-bit Windows 7 machines with 16 and 32 GB RAM and quad-core (single and dual) processors to maximize speed and computational storage during simulations. Nasal inhalation was represented with uniform inlet velocities applied to the surface of the nostril, to represent a steady suction with velocities equivalent to mean inhalation rates of 7.5 and 20.8 l min⁻¹, at-rest and moderate breathing rates, respectively. Velocity was adjusted by geometry (nose size, orientation) to ensure these volumetric flow rates were identical in matched simulations (i.e. small nose–small lip was 2.4 m s⁻¹ for at-rest and 5.7 m s⁻¹ for moderate; see Supplemental details, at Annals of Occupational Hygiene online, for exact settings). Uniform velocities of 0.1, 0.2, or 0.4 m s⁻¹ were applied to the wind tunnel entrance to represent the range of indoor velocities reported in occupational settings (Baldwin and Maynard, 1998). The wind tunnel exit was assigned as outflow to enforce zero acceleration through the surface while computing exit velocities. A plane of symmetry was placed at the floor of the wind tunnel, allowing flow along but not through the surface. The no-slip condition (‘wall’) was assigned to all other surfaces in the domain.

Fluid flow simulations used standard k-epsilon turbulence models with standard wall functions and full buoyancy effects. Additional investigations examined the effect of realizable k-epsilon turbulence models (small nose–small lip at 0.2 m s⁻¹ at moderate breathing, over all orientations) and enhanced wall functions (large nose–large lip at 0.1 m s⁻¹ and moderate breathing, 0.4 m s⁻¹, at-rest breathing) to evaluate the effect of different turbulence models on aspiration efficiency estimates. The realizable turbulence model has shown to be a better predictor of flow separation compared to the standard k-epsilon models and was examined to evaluate whether it improved simulations with back-to-the wind orientations (Anderson and Anthony, 2013).

A pressure-based solver with the SIMPLE algorithm was used, with least squares cell based gradient discretization. Pressure, momentum, and turbulence used second-order upwinding discretization methods. All unassigned nodes in the computational domain were initially assigned streamwise velocities equivalent to the inlet freestream velocity under investigation. Turbulent intensity of 8% and the ratio of eddy to laminar viscosity of 10, typical of wind tunnel studies, were used.

Velocity, turbulence, and pressure estimates were extracted over 3200 points ranging in heights from 0.3 m below to 0.6 m above the mouth center, laterally from ±0.75 m and 0.75 m upstream to just in front of the mouth opening (coordinates provided in Supplementary materials, at Annals of Occupational Hygiene online). Data were extracted from each simulation at each mesh density at global solution error (GSE) tolerances of 10⁻³, 10⁻⁴, and 10⁻⁵. Nonlinear iterative convergence was assessed by computing L2 error norms for each degree of freedom between successively smaller GSE values within a given mesh, and the target of <5% change was established a priori. Mesh independence was assessed using three-mesh error norms (R ₂, Stern et al., 2001) within a given simulation setup (orientation, freestream velocity, inhalation velocity). When local R ₂ was less than unity for all degrees of freedom, mesh independence was indicated (Stern et al., 2001). Once simulations met both convergence criterion (L2 < 5%, R ₂ < 1), particle simulations were performed.

Particle simulations

Particle simulations were performed using the solution from the most refined mesh with global solution tolerances of 10⁻⁵. Laminar particle simulations were conducted to locate the upstream critical area through which particles in the freestream would be transported prior terminating on one of the two nostril planes. Particle releases tracked single, laminar trajectories (no random walk) with 5500 (facing the wind) to 10000 steps (back to the wind) with 5×10⁻⁵ m length scale using spherical drag law and implicit (low order) and trapezoidal (high order) tracking scheme, with accuracy control tolerance of 10⁻⁶ and 20 maximum refinements. In order to fulfill the assumption of uniform particle concentration upstream of the humanoid, particles were released with horizontal velocities equal to the freestream velocity at the release location and vertical velocities equivalent to the combination of the terminal settling velocity and freestream velocity at that release location. Nonevaporating, unit density particles for aerodynamic diameters of 7, 22, 52, 68, 82, 100, and 116 µm were simulated to match particle diameters from previously published experimental aspiration data (Kennedy and Hinds, 2002) and to compare to previously simulated mouth-breathing aspiration data (Anthony and Anderson, 2013). This study did not quantify the contribution of secondary aspiration on nasal aspiration; thus particles that contacted any surface other than the nostril inlet surface were presumed to deposit on that surface.

Particle release methods were identical to that of the previous mouth-breathing simulations (Anthony and Anderson, 2013), summarized briefly here. Initial positions of particle releases were upstream of the humanoid away from bluff body effects in the freestream and effects of suction from the nose, confirmed to differ by <1% from the prescribed freestream velocity. Sets of 100 particles were released across a series of upstream vertical line releases (Z = 0.01 m, for spacing between particles ΔZ = 0.0001 m), stepped through fixed lateral positions (ΔY = 0.0005 m). The position coordinates and number of particles that terminated on the nostril surface were identified and used to define the critical area for each simulation. The size of the critical area was computed using:

$$A_{\text{critical}}\text{ = }{\displaystyle {\sum }_{\text{All }Y\text{,}Z}\Delta Y\Delta Z{N}_{\text{trapped}}}$$ (2)

where ΔY is the distance between successive lateral release locations (0.0005 m), ΔZ is the spacing between particles release (0.0001 m), and N _trapped is the number of particles terminating at the nostril surface. In addition, these coordinates were plotted to examine the shape of the critical areas associated with particle inhalation into the nose. We also examined the uncertainty in estimates of aspiration efficiency using this method by identifying the area one particle position beyond the last particle that was aspirated and computing the maximum critical area.

Aspiration efficiency calculation

Aspiration efficiency was calculated using the ratio of the critical area and upstream area to the nostril inlet area and inhalation velocity, using the method defined by Anthony and Flynn (2006):

$$A\text{ = }\frac{A_{\text{critical}}{U}_{\text{critical}}}{A_{\text{nose}}{U}_{\text{nose}}}$$ (3)

where A _critical is the upstream critical area, A _nose is the total area of the nostril openings, U _critical is the upstream freestream velocity within in the critical area, and U _nose is the inhalation velocity assigned to the total nostril areas.

Comparison of inhalability to the IPM criterion to rotating mannequin studies requires omnidirectional inhalability estimates. For this study, simulations were conducted at discrete angles (0, 15, 30, 60, 90, 135, and 180°) relative to the oncoming wind for each velocity condition. Orientation-averaged aspiration was calculated by weighting the orientation-specific aspiration by the proportion of a full rotation represented by that orientation, namely:

$$A\text{ = }\frac{\text{1}}{\text{24}}{A}_{\text{0}}\text{+}\frac{\text{1}}{\text{12}}{A}_{\text{15}}\text{+}\frac{\text{1}}{\text{8}}{A}_{\text{30}}\text{+}\frac{\text{1}}{\text{6}}{A}_{\text{60}}\text{+}\frac{\text{1}}{\text{24}}{A}_{\text{90}}\text{+}\frac{\text{1}}{\text{4}}{A}_{\text{135}}\text{+}\frac{\text{1}}{\text{8}}{A}_{\text{180}}$$ (4)

This method assumes lateral symmetry for left- and right-facing mannequins during rotation through 360°. A forward-facing estimate for aspiration was also computed using only orientations through 90°, weighed by the proportion of 180° covered:

$$A\text{ = }\frac{\text{1}}{\text{12}}{A}_{\text{0}}\text{+}\frac{\text{1}}{\text{6}}{A}_{\text{15}}\text{+}\frac{\text{1}}{\text{4}}{A}_{\text{30}}\text{+}\frac{\text{1}}{\text{3}}{A}_{\text{60}}\text{+}\frac{\text{1}}{\text{6}}{A}_{\text{90}}$$ (5)

Differences between the forward facing [equation (5)] and full rotation [equation (4)] allowed for an examination of the contribution of the back-to-the wind aspiration in the overall omnidirectional aspiration.

Data analysis

For each set of simulation parameters (i.e. breathing velocity, freestream velocity, facial feature dimensions), aspiration efficiency estimates for facing-the-wind (0°), forward-facing (±90°), and orientation-averaged (±180°) were generated and compared graphically and to the experimental data of Kennedy and Hinds (2002) and Sleeth and Vincent (2011). Comparisons between simulated aspiration estimates were made to quantify differences between turbulent model formulations, inlet surface position, and nose size, to understand the effect of model simplifications and formulations on the estimates for aspiration.

RESULTS AND DISCUSSION

Fluid dynamics

Fluid solutions were generated for the 83 unique fluid flow models indicated in Table 1. Approximately 6–10 days of simulation run time were require to achieve solutions at 10⁻⁵ tolerances for the most refined mesh densities for each geometry, velocity, and orientation combination.

Nonlinear convergence and mesh independence were evaluated (full data in Supplemental materials, at Annals of Occupational Hygiene online). The local L2 error norms were sufficiently below the a priori 5% level for all test conditions, indicating that the estimates of velocity, pressure, and turbulence parameters were changing <5% with subsequently lower GSE tolerances. The R ₂ error norms were below unity for all simulations except the 60° orientation at 0.4 m s⁻¹ freestream velocity and moderate breathing velocity, where exceedances were identified for all degrees of freedom.

To assess the performance of the wall functions in turbulence models, the Y+ values on all solid surfaces were examined throughout the domain. Although the Y+ values were >5 for simulations using the standard wall functions, tests showed that aspiration efficiency differed by <1% between simulations using standard wall functions and those using the enhanced wall functions.

Particle simulations and critical areas

The solution from most refined mesh at GSE tolerances of 10⁻⁵ were used to perform particle simulations. Aspiration estimates were determined for 581 combinations of particle and simulated fluid flow field. To determine critical areas, particle simulations required ~4–8h for a given particle per flow field-geometry solution. Longer times were necessary for the moderate breathing rate and lower freestream velocities, as critical areas were larger for these conditions.

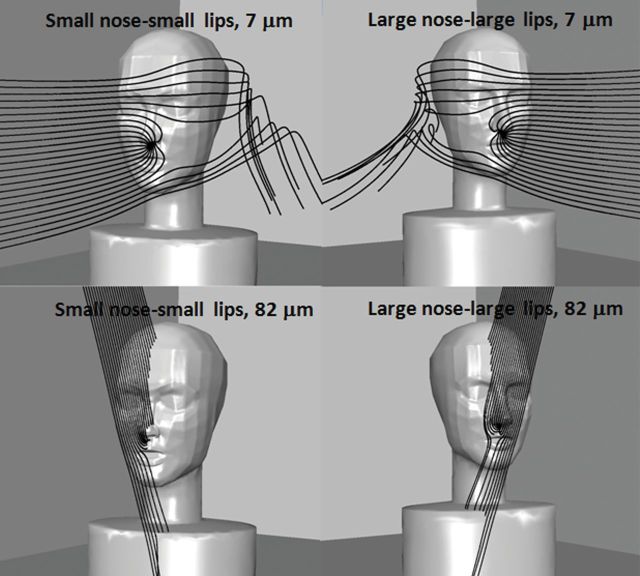
Illustrations of particle trajectory simulations are provided in Fig. 3, using 7- and 82-µm particles released in the 0.1 m s⁻¹ freestream velocity, and moderate breathing for both the small and large nose humanoid forms. The lines represent the path of particles from the upstream release location (Y = 0.02 m) with ΔZ spacing of 0.01 m between the initial position of each particle. The spacing for illustrations is coarser than those used for critical area determination, but illustrate particle movement around the head and torso. Particles terminating within the nose indicate particles were contained within the upstream critical area. Particle trajectories were similar to those seen for mouth-breathing simulations, where small (7 µm) particles followed the streamlines closely and particles with greater settling velocities (≥68 µm) had significantly downward trajectories prior to being inhaled through the nostril. These trends were similar regardless of nose geometry (small nose–small lips and large nose–large lip).

3.

Example particle trajectories for 0.1 m s⁻¹ freestream velocity and moderate inhalation simulations at 15° orientation. Each image shows 25 particles released upstream, at 0.02 m laterally from the mouth center. On the left is the small nose–small lips geometry; on the right is the large nose–large lips geometry.

Figs 4–6 provide an illustration of the shapes of upstream critical areas. Overall, as particle size increased, critical area size decreased, regardless of freestream velocity or inhalation velocity, as illustrated in the facing-the-wind critical areas in Fig. 4. This figure has expanded the horizontal scale relative to the vertical scale to illustrate features of the critical areas over all particle sizes studied. As freestream velocity increased, the size of the critical area decreased within a given particle size. The shape of the critical area was similar to the critical area shapes for mouth-breathing simulations for the facing-the-wind orientation (Anthony and Anderson, 2013), with the characteristic notch at the top center, caused by particles depositing on the nose tip for 7- and 22-µm particles. For particles >22 µm, the critical area separated into two distinct critical areas, one associated with each nostril. The separation of critical area into left and right illustrates the effect of particles impacting the surface of the nose (tip and subnasale), which is of particular interest for large particles that are affected by both convective and gravitational forces in low velocity environments. However, in truly turbulent air, the bifurcated critical areas might be less important when the random aspect of particle transport is incorporated into the particle simulations compared to the mean transport paths examined through the laminar simulations presented here. These critical areas are similar in shape to those presented for low breathing rate nose-breathing simulations of King Se et al. (2010; Fig. 8a).

4.

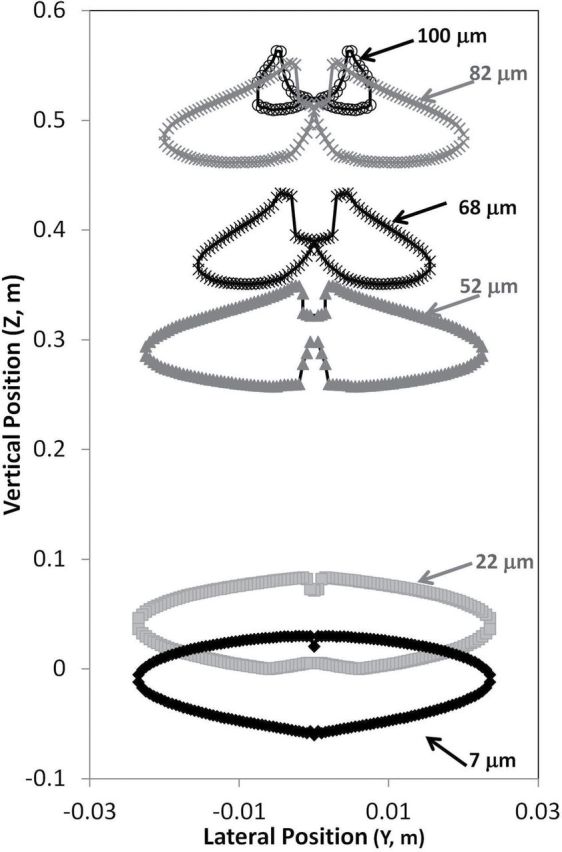
Upstream critical areas for small nose–small lips, surface nostril, at 0.2 m s⁻¹ freestream velocity, with mouth inhalation velocity equivalent to moderate breathing at facing-the-wind orientation for all particles sizes.

6.

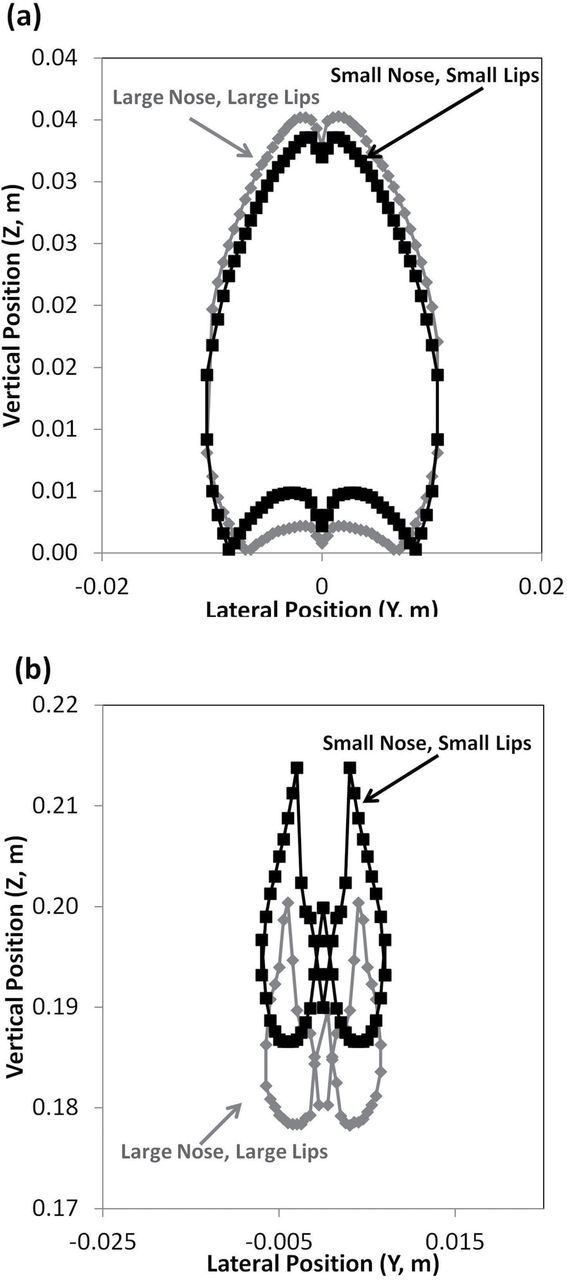
Upstream critical areas at 0.4 m s⁻¹ freestream velocity, with mouth inhalation velocity equivalent to at-rest breathing for facing-the-wind orientation for (a) 7-µm aerodynamic diameter particles and (b) 82-µm aerodynamic diameter particles.

8.

Representative illustration of velocity vectors for 0.2 m s⁻¹ freestream velocity, moderate breathing for small nose–small lip surface nostril (left side) and small nose–small lip interior nostril (right side). Regions of higher velocity (grey) are identified only immediately in front of the nose openings.

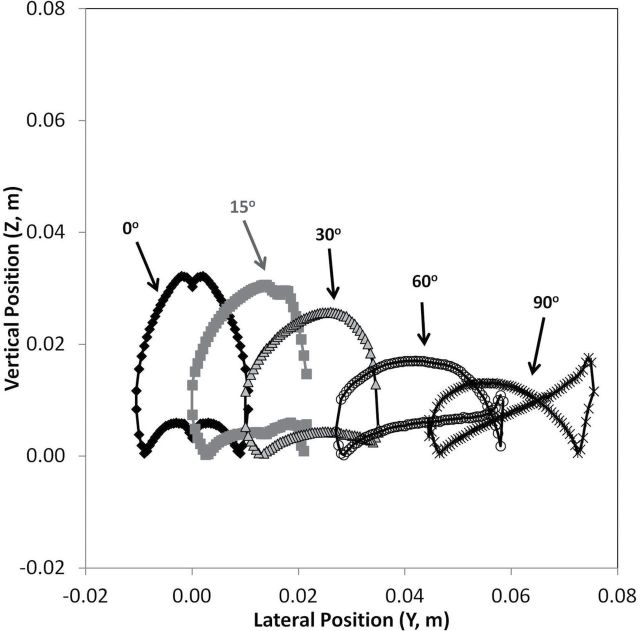
Fig. 5 illustrates the decreasing size and changing shapes for the critical areas with rotation. Similar to the previously reported mouth-breathing simulations, as the humanoid form rotated beyond 90°, inhaled particles terminated at the nostril by travelling both (i) above the top of the head and were transported back to the nose when caught in the wake and (ii) at lower positions and were transported directly to the face where they were captured by the suction from the nose. This trend continued for larger particles, with particles for the rear-facing orientations traveling over the top of the head to be aspirated. For the rear-facing orientations, suction velocity became more important to capture the particles moving in front of the nose.

5.

Upstream critical areas for small nose–small lips, surface nostril, at 0.2 m s⁻¹ freestream velocity, with moderate breathing for forward-facing orientations (0–90°) for 7-µm aerodynamic diameter particles.

Fig. 6 allows a visual comparison of the effect of nose size on critical area. While the critical areas for the large nose–large lip geometry were slightly larger (0.003008 m²) than the small nose–small lip geometry, the same overall trends were seen. Fig. 6 illustrates the position of the critical areas for the two nose size geometries: the areas are similar for the 7-µm particles, but at 82-µm particles, the position of the critical area was shifted downward ~1mm for the large nose–large lip geometry.

Aspiration efficiencies

Table 2 summarizes fractional aspiration efficiencies for all test conditions with standard k-epsilon simulations with the surface plane. The uncertainty in the size of critical areas associated with the particle release spacing in trajectory simulations was ±2%. Aspiration efficiency decreased with increasing particle size over all orientations, freestream velocities and inhalation velocities, for all geometries, as anticipated. In order for particles to be captured by the nose, an upward turn >90° above the horizon into the nasal opening was required. Low aspirations for 100- and 116-µm particles for all freestream and breathing rate conditions were observed, as inhalation velocities could not overcome the particle inertia.

Table 2.

Aspiration efficiency fraction for standard k-epsilon simulations by freestream velocity, breathing rate, nose size, orientation, and particle size

	Particle size, µm	Small nose–small lip, surface nostril plane			Large nose–large lip, surface nostril plane
		Facing the wind	Forward facinga	Orientation averagedb	Facing the wind	Forward facinga	Orientation averagedb
0.1 m s−1 freestream, moderate breathing	7	1.00	0.98	0.94	0.99	0.95	0.90
	22	0.98	0.96	0.87	0.96	0.93	0.85
	52	0.88	0.70	0.72	0.80	0.74	0.65
	68	0.74	0.71	0.68	0.64	0.59	0.56
	82	0.47	0.49	0.48	0.39	0.41	0.39
	100	0.11	0.11	0.11	0.04	0.17	0.16
	116	0.02	0.00	0.00	0.00	0.00	0.00
0.1 m s−1 freestream, at-rest breathing	7	1.01	0.97	0.93
	22	1.00	0.95	0.89
	52	0.87	0.80	0.78
	68	0.66	0.61	0.59
	82	0.31	0.31	0.30
	100	0.02	0.01	0.00
	116	0.00	0.00	0.00
0.2 m/s freestream, at-rest breathing	7	1.02	0.97	0.89
	22	1.01	0.93	0.86
	52	0.87	0.74	0.68
	68	0.67	0.53	0.52
	82	0.33	0.28	0.30
	100	0.00	0.02	0.04
	116	0.00	0.00	0.00
0.2 m s−1 freestream, moderate breathing	7	1.01	0.98	0.91
	22	0.99	0.95	0.89
	52	0.88	0.81	0.72
	68	0.73	0.66	0.60
	82	0.48	0.45	0.44
	100	0.13	0.13	0.15
	116	0.00	0.00	0.01
0.4 m s−1 freestream, at-rest breathing	7	1.03	0.96	0.87	0.99	0.95	0.79
	22	1.01	0.86	0.79	0.96	0.84	0.72
	52	0.85	0.42	0.45	0.71	0.35	0.29
	68	0.60	0.35	0.35	0.48	0.14	0.08
	82	0.31	0.16	0.19	0.23	0.02	0.01
	100	0.00	0.02	0.01	0.00	0.00	0.00
	116	0.00	0.00	0.00	0.00	0.00	0.00
0.4 m s−1 freestream, moderate breathing	7	1.02	0.98	0.93
	22	0.99	0.92	0.85
	52	0.86	0.66	0.56
	68	0.64	0.48	0.40
	82	0.42	0.24	0.23
	100	0.16	0.12	0.13
	116	0.00	0.02	0.01

^aEquation (5) was used to compute forward facing aspiration.

^bEquation (4) was used to compute orientation-averaged aspiration.

As seen in previous CFD investigations of mouth-breathing simulations (Anthony and Anderson, 2013), aspiration efficiency was highest for the facing-the-wind orientation and decreased with increasing rotation away from the centerline. As air approaches a bluff body, velocity streamlines have an upward component near the surface: for facing-the-wind orientations, this helped transport small particles vertically towards the nose. For rear-facing orientations, the bluff body effect is less important: to be aspirated into the nose, particles needed to travel over the head, then settle through the region of the nose, and finally make a 150° vertical turn into the nostril. The suction association with inhalation was insufficient to overcome the inertial forces of large particles that were transported over the head and into the region of the nose.

The nose size had a significant effect on aspiration efficiency, with the small nose–small lip geometry having consistently higher aspiration efficiencies compared to the large nose–large lip geometry for both velocity conditions investigated (Fig. 7). Because the nostril opening areas were proportional to the overall nose size, the larger nose had a larger nostril opening, resulting in a lower nostril velocity to match the same flow rate through the smaller nose model. These lower velocities resulted in less ability to capture particles. Differences in aspiration between the nose size geometry were more apparent at 0.4 m s⁻¹ freestream, at-rest breathing, where they ranged up to 27% (7.6% on average).

7.

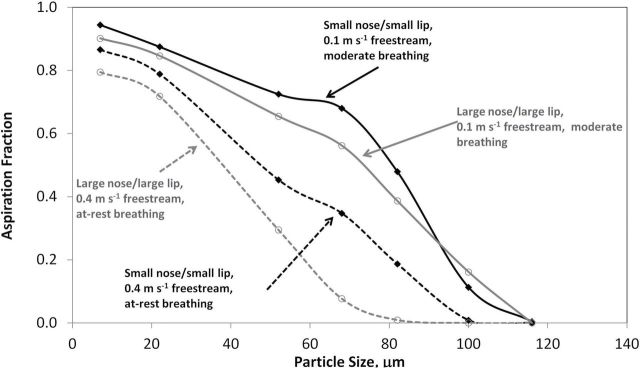
Orientation-averaged aspiration efficiency estimates from standard k-epsilon models. Solid lines represent 0.1 m s⁻¹ freestream, moderate breathing; dashed lines represent 0.4 m s⁻¹ freestream, at-rest breathing. Solid black markers represent the small nose–small lip geometry, open markers represent large nose–large lip geometry.

Assessment of simulation methods

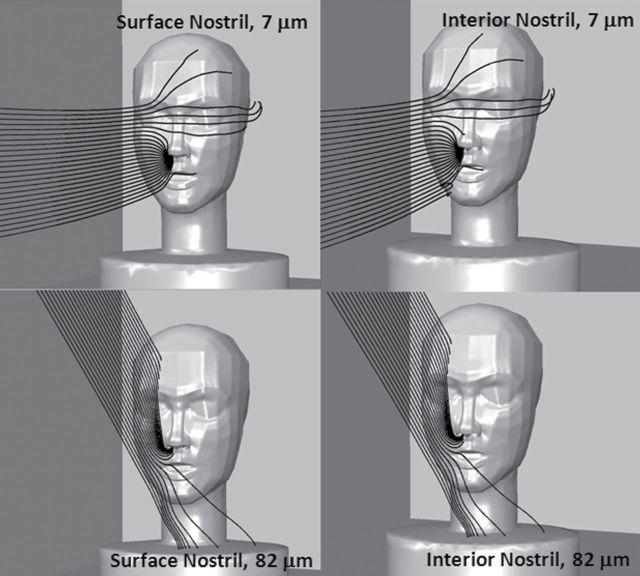
First examined was the effect of nostril depth on simulations of particle transport from the freestream into the nostrils. Fig. 8 illustrates that no discernible differences were identified in velocity contours approaching the nostril opening between simulations with a uniform velocity profile (surface nostril) and a fully developed velocity profile at the nose opening by setting a uniform velocity profile on a surface 10mm inside the nostril (interior nostril). Particle trajectories approaching the nose opening were similar for both nostril configuration methods (Fig. 9). However, once penetrating through the nostril opening, fewer large particles actually reached the interior nostril plane, as particles deposited on the simulated cylinder positioned inside the nostril. Fig. 8 illustrates 25 particle releases for two particle sizes for the two nostril configurations. For the 7-µm particles, the same particle counts were identified for both the surface and interior nostril planes, indicating less deposition within the surrogate nasal cavity. For the 82-µm particles, 18 of the 25 in Fig. 8 passed through the surface nostril plane, but none of them reached the internal nostril. Closer examination of the particle trajectories reveled that 52-µm particles and larger particles struck the interior nostril wall but were unable to reach the back of the nasal opening. All surfaces inside the opening to the nasal cavity should be set up to count particles as inhaled in future simulations. More importantly, unless interested in examining the behavior of particles once they enter the nose, simplification of the nostril at the plane of the nose surface and applying a uniform velocity boundary condition appears to be sufficient to model aspiration.

9.

Example particle trajectories (82 µm) for 0.1 m s⁻¹ freestream velocity and moderate nose breathing. Humanoid is oriented 15° off of facing the wind, with small nose–small lip. Each image shows 25 particles released upstream, at 0.02 m laterally from the mouth center. On the left is surface nostril plane model; on the right is the interior nostril plane model.

The second assessment of our model specifically evaluated the formulation of k-epsilon turbulence models: standard and realizable (Fig. 10). Differences in aspiration between the two turbulence models were most evident for the rear-facing orientations. The realizable turbulence model resulted in lower aspiration efficiencies; however, over all orientations differences were negligible and averaged 2% (range 0–14%). The realizable turbulence model resulted in consistently lower aspiration efficiencies compared to the standard k-epsilon turbulence model. Although standard k-epsilon resulted in slightly higher aspiration efficiency (14% maximum) when the humanoid was rotated 135 and 180°, differences in aspiration efficiency for the forward-facing orientations were −3.3 to 7%.

10.

Comparison of orientation-averaged aspiration for 0.2 m s⁻¹ freestream, moderate breathing by turbulence model. Solid line represents standard k-epsilon turbulence model aspiration fractions, and dashed line represents realizable turbulence model aspiration fractions.

Comparison to mannequin study findings

Simulated aspiration efficiency estimates were compared to published data in the literature, particularly the ultralow velocity (0.1, 0.2, and 0.4 m s⁻¹) mannequin wind tunnel studies of Sleeth and Vincent (2011) and 0.4 m s⁻¹ mannequin wind tunnel studies of Kennedy and Hinds (2002).

Sleeth and Vincent (2011) investigated orientation-averaged inhalability for both nose and mouth breathing at 0.1, 0.2, and 0.4 m s⁻¹ freestream velocities. Cyclical breathing rates with minute volumes of 6 and 20 l were used, which is comparable to the at-rest and moderate breathing continuous inhalation rates investigated in this work. Fig. 11 compares the simulated and wind tunnel measures of orientation-averaged aspiration estimates, by freestream velocity for the (i) moderate and (ii) at-rest nose-breathing rates. Similar trends were seen between the aspiration curves, with aspiration decreasing with increasing freestream velocity. Aspiration estimates for the simulations were higher compared to estimates from the wind tunnel studies, but were mostly within 1 SD of the wind tunnel data. The simulated and wind tunnel curves compared well at the 0.2 and 0.4 m s⁻¹ freestream velocity. At 0.1 m s⁻¹ freestream, aspiration for 28 and 37 µm for the wind tunnel data was lower compared to the simulated curve. Simulated aspiration efficiency for ≥68 µm was lower compared to the wind tunnel results.

11.

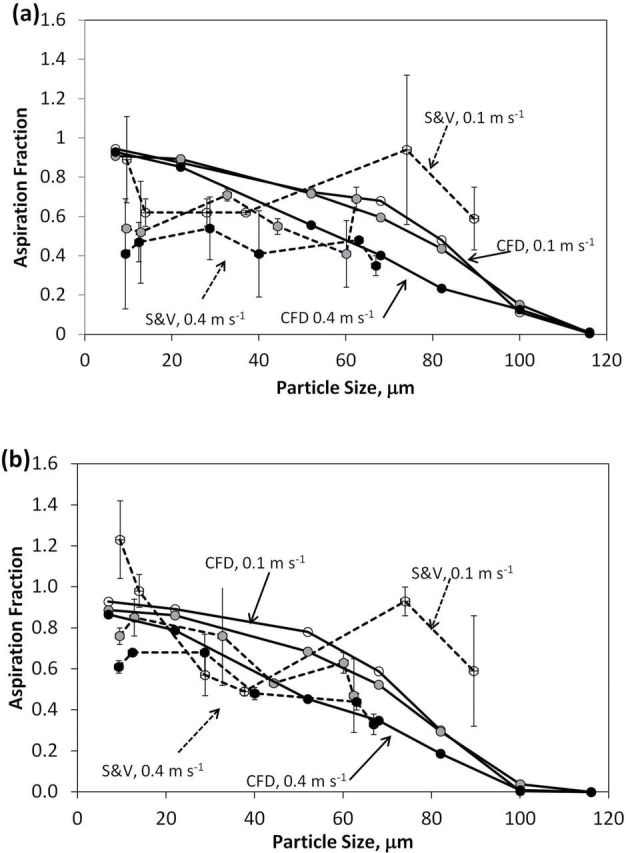
Orientation-averaged aspiration efficiency by freestream velocity, for moderate nose-breathing velocity for (a) moderate breathing and (b) at-rest breathing for CFD simulations (solid lines) compared to Sleeth and Vincent (2011) data (dashed lines). Open markers represent 0.1 m s⁻¹, grey markers represent 0.2 m s⁻¹, and black markers represent 0.4 m s⁻¹ freestream velocities.

Kennedy and Hinds (2002) investigated both orientation-averaged and facing-the-wind nasal inhalability using a full-sized mannequin rotated continuously in wind tunnel experiments. Simulated aspiration estimates for orientation-averaged, at 0.4 m s⁻¹ freestream velocity and at-rest nasal breathing, were compared to Kennedy and Hinds (2002) (Fig. 12). Simulated aspiration efficiency was within measurement uncertainty of wind tunnel data for particle sizes ≤22 µm, but simulated aspiration efficiency did not decrease as quickly with increasing particle size as wind tunnel tests. These differences may be attributed to differences in breathing pattern: the simulation work presented here identified suction velocity is required to overcome downward particle trajectories, and cyclical breathing maintains suction velocities above the modeled values for less than half of the breathing cycle. For nose breathing, continuous inhalation may be insufficient to adequately represent the human aspiration efficiency phenomenon for large particles, as simulations overestimated aspiration efficiency compared to both mannequin studies using cyclical breathing. The use of continuous inhalation velocity in these simulations also ignored the disturbance of air and particles from exhalation, which has been shown by Schmees et al. (2008) to have an impact on the air immediately upstream of the mannequin’s face which could affect particle transport and aspiration in this region.

12.

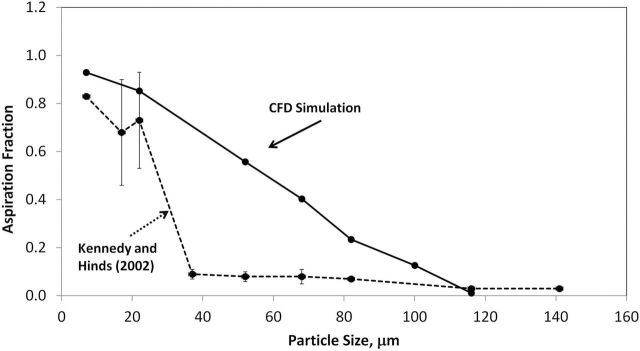
Orientation-averaged aspiration efficiency for 0.4 m s⁻¹ freestream, at-rest nose breathing compared for 0.4 m s⁻¹ freestream of Kennedy and Hinds (2002).

Fig. 13 compares the single orientation nasal aspiration from CFD simulations of King Se et al. (2010) to the matched freestream simulations (0. 2 m s⁻¹) of this work. Aspiration using laminar particle trajectories in this study yielded larger aspirations compared to turbulent simulations of King Se et al., employing a stochastic approach to simulations of critical area and which used larger nose and head than the female form studied here.

13.

Comparison of facing-the-wind orientation aspiration simulations at 0.2 m s⁻¹ freestream for nose breathing by King Se et al. (2010).

Other differences in this work include simplification of humanoid rotation. Instead of rotating the humanoid through all orientations in the current simulation, this investigation examined aspiration over discrete orientations relative to the oncoming wind and reported an angle-weighted average. This is a simplification from the real world where random motion of the workers would impact the freestream velocity. However, solving fluid flows for discrete orientations, inhalation, and freestream velocities allows for the examination of the relative contribution of each of these factors to the overall particle aspiration.

Finally, particle simplifications in these simulations excluded the secondary aspiration phenomenon and examination of only laminar (mean) trajectories to examine aspiration. Secondary aspiration, in this context, would occur when particles strike a surface, such as the face, and rebound back into the freestream prior to subsequently being inhaled. While wind tunnel studies have typically not attempted to reduce bounce on mannequin surfaces, the modeling of bounce would have resulted in increases in aspiration estimates, further separating the results of wind tunnel to simulation. In addition, turbulent particle tracking was not used in these simulations, and aspiration efficiencies of only mean transport paths (laminar) were evaluated. Thus, the effect of random motion of the velocity field on the particle paths cannot be assessed using laminar particle simulations.

While simplifications in the CFD simulations may have resulted in overestimates of aspiration efficiency compared to mannequin studies, the stepwise investigation of orientation and suction velocity provide insights into the phenomenon of aspiration into the nose and provide guidance into future modeling efforts. Using a simple nostril plane, just inside of the nose, provides reasonable agreement with setting internal plane. A larger nostril opening, associated with larger nose dimensions, resulted in decreased nasal aspiration given the same breathing rate, which may account for between-researcher differences in nose-breathing aspiration efficiency estimates.

CONCLUSIONS

This work expanded previous CFD simulations of large particle inhalability to include orientation-averaged aspiration estimates for nasal breathing. The same trends as seen in mouth-breathing CFD simulations were observed, namely that aspiration decreased with increasing particle size, that rotating in back toward the wind reduces the aspiration efficiency of the nose, and that there appears to be an upper size limit for aspiration efficiency with nose breathing (~100 µm). The CFD models identified the same trend of increased aspiration efficiency as freestream velocity decreases from 0.4 to 0.1 m s⁻¹. However, the orientation-averaged increase in aspiration with increasing particle size demonstrated in wind tunnel work (Sleeth and Vincent, 2011) was not observed in CFD simulations. Differences in breathing pattern (sinusoidal versus continuous inhalation) and rotation pattern (continuous rotation through ±180 versus stepwise evaluation at fixed intervals) may account for differences between simulated and laboratory studies of aspiration efficiency. From these CFD estimates, the impact of the breathing rate (as continuous velocity), freestream velocity, and nose size altered the estimates of nose-breathing aspiration efficiency by 5.7, 7.2, and 7.6%, respectively.

SUPPLEMENTARY DATA

Supplementary data can be found at http://annhyg.oxfordjournals.org/.

FUNDING

National Institute for Occupational Safety and Health, Centers for Disease Control (R01 OH009290).