Abstract
All aqueous humor draining through the conventional outflow pathway must cross the endothelium of Schlemm’s canal (SC), likely by passing through micron-sized transendothelial pores. SC pores are non-uniformly distributed along the inner wall endothelium, but it is unclear how the distribution of pores relates to the non-uniform or segmental distribution of aqueous humor outflow through the trabecular meshwork. It is hypothesized that regions in the juxtacanalicular tissue (JCT) with higher local outflow should coincide with regions of greater inner wall pore density compared to JCT regions with lower outflow.
Three pairs of non-glaucomatous human donor eyes were perfused at 8 mmHg with fluorescent tracer nanospheres to decorate local patterns of outflow segmentation through the JCT. The inner wall was stained for CD31 and/or vimentin and imaged en face using confocal and scanning electron microscopy (SEM). Confocal and SEM images were spatially registered to examine the spatial relationship between inner wall pore density and tracer intensity in the underlying JCT. For each eye, tracer intensity, pore density (n) and pore diameter (D) (for both transcellular “I” and paracellular “B” pores) were measured in 4-7 regions of interest (ROIs; 50 × 150 μm each). Analysis of covariance was used to examine the relationship between tracer intensity and pore density, as well as the relationship between tracer intensity and three pore metrics (nD, nD2 and nD3) that represent the local hydraulic conductivity of the outflow pathway as predicted by various hydrodynamic models.
Tracer intensity in the JCT correlated positively with local pore density when considering total pores (p = 0.044) and paracellular B pores on their own (p = 0.016), but not transcellular I-pores on their own (p = 0.54). Local hydraulic conductivity as predicted by the three hydrodynamic models all showed a significant positive correlation with tracer intensity when considering total pores and B-pores (p < 0.0015 and p < 10−4) but not I-pores (p > 0.38).
These data suggest that aqueous humor passes through micron-sized pores in the inner wall endothelium of SC. Paracellular B-pores appear to have a dominant contribution towards transendothelial filtration across the inner wall relative to transcellular I-pores. Impaired pore formation, as previously described in glaucomatous SC cells, may thereby contribute to greater outflow heterogeneity, outflow obstruction, and IOP elevation in glaucoma.
Introduction
The conventional outflow pathway is the predominant route of aqueous humor outflow, and the increase in intraocular pressure (IOP) associated with many cases of primary open angle glaucoma (POAG) is due to increased conventional outflow resistance (Grant, 1963). Within the conventional outflow pathway, the majority of outflow resistance appears to be generated in the vicinity of the inner wall endothelium of Schlemm’s canal (SC) and the juxtacanalicular tissue (JCT) (Lütjen-Drecoll, 1973; Mäepea and Bill, 1992), but the hydrodynamic details of how aqueous humor flows through these tissues remain unclear.
All conventional aqueous outflow must somehow filter across the inner wall endothelium of SC, presumably by passing through micron-sized pores in an otherwise continuous endothelium containing tight junctions (M. C. Johnson, 2006). In glaucoma, inner wall pore density is reduced by up to five-fold compared to normal eyes (Allingham et al., 1992; M. C. Johnson et al., 2002), suggesting that impaired pore formation may contribute to outflow obstruction and IOP elevation characteristic of glaucoma. Two types of pores exist: transcellular “I” pores that pass through individual SC cells, and paracellular “B” pores that pass through the junction between neighboring SC cells (Ethier et al., 1998). However, the contribution of each pore type to filtration across the inner wall and whether one pore type has a dominant role remain unknown.
Drainage through the conventional outflow pathway is non-uniform or segmental around the circumference of the trabecular meshwork (TM) (de Kater et al., 1989), over both a “macro” scale (order of mm) and over a “micro” scale (order of a few μm; Figure 1) (Chang et al., 2014; Lu et al., 2008). Furthermore, inner wall pores are non-uniformly distributed along the inner wall endothelium (Allingham et al., 1992). This study investigated the hypothesis that regions of higher local outflow co-localize with regions of higher local pore density along the inner wall of SC (Figure 2). To test this hypothesis, fluorescent tracer nanospheres were perfused into post mortem human eyes, SC was micro-dissected to visualize the inner wall en face, and correlative light and electron microscopy was used to image the distribution of tracer and location of pores along the inner wall. A spatial correlation was observed between local tracer intensity and local pore density, suggesting that at least some pores are fluid-conducting structures that respond to local mechanical stimuli induced by flow and/or pressure drop across the inner wall.
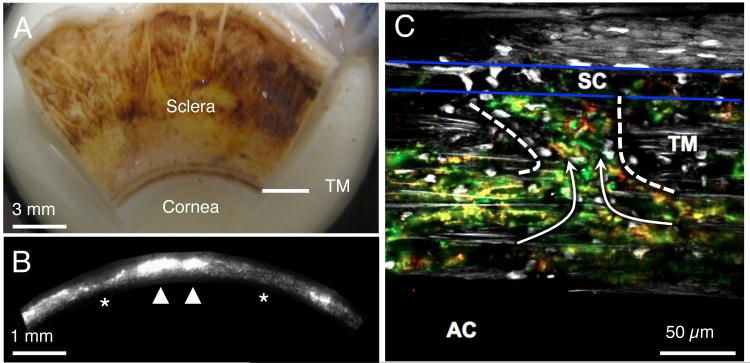
Figure 1.
Aqueous humor outflow is non-uniform, or segmental, around the circumference of the trabecular meshwork (TM) over both macroscopic (order of a few mm) and microscopic length scales (order of a few tens of μm). A) The internal face of a corneoscleral wedge of a human eye after removing the iris, ciliary body, retina and choroid. The TM is seen as a dense band of pigmented tissue located near the corneoscleral junction. B) A fluorescent micrograph of the internal surface of the TM in a human eye after perfusion with fluorescent tracer particles. The orientation is similar to the TM shown in panel A. Macroscopic segmental outflow variations are detected as variations in fluorescence intensity around the circumference of the TM containing active (arrowheads, stronger signal, more accumulated tracer) and less active (asterisks, weaker signal, less accumulated tracer) outflow regions. C) When looking at a microscopic section through the TM and SC (between blue lines), red and green tracer particles can be seen to pass through the TM and into SC (arrows) through the preferential pathway (within dashed lines Panels A-C are reproduced from Chang et al. 2014 (Chang et al., 2014) and permission will be requested from the publisher.
Figure 2.
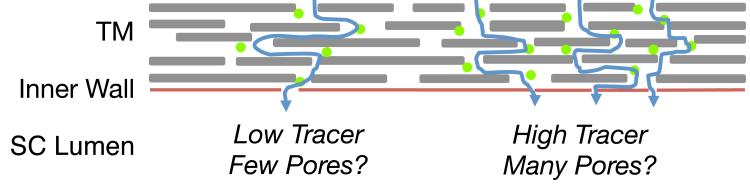
Schematic illustration of the hypothesis motivating this study. Outflow through the trabecular meshwork (TM) is non-uniform or segmental (curved blue arrows) such that some regions of the TM have high local outflow, and hence high local tracer accumulation, relative to regions with low outflow and low tracer accumulation. We hypothesize that regions of high local tracer intensity colocalize with regions of high local pore density along the inner wall of Schlemm’s canal (SC).
Methods
Reagents
Dulbecco’s phosphate buffered saline (DPBS), glucose, gelatin, Triton X-100, tannic acid, guanidine hydrochloride and goat serum were acquired from Sigma Aldrich (Austin, TX, USA). Glutaraldehyde, formaldehyde, ethanol, osmium tetroxide and hexamethyldisilazane were purchased from EMS Diasum (Hatfield, PA, USA). Fluorescent tracer nanospheres (20 nm, sulfate-coated; F8845), Alexa647 goat anti-mouse IgG, Alexa 546 goat anti-rabbit and DAPI were obtained from Life Technologies (Austin, TX, USA). Mounting medium and mouse anti-human CD31 antibody (clone JC70A) were obtained from DAKO (Glostrup, Denmark). Rabbit anti-human vimentin antibodies (clone EPR3776) were obtained from Abcam (Cambridge, MA, USA).
Whole Eye Perfusion
Three pairs of ostensibly normal human eyes were obtained from donors aged 67, 78 and 80 through the Eye Bank of Canada (Ontario Division, Toronto, Canada), Table 1. The temperature of the eye was maintained by submersion in a bath of DPBS at 34°C. A needle was inserted through the cor nea with the tip positioned in the posterior chamber, and the eye was perfused at a constant pressure of 8 mmHg following established methods (Ethier et al., 1998; 1993). The perfusion fluid was DPBS containing CaCl2, MgCl2 and 5.5 mM glucose that was filtered through a 0.22 μm syringe filter prior to use (referred to as ‘DBG’). After perfusion with DBG for 45 – 90 minutes to measure baseline outflow facility (Table 1), the anterior chamber was exchanged with DBG containing 0.005% w/v fluorescent tracer nanospheres. After the exchange, the eye was perfused for 30 minutes with tracer to label the patterns of outflow through the TM, while recording ‘tracer’ facility (Table 1). The anterior chamber was then exchanged with either DBG alone or DBG containing 2% gelatin, and the eye was perfused until it reached a steady ‘post-tracer’ facility (Table 1) typically within 30 – 40 minutes. Gelatin was used to preserve the distribution of tracer within the tissue, following Johnson et al. (M. C. Johnson et al., 1990), but gelatin did not appear to affect outflow facility when compared to the paired control eye. The perfusion was terminated by clamping the perfusion tubing and then immediately placing the eyes on wet ice for 15 – 20 minutes. The perfusion needles were kept in place during the cooling period, but with the tubing clamped, the pressure in the eye decreased slowly over several minutes on account of drainage through the conventional outflow pathway. Following the cooling period, the globes were cut open near the equator and immersion fixed in ice cold 3% formaldehyde in DBG.
Table 1.
Donor and perfusion information. “Tracer” facility was the average facility measured during tracer perfusion. “Post-Tracer” facility was the average facility measured during the period after the anterior chamber was exchanged and perfused with DBG (with or without gelatin).
| Eye | Sex | Age | Time [hrs Post Mortem] | Facility [μL/min/mmHg] | Gelatin | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Number | L/R | Comments | Enucleation | Perfusion | Baseline | Tracer | Post-Tracer | Present | ||
| 649 | L | None | M | 67 | 5 | 34 | 0.30 | 0.20 | 0.17 | No |
| 650 | R | Aphakic | 0.16 | 0.10 | 0.10 | Yes | ||||
|
| ||||||||||
| 669 | L | None | F | 80 | 1 | 22 | 0.10 | 0.15 | 0.09 | No |
| 670 | R | None | 0.12 | 0.20 | 0.16 | Yes | ||||
|
| ||||||||||
| 681 | R | Pseudophakic | M | 78 | 6 | 28 | 0.30 | 0.25 | 0.17 | No |
| 682 | L | Pseudophakic | 0.19 | 0.18 | 0.18 | Yes | ||||
Dissection
The eyes were hemisected, the vitreous humor and lens were removed and the anterior segment was cut into quadrants. Each quadrant was cut into wedges for microdissection to expose approximately 2-3 mm along the circumference of the inner wall en face, as previously described (Ethier et al., 2004). Briefly, the tissue wedges containing the inner wall, JCT and TM, were separated from the ciliary body and iris root. SC was incised along its posterior margin and opened such that the TM and adherent inner wall of SC could be reflected anteriorly. The inner wall and underlying TM were fluorescently stained for the endothelial marker CD31, the intermediate filament vimentin, and the nuclear stain DAPI. Specifically, the tissue was permeabilized at room temperature (RT) for 5 minutes with 0.2% Triton X-100 in DPBS and blocked at RT for 30 minutes with 10% goat serum. Tissue was then labeled with mouse anti-human CD31 IgG (dilution 1:30) and rabbit anti-human Vimentin IgG (1:200) overnight at 4°C. After three 5 minute washes with DPBS, the tissue was incubated with Alexa 647 goat anti-mouse IgG (1:150) and Alexa 546 goat anti-rabbit IgG (1:150) overnight at 4°C. Nega tive controls were prepared as above, omitting the primary antibodies. Finally, nuclei were labeled by incubating the tissue for 5 min at RT in 2 μg/mL DAPI in DPBS.
Imaging
One tissue wedge was imaged per eye using first confocal microscopy (to visualize tracer, CD31, vimentin and DAPI) and then scanning electron microscopy (SEM; to visualize pores). For confocal imaging, each wedge was mounted in fluorescent mounting medium and oriented such that the inner wall of SC faced upwards, overlying the adjacent JCT/TM. The tracer (Ex: 505nm/Em: 515nm), CD31 (650/665), vimentin (556/573) and DAPI (358/461) were imaged en face using a Zeiss LSM 510 meta confocal microscope with a 25x/0.8NA objective. Images were obtained as a z-stack starting several microns above the inner wall and stretching 50 – 80 μm deep into the TM. Each confocal image was corrected for uneven illumination by dividing local intensities by those from the corresponding location of a reference image taken from a well-mixed solution of fluorescent tracer. The entire surface of the inner wall (as indicated by CD31) was imaged, such that the z-stacks could be tiled together to create a complete montage for each wedge using a plug-in executed in FIJI (NIH, MD, USA) and developed by Preibisch et al. (Preibisch et al., 2009). Montages of CD31 and vimentin were created using tiles based on the maximum intensity projection through each stack. However, the tracer stacks were processed to create tiles that showed tracer in only the JCT lying within 10 μm of the inner wall. To do this, the z-position of the inner wall was defined for each pixel using a surface spline that was fit through the z-position of the maximum CD31 intensity for each x,y pixel location. The tracer pixel intensity values were then averaged across the voxels lying within 10 μm below the inner wall for each pixel location, and this value was defined as the JCT tracer intensity for the corresponding pixel. Note that this approach eliminates the influence of tracer that lies outside of the JCT while allowing the z-position of the inner wall to change across the montage, thus accounting for inner wall undulations.
After the confocal montage was complete, the tissue was unmounted and prepared for SEM to visualize pores along the inner wall. The tissue was rinsed in DPBS overnight at 4°C to remove the mounting media and then post-fixed in universal fixative (2.5% (v/v) glutaraldehyde and 2% (w/v) formaldehyde in Sørensen’s Buffer) overnight at 4°C. The tissue was then incubated in 2% (w/v) tannic acid, 2% (w/v) guanidine hydrochloride in DPBS for two hours, followed by one hour in 1% (w/v) osmium tetroxide in DPBS. Between each solution change, the tissue was rinsed thoroughly in DPBS. The tissue specimen was then dehydrated through a graded ethanol series, followed by two changes in hexamethyldisilazane, air-dried, mounted on stubs with carbon cement, and sputter-coated with gold. An overview montage, composed of several contiguous smaller image tiles, was acquired to show the entire inner wall surface within the wedge at 300x magnification by SEM (Hitachi S-3400N VP). The overview montage was used to identify regions of damaged inner wall, to guide the selection of regions for analysis, and to perform the image registration between the confocal and SEM montages (described below). Pore counting was not performed using the overview montage but rather using SEM micrographs that were re-imaged at higher magnification (10,000x; see below).
Image Registration
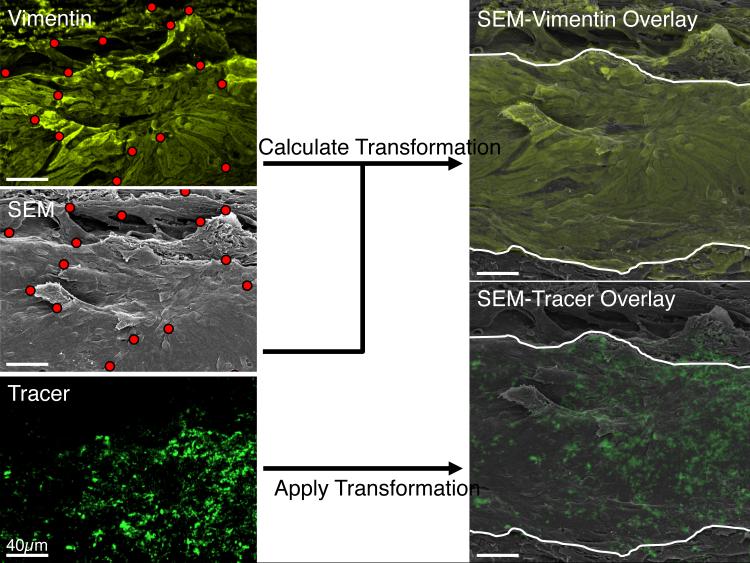
In order to investigate the spatial relationship between tracer and pores, it was necessary to spatially register the confocal and SEM montages such that the same physical point along the inner wall appeared at the same location in both images. However, tissue shrinkage during processing and differences in tissue orientation between imaging sessions led to image distortion that prevented a simple overlay of the confocal and SEM micrographs. This distortion was corrected by mapping each confocal montage onto the corresponding SEM montage using an image registration algorithm. Briefly, the image registration algorithm used common landmarks that were manually identified in the confocal and SEM montages to establish a transformation function that, when applied to the confocal montage, deformed the confocal montage in such a way that the common landmarks overlapped with those in the SEM montage. To do this, between 48 and 80 reference points were selected in the CD31 montage (for eyes 649C and 650D) or in the vimentin montage (for eyes 669B, 670B, 681B and 682D) and manually matched to corresponding reference points on the SEM montage. The coordinate positions of the pixels at each reference point were used to calculate the mathematical mapping transformation using the ‘cp2tform’ function in MATLAB (v2014a, Mathworks, Natick, MA, USA) with a linear weighted mean optimization (Goshtasby, 1988). The same mapping transformation was then applied to the tracer montage so as to spatially register the tracer and SEM montages (Figure 3).
Figure 3.
A summary of the image registration algorithm used to map the confocal montage onto the overview scanning electron microscopic (SEM) montage so as to allow colocalization analysis between tracer intensity and inner wall pore density. Common landmarks (red dots) observed along the inner wall within the vimentin (top left) or CD31 montage (not shown) were manually selected and matched to the same physical landmarks in the SEM montage (middle left). A mapping algorithm then calculated the mathematical transformation that, when applied to the vimentin (or CD31) montage, allowed the corresponding landmarks to overlap those in the SEM montage (top right) with good precision (cf. Figure 4). The same mathematical transformation was then applied to the tracer montage (bottom left), providing a co-registered SEM-tracer overlay that was used for colocalization analysis between tracer intensity and pore density (bottom right). The white curves in the right panels represent the anterior and posterior boundaries of the inner wall, determined from the CD31 labeling (not shown).
Colocalization Analysis
This study compared the fluorescent tracer intensity and pore density measured within individual regions of interest (ROIs) along the inner wall of SC. Typically, 4 – 7 ROIs were examined per tissue wedge, with 31 ROIs in total, and data from each ROI yielded a single data-point for the colocalization analysis between tracer intensity and pore density. The ROI area (7,500 μm2) was chosen to contain a sufficient number of pores (~ 62 pores, assuming a pore density of 835 pores/mm2 (M. C. Johnson et al., 2002)) to allow a robust sampling of the local pore density. The ROI aspect ratio (50 μm × 150 μm) was chosen to approximate the aspect ratio of the inner wall as viewed en face, with the long edge of the ROI oriented parallel to the long axis of the inner wall. Each ROI was defined within the SEM and transformed confocal montages, and the location of each ROI was chosen based on the presence of continuous CD31 staining, representing a continuous region of the inner wall that was free of cracks, debris or other damage as seen in the SEM montage. To maximize the range and provide sufficient leverage for the colocalization analysis, ROIs were typically chosen from regions with very high or very low tracer intensity, with some ROIs covering regions of moderate tracer intensity. Within each ROI the tracer intensity (TI) was measured as the average pixel intensity over the ROI area in the transformed tracer montage. Note that the pixel intensities in the tracer montage represent the depth-wise averaged pixel intensity of the tracer channel in the JCT region within 10 μm of the inner wall (see above).
After ROIs were defined, each ROI was then re-imaged by SEM for pore counting. First, an image at 1500x magnification was acquired to identify any potential pore-like object, and all pore-like objects were then re-imaged at 10,000x magnification. Each 10,000x image was assigned a random identification number to mask any relationship with the ROI, and the masked images were distributed to at least three observers who independently assessed each pore-like object to distinguish true pores from artifacts and to identify pore type (I or B). Pore-like objects were identified as pores if they had a smooth, flat, approximately elliptical boundary and a dark interior. Pores that fell on the border of the ROI were included only if they fell on the left or upper border. Any discrepancies in pore identification were discussed during a panel meeting until a consensus was reached, and only after all pore decisions were finalized was the image key broken. The number of pores and pore density (n, equal to the number of pores divided by the ROI area) was then calculated for each ROI, and pore diameter (D) was computed from the measured pore area A as: . Several higher order moments of the pore diameter (nD, nD2, nD3) were also calculated, motivated by hydrodynamic models of flow through pores, as described below.
Hydrodynamic models of inner wall hydraulic conductivity
In addition to pore density, the pore diameter may also influence the local accumulation of tracer along the inner wall. Under the assumption that the tracer distribution represents the distribution of aqueous humor filtration across the inner wall, the local tracer intensity should be proportional to the local hydraulic conductivity (Lp1) of the outflow pathway that includes the JCT and the inner wall endothelium. Because this study did not directly assess the hydraulic properties of the JCT, the hydraulic conductivity of the JCT was assumed to be uniform. Several models to describe Lp of the inner wall with or without the JCT have been proposed including the funneling model (M. C. Johnson et al., 1992) and Sampson’s law (Bill and Svedbergh, 1972; Ethier et al., 1998; Grant, 1963). Each of these models expresses Lp in terms of the product of pore density (n) and a moment of pore diameter. Specifically, for Sampson’s law, Lp ~ nD3 (Happel and Brenner, 1983; Lütjen-Drecoll, 1973; Mäepea and Bill, 1992), and for the funneling model, Lp ~ nD (Ethier and Coloma, 1999; Ethier et al., 2006; M. C. Johnson, 2006). Additionally, a model was considered where the hydraulic conductivity was proportional simply to inner wall porosity (total pore area/analyzed area), and hence Lp ~ nD2. The relationship between TI and each of n, nD, nD2 and nD3 (which we refer to as pore metrics) was examined for total pores, I-pores and B-pores.
Statistical Analysis
To test whether there was a relationship between TI and any given pore metric, two separate methods were used. First, an analysis of covariance (ANCOVA) was applied to the raw data. Essentially, ANCOVA performs a linear regression on a particular pore metric as a function of TI, with each ROI contributing a single data point to the regression analysis. The linear regression was performed separately for each wedge (4-7 ROIs per wedge), but ANCOVA forces the slope of the linear regression to be the same for all wedges. ANCOVA therefore provides an estimate of the optimal slope that best describes the relationship between the pore metric and TI across all wedges, and the confidence intervals on this slope are used to determine statistical significance compared to the null hypothesis of zero slope. However, because ANCOVA operates on raw data and because the raw TI and pore metrics may vary considerably between wedges of different eyes, wedges that have particularly large data values may have a disproportionate leverage on the estimated slope.
To account for any potential bias that may occur when analyzing raw data with ANCOVA, a second method of analysis was applied using normalized data. Importantly, data normalization (described below) eliminates the variation between wedges, while preserving the variation within each wedge, such that all of the ROI data points span a similar numerical range and can be fit by a single linear regression. Because TI was normally distributed between ROIs within each wedge (p > 0.12, Shapiro-Wilk test), TI was normalized (or, more accurately, studentized) according to , where asterisks represent normalized values, the subscript i and j refer to the ith ROI of the jth eye, and represent the estimated population mean and standard deviation of TI values over all i ROIs within the jth eye. Note that the normalization of TI expresses TI* in terms of units of standard deviation from the mean for each corresponding wedge. Because the pore density and diameter have been shown to be skewed distributions (Allingham et al., 1992; Braakman et al., 2014; M. C. Johnson et al., 2002), pore metrics (n, nD, nD2, nD3) were normalized by dividing the raw value by the mean value, where the mean for each pore metric was calculated by averaging the pore metric itself over the ROIs of the corresponding wedge. Normalized pore metrics (n*, nD*, nD2*, nD3*) were plotted as a function of TI* including data from all wedges, and the relationship between each pore metric versus TI* was analyzed by a single linear regression. A two-tailed Student’s t-test was used to determine whether the slope of the linear regression was significantly different from zero, with significance defined at p < 0.05. All statistical analyses was performed using MATLAB (v2014a, MathWorks, MA, USA).
The statistical power of a regression analysis represents the probability of finding a statistically significant correlation assuming that one exists. Because only a limited number of ROIs (typically 4-7) can be physically placed within each wedge, the statistical power of a regression analysis applied to a single wedge is relatively low (~25% assuming that R2 = 0.5 and α = 0.05). To overcome this limitation, we acquired data from 31 ROIs from 6 different wedges from separate eyes, and performed the analysis on the aggregated data. This approach increased the statistical power to approximately 71% for the ANCOVA approach and 73% for the single linear regression on the normalized data (Cohen et al., 2013; Ethier et al., 1998).
Results
Image Registration
The transformed vimentin and CD31 images co-registered well with the SEM images (Figure 4). The distance between corresponding features was typically less than 5 μm, and the vimentin staining around nuclei and GVs corresponded very well with the same structures seen by SEM. The accuracy of the registration algorithm was therefore judged to be within a few μm and thus considered to be sufficient for a colocalization analysis between tracer intensity and pore density over length scales of the ROI (50 μm × 150 μm).
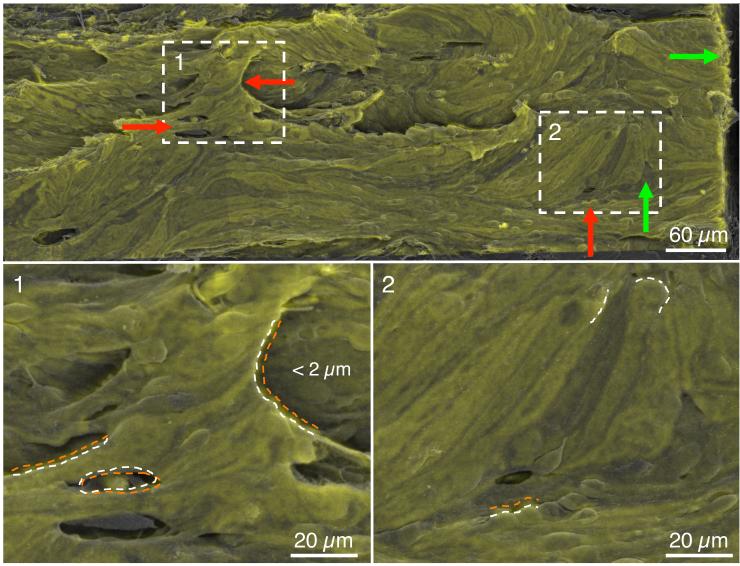
Figure 4.
Quality of the image registration algorithm based on a transformed CD31 montage (green) overlaid onto the corresponding scanning electron microscopy (SEM) overview montage (grey) from eye 649C. The white boxes labeled 1-2 are shown at higher magnification in the lower panels. Green arrows indicate regions of good co-registration (< 2 μm) while red arrows indicate regions of larger deviation (typically < 5 μm). Macroscopic features of the inner wall are largely preserved and overlap between transformed CD31 and SEM images. Coincident structures are marked with an orange dotted curve for the CD31 image and a white dashed curve for the SEM image.
Outflow Facility and Pore Density
Baseline outflow facilities were within the typical range for non-glaucomatous eyes (0.1 – 0.3 μL/min/mmHg, see Table 1). Perfusion with tracer tended to decrease facility (Table 1), but tracer did not have a consistent or statistically significant effect across all eyes. Perfusion with gelatin did not significantly decrease outflow facility relative to the contralateral eye that was perfused without gelatin (Table 1).
The average total pore density observed across all six eyes was 2173 ± 471 pores/mm2 (mean ± standard error of the mean). The average I-pore density was 866 ± 153 pores/mm2, and the average B-pore density was 1231 ± 354 pores/mm2 (Table 2). Although B-pores constituted the overall majority of pores (53 ± 6.2% vs. 44 ± 6.7%, weighted mean), one pair of eyes (681/682) showed more I-pores than B-pores (62 ± 7.2 % I-pores vs. 36 ± 5.1 % B-pores). The other two pairs had a majority of B-pores (35 ± 4.9 % I-pores vs. 62 ± 3.7 % B-pores). The remainder of pores (typically 3-7%) were U-pores that could not be clearly classified, usually because part of the pore was obscured from view preventing definitive identification of a cell border.
Table 2.
Summary of the measured pore densities, the absolute number of pores and the percentage of I-pores and B-pores. Note that the total pore densities and percentages of I-pores and B-pores are provided as mean ± standard error of the mean, whereas the total number of observed pores is a sum of all the observed pores.
| Eye |
|
|||||||
|---|---|---|---|---|---|---|---|---|
| Total pores | I-pores | B-pores | Total pores | I-pores | B-pores | % I-pores | % B-pores | |
| 649C | 3635 | 911 | 2440 | 105 | 26 | 71 | 25% | 68% |
| 650D | 704 | 320 | 384 | 20 | 9 | 11 | 45% | 55% |
| 669B | 3333 | 1400 | 1867 | 150 | 63 | 84 | 42% | 56% |
| 670B | 2378 | 689 | 1644 | 107 | 31 | 74 | 29% | 69% |
| 681B | 1352 | 743 | 552 | 71 | 39 | 29 | 55% | 41% |
| 682D | 1633 | 1133 | 500 | 49 | 34 | 15 | 69% | 31% |
|
| ||||||||
| Total | 2173±471 | 866±153 | 1231±354 | 382 | 129 | 240 | 44±6.7% | 53±6.2% |
Relationship between Pore Density and Tracer Intensity
An ANCOVA analysis applied to all 31 ROIs from 6 eyes showed a positive correlation between TI and total pore density (p = 0.044, Table 3). When ANCOVA was applied to each pore type separately, there was a statistically significant correlation between paracellular (B-pore) density and TI (p = 0.016), but no relationship between transcellular (I-pore) density and TI (p = 0.54; Table 3).
Table 3.
Summary of the correlations between tracer intensity and pore metrics. Bolded p-values highlighted in green indicate statistically significant correlations (p < 0.05); bold-italicized p-values highlighted in yellow indicate borderline significant correlations (0.10 < p < 0.05); and p-values highlighted in red are not statistically significant (p > 0.10).
| Model | Total pores | I-pores | B-pores | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
ANCOVA
Raw Data |
p | Partial η2 | Slope | p | Partial η2 | Slope | p | Partial η2 | Slope | |
|
|
||||||||||
| n | 0.044 | 0.16 | + | 0.54 | 0.02 | + | 0.016 | 0.22 | + | |
| nD | 1.5E-03 | 0.35 | + | 0.38 | 0.03 | + | 2.5E-05 | 0.53 | + | |
| nD2 | 3.2E-04 | 0.42 | + | 0.84 | 0.00 | + | 4.8E-07 | 0.66 | + | |
| nD3 | 4.0E-04 | 0.41 | + | 0.81 | 0.00 | + | 1.9E-06 | 0.62 | + | |
|
| ||||||||||
|
t-test
Normalized Data |
p | R2 | Slope | p | R2 | Slope | p | R2 | Slope | |
|
|
||||||||||
| n* | 0.054 | 0.12 | + | 0.27 | 0.04 | + | 0.051 | 0.12 | + | |
| nD* | 0.006 | 0.22 | + | 0.10 | 0.09 | + | 3.7E-03 | 0.25 | + | |
| nD2* | 0.007 | 0.22 | + | 0.21 | 0.05 | + | 1.1E-03 | 0.30 | + | |
| nD3* | 0.027 | 0.15 | + | 0.31 | 0.03 | + | 7.8E-04 | 0.32 | + | |
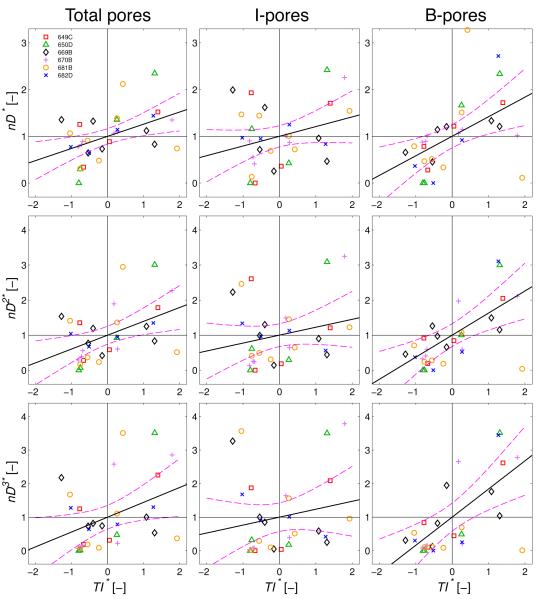
Because ANCOVA operates on raw pore density and TI values, and because there may be significant variability in the numerical values of these data between eyes, the outcome of the ANCOVA analysis may be biased by extreme values of pore density or TI that may exert high statistical leverage on the common slope of the ANCOVA regressions. Indeed, total pore density (p = 0.0003, ANOVA), B-pore density (p = 0.0008) and TI (p = 0.0007) were all significantly different between eyes. To account for this potential confounding factor, TI and pore density data were normalized as described in Methods, and normalized data from all eyes were aggregated together and analyzed using a single linear regression. Note that, as a result of the normalization, all data values are non-dimensional and are centered around 0 for TI* and around 1 for normalized pore metrics (Figures 5 and 6).
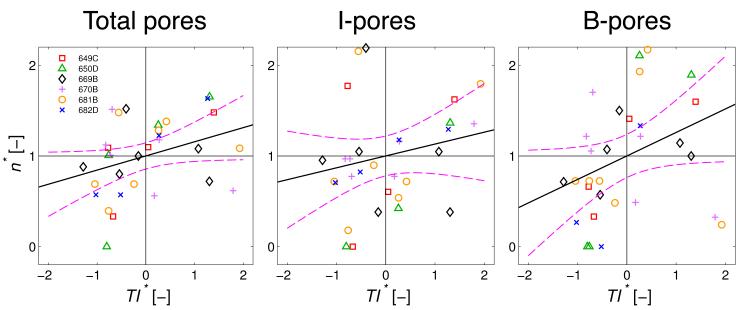
Figure 5.
Normalized pore density (n*) plotted versus normalized tracer intensity (TI*) in the juxtacanalicular tissue (JCT) for total pores, transcellular I-pores and paracellular B-pores. Black lines through the data represent the optimal linear regressions of n* vs TI* with the purple dashed curves representing the 95% confidence bounds on each regression. The linear regressions were borderline significant for total pores (p = 0.054) and B-pores (p = 0.051), but not for I-pores (p = 0.27). Each point represents an individual region-of-interest (N = 31) from the 6 eyes. See methods for details of the normalization.
Figure 6.
Normalized pore metrics from the hydrodynamic models plotted versus normalized tracer intensity (TI*) in the juxtacanalicular tissue (JCT) for total pores, transcellular I-pores and paracellular B-pores. Pore metrics represent the local hydraulic conductivity of the outflow pathway based on the funneling model (nD*), the porosity model (nD2*) and the Sampson’s law model (nD3*) as described in Methods. Black lines through the data represent the optimal linear regressions, and the purple dashed curves represent the 95% confidence bounds on each regression. All linear regressions were statistically significant for total pores (p < 0.027) and B-pores (p < 0.0037), but not for I-pores (p > 0.10; see Table 3). Each point represents an individual region-of-interest (N = 31) from the 6 eyes. See methods for details of the normalization.
There was a borderline significant correlation between the normalized pore density and TI* when applied to total pores (p = 0.054; Table 3), with a positive slope for the linear regression suggesting that pore density tends to increase with increasing TI* across the entire population of ROIs (Figure 5). When analyzed in terms of pore subtypes, there was a slightly stronger statistical relationship for B-pores (p = 0.051) but not for I-pores (p = 0.27; Table 3 and Figure 5), consistent with the ANCOVA results above. These results suggest that B-pores, more so than I-pores, tend to co-localize with regions of elevated tracer accumulation, presumably representing sites of greater fluid transport across the inner wall.
Hydrodynamic models
To understand how pore density (n) and diameter (D) may influence the local hydraulic conductivity (Lp) of the outflow pathway, we examined the relationship between tracer intensity and Lp as predicted by the funneling model (Lp ~ nD), the porosity model (Lp ~ nD2) and the Sampson’s law model (Lp ~ n D3). Statistics were determined using both raw data analyzed by ANCOVA and normalized data analyzed by single linear regression. All regressions, regardless of the statistical approach, had a positive slope, and the correlations for the hydrodynamic models (nD, nD2 and nD3) were all statistically stronger than those for the pore density alone (Table 3). By ANCOVA, a clear trend emerged: TI showed a highly significant positive correlation for all hydrodynamic models involving total pores (p < 0.0015) and B-pores (p < 0.000025) but not for those involving I-pores (p < 0.38; Table 3). The same trend was observed using normalized data, where all hydrodynamic models correlated strongly with TI* for total pores (p < 0.027) and B-pores (p < 0.0037) but not for I-pores (p > 0.10; Table 3 and Figure 6). Presumably, the stronger correlations with B-pores overcame the weaker correlations with I-pores and contributed to the statistically significant correlations observed when both pore subtypes were aggregated and analyzed together as total pores.
To determine which hydrodynamic model gave the best fit to the tracer data, we compared the partial η2 values from the ANCOVA analysis and the R2 values from the normalized analysis. For all hydrodynamic models the partial η2 and R2 values were typically 45-fold and 5-fold greater for B-pores (η2 > 0.53, R2 > 0.25) than I-pores (η2 < 0.03, R2 < 0.09), consistent with the stronger statistical relationships with B-pores presented above. The largest partial η2 value was observed for the B-pore porosity (nD2*) model (η2 = 0.66), while the largest R2 value was observed for the B-pore Sampson’s law (nD3) model (R2 = 0.32; Table 3). However, the values of partial η2 and R2 were relatively similar between all three models, making it difficult to definitively determine which specific model best fit the data.
Discussion
Several studies have investigated how tracer particles pass through the trabecular outflow pathway, mostly by imaging transverse sections through the TM, JCT and SC endothelium (de Kater et al., 1989; Epstein and Rohen, 1991; Ethier and Chan, 2001; Lu et al., 2008; Overby et al., 2002). Some of these studies observed tracer particles close to pores (Chang et al., 2014; Ethier and Chan, 2001; Lu et al., 2008) or passing through pores (Allingham et al., 1992; Yang et al., 2013). However, the small number of pores typically observed in individual sections has prevented any detailed quantitative analysis of the relationship between tracer accumulation in the JCT and pores in the inner wall of SC. In the present work, this problem was overcome by sampling a large area of the inner wall using correlative microscopy to acquire co-registered images of inner wall pores (by SEM) and tracer distribution in the JCT (by confocal microscopy). Using this approach, a strong correlation was observed between tracer intensity and B-pore density and pore metrics, but no correlation was observed with I-pore density or pore metrics. These observations strongly argue that aqueous humor passes through micron-sized pores in the inner wall endothelium of SC, with a dominant hydrodynamic contribution from paracellular B-pores compared to transcellular I-pores. Furthermore, these observations demonstrate that the location of B-pores and the local hydraulic conductivity arising due to B-pores co-localizes with the non-uniform or segmental distribution of outflow through the JCT.
The fundamental assumption underlying this tracer study (and any tracer study) is that the tracer distribution reflects the pattern of aqueous humor outflow through the TM/JCT, such that regions of higher tracer accumulation correspond to regions of higher outflow. Indeed, prior tracer studies have shown that tracer accumulation coincides with the location of collector channel ostia (Ethier et al., 1998; 1993; Hann and Fautsch, 2009; Zhang et al., 2009) and with regions of JCT containing less versican (M. C. Johnson et al., 1990; Keller et al., 2011), supporting this assumption.
Rationale for Immersion Fixation
The current study used immersion fixation, although it is generally believed that perfusion fixation is necessary to preserve pores and giant vacuoles along the inner wall (Ethier et al., 2004; Overby, 2011). Pores and giant vacuoles, however, were commonly observed in the immersion-fixed samples of this study, suggesting that the two-step method of first immersing the eye in wet ice followed by immersion in ice cold fixative was able to preserve inner wall structure.
The motivation for the immersion fixation approach was three-fold. Firstly, perfusion fixation is believed to artificially increase inner wall pore density (Ethier et al., 1998; M. C. Johnson et al., 2002; Preibisch et al., 2009; Sit et al., 1997), and we wished to avoid this artifact so as to best examine the relationship between pore density and tracer intensity. Secondly, in the eyes perfused with gelatin, wet ice was necessary to ‘set’ the gelatin prior to aldehyde fixation. Thirdly, the rapid drop in temperature would quickly inhibit metabolic activity at the inner wall and decrease the fluidity of lipid membranes, which we presumed would inhibit pore closure and giant vacuole retraction and thereby preserve these structures until the inner wall was aldehyde fixed. Indeed, using estimates of the heat transfer rate through sclera, the temperature of the inner wall should decrease from 34°C to 4°C within 30 seconds to 5 minutes2 following immersion in ice cold water at 0°C. While the eye is cooling, however, IOP decreases as fluid drains through the outflow pathway (recall that the perfusion tubes were clamped, preventing backflow through that route). Conservative estimates of the IOP decay indicate that it takes at least 20 minutes for IOP to decrease from 8 to 4 mmHg after clamping the perfusion tubing3. Even if the IOP was reduced immediately to 0 mmHg, pore closure would still likely require several minutes, based on best estimates of the giant vacuole retraction time (Brilakis and D. H. Johnson, 2001) and pore formation in other endothelia (Martinelli et al., 2013). Thus, the ‘cooling’ rate of the inner wall was likely faster than the turnover time for pore formation and closure, and this rapid cooling may have preserved the inner wall structure despite the absence of perfusion fixation.
We cannot eliminate the possibility that the rapid decrease in temperature somehow induced pore formation. Indeed, the pore densities observed in this study were consistent, but somewhat higher (2181 ± 1336 pores/mm2), than prior reports of inner wall pore density (835 – 1437 pores/mm2), even when prior values were corrected to account for the artificial increase in pore density caused by perfusion fixation (Allingham et al., 1992; M. C. Johnson et al., 2002). Alternatively, the temperature decrease may have differentially affected each pore type. Indeed, higher proportions of B-pores relative to I-pores were typically observed in this study, opposite to the ratio observed in other studies. Specifically, in this study 53% of all observed pores were B-pores (Table 2), whereas in a prior study 30% of all observed pores were B-pores (Ethier et al., 1998). Importantly however, because the current study compared ROIs from within individual wedges, any temperature-induced pore formation needed to have affected each ROI differentially to influence our results, since any artifact that affected all ROIs uniformly would have been effectively eliminated by the statistical normalization. Furthermore, if temperature-induced pore formation were to account for the observed relationship between pore metrics and tracer intensity, it would have to occur preferentially in regions of higher tracer accumulation. While this possibility cannot be eliminated, it seems unlikely, and considering that perfusion fixation is already known to artificially increase pore density, immersion fixation on ice seems a reasonable alternative for preserving inner wall pore structure.
The Spatial Relationship Between Pores and Local Filtration
The spatial correlation observed between pores and tracer suggests that pores are related to outflow segmentation, but does not provide insight as to the nature of such a relationship. There are two limiting scenarios for how pores may interact with flow. First, local filtration may trigger pore formation. In our prior work (Braakman et al., 2014), we established that cellular strain can induce pore formation in cultured SC cells, so it is possible that pore formation results from the cellular strain imposed by giant vacuole formation or inner wall ‘ballooning’ associated with transendothelial filtration as occurs in vivo. In this scenario, the inner wall functions as a “smart” filter, adjusting its porosity and local hydraulic conductivity to accommodate local variations in filtration demand arising from outflow segmentation, with biomechanical strain acting as the local signal for pore formation. The second scenario is that pore formation may regulate local filtration. Because the hydraulic conductivity of a non-porous region of the inner wall is low due to tight junctions between SC cells, micron-sized pores are an apparent requirement for aqueous humor filtration across the inner wall (M. C. Johnson, 2006; M. C. Johnson et al., 1992). Local pore formation, possibly induced by paracrine or autocrine signals released by JCT, TM or SC cells, may thereby determine filtration patterns to influence outflow segmentation.
The current study is unable to determine which of these scenarios is most correct. However, we speculate that the physiological situation is a mix of both extremes, representing a coupled interaction between local filtration demands and the cellular biomechanics involved in giant vacuole and pore formation. For example, a recent study by Overby et al. (Overby et al., 2014) has shown that pore formation correlates with the stiffness of the subcortical cytoskeleton in SC cells and, in line with this observation, that glaucomatous SC cells eyes exhibit both a stiffer subcortical cytoskeleton and a reduced ability to form pores. This leads to an interesting question of whether variations in SC cell stiffness exist along the inner wall, and whether such variations in stiffness may coincide with variations in pore density. Regardless of the precise mechanism, the fact that pore density is reduced in glaucomatous eyes, and that impaired pore formation persists in glaucomatous SC cells in culture, suggests that disrupting the normal mechanism of SC pore formation leads to impaired filtration, contributing to outflow obstruction and IOP elevation in glaucoma.
Differential Responses of I-pores and B-pores
The relationships between pore metrics and tracer were much stronger for paracellular B-pores compared to transcellular I-pores, and the strong relationship with B-pores likely contributed to the overall relationship that was observed between tracer and total pores. These results suggest that B-pores provide the dominant pathway for aqueous humor filtration across the inner wall. In contrast, I-pores showed no correlation with tracer intensity. While these data cannot exclude any potential role for I-pores, the data do suggest that I-pores function differently so as to be less conductive than B-pores at physiological pressure drops across the inner wall, as examined in this study. For example, the ultrastructure of the JCT or extracellular matrix underlying I-pores may be more resistive than that underlying B-pores. Alternatively, B-pores and I-pores may operate at different ranges of pressure drop across the inner wall or function under different time or length scales. For example, I-pores might require more time to become fully conductive or have smaller or larger hydrodynamic radii of influence than is captured by the 150 × 50 μm size of the ROI. Regardless, the data strongly support a hydrodynamic role for B-pores, but we would caution against using these data to argue against any potential role of I-pores.
Like the two pore sub-types observed in SC, vascular and lymphatic endothelia also exhibit two pathways for transport, particularly for leukocyte diapedesis that may proceed via transcellular or paracellular routes. In endothelia that form well-developed intercellular junctions such as in the blood-brain barrier, leukocyte diapedesis occurs predominantly transcellularly, allowing the junctions to be maintained and barrier function to be preserved (Wedel-Parlow et al., 2011). In microvascular and lymphatic endothelia with less well-developed intercellular junctions, leukocyte diapedesis occurs predominantly paracellularly (Carman et al., 2007). Similarly, the pore type in SC endothelium may depend on the quality of the local junctions or paracrine or autocrine signals from TM, JCT and/or SC cells potentially mediated by physical cues related to IOP or outflow (Alvarado et al., 2005).
In conclusion, this study demonstrated a colocalization between paracellular B-pores and local tracer accumulation along the inner wall of SC in human eyes perfused with fluorescent tracer nanospheres. These results strongly argue that pores provide a pathway for aqueous humor filtration across the inner wall and that the location of pores may contribute to the segmental distribution of aqueous humor outflow in the JCT. Increasing pore density is therefore a promising strategy to promote outflow and lower IOP in glaucoma.
Highlights.
Enucleated human eyes were perfused with fluorescent tracer nanospheres to visualize the patterns of outflow through the juxtacanalicular tissue (JCT).
Correlative microscopy was used to spatially register fluorescent images of tracer intensity in the JCT with scanning electron micrographs of micron-sized pores along the inner wall endothelium of Schlemm’s canal (SC).
Regions of greater tracer intensity coincided with regions of greater pore density, suggesting that aqueous humor passes through pores in the inner wall endothelium of SC.
Paracellular “B” pores appeared to have a dominant contribution towards transendothelial filtration across the inner wall relative to transcellular “I” pores.
Impaired pore formation, as previously described in glaucomatous SC cells, may thereby contribute to greater outflow heterogeneity, outflow obstruction, and IOP elevation in glaucoma.
Acknowledgments
Support: A grant from National Glaucoma Research, (G2009-032) a Program of The BrightFocus Foundation (Formerly the American Health Assistance Foundation), and the National Eye Institute (EY019696).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
The hydraulic conductivity (Lp) is defined as the ratio of the flow rate (Q) to the pressure drop (ΔP) across a hydraulically resistive barrier, normalized by the area (A) of the barrier. Hence, Lp = Q/(ΔP A).
This is a heat transfer problem. We modelled the eye as a sphere of radius 12 mm with SC endothelium located 0.5 mm beneath the scleral surface (Goshtasby, 1988; Irshad et al., 2010), and assumed that the thermal conductivity of the sclera was 0.53 W/mK (Barton and Trembly, 2013; M. C. Johnson et al., 2002), that the specific heat capacity of the sclera was 4181 W/kg K, and that the surface of the sclera was either at a constant temperature (0°C; correspondin g to the lower time limit) or at a constant heat flux with a heat transfer coefficient 44 W/m2K (corresponding to the upper time limit, neglecting natural convection) (Incropera and DeWitt, 2002; M. C. Johnson et al., 1992). Both boundary conditions have an analytical solution given by Schneider (Schneider, 1955) that, when using the parameter values given above, yield the time limits given in the main text.
The eye was treated as an RC circuit with an outflow resistance of 5 mmHg min/μL and an ocular compliance of C = 1/(Kr P) with P = 6 mmHg and Kr = 0.0215 1/μL (McBain, 1958). The IOP therefore decreases according to Po = e−t/RC, where P0 is the initial pressure (8 mmHg), predicting that the eye reaches 4 mmHg at t = 20 min. Note that the compliance increases as the pressure decreases, suggesting that this calculation slightly underestimates the actual time required for IOP to reach 4 mmHg.
References
- Allingham RR, de Kater AW, Ethier CR, Anderson PJ, Hertzmark E, Epstein DL. The relationship between pore density and outflow facility in human eyes. Investigative Ophthalmology & Visual Science. 1992;33:1661–1669. [PubMed] [Google Scholar]
- Alvarado JA, Yeh R-F, Franse-Carman L, Marcellino G, Brownstein MJ. Interactions between endothelia of the trabecular meshwork and of Schlemm’s canal: a new insight into the regulation of aqueous outflow in the eye. Transactions of the American Ophthalmological Society. 2005;103:148. [PMC free article] [PubMed] [Google Scholar]
- Barton MD, Trembly BS. Experimental Eye Research. Experimental Eye Research. 2013;115:216–223. doi: 10.1016/j.exer.2013.07.029. doi:10.1016/j.exer.2013.07.029. [DOI] [PubMed] [Google Scholar]
- Bill A, Svedbergh B. Scanning electron microscopic studies of the trabecular meshwork and the canal of Schlemm. Acta Ophthalmol (Copenh) 1972;50:295–320. doi: 10.1111/j.1755-3768.1972.tb05954.x. [DOI] [PubMed] [Google Scholar]
- Braakman ST, Pedrigi RM, Read AT, Smith JAE, Stamer WD, Ethier CR, Overby DR. Experimental Eye Research. Experimental Eye Research. 2014;127:224–235. doi: 10.1016/j.exer.2014.08.003. doi:10.1016/j.exer.2014.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brilakis HS, Johnson DH. Giant vacuole survival time and implications for aqueous humor outflow. Journal of Glaucoma. 2001;10:277–283. doi: 10.1097/00061198-200108000-00006. [DOI] [PubMed] [Google Scholar]
- Carman CV, Sage PT, Sciuto TE, la Fuente, de MA, Geha RS, Ochs HD, Dvorak HF, Dvorak AM, Springer TA. Transcellular Diapedesis Is Initiated by Invasive Podosomes. Immunity. 2007;26:784–797. doi: 10.1016/j.immuni.2007.04.015. doi:10.1016/j.immuni.2007.04.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang JYH, Folz SJ, Laryea SN, Overby DR. Multi-Scale Analysis of Segmental Outflow Patterns in Human Trabecular Meshwork with Changing Intraocular Pressure. Journal of Ocular Pharmacology and Therapeutics. 2014;30:213–223. doi: 10.1089/jop.2013.0182. doi:10.1089/jop.2013.0182. [DOI] [PubMed] [Google Scholar]
- Cohen J, Cohen P, West SG, Aiken LS. Applied multiple regression/correlation analysis for the behavioral sciences. Routledge; 2013. [Google Scholar]
- de Kater AW, Melamed S, Epstein DL. Patterns of aqueous humor outflow in glaucomatous and nonglaucomatous human eyes. A tracer study using cationized ferritin. Archives of Ophthalmology. 1989;107:572. doi: 10.1001/archopht.1989.01070010586035. [DOI] [PubMed] [Google Scholar]
- Epstein DL, Rohen JW. Morphology of the trabecular meshwork and inner-wall endothelium after cationized ferritin perfusion in the monkey eye. Investigative Ophthalmology & Visual Science. 1991;32:160–171. [PubMed] [Google Scholar]
- Ethier CR, Ajersch P, Pirog R. An improved ocular perfusion system. Current eye research. 1993;12:765–770. doi: 10.3109/02713689308995773. [DOI] [PubMed] [Google Scholar]
- Ethier CR, Chan DWH. Cationic ferritin changes outflow facility in human eyes whereas anionic ferritin does not. Investigative Ophthalmology & Visual Science. 2001;42:1795–1802. [PubMed] [Google Scholar]
- Ethier CR, Coloma FM. Effects of ethacrynic acid on Schlemm's canal inner wall and outflow facility in human eyes. Investigative Ophthalmology & Visual Science. 1999;40:1599–1607. [PubMed] [Google Scholar]
- Ethier CR, Coloma FM, Sit AJ, Johnson MC. Two pore types in the inner-wall endothelium of Schlemm's canal. Investigative Ophthalmology & Visual Science. 1998;39:2041–2048. [PubMed] [Google Scholar]
- Ethier CR, Read AT, Chan DWH. Biomechanics of Schlemm's Canal Endothelial Cells: Influence on F-Actin Architecture. Biophysical Journal. 2004;87:2828–2837. doi: 10.1529/biophysj.103.038133. doi:10.1529/biophysj.103.038133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ethier CR, Read AT, Chan DWH. Effects of Latrunculin-B on Outflow Facility and Trabecular Meshwork Structure in Human Eyes. Investigative Ophthalmology & Visual Science. 2006;47:1991–1998. doi: 10.1167/iovs.05-0327. doi:10.1167/iovs.05-0327. [DOI] [PubMed] [Google Scholar]
- Goshtasby A. Image registration by local approximation methods. Image and Vision Computing. 1988;6:255–261. [Google Scholar]
- Grant WM. Experimental aqueous perfusion in enucleated human eyes. Archives of Ophthalmology. 1963;69:783. doi: 10.1001/archopht.1963.00960040789022. [DOI] [PubMed] [Google Scholar]
- Hann CR, Fautsch MP. Preferential fluid flow in the human trabecular meshwork near collector channels. Investigative Ophthalmology & Visual Science. 2009;50:1692–1697. doi: 10.1167/iovs.08-2375. doi:10.1167/iovs.08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Happel J, Brenner H. Low Reynolds number hydrodynamics: with special applications to particulate media. Springer; 1983. [Google Scholar]
- Incropera FP, DeWitt DP. Heat and Mass Transfer. Fifth John Wiley and Sons; NJ: 2002. External Flow around a Sphere; pp. 533–593. [Google Scholar]
- Irshad FA, Mayfield MS, Zurakowski D, Ayyala RS. Variation in Schlemm’s Canal Diameter and Location by Ultrasound Biomicroscopy. Ophthalmology. 2010;117:916–920. doi: 10.1016/j.ophtha.2009.09.041. doi:10.1016/j.ophtha.2009.09.041. [DOI] [PubMed] [Google Scholar]
- Johnson MC. What controls aqueous humour outflow resistance? Experimental Eye Research. 2006;82:545–557. doi: 10.1016/j.exer.2005.10.011. doi:10.1016/j.exer.2005.10.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson MC, Chan DWH, Read AT, Christensen C, Sit AJ, Ethier CR. Glaucomatous eyes have a reduced pore density in the inner wall endothelium of Schlemm's canal. Investigative Ophtalmology and Visual Science. 2002;43:3961. [PubMed] [Google Scholar]
- Johnson MC, Johnson DH, Kamm RD, DeKater AW, Epstein DL. The filtration characteristics of the aqueous outflow system. Experimental Eye Research. 1990;50:407–418. doi: 10.1016/0014-4835(90)90142-h. [DOI] [PubMed] [Google Scholar]
- Johnson MC, Shapiro A, Ethier CR, Kamm RD. Modulation of outflow resistance by the pores of the inner wall endothelium. Investigative Ophthalmology & Visual Science. 1992;33:1670–1675. [PubMed] [Google Scholar]
- Keller KE, Bradley JM, Vranka JA, Acott TS. Segmental Versican Expression in the Trabecular Meshwork and Involvement in Outflow Facility. Investigative Ophthalmology & Visual Science. 2011;52:5049–5057. doi: 10.1167/iovs.10-6948. doi:10.1167/iovs.10-6948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu Z, Overby DR, Scott PA, Freddo TF, Gong H. The mechanism of increasing outflow facility by rho-kinase inhibition with Y-27632 in bovine eyes. Experimental Eye Research. 2008;86:271–281. doi: 10.1016/j.exer.2007.10.018. doi:10.1016/j.exer.2007.10.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lütjen-Drecoll E. Structural Factors Influencing Outflow Facility and its Changeability Under Drugs A Study in Macaca Arctoides. Investigative Ophthalmology & Visual Science. 1973;12:280–294. [PubMed] [Google Scholar]
- Martinelli R, Kamei M, Sage PT, Massol R, Varghese L, Sciuto T, Toporsian M, Dvorak AM, Kirchhausen T, Springer TA, Carman CV. Release of cellular tension signals self-restorative ventral lamellipodia to heal barrier micro-wounds. The Journal of Cell Biology. 2013;201:449–465. doi: 10.1083/jcb.201209077. doi:10.1182/blood-2004-12-4942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mäepea O, Bill A. Pressures in the juxtacanalicular tissue and Schlemm's canal in monkeys. Experimental Eye Research. 1992;54:879–883. doi: 10.1016/0014-4835(92)90151-h. [DOI] [PubMed] [Google Scholar]
- McBain EH. Tonometer Calibration. AMA Arch Ophthalmol. 1958;1080;60 doi: 10.1001/archopht.1958.00940081100015. doi:10.1001/archopht.1958.00940081100015. [DOI] [PubMed] [Google Scholar]
- Overby DR. The mechanobiology of aqueous humor transport across Schlemm’s canal endothelium. Mechanobiology Handbook. 2011:367–390. [Google Scholar]
- Overby DR, Gong H, Qiu G, Freddo TF, Johnson MC. The mechanism of increasing outflow facility during washout in the bovine eye. Investigative Ophthalmology & Visual Science. 2002;43:3455–3464. [PubMed] [Google Scholar]
- Overby DR, Zhou EH, Vargas-Pinto R, Pedrigi RM, Fuchshofer R, Braakman ST, Gupta R, Perkumas KM, Sherwood JM, Vahabikashi A, Dang Q, Kim JH, Ethier CR, Stamer WD, Fredberg JJ, Johnson MC. Altered mechanobiology of Schlemm's canal endothelial cells in glaucoma. Proceedings of the national Academy of Sciences. 2014 doi: 10.1073/pnas.1410602111. doi:10.1073/pnas.1410602111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Preibisch S, Saalfeld S, Tomancak P. Globally optimal stitching of tiled 3D microscopic image acquisitions. Bioinformatics. 2009;25:1463–1465. doi: 10.1093/bioinformatics/btp184. doi:10.1093/bioinformatics/btp184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider PJ. Conduction Heat Transfer. Addison-Wesley Publishing Company; 1955. [Google Scholar]
- Sit AJ, Coloma FM, Ethier CR, Johnson MC. Factors affecting the pores of the inner wall endothelium of Schlemm's canal. Investigative Ophthalmology & Visual Science. 1997;38:1517–1525. [PubMed] [Google Scholar]
- Wedel-Parlow, von M, Schrot S, Lemmen J, Treeratanapiboon L, Wegener J, Galla H-J. Neutrophils cross the BBB primarily on transcellular pathways: An in vitro study. Brain Research. 2011;1367:62–76. doi: 10.1016/j.brainres.2010.09.076. doi:10.1016/j.brainres.2010.09.076. [DOI] [PubMed] [Google Scholar]
- Yang CYC, Liu Y, Lu Z, Ren R, Gong H. Effects of Y27632 on Aqueous Humor Outflow Facility With Changes in Hydrodynamic Pattern and Morphology in Human Eyes. Multiple values selected. 2013;54:5859–5870. doi: 10.1167/iovs.12-10930. doi:10.1167/iovs.12-10930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Toris CB, Liu Y, Ye W, Gong H. Morphological and hydrodynamic correlates in monkey eyes with laser induced glaucoma. Experimental Eye Research. 2009;89:748–756. doi: 10.1016/j.exer.2009.06.015. doi:10.1016/j.exer.2009.06.015. [DOI] [PubMed] [Google Scholar]