Median Modified Wiener Filter for nonlinear adaptive spatial denoising of protein NMR multidimensional spectra

Abstract

Denoising multidimensional NMR-spectra is a fundamental step in NMR protein structure determination. The state-of-the-art method uses wavelet-denoising, which may suffer when applied to non-stationary signals affected by Gaussian-white-noise mixed with strong impulsive artifacts, like those in multi-dimensional NMR-spectra. Regrettably, Wavelet's performance depends on a combinatorial search of wavelet shapes and parameters; and multi-dimensional extension of wavelet-denoising is highly non-trivial, which hampers its application to multidimensional NMR-spectra. Here, we endorse a diverse philosophy of denoising NMR-spectra: less is more! We consider spatial filters that have only one parameter to tune: the window-size. We propose, for the first time, the 3D extension of the median-modified-Wiener-filter (MMWF), an adaptive variant of the median-filter, and also its novel variation named MMWF*. We test the proposed filters and the Wiener-filter, an adaptive variant of the mean-filter, on a benchmark set that contains 16 two-dimensional and three-dimensional NMR-spectra extracted from eight proteins. Our results demonstrate that the adaptive spatial filters significantly outperform their non-adaptive versions. The performance of the new MMWF* on 2D/3D-spectra is even better than wavelet-denoising. Noticeably, MMWF* produces stable high performance almost invariant for diverse window-size settings: this signifies a consistent advantage in the implementation of automatic pipelines for protein NMR-spectra analysis.

Nuclear magnetic resonance (NMR) spectroscopy is one of the two main techniques to experimentally determine protein three-dimensional (3D) structures. In contrast to X-ray crystallography that requires the target protein to be crystallized, NMR can detect the 3D structure of the target protein in vivo, which can provide information about the living form and dynamics of the protein.

The physical principle of NMR is that when an isotope nucleus that have an odd atomic number and/or odd atomic mass (e.g., 1H, 13C and 15N) is placed in a strong magnetic field, it absorbs and re-emits electromagnetic radiation due to its intrinsic magnetic moment. The same type of nucleus, however, often has different resonance depending on the local chemical and geometric environment, such as binding partners, bond lengths and bond angles. The resonance frequency of a nucleus relative to a standard frequency is called the chemical shift of this nucleus. If two or multiple nucleic are close to each other in the 3D space, their resonance can be coupled and such coupling can be captured by NMR spectrometers. According to the way the resonance is coupled, there can be both through-bond and through-space spectra. Mathematically speaking, an NMR spectrum can be considered as a multi-dimensional matrix, in which the coordinates of each dimension are the discrete chemical shift values of a certain nucleus and the signals (i.e., peaks) of the matrix are the intensity values of the coupling.

Wüthrich (1986) proposed a multi-step pipeline for NMR protein 3D structure determination that takes a set of multi-dimensional spectra (usually 2D and 3D spectra) as input and generates an ensemble of 3D structures as output¹. The idea is to use the physical principle of the NMR technique to extract short distance constraints from through-space spectra, such as nuclear Overhauser effect (NOE) spectra, and solve the 3D structure of the target protein as a constrained optimization problem accordingly. In order to interpret NOE peaks, the resonance assignment of the atoms of the target protein is needed. Such an assignment can be obtained from picked peaks of a set of through-bond spectra that share certain common nucleic as root, such as the 2D¹⁵N-HSQC, and the 3D CBCA(CO)NH and HNCACB. This entire procedure, unfortunately, is a costly and time-consuming one that, up to now, mainly depends on manual or semi-automated work with expert knowledge.

In the last two decades, computational community has played more and more important roles to simplify and accelerate this tedious structure determination process²,³,⁴,⁵,⁶,⁷,⁸,⁹. Peak picking has been treated as a signal processing problem and has been tackled by a variety of methods¹⁰,¹¹,¹²,¹³,¹⁴,¹⁵,¹⁶,¹⁷,¹⁸,¹⁹,²⁰,²¹,²²,²³,²⁴,²⁵,²⁶,²⁷. Resonance assignment, on the other hand, is often formulated as a graph-based problem to find the best mapping between spin systems and residues of the target protein. Different types of graph algorithms and optimization algorithms have been proposed accordingly²⁸,²⁹,³⁰,³¹,³²,³³,³⁴,³⁵,³⁶,³⁷,³⁸,³⁹,⁴⁰,⁴¹,⁴²,⁴³,⁴⁴. Once the NOE distance constraints are extracted from NOE spectra, the structure calculation is considered as a constraint satisfaction problem, for which a number of efficient searching algorithms have been developed⁵,⁶,⁷,⁴⁵,⁴⁶,⁴⁷,⁴⁸. Recently, it was shown that accurate structures for small and medium sizes proteins can be determined directly from their resonance assignments⁴⁹,⁵⁰.

Peak picking, as the first step in NMR protein structure determination, is a key to all the subsequent steps. On one hand, if the picked peaks contain a large number of false positives, it will introduce too much noise and ambiguities to the following steps, which makes their search space prohibitively large. On the other hand, if the picked peaks contain many false negatives, it will bring too much missing information that is impossible for the following steps to recover. A practically useful peak picking method thus must provide a good tradeoff between recall and precision. Peak picking is a computationally challenging problem due to various sources of noise, including: Gaussian white noise, low signal-to-noise ratios, peak overlaps, sample impurities, water bands, and artifacts. Therefore, the most crucial step in peak picking is the initial denoising of the spectra. It has been shown that once denoising is done, it is relatively straightforward to identify peaks²⁴,²⁶. There are two types of commonly used denoising techniques for NMR spectra, i.e., hard denoising and soft denoising. AUTOPSY¹⁶ and PICKY²² both use hard denoising. The background noise in NMR spectra is assumed to be white Gaussian noise in these methods. The mean is assumed to be zero and the standard deviation is estimated in local spectrum regions that do not contain signals. The noise level is then defined as a small constant (usually 5) times the standard deviation. Any data points that have intensity values below the noise level are eliminated. The advantage of hard denoising is that the denoised spectra become very sparse, which make the following peak selection step trivial. However, hard denoising has risks of eliminating weak peaks, especially when signal-to-noise ratio is low. WaVPeak²⁶, the state of-the-art method on peak picking, is based on soft denoising. It decomposes a spectrum by wavelet decompositions. The low frequency components are kept and the high frequency ones are eliminated. In this way, it smoothes the entire spectrum without eliminating any data point. However, wavelet denoising requires several parameters to be tuned for different proteins and different types of spectra. A combinatorial search of such parameters is infeasible due to the slow speed of wavelet decomposition and reconstruction, especially for 3D spectra. This issue becomes a serious obstacle to adopt wavelet denoising in the near future, when multi-dimensional protein NMR spectra with more than three dimensions will be of common use.

Here, we open the way to address this wavelet denoising limitation with a radical change of strategy that stems from a consciousness raising. Wavelet denoising became in the last decade a sort of ‘moda', rapidly substituting classical adaptive spatial filtering like the Wiener filter. This replacement was often supported by studies that clearly demonstrate the superiority of wavelet denoising in some contexts. However, in many other cases wavelet denoising was de facto chosen as the strategy to adopt because considered by principle superior to classical adaptive spatial filtering. Yet, this superiority is very signal/noise-dependent⁵¹. In particular, when non-stationary signals are affected by a mixture of Gaussian white noise and strong impulsive artifacts (like small false peaks in protein NMR spectra), wavelets denoising might be significantly outperformed by nonlinear adaptive spatial filtering like the one provided by the Median Modified Wiener Filter (MMWF)⁵¹. In addition, wavelet denoising is a very sophisticated technique that requires the ‘mining' of the proper wavelet shape, and the combinatorial tuning of at least three parameters. In contrast, adaptive spatial filtering is very simple and in most cases like the Wiener filter and the MMWF requires just the tuning of one parameter. In conclusion, we might argue that more sophisticated method does not necessarily mean more accurate or time efficient. In this article we want to endorse a diverse philosophy of denoising protein NMR spectra: less is more! We believe that engineering needs freedom of choice on the strategies used to design computational tools. In the end what really make the difference are the results and, as a matter of fact, here we propose new and interesting results, stemmed from a simple, but not for this reason less powerful, designing philosophy.

Results

Classical and adaptive spatial filters

One of the most used denoising techniques in digital signal and image processing are linear and nonlinear local filters, also defined: spatial filters. The common parameter in spatial filtering is the size of the window, also called kernel or mask, which, in case of 2D signals, is the small n × m pixels area around a given processed point, pixel or voxel (for simplicity in the rest of the text we will refer just to pixels). The filter uses the pixel intensity values of the area to re-compute the new value of the processed pixel at the centre. In general, some spatial filters might also have more than one adjunctive parameter, as the variance in the Gaussian filter or the polynomial degree in the polynomial filter.

The first two spatial filters that we considered are the mean and median filters. The mean is a linear filter while the median is a nonlinear filter. Then, we considered their respective adaptive variations. The Wiener filter is a linear adaptive spatial filter that derives from the mean operator; and the MMWF is a nonlinear adaptive spatial filter that derives from the median operator.

The mean filter is the simplest linear spatial filter and, to compute the denoised signal value, assigns to the pixel at the centre of the window the average value of the pixels in the window. Moving the window across the signals, a new denoised signal value is recomputed for each pixel. For this reason the mean filter is also called moving average filter. The median filter is the simplest nonlinear spatial filter, and it is often used to reduce impulsive noise like ‘salt and pepper' noise. It is more effective than convolution filter when the goal is to simultaneously reduce noise and preserve edges⁵¹. The reason why the median filter is so efficient to remove impulsive noise comes from the fact that the median operator is much less sensitive than the mean operator to outlier values (like small false peaks in the signal). Therefore, median filter is better able to remove these outlier values without reducing the sharpness of the signal. Even though the median filter provides smooth signals, in particular for large windows in 2D signals it erodes the edge of isolated spots and tends to fill the space between close-set spots. For clarity, with the expression ‘spots', we refer to zones of the background of a 2D signals that emerge indicating the presence of a significant pattern with the form of a peak. The evidence that median filter causes signal erosion is extensively treated in literature⁵¹. In contrast, the signal dilatation (that tends to fill the space between spots in 2D signals) was firstly shown by Cannistraci et al⁵¹. as a paradoxical effect caused by the median operator in the particular case where it is applied in proximity of narrow 2D signal depressions. This is an important side effect of the median operator, which earns significance in case of close peaks in 2-D signals like protein NMR 2D spectra. Thus, the median filter is expected to perform poorly, especially for large window settings, in denoising of multidimensional protein NMR spectra.

Another linear technique for spatial filtering is the Wiener filter. It is considered a more advanced technique because it is adaptive. Wiener filter is applied to a signal adaptively, tailoring itself to the local signal variance. Where the variance is large, it performs less smoothing, while where the variance is small, it performs more smoothing. The estimate of the local (i.e. considered in the sliding window) mean μ and variance σ² around each pixel in a 2D signal is:

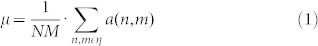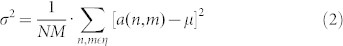where N-by-M is the size of the local neighbourhood area, η, contained in the window, and a(n,m) is a notation to identify each pixel contained in the area η of the 2D signal. Then a pixel-wise Wiener filter is implemented using these estimates to calculate the new pixel value b:

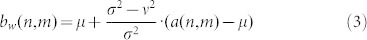where ν² is the noise variance. If the Gaussian noise variance is not given as input, the average of all the local variances estimated for each window is used⁵¹: in our study we exploited this second variance setting. Wiener filter often produces better results than standard non-adaptive linear filtering. In fact, the adaptive filter procedure is more selective (preserving edges in 2D signals) than a comparable linear filter⁵¹. Some of the inconvenience of the Wiener denoising (especially for large windows) is that it does not respect the morphology of the signal and thus causes fuzzification/dilatation of edges, noise-small-features and spikes (small peaks).

Median Modified Wiener Filter (MMWF): extension to the case of multi-dimensional signals

The MMWF was invented as an informational filter by Cannistraci, and was proposed for the first time for denoising application in the work of Cannistraci et al⁵¹. Specifically, it was applied for denoising of 2D signals in image proteomics, and the source of the signal were 2D-gel-electrophoresis maps.

This nonlinear adaptive spatial filter was introduced with the aim to merge the complementary qualities and abilities of median filter and the Wiener filter, reciprocally nullifying the respective defects. In particular, the objective was to facilitate the efficacy in removing spike noise from the 2D signal background (typical of the median filter) while preserving unaltered spot edges (a property partially provided by the Wiener filter that preserves edges but unfortunately modifying their morphology). The mathematical formula for the MMWF in case of 2D signals, considering the notation 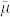to indicate the local window median around each pixel μ:

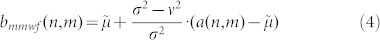The rest of the notation is the same already introduced for the Wiener filter. The consequences of this modification in the original Wiener filter formula are very significant and are mainly caused by the introduction in an adaptive contest of the nonlinear behaviour due to the median operator. A deep mathematical discussion of this modification in the Wiener formula is offered in the article of Cannistraci et al⁵¹. Here for simplicity we summarize the main effects of this mathematical modification from the denoising point of view, in 2D signals.

The main effect is that after denoising the edge morphology is well preserved (in contrast to the result of the median and Wiener filter). This effect was named drop-off-effect because the slope of the sides of the spots in the 2D signals is preserved. The second crucial result is that MMWF showed high performance in global denoising of different types of noise, being its best window setting invariant of the type of noise. In general, the median filter erodes the edge of isolated spots and fills the space between close-set spots, while the MMWF because of the drop-off-effect does not suffer from erosion problems, preserves the morphology of close-set spots, and avoids spot and spike fuzzification, an aberration frequently encountered for Wiener filter⁵¹. In conclusion, the MMWF should theoretically improve the precision in detection of real peaks in protein NMR 2D-spectra, although it might also slightly decrease the recall, because of excessive denoising of small real peaks erroneously smoothed. This kind of problem was less probable in signals of 2D-gel-electrophoresis maps, because the smallest size of the signal spots in the 2D-gel-electrophoresis maps was generally wider than the largest size of false and noisy peaks distributed both in the background and over the spots.

Here, for the first time, we introduce the extension of the MMWF to the case of multidimensional signals, with the aim to test its performance in case of protein NMR 3D-spectra. The generalized mathematical formula is:

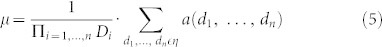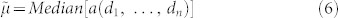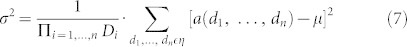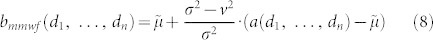where in respect to the previous formulation we introduced the new notations, d₁, …, d_n, to intend a combination of values that indicate the location of a discrete point in an n-dimensional hypercube, and D_i to intend the size of the length of the i-th dimension of the hypercube.

MMWF*: a novel variation of the Median Modified Wiener Filter

Here, we introduce MMWF* that is a new variation of the MMWF. We report the formula of this new filter for multidimensional signals, however the formulation in case of 2D-signals can be easily derived.

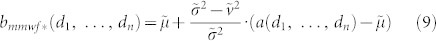Where 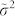is the variance computed as average squared deviation from the median :

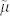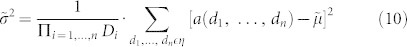This first variation is significant because, since the variance operator is an edge detector, the replacement in the formula of the mean with median provides a more robust estimation of the background value inside the window. As a consequence, a better detection of the signal's edges is obtained, for instance: the edge of a spot in an image or the edge of a real peak in a 2D NMR spectrum.

The 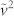is the noise variance, estimated as the median of all the local variances 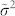, which are computed for each window defined around each point in the multidimensional signal. This second variation is even more important because the noise variance should be window-size independent. As a matter of fact, in non-stationary and sparse signals like 2D-gel-electrophoresis maps and NMR-spectra, the mean of all the local variances is an unstable estimator of the noise variance, and tends to decrease performance for increasing window-sizes. The motivation lies in the fact that, since the real peak signals are sparse, for small window sizes we have a good sampling of the noise in the background, while for large window-sizes several windows will sample also real peaks, and the mean of all the local variances will be affected by the presence of many outlier-values that will introduce nonlinearity in the distribution of all the local variances 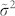. The median operator will be much less affected by these outlier-values in the distribution of the local variances, thus will provide a more robust estimation of the noise variance also with increasing window-sizes.

Evaluations and comparisons

We evaluated the denoising performance of the spatial filters and wavelet on a similar benchmark NMR spectrum set used in refs ^{22, 26}. The details on the evaluation procedure are provided in the Methods section. Our spectrum set contains 16 raw 2D and 3D spectra in the UCSF format extracted from eight proteins, i.e., TM1112 (PDB ID: 1LKN), YST0336 (PDB ID: 2JYN), RP3384 (PDB ID: 2JTV), ATC1776 (PDB ID: 2JYA), CASKIN (PDB ID: 2KE9), HACS1 (PDB ID: 2KEA), VRAR (PDB ID: 2RNJ), and COILIN (unpublished data). The sizes of these proteins range from 64aa to 146aa. The spectra contains eight 2D ¹⁵N-HSQC spectra and eight 3D CBCA(CO)NH spectra, one for each protein, respectively.

First, we compared the performance of the five different spatial filters for denoising of NMR 2D protein spectra. As mentioned, we selected spatial filters that present just one tuning parameter: the size of the sliding window. This window is introduced in the spatial filter algorithm for sampling the information stored around a signal region that should be denoised. The rationale to select spatial filters with just this simple tuning parameter is in adopting algorithms that are computationally fast and easy to generalize to NMR protein spectra with dimension higher than two. On the other side, algorithms with several parameters like wavelets, although in principle more powerful, present the drawback that they might require a combinatorial tuning of their parameters in relation to different protein spectra. This combinatorial tuning might be complicated if implemented in an automatic pipeline where there is not intervention of an external human operator. In addition, extension of these last algorithms to protein spectra with dimension higher than 2D can be theoretically very complicated and might require a significant increase of computational time and memory allocation.

The first two spatial filters that we considered are the mean and median filters. The mean is a linear filter while the median is a nonlinear filter. Then, we considered their respective adaptive variations. The Wiener filter is a linear adaptive spatial filter that derives from the mean operator; and the Median Modified Wiener Filter (MMWF) is a nonlinear adaptive spatial filter that derives from the median operator. We also evaluated the performance of the MMWF* (which is a variation of the MMWF) here introduced for the first time. We tested the performance of these five filters for a range of squared window size that is from 3 × 3 to 31 × 31 pixels. We considered squared windows because the shape of each peak in the spectra is, as first approximation, isotropic. For the evaluation we considered as main reference the F-score measure, because it is a balanced estimation that merges together precision and recall performance.

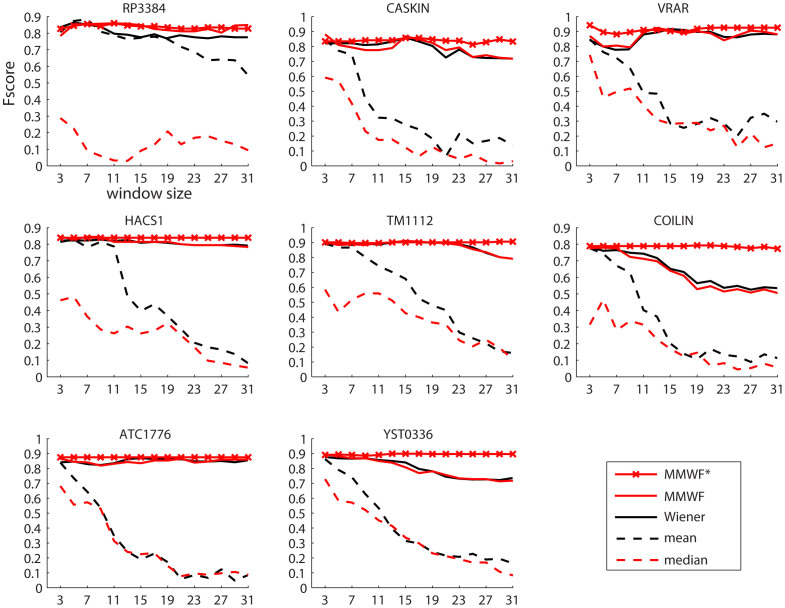
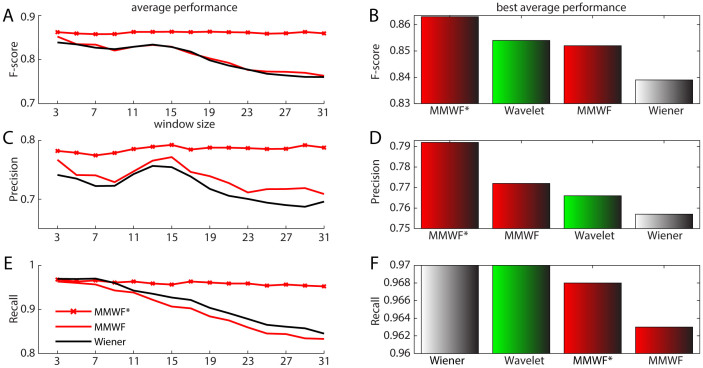
The results presented in Fig. 1 for eight different 2D protein spectra clearly point out that adaptive filters make a significant difference in denoising task at least in the context of the analyzed proteins. We are aware that eight proteins are not a sufficient number for generalizing our result, however since this significant discrepancy in performance are confirmed also by the plots of Precision (see Suppl. Info Fig. 1) and Recall (see Suppl. Info Fig. 2), we feel confident on the importance of this result. In particular, our experimental results are also supported by the theory, in fact adaptive filters such as Wiener, MMWF and MMWF* should theoretically maintain their performance quite stable for different window sizes compared to non-adaptive filters such as mean and median, and this is evident in Fig. 1. In order to discriminate the difference in performance between Wiener, MMWF and MMWF*, we considered the average F-score, Precision and Recall across the different 2D spectra. This result is displayed in Fig. 2A, C, E. The difference of performance between the Wiener and MMWF does not look really significant; however MMWF offers a higher F-score and precision, while the difference in Recall is negligible. Interestingly, MMWF offers the best F-score performance for window size 3 × 3 with a monotonically decreasing slope. This is an important result because it suggests that using the MMWF with windows size 3 × 3 might be a smart selection in many cases where we want to implement an automatic pipeline. Particularly impressive is the result of the novel MMWF*, which offers very stable and high performance with a trend that is almost invariant to the window size setting (Fig. 2A, C, E). This is a confirmation of the result we were theoretically expecting according to the new MMWF* mathematical formulation that we discussed in the paragraph above. Therefore, using MMWF* should offer even a better solution than using MMWF for implementation of automatic pipeline. We also decided to compare the average performance of these two adaptive filters with wavelet denoising (Fig. 2B, D, F). For the wavelet denoising, we used the best parameters of the wavelet proposed in Liu et al²⁶. For this comparison we considered the best average performance offered by the adaptive filters at a fixed window size, as example for MMWF it was window 3 × 3 (Fig. 2A). We were surprised to notice that the performance of MMWF* was higher than wavelet denoising, while the performance of the other adaptive filters were not that far from a more complicated and advanced algorithm such as wavelet denoising: in practice, there was not any significant performance difference. This key result was an important achievement because to the best of our knowledge it is the first time that spatial filtering is demonstrated to be so competitive in denoising of such type of signals (like protein NMR multi-dimensional spectra). We were then encouraged to continue our study investigating whether the denoising performance of these algorithms would dramatically change in case we considered the 3D NMR spectra of the same eight proteins analyzed in Fig. 1 and Fig. 2. The rationale for selecting the same eight proteins in a higher dimensional space is coming from the intention to reduce any change or bias in evaluation performance related with modifying the original dataset characteristics. This simplifies the comparison between the results obtained in 2D and 3D spectra denoising. To notice, we introduce in this article for the first time MMWF* and the generalization of the MMWF to the case of multi-dimensional signals, and this was an important test to verify their behavior on 3D signals like protein NMR spectra.

Figure 1. F-score curves for 2D spectra.

F-score curves of peak picking when using four different spatial filters for denoising NMR 2D spectra (¹⁵N-HSQC) of the eight proteins. The filters used are the Mean and Median filters (dashed lines), and their respective adaptive variations (full lines) Wiener and Median Modified Wiener Filter (MMWF). MMWF*, the new variation of the MMWF, is distinguished by a red line marked by red crosses. Each filter is tested for a range of squared window size that is varying from 3 × 3, 5 × 5, 7 × 7,… to 31 × 31 pixels. The figures show that adaptive filters outperform the non-adaptive ones significantly in the denoising task. It is also clear that adaptive filters maintain their performance quite stable for different window sizes.

Figure 2. Average performance for 2D spectra.

Subfigures (A), (C), and (E): Average performance curves of the three adaptive spatial filters over the 2D spectra with respect to the window size. (A). average F-score curves; (C). average precision curves; and (E). average recall curves. Subfigures (B), (D), and (F): Bar charts of average performance of the wavelet denoising in Liu et al²⁶ and the three adaptive spatial filters with the best window size on the 2D spectra. (B). average F-score bar charts; (D). average precision bar charts; and (F). average recall bar charts.

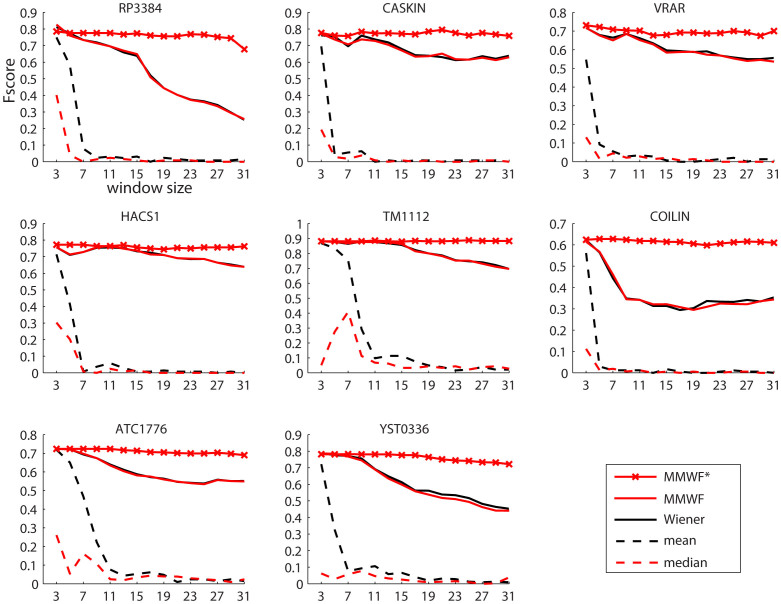
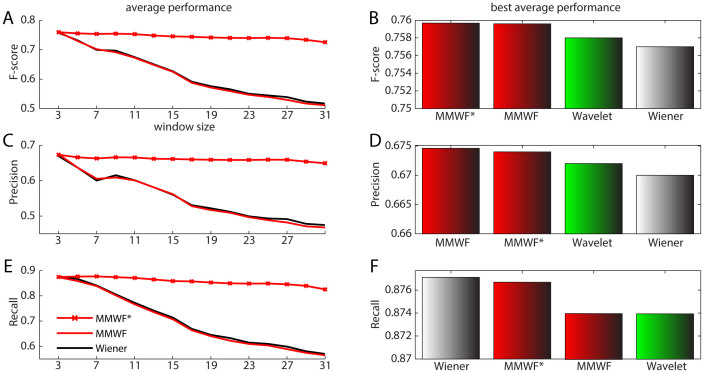
The supremacy of adaptive spatial filtering on the non-adaptive one (Fig. 3, and Suppl Info: Fig. 3 and Fig. 4) is as expected confirmed also in 3D spectra denoising. Additionally, it is confirmed also the robustness of adaptive spatial filtering to changes in the window size, particularly for MMWF* (Fig. 3; and Suppl Info: Fig. 3 and Fig. 4). Surprisingly, although it is not detected any significant difference between adaptive spatial filters and wavelet performance, the MMWF and MMWF* in this case gave higher performance in F-score and Precision than wavelet. However, these results should be taken with the congruous reserve. Since the number of the available analyzed spectra is low (just eight proteins) though it is the largest in NMR peak picking studies, we expect that changing the context of the analysis, an example considering different type and number of proteins, might modify the fact that MMWF and MMWF* resulted the first in this 3D denoising comparison. The most interesting information regarding MMWF is not related with the fact that it gave a slightly (and likely not statistical significant) higher performance, but is connected with the fact that this best average performance was achieved again for window size 3 × 3 (Fig. 4A, C, E). Also 3D experiments advocated the use of the MMWF with windows size 3 × 3 to get the best performance in most of the cases in automatic computational pipelines. This is even more valid for MMWF* that also in the context of 3D denoising confirmed a very stable performance almost invariant to the window size setting. Somehow, we can summarize that considering the nature of the signal present in the 2D and 3D protein spectra, the MMWF produced a stable performance at least for a fixed and well determined window size that was 3 × 3, while MMWF* produced high and stable performance for all the range of window settings. This MMWF's window invariance was also a main finding of the previous proteomic study on signals of 2D-gel-electrophoresis maps⁵¹, a result that now is even reinforced by the introduction of the new MMWF*. Here, the window invariance might represent a consistent advantage for introducing nonlinear adaptive spatial filtering in the implementation of automatic pipelines for NMR protein spectra analysis.

Figure 3. F-score curves for 3D spectra.

F-score curves of peak picking when using four different spatial filters for denoising NMR 3D spectra (CBCA(CO)NH) of the eight proteins. The filters used are the Mean and Median filters (dashed lines), and their respective adaptive variations (full lines) Wiener and Median Modified Wiener Filter (MMWF). MMWF*, the new variation of the MMWF, is distinguished by a red line marked by red crosses. Each filter is tested for a range of squared window size that is varying from 3 × 3, 5 × 5, 7 × 7,… to 31 × 31 pixels. The figures show that adaptive filters outperform the non-adaptive ones significantly in the denoising task. It is also clear that adaptive filters maintain their performance quite stable for different window sizes.

Figure 4. Average performance for 3D spectra.

Subfigures (A), (C), and (E): Average performance curves of the three adaptive spatial filters over the 3D spectra with respect to the window size. (A). average F-score curves; (C). average precision curves; and (E). average recall curves. Subfigures (B), (D), and (F): Bar charts of average performance of the wavelet denoising in Liu et al²⁶ and the three adaptive spatial filters with the best window size on the 3D spectra. (B). average F-score bar charts; (D). average precision bar charts; and (F). average recall bar charts.

Discussion

From the results presented in this study on the denoising of 2D and 3D protein spectra, we can gather that unexpectedly a simple and efficient procedure like adaptive spatial filtering offers a valid alternative to complicated and time-consuming techniques like wavelet-denoising, which suffers from the problem of the combinatorial tuning of multiple parameters and settings. In addition, we propose, for the first time, the 3D extension of the Median Modified Wiener Filter (MMWF) and its new variation named MMWF*: nonlinear adaptive spatial filters that are adaptive variants of the median filter. Our results demonstrate that performance of MMWF is comparable to that of wavelet and Wiener filter on 2D spectra, but noticeably better on 3D spectra. The performance of the new MMWF* on 2D/3D-spectra is even better than MMWF and wavelet-denoising. Noticeably, MMWF* gains stable high performance almost invariant to diverse window-size settings, which might represent a consistent advantage in automatic computational pipelines for protein NMR-spectra analysis.

Non-stationary signals, such as protein NMR spectra, are difficult to treat due to the large and unstructured variations in intensity and size. Nonlinear adaptive spatial filters, like MMWF and MMWF*, perform well also on non-stationary signals, are easy to implement and fast to use, and theoretically can be implemented in any multidimensional space without the need of a strong theoretical revision on their original equations or algorithms. We hope that this study (and the computational codes here released) might trigger further interests in the development of novel and most refined adaptive spatial filters for denoising of protein NMR-spectra and of non-stationary signals in general.

Methods

Since the main focus of this paper is on denoising of NMR spectra, in all the experiments, as described above, we apply different methods on denoising the original, raw 2D and 3D NMR spectra only. The settings of these denoising techniques were all specified and commented during the presentations of the results together with the respective references. Then, we followed Liu et al²⁶ to use a brute force algorithm to select all the local maxima in the denoised spectra, ranked them according to their estimated volumes, and selected the top K predicted peaks, where K is a number determined by the Benjamini-Hochberg algorithm²⁵. The peak lists returned by each denoising method was compared with the manually picked peaks (obtained from the Biological Magnetic Resonance Bank) to calculate precision, recall and F-scores. A predicted 2D peak is considered correct if and only if its coordinate in dimension N (nitrogen) is within 0.5 ppm with a true peak and its coordinate in dimension H (hydrogen) is within 0.05 ppm with the same true peak. A predicted 3D peak is considered correct if and only if its coordinate in dimensions N and C (carbon) is within 0.5 ppm with a true peak and its coordinate in dimension H (hydrogen) is within 0.05 ppm with the same true peak.

The MATLAB codes for running MMWF and MMWF* for general denoising of 2D and 3D signals are available at: https://sites.google.com/site/carlovittoriocannistraci/5-datasets-and-matlab-code/median-modified-wiener-filter-for-2d-and-multidimensional-signal-denosing.

The proposed MMWF and MMWF* have been also incorporated into the WaVPeak program as options for the spectrum denoising step, and available at http://sfb.kaust.edu.sa/Pages/Software.aspx.

Author Contributions

C.V.C. and X.G. envisioned the study. C.V.C. invented MMWF* that is a novel variation of the MMWF. C.V.C., A.A. and X.G. designed the experiments. C.V.C. and A.A. designed the codes and performed the computational analysis. C.V.C., A.A. and X.G. analysed the results. C.V.C., A.A. and X.G. wrote the article.

Supplementary Material

Supplementary Information

Suppl Info

Funding: This work was supported by the independent group leader starting grant of the Technische Universita¨t Dresden (TUD), and Award No. GRP-CF-2011-19-P-Gao-Huang and a GMSV-OCRF award from King Abdullah University of Science and Technology (KAUST).