Parameterization of Highly Charged Metal Ions Using the 12-6-4 LJ-Type Nonbonded Model in Explicit Water

Abstract

Highly charged metal ions act as catalytic centers and structural elements in a broad range of chemical complexes. The nonbonded model for metal ions is extensively used in molecular simulations due to its simple form, computational speed, and transferability. We have proposed and parametrized a 12-6-4 LJ (Lennard-Jones)-type nonbonded model for divalent metal ions in previous work, which showed a marked improvement over the 12-6 LJ nonbonded model. In the present study, by treating the experimental hydration free energies and ion–oxygen distances of the first solvation shell as targets for our parametrization, we evaluated 12-6 LJ parameters for 18 M(III) and 6 M(IV) metal ions for three widely used water models (TIP3P, SPC/E, and TIP4P_EW). As expected, the interaction energy underestimation of the 12-6 LJ nonbonded model increases dramatically for the highly charged metal ions. We then parametrized the 12-6-4 LJ-type nonbonded model for these metal ions with the three water models. The final parameters reproduced the target values with good accuracy, which is consistent with our previous experience using this potential. Finally, tests were performed on a protein system, and the obtained results validate the transferability of these nonbonded model parameters.

Introduction

Highly charged (trivalent and tetravalent) metal ions are of great interest in both supramolecular,¹ biomolecular,² and rare-earth chemistry.³ Some of these serve as the coordination center that performs structural, catalytic, or electron-transfer functions, while others are well-known biotoxins.⁴⁻⁶ For example, iron–sulfur clusters have biochemical functions involving the respiration and photosynthesis processes.⁷ Iron in hemoglobin is involved in the transport and transfers oxygen within organisms.⁸ Lanthanide series elements have attracted significant attention due to their specific electromagnetic and optical characteristics.⁹ Their complexes serve as luminescent probes because of their large Stokes shifts and emission lifetimes.² The actinide series elements, such as Th, U, and Pu, are well known for their radioactivity.¹⁰ All of these can form highly charged metal ions, which pose a major challenge to computational modeling. Indeed, effective and accurate modeling of these ions will give insight into separation and recycling process aimed at reducing their harmfulness to the environment.

There are several theoretical methods to model metal ions: quantum mechanics (QM),^11,12 molecular mechanics (MM),¹³⁻²⁸ and the hybrid QM/MM method.^29,30 Classical force fields, which use an analytical function to represent the relationship between the energy and configuration of a system, have a significant speed advantage over the quantum-based methods. It is the state-of-the-art tool to study systems at the molecular level when combined with molecular dynamics^31,32 or Monte Carlo methods.^33,34 For metal ions, there are several widely used models including the bonded model,¹⁹⁻²⁴ nonbonded model,¹³⁻¹⁸ and cationic dummy model.²⁵⁻²⁷ The bonded model represents the interaction between the ion and its surrounding residues via the bond, angle, torsion, coulombic, and van der Waals (VDW) terms. Because of the harmonic approximation used in the bonded model, it does not simulate the processes involving chemical bond formation and dissociation.¹⁹ The nonbonded model usually places an integer charge on the metal ion and only uses the coulombic and VDW terms to represent the intermolecular interactions between the metal ion and surrounding particles. This simplification can result in a notable underestimation for modeling systems with strong covalent bonds.¹⁴ The dummy cationic model places the charge between the metal ions and the ligating atoms to mimic the covalent bond.²⁵ Besides the models previously discussed, there are also some polarizable force fields that have been developed for metal ions in recent years.³⁵⁻⁴¹

Even though more accurate models exist, the 12-6 Lennard-Jones nonbonded model is widely used due to its simple form, computational efficiency, and excellent transferability characteristics.^13,15,16,42 However, in previous research, we found that the 12-6 Lennard-Jones (LJ) nonbonded model could not reproduce several experimental properties across a series of divalent metal ions due to the neglect of the ion-induced dipole interaction.¹⁸ For the divalent metal ions, on average, there is a 50 kcal/mol underestimation for the hydration free energy (HFE) if we want to reproduce the experimental ion–oxygen distance (IOD) values, while there is ∼0.27 Å reduction for the IOD values if we reproduce the experimental HFE values. In light of this, we proposed a 12-6-4 LJ-type nonbonded model to account for the charge-induced dipole interaction.¹⁸ After picking suitable parameters, it was demonstrated that it was possible to reproduce the experimental HFE, IOD, and coordination number (CN) values simultaneously for a series of divalent metal ions. Furthermore, it was shown the new nonbonded model was readily transferable to mixed systems such as salt solutions and nucleic acid systems.

In the present work, we have estimated the 12-6 LJ parameters for 24 highly charged metal ions (18 M(III) ions and 6 M(IV) ions) for three widely used water models (TIP3P,⁴³ SPC/E,⁴⁴ and TIP4P_EW⁴⁵), respectively. This illustrated that the 12-6 LJ nonbonded model has a much larger underestimation of the ion–water interactions for the highly charged ions than for the mono and dications. We next parametrized the 12-6-4 LJ-type nonbonded model for the 24 highly charged metal ions for the same three water models. In general, these parameters simultaneously reproduce both the experimental HFE, IOD, and CN values with good accuracy. Moreover, they are consistent with previous research.^30,46−48 This work opens up new opportunities to simulate M(III) and M(IV) ions in aqueous solution using classical models. Furthermore, we carried out test simulations on a Fe(III)-containing protein system. Stable trajectories were obtained with the metal binding site being well-conserved, further supporting the excellent transferability of these parameters.

Method

Potential Form

In present work, we employed the nonbonded model in the AMBER force field⁴⁹

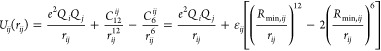1

In eq 1, the U_ij(r_ij) is the nonbonded interaction potential between atoms i and j at distance r_ij. It consists of electrostatic and VDW terms. Herein e represents the charge of the proton, while Q_i and Q_j are the partial charge of atoms i and j. The partial charge of metal ions is always treated as an integer number in the nonbonded model. The VDW interaction part uses a 12-6 Lennard-Jones (LJ) potential, in which there are two parameters (ε_ij and R_min,ij) that need to be determined. Using the geometric combining rule, the well depth of the LJ potential is

2

For the R_min,ij parameters, there are two widely used combining rules

3

and

4

Equation 3 is employed in the AMBER⁵⁰ and CHARMM⁵¹ force fields, while eq 4 is used in the OPLS force field.⁵² In the present work, we employed the Lorentz–Berthelot combining rules, which is the union of eqs 2 (Lorentz combining rule) and 3 (Berthelot combining rule).

For the 12-6-4 LJ-type potential, we employed the following expression

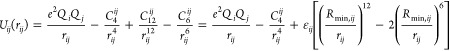5

An r^–4 term was added to describe the ion-induced dipole interaction, which cannot be overlooked for highly charged systems. The parametrization work concentrated on the determination of the R_min,i, ε_i for the different metal ions, and the C₄^ij term between the metal ion and oxygen atoms of the different water models. In the present work, we have determined the parameters for three widely used water models (TIP3P,⁴³ SPC/E,⁴⁴ and TIP4P_EW⁴⁵) independently. Previous work demonstrated that it is necessary to design different parameters for these water models due to their different geometries, charge distributions, and VDW parameters.^14,18,53

HFE Calculation

The thermodynamic integration (TI) method⁵⁴⁻⁵⁷ was used to simulate the HFE values. TI calculates the free-energy change between two different states of a system. An initial-state/final-state mixing potential was used during the simulation, in which V₀ and V₁ represent the potential of the initial and final state, respectively, while λ governs the mixing between the two states. k determines whether the mixing is linear or of higher order (k = 1 is linear).

6

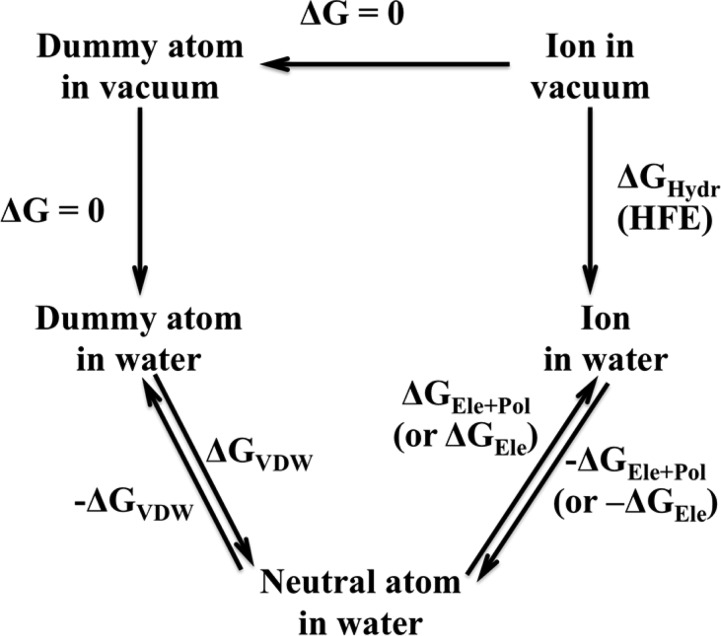
The ion solvation process is modeled as transfer of an isolated metal ion from the gas to liquid phase. In the present work, we employed the thermodynamic cycle depicted in Figure 1. To avoid the “end-point catastrophe”, we employed the linear scaling soft-core TI method⁵⁸ to obtain the ΔG_VDW term.

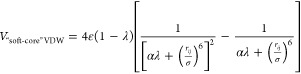7

Figure 1.

Thermodynamic cycle describing the determination of the hydration free energy of ions.

In eq 7, r_ij is the distance between the dummy atom and the surrounding particles, while σ is the distance at which the two particles’ VDW interaction is equal to zero. Here the ε is the well depth and α is a constant set to 0.5. The “end-point catastrophe” problem is largely avoided because there is limited energy penalty induced between the dummy atom and proximal particles when the VDW potential of the dummy atom is turned on.

8

9

As seen from eq 8, the free-energy of each process is obtained via the integration of the derivative of the potential with respect to λ. Herein we employed Gaussian quadrature⁵⁹ (eq 9) to evaluate the integral in an efficient way.

As illustrated in Figure 1, we obtained the HFE values based on the free-energy changes associated with four processes: ΔG_VDW, ΔG_Ele+Pol, −ΔG_Ele+Pol, and −ΔG_VDW. Herein the HFE value is computed using HFE = 1/2 × (ΔG_VDW + ΔG_Ele+Pol – (−ΔG_Ele+Pol – ΔG_VDW)). The ΔG_Ele+Pol and −ΔG_Ele+Pol are ΔG_Ele and −ΔG_Ele respectively, when the 12-6 nonbonded model is employed. At first, a dummy atom was placed in the center of a cubic water box (with size ∼32 Å × 32 Å × 32 Å) with the closest water molecule ∼1.5 Å away from it. There are in total 722 water molecules in the TIP3P or SPC/E water boxes, while there are 732 water molecules in the TIP4P_EW water box. Afterward 1000 steps of steepest descent minimization were performed, followed by 1000 steps conjugate gradient minimization. Then, a 500 ps heating procedure was performed to heat the system from 0 to 300 K in the NVT ensemble. Next, we equilibrated the system for 500 ps at 300 K and 1 atm using the NPT ensemble. The final snapshot from the equilibration simulation was used as the initial structure for the calculation of ΔG_VDW. To balance accuracy and speed, we used the four-window linear soft-core scaling process to obtain the ΔG_VDW value with λ values of 0.1127, 0.5, 0.88729, and 0.98, respectively. The simulation of last window was used to further equilibrate the system but was not used in the free-energy evaluation. The final snapshot was used to initiate the determination of ΔG_Ele+Pol. For the ΔG_Ele+Pol calculation process, a nine-window linear scaling scheme was utilized with λ values of 0, 0.2544, 0.12923, 0.29707, 0.5, 0.70292, 0.87076, 0.97455, and 1, respectively. Afterward, the −ΔG_Ele+Pol calculation process was carried out in a similar manner. In these simulations, the first and last windows (λ equal to 0 and 1) are not used in the final free-energy calculation but to further equilibrate the system. Finally, the −ΔG_VDW simulation procedure was carried out using a three-window linear soft-core scaling process in which λ was set at 0.1127, 0.5, and 0.88729, respectively. For the determination of ΔG_VDW and −ΔG_VDW, each window was simulated for 300 ps, with the last 200 ps used for data collection. The ΔG_Ele+Pol and −ΔG_Ele+Pol simulations covered 200 ps, with the last 150 ps used for data collection in each window. All TI simulations were performed in the NPT ensemble.

We have employed two different methods to evaluate the uncertainty of the simulated HFE values in the present work. These results are gathered in the Supporting Information (SI). The first method (Set 1) divided each sampling segment (ΔG_VDW, ΔG_Ele+Pol, −ΔG_Ele+Pol, and −ΔG_VDW) into two even portions and estimated the uncertainties for the VDW and electrostatic plus polarization free-energy determinations. For example, we have 200 ps of sampling for each window for the determination of ΔG_VDW and −ΔG_VDW. We used the first 100 ps of sampling to calculate the ΔG_VDW-part 1 and −ΔG_VDW-part 1 values, while we used the later 100 ps of sampling to obtain the ΔG_VDW-part 2 and −ΔG_VDW-part 2. Then, we assessed the uncertainty of the VDW free-energy determination by calculating the standard deviation based on these four values. The uncertainty of the electrostatic plus polarization free-energy determination was obtained in a similar manner with each fragment using 75 ps of sampling. Subsequently, we obtain the total uncertainty in the HFE value by adding the uncertainties of the VDW and electrostatic plus polarization free-energy determinations.

The second method (Set 2) uses eq 10, in which the τ_A is the autocorrelation time of observable A while (⟨A²⟩_c)^1/2 is the standard deviation of A. T is the sampling time of the simulation and δA is the final uncertainty of the observable A. The final HFE values given in the spreadsheets given in the SI are depicted as ⟨A⟩ ± σ. Again, the uncertainty of the VDW and electrostatic plus polarization free-energy determinations were evaluated separately, and the final uncertainty was treated as their sum. Herein we used a τ_A value equal to 500 fs for the VDW free-energy determinations, while we used 250 fs for the electrostatic plus polarization scaling part. We obtained these values based on test simulations, and they are consistent with previous work.⁶⁰

10

The Set 1 approach yields uncertainties in the range of 0.1–7.5 kcal/mol with an average of ∼1.2 kcal/mol, while Set 2 gives uncertainties in the range of 1.1 to 2.0 kcal/mol with an average of ∼1.4 kcal/mol. On the basis of these analyses, we estimate that the HFE uncertainty is in the ±2.0 kcal/mol range, which is quite small given the magnitude of HFEs we are computing.

IOD and CN Calculation

A metal ion (with an integer +3 or +4 partial charge) was solvated in the center of a cubic water box (with the same size as described in the HFE simulation part). Then, 1000 steps of steepest descent and 1000 steps of conjugated gradient minimization were carried out to relax the initial structure. Afterward, a 500 ps “heating” simulation was performed in the NVT ensemble that took the system from 0 to 300 K. Next, 500 ps of equilibration, followed by 2 ns of sampling were performed at 300 K and 1 atm. Snapshots were stored every 0.5 ps (every 500 steps for 4000 snapshots in total) for the subsequent IOD and CN analysis. The radial distribution function (RDF) of the ion and water oxygen atom was then calculated based on the average volume of the entire trajectory in the range of 0−5.0 Å with a grid resolution of 0.01 Å. The IOD value was evaluated based on two quadratic fits of the RDF. The first quadratic fit was performed using the points within ±0.1 Å of the first peak of RDF. In this way, the apex value was obtained with an accuracy of 0.01 Å. The second quadratic fitting was done based on the points within ±0.1 Å of the apex obtained from the first fitting. In total, 21 points were used for each fit. The maximum given by the second fitting was treated as the final IOD value to two decimal places. The CN value was obtained by integrating from the origin to the first minimum of the RDF.

The AMBER 12 suite of programs⁴⁹ was used to perform the simulations, while the Amber Tools suite of programs⁴⁹ was utilized to carry out the data analysis. The particle mesh Ewald (PME)⁶¹⁻⁶³ method and periodic boundary condition (PBC) were employed throughout. The time-step was 1 fs, while the cutoff was set to 10 Å. For the temperature control, the Langevin algorithm was utilized with a collision frequency equal to 5.0 ps^–1. The isotropic pressure algorithm was used to control the pressure. The pressure relaxation time was set to 10 and 1 ps in the TI and standard MD simulations, respectively. The SHAKE^64,65 algorithm was employed to restrain the bond lengths involving hydrogen atoms. Herein the “three-point” algorithm was used for the water molecules.⁶⁵

Results and Discussion

Experimental Values

The HFE values for all M(III) and M(IV) ions investigated were taken from Marcus.⁶⁶ They were determined based on using Δ_hydG⁰[H⁺] = −1056 kJ/mol.⁶⁶ It is one of the most complete databases regarding the thermodynamic properties of ions. The IOD and CN values for M(III) ions were taken from Marcus’ review,⁶⁷ while the IOD and CN values for the M(IV) ions were taken from a number of sources.⁶⁸⁻⁷¹ The experimental effective ionic radii were obtained from Shannon.⁷² On the basis of the IOD values and effective ionic radii, we estimated the effective radii of the coordinated water and display the data in Table 1. Some highly charged ions that readily hydrolyze water such as As³⁺, Sn⁴⁺, and Pb⁴⁺ ions³⁰ were not considered in the present work.

Table 1. Experimental HFE and IOD Values of M(III) and M(IV) Metal Ions.

metal ion	electron configuration	HFE (kcal/mol)a	IOD (Å)b	CNb	effective ion radii (Å)	first shell water radii (Å)
Al3+	[Ne]	–1081.5	1.88	6	0.54	1.34
Fe3+	[Ar]3d5	–1019.4	2.03	6	0.65	1.38
Cr3+	[Ar]3d3	–958.4	1.96	6	0.62	1.34
In3+	[Kr]4d10	–951.2	2.15	6	0.80	1.35
Tl3+	[Xe]4f145d10	–948.9	2.23	4–6	0.89	1.34
Y3+	[Kr]	–824.6	2.36	8	0.90	1.46
La3+	[Xe]	–751.7	2.52	8.0–9.1	1.03	1.49
Ce3+	[Xe]4f1	–764.8	2.55	7.5	1.01	1.54
Pr3+	[Xe]4f2	–775.6	2.54	9.2	0.99	1.55
Nd3+	[Xe]4f3	–783.9	2.47	8.0–8.9	0.98	1.49
Sm3+	[Xe]4f5	–794.7	2.44	8.0–9.9	0.96	1.48
Eu3+	[Xe]4f6	–803.1	2.45	8.3	0.95	1.50
Gd3+	[Xe]4f7	–806.6	2.39	8.0–9.9	0.94	1.45
Tb3+	[Xe]4f8	–812.6	2.40	8.0–8.2	0.92	1.48
Dy3+	[Xe]4f9	–818.6	2.37	7.4–7.9	0.91	1.46
Er3+	[Xe]4f11	–835.3	2.36	6.3–8.2	0.89	1.47
Tm3+	[Xe]4f12	–840.1	2.36	8.1	0.88	1.48
Lu3+	[Xe]4f14	–840.1	2.34	8	0.86	1.48
Hf4+	[Xe]4f14	–1664.7	2.16c	8c	0.85	1.31
Zr4+	[Kr]	–1622.8	2.19c	8c	0.86	1.33
Ce4+	[Xe]	–1462.7	2.42d	9d	0.87	1.55
U4+	[Rn]6d15f1	–1567.9	2.42e	9–11e	0.89	1.53
Pu4+	[Rn]5f4	–1520.1	2.39f	8f	0.86	1.53
Th4+	[Rn]	–1389.8	2.45e	9–11e	0.94	1.51

^aReferenced from Marcus.⁶⁶

^bReferenced or calculated from Marcus.⁶⁷

^cFrom Hagfeldt et al.⁷¹

^dFrom Sham.⁶⁸

^eFrom Moll et al.⁷⁰

^fFrom Ankudinov et al.⁶⁹

Scanning Parameter Space

To balance time and accuracy, we performed parameter scanning using two parallel curves. One is for R_min/2 from 0.9 to 2.3 Å with 0.1 Å intervals without the C₄ term (namely using the 12-6 LJ nonbonded model), while the other is for the same R_min/2 value sets with a constant C₄ term equal to 500 kcal/mol·Å⁴. The ε values are obtained for each R_min/2 value based on the noble gas curve (NGC), which was previously developed.¹⁴ The HFE, IOD, and CN values for each parameter point are collected in Tables SI.1 and SI.2 in the Supporting Information (SI). These data points might be useful to those who want to parametrize the 12-6 LJ or 12-6-4 LJ-type nonbonded model with different target values from the present work.

12-6 LJ Parameters Estimation

On the basis of the quadratic fitting of the data points from the parameter scans without the C₄ term (see the SI), we estimated the HFE and IOD parameter sets. The two parameter sets are shown in Tables 2 and 3, while the estimated absolute and percent errors are shown in Table SI.3. Similar to our parametrization of divalent metal ions using the 12-6 LJ nonbonded model,¹⁴ the R_min/2 parameters in the HFE parameter set are in excellent agreement with the VDW radii calculated using the quantum-mechanical scaling principle (QMSP) method.⁷³ For the Al³⁺, Y³⁺, and La³⁺ ions, the estimated R_min/2 values in the estimated HFE parameter set for the TIP3P water model are 0.981, 1.454, and 1.628 Å respectively. The calculated VDW radii are 1.046, 1.481, and 1.642 Å, respectively, based on the QMSP method. There is only a 6.2, 1.8, and 0.9% difference between these two sets of values. This further validates the physical meaningful of our parametrization work. Moreover, the estimated R_min/2 values used in the 12-6 LJ parameter sets could be used as the VDW radii for RESP charge-fitting procedures. For example, in the work of Kuznetsov et al.,⁷⁴ they used 1.4 Å as the VDW radius for the RESP charge fitting for both the Fe²⁺ and Fe³⁺ ions, while for the IOD parameter set the Fe²⁺ radius was determined to be 1.409 Å in our previous research.¹⁸ Herein, the IOD parameter sets for the Fe³⁺ ion estimated the radius as 1.386, 1.386, and 1.375 for the TIP3P, SPC/E, and TIP4P_EW water models, respectively.

Table 2. Estimated HFE Parameter Set for M(III) and M(IV) Metal Ions Using the 12-6 LJ Nonbonded Potential.

	TIP3P		SPC/E		TIP4PEW
	Rmin/2 (Å)	ε (kcal/mol)	Rmin/2 (Å)	ε (kcal/mol)	Rmin/2 (Å)	ε (kcal/mol)
Al3+	0.981	0.00000832	0.991	0.00001107	0.876	0.00000026
Fe3+	1.082	0.00011017	1.091	0.00013462	0.984	0.00000907
Cr3+	1.188	0.00089969	1.196	0.00103208	1.096	0.00015019
In3+	1.202	0.00114198	1.209	0.00128267	1.110	0.00020260
Tl3+	1.206	0.00122067	1.213	0.00136949	1.114	0.00022027
Y3+	1.454	0.02639002	1.459	0.02759452	1.375	0.01205473
La3+	1.628	0.09399072	1.629	0.09454081	1.553	0.05807581
Ce3+	1.595	0.07688443	1.597	0.07786298	1.519	0.04525501
Pr3+	1.568	0.06441235	1.571	0.06573030	1.492	0.03655251
Nd3+	1.548	0.05605698	1.551	0.05726270	1.471	0.03064622
Sm3+	1.522	0.04630154	1.526	0.04772212	1.445	0.02431873
Eu3+	1.503	0.03994409	1.507	0.04122946	1.425	0.02014513
Gd3+	1.495	0.03745682	1.499	0.03868661	1.417	0.01863432
Tb3+	1.481	0.03336723	1.485	0.03450196	1.403	0.01619682
Dy3+	1.468	0.02986171	1.472	0.03091095	1.389	0.01400886
Er3+	1.431	0.02133669	1.436	0.02236885	1.350	0.00909668
Tm3+	1.421	0.01937874	1.426	0.02034021	1.340	0.00808758
Lu3+	1.421	0.01937874	1.426	0.02034021	1.340	0.00808758
Hf4+	1.087	0.00012321	1.098	0.00015685	0.977	0.00000741
Zr4+	1.139	0.00036479	1.149	0.00044254	1.031	0.00003240
Ce4+	1.353	0.00941798	1.360	0.01020237	1.257	0.00270120
U4+	1.209	0.00128267	1.218	0.00148497	1.105	0.00018227
Pu4+	1.273	0.00339720	1.281	0.00379705	1.172	0.00067804
Th4+	1.463	0.02858630	1.468	0.02986171	1.370	0.01141046

Table 3. Estimated IOD Parameter Set for M(III) and M(IV) Metal Ions Using the 12-6 LJ Nonbonded Potential.

	TIP3P		SPC/E		TIP4PEW
	Rmin/2 (Å)	ε (kcal/mol)	Rmin/2 (Å)	ε (kcal/mol)	Rmin/2 (Å)	ε (kcal/mol)
Al3+	1.297	0.00471279	1.296	0.00465074	1.285	0.00401101
Fe3+	1.386	0.01357097	1.386	0.01357097	1.375	0.01205473
Cr3+	1.344	0.00848000	1.343	0.00838052	1.333	0.00743559
In3+	1.461	0.02808726	1.461	0.02808726	1.450	0.02545423
Tl3+	1.513	0.04321029	1.513	0.04321029	1.502	0.03962711
Y3+	1.602	0.08034231	1.602	0.08034231	1.590	0.07447106
La3+	1.718	0.15060822	1.718	0.15060822	1.707	0.14295367
Ce3+	1.741	0.16721338	1.741	0.16721338	1.729	0.15845086
Pr3+	1.733	0.16134811	1.734	0.16207614	1.722	0.15343866
Nd3+	1.681	0.12564307	1.681	0.12564307	1.669	0.11803919
Sm3+	1.659	0.11189491	1.659	0.11189491	1.647	0.10475707
Eu3+	1.666	0.11617738	1.666	0.11617738	1.655	0.10948690
Gd3+	1.623	0.09126804	1.623	0.09126804	1.612	0.08544204
Tb3+	1.630	0.09509276	1.630	0.09509276	1.619	0.08912336
Dy3+	1.609	0.08389240	1.609	0.08389240	1.597	0.07786298
Er3+	1.602	0.08034231	1.602	0.08034231	1.590	0.07447106
Tm3+	1.602	0.08034231	1.602	0.08034231	1.590	0.07447106
Lu3+	1.588	0.07351892	1.588	0.07351892	1.577	0.06841702
Hf4+	1.499	0.03868661	1.501	0.03931188	1.483	0.03393126
Zr4+	1.519	0.04525501	1.521	0.04595090	1.503	0.03994409
Ce4+	1.684	0.12758274	1.689	0.13084945	1.667	0.11679623
U4+	1.684	0.12758274	1.689	0.13084945	1.667	0.11679623
Pu4+	1.662	0.11371963	1.666	0.11617738	1.645	0.10359269
Th4+	1.708	0.14364160	1.713	0.14710519	1.690	0.13150785

Combining the data with previous work on M(II) metal ions, we summarized the absolute and percent errors for the 12-6 LJ nonbonded model for M(II), M(III), and M(IV) ions in Tables 4 and 5. These results, taken as a whole, show that the underestimation of the 12-6 LJ nonbonded model increases dramatically as the charge on the metal ion increases. For example, for the TIP3P water model, the average absolute error goes from ∼50 kcal/mol for M(II) ions to ∼80 kcal/mol for M(III) and ∼240 kcal/mol for M(IV) ions for the IOD parameter set, while the average absolute error of the IOD values for the HFE parameter set increases from −0.27 Å for M(II) ions to −0.29 Å for M(III) ions and −0.58 Å for M(IV) ions. For some of the monovalent ions, it is possible to reproduce both the experimental HFE and IOD values at the same time;⁵³ this underestimation of the 12-6 LJ nonbonded model is pretty small and can almost be neglected. Because there are significant errors associated with the 12-6 LJ nonbonded model for highly charged ions, we did not carry out further refinement work on the estimated 12-6 LJ parameters because the resultant parameters would be of limited usefulness.

Table 4. Estimated Average Absolute and Percent IOD Errors (in Brackets) for the 12-6 HFE Parameter Set against Experimental Values for Divalent, Trivalent, and Tetravalent Metal Ions^a.

		M(II)	M(III)	M(IV)
TIP3P	avg. IOD error	–0.27 (−12.4%)	–0.29 (−12.8%)	–0.58 (−25.0%)
	IOD error SD	0.14 (7.8%)	0.14 (7.4%)	0.15 (7.0%)
SPC/E	avg. IOD error	–0.26 (−12.3%)	–0.28 (−12.4%)	–0.57 (−24.5%)
	IOD error SD	0.14 (7.6%)	0.13 (7.2%)	0.14 (6.6%)
TIP4PEW	avg. IOD error	–0.36 (−16.8%)	–0.41 (−18.1%)	–0.74 (−32.0%)
	IOD error SD	0.17 (10.2%)	0.16 (9.2%)	0.17 (8.2%)

^aAbsolute IOD errors are in angstroms.

Table 5. Estimated Average Absolute and Percent HFE Errors (in brackets) for the 12-6 IOD Parameter Set against Experimental Values for Divalent, Trivalent, and Tetravalent Metal Ions^a.

		M(II)	M(III)	M(IV)
TIP3P	avg HFE error	51.1 (−11.5%)	82.7 (−9.3%)	244.3 (−15.7%)
	HFE error SD	25.2 (4.5%)	42.7 (3.6%)	62.7 (3.3%)
SPC/E	avg HFE error	51.9 (−11.7%)	81.8 (−9.2%)	244.9 (−15.8%)
	HFE error SD	24.3 (4.3%)	41.6 (3.5%)	61.8 (3.2%)
TIP4PEW	avg HFE error	67.2 (−15.2%)	108.0 (−12.3%)	283.0 (−18.2%)
	HFE error SD	27.5 (4.5%)	46.4 (3.7%)	65.1 (3.3%)

^aAbsolute HFE errors are in kilocalories per mole.

12-6-4 Parameter Determination

After initial parameter selection and subsequent fine-tuning, the final 12-6-4 parameters were determined. The final optimized 12-6-4 parameters are given in Table 6 while the simulated HFE, IOD, and CN values are shown in Table SI.4. These parameters reproduce the experimental HFE values by ±1 kcal/mol and the IOD values by ±0.01 Å for the M(III) ions, while they reproduce the HFE values by ±2 kcal/mol and the IOD values by ±0.01 Å for the M(IV) ions. Just as in the 12-6-4 parameter sets for divalent metal ions, the R_min/2 terms are similar between the three water models, while the C₄ term for TIP4P_EW water is generally larger than for the other two water models for the same metal ion. This may due to the smaller dipole of the TIP4P_EW water model (2.32 D) relative to the TIP3P (2.35 D) and SPC/E (2.35 D) water models. Figure 2 shows the accuracy comparison between the 12-6-4 parameter set and the 12-6 parameter sets for divalent, trivalent, and tetravalent metal ions. We can see that there is significant improvement in the accuracy using the 12-6-4 parameter set, which is able to reproduce the experimental HFE and IOD values simultaneously. While for the 12-6 LJ nonbonded model, if you want to reproduce the experimental HFE values, the error in the simulated IOD values would increase along with the formal charge of the metal ions. Vice versa, if you simulate the IOD values using the 12-6 LJ nonbonded model, the error of the calculated HFE would increase markedly with an increase in the oxidation state of the metal ion in question.

Table 6. Final Parameters for the 12-6-4 LJ-Type Nonbonded Model for Metal Ions in Three Water Models.

	TIP3P			SPC/E			TIP4PEW
	Rmin/2 (Å)	ε (kcal/mol)	C4 (kcal/mol·Å4)	Rmin/2 (Å)	ε (kcal/mol)	C4 (kcal/mol·Å4)	Rmin/2 (Å)	ε (kcal/mol)	C4 (kcal/mol·Å4)
Al3+	1.369	0.01128487	399	1.375	0.01205473	406	1.377	0.01232018	488
Fe3+	1.443	0.02387506	428	1.450	0.02545423	442	1.448	0.02499549	519
Cr3+	1.415	0.01827024	258	1.414	0.01809021	254	1.408	0.01703790	322
In3+	1.491	0.03625449	347	1.487	0.03507938	349	1.486	0.03478983	425
Tl3+	1.571	0.06573030	456	1.569	0.06484979	455	1.564	0.06268139	535
Y3+	1.630	0.09509276	216	1.624	0.09180886	209	1.624	0.09180886	294
La3+	1.758	0.17997960	152	1.763	0.18380968	165	1.755	0.17769767	243
Ce3+	1.782	0.19865859	230	1.786	0.20184160	242	1.776	0.19392043	315
Pr3+	1.780	0.19707431	264	1.782	0.19865859	272	1.774	0.19235093	348
Nd3+	1.724	0.15486311	213	1.735	0.16280564	235	1.720	0.15202035	297
Sm3+	1.711	0.14571499	230	1.703	0.14021803	224	1.706	0.14226734	314
Eu3+	1.716	0.14920231	259	1.721	0.15272873	273	1.711	0.14571499	345
Gd3+	1.658	0.11129023	198	1.646	0.10417397	186	1.652	0.10769970	280
Tb3+	1.671	0.11928915	235	1.666	0.11617738	227	1.665	0.11556030	313
Dy3+	1.637	0.09900804	207	1.637	0.09900804	206	1.639	0.10014323	298
Er3+	1.635	0.09788018	251	1.629	0.09454081	247	1.628	0.09399072	328
Tm3+	1.647	0.10475707	282	1.633	0.09675968	262	1.638	0.09957472	356
Lu3+	1.625	0.09235154	249	1.620	0.08965674	247	1.617	0.08806221	331
Hf4+	1.600	0.07934493	827	1.592	0.07543075	810	1.599	0.07884906	956
Zr4+	1.609	0.08389240	761	1.609	0.08389240	760	1.610	0.08440707	895
Ce4+	1.766	0.18612361	706	1.761	0.18227365	694	1.761	0.18227365	835
U4+	1.792	0.20665151	1034	1.791	0.20584696	1043	1.791	0.20584696	1183
Pu4+	1.752	0.17542802	828	1.750	0.17392181	828	1.753	0.17618319	972
Th4+	1.770	0.18922704	512	1.773	0.19156806	513	1.758	0.17997960	625

Figure 2.

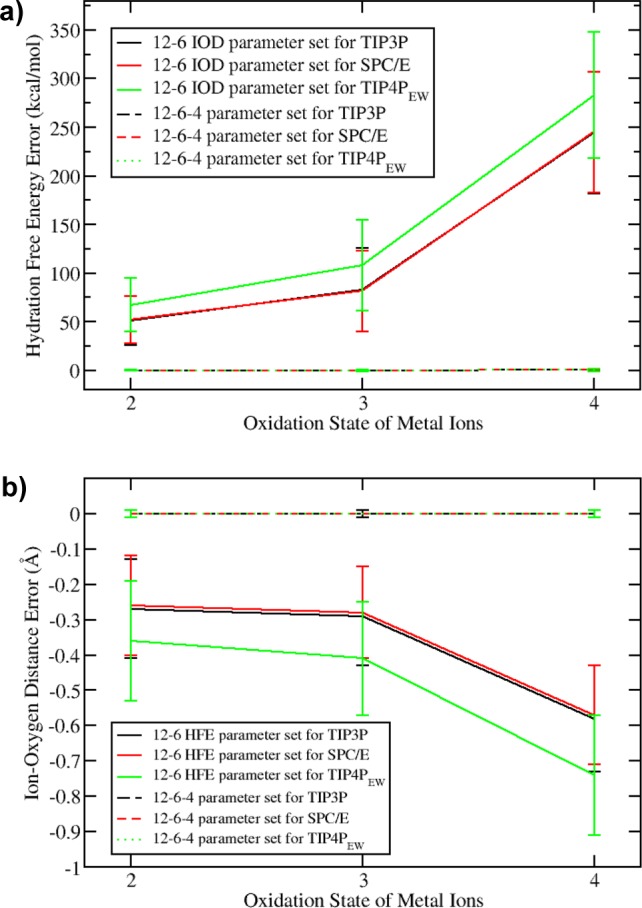
(a) HFE errors for the 12-6 IOD and 12-6-4 parameter sets for M(II), M(III), and M(IV) metal ions. (b) IOD errors for the 12-6 HFE and 12-6-4 parameter sets for the M(II), M(III), and M(IV) metal ions.

1. Trivalent Metal Ions

Main Group and Transition-Metal Ions

These metal ions have much stronger ion–water interactions than the Ln³⁺ ions. Some of them are extremely inert ions. They form a stable octahedral structure with water molecules in the first solvation shell. Data in Table 1 indicate that the average effective radius of the first solvation shell water is ∼1.35 Å for the first several metal ions, which is consistent with strong interactions between the coordinated water molecules and these metal ions. These values are close to previously proposed coordinated water radius (∼1.34 Å).⁷⁵ The corresponding average values are ∼1.49 Å and ∼1.46 Å for the Ln³⁺ and the M(IV) metal ions, respectively, which implies a smaller electronic cloud overlap between the metal ion center and each of the coordinated water molecules.

Al³⁺, In³⁺, and Tl³⁺ are group IV ions. For the C₄ parameters derived herein, we obtained a sequence of Tl³⁺ > Al³⁺ > In³⁺. The Al³⁺ ion is the smallest M(III) ion, resulting in a relatively larger C₄ term due to its strong covalent interaction with coordinated water molecules. Tl has two oxidation states, +1 and +3, and the HFE values of the Tl⁺ and K⁺ are almost the same in Marcus’ HFE set.⁶⁶ Tl³⁺ could have very strong covalent interactions with the surrounding residues. The reduced electric potential of M(III) + 3e^– = M is −1.67, −0.3382, and +0.72 eV for Al³⁺, In³⁺, and Tl³⁺, respectively.⁷⁶ The positive reduction potential of Tl³⁺ makes it a very reactive species. It readily obtains electrons from its surroundings, which may be the reason for a strong charge-transfer effect between the Tl³⁺ ion and the surrounding water molecules. The 12-6-4 parameters of In³⁺ and Tl³⁺ ions gave an excellent prediction for the HFE and IOD values but overestimated the CN value (8 instead of 6), and this is mainly due to the lack of a correction for the water–water interactions in the first solvation shell during the simulations. The water–water interactions were parametrized to reproduce the pure liquid water properties in the original parameter design. However, the first solvation shell water molecules of the highly charged metal ions should more strongly repel one another due to their bigger charge separations. This effect is smaller for M(I) and M(II) metal ions, but it dramatically increases for the highly charged ions. Meanwhile, this kind of effect may decrease in protein systems due to the preorganization of the metal ion binding sites.

Fe³⁺ has a larger C₄ term than Al³⁺, the smallest M(III) ion, which suggests that Fe³⁺ has a stronger interaction with its surrounding water molecules. This is consistent with quantum-mechanical charge-field molecular dynamics (QMCF-MD) simulations, which shows that the force constant between the ion and the oxygen of first solvation shell water molecules (k_ion-O) is 198 N/m for Fe³⁺ compared with 185 N/m for Al³⁺.³⁰ This is a consequence of both electrostatic and covalent interactions. The Fe³⁺ ion has an average 1.85e⁴⁷ charge (from a Mulliken analysis) in the QMCF simulation, while Al³⁺ ion has a corresponding value of 2.5 e,⁷⁷ which implies that there is a stronger charge-transfer effect for the Fe³⁺ ion and its surrounding water molecules than for the Al³⁺ ion. There is a slight overestimation of the CN for Fe³⁺ ions. Also, as previously discussed, this may be due to the underestimation of the interactions between the first solvation water molecules. While this effect is operative in aqueous solution, it will likely be less of an issue in protein systems (see discussion below).

Y³⁺ and Ln³⁺ Ions

The +3 oxidation state is the typical oxidation state of the Ln elements, with the exception that Eu²⁺ and Ce⁴⁺ could also be observed. This is because Eu²⁺ has a half-filled 4f orbital while Ce⁴⁺ has the same electronic configuration as Xe. The interaction of the Ln³⁺ ions with surrounding water molecules would be expected to have more ionic character than the M(III) ions previously discussed. For example, the C₄ terms between the Ln³⁺ ions and water molecules are between 152 and 282 kcal/mol·Å⁴, which is smaller than the 258–456 kcal/mol·Å⁴ range seen for the other +3 metal ions previously discussed. Previous simulations found that the k_ion-O values are much smaller for the Ln³⁺ ions; for example, La³⁺, Ce³⁺, Lu³⁺, and Er³⁺ have k_ion-O values ∼110 N/m, while the values for the Al³⁺ and Fe³⁺ ions are 185 and 203 N/m, respectively.⁴⁶ The Ln³⁺ ions have effective ionic radii in the range of 0.86 to 1.03 Å and IOD values in the range of 2.34 to 2.55 Å. These values are similar to that of the Ca²⁺ ion (whose effective ionic radius and IOD value is 1.00⁷² and 2.46 Å,⁷⁸ respectively). Therefore, they have been used as probes to investigate the role of Ca²⁺ ions in biological systems.⁷⁹

From Table 6, we observe that the La³⁺ and Gd³⁺ ions have the smallest C₄ terms among the Ln³⁺ ions. This may be because they have either totally empty or half-filled 4f orbitals, making them more likely to form isolated ions, which reduces the covalent character of their bonds with coordinated water molecules. It is easy to see the “lanthanide contraction” effect from Table 1. The effective ion radius decreases monotonically with an increase in the metal ions’ atomic number due to the poor shielding of the 4f electrons toward 5s and 5p orbitals.⁸⁰ A similar tendency can also be seen for the HFE and IOD values along the series. Our final R_min/2 parameters are consistent with this pattern as well. Meanwhile, the CN also decreases along the Ln³⁺ ion series. Previous work reached the conclusion that the lighter Ln³⁺ ions (La³⁺ to Nd³⁺) prefer a CN of ∼9 and the heavier ions (Gd³⁺ to Tb³⁺) prefer a CN of ∼8, while the middle ions such as Sm³⁺ and Eu³⁺ have CN between these two values.⁸¹⁻⁸⁶ It was proposed that the former Ln³⁺ ions have a tricapped trigonal prism structure, which then shifts to a distorted bicapped trigonal prism structure for the heavier elements as one of the two capping water molecules leaves the first solvation shell.⁸⁷ Generally speaking, there is a good agreement between the 12-6-4 parameters for the HFE, IOD, and CN values with experiment, with the exception that some of the CN values were slightly overestimated. The final parameters gave a CN in the range of 9 to 10 for Ln³⁺ ions rather than the range of 8 to 9 reported in the literature. As previously discussed, this may be due to the fact that there is no water–water interaction correction term in the present parametrization process. Moreover, the CN values given by Marcus (as shown in Table 1) likely also vary under different experimental conditions (counterions used solute concentration, etc.). Among all ions, Al³⁺, Y³⁺, and La³⁺ have the same electron configurations as the noble gas atoms Ne, Kr, and Xe, respectively. Using the TIP3P water model as an example, we can see their C₄ values decrease from 399 to 216 and 152 kcal/mol·Å⁴, respectively.

2. Tetravalent Metal Ions

There are only a few M(IV) ions that exist in aqueous solution, while the others are readily hydrolyzed into polynuclear complexes in water.⁶⁸⁻⁷¹ Table 1 shows the M(IV) ions examined herein. These ions exist in at least highly acidic solution. The CN values of these metal ions are greater than 8, with some of them being ∼10 according to experiment.⁶⁸⁻⁷¹ Previous work found that Pu(IV), Th(IV), and U(IV) could strongly bind to transferrin, an iron-transport protein.⁸⁸ Hence, the parameters developed herein might facilitate theoretical research on the biotoxicity of these M(IV) ions.

The Zr⁴⁺ and Hf⁴⁺ are in the IVB group. Even though Hf⁴⁺ has a larger atomic number than Zr⁴⁺, due to the “lanthanide contraction” effect, it has a smaller effective radius, smaller IOD, smaller HFE, and a bigger C₄ term than Zr⁴⁺. These observations reflect its stronger interaction with the surrounding water molecules. In contrast, Ce⁴⁺ and Th⁴⁺ are in the same group where the larger atomic number (Th⁴⁺) has the bigger ionic radius, bigger HFE, and smaller C₄ terms. This may be because they share the same electronic structure as Xe and Rn, respectively. Besides these ions, Zr⁴⁺ is another M(IV) ion that has a noble gas atom’s electronic structure (the same as Kr). There is also a single trend for the C₄ terms of Zr⁴⁺, Ce⁴⁺, and Th⁴⁺ ions for each specific water model. For instance, the C₄ terms for the TIP3P water model are 761, 706, and 512 kcal/mol·Å⁴, respectively.

Th, U, and Pu are in the An series and are the largest elements investigated in the present work. Their tetravalent metal ions exist only in highly acidic solutions. Canaval et al. investigated Th⁴⁺ in aqueous solutions using the QMCF-MD method. They found a stable nine-coordinate complex, and even the third layer of water molecules has a bigger mean residence time than that of pure water, implying they are stabilized by the highly charged Th⁴⁺ ion.⁴⁸ U⁴⁺ fluoresces due to the electron transition between the 6d¹5f¹ and 5f² electronic configurations.²⁰⁰ The U⁴⁺ ion has the largest C₄ term of all of the M(IV) metal ions investigated. Frick et al. investigated the U⁴⁺ ion in aqueous solution using the QMCF-MD method, and the CN value was characterized as 9, while the average charge of U⁴⁺ was predicted to be +2.68 from Mulliken population analyses.³⁰⁰ Odoh et al. simulated the Pu³⁺, Pu⁴⁺, PuO₂⁺, and PuO₂²⁺ ions in water solution using the Car–Parrinello molecular dynamics method.⁸⁹ They predicted that the pK_a value for the first hydrolysis step for the Pu³⁺, Pu⁴⁺, PuO₂⁺, and PuO₂²⁺ ions is 6.65, 0.17, 9.51, and 5.70, respectively, showing a general tendency that the larger the charge of the metal center, the lower the pK_a value of the first hydrolysis reaction. Hf⁴⁺, Zr⁴⁺, and Pu⁴⁺ have relatively smaller IOD values among the tetravalent ions, where they all have experimental CNs of ∼8.⁷¹ Ce⁴⁺ was determined to have an experimental CN of ∼9,⁶⁸ while U⁴⁺ and Th⁴⁺ have CNs between 9 and 11.⁷¹ Soderholm et al. proposed that counterions also play a key role in the first solvation shell structure, while the 9-, 10-, or 11-coordinated Th⁴⁺ have very small energy differences and are in a dynamic equilibration.⁹⁰ The simulated HFE and IOD values of the 12-6-4 parameter set are in excellent agreement with the experiment. The simulated CN values of most of the M(IV) ions are ∼10, with Hf⁴⁺ having a CN ∼8 for the TIP4P_EW and SPC/E water models. Herein, the TIP3P model always predicted a larger CN value than the other two water models, which may be because it has a smaller C₁₂ term (∼582.0 × 10⁵ kcal·Å¹²/mol) than that of the SPC/E (∼629.4 × 10⁵ kcal·Å¹²/mol) and TIP4P_EW (∼656.1 × 10⁵ kcal·Å¹²/mol) models.

3. Redox Ion Pairs

Later, we analyze several redox pairs to explore the consistency of the C₄ parameters we determined with respect to the behavior of these pairs in aqueous solution. We also calculated the relative HFE between each redox pair for the TIP3P water model (see below). The divalent metal ions’ 12-6-4 parameters are from previous work.¹⁸ A nine-windows TI simulation (50 ps of equilibration and 150 ps of sampling for each window) was performed forward and backward, respectively, to obtain the final results. The results further validate the method employed in the present work. For example, the simulated relative HFEs of Fe²⁺/Fe³⁺, Cr²⁺/Cr³⁺, and Ce³⁺/Ce⁴⁺ ion pairs were 580.2, 516.9, and 698.2 kcal/mol, while the experimental values are 579.6, 516.2, and 697.6 kcal/mol, respectively.⁶⁶

Fe^2+/Fe³⁺ Ion Pairs

The experimental IOD values shrink ∼0.08 Å from 2.11 Å of Fe²⁺ to 2.03 Å of Fe³⁺ ion. Moin et al. investigated ferrous and ferric ions in water using the QMCF-MD method. They obtained a force constant k_ion-O of 193 N/m for Fe³⁺, which is almost twice as strong as that of Fe²⁺ (93 N/m), while the effective charges (from a Mulliken population analysis) for the Fe²⁺ ion are in the range of 1.25 to 1.45 (with an average of 1.36), and for the Fe³⁺ ion it is in the range of 1.70 to 1.95 (with an average of 1.85).⁴⁷ Fe²⁺/Fe³⁺ redox pairs exist broadly in biologically related system such as the Fe–S proteins and heme structures.^7,91 Moreover, Fe²⁺/Fe³⁺ redox pairs play fundamental roles in many electron-transfer processes. We have determined the 12-6-4 parameters for Fe²⁺ ion with three different water models in previous work.¹⁸ For the TIP3P water model, the final optimized parameters were R_min/2 = 1.457 Å, ε = 0.02710805 kcal/mol, and C₄ = 163 kcal/mol·Å⁴.¹⁸ From the 12-6-4 parameters determined for the Fe³⁺ ion herein, we find that the R_min/2 decreases slightly as the outer shell electron number decreases, while the C₄ term increases by ∼2.5 times relative to Fe²⁺. This is consistent with a ratio between the C₄ terms for a trivalent and divalent ion of [3/2]² = 2.25, which is derived from the original ion-induced dipole equation (eq 11 in a prior publication¹⁸).

Cr^2+/Cr³⁺ Ion Pairs

Cr³⁺ forms a stable Cr(H₂O)₆³⁺ complex in the aqueous phase. The Cr²⁺ and Cr³⁺ ions have [Ar]3d⁴ and [Ar]3d⁵ electronic structures, respectively, where the Cr(H₂O)₆²⁺ complex has a strong Jahn–Teller effect while the Cr(H₂O)₆³⁺ molecule has a standard octahedral configuration. The IOD values decreases from 2.08 to 1.96 Å for the Cr²⁺ and Cr³⁺ ions. Using the TIP3P water model as a representative example, we observe that the R_min/2 parameter decreases from 1.431 to1.405 Å, while the C₄ term increases from ∼137 to ∼258 kcal/mol·Å⁴ for the Cr²⁺ and Cr³⁺ ions (the Cr²⁺ parameters are reported in reference (18)).

Ce^3+/Ce⁴⁺ Ion Pairs

Cerium has both +3 and +4 oxidation states. Ce⁴⁺ is the most stable state because it shares the same electronic configuration with Xe. Just like the two oxidation pairs previously discussed we find that the R_min/2 value decreases while the C₄ term increases significantly with increasing charge. For example, for the parameters determined for the TIP3P water model, the R_min/2 decreased ∼0.03 Å, while the C₄ term increased by ∼480 kcal/mol·Å⁴.

Validation on a Protein System

PDB entry 4BV1 was used to obtain the starting coordinates for this modeling exercise. It is a superoxide reductase (SOD) found in Nanoarchaeum equitans. It is a protein tetramer with each monomer having a metal site containing an Fe³⁺ ion. The structure has been determined by using X-ray crystallography to a resolution of 1.90 Å. The tetramer structure is shown in Figure 3, while Chain C with its metal site is shown in Figure 4. The metal site contains four histidine groups, one cysteine group, and one water molecule. By treating Chain C as the initial structure, we performed three simulations with different parameter sets (the HFE, IOD, and 12-6-4 parameter sets). For the 12-6-4 parameter set, the C₄ terms between the Fe³⁺ ion and atom types other than water oxygen were evaluated using eq 11. The TIP3P water model was employed during the simulations. Details of the simulation procedures and the polarizability of each atom type are given in the SI.

11

Figure 3.

PDB entry 4BV1. Water molecules are not shown in the Figure, the ferric ion is shown as a sliver sphere. This picture was created by VMD.⁹²

Figure 4.

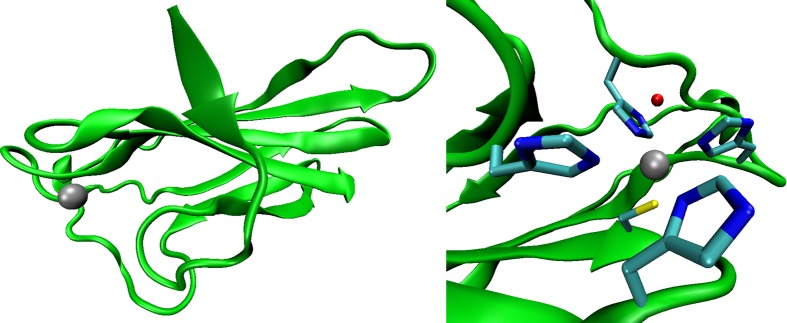
Chain C in PDB entry 4BV1 (left) and a close up of the metal site in Chain C (right). The ferric ion is represented as a silver sphere, and it is coordinated by one Cys, four His, and one water molecule. The figures were made using VMD.⁹²

A total of 10 ns of sampling was performed during the simulation, and snapshots were stored after each 500 fs. The HFE parameter set prefers a smaller CN (of 4), and the metal ion moves out from the binding pocket, while stable metal complex structures were obtained for the simulations using the IOD and 12-6-4 parameter sets. An RMSD analysis was performed over the heavy atoms of the backbone and the metal site for the simulations by treating the initial structure (experimental structure) as reference. The results are depicted in Figure 5. The RMSD of the heavy backbone atoms fluctuated around ∼1.2 Å, while the RMSD of the metal site was ∼0.5 Å. These values illustrate that the metal binding site is stable during the course of the simulations.

Figure 5.

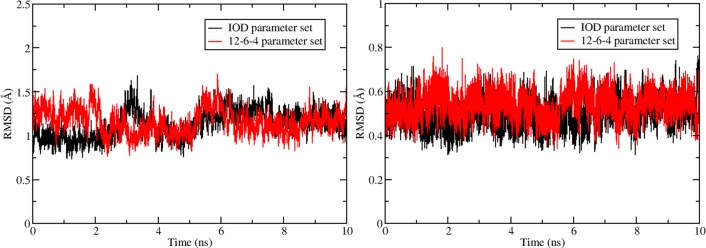
RMSD of heavy atoms of backbone (left) and the metal site (right, including the binding water molecule) for simulations with IOD and 12-6-4 parameter sets using the initial structure (experimental structure) as reference.

We have also performed an RMSF analysis of the backbone heavy atoms for each residue together with the oxygen atom in the metal site binding water. The results are shown in Figure 6. From this Figure it can be seen that the metal site residues: residue His10 (residue number 11), His 35 (residue number 36), His 41 (residue number 42), Cys 97 (residue number 98), and His 100 (residue number 101), all have relatively small RMSF values (∼0.5 Å). The metal site binding water (residue number 115, is not shown in the Figure since the protein ends at residue number 112) has a RMSF of ∼0.6 Å for both the simulations with the IOD and the 12-6-4 parameter sets. These results further validated that the metal ion site is stable over the course of the simulations.

Figure 6.

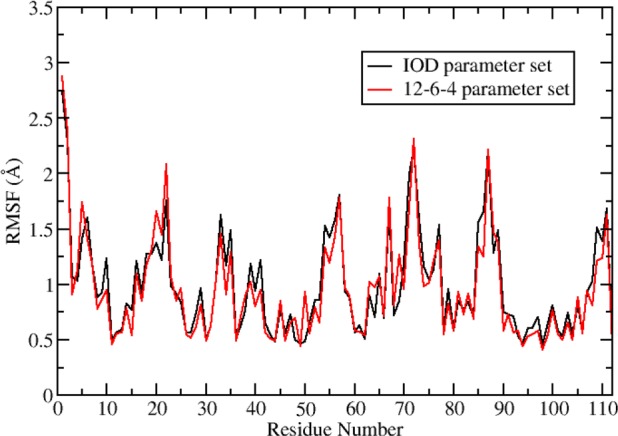
RMSF of heavy atoms of the protein residues in the simulations using IOD and 12-6-4 parameter sets.

Conclusions

In this work, we have estimated the 12-6 LJ parameters and determined the 12-6-4 LJ-type parameters for 24 highly charged metal ions (18 M(III) ions and 6 M(IV) ions) with three water models (TIP3P, SPC/E and TIP4P_EW) based on a parameter scanning protocol. We have shown that with the increasing charge of the metal ions there is a notable decrease in the accuracy of the 12-6 LJ nonbonded model. Using TIP3P as an example, the average underestimation of the HFE values increases from ∼50 kcal/mol for M(II) ions to ∼80 kcal/mol for M(III) ions and to ∼240 kcal/mol for M(IV) ions when trying to reproduce the experimental IOD values. The average underestimation of the IOD values increases from −0.27 to −0.29 Å and −0.58 Å for the M(II), M(III), and M(IV) ions, respectively, when trying to reproduce the experimental HFE values.

The 12-6-4 LJ-type nonbonded model, which we previously described, addresses this problem in a consistent manner. It improves the accuracy of the 12-6 LJ nonbonded model remarkably with just a slight increase in computational cost. This parameter set, derived in this work, reproduced several experimental values (HFE, IOD, and CN) with good accuracy. They reproduce the HFE within ±1 kcal/mol for the M(III) ions and ±2 kcal/mol for M(IV) ions while reproducing the experimental IOD values to within ±0.01 Å. Moreover, excellent quantitative and qualitative agreement with previous experimental and computational work supports the validity of the 12-6-4 LJ-type nonbonded model. Testing in a protein system also revealed good transferability of the parameters determined herein.

Glossary

Abbreviations

VDW

van der Waals

LJ

Lennard-Jones

PME

particle mesh Ewald

HFE

hydration free energy

TI

thermodynamic integration

RDF

radial distribution function

IOD

ion–oxygen distance

CN

coordination number

Supporting Information Available

Simulated HFE, IOD, and CN values obtained using parameter scanning and the final determined 12-6-4 parameters; estimated percentage errors of the 12−6 HFE and IOD parameter sets; and procedures used in the protein simulations may be accessed in file (jp505875v_si_003.pdf). Uncertainty of each simulated HFE value may be viewed in files (jp505875v_si_001.xlsx and jp505875v_si_002.xlsx). This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States