Calibrated Precision Matrix Estimation for High-Dimensional Elliptical Distributions

Abstract

We propose a semiparametric method for estimating a precision matrix of high-dimensional elliptical distributions. Unlike most existing methods, our method naturally handles heavy tailness and conducts parameter estimation under a calibration framework, thus achieves improved theoretical rates of convergence and finite sample performance on heavy-tail applications. We further demonstrate the performance of the proposed method using thorough numerical experiments.

I. Introduction

We Consider the problem of precision matrix estimation. Let X = (X₁, …, X_d)^T be a d-dimensional random vector with mean μ ∈ ℝ^d and covariance matrix Σ ∈ ℝ^d×d, where ${\Sigma }_{kj}=𝔼X_k{X}_j-𝔼X_k𝔼X_j$. We want to estimate the precision matrix Ω = Σ⁻¹ based on n independent observations. In this paper we focus on high dimensional settings where d/n → ∞. To handle the curse of dimensionality, we assume that Ω is sparse (i.e., many off-diagonal entries of Ω are zero).

A popular statistical model for precision matrix estimation is multivariate Gaussian, i.e., X ~ N(μ, Σ). Under Gaussian models, sparse precision matrix encodes the conditional independence relationship of the random variables [8], [21], which has motivates numerous applications in different research areas [3], [15], [36]. In the past decade, many precision matrix estimation methods have been proposed for Gaussian distributions. For more details, let x₁, …, x_n ∈ ℝ^d be n independent observations of X, we define the sample covariance matrix as

$$\mathbf{S}=\frac{1}{n}\sum _{i=1}^n(x_i-\stackrel{‒}{x}){(x_i-\stackrel{‒}{x})}^T,$$ (1)

where $\stackrel{‒}{x}=\frac{1}{n}{\sum }_{i=1}^n{x}_i$. [1], [11], [38] propose the penalized Gaussian log-likelihood method named graphical lasso (GLASSO), which solves

$$\widehat{\Omega }=\underset{\Omega }{\mathrm{argmin}}-\log \mid \Omega \mid +\mathrm{tr}\left(\mathbf{S}\Omega \right)+\lambda \sum _{k,j}\mid {\Omega }_{\mathit{kj}}\mid ,$$ (2)

where λ > 0 is a regularization parameter for controlling the bias-variance tradeoff. In another line of research, [5], [37] propose pseudo-likelihood methods to estimate the precision matrix. Their methods adopt a column-by column estimation scheme and are more amenable to theoretical analysis. More specifically, given a matrix A ∈ ℝ^d×d, let A_*j = (A_1j,…,A_dj)^T denote the j^th column of A, we define ${\mid \mid {\mathbf{A}}_{\ast j}\mid \mid }_1={\Sigma }_k\mid {\mathbf{A}}_{kj}\mid$ and ${\mid \mid {\mathbf{A}}_{\ast j}\mid \mid }_{\infty }={\max }_k\mid {\mathbf{A}}_{kj}\mid$. [5] propose CLIME estimator, which solves

$$\begin{array}{cc}\hfill & {\widehat{\Omega }}_{\ast j}=\underset{{\Omega }_{\ast j}}{\mathrm{argmin}}{\mid \mid {\Omega }_{\ast j}\mid \mid }_1\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.{\mid \mid \mathbf{S}{\Omega }_{\ast j}-{\mathbf{I}}_{\ast j}\mid \mid }_{\infty }\le \lambda ,\forall j=1,\dots ,d,\hfill \end{array}$$ (3)

to estimate the j^th column of the precision matrix. Moreover, let ||A||₁ = max_j ||A_*j||₁ be the matrix ℓ₁ norm of A, and ||A||₂ be the largest singular value of A, (i.e., the spectral norm of A), [5] show that if we choose

$$\lambda \asymp {\mid \mid \Omega \mid \mid }_1\cdot \sqrt{\frac{\log d}{n}},$$ (4)

the CLIME estimator in (3) attains the rates of convergence

$${\mid \mid \widehat{\Omega }-\Omega \mid \mid }_p=O_P\left({\mid \mid \Omega \mid \mid }_1^2\cdot s\sqrt{\frac{\log d}{n}}\right),$$ (5)

where $s={\max }_j{\Sigma }_{k}I({\Omega }_{kj}\ne 0)$, and p = 1, 2. Scalable software packages for GLASSO and CLIME=have been developed which scale to thousands of dimensions [16], [22], [40].

Though significant progress has been for estimating Gaussian graphical models, most existing methods have two drawbacks: (i) They generally require the underlying distribution to be light-tailed [5], [7]. When this assumption is violated, these sample covariance matrix-based methods may have poor performance. (ii) They generally use the same tuning parameter to regularize the estimation, which is not adaptive to the individual sparseness of each column (More details will be provided in §III.B) and may lead to inferior finite sample performance. In another word, the regularization for estimating different columns of the precision matrix is not calibrated.

To overcome the above drawbacks, we propose a new sparse precision matrix estimation method, named EPIC (Estimating Precision matrIx with Calibration), which simultaneously handles data heavy-tailness and conducts calibrated estimation. To relax the tail conditions, we adopt a combination of the rank-based transformed Kendall’s tau estimator and Catoni’s M-estimator [7], [18]. Such a semiparametric combination has shown better statistical properties than those of the sample covariance matrix for the heavy-tailed elliptical distributions [6], [7], [10], [17]. We will explain more details in § II and § IV. To calibrate the parameter estimation, we exploit a new framework proposed by [12]. Under this framework, the optimal tuning parameter does not depend on any unknown quantity of the data distribution, thus the EPIC estimator is tuning insensitive [25]. Computationally, the EPIC estimator is formulated as a convex program, which can be efficiently solved by the parametric simplex method [34]. Theoretically, we show that the EPIC estimator attains improved rates of convergence than the one in (5) under mild conditions. Numerical experiments on both simulated and real datasets show that the EPIC method outperforms existing precision matrix estimation methods.

The rest of this paper is organized as follows: In §II, we briefly review the elliptical family; In §III, we describe the proposed method and derive the computational algorithm; In §IV, we analyze the statistical properties of the EPIC estimator; In §V and §VI, we conduct numerical experiments on both simulated and real datasets to illustrate the effectiveness of the proposed method; In §VII, we discuss other related precision matrix estimation methods and compare them with our method [23]-[25].

II. Background

We start with some notations. Let v = (v₁, …, v_d)^T ∈ ℝ^d be a vector, we define vector norms: ${\mid \mid v\mid \mid }_1={\Sigma }_{i=1}^d\mid v_j\mid$, ${\mid \mid v\mid \mid }_2^2={\Sigma }_{j=1}^d{v}_j^2$, $\mid \mid v\mid {\mid }_{\infty }={\max }_{1\le j\le d}\mid v_j\mid$. Let $\mathcal{S}$ be a subspace of ℝ^d, we use $v_{\mathcal{S}}$ to denote the projection of v onto $\mathcal{S}:v_{\mathcal{S}}={\mathrm{argmin}}_{u\in \mathcal{S}}{\mid \mid u-v\mid \mid }_2^2$. We also define orthogonal complement of $\mathcal{S}$ as ${\mathcal{S}}^{\perp }=\{u\in {ℝ}^d\mid u^{T}v=0,\text{for any}v\in \mathcal{S}\}$. Given a matrix A ∈ ℝ^d×d, let A_*j = (A_1j,…,A_dj)^T and A_k* = (A_k1, …, A_kd)^T denote the j^th column and k^th row of A in vector forms, we define matrix norms: ||A||₁ = max_j||A_*j||₁, ||A||₂ = ψ_max(A), ||A||_∞ = max_k||A_k*||₁, ${\mid \mid A\mid \mid }_{\mathrm{F}}^2={\Sigma }_j{\mid \mid {\mathbf{A}}_{\ast j}\mid \mid }_2^2$, ||A||_max = max_j||A_*j||_∞, where ψ_max(A) is the largest singular value of A. We use Λ_max(A) and Λ_min(A) to denote the largest and smallest eigenvalues of A. Moreover, we define the projection of A_*j onto $\mathcal{S}$ as ${\mathbf{A}}_{\mathcal{S}j}={\mathrm{argmin}}_{u\in \mathcal{S}}{\mid \mid u-{\mathbf{A}}_{\ast j}\mid \mid }_2^2$.

We then briefly review the elliptical family, which has the following definition.

Definition 2.1 ([10]): Given μ ∈ ℝ^d and a symmetric positive semidefinite matrix Σ with rank (Σ) = r ≤ d, we say that a d-dimensional random vector X = (X₁, …,X_d)^T follows an elliptical distribution with parameter μ, ξ, and Σ denoted by

$$\mathit{X}~\mathit{EC}(\mu ,\xi ,\Sigma ),$$ (6)

if X has a stochastic representation

$$\mathit{X}\underset{=}{d}\mu +\xi \mathbf{A}\mathit{U}$$ (7)

where ξ ≥ 0 is a continuous random variable independent of U. Here $U\in {𝕊}^{r-1}$ is uniformly distributed on the unit sphere in ℝ^r, and Σ = AA^T.

Note that A and ξ in (7) can be properly rescaled without changing the distribution. Thus existing literature usually imposes an additional constraint ||Σ||_max 1 to make the distribution identifiable [10]. However, such=a constraint does not necessarily make Σ the covariance matrix of X. Since we are interested in estimating the precision matrix in this paper, we require $𝔼\left({\xi }^2\right)<\infty$ and rank (Σ) = d such that the precision matrix of the elliptical distribution exists. Under this assumption, we use an alternative constraint $𝔼\left({\xi }^2\right)=d$, which not only makes the distribution identifiable but also has Σ defined as the conventional covariance matrix (e.g., as in the Gaussian distribution).

Remark 1: Σ can be factorized as Σ = ΘZΘ, where Z is the Pearson correlation matrix, and Θ = diag(θ₁, …, θ_d) with θ_j as the standard deviation of X_j. Since Θ is a diagonal matrix, we can rewrite the precision matrix Ω as Ω = Θ⁻¹ΓΒ⁻¹, where Γ = Z⁻¹ is the inverse correlation matrix.

Remark 2: As a generalization of the Gaussian family, the elliptical family has been widely applied to many research areas such as dimensionality reduction [19], portfolio theory [14], and data visualization [33]. Many of these applications rely on an effective estimator of the precision matrix for elliptical distributions.

III. Method

Motivated by the above discussion, the EPIC method has three steps: We first use the transformed Kendall’s tau estimator and Catoni’s M-estimator to obtain $\widehat{\mathbf{Z}}$ and $\widehat{ϴ}$ respectively; We then plug $\widehat{\mathbf{Z}}$ into a calibrated inverse correlation matrix estimation procedure to obtain $\widehat{\Gamma }$; At last we assemble $\widehat{\Gamma }$ and $\widehat{ϴ}$ to obtain $\widehat{\Omega }$. We explain more details about these three steps in the following subsections.

A. Correlation Matrix and Standard Deviation Estimation

To estimate Z, we adopt the transformed Kendall’s tau estimator proposed in [10] and [23]. More specifically, we define a population version of the Kendall’s tau statistic between X_j and X_k as follows,

$$\begin{array}{cc}\hfill {\tau }_{\mathit{kj}}=& \mathbb{P}\left(\right(X_j-{\tilde{X}}_j\left)\right(X_k-{\tilde{X}}_k)>0)\hfill \\ \hfill & -\mathbb{P}\left(\right(X_j-{\tilde{X}}_j\left)\right(X_k-{\tilde{X}}_k)<0),\hfill \end{array}$$

where ${\tilde{X}}_j$ and ${\tilde{X}}_k$ are independent copies of X_j and X_k respectively. For elliptical distributions, [10], [23] show that Z_kj’s and τ_kj’s have the following relationship

$$\mathbf{Z}=\left[{\mathbf{Z}}_{\mathit{kj}}\right]=\left[\sin \left(\frac{\pi }{2}{\tau }_{\mathit{kj}}\right)\right].$$ (8)

Therefore given x₁, …, x_n be n independent observations of X, where x_i = (x_i1,…, x_id)^T, we first calculate a sample version of the Kendall’s tau statistic between X_j and X_k by

$${\widehat{\tau }}_{\mathit{kj}}=\frac{2{\Sigma }_{i<i^{\prime }}\mathrm{sign}\left(\right(x_{\mathit{ik}}-x_{i^{\prime }k}\left)\right(x_{\mathit{ij}}-x_{i^{\prime }j}\left)\right)}{n(n-1)}$$

for all k ≠ j, and 1 otherwise. We then obtain a correlation matrix estimator by the same entrywise transformation as (8),

$$\widehat{\mathbf{Z}}=\left[{\widehat{\mathbf{Z}}}_{\mathit{kj}}\right]=\left[\sin \left(\frac{\pi }{2}{\widehat{\tau }}_{\mathit{kj}}\right)\right].$$ (9)

To estimate Θ, we exploit the Catoni’s M-estimator proposed in [7]. For heavy-tailed distributions, [7] show that the Catoni’s M-estimator has better theoretical and empirical performance than the sample moment-based estimator. In particular, let ψ(t) = sign(t) · log(1 + |t| + t²/2) be a univariate function where sign(0) = 0. Let ${\widehat{\mu }}_j$ and ${\widehat{m}}_j$ be the estimatior of $𝔼X_j$ and $𝔼X_j^2$ respectively which solve the following two equations:

$$\sum _{i=1}^n\psi \left((x_{\mathit{ij}}-{\mu }_j)\sqrt{\frac{2}{{\mathit{nK}}_{\max }}}\right)=0,$$ (10)

$$\sum _{i=1}^n\psi \left((x_{\mathit{ij}}^2-m_j)\sqrt{\frac{2}{{\mathit{nK}}_{\max }}}\right)=0.$$ (11)

Here K_max is a preset upper bound of max_j Var(X_j) and ${\max }_j\mathrm{Var}\left(X_j^2\right)$. [7] shows that the solutions to (10) and (11) must exist and can be efficiently solved by the Newton-Raphson algorithm [31]. Once we obtain ${\widehat{m}}_j$ and ${\widehat{\mu }}_j$, we estimate the marginal standard deviation θ_j by

$${\widehat{\theta }}_j=\sqrt{\max \{{\widehat{m}}_j-{\widehat{\mu }}_j^2,{\mathit{K}}_{\min }\}},$$ (12)

where K_min is a preset lower bound of ${\min }_j{\theta }_j^2$.

Remark 3: We choose the combination of the transformed Kendall’s tau estimator and Catoni’s M-estimator instead of sample covariance matrix, because we are handling heavy-tailed elliptical distributions. For light-tailed distributions (e.g. Gaussian distribution), we can still use the sample correlation matrix and sample standard deviation to estimate the Z and Θ. The extension of our proposed methodology and theory is straightforward. See more details in §IV.

B. Calibrated Inverse Correlation Matrix Estimation

We then plug the transformed Kendall’s tau estimator $\widehat{\mathbf{Z}}$ into the following convex program,

$$\begin{array}{cc}\hfill & ({\widehat{\Gamma }}_{\ast j},{\widehat{\tau }}_j)=\underset{{\Gamma }_{\ast j},{\tau }_j}{\mathrm{argmin}}{\Vert {\Gamma }_{\ast j}\Vert }_1+c{\tau }_1\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.{\Vert \widehat{Z}{\Gamma }_{\ast j}-{\mathbf{I}}_{\ast j}\Vert }_{\infty }\le \lambda {\tau }_j,{\Vert {\Gamma }_{\ast j}\Vert }_1\le {\tau }_j,\hfill \end{array}$$ (13)

for all j = 1, …, d, where c can be any constant between 0 and 1 (e.g., c = 0.5). Here τ_j serves as an auxiliary variable to calibrate the regularization [12], [32]. Both the objective function and constraints in (13) contain τ_j to prevent from choosing τ_j either too large or too small.

To gain more intuition of the formulation of (13), we first consider estimating the j^th column of the inverse correlation matrix using the CLIME method in a regularization form as follows,

$${\widehat{\Gamma }}_{\ast j}=\underset{{\Gamma }_{\ast j}}{\mathrm{argmin}}{\Vert {\Gamma }_{\ast j}\Vert }_1+\nu {\Vert \widehat{\mathbf{Z}}{\Gamma }_{\ast j}-{\mathbf{I}}_{\ast j}\Vert }_{\infty },$$ (14)

where ν > 0 is the regularization parameter. The next proposition presents an alternative formulation of (14).

Proposition III.1: The following optimization problem

$$\begin{array}{cc}\hfill & ({\widehat{\Gamma }}_{\ast j},{\widehat{\tau }}_j)=\underset{{\Gamma }_{\ast j},{\tau }_j}{\mathrm{argmin}}{\Vert {\Gamma }_{\ast j}\Vert }_1+c{\tau }_j\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.{\Vert \widehat{\mathbf{Z}}{\Gamma }_{\ast j}-{\mathbf{I}}_{\ast j}\Vert }_{\infty }\le \frac{c}{\nu }{\tau }_j.\hfill \end{array}$$ (15)

has the same solution as (14).

The proof of Proposition III.1 is provided in Appendix A. If we set ν/c = λ, then the only difference between (13) and (15) is that (13) contains a constraint ||Γ_*j||₁ ≤ τ_j. Due to the complementary slackness, this additional constraint encourages the regularization λτ_j to be proportional to the ℓ₁ norm of the j^th column (weak sparseness). From the theoretical analysis in §IV, we see that the regularization is calibrated in this way.

In the rest of this subsection, we omit the index j in (13) for notational simplicity. We denote Γ_*j, I_*j, and τ_j by γ, e, and τ respectively. By reparametrizing γ = γ⁺−γ⁻, we can rewrite (13) as the following linear program,

$$\begin{array}{cc}\hfill & ({\widehat{\gamma }}^{+},{\widehat{\gamma }}^{-},\widehat{\tau })=\underset{{\gamma }^{+},{\gamma }^{-},\tau }{\mathrm{argmin}}{1}^T{\gamma }^{+}+1^T{\gamma }^{-}+c\tau \hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\left[\begin{array}{ccc}\hfill \widehat{\mathbf{Z}}\hfill & \hfill -\widehat{\mathbf{Z}}\hfill & \hfill -\lambda \hfill \\ \hfill -\widehat{\mathbf{Z}}\hfill & \hfill \widehat{\mathbf{Z}}\hfill & \hfill -\lambda \hfill \\ \hfill 1^T\hfill & \hfill 1^T\hfill & \hfill -1\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\gamma }^{+}\hfill \\ \hfill {\gamma }^{-}\hfill \\ \hfill \tau \hfill \end{array}\right]\le \left[\begin{array}{c}\hfill e\hfill \\ \hfill -e\hfill \\ \hfill 0\hfill \end{array}\right],\hfill \\ \hfill & {\gamma }^{+}\ge 0,{\gamma }^{-}\ge 0,\tau \ge 0,\hfill \end{array}$$ (16)

where λ = λ1. Though (16) can be solved by general linear program solvers (e.g. the simplex method as suggested in [5]), these general solvers cannot scale to large problems. In Appendix B, we provide a more efficient parametric simplex method [34], which naturally exploits the underlying sparsity structure, and attains better empirical performance than the simplex method.

C. Symmetric Precision Matrix Estimation

Once we get the inverse correlation matrix estimate $\widehat{\Gamma }$, we estimate the precision matrix by

$$\tilde{\Omega }={\widehat{ϴ}}^{-1}\widehat{\Gamma }{\widehat{ϴ}}^{-1}.$$

Remark 4: A possible alternative is that we first assemble a covariance matrix estimator

$$\widehat{\mathbf{S}}=\widehat{ϴ}\widehat{\mathbf{Z}}\widehat{ϴ},$$ (17)

then directly estimate Ω by solving

$$\begin{array}{cc}\hfill & ({\widehat{\Omega }}_{\ast j},{\widehat{\tau }}_j)=\underset{{\Omega }_{\ast j},{\tau }_j}{\mathrm{argmin}}{\Vert {\Omega }_{\ast j}\Vert }_1+c{\tau }_j\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.{\Vert \widehat{\mathbf{S}}{\Omega }_{\ast j}-{\mathbf{I}}_{\ast j}\Vert }_{\infty }\le \lambda {\tau }_j,{\Vert {\Omega }_{\ast }j\Vert }_1\le {\tau }_j\hfill \end{array}$$

for all j = 1, …, d. However, such a direct estimation procedure makes the regularization parameter selection sensitive to marginal variability. See [20], [26], [29] for more discussions of the ensemble rule.

The EPIC method does not guarantee the symmetry of $\tilde{\Omega }$. To get a symmetric estimate, we take an additional projection procedure to obtain a symmetric estimator

$$\widehat{\Omega }=\underset{\Omega }{\mathrm{argmin}}{\Vert \Omega -\tilde{\Omega }\Vert }_{\ast }\mathrm{s}.\mathrm{t}.\Omega ={\Omega }^T,$$ (18)

where ||·||_∗ can be the matrix ℓ₁, Frobenius, or max norm. More details about how to choose a suitable norm will be explained in the next section.

Remark 5: For the Frobenius and max norms, (18) has a closed form solution as follows,

$$\widehat{\Omega }=\frac{1}{2}\left(\tilde{\Omega }+{\tilde{\Omega }}^T\right).$$

For the matrix #x2113;₁ norm, see our proposed smoothed proximal gradient algorithm in Appendix C. More details about how to choose a suitable norm will be explained in the next section.

IV. Statistical Properties

To analyze the statistical properties of the EPIC estimator, we define the following class of sparse symmetric matrices,

$$\begin{array}{cc}\hfill \mathcal{U}(s,M,k_u)=& \{\Gamma \in {ℝ}^{d\times d}\mid \Gamma \succ 0,{\Lambda }_{\max }\left(\Gamma \right)\le k_u,\phantom{\mid }\phantom{\}}\hfill \\ \hfill & \phantom{\{}\underset{j}{\max }\sum _k\mathit{I}({\Gamma }_{\mathit{kj}}\ne 0)\le s,{\Vert \Gamma \Vert }_1\le \mathit{M}\},\hfill \end{array}$$

where κ_u is a constant, and (s, d, M) may scale with the sample size n. We assume that the following conditions hold:

• (A.1)$\Gamma \in \mathcal{U}(s,M,{\kappa }_u)$,

• (A.2) θ_min ≤ min_j θ_j ≤ max_j θ_j ≤ θ_max,

• (A.3)max_j |μ_j| ≤ μ_max, max_j $𝔼X_j^4\le K$,
• (A.4)s² log d/n→0,

where θ_max, θ_min, μ_max, and K are constants.

Remark 6: Condition (A.3) only requires the fourth moment of the distribution to be finite. In contrast, sample covariance-based estimation methods can not achieve such theoretical results. See more details in [5] and [7].

Remark 7: The bounded mean in Condition (A.3) is actually a mild assumption. Existing high dimensional theories (Cai et al. 2011; Yuan, 2010; Rothman et al. 2008) on sparse precision matrix estimation all require the distribution to be light-tailed. For example, there exists some constant K such that ${\max }_j𝔼{\mid X_j\mid }^r\le K<\infty$ for some r >> 4. By Jessen’s inequality, we have ${(𝔼\mid X_j\mid )}^r\le 𝔼{\mid X_j\mid }^r\le K<\infty$, which implies that ${\max }_j𝔼\mid X_j\mid \le K^{1∕r}<\infty$. In another word, they also require max_j|μ_j| to be bounded

Before we proceed with main results, we first present the following important lemma.

Lemma 1: We assume that X ~ EC(μ, ξ, Σ) and (A.2)-(A.4) hold. Let $\widehat{\mathbf{Z}}$ and ${\widehat{\theta }}_j$ be defined in (9) and (12). There exist universal constants κ₁ and κ₂ such that for large enough n,

$$\mathbb{P}\left(\underset{k,j}{\max }\mid {\widehat{\mathbf{Z}}}_{\mathit{kj}}-{\mathbf{Z}}_{\mathit{kj}}\mid \le k_1\sqrt{\frac{\log d}{n}}\right)\ge 1-\frac{1}{d},$$ (19)

$$\mathbb{P}\left(\underset{j}{\max }\mid {\widehat{\theta }}_j^{-1}-{\theta }_j^{-1}\mid \le k_2\sqrt{\frac{\log d}{n}}\right)\ge 1-\frac{2}{d}.$$ (20)

The proof of Lemma 1 is provided in Appendix D.

Remark 8: Lemma 1 shows that the transformed Kendall’s tau estimator and Catoni’s M-estimator possess good concentration properties for heavy-tailed elliptical distributions. That enables us to obtain a consistent precision matrix estimator in high dimensions.

A. Parameter Estimation Consistency

Theorem IV.1 provides the rates of convergence for precision matrix estimation under the matrix #x2113;₁, spectral, and Frobenius norms.

Theorem IV.1: Suppose that X ~ EC(μ, ξ, σ) and (A.1)-(A.4) hold, if we take $\lambda ={\kappa }_1∕\sqrt{logd∕n}$ and choose the matrix #x2113;₁ norm as ||·||_* in (18), then for large enough n and p = 1,2, there exists a universal constant C₁ such that

$$\mathbb{P}\left({\Vert \widehat{\Omega }-\Omega \Vert }_p\le C_1\mathit{Ms}\sqrt{\frac{\log d}{n}}\right)\ge 1-\frac{3}{d}.$$ (21)

Moreover, if we choose the Forbenius norm as ||·||_* in (18), then for large enough n, there exists a universal constant C₂ such that

$$\mathbb{P}\left(\frac{1}{d}{\Vert \widehat{\Omega }-\Omega \Vert }_{\mathrm{F}}^2\le C_2{M}^2\frac{\log d}{n}\right)\ge 1-\frac{3}{d}.$$ (22)

The proof of Theorem IV.1 is provided in Appendix E. Note that the rates of convergence obtained in the above theorem are faster than those in [5].

B. Model Selection Consistency

Theorem IV.2 provides the rate of convergence under the elementwise max norm.

Theorem IV.2: Suppose that X ~ EC(μ, ξ, Σ) and (A.1)-(A.4) hold. If we take $\lambda ={\kappa }_1∕\sqrt{logd∕n}$ and choose the max norm for (18), then for large enough n, there exists a universal constant C₃ such that

$$\mathbb{P}\left({\Vert \widehat{\Omega }-\Omega \Vert }_{\max }\le C_3{M}^2\sqrt{\frac{\log d}{n}}\right)\ge 1-\frac{3}{d}.$$ (23)

Moreover, let E = {(k, j)|Ω_kj ≠ 0}, and $\widehat{E}=\left\{\right(k,j)\mid {\widehat{\Omega }}_{kj}\ne 0\}$, if there exists large enough constant C₄ such that

$$\underset{(k,j)\in E}{\min }\mid {\Omega }_{\mathit{kj}}\mid \ge C_4{M}^2\sqrt{\frac{\log d}{n}},$$

then we have $\mathbb{P}(E\subseteq \widehat{E})\to 1$.

The proof of Theorem IV.2 is provided in Appendix G. The obtained rate of convergence in Theorem IV.2 is comparable to that of [5].

Remark 9: Our selected regularization parameter $\lambda ={\kappa }_1∕\sqrt{logd∕n}$ in Theorems IV.1 and IV.2 does not contain any unknown parameter of the underlying distribution (e.g. ||Γ₁||). Note that κ₁ comes from (19) in Lemma 1. Theoretically we can choose κ₁ as a reasonably large without any additional tuning (e.g. $\sqrt{2}\pi$. See more details in [23]). In practice, we found that a fine tuning of κ₁ delivers better finite sample performance.

V. Numerical Results

In this section, we compare the EPIC estimator with several competing estimators including:

1. CLIME.RC: We obtain the sparse precision matrix estimator by plugging the covariance matrix estimator $\widehat{\mathbf{S}}$ defined in (17) into (3).

2. CLIME.SC: We obtain the sparse precision matrix estimator by plugging the sample covariance matrix estimator S defined in (1) into (3).

3. GLASSO.RC: We obtain the sparse precision matrix estimator by plugging the covariance matrix estimator $\widehat{\mathbf{S}}$ defined in (17) into (2).

Moreover, (3) is also solved by the parametric simplex method as our proposed EPIC method, and (2) is solved by the block coordinate descent algorithm. All experiments are conducted on a PC with Core i5 3.3GHz CPU and 16GB memory. All programs are coded using C using double precision, and further called from R.

A. Data Generation

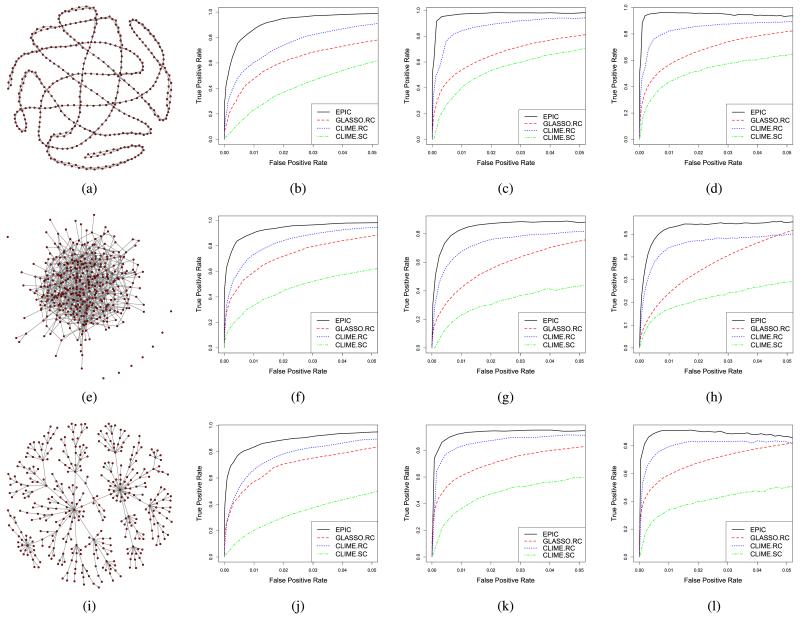
We consider three different settings for comparison: (1) d = 101; (2) d = 201; (3) d = 401. We adopt the following three graph generation schemes, as illustrated in Figure 1, to obtain precision matrices:

• Band. Each node is assigned an index j with j = 1, …, d. Two nodes are connected by an edge if the difference between their indices is no larger than 2.

• Erdös-Rényi. We set an edge between each pair of nodes with probability 4/d, independently of the other edges.

• Scale-free. The degree distribution of the graph follows a power law. The graph is generated by the preferential attachment mechanism.

Fig. 1.

Three different graph patterns and corresponding average ROC curves. EPIC outperforms the competitors throughout all settings. (a) Band (d = 401). (b) Band (d = 101). (c) Band (d = 201). (d) Band (d = 401). (e) Erdös-Rényi (d = 401). (f) Erdös-Rényi (d = 101). (g) Erdös-Rényi (d = 201). (h) Erdös-Rényi (d = 401). (i) Scale-free (d = 401). (j) Scale-free (d = 101). (k) Scale-free (d = 201). (l) Scale-free (d = 401).

The graph begins with an initial chain graph of 10 nodes. New nodes are added to the graph one at a time. Each new node is connected to an existing node with a probability that is proportional to the number of degrees that the existing nodes already have. Formally, the probability p_i that the new node is connected to the i^th existing node is $p_i=\frac{k_i}{{\Sigma }_j{k}_j}$ where k_i is the degree of node i.

Let G be the adjacency matrix of the generated graph, we calculate $\tilde{\mathbf{G}}=\left[{\tilde{\mathbf{G}}}_{jk}\right]$ as

$${\tilde{\mathbf{G}}}_{\mathit{jk}}={\tilde{\mathbf{G}}}_{\mathit{kj}}=\{\begin{array}{cc}\hfill {\mathbf{U}}_{\mathit{kj}}\hfill & \hfill \text{if}{\mathbf{G}}_{\mathit{jk}}={\mathbf{G}}_{\mathit{kj}}=1\hfill \\ \hfill 0\hfill & \hfill \text{if}{\mathbf{G}}_{\mathit{jk}}={\mathbf{G}}_{\mathit{kj}}=0\hfill \end{array}\phantom{\}}$$

where all U_kj’s are independently sampled from the uniform distribution Uniform (−1, +1). Let ${\mathcal{C}}_2$ be the rescaling operator that converts a symmetric positive definite matrix to the corresponding correlation matrix, we further calculate

$$\Sigma =ϴ{\mathcal{C}}_2\left[{(\tilde{\mathbf{G}}+(0.1-{\Lambda }_{\min }\left(\tilde{\mathbf{G}}\right))\cdot \mathbf{I})}^{-1}\right]ϴ,$$

where Θ is the diagonal standard deviation matrix with ${ϴ}_{jj}=2^{\frac{2j-d-1}{2(d-1)}}$ for j = 1,…, d.

We then generate $n=\lceil 14\sqrt{d}\rceil$ independent samples from the t-distribution with 6 degrees of freedom, mean 0, and covariance Σ. For the EPIC estimator, we set c = 0.5 in (13). For the Catoni’s M-estimator, we set K_max = 10 and K_min = 0.1.

B. Timing Performance

We first evaluate the computational performance of the parametric simplex method. For each model, we choose a regularization parameter, which yields approximate 0.05 · d(d − 1) nonzero off-diagonal entries. The EPIC and CLIME methods are solved by the parametric simplex method, which is described in Appendix B. The GLASSO is solved by the dual block coordinate descent algorithm, which is described in [11]. Table I summarizes the timing performance averaged over 100 replications. To obtain the baseline performance, we solve the CLIME.SC method using the simplex method¹ as suggested in [5]. We see that all four methods greatly outperform the baseline. The EPIC, CLIME.RC, and CLIME.SC methods attain similar timing performance for all settings, and the GLASSO.RC method is more efficient than the others for d = 201 and d = 401.

TABLE I. Timing Performance of Different Estimators on the Band, Erdös-Rényi, and Scale-Free Models (in Seconds). The Baseline Performance Is Obtained by Solving the CLIME.SC Method Using the Simplex Method.

Model	d	EPIC	GLASSO.RC	CLIME.RC	CLIME.SC	BASELINE
	101	0.1561(0.0248)	0.3633(0.0070)	0.1233(0.0057)	0.1701(0.0119)	49.467(1.7862)
Band	201	1.6622(0.1253)	0.4417(0.0122)	1.5897(0.1249)	1.6085(0.0518)	687.57(23.720)
	401	23.061(0.5777)	1.0864(0.1403)	24.441(1.5344)	25.445(3.8066)	4756.4(170.25)
	101	0.1414(0.0079)	0.3703(0.0072)	0.1309(0.0331)	0.2073(0.0925)	59.775(2.0521)
Erdös-Rényi	201	1.6214(0.5175)	0.4448(0.0164)	1.5992(0.1840)	1.6155(0.2957)	803.51(29.835)
	401	21.722(0.5470)	1.1517(0.0959)	22.795(0.6999)	24.230(3.1871)	4531.7(151.46)
	101	0.2245(0.0514)	0.4398(0.0843)	0.1509(0.0054)	0.1871(0.0149)	55.112(1.7109)
Scale-free	201	1.8682(0.1078)	0.4632(0.0067)	1.5472(0.1350)	1.7235(0.1778)	865.98(31.399)
	401	21.926(0.7112)	1.0093(0.1140)	23.135(1.4318)	25.596(3.3401)	4991.2(202.44)

C. Parameter Estimation

To select the regularization parameter, we independently generate a validation set of n samples from the same distribution. We tune λ over a refined grid, then the selected optimal regularization parameter is $\widehat{\lambda }={\mathrm{argmin}}_{\lambda }{\mid \mid {\widehat{\Omega }}^{\lambda }\widehat{\Sigma }-\mathbf{I})}_{\max }$, where ${\widehat{\Omega }}^{\lambda }$ denotes the estimated precision matrix of the training set using the regularization parameter λ, and $\widehat{\Sigma }$ denotes the estimated covariance matrix of the validation set using either (1) or (17). Tables II and III summarize the numerical results averaged over 100 replications. We see that the EPIC estimator outperforms the GLASSO.RC and CLIME.RC estimators in all settings.

TABLE II.

Quantitive Comparison of Different Estimators on the Band, Erdös-Rényi, and Scale-Free Models. The EPIC Estimator Outperforms the Competitors in all Settings

		Spectral Norm: ${\mid \mid \widehat{\Omega }-\Omega \mid \mid }_2$
Model	d	EPIC	GLASSO.RC	CLIME.RC	CLIME.SC
	101	3.3748(0.2081)	4.4360(9,1445)	3.3961(0.4403)	3.6885(0.5850)
Band	201	3.3283(0.1114)	4.8616(0.0644)	3.4559(0.0979)	4.4789(0.3399)
	401	3.5933(0.5192)	5.1667(0.0354)	4.0623(0.2397)	5.7164(0.9666)
	101	2.1849(0.2281)	2.6681(0.1293)	2.6787(0.8414)	2.3391(0.2976)
Erdös-Rényi	201	1.8322(0.0769)	2.3753(0.0949)	2.0106(0.3943)	2.0528(0.1548)
	401	1.3322(0.1294)	2.4265(0.0564)	2.0051(0.4144)	4.0667(1.1174)
	101	2.1113(0.3081)	2.9979(0.1654)	2.0401(0.3703)	2.6541(0.5882)
Scale-free	201	2.3519(0.1779)	3.2394(0.1078)	2.3785(0.4186)	2.5789(0.5139)
	401	3.2273(0.1201)	4.0105(0.5812)	3.3139(0.5812)	3.9287(1.1750)

TABLE III.

Quantitive Comparison of Different Estimators on the Band, Erdös-Rényi, and Scale-Free Models. The EPIC Estimator Outperforms the Competitors in All Settings

		Frobenius Norm: ${\mid \mid \widehat{\Omega }-\Omega \mid \mid }_2$
Model	d	EPIC	GLASSO.RC	CLIME.RC	CLIME.SC
	101	9.4307(0.3245)	11.069(0.2618)	9.7538(0.3949)	11.392(0.8319)
Band	201	12.720(0.2282)	16.135(0.1399)	13.533(0.1898)	14.850(0.6167)
	401	18.298(1.0537)	23.177(0.1957)	20.412(0.2366)	25.254(1.0002)
	101	6.0660(0.1552)	6.8777(0.2115)	6.7097(0.3672)	7.3789(0.4390)
Erdös-Rényi	201	6.7794(0.1632)	8.1531(0.1828)	7.6175(0.2616)	8.3555(0.2844)
	401	7.3497(0.1743)	10.795(0.1323)	8.3869(0.4755)	11.104(0.6069)
	101	4.6695(0.2435)	5.6689(0.2344)	4.9658(0.1762)	6.2264(0.3841)
Scale-free	201	5.6732(0.1782)	7.2768(0.0940)	6.2343(0.2401)	7.2842(0.3310)
	401	7.2979(0.1094)	9.0940(0.0935)	7.3765(0.2328)	9.5396(0.5636)

D. Model Selection

To evaluate the model selection performance, we calculate the ROC curve of each obtained regularization path using the false positive rate (FPR) and true positive rate (FNR) defined as follows,

$$\begin{array}{cc}\hfill & \mathrm{F}.\mathrm{P}.\mathrm{R}.=\frac{{\sum }_{k,j}\mathit{I}\left({\widehat{\Omega }}_{\mathit{kj}}^{\left(\lambda \right)}\ne 0,{\Omega }_{\mathit{kj}}=0\right)}{{\sum }_{k,j}\mathit{I}({\Omega }_{\mathit{kj}}=0)},\hfill \\ \hfill & \mathrm{T}.\mathrm{P}.\mathrm{R}.=\frac{{\sum }_{k,j}\mathit{I}\left({\widehat{\Omega }}_{\mathit{kj}}^{\left(\lambda \right)}\ne 0,{\Omega }_{\mathit{kj}}\ne 0\right)}{{\sum }_{k,j}\mathit{I}\left({\widehat{\Omega }}_{\mathit{kj}}^{\left(\lambda \right)}\ne 0\right)}.\hfill \end{array}$$

Figure 1 summarizes ROC curves of all methods averaged over 100 replications.² We see that the EPIC estimator outperforms the competing estimators throughout all settings. Similarly, our method outperforms the sample covariance matrix-based CLIME estimator.

VI. Real Data Example

To illustrate the effectiveness of the proposed EPIC method, we adopt the sonar dataset from UCI Machine Learning Repository³ [13]. The dataset contains 101 patterns obtained by bouncing sonar signals off a metal cylinder at various angles and under various conditions, and 97 patterns obtained from rocks under similar conditions. Each pattern is a set of 60 features. Each feature represents the logarithm of the energy integrated over a certain period of time within a particular frequency band. Our goal is to discriminate between sonar signals bounced off a metal cylinder and those bounced off a roughly cylindrical rock.

We randomly split the data into two sets. The training set contains 80 metal and 77 rock patterns. The testing set contains 21 metal and 20 rock patterns. Let μ^(k) be the class conditional means of the data where k = 1 represents the metal category and k = 0 represents the rock category. [5] assume that two classes share the same covariance matrix, and then adopt the sample mean for estimating μ_k’s and the sample covariance matrix-based CLIME estimator for estimating Ω. In contrast, we adopt the Catoni’s M-estimator for estimating μ_k’s and the EPIC estimator for estimating Ω. We classify a sample x to the metal category if

$${\left(x-\frac{{\widehat{\mu }}^{\left(1\right)}+{\widehat{\mu }}^{\left(0\right)}}{2}\right)}^T\widehat{\Omega }\left({\widehat{\mu }}^{\left(1\right)}-{\widehat{\mu }}^{\left(0\right)}\right)\ge 0,$$

and to the rock category otherwise. We use the testing set to evaluate the performance of the EPIC estimator. For tuning parameter selection, we use a 5-fold cross validation on the training set to pick the regularization parameter λ.

To evaluate the classification performance, we use the criteria of misclassification rate, specificity, sensitivity, and Mathews Correlation Coefficient (MCC). More specifically, let y_i’s and ${\widehat{\lambda }}_i$’s be true labels and predicted labels of the testing samples, we define

$$\begin{array}{cc}\hfill & \text{Misclassification Rate}\hfill \\ \hfill & =\frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{TN}+\mathrm{TP}+\mathrm{FN}+\mathrm{FP}},\hfill \\ \hfill & \text{Specificity}=\frac{\mathrm{TN}}{\mathrm{TN}+\mathrm{FP}},\text{Sensitivity}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}},\hfill \\ \hfill & \mathrm{MCC}=\frac{\mathrm{TP}\cdot \mathrm{TN}-\mathrm{FP}\cdot \mathrm{FN}}{\sqrt{(\mathrm{TP}+\mathrm{FP})(\mathrm{TP}+\mathrm{FN})(\mathrm{TN}+\mathrm{FP})(\mathrm{TN}+\mathrm{FN})}},\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill & \mathrm{TP}=\sum _i\mathit{I}({\widehat{y}}_i=y_i=1),\mathrm{FP}=\sum _i\mathit{I}({\widehat{y}}_i=1,y_i=0),\hfill \\ \hfill & \mathrm{TN}=\sum _i\mathit{I}({\widehat{y}}_i=y_i=0),\mathrm{FN}=\sum _i\mathit{I}({\widehat{y}}_i=0,y_i=1).\hfill \end{array}$$

Table IV summarizes the performance of both methods averaged over 100 replications (with standard errors in parentheses). We see that the EPIC estimator significantly outperforms the competitor on the sensitivity and misclassification rate, but slightly worse on the specificity. The overall classification performance measured by MCC shows that the EPIC estimator has about 8% improvement over the competitor.

TABLE IV.

Quantitive Comparison of the EPIC and Sample Covariance Matrix-Based CLIME Estimators in the Sonar Data Classification

Method	Misclassification Rate	Specificity	Sensitivity	MCC
EPIC	0.1990(0.0285)	0.7288(0.0499)	0.8579(0.0301)	0.6023(0.0665)
CLIME.SC	0.2362(0.0317)	0.7460(0.0403)	0.7791(0.0429)	0.5288(0.0631)

VII. Discussion and Conclusion

In this paper, we propose a new sparse precision matrix estimation method for the elliptical family. Our method handles heavy-tailness, and conducts parameter estimation under a calibration framework. We show that the proposed method achieves improved rates of convergence and better finite sample performance than existing methods. The effectiveness of the proposed method is further illustrated by numerical experiments on both simulated and real datasets.

[25] proposed another calibrated graph estimation method named TIGER for Gaussian family. However, unlike the EPIC estimator, the TIGER method can not handle the elliptical family due to two reasons: (1) The transformed Kendall’s tau estimator cannot guarantee the positive semidefiniteness. If we directly plug it into the TIGER method, it makes the TIGER formulation nonconvex. Existing algorithms may not obtain a global solution in polynomial time. (2) The theoretical analysis in [25] is only applicable to the Gaussian family. Theoretical properties of the TIGER method for the elliptical family is unclear.

Another closely related method is the rank-based CLIME method for estimating inverse correlation matrix estimation for the elliptical family [24]. The rank-based CLIME method is based on the formulation in (3) and cannot calibrate the regularization. Furthermore, the rank-based CLIME method can only estimate the inverse correlation matrix. Thus for applications such as the linear discriminant analysis (as is demonstrated in §6) which requires the input to be a precision matrix [2], [30], [35], the rank-based CLIME method is not applicable.

Biographies

Tuo Zhao received his B.S. and M.S. degrees in Computer Science from Harbin Institute of Technology, and his second M.S. degree in Applied Math from University of Minnesota.

He is currently a Ph.D. Candidate in Department of Computer Science at Johns Hopkins University. He is also a visiting student in Department of Operations Research and Financial Engineering at Princeton University. His research focuses on large-scale semiparametric and nonparametric learning and applications to high throughput genomics and neuroimaging.

Han Liu received a joint Ph.D. degree in Machine Learning and Statistics from the Carnegie Mellon University, Pittsburgh, PA, USA in 2011.

He is currently an Assistant Professor of Statistical Machine Learning in the Department of Operations Research and Financial Engineering at Princeton University, Princeton, NJ. He is also an adjunct Professor in the Department of Biostatistics and Department of Computer Science at Johns Hopkins University. He built and is serving as the principal investigator of the Statistical Machine Learning (SMiLe) lab at Princeton University. His research interests include high dimensional semiparametric inference, statistical optimization, Big Data inferential analysis.

APPENDIX A PROOF OF PROPOSITION III.1

Proof: To show the equivalence between (14) and (15), we only need to verify that the optimal solution $({\widehat{\Gamma }}_{\ast j},{\widehat{\tau }}_j)$ to (15) satisfies

$${\Vert \widehat{\mathbf{Z}}{\widehat{\Gamma }}_{\ast j}-{\mathbf{I}}_{\ast j}\Vert }_{\infty }=\frac{c}{\nu }{\widehat{\tau }}_j.$$ (A.1)

We then prove (A.1) by contradiction. Assuming that there exists some ${\stackrel{‒}{\tau }}_j\ge 0$ such that

$${\Vert \widehat{\mathbf{Z}}{\widehat{\Gamma }}_{\ast j}-{\mathbf{I}}_{\ast j}\Vert }_{\infty }=\frac{c}{\nu }{\stackrel{‒}{\tau }}_j<\frac{c}{\nu }{\widehat{\tau }}_j,$$ (A.2)

(A.2) implies that $({\widehat{\Gamma }}_{\ast j},{\stackrel{‒}{\tau }}_j)$ is also a feasible solution to (15) and

$${\Vert {\widehat{\Gamma }}_{\ast j}\Vert }_1+c{\stackrel{‒}{\tau }}_j<{\Vert {\widehat{\Gamma }}_{\ast j}\Vert }_1+c{\widehat{\tau }}_j.$$ (A.3)

(A.3) contradicts with the fact that $({\widehat{\Gamma }}_{\ast j},{\widehat{\tau }}_j)$ minimizes (15). Thus (A.1) must hold, and (15) is equivalent to (14).

Appendix B Parametric Simplex Method

We provide a brief description of the parametric simplex method only for self-containedness. More details of the derivation can be found in [34]. We consider the following generic form of linear program,

$$\underset{x\in {ℝ}^m}{\max }{\mathit{c}}^T\mathit{x}\mathrm{s}.\mathrm{t}.\mathbf{A}\mathit{x}\le \mathit{b},\mathit{x}\ge 0,$$ (B.1)

where c ∈ ℝ^m, A ∈ ℝ^n×m, and b ∈ ℝⁿ. It is well known that (B.1) has a dual formulation as ∈follows,

$$\underset{y\in {ℝ}^n}{\min }{\mathit{b}}^T\mathit{y}\mathrm{s}.\mathrm{t}.{\mathbf{A}}^{\mathit{T}}\mathit{y}\le \mathit{c},\mathit{y}\ge 0,$$ (B.2)

where y = (y₁, …, y_n)^T ∈ ℝⁿ are dual variables. The simplex method usually solves either (B.1) or (B.2). It contains two phases: Phase I is to find a feasible initial solution for Phase II; Phase II is an iterative procedure to recover the optimal solution based on the given initial solution.

Different from the simplex method, the parametric simplex method adds some perturbation to (B.1) and (B.2) such that the optimal solutions can be trivially obtained. More specifically, the parametric simplex method solves the following pair of linear programs

$$\underset{x\in {ℝ}^m}{\max }(\mathit{c}+\beta \mathit{q}){}^{T}x\mathrm{s}.\mathrm{t}.\mathbf{A}\mathit{x}\le \mathit{b}+\beta \mathit{p},\mathit{x}\ge 0,$$ (B.3)

$$\underset{x\in {ℝ}^n}{\min }{(\mathit{b}+\beta \mathit{p})}^T\mathit{y}\mathrm{s}.\mathrm{t}.{\mathbf{A}}^{\mathit{T}}\mathit{y}\ge \mathit{c}+\beta \mathit{q},\mathit{y}\ge 0,$$ (B.4)

where β ≥ 0 is a perturbation parameter, p ∈ ℝⁿ and q ∈ ℝ^m are perturbation vectors. When β, p, and q are suitably chosen such that b + βp ≥ 0 and c + βq ≤ 0, x = 0 and y = 0 are the optimal solutions to (B.3) and (B.4) respectively. The parametric simplex method is an iterative procedure, which gradually reduces β to 0 (corresponding to no perturation) and eventually recovers the optimal solution to (B.1).

To derive the iterative procedure, we first add slack variables w = (w₁, …, w_n)^T ∈ ℝⁿ, and rewrite (B.3) as

$$\underset{\tilde{x}\in {ℝ}^{m+n}}{\max }{(\tilde{c}+\beta \tilde{\mathit{q}})}^T\tilde{x}\mathrm{s}.\mathrm{t}.\mathbf{H}\tilde{x}=\mathit{b}+\beta \mathit{p},\tilde{x}\ge 0.$$ (B.5)

where H = [AI], $\tilde{c}={(c^T,0^T)}^T$, $\tilde{q}={(q^T,0^T)}^T$ and

$$\begin{array}{cc}\hfill \tilde{\mathit{x}}=& {({\tilde{x}}_1,\dots ,{\tilde{x}}_m,{\tilde{x}}_{m+1},\dots ,{\tilde{x}}_{m+n})}^T\hfill \\ \hfill =& {(x_1,\dots ,x_m,w_1,\dots ,w_n)}^T\in {ℝ}^{m+n}.\hfill \end{array}$$

Since b + βp ≥ 0 and c + βq ≤ 0, $\tilde{x}={(0,b+\beta p)}^T$ is the optimal solution to (B.5). We then divide all variables in $\tilde{x}$ into a nonbasic group $\mathcal{N}$ and a basic group $\mathcal{B}$. In particular,${\tilde{x}}_1,\dots ,{\tilde{x}}_m$ belong to the nonbasic group denoted by ${\tilde{x}}_{\mathcal{N}}$, and ${\tilde{x}}_{m+1},\dots ,{\tilde{x}}_{m+n}$ belong to the basic group denoted by ${\tilde{x}}_{\mathcal{B}}$. We also divide H into two submatrices ${\mathbf{H}}_{\mathcal{N}}$ and ${\mathbf{H}}_{\mathcal{B}}$, where ${\mathbf{H}}_{\mathcal{N}}$ contains all columns of H corresponding to ${\tilde{x}}_{\mathcal{N}}$, and ${\mathbf{H}}_{\mathcal{B}}$ contains all columns of H corresponding to ${\tilde{x}}_{\mathcal{N}}$. We then rewrite the constraint in (B.5) as ${\mathbf{H}}_{\mathcal{N}}{\tilde{x}}_{\mathcal{N}}+{\mathbf{H}}_{\mathcal{B}}{\tilde{x}}_{\mathcal{B}}=b+\beta p$. Consequently, we obtain the primal dictionary associated with the basic group $\mathcal{B}$ by

$${\tilde{\mathit{x}}}_{\mathcal{B}}={\tilde{\mathit{x}}}_{\mathcal{B}}^{\ast }+\beta {\stackrel{‒}{\mathit{x}}}_{\mathcal{B}}-{\mathbf{H}}_{\mathcal{B}}^{-1}{\mathbf{H}}_{\mathcal{N}},$$ (B.6)

$${\varphi }_P={\varphi }^{\ast }-{({\tilde{z}}^{\ast }+\beta \stackrel{‒}{z})}^T{\tilde{\mathit{x}}}_{\mathcal{N}}.,$$ (B.7)

where ${\tilde{x}}_{\mathcal{B}}^{\ast }={\mathbf{H}}_{\mathcal{B}}^{-1}b$, ${\stackrel{‒}{x}}_{\mathcal{B}}={\mathbf{H}}_{\mathcal{B}}^{-1}p$, ${\varphi }_P^{\ast }={\tilde{c}}_{\mathcal{B}}^T{\mathbf{H}}_{\mathcal{B}}b$, ${\tilde{z}}^{\ast }={\left({\mathbf{H}}_{\mathcal{B}}^{-1}{\mathbf{H}}_{\mathcal{N}}\right)}^T{\tilde{c}}_{\mathcal{B}}-{\tilde{c}}_{\mathcal{N}}$, ${\stackrel{‒}{z}}_{\mathcal{N}}={\left({\mathbf{H}}_{\mathcal{B}}^{-1}{\mathbf{H}}_{\mathcal{N}}\right)}^T\tilde{q}\mathcal{B}-\tilde{q}\mathcal{N}$ and φ_P is the objective value of (B.5) at current iteration.

We then add slack variables z = (z₁, … , z_m)^T, and rewrite (16) as

$$\begin{array}{cc}\hfill & \underset{\mathit{y}\in {ℝ}^n}{\min }{(\tilde{\mathit{b}}+\beta \tilde{\mathit{p}})}^T\mathit{y}\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\mathbf{A}-z^T\tilde{y}\ge \mathit{c}+\beta \mathit{q},\tilde{y}\ge 0.\hfill \end{array}$$ (B.8)

To make the notation consistent with the primal problem, we define

$$\begin{array}{cc}\hfill \tilde{z}=& ({\tilde{z}}_1,\dots ,{\tilde{z}}_m,{\tilde{z}}_{m+1},\dots ,{\tilde{z}}_{m+n})\hfill \\ \hfill =& {(z_1,\dots ,z_m,y_1,\dots ,y_n)}^T\in {ℝ}^{m+n}.\hfill \end{array}$$

Similarly we can obtain the dual dictionary associated with the nonbasic variable $\mathcal{N}$ by

$${\tilde{z}}_{\mathcal{N}}=({\tilde{z}}_{\mathcal{N}}^{\ast }+\beta {\stackrel{‒}{z}}_{\mathcal{N}})+{\left({\mathbf{H}}_{\mathcal{B}}^{-1}{\mathbf{H}}_{\mathcal{N}}\right)}^T{\tilde{z}}_{\mathcal{B}},$$ (B.9)

$$-{\varphi }_D=-{\varphi }_D^{\ast }-{({\mathit{x}}_{\mathcal{B}}^{\ast }+\beta {\stackrel{‒}{x}}_{\mathcal{B}})}^T{\tilde{z}}_{\mathcal{B}},$$ (B.10)

where ${\varphi }_D^{\ast }={\tilde{c}}_{\mathcal{B}}^T{\mathbf{H}}_{\mathcal{B}}^{-1}b$, and φ_D is the objective value of the dual problem at current iteration.

Once we obtain (B.6), (B.7), (B.9), and (B.10), we start to decrease β, and the smallest value of β at current iteration is obtained by

$${\beta }^{\ast }=\min \{\beta \mid {\tilde{\mathit{x}}}_{\mathcal{B}}^{\ast }+\beta {\stackrel{‒}{\mathit{x}}}_{\mathcal{B}}\ge 0,{\tilde{z}}_{\mathcal{N}}^{\ast }+\beta {\stackrel{‒}{z}}_{\mathcal{N}}\ge 0\}.$$

we then swap a pair of basic and nonbasic variables in B and N and update the primal and dual dictionaries such that β can be decreased to β*. See more details on updating the dictionaries in [34]. By repeating the above procedure, we eventually decrease β to 0. The parametric simplex method guarantees the feasibility and optimality for both (B.3) and (B.4) in each iteration, and eventually obtain the optimal solution to the original problem (B.3).

Since the parametric simplex method starts with all zero solutions, it can recover the optimal solution only in a few iterations when the optimal solution is very sparse. That naturally fits into the sparse estimation problems such as the EPIC method. Moreover, if we rewrite (16) in the same form as (B.3), we need to set p = (0^T, e^T, 0)^T and start with β = 1. Since c = (−1^T, −c)^T, we can set q = 0 i.e., we do not need perturbation on c. Thus the computation in each iteration can be further simplified due to the sparsity of p and q.

Remark B.1: For sparse estimation problems, Phase I of the simplex method does not guarantee the sparseness of the initial solution. As a result, Phase II may start with a dense initial solution, and gradually reduce the sparsity of the solution. Thus the overall convergence of the simplex method often requires a large number of iterations when the optimal solution is very sparse.

APPENDIX C Smoothed Proximal Gradient Algorithm

We first apply the smoothing approach in [28] to obtain a smooth surrogate of the matrix #x2113;₁ norm based on the Fenchel dual representation,

$${\Vert \Omega -\tilde{\Omega }\Vert }_{\eta }=\underset{{\Vert \mathbf{U}\Vert }_{\infty \le 1}}{\min }\mathrm{tr}\left({\mathbf{U}}^T\right(\Omega -\tilde{\Omega }\left)\right)+\frac{\eta }{2}{\Vert \mathbf{U}\Vert }_{\mathrm{F}}^2,$$ (C.1)

where η > 0 is a smoothing parameter. (C.1) has a closed form solution $\widehat{\mathbf{U}}$ as follows,

$${\widehat{\mathbf{U}}}_{\mathit{kj}}^{\Omega }=\text{sign}\left({\tilde{\mathbf{U}}}_{\mathit{kj}}^{\Omega }\right)\cdot \max \{\mid {\tilde{\mathbf{U}}}_{\mathit{kj}}^{\Omega }\mid -\gamma k\}.$$ (C.2)

where ${\tilde{\mathbf{U}}}^{\Omega }=(\Omega -\tilde{\Omega })∕\eta$, and γk is the minimum positive value such that ${\mid \mid \widehat{\mathbf{U}}\mid \mid }_{\infty }={\max }_k{\mid \mid {\widehat{\mathbf{U}}}_{k\ast }\mid \mid }_1\le 1$. See [9] for an efficient algorithms to find γk with the average computational complexity of O(d²). As is shown in [28], the smooth surrogate ${\mid \mid \Omega -\tilde{\Omega }\mid \mid }_{\eta }$ is smooth, convex, and has a simple form gradient as

$$\mathbf{G}\left(\Omega \right)=\frac{\partial {\Vert \Omega -\tilde{\Omega }\Vert }_{\eta }}{\partial \Omega }={\widehat{\mathbf{U}}}_{\mathit{kj}}^{\Omega }$$

Since ${\widehat{\mathbf{U}}}_{kj}^{\Omega }$ is obtained by the soft-thresholding in (C.2), we have G(Ω) continuous in Ω with the Lipschitz constant η⁻¹. Motivated by these good computational properties, we consider the following optimization problem instead of (18),

$$\overline{\Omega }=\underset{\Omega ={\Omega }^T}{\mathrm{argmin}}{\Vert \Omega -\tilde{\Omega }\Vert }_{\eta }.$$ (C.3)

To solve (C.3), we adopt the accelerated projected gradient algorithm proposed in [27]. More specifically, we define two sequences of auxiliary variables {M^(t)} and {W^(t)} with M⁽⁰⁾ = W⁽⁰⁾ = Ω⁽⁰⁾, and a sequence of weights {θ_t = 2/(1+t)}. For the t^th iteration, we first calculate the auxiliary variable M^(t) as

$${\mathbf{M}}^{\left(t\right)}=(1-{\theta }_t){\Omega }^{(t-1)}+{\theta }_t{\mathbf{W}}^{(t-1)}.$$

We then calculate the auxiliary variable W^(t) as

$$\begin{array}{cc}\hfill {\mathbf{W}}^{\left(t\right)}=& \underset{\mathbf{W}={\mathbf{W}}^T}{\mathrm{argmin}}{\Vert {\mathbf{W}}^{(t-1)}-\tilde{\Omega }\Vert }_{\eta }+\mathrm{tr}\left({(\mathbf{W}-{\mathbf{W}}^{(t-1)})}^T\mathbf{G}\left({\mathbf{M}}^{\left(t\right)}\right)\right)\hfill \\ \hfill & +\frac{1}{2{\eta }_t{\theta }_t}{\Vert \mathbf{W}-{\mathbf{W}}^{(t-1)}\Vert }_{\mathrm{F}}^2=\frac{1}{2}\left({\mathbf{W}}^{(t-1)}-\frac{{\eta }_t}{{\theta }_t}\mathbf{G}\left({\mathbf{M}}^{\left(t\right)}\right)\right)\hfill \\ \hfill & +\frac{1}{2}{\left({\mathbf{W}}^{(t-1)}-\frac{{\eta }_t}{{\theta }_t}\mathbf{G}\left({\mathbf{M}}^{\left(t\right)}\right)\right)}^T,\hfill \end{array}$$

where η_t is the step size. We can either choose η_t = η in all iterations or estimate η_t’s by the back-tracking=line search for better empirical performance [4]. At last, we calculate Ω^(t) as,

$${\Omega }^{\left(t\right)}=(1-{\theta }_t){\Omega }^{(t-1)}+{\theta }_t{\mathbf{W}}^{\left(t\right)}.$$

The next theorem provides the convergence rate of the algorithm with respect to minimizing (18).

Theorem C.1: Given the desired accuracy ε such that ${\mid \mid {\Omega }^{\left(t\right)}-\tilde{\Omega }\mid \mid }_1-{\mid \mid \widehat{\Omega }-\tilde{\Omega }\mid \mid }_1<\epsilon$, let η = d⁻¹ε/2, we need the number of iterations to be at most

$$t=2\sqrt{2d}{\Vert {\Omega }^{\left(0\right)}-\overline{\Omega }\Vert }_{\mathrm{F}}\cdot {\epsilon }^{-1}-1=O\left({\epsilon }^{-1}\right).$$

Proof: Due to the fact that ||A||_F ≤ d||A||∞, a direct consequence of (C.1) is the following uniform bound

$${\Vert \Omega -\tilde{\Omega }\Vert }_1-d\eta \le {\Vert \Omega -\tilde{\Omega }\Vert }_{\eta }\le {\Vert \Omega -\tilde{\Omega }\Vert }_1.$$

Then we consider the following decomposition

$$\begin{array}{cc}\hfill & {\Vert {\Omega }^{\left(t\right)}-\tilde{\Omega }\Vert }_1-{\Vert \widehat{\Omega }-\tilde{\Omega }\Vert }_1\hfill \\ \hfill & ={\Vert {\Omega }^{\left(t\right)}-\tilde{\Omega }\Vert }_1-{\Vert \overline{\Omega }-\tilde{\Omega }\Vert }_{\eta }+{\Vert \overline{\Omega }-\tilde{\Omega }\Vert }_{\eta }-{\Vert \widehat{\Omega }-\tilde{\Omega }\Vert }_1\hfill \\ \hfill & \le {\Vert {\Omega }^{\left(t\right)}-\tilde{\Omega }\Vert }_{\eta }-{\Vert \overline{\Omega }-\tilde{\Omega }\Vert }_{\eta }+d\eta \hfill \\ \hfill & \le \frac{2{\Vert {\Omega }^t-\tilde{\Omega }\Vert }_{\mathrm{F}}^2}{{(t+1)}^2\eta }+d\eta ,\hfill \end{array}$$

where the last inequality comes from the result established in [27],

$${\Vert {\Omega }^{\left(t\right)}-\tilde{\Omega }\Vert }_{\eta }-{\Vert \overline{\Omega }-\tilde{\Omega }\Vert }_{\eta }\le \frac{2{\Vert {\Omega }^{\left(0\right)}-\overline{\Omega }\Vert }_{\mathrm{F}}^2}{{(t+1)}^2\eta }.$$

Thus given dη = ε/2, we only need

$$\frac{4d{\Vert {\Omega }^{\left(0\right)}-\overline{\Omega }\Vert }_{\mathrm{F}}^2}{{(t+1)}^2}\le \frac{{∊}^2}{2}.$$ (C.4)

By solving (C.4), we obtain

$$t\le \frac{2\sqrt{2d}{\Vert {\Omega }^{\left(0\right)}-\overline{\Omega }\Vert }_{\mathrm{F}}}{∊}-1.$$

Theorem C.1 guarantees that the above algorithm achieves the optimal rate of convergence for minimizing (18) over the class of all first-order computational algorithms.

APPENDIX D Proof of Lemma 1

Proof: [7] shows that there exist universal constants κ₃ and κ₄ such that

$$\mathbb{P}(\mid {\widehat{\mu }}_j-{\mu }_j\mid \le k_3{\theta }_{\max }∊)\ge 1-\exp (-n{∊}^2),$$ (D.1)

$$\mathbb{P}\left(\mid {\widehat{m}}_j-𝔼X_j^2\mid \le k_4\sqrt{K}∊\right)\ge 1-\exp (-n{∊}^2).$$ (D.2)

We then define the following events

$$\begin{array}{cc}\hfill & {\mathcal{C}}_1=\{\mid {\widehat{\mu }}_j-{\mu }_j\mid \le {\mu }_{\max }\},\hfill \\ \hfill & {\mathcal{C}}_2=\{\mid {\widehat{\mu }}_j-{\mu }_j\mid \le k_3{\theta }_{\max }∊\},\hfill \\ \hfill & {\mathcal{C}}_3=\{{\widehat{m}}_j-𝔼X_j^2\mid \le k_4\sqrt{K}∊\},\hfill \\ \hfill & {\mathcal{C}}_4=\{\mid {\widehat{\theta }}_j-{\theta }_j\mid \le {\theta }_{\min }\}.\hfill \end{array}$$

Conditioning on ${\mathcal{C}}_1$, we have

$$\begin{array}{cc}\hfill \mid {\widehat{\mu }}_j^2-{\mu }_j^2\mid & =\mid {\widehat{\mu }}_j-{\mu }_j\mid \cdot \mid {\widehat{\mu }}_j+{\mu }_j\mid \hfill \\ \hfill & \le \mid {\widehat{\mu }}_j-{\mu }_j\mid \cdot \mid {\widehat{\mu }}_j-{\mu }_j\mid +\mid {\widehat{\mu }}_j-{\mu }_j\mid \cdot \mid 2{\mu }_j\mid \hfill \\ \hfill & \le (2{\mu }_{\max }+\mid {\widehat{\mu }}_j-{\mu }_j\mid )\mid {\widehat{\mu }}_j-{\mu }_j\mid \hfill \\ \hfill & \le 3{\mu }_{\max }\mid {\widehat{\mu }}_j-{\mu }_j\mid .\hfill \end{array}$$ (D.3)

Conditioning on ${\mathcal{C}}_2$ and ${\mathcal{C}}_3$, (D.3) implies

$$\begin{array}{cc}\hfill \mid {\widehat{\theta }}_j^2-{\theta }_j^2\mid & =\mid {\widehat{m}}_j-{\widehat{\mu }}_j^2-𝔼X_j^2+{\mu }_j^2\mid \hfill \\ \hfill & \le \mid {\widehat{m}}_j-𝔼X_j^2\mid +\mid {\mu }_j^2-{\mu }_j^2\mid \hfill \\ \hfill & \le (3{\mu }_{\max }{k}_3{\theta }_{\max }+k_4\sqrt{K})∊.\hfill \end{array}$$ (D.4)

(D.4) further implies

$$\begin{array}{cc}\hfill \mid {\widehat{\theta }}_j-{\theta }_j\mid & \le \frac{\mid {\widehat{\theta }}_j^2-{\theta }_j^2\mid }{{\widehat{\theta }}_j+{\theta }_j}\le \frac{\mid {\widehat{\theta }}_j^2-{\theta }_j^2\mid }{{\theta }_j}\hfill \\ \hfill & \le \frac{(3{\mu }_{\max }{k}_3{\theta }_{\max }+k_4\sqrt{K})∊}{{\theta }_{\min }}.\hfill \end{array}$$ (D.5)

Conditioning ${\mathcal{C}}_4$, (D.5) implies

$$\begin{array}{cc}\hfill \mid {\widehat{\theta }}_j^{-1}-{\theta }_j^{-1}\mid =& \frac{\mid {\widehat{\theta }}_j-{\theta }_j\mid }{{\widehat{\theta }}_j{\theta }_j}=\frac{\mid {\widehat{\theta }}_j-{\theta }_j\mid }{({\widehat{\theta }}_j-{\theta }_j){\theta }_j+2{\theta }_j^2}\hfill \\ \hfill & \le \frac{(3{\mu }_{\max }{k}_3{\theta }_{\max }+k_4\sqrt{K})∊}{({\widehat{\theta }}_j-{\theta }_j){\theta }_j{\theta }_{\min }+2{\theta }_j^2{\theta }_{\min }}\hfill \\ \hfill & \le \frac{(3{\mu }_{\max }{k}_3{\theta }_{\max }+k_4\sqrt{K})∊}{2{\theta }_j^2{\theta }_{\min }}\hfill \\ \hfill & \le \frac{(3{\mu }_{\max }{k}_3{\theta }_{\max }+k_4\sqrt{K})∊}{2{\theta }_{\min }^3}.\hfill \end{array}$$ (D.6)

Combining (D.1), (D.2), and (D.6), for small enough ε such that

$$∊\le \min \left\{\frac{{\mu }_{\max }}{k_3{\theta }_{\max }},\frac{{\theta }_{\min }^2}{3{\mu }_{\max }{k}_3{\theta }_{\max }+k_4\sqrt{K}}\right\},$$ (D.7)

we have

$$\mathbb{P}\left(\mid {\widehat{\theta }}_j^{-1}-{\theta }_j^{-1}\mid \le \frac{(3{\mu }_{\max }{k}_3{\theta }_{\max }+k_4\sqrt{K})∊}{{\theta }_{\min }^3}\right)\ge 1-2\exp (-4n{∊}^2).$$ (D.8)

By taking the union bound of (D.8), we have

$$\mathbb{P}\left(\underset{1\le j\le d}{\max }\mid {\widehat{\theta }}_j^{-1}-{\theta }_j^{-1}\mid \le \frac{(3{\mu }_{\max }{k}_3{\theta }_{\max }+k_4\sqrt{K})∊}{{\theta }_{\min }^3}\right)\ge 1-2\exp (-4n{∊}^2+\log d).$$

If we take $∊=\sqrt{\log d∕n}$, then (D.7) implies that we need n large enough such that

$$n\ge \max \left\{\frac{k_3^2{\theta }_{\max }^2}{{\mu }_{\max }^2},\frac{{(3{\mu }_{\max }{k}_3{\theta }_{\max }+k_4\sqrt{K})}^2}{{\theta }_{\min }^4}\right\}\cdot \log d.$$

Taking ${\kappa }_2=(3_{{\mu }_{\max }{\kappa }_3}{\theta }_{\max }+{\kappa }_4\sqrt{K})∕{\theta }_{\min }^3$, we then have

$$\mathbb{P}\left(\underset{1\le j\le d}{\max }\mid {\widehat{\theta }}_j^{-1}-{\theta }_j^{-1}\mid \le k_2\sqrt{\frac{\log d}{n}}\right)\ge 1-\frac{2}{d}.$$

(19) is a direct result in [24], therefore its proof is omitted.

Appendix E Proof Of Theorem IV.1

Proof: We first define the following pair of orthogonal subspaces $({\mathcal{S}}_j,{\mathcal{S}}_j^{\perp })$,

$$\begin{array}{cc}\hfill & {\mathcal{S}}_j=\{\mathit{v}\in {ℝ}^d\mid v_k=0\text{for all}{\Gamma }_{\mathit{kj}}=0\},\hfill \\ \hfill & {\mathcal{S}}_j^{\perp }=\{\mathit{v}\in {ℝ}^d\mid v_k=0\text{for all}{\Gamma }_{kj}\ne 0\}.\hfill \end{array}$$

We will use $({\mathcal{S}}_j,{\mathcal{S}}_j^{\perp })$ to exploit the sparseness of Γ_*j. We then define the following event

$${\mathcal{D}}_1-\{{\Vert \widehat{\mathbf{Z}}-\mathbf{Z}\Vert }_{\max }\le \lambda \}.$$

Conditioning on ${\mathcal{D}}_1$, we haveis

$$\begin{array}{cc}\hfill {\Vert \widehat{\mathbf{Z}}{\Gamma }_{\ast j}-{\mathbf{I}}_{\ast j}\Vert }_{\infty }=& {\Vert (\widehat{\mathbf{Z}}-\mathbf{Z}){\Gamma }_{\ast j}\Vert }_{\infty }\hfill \\ \hfill & \le {\Vert {\Gamma }_{\ast j}\Vert }_1{\Vert \widehat{\mathbf{Z}}-\mathbf{Z}\Vert }_{\max }\le \lambda {\Vert {\Gamma }_{\ast j}\Vert }_1.\hfill \end{array}$$ (E.1)

Now let τ_j = ||Γ_*j||₁, (E.1) implies that (Γ_*j, τ_j) is a feasible solution to (13). Since $({\widehat{\Gamma }}_{\ast j},{\widehat{\tau }}_j)$ is the empirical minimizer, we have

$$\begin{array}{cc}\hfill {\Vert {\widehat{\Gamma }}_{{\mathcal{S}}_{i}j}\Vert }_1+& {\Vert {\widehat{\Gamma }}_{{\mathcal{S}}_j^{\perp }j}\Vert }_1+c{\widehat{\tau }}_j={\Vert {\widehat{\Gamma }}_{\ast j}\Vert }_1+c{\widehat{\tau }}_j\hfill \\ \hfill & \le {\Vert {\Gamma }_{\ast j}\Vert }_1+c{\tau }_j={\Vert {\Gamma }_{{\mathcal{S}}_{j}j}\Vert }_1+c{\tau }_j,\hfill \end{array}$$ (E.2)

where the last equality comes from the fact that ${\Gamma }_{{\mathcal{S}}_j^{\perp }j}=0$.

Let $\widehat{\Delta }=\widehat{\Gamma }-\Gamma$ be the estimation error, (E.2) implies

$$\begin{array}{cc}\hfill {\Vert {\widehat{\Gamma }}_{{\mathcal{S}}_j^{\perp }j}\Vert }_1\le & {\Vert {\Gamma }_{{\mathcal{S}}_{j}j}\Vert }_1-{\Vert {\widehat{\Gamma }}_{{\mathcal{S}}_{j}j}\Vert }_1+c({\tau }_j-{\widehat{\tau }}_j)\hfill \\ \hfill \le & {\Vert {\widehat{\Delta }}_{{\mathcal{S}}_{j}j}\Vert }_1+c({\tau }_j-{\widehat{\tau }}_j)\hfill \\ \hfill \le & {\Vert {\widehat{\Delta }}_{{\mathcal{S}}_{j}j}\Vert }_1+c({\Vert {\Gamma }_{\ast j}\Vert }_1-{\Vert {\widehat{\Gamma }}_{\ast j}\Vert }_1)\hfill \\ \hfill \underset{\le }{\left(\mathrm{i}\right)}& {\Vert {\widehat{\Delta }}_{{\mathcal{S}}_{j}j}\Vert }_1+c{\Vert {\widehat{\Delta }}_{\ast j}\Vert }_1\hfill \\ \hfill \underset{\le }{\left(\mathrm{ii}\right)}& (1+c){\Vert {\widehat{\Delta }}_{{\mathcal{S}}_{j}j}\Vert }_1+c{\Vert {\widehat{\Delta }}_{{\mathcal{S}}_j^{\perp }j}\Vert }_1,\hfill \end{array}$$ (E.3)

where (i) comes from the constraint in (13):${\mid \mid {\widehat{\Gamma }}_{\ast j}\mid \mid }_1\le {\widehat{\tau }}_j$ and (ii) comes from the fact ${\mid \mid {\widehat{\Delta }}_{\ast j}\mid \mid }_1={\mid \mid {\widehat{\Delta }}_{{\mathcal{S}}_{i}j}\mid \mid }_1+{\mid \mid {\widehat{\Delta }}_{{\mathcal{S}}_j^{\perp }j}\mid \mid }_1$ Combining the fact ${\mid \mid {\widehat{\Delta }}_{{\mathcal{S}}_j^{\perp }j}\mid \mid }_1={\mid \mid {\widehat{\Gamma }}_{{\mathcal{S}}_j^{\perp }j}-0\mid \mid }_1={\mid \mid {\widehat{\Gamma }}_{{\mathcal{S}}_j^{\perp }j}\mid \mid }_1$ with (E.3), we have

$${\Vert {\widehat{\Delta }}_{{\mathcal{S}}_j^{\perp }j}\Vert }_1\le \stackrel{‒}{c}{\Vert {\widehat{\Delta }}_{{\mathcal{S}}_{j}j}\Vert }_1,$$ (E.4)

where $\stackrel{‒}{c}=(1+c)∕(1-c)$. (E.4) implies that ${\Delta }_{\ast j}$ belongs the following cone shape set

$${\mathcal{M}}_j^{\stackrel{‒}{c}}=\left\{\mathit{v}\in {ℝ}^d\setminus \left\{0\right\}\mid {\Vert {\mathit{v}}_{{\mathcal{S}}_j^{\perp }}\Vert }_1\le \stackrel{‒}{c}{\Vert v_{{\mathcal{S}}_j}\Vert }_1\right\}.$$

The following lemma characterizes an important property of ${\mathcal{M}}_j^{\stackrel{‒}{c}}$ when ${\mathcal{D}}_1$ holds.

Lemma E.1: Suppose that X ~ EC(μ, ξ, Σ), and (A.1) and ${\mathcal{D}}_1$ hold. Given any $\mathcal{v}\in {\mathcal{M}}_j^{\stackrel{‒}{c}}$, for small enough λ such that $2{(1+\stackrel{‒}{c})}^{2}s\lambda {\kappa }_u\le 1$, we have

$$\underset{v\in {\mathcal{M}}_j^{\stackrel{‒}{c}}}{\min }{v}^T\widehat{\mathbf{Z}}v\ge \frac{{\Vert v\Vert }_2^2}{2k_u}.$$ (E.5)

The proof of Lemma E.1 is provided in Appendix E.1. Since Δ_*j exactly belongs to ${\mathcal{M}}_j^{\stackrel{‒}{c}}$, we have a simple variant of (E.5) as

$$\begin{array}{cc}\hfill {\Vert {\widehat{\Delta }}_{\ast j}\Vert }_1{\Vert \widehat{\mathbf{Z}}{\widehat{\Delta }}_{\ast j}\Vert }_{\infty }\ge & {\widehat{\Delta }}_{\ast j}^T\widehat{\mathbf{Z}}{\widehat{\Delta }}_{\ast j}\ge \frac{{\Vert {\widehat{\Delta }}_{\ast j}\Vert }_2^2}{2k_u}\hfill \\ \hfill \ge & \frac{{\Vert {\widehat{\Delta }}_{{\mathcal{S}}_{j}j}\Vert }_2^2}{2k_u}\ge \frac{{\Vert {\widehat{\Delta }}_{{\mathcal{S}}_{j}j}\Vert }_1^2}{2{\mathit{sk}}_u},\hfill \end{array}$$ (E.6)

where the last inequality comes from the fact that ${\widehat{\Delta }}_{{\mathcal{S}}_{j}j}$ has at most s nonzero entries. Since

$$\begin{array}{cc}\hfill {\Vert \widehat{\mathbf{Z}}{\widehat{\Delta }}_{\ast j}\Vert }_{\infty }\le & {\Vert \widehat{\mathbf{Z}}{\widehat{\Gamma }}_{\ast j}-{\mathbf{I}}_{\ast j}\Vert }_{\infty }+{\Vert \widehat{\mathbf{Z}}{\Gamma }_{\ast j}-{\mathbf{I}}_{\ast j}\Vert }_{\infty }\hfill \\ \hfill \le & \lambda ({\widehat{\tau }}_j+{\tau }_j)\hfill \\ \hfill \le & \lambda (2{\widehat{\tau }}_j+{\tau }_j-{\widehat{\tau }}_j)\hfill \\ \hfill \le & \lambda (2{\widehat{\tau }}_j+{\Vert {\widehat{\Delta }}_{\ast j}\Vert }_1)\hfill \\ \hfill \le & \lambda (2{\widehat{\tau }}_j+(1+\stackrel{‒}{c}\left){\Vert {\widehat{\Delta }}_{{\mathcal{S}}_{j}j}\Vert }_1\right),\hfill \end{array}$$ (E.7)

where the last inequality comes from (E.4). Combining (E.6) and (E.7), we have

$${\Vert \widehat{\mathbf{Z}}{\widehat{\Delta }}_{\ast j}\Vert }_{\infty }\le \lambda (2{\widehat{\tau }}_j+2(1+\stackrel{‒}{c}\left)k_{u}s{\Vert \widehat{\mathbf{Z}}{\widehat{\Delta }}_{\ast j}\Vert }_{\infty }\right).$$ (E.8)

Assuming that $1-2(1+\stackrel{‒}{c}){\kappa }_{u}s\lambda ={\delta }_1>0$, (E.8) implies

$${\Vert \widehat{\mathbf{Z}}{\widehat{\Delta }}_{\ast j}\Vert }_{\infty }\le 2{\delta }_1^{-1}\lambda \widehat{\tau }j.$$ (E.9)

Combining (E.6) and (E.9), we have

$$\begin{array}{cc}\hfill c{\widehat{\tau }}_j& \le {\Vert {\widehat{\Delta }}_{{\mathcal{S}}_{j}j}\Vert }_1+c{\tau }_j\le 2k_{u}s{\Vert \widehat{\mathbf{Z}}{\widehat{\Delta }}_{\ast j}\Vert }_{\infty }+c{\tau }_j\hfill \\ \hfill & \le 4k_{u}s{\delta }_1^{-1}\lambda {\widehat{\tau }}_j+c{\tau }_j.\hfill \end{array}$$ (E.10)

Assuming that $1-4{\kappa }_{u}s{\delta }_1^{-1}{c}^{-1}\lambda ={\delta }_2>0$, (E.10) implies

$${\widehat{\tau }}_j\le {\delta }_2^{-1}{\tau }_j.$$ (E.11)

Recall $\lambda ={\kappa }_1\sqrt{\log d∕n}$, in order to secure

$$\begin{array}{cc}\hfill 1-2& (1+\stackrel{‒}{c})k_{u}s\lambda ={\delta }_1>0,\hfill \\ \hfill & c-4k_{u}s{\delta }_1^{-1}\lambda ={\delta }_2>0,\hfill \\ \hfill & 2{(1+\stackrel{‒}{c})}^{2}s\lambda k_u\le 1,\hfill \end{array}$$

we need large enough n such that

$$\begin{array}{cc}\hfill n\ge \max & \{4{(1-{\delta }_1)}^{-2}{(1+\stackrel{‒}{c})}^2{k}_u^2,16{(c-{\delta }_2)}^{-2}{k}_u^2{\delta }_1^{-2},\phantom{\}}\hfill \\ \hfill & \phantom{\{}4{(1+\stackrel{‒}{c})}^4{k}_u{k}_1\}\cdot s^2\log d.\hfill \end{array}$$

Combining (E.9) and (E.11), we have

$${\Vert \widehat{\mathbf{Z}}{\widehat{\Delta }}_{\ast j}\Vert }_{\infty }\le 2{\delta }_1^{-1}{\delta }_2^{-1}\lambda {\tau }_j.$$ (E.12)

Combining (E.4), (E.6), and (E.12), we obtain

$${\Vert {\widehat{\Delta }}_{\ast j}\Vert }_1\le 4(1+\stackrel{‒}{c})k_u{\delta }_1^{-1}{\delta }_2^{-1}s\lambda {\tau }_j.$$ (E.13)

Combining (E.12) and (E.13), we have

$$\begin{array}{cc}\hfill {\widehat{\Delta }}_{\ast j}^T\widehat{\mathbf{Z}}{\widehat{\Delta }}_{\ast j}\le & {\Vert {\widehat{\Delta }}_{\ast j}\Vert }_1\cdot {\Vert \widehat{\mathbf{Z}}{\widehat{\Delta }}_{\ast j}\Vert }_{\infty }\hfill \\ \hfill \le & 8(1+\stackrel{‒}{c})k_u{\delta }_1^{-2}{\delta }_2^{-2}s{\lambda }^2{\tau }_j^2.\hfill \end{array}$$ (E.14)

By Lemma E.1 again, (E.14) implies

$${\Vert {\widehat{\Delta }}_{\ast j}\Vert }_2^2\le 16(1+\stackrel{‒}{c})k_u^2{\delta }_1^{-2}{\delta }_2^{-2}s{\lambda }^2{\tau }_j^2.$$ (E.15)

Let ${\kappa }_5=4(1+\stackrel{‒}{c}){\kappa }_u{\delta }_1^{-1}{\delta }_2^{-1}{\kappa }_1$ and ${\kappa }_6=16(1+\stackrel{‒}{c}){\kappa }_u^2{\delta }_1^{-2}{\delta }_2^{-2}{\kappa }_1^2$. Recall $\lambda ={\kappa }_1\sqrt{\log d∕n}$, by definition of the matrix #x2113;₁ and Frobenius norms, (E.13) and (E.15) imply

$$\begin{array}{cc}\hfill {\Vert \widehat{\Delta }\Vert }_1=& \underset{j}{\max }{\Vert {\widehat{\Delta }}_{\ast j}\Vert }_1\le 4(1+\stackrel{‒}{c})k_u{\delta }_1^{-1}{\delta }_2^{-1}s\lambda \underset{j}{\max }{\tau }_j\hfill \\ \hfill \le & k_5\cdot M\cdot s\sqrt{\frac{\log d}{n}},\hfill \end{array}$$ (E.16)

and

$$\begin{array}{cc}\hfill \frac{1}{\mathit{d}}{\Vert \widehat{\Delta }\Vert }_{\mathrm{F}}^2=& \frac{1}{\mathit{d}}\sum _j{\Vert {\widehat{\Delta }}_{\ast j}\Vert }_2^2\le 16(1+\stackrel{‒}{c})k_u^2{\delta }_1^{-2}{\delta }_2^{-2}s{\lambda }^2{\tau }_j^2\hfill \\ \hfill \le & k_6\cdot M^2\cdot \frac{s\log d}{n}.\hfill \end{array}$$ (E.17)

Now we start to derive the error bound of $\tilde{\Omega }$ obtained by the ensemble rule. We have the following decomposition

$$\begin{array}{cc}\hfill \tilde{\Omega }-\Omega =& {\widehat{\Theta }}^{-1}\widehat{\Gamma }{\widehat{\Theta }}^{-1}-{\Theta }^{-1}\Gamma {\Theta }^{-1}\hfill \\ \hfill =& ({\widehat{\Theta }}^{-1}-{\Theta }^{-1}+{\Theta }^{-1})(\widehat{\Gamma }-\Gamma +\Gamma )\hfill \\ \hfill & \cdot ({\widehat{\Theta }}^{-1}-{\Theta }^{-1}+{\Theta }^{-1})-{\Theta }^{-1}\Gamma {\Theta }^{-1}\hfill \\ \hfill =& ({\widehat{\Theta }}^{-1}-{\Theta }^{-1})(\widehat{\Gamma }-\Gamma )({\widehat{\Theta }}^{-1}-{\Theta }^{-1})\hfill \\ \hfill & +({\widehat{\Theta }}^{-1}-{\Theta }^{-1})(\widehat{\Gamma }-\Gamma ){\Theta }^{-1}+({\widehat{\Theta }}^{-1}-{\Theta }^{-1})\Gamma {\Theta }^{-1}\hfill \\ \hfill & +({\widehat{\Theta }}^{-1}-{\Theta }^{-1})\Gamma ({\widehat{\Theta }}^{-1}-{\Theta }^{-1})+{\Theta }^{-1}(\widehat{\Gamma }-\Gamma ){\Theta }^{-1}\hfill \\ \hfill & +{\Theta }^{-1}(\widehat{\Gamma }-\Gamma )({\widehat{\Theta }}^{-1}-{\Theta }^{-1})\hfill \\ \hfill & +{\Theta }^{-1}\Gamma ({\widehat{\Theta }}^{-1}-{\Theta }^{-1}).\hfill \end{array}$$ (E.18)

Moreover, for any A, B, C ∈ ℝ^d×d, where A and C are diagonal matrices, we have

$${\Vert \mathbf{ABC}\Vert }_1\le {\Vert \mathbf{A}\Vert }_{\max }\cdot {\Vert \mathbf{B}\Vert }_1\cdot {\Vert \mathbf{C}\Vert }_{\max },$$ (E.19)

$${\Vert \mathbf{ABC}\Vert }_{\mathrm{F}}\le {\Vert \mathbf{A}\Vert }_{\max }\cdot {\Vert \mathbf{B}\Vert }_{\mathrm{F}}\cdot {\Vert \mathbf{C}\Vert }_{\max }.$$ (E.20)

Here we define the following event

$${\mathcal{D}}_2=\left\{{\Vert {\widehat{\Theta }}^{-1}-{\Theta }^{-1}\Vert }_{\max }\le {\kappa }_2\sqrt{\frac{\log d}{n}}\right\}.$$

Thus conditioning ${\mathcal{D}}_2$, (E.16), (E.18), and (E.19) imply

$$\begin{array}{cc}\hfill {\Vert \tilde{\Omega }-\Omega \Vert }_{-1}\le & {\kappa }_2^2{\kappa }_5\cdot \frac{\log d}{n}\cdot M\cdot s\sqrt{\frac{\log d}{n}}\hfill \\ \hfill & +\frac{{\kappa }_2{\kappa }_5}{{\theta }_{\min }}\cdot \sqrt{\frac{\log d}{n}}\cdot M\cdot s\sqrt{\frac{\log d}{n}}\hfill \\ \hfill & +{\kappa }_2^2\cdot M\cdot \frac{\log d}{n}+\frac{{\kappa }_2}{{\theta }_{\min }}\cdot M\cdot \sqrt{\frac{\log d}{n}}\hfill \\ \hfill & +\frac{{\kappa }_2{\kappa }_5}{{\theta }_{\min }}\cdot \sqrt{\frac{\log d}{n}}\cdot M\cdot s\sqrt{\frac{\log d}{n}}\hfill \\ \hfill & +\frac{{\kappa }_5}{{\theta }_{\min }^2}M\cdot s\sqrt{\frac{\log d}{n}}+\frac{{\kappa }_2}{{\theta }_{\min }}\cdot M\cdot \sqrt{\frac{\log d}{n}}.\hfill \end{array}$$ (E.21)

If (A.4): s²logd/n → 0 holds, then (E.21) is determined by the slowest rate $Ms\sqrt{\log d∕n}$. Thus for large enough n, there exists a universal constant C₄ such that

$${\Vert \tilde{\Omega }-\Omega \Vert }_{-1}\le C_4\cdot M\cdot s\sqrt{\frac{\log d}{n}}.$$ (E.22)

Similarly, conditioning on ${\mathcal{D}}_2$, (E.17), (E.18), (E.20) and the fact ${\mid \mid \Gamma \mid \mid }_{\mathrm{F}}\le M\sqrt{d}$ imply

$$\begin{array}{cc}\hfill {\Vert \tilde{\Omega }-\Omega \Vert }_{\mathrm{F}}\le & {\kappa }_2^2{\kappa }_6\cdot \frac{\log d}{n}\cdot M\cdot \sqrt{\frac{\mathit{ds}\log d}{n}}\hfill \\ \hfill & +\frac{{\kappa }_2{\kappa }_6}{{\theta }_{\min }}\cdot \sqrt{\frac{\log d}{n}}\cdot M\cdot \sqrt{\frac{\mathit{ds}\log d}{n}}\hfill \\ \hfill & +{\kappa }_2^2\cdot M\sqrt{d}\cdot \frac{\log d}{n}+\frac{{\kappa }_2}{{\theta }_{\min }}\cdot M\sqrt{d}\cdot \sqrt{\frac{\log d}{n}}\hfill \\ \hfill & +\frac{{\kappa }_2{\kappa }_6}{{\theta }_{\min }}\cdot \sqrt{\frac{\log d}{n}}\cdot M\cdot \sqrt{\frac{\mathit{ds}\log d}{n}}\hfill \\ \hfill & +\frac{{\kappa }_6}{{\theta }_{\min }^2}M\cdot \sqrt{\frac{\mathit{ds}\log d}{n}}+\frac{{\kappa }_2}{{\theta }_{\min }}\cdot M\sqrt{d}\cdot \sqrt{\frac{\log d}{n}}.\hfill \end{array}$$ (E.23)

Again if (A.4) holds, then (E.23) is determined by the slowest rate $M\sqrt{ds\log d∕n}$. Thus for large enough n, there exists a universal constant C₂ such that

$$\frac{1}{d}{\Vert \tilde{\Omega }-\Omega \Vert }_{\mathrm{F}}^2\le C_2\cdot M^2\cdot \frac{s\log d}{n}.$$ (E.24)

We then proceed to prove the error bound of $\widehat{\Omega }$ obtained by the symmetrization procedure (18). Let C₁ = 2C₄, if we choose the matrix #x2113;₁ norm as ||·||_* in (18), we have

$$\begin{array}{cc}\hfill {\Vert \widehat{\Omega }-\Omega \Vert }_1& \le {\Vert \tilde{\Omega }-\widehat{\Omega }\Vert }_1+{\Vert \tilde{\Omega }-\Omega \Vert }_1\hfill \\ \hfill & \le 2{\Vert \tilde{\Omega }-\Omega \Vert }_1\le C_1\cdot M\cdot s\sqrt{\frac{\log d}{n}},\hfill \end{array}$$ (E.25)

where the second inequality comes from the fact that Ω is a feasible solution to (18), and $\widehat{\Omega }$ is the empirical minimizer. If we choose the Frobenius norm as ||·||_* in (18), using the fact that the Frobenius norm projection is contractive, we have

$$\frac{1}{d}{\Vert \widehat{\Omega }-\Omega \Vert }_{\mathrm{F}}^2\le \frac{1}{d}{\Vert \tilde{\Omega }-\Omega \Vert }_{\mathrm{F}}^2\le C_2{M}^2\frac{s\log d}{n}.$$ (E.26)

All above analysis are conditioned on ${\mathcal{D}}_1$ and ${\mathcal{D}}_2$. Thus combining Lemma 1 with (E.25) and (E.26), we have

$$\mathbb{P}\left({\Vert \widehat{\Omega }-\Omega \Vert }_p\le C_1\mathit{Ms}\sqrt{\frac{\log d}{n}}\right)\ge 1-\frac{3}{d},$$ (E.27)

$$\mathbb{P}\left(\frac{1}{d}{\Vert \widehat{\Omega }-\Omega \Vert }_{\mathrm{F}}^2\le C_2{M}^2\frac{s\log d}{n}\right)\ge 1-\frac{3}{d}.$$ (E.28)

where p = 1, 2, and (E.27) comes from the fact that ||A||₂ ≤ ||A||₁ for any symmetric matrix A.

APPENDIX F Proof of Lemma E.1

Proof: Since ${\Lambda }_{\min }\left(\mathrm{Z}\right)=1∕{\Lambda }_{\max }\left(\Gamma \right)\ge {\kappa }_u^{-1}$, we have

$$\begin{array}{cc}\hfill {\mathit{v}}^T\widehat{\mathbf{Z}}\mathit{v}& ={\mathit{v}}^T\mathbf{Z}\mathit{v}-{\mathit{v}}^T(\mathbf{Z}-\widehat{\mathbf{Z}})\mathit{v}\hfill \\ \hfill & \ge {\kappa }_u^{-1}{\Vert \mathit{v}\Vert }_2^2-{\Vert \mathit{v}\Vert }_1^2\cdot {\Vert \mathbf{Z}-\widehat{\mathbf{Z}}\Vert }_{\max }.\hfill \end{array}$$ (F.1)

Since $v\in {\mathcal{M}}_j^{\stackrel{‒}{c}}$, we have ${\mid \mid v_{{\mathcal{S}}_j^{\perp }}\mid \mid }_1\le \stackrel{‒}{c}{\mid \mid v_{{\mathcal{S}}_j}\mid \mid }_1$, which implies

$$\begin{array}{cc}\hfill {\Vert \mathit{v}\Vert }_1& ={\Vert {\mathit{v}}_{{\mathcal{S}}_j}\Vert }_1+{\Vert {\mathit{v}}_{{\mathcal{S}}_j^{\perp }}\Vert }_1\le (1+\stackrel{‒}{c}){\Vert {\mathit{v}}_{{\mathcal{S}}_j}\Vert }_1\hfill \\ \hfill & \le (1+\stackrel{‒}{c})\sqrt{s}{\Vert {\mathit{v}}_{{\mathcal{S}}_j}\Vert }_2,\hfill \end{array}$$ (F.2)

where the last inequality comes from the fact that there are at most s nonzero entries in $v_{{\mathcal{S}}_j}$. Then combining (F.1) and (F.2), we have

$$\begin{array}{cc}\hfill {\mathit{v}}^T\widehat{\mathbf{Z}}\mathit{v}& \ge {\kappa }_u^{-1}{\Vert \mathit{v}\Vert }_2^2-{(1+\stackrel{‒}{c})}^2{\Vert {\mathit{v}}_{\mathcal{S}}\Vert }_1^2\cdot {\Vert \mathbf{Z}-\widehat{\mathbf{Z}}\Vert }_{\max }\hfill \\ \hfill & \ge {\kappa }_u^{-1}{\Vert \mathit{v}\Vert }_2^2-{(1+\stackrel{‒}{c})}^{2}s\lambda {\Vert {\mathit{v}}_{\mathcal{S}}\Vert }_2^2.\hfill \end{array}$$ (F.3)

Since we have $2{(1+\stackrel{‒}{c})}^{2}s\lambda {\kappa }_u\le 1$, (F.3) implies

$${\mathit{v}}^T\widehat{\mathbf{Z}}\mathit{v}\ge \frac{{\Vert \mathit{v}\Vert }_2^2}{2{\kappa }_u}.$$

APPENDIX G Proof Of Theorem IV.2

Proof: Our following analysis also assumes that ${\mathcal{D}}_1=\{{\mid \mid \widehat{\mathbf{Z}}-\mathbf{Z}\mid \mid }_{\max }\le \lambda \}$ holds. Since ${\mathcal{D}}_1$ implies (E.1),

$${\Vert \widehat{\mathbf{Z}}{\Gamma }_{\ast j}-{\mathbf{I}}_{\ast j}\Vert }_{\infty }\le \lambda {\tau }_j,\forall j=1,\dots ,d,$$

where τ_j = ||Γ_*j||₁. Then (Γ_*j, τ_j) is a feasible solution to (13), which implies

$$\begin{array}{cc}\hfill {\Vert \widehat{\mathbf{Z}}({\widehat{\Gamma }}_{\ast j}-{\Gamma }_{\ast j})\Vert }_{\infty }\le & {\Vert \widehat{\mathbf{Z}}{\widehat{\Gamma }}_{\ast j}-{\mathbf{I}}_{\ast j}\Vert }_{\infty }+{\Vert \widehat{\mathbf{Z}}{\Gamma }_{\ast j}-{\mathbf{I}}_{\ast j}\Vert }_{\infty }\hfill \\ \hfill \le & \lambda {\widehat{\tau }}_j+\lambda {\tau }_j.\hfill \end{array}$$ (G.1)

Moreover, we have

$$\begin{array}{cc}\hfill (1+c){\Vert {\widehat{\Gamma }}_{\ast j}\Vert }_1\le & {\Vert {\widehat{\Gamma }}_{\ast j}\Vert }_1+c{\widehat{\tau }}_j\le {\Vert {\Gamma }_{\ast j}\Vert }_1+c{\tau }_j\hfill \\ \hfill =& (1+c){\Vert {\Gamma }_{\ast j}\Vert }_1=(1+c){\tau }_j,\hfill \end{array}$$

which further implies

$${\Vert {\widehat{\Gamma }}_{\ast j}\Vert }_1\le {\Vert {\Gamma }_{\ast j}\Vert }_1,{\Vert {\widehat{\Gamma }}_{\ast j}-{\Gamma }_{\ast j}\Vert }_1\le 2{\Vert {\Gamma }_{\ast j}\Vert }_1.$$ (G.2)

Combing (G.1) and (G.2), we have where the last inequality comes from

$$\begin{array}{cc}\hfill & {\Vert \mathbf{Z}({\widehat{\Gamma }}_{\ast j}-{\Gamma }_{\ast j})\Vert }_{\infty }\hfill \\ \hfill & \le {\Vert \widehat{\mathbf{Z}}({\widehat{\Gamma }}_{\ast j}-{\Gamma }_{\ast j})\Vert }_{\infty }+{\Vert (\widehat{\mathbf{Z}}-\mathbf{Z})({\widehat{\Gamma }}_{\ast j}-{\Gamma }_{\ast j})\Vert }_{\infty }\hfill \\ \hfill & \le \lambda \tau +\lambda {\widehat{\tau }}_j+{\Vert \widehat{\mathbf{Z}}-\mathbf{Z}\Vert }_{\max }{\Vert {\widehat{\Gamma }}_{\ast j}-{\Gamma }_{\ast j}\Vert }_1\hfill \\ \hfill & \le 3\lambda \tau +\lambda {\widehat{\tau }}_j\le \frac{(1+4c)\lambda {\tau }_j}{c},\hfill \end{array}$$ (G.3)

where the last inequality comes from

$$c{\widehat{\tau }}_j\le {\Vert {\widehat{\Gamma }}_{\ast j}\Vert }_1+c{\widehat{\tau }}_j\le {\Vert {\Gamma }_{\ast j}\Vert }_{1}c{\tau }_j=(1+c){\tau }_j.$$

By (G.3), we have

$$\begin{array}{cc}\hfill {\Vert {\widehat{\Gamma }}_{\ast j}-{\Gamma }_{\ast j}\Vert }_{\infty }\le & {\Vert {\Gamma }_{\ast j}\Vert }_1{\Vert \mathbf{Z}({\widehat{\Gamma }}_{\ast j}-{\Gamma }_{\ast j})\Vert }_{\infty }\hfill \\ \hfill \le & \frac{\lambda (1+4c){\tau }_j}{c}\cdot {\Vert {\Gamma }_{\ast j}\Vert }_1\le \frac{\lambda (1+4c){\tau }_j^2}{c}.\hfill \end{array}$$ (G.4)

Recall $\lambda ={\kappa }_1\sqrt{\log d∕n}$, by the definition of the max norm and (G.4), we have

$${\Vert \widehat{\Gamma }-\Gamma \Vert }_{\max }\le k_6\cdot M^2\cdot \sqrt{\frac{\log d}{n}},$$ (G.5)

where κ₇ = κ₁(1 + 4c)/c. Since for any A, B, C ∈ ℝ^d×d, where A and C are diagonal matrices, we have

$${\Vert \mathbf{ABC}\Vert }_{\max }\le {\Vert \mathbf{A}\Vert }_{\max }\cdot {\Vert \mathbf{B}\Vert }_{\max }\cdot {\Vert \mathbf{C}\Vert }_{\max }.$$ (G.6)

Conditioning on

$${\mathcal{D}}_2=\left\{{\Vert {\widehat{ϴ}}^{-1}-{ϴ}^{-1}\Vert }_{\max }\le k_2\sqrt{\frac{\log d}{n}}\right\},$$ (G.7)

(G.6), (E.18) and the fact ||Γ||_max ≤ M imply

$$\begin{array}{cc}\hfill {\Vert \tilde{\Omega }-\Omega \Vert }_{\max }\le & k_2^2{k}_7\cdot \frac{\log d}{n}\cdot M^2\cdot \sqrt{\frac{\log d}{n}}\hfill \\ \hfill & +\frac{k_2{k}_7}{{\theta }_{\min }}\cdot \sqrt{\frac{\log d}{n}}\cdot M^2\cdot \sqrt{\frac{\log d}{n}}\hfill \\ \hfill & +k_2^2\cdot \mathit{M}\cdot \frac{\log d}{\mathit{b}}+\frac{k_2}{{\theta }_{\min }}\cdot \mathit{M}\cdot \sqrt{\frac{\log d}{\mathit{n}}}\hfill \\ \hfill & +\frac{k_2{k}_7}{{\theta }_{\min }}\cdot \sqrt{\frac{\log d}{n}}\cdot {\mathit{M}}^2\cdot \sqrt{\frac{\log d}{\mathit{n}}}\hfill \\ \hfill & +\frac{k_7}{{\theta }_{\min }^2}{\mathit{M}}^2\cdot \sqrt{\frac{\log d}{n}}+\frac{k_2}{{\theta }_{\min }}\cdot \mathit{M}\cdot \sqrt{\frac{\log d}{n}}.\hfill \end{array}$$ (G.8)

Again if (A.4): s² log d/n → 0 holds, then (G.8) determined by the slowest rate $M^2\sqrt{\log d∕n}$. Thus for large enough n, if we choose the max norm as ||·||_* in (18), we have

$$\begin{array}{cc}\hfill {\Vert \widehat{\Omega }-\Omega \Vert }_{\max }\le & {\Vert \tilde{\Omega }-\widehat{\Omega }\Vert }_{\max }+{\Vert \tilde{\Omega }-\Omega \Vert }_{\max }\hfill \\ \hfill \le & 2{\Vert \tilde{\Omega }-\Omega \Vert }_{\max }\le 2k_7\cdot {\mathit{M}}^2\cdot \sqrt{\frac{\log d}{n}},\hfill \end{array}$$ (G.9)

where the second inequality comes from the fact that Ω is a feasible solution to (18), and $\widehat{\Omega }$ is the empirical minimizer.

Note that the results obtained here only depend on ${\mathcal{D}}_1$ and ${\mathcal{D}}_2$. Thus by Lemma 1 and (G.9), let C₃ = 2κ₇, we have

$$\mathbb{P}\left({\Vert \widehat{\Omega }-\Omega \Vert }_{\max }\le C_3\cdot M^2\cdot \sqrt{\frac{\log d}{n}}\right)\ge 1-\frac{3}{d}.$$

To show the partial consistency in graph estimation $\mathbb{P}(E\subseteq \widehat{E})\to 1$, we follow a similar argument to Theorem 4 in [25]. Therefore the proof is omitted.