Abstract
Background
The accurate prediction of surgical risk is important to patients and physicians. Logistic regression (LR) models are typically used to estimate these risks. However, in the fields of data mining and machine-learning, many alternative classification and prediction algorithms have been developed. This study aimed to compare the performance of LR to several data mining algorithms for predicting 30-day surgical morbidity in children.
Methods
We used the 2012 National Surgical Quality Improvement Program-Pediatric dataset to compare the performance of 1) a LR model that assumed linearity and additivity (simple LR model) 2) a LR model incorporating restricted cubic splines and interactions (flexible LR model) 3) a support vector machine, 4) a random forest and 5) boosted classification trees for predicting surgical morbidity.
Results
The ensemble-based methods showed significantly higher accuracy, sensitivity, specificity, PPV, and NPV than the simple LR model. However, none of the models performed better than the flexible LR model in terms of the aforementioned measures or in model calibration or discrimination.
Conclusion
Support vector machines, random forests, and boosted classification trees do not show better performance than LR for predicting pediatric surgical morbidity. After further validation, the flexible LR model derived in this study could be used to assist with clinical decision-making based on patient-specific surgical risks.
Keywords: data mining, machine learning, prediction, boosting, random forests, support vector machines, logistic regression, surgical morbidity, pediatrics
INTRODUCTION
Data mining algorithms, sometimes called machine learning or statistical learning algorithms, have been increasingly used in biomedical research in recent years. Data mining is broadly defined as the process of selecting, exploring, and modeling large amounts of data to discover unknown and useful patterns or relationships.[1, 2] Data mining algorithms arose from the fields of statistics and computer science, and are widely used in marketing, banking, engineering, and bioinformatics. Their application to clinical research, however, has been limited.
In clinical research, logistic regression models are by far the most commonly used algorithm for predicting the probability of occurrence of an event. While these models can provide unbiased estimates of the associations between predictors and the outcome, they have some limitations. First, they assume a particular parametric form of the relationships between the predictors and the outcome; namely, the assumption is made that the logit of the outcome is equal to a linear combination of the independent variables.[3] These models also assume additivity of the predictors’ effects on the outcome. These assumptions are usually incorrect, though the extent to which they are incorrect varies. Furthermore, in small datasets, these assumptions may be necessary to avoid overfitting. In larger datasets, these assumptions can be circumvented by using transformations or splines to model continuous predictors and by including interactions between variables. These techniques can improve model fit, but they are infrequently used, partly because they tend to reduce model interpretability.[4] Another limitation of regression models is that they do not always provide optimal predictive accuracy. In clinical research, these models are typically built to describe the nature of the relationship between specific covariates and the outcome.[2] While estimating such relationships is clearly important in biomedical research, accurate prediction is also very important. In fact, in certain situations in which the primary aim is to achieve optimal predictive accuracy, a reduction in clinical interpretability may be acceptable.
One area of biomedical research in which data mining may be particularly useful is in outcome prediction using large clinical databases, such as the American College of Surgeons’ National Surgical Quality Improvement Program (ACS NSQIP) database.[2] Of the few studies investigating the performance of data mining algorithms for predicting surgical morbidity or mortality, most have been small (several hundred or several thousand patients)[5–10], though a few larger studies have been reported.[11–17] These studies have been inconsistent in their findings, in that some have shown data mining algorithms to perform better than traditional logistic regression in terms of overall accuracy[13, 14, 16, 18], discrimination[13, 14, 16], or calibration[11], whereas some have reported similar performance according to these measures.[11, 18–20] Data from the ACS NSQIP has been used to create risk calculators to predict post-operative outcomes for adult surgery patients overall [21] and for patients undergoing specific procedures.[22–25] Several of these calculators are freely available online, and their use by both physicians and patients has the potential to improve shared decision making and informed consent.[21–25] All of these calculators are based on logistic regression models that are reported to have good discrimination and calibration. However, none of the studies in which these prediction models were derived reported investigating whether other statistical algorithms might perform as well as or better than logistic regression, and none included pediatric patients. The objective of this study was to compare the performance of five different statistical algorithms for predicting surgical morbidity in pediatric surgical patients. The algorithms evaluated were chosen because of their infrequent use in the clinical research literature and their straightforward implementation in freely available software and included 1) a logistic regression model that assumed linearity and additivity (simple logistic regression model) 2) a logistic regression model incorporating restricted cubic splines and interactions (flexible logistic regression model) 3) a support vector machine, 4) a random forest and 5) boosted classification trees.
METHODS
This study used the 2012 NSQIP Pediatric (NSQIP-Peds) Participant Use Data File, which contains patient-level data on 51,008 pediatric surgery cases submitted in 2012 by 50 US and Canadian children’s hospitals. The NSQIP-Peds program is a multi-specialty program with cases sampled from pediatric general/thoracic surgery, pediatric otolaryngology, pediatric orthopedic surgery, pediatric urology, pediatric neurosurgery, and pediatric plastic surgery. Launched in October 2008 with 4 sites, NSQIP-Peds has since expanded, with 50 institutions participating in 2012. The program provides peer-reviewed, risk-adjusted 30-day postoperative outcomes to participating institutions, for the purposes of benchmarking and quality improvement.[26–28] Included cases are selected based on Current Procedural Terminology codes using NSQIP 8-day cycle-based systematic sampling of 35 procedures per cycle. One hundred and twenty-nine variables are collected from the medical records and the patients and their families, including information on demographics, surgical profile, preoperative and intraoperative variables, and postoperative occurrences.[26–28] The conduct of this study was approved by Nationwide Children’s Hospital Institutional Research Board with a waiver of informed consent.
In this study, we considered the question of which model most accurately predicts the occurrence of surgical morbidity within 30 days of surgery. Neonates were excluded, because of the known differences in risk of surgical morbidity between neonates and non-neonates and because of the relatively small number of neonates (N=2919) and larger amount of missing data in neonates compared to non-neonates (N=48089) in the 2012 NSQIP-Peds sample. The 49 preoperative variables in pediatric patients considered for inclusion in each model are shown in Table 1. This list consists of all preoperative patient characteristics available in the database, though some rare characteristics were eliminated or grouped with other similar characteristics. Of note, procedures that occurred concurrently with the principal operative procedure were not considered as predictors because whether these additional procedures would be performed was not necessarily known preoperatively. In addition, 60 individual procedures (designated by CPT codes) that were performed in the total cohort at least 200 times were also included as indicator variables in the models, resulting in a total of 109 predictor variables. A frequency of 200 times was chosen to maximize the external validity of the models by enabling the risk of surgical morbidity associated with each procedure to be estimated accurately in the training dataset. Many of the procedures performed less frequently had no associated cases of surgical morbidity in the sample, whereas all procedures performed 200 or more times were associated with at least one case of surgical morbidity. No observations were removed from the analyses due to the use of this criterion as each type of procedure included as a predictor was treated as an individual binary variable. The outcome variable was the occurrence of intra-operative or post-operative morbidity within 30 days of the surgery, which was defined as any of the following events: SSI (superficial, deep, or organ/space without open wound), wound disruption, pneumonia without preoperative pneumonia, unplanned intubation, pulmonary embolism, renal insufficiency or failure without preoperative renal failure or dialysis, urinary tract infection, central line associated bloodstream infection, coma > 24 hours without preoperative coma, seizure, nerve injury, any cerebral intra-ventricular hemorrhage, CVA/stroke or intracranial hemorrhage, cardiac arrest requiring CPR, venous thrombosis requiring therapy, bleeding/transfusion, graft/prosthesis/flap failure, or the development or worsening of sepsis.[26, 29] Patients who died within 30 days of their surgery (0.1%) were included in all analyses because the outcome under examination, surgical morbidity, could occur either intraoperatively or postoperatively.
Table 1.
Pre-operative patient characteristics
| Training Sample (N=33662) | Validation Sample (N=14427) | |||||
|---|---|---|---|---|---|---|
|
| ||||||
| Characteristic | No Surgical Morbidity (N=43858) | Surgical Morbidity (N=4231) | P | No Surgical Morbidity (N=13209) | Surgical Morbidity (N=1218) | P |
| Age at surgery (years) | 6.6(1.8, 12.1) | 9.5(1.6, 14.0) | <.001 | 6.3(1.8, 11.8) | 10.3(1.6, 14.4) | <.001 |
| Pre-op length of stay (days) | 0.0(0.0, 0.0) | 0.0(0.0, 0.0) | <.001 | 0.0(0.0, 0.0) | 0.0(0.0, 0.0) | <.001 |
| Male | 17749(57.9) | 1438(47.7) | <.001 | 7647(57.9) | 564(46.3) | <.001 |
| Race | 0.13 | 0.025 | ||||
| White | 22096(72.1) | 2149(71.3) | 9522(72.1) | 878(72.1) | ||
| Black or African American | 3605(11.8) | 391(13.0) | 1504(11.4) | 152(12.5) | ||
| Asian | 962(3.1) | 78(2.6) | 410(3.1) | 23(1.9) | ||
| Other | 184(0.6) | 22(0.7) | 76(0.6) | 13(1.1) | ||
| Unknown | 3802(12.4) | 373(12.4) | 1697(12.8) | 152(12.5) | ||
| Hispanic Ethnicity | 3729(12.2) | 323(10.7) | 0.020 | 1722(13.0) | 124(10.2) | 0.004 |
| Admission Status | <.001 | <.001 | ||||
| Inpatient | 16116(52.6) | 2678(88.9) | 6909(52.3) | 1107(90.9) | ||
| Outpatient | 14533(47.4) | 335(11.1) | 6300(47.7) | 111(9.1) | ||
| Transfer Status | <.001 | <.001 | ||||
| Admitted from home, clinic, or doctor’s office | 22136(72.2) | 2304(76.5) | 9600(72.7) | 919(75.5) | ||
| Admitted through ER | 7521(24.5) | 524(17.4) | 3195(24.2) | 212(17.4) | ||
| Transferred from outside hospital | 833(2.7) | 153(5.1) | 345(2.6) | 76(6.2) | ||
| Other | 159(0.5) | 32(1.1) | 69(0.5) | 11(0.9) | ||
| Surgical Specialty | <.001 | <.001 | ||||
| General or cardiothoracic surgery | 11300(36.9) | 963(32.0) | 4749(36.0) | 398(32.7) | ||
| Neurosurgery | 2508(8.2) | 397(13.2) | 1100(8.3) | 154(12.6) | ||
| Orthopedic Surgery | 5730(18.7) | 1138(37.8) | 2535(19.2) | 469(38.5) | ||
| Otolaryngology (ENT) | 3437(11.2) | 89(3.0) | 1490(11.3) | 27(2.2) | ||
| Plastics | 3451(11.3) | 273(9.1) | 1523(11.5) | 104(8.5) | ||
| Urologic or gynecologic surgery | 4223(13.8) | 153(5.1) | 1812(13.7) | 66(5.4) | ||
| Case Type | <.001 | <.001 | ||||
| Elective | 22930(74.8) | 2494(82.8) | 9905(75.0) | 984(80.8) | ||
| Emergent | 4704(15.3) | 320(10.6) | 2070(15.7) | 152(12.5) | ||
| Urgent | 3015(9.8) | 199(6.6) | 1234(9.3) | 82(6.7) | ||
| Diabetes | 113(0.4) | 10(0.3) | 0.75 | 43(0.3) | 6(0.5) | 0.34 |
| Premature birth | <.001 | <.001 | ||||
| No | 24443(79.8) | 2282(75.7) | 10460(79.2) | 918(75.4) | ||
| ≤ 24 weeks | 199(0.6) | 28(0.9) | 83(0.6) | 19(1.6) | ||
| 25–26 weeks | 301(1.0) | 53(1.8) | 123(0.9) | 13(1.1) | ||
| 27–28 weeks | 270(0.9) | 41(1.4) | 135(1.0) | 25(2.1) | ||
| 29–30 weeks | 247(0.8) | 43(1.4) | 123(0.9) | 11(0.9) | ||
| 31–32 weeks | 357(1.2) | 56(1.9) | 177(1.3) | 25(2.1) | ||
| 33–34 weeks | 510(1.7) | 73(2.4) | 249(1.9) | 24(2.0) | ||
| 35–36 weeks | 1130(3.7) | 139(4.6) | 453(3.4) | 57(4.7) | ||
| Unknown | 3192(10.4) | 298(9.9) | 1406(10.6) | 126(10.3) | ||
| Pulmonary: | ||||||
| Ventilator dependence | 341(1.1) | 170(5.6) | <.001 | 119(0.9) | 77(6.3) | <.001 |
| Pneumonia | 113(0.4) | 30(1.0) | <.001 | 47(0.4) | 11(0.9) | 0.004 |
| Asthma | 1889(6.2) | 245(8.1) | <.001 | 759(5.7) | 90(7.4) | 0.020 |
| COPD | 715(2.3) | 201(6.7) | <.001 | 291(2.2) | 80(6.6) | <.001 |
| Oxygen support | 545(1.8) | 212(7.0) | <.001 | 216(1.6) | 94(7.7) | <.001 |
| Cystic fibrosis | 77(0.3) | 14(0.5) | 0.031 | 26(0.2) | 1(0.1) | 0.38 |
| Tracheostomy | 276(0.9) | 76(2.5) | <.001 | 116(0.9) | 36(3.0) | <.001 |
| Structural pulmonary/airway abnormality | 1425(4.6) | 293(9.7) | <.001 | 576(4.4) | 129(10.6) | <.001 |
| Gastrointestinal: | ||||||
| Esophageal, gastric, or intestinal disease | 4654(15.2) | 775(25.7) | <.001 | 1996(15.1) | 319(26.2) | <.001 |
| Biliary, liver, or pancreatic disease | 757(2.5) | 118(3.9) | <.001 | 304(2.3) | 41(3.4) | 0.020 |
| Cardiac: | ||||||
| Cardiac risk factors | <.001 | <.001 | ||||
| None | 28576(93.2) | 2612(86.7) | 12381(93.7) | 1045(85.8) | ||
| Minor | 1367(4.5) | 215(7.1) | 535(4.1) | 102(8.4) | ||
| Major | 520(1.7) | 123(4.1) | 216(1.6) | 54(4.4) | ||
| Severe | 186(0.6) | 63(2.1) | 77(0.6) | 17(1.4) | ||
| Previous cardiac surgery/cardiac intervention | 858(2.8) | 180(6.0) | <.001 | 360(2.7) | 76(6.2) | <.001 |
| Any renal comorbidity | 88(0.3) | 35(1.2) | <.001 | 40(0.3) | 20(1.6) | <.001 |
| Central nervous system: | ||||||
| CVA/Stroke or traumatic/acquired brain injury with neurological deficit | 632(2.1) | 158(5.2) | <.001 | 264(2.0) | 54(4.4) | <.001 |
| Tumor involving CNS | 494(1.6) | 130(4.3) | <.001 | 227(1.7) | 59(4.8) | <.001 |
| Developmental delay/impaired cognition | 3860(12.6) | 703(23.3) | <.001 | 1723(13.0) | 272(22.3) | <.001 |
| Seizure | 1328(4.3) | 326(10.8) | <.001 | 600(4.5) | 124(10.2) | <.001 |
| Cerebral palsy | 1053(3.4) | 251(8.3) | <.001 | 490(3.7) | 94(7.7) | <.001 |
| Structural Central Nervous System abnormality | 3163(10.3) | 600(19.9) | <.001 | 1365(10.3) | 269(22.1) | <.001 |
| Neuromuscular disorder | 1278(4.2) | 410(13.6) | <.001 | 556(4.2) | 176(14.4) | <.001 |
| Intraventricular hemorrhage | 404(1.3) | 77(2.6) | <.001 | 191(1.4) | 27(2.2) | 0.035 |
| Immunology: | ||||||
| Immune disease/immunosuppressant use | 281(0.9) | 75(2.5) | <.001 | 133(1.0) | 23(1.9) | 0.004 |
| Steroid use within 30 days | 654(2.1) | 189(6.3) | <.001 | 277(2.1) | 84(6.9) | <.001 |
| Bone marrow or solid organ transplant | 134(0.4) | 32(1.1) | <.001 | 61(0.5) | 9(0.7) | 0.18 |
| Nutritional/immune/oncology/other: | ||||||
| History of or current malignancy | 789(2.6) | 240(8.0) | <.001 | 331(2.5) | 104(8.5) | <.001 |
| Open wound with or without infection | 337(1.1) | 48(1.6) | 0.015 | 112(0.8) | 19(1.6) | 0.012 |
| Weight loss >10%/failure to thrive | 894(2.9) | 167(5.5) | <.001 | 405(3.1) | 59(4.8) | <.001 |
| Nutritional support | 1607(5.2) | 532(17.7) | <.001 | 653(4.9) | 200(16.4) | <.001 |
| Bleeding disorder | 131(0.4) | 47(1.6) | <.001 | 48(0.4) | 22(1.8) | <.001 |
| Hematologic disorder | 633(2.1) | 213(7.1) | <.001 | 258(2.0) | 89(7.3) | <.001 |
| Chemotherapy for malignancy within 30 days or radiotherapy for malignancy within 90 days before surgery | 167(0.5) | 63(2.1) | <.001 | 58(0.4) | 27(2.2) | <.001 |
| SIRS, Sepsis, or Septic shock within 48 hours before surgery | 1494(4.9) | 169(5.6) | 0.08 | 675(5.1) | 123(10.1) | <.001 |
| Inotropic support at time of surgery | 140(0.5) | 123(4.1) | <.001 | 59(0.4) | 49(4.0) | <.001 |
| Prior operation within 30 days before surgery | 371(1.2) | 98(3.3) | <.001 | 140(1.1) | 34(2.8) | <.001 |
| History of or current congenital malformation | 10363(33.8) | 1358(45.1) | <.001 | 4527(34.3) | 531(43.6) | <.001 |
| Blood transfusions within 48 hours before surgery | 183(0.6) | 85(2.8) | <.001 | 77(0.6) | 45(3.7) | <.001 |
| ASA classification | <.001 | <.001 | ||||
| 1 Normal | 11822(38.6) | 445(14.8) | 5150(39.0) | 188(15.4) | ||
| 2 Mild disease | 13055(42.6) | 1129(37.5) | 5582(42.3) | 472(38.8) | ||
| 3 Severe disease | 5361(17.5) | 1245(41.3) | 2298(17.4) | 464(38.1) | ||
| 4/5 Life-threatening/moribund | 342(1.1) | 189(6.3) | 142(1.1) | 89(7.3) | ||
| None assigned | 69(0.2) | 5(0.2) | 37(0.3) | 5(0.4) | ||
| Wound classification | <.001 | <.001 | ||||
| Clean | 15099(49.3) | 1979(65.7) | 6579(49.8) | 777(63.8) | ||
| Clean/contaminated | 11952(39.0) | 747(24.8) | 5097(38.6) | 301(24.7) | ||
| Contaminated | 2140(7.0) | 109(3.6) | 910(6.9) | 38(3.1) | ||
| Dirty/infected | 1458(4.8) | 178(5.9) | 623(4.7) | 102(8.4) | ||
Values are shown as frequency (%) or median (1 quartile, 3 quartile). P-values are from Wilcoxon rank sum tests for continuous variables and Pearson chi square tests for categorical variables.
Statistical Analysis
In order to avoid overfitting, which occurs when a model has excellent fit to the data used in model fitting but poor fit to external data, [4, 30] the 2012 NSQIP-Peds PUF dataset was split into training and validation datasets. Seventy percent of the observations were chosen randomly for use as the training dataset, and the other 30% were used as the test (validation) dataset. Each algorithm incorporated all 109 pre-operative variables of interest. The 5 statistical algorithms compared were: 1) a logistic regression model that assumed a linear relationship between each covariate and the log-odds of morbidity, with no interaction terms (simple logistic regression model), 2) a logistic regression model fit with the relationship between continuous variables and the log-odds of morbidity expressed using restricted cubic splines with decile knots and with interactions between any two predictors included if statistically significant at p<0.01 in stepwise selection when added to the model containing all main effects (flexible logistic regression model), 3) a support vector machine (SVM), 4) a random forest (RF) and 5) boosted classification trees.[4, 30]
The relative performance of the 5 models in the validation dataset was first assessed by examining overall accuracy, sensitivity, specificity, negative predictive value (NPV), and positive predictive value (PPV). In the logistic regression models, a cutoff outcome probability of 50% was used for classification. The McNemar test was used to compare accuracy, sensitivity, and specificity between each of the machine learning algorithms and the logistic regression models. Marginal logistic regression models were used to compare NPV and PPV between the machine learning algorithms and the logistic regression models.[31] This method is analogous to McNemar’s test but for the problem of comparing predictive values, which condition on the test outcome. Because the predictive algorithms do not necessarily all predict the same outcome for a given patient, some patients may contribute zero, one, or two observations to the comparisons, thus the variance estimator for the difference in PPVs and NPVs between algorithms is not straightforward. Marginal regression models provide a natural test statistic to assess these differences. The discriminative ability of the algorithms was determined using the area under the receiver operating characteristic curve (AUROC).[3] The nonparametric test of DeLong et al. was used to compare the AUROC between the machine learning algorithms and the logistic regression models.[32] The calibration of each model was assessed by first comparing the mean predicted probability of morbidity to the observed probability of morbidity in the validation sample. This provides a measure of the calibration intercept, also known as calibration-in-the-large.[33] Secondly, the calibration slope was calculated; this slope assesses deviation between observed and expected probabilities of surgical morbidity across the entire range of predicted risk; it equals one if the model is perfectly calibrated. Lastly, a lowess scatterplot smoother was used to graphically describe the relationship between observed and predicted morbidity in the validation sample. Deviation of this curve from a diagonal line with unit slope is indicative of poor calibration.[33] Logistic regression modeling was performed using the logistic procedure in SAS v9.3 (SAS Institute Inc., Cary, NC) and the glm function in the stats package in the R statistical environment (R Foundation for Statistical Computing, Vienna, Austria). SVM models were fit using the svm function in the e1071 package in R.[34] Random forest models were fit using the randomForest function in the randomForest package in R.[35] Boosted classification tree models were built using the gbm function in the gbm package in R.[36] AUROC was calculated and compared between models using the roc.test function in the pROC package in R.[37] Assessment of model calibration was performed using the val.prob function in the rms package in R.[38]
Logistic Regression Models
Logistic regression is the most common statistical algorithm employed in clinical research studies to assess associations between patient characteristics and binary outcomes. These models are a type of generalized linear model, and are fit using maximum likelihood estimation. In generalized linear models, the expected value of the outcome is a function of a linear combination of the predictors; in logistic regression the logit function is used.[3] Logistic regression models yield odds ratios for the associations between the dependent and independent variables. They also generate a risk score, or an estimated probability of the outcome, that can be used for classification and prediction.
Support Vector Machine
The idea behind SVMs is the construction of an optimal separating hyperplane between two classes.[4, 39, 40] Each observation is treated as a point in high-dimensional feature (predictor) space, with the dimension of this space determined by the number of predictors. The SVM model uses mathematical functions (kernels) to project the original data into higher-dimensional space in order to improve the separability of the two classes. The SVM model also uses a ‘soft margin’ around the separating hyperplane, the size of which is chosen using cross-validation. This margin allows some observations to violate the separating hyperplane in order to achieve better overall performance.[4, 40] Radial kernels often deliver excellent results in high dimensional problems[4], and these were used in this study. SVMs with radial kernels require the specification of two parameters: C, which controls the overfitting of the model, and γ, which controls the degree of non-linearity of the model.[30] To optimize these parameters, 10-fold cross-validation of the training data was performed; the C and γ values that minimized the overall misclassification rate were chosen using a grid search in the intervals [1; 1000] and [0.001; 100] respectively. Finally, the output values of the SVM were converted into probabilities using the sigmoid function as described by Lin et. al.[41]
Random Forest
A random forest is a collection, or “ensemble”, of classification trees[42] with the predictions from all trees combined to make the overall prediction by “majority vote”.[43] A series of classification trees is built, with each tree being fit using a random bootstrap sample of the original training dataset and a random subset of the predictors that maximize the classification criterion at each node. An estimate of the misclassification rate is obtained without cross-validation by using each classification tree to predict the outcome of the observations not in the bootstrap sample used to grow that particular tree (“out-of-bag” observations), then taking a majority vote of the out-of-the-bag predictions from the collection of trees. Random forests typically have substantially greater predictive accuracy than single classification trees, which have very high variance.[43, 44] Random forests require just two parameters to be defined: the number of random trees in the forest, and the number of predictive variables randomly selected for consideration at each node.[43] In this study, these parameters were optimized by a grid search in the intervals [400; 1000] and [6; 16] respectively; the parameters yielding the lowest out-of-bag misclassification rate were selected for the final models.
Boosted classification trees
Similar to the random forest algorithm, boosting involves the combining of predictions from a large number of ‘weak’ classifiers, each with error rates only slightly better than random guessing, to produce a final more accurate prediction.[4] Boosting can be applied with any base algorithm, but is most often used with classification and regression trees. Unlike random forests, boosted classification trees are grown sequentially using information from previously grown trees. Boosting does not involve bootstrap sampling or the random selection of predictors to be considered at each node. Rather, the boosted classification tree algorithm fits a small tree to a sequence of reweighted versions of the data. In the building of each new tree, patients whose outcomes were incorrectly classified by the previous tree are weighted more heavily than patients who were correctly classified. In this study, we will fit a gradient boosted model with binomial deviance loss function as this algorithm is particularly robust to overlapping class distributions.[4, 45] Boosted classification trees fit with the gradient boosting algorithm and incorporating regularization through shrinkage require the defining of three parameters: the number of component trees (M), the shrinkage parameter (ν), and the maximum interaction depth or number of terminal nodes of each tree.[45] To optimize the first two of these parameters, 10-fold cross-validation of the training data was performed; M and ν values that minimized the overall misclassification rate were chosen using a grid search in the intervals [1; 10000] and [0.001; 0.1] respectively. Although there is no consensus on the optimal tree depth, interaction depths between 3 and 7 are often found to yield similar results, with cross-validation error rates being relatively insensitive to particular choices in this range.[4] We chose to use classification trees of depth 4.
RESULTS
Description of study sample
Comparisons of pre-operative characteristics between patients with and without surgical morbidity in both the training and validation datasets are shown in Table 1. Forty-six of the 49 evaluated pre-operative characteristics differed significantly between patients with and without surgical morbidity in both datasets, and these differences were fairly consistent across the two datasets. Substantial heterogeneity was found across procedures in the rates of surgical morbidity. The 10 most common procedures in the study cohort are shown in Table 2. Spinal fusion (arthrodesis) procedures had much higher rates of surgical morbidity than other common procedures.
Table 2.
Ten most common principal operative procedures
| Training Sample (N=33662) | Validation Sample (N=14427) | |||||
|---|---|---|---|---|---|---|
|
| ||||||
| Procedure | Overall (% of total procedures) | No Surgical Morbidity (row %) (N=43858) | Surgical Morbidity (row %) (N=4231) | Overall (% of total procedures) | No Surgical Morbidity (row %) (N=13209) | Surgical Morbidity (row %) (N=1218) |
| Laparoscopic appendectomy | 3489 (10.4) | 3343 (95.8) | 146 (4.2) | 1555 (10.8) | 1478 (95.1) | 77 (4.9) |
| Percutaneous skeletal fixation of supracondylar or transcondylar humeral fracture | 1611 (4.8) | 1595 (99.0) | 16 (1.0) | 669 (4.6) | 665 (99.4) | 4 (0.6) |
| Arthrodesis, posterior, for spinal deformity, 7–12 vertebral segments | 736 (2.2) | 244 (33.2) | 492 (66.9) | 313 (2.2) | 108 (34.5) | 205 (65.5) |
| Tympanoplasty without mastoidectomy or ossicular chain reconstruction | 677 (2) | 667 (98.5) | 10 (1.5) | 303 (2.1) | 297 (98.0) | 6 (2.0) |
| Laparoscopic cholecystectomy | 675 (2) | 662 (98.1) | 13 (1.9) | 282 (2.0) | 281 (99.7) | 1 (0.4) |
| Palatoplasty for cleft palate, soft and/or hard palate only | 618 (1.8) | 606 (98.1) | 12 (1.9) | 264 (1.8) | 258 (97.7) | 6 (2.3) |
| Pyloromyotomy, cutting of pyloric muscle | 611 (1.8) | 601 (98.4) | 10 (1.6) | 262 (1.8) | 259 (98.9) | 3 (1.2) |
| Ureteroneocystostomy; anastomosis of single ureter to bladder | 589 (1.8) | 585 (99.3) | 4 (0.7) | 262 (1.8) | 261 (99.6) | 1 (0.4) |
| One-stage distal hypospadias repair with urethroplasty by local skin flaps | 583 (1.7) | 560 (96.1) | 23 (3.9) | 236 (1.6) | 232 (98.3) | 4 (1.7) |
| Arthrodesis, posterior, for spinal deformity, 13 or more vertebral segments | 524 (1.6) | 129 (24.6) | 395 (75.4) | 220 (1.5) | 52 (23.6) | 168 (76.4) |
Data are shown as frequencies and percentages. This list contains the 10 most common procedures according to CPT codes, but all 60 procedures with a frequency of greater than 200 cases in the total study cohort were included as indicator variables in the statistical models.
Patients in the training and validation samples had similar characteristics, with only a few exceptions. Children in the validation sample were slightly more likely to be of Hispanic ethnicity (12.8 vs. 12.0%, p=0.02) and to have had SIRS, sepsis, or septic shock within 48 hours before surgery (5.5 vs. 4.9%, p=0.007), and they were slightly less likely to have an open wound at the time of surgery (0.9 vs. 1.1%, p=0.02). The proportions of patients who had each procedure were similar in the two samples when considering procedures performed in at least 200 cases in the overall cohort. The proportion of patients who experienced surgical morbidity was also similar in the two samples (Table 3).
Table 3.
Thirty day surgical morbidity
| Training Sample (N=33662) | Validation Sample (N=14427) | |
|---|---|---|
|
| ||
| Outcome | N (%) | N (%) |
| Any surgical morbidity | 3013(9.0) | 1218 (8.4) |
| Central nervous system | ||
| Coma (>24 hours) | 3(0.0) | 2 (0.0) |
| Cardiac arrest requiring CPR | 39(0.1) | 14 (0.1) |
| Cerebral Vascular Accident/Stroke or intracranial hemorrhage | 20(0.1) | 5 (0.0) |
| Seizure | 45(0.1) | 29 (0.2) |
| Nerve injury | 23(0.1) | 10 (0.1) |
| Pulmonary | ||
| Pneumonia | 130(0.4) | 49 (0.3) |
| Unplanned intubations | 142(0.4) | 54 (0.4) |
| Pulmonary embolism | 3(0.0) | 0 (0.0) |
| Renal | ||
| Renal insufficiency | 15(0.0) | 5 (0.0) |
| Renal failure | 9(0.0) | 4 (0.0) |
| Urinary tract infection | 189(0.6) | 78 (0.5) |
| Infection/other | ||
| Sepsis | 169(0.5) | 49 (0.3) |
| Superficial incisional surgical site infection (SSI) | 353(1.0) | 123 (0.9) |
| Deep incisional SSI | 85(0.3) | 38 (0.3) |
| Organ/space SSI | 233(0.7) | 118 (0.8) |
| Central line associated blood infections (CLABSI) | 40(0.1) | 7 (0.0) |
| Wound disruption | 177(0.5) | 71 (0.5) |
| Bleeding or transfusion | 1850(5.5) | 748 (5.2) |
| Graft/prosthesis/flap failure | 14(0.0) | 7 (0.0) |
| Venous thrombosis | 37(0.1) | 14 (0.1) |
Comparison of accuracy of classification of the models
The classification accuracy, sensitivity, specificity, PPV, and NPV of the different models fit to the training sample and evaluated in the validation sample are shown in Table 4. Accuracy was highest in the flexible logistic regression model. This model incorporated restricted cubic regression splines for the two continuous pre-operative variables and also included eight statistically significant interactions between preoperative variables. The included interactions were those between surgical specialty and age at surgery, inpatient status, blood transfusion within 48 hours before surgery, and wound classification, as well as those between baseline patient characteristics and particular procedures; namely, between spinal fusion of 7–12 vertebral segments and the presence of a structural central nervous system abnormality, palatoplasty for cleft palate and inpatient status, laminectomy with the release of a tethered spinal cord and inpatient status, and adjacent tissue transfer of 10 cm2 or less and steroid use in the 30 days preceding surgery (p<.01 for all). Importantly, the accuracies of the ensemble tree-based algorithms, random forests and boosted classification trees were not statistically significantly different from that of the flexible logistic regression model, and all models had accuracies within 0.5% of each other. Sensitivity was poor but varied substantially across the models, with the flexible logistic regression model performing best. Specificity was excellent and varied by less than 1% across all models. PPV was lower in the simple logistic regression model compared to all other models. NPV differed by less than 1% among all models but was highest in the flexible logistic regression model. The flexible logistic regression model performed at least as well as or better than the other models on all classification accuracy criteria except specificity, for which the support vector machine and random forest were slightly superior.
Table 4.
Comparison of model accuracy, sensitivity, specificity, and positive and negative predictive values
| Model | Accuracy (%) | Sensitivity (%) | Specificity (%) | PPV (%) | NPV (%) |
|---|---|---|---|---|---|
| Simple logistic regression model | 93.2 | 37.5 | 98.4 | 68.0 | 94.5 |
| Flexible logistic regression model | 93.7a | 41.5a | 98.5a | 72.0a | 94.8a |
| Support vector machinec | 93.3b | 32.9ab | 98.8ab | 72.4a | 94.1ab |
| Random forestd | 93.6a | 39.0ab | 98.7ab | 73.2a | 94.6b |
| Boosted treese | 93.6a | 39.8ab | 98.5a | 71.5a | 94.7ab |
P<.05 vs. simple logistic regression model
P<.05 vs. flexible logistic regression model
Cost=1, γ=0.1
Number of trees=500, number of variables considered at each split=16
Number of trees=7762, shrinkage parameter=0.001, interaction depth=4
Comparison of predictive ability of the models
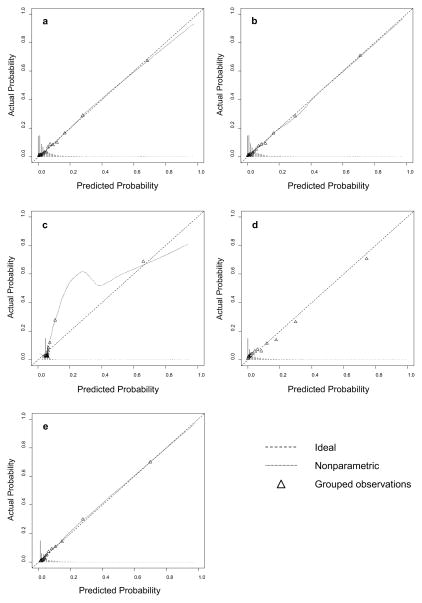
All models showed good discrimination, with areas under the receiver operating characteristic curve (c-statistics) ranging from 0.818 for the support vector machine to 0.880 for the boosted classification trees. The flexible logistic regression model and boosted classification trees had statistically equivalent c-statistics. The calibration of each model is described in Table 6 and Figure 1. The support vector machine demonstrated the worst calibration, and the logistic regression models demonstrated the best calibration of all models. Boosted classification trees also showed good calibration but tended to slightly underestimate the probability of surgical morbidity.
Table 6.
Model calibration
| Model | Calibration intercept | Calibration slope |
|---|---|---|
| Simple logistic regression model | −0.051 | 0.988 |
| Flexible logistic regression model | −0.050 | 0.960 |
| Support vector machine | −0.090a | 1.050 |
| Random forest | 0.033 | 0.765a |
| Boosted trees | −0.046 | 1.068a |
p<.05 vs. ideal value of 0 for the calibration intercept and 1 for the calibration slope
Figure 1.
Calibration plots of all prediction models: a) simple logistic regression model b) flexible logistic regression model c) support vector machine d) random forest e) boosted classification trees
Important predictors of surgical morbidity
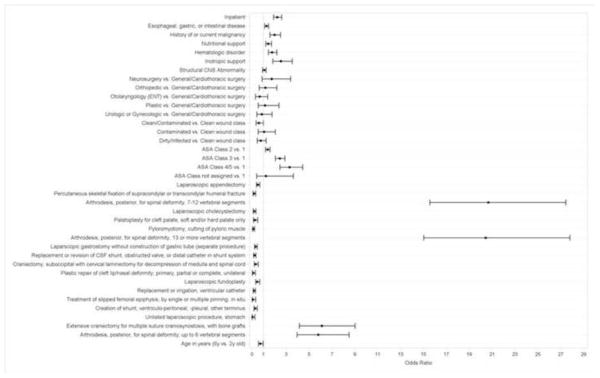
Figure 2 shows marginal odds ratios from the flexible logistic regression model for several important predictors. The marginal effects of predictors that were considered to be both clinically important and either statistically significant at p<.001 or involved in interactions statistically significant at p<.001 are shown. The predictors with the highest estimated odds ratios were two particular procedures, namely spinal fusions and craniectomy. As expected, many individual procedures were found to be significant independent predictors of surgical morbidity. Other factors strongly associated with an increased risk of surgical morbidity in the overall study cohort included higher ASA class, which is a measure of a patient’s preoperative physical state, and having a procedure as an inpatient, which is the setting in which higher risk procedures are typically performed. In addition, particular gastrointestinal, nutritional, or oncologic comorbidities were associated with an increased risk of surgical morbidity. These comorbidities included esophageal, gastric, or intestinal disease, history of or current malignancy, hematologic disorders, and structural central nervous system abnormalities, all of which, in addition to being potential indications for high risk procedures, are often present in high risk complex patients who are at increased risk for postoperative bleeding and infections. Patients who required preoperative nutritional or inotropic support, which are often required to keep complex and critically ill patients stable, were also at greater risk for surgical morbidity. Being younger was also associated with an increased risk of surgical morbidity, as these patients are more likely to undergo high risk procedures for serious congenital anomalies or conditions related to prematurity than older patients; however, the effect of age was mainly evident when comparing children older vs. younger than 2 years of age.
Figure 2.
Relationships between key predictors and the odds of surgical morbidity in the flexible logistic regression model. Marginal odds ratios and 95% Wald confidence intervals are shown for all predictors that either had main effects significant at p<.001 or were included in interactions significant at p<.001. ASA=American Society of Anesthesiologists, CSF=cerebrospinal fluid.
DISCUSSION
This study compared five different statistical algorithms for the prediction of surgical morbidity in pediatric patients. The primary finding was that a flexible logistic regression model that incorporated restricted cubic regression splines and statistically significant and clinically meaningful interactions had the highest out-of-sample accuracy and sensitivity of all algorithms examined. This model also had excellent discrimination and calibration. Given the large number of patients and hospitals included in both the training and validation samples, as well as the highly standardized and validated method of data collection used in NSQIP-Peds, the model derived in this study is likely to be applicable to the general population of pediatric surgery patients. However, as with any statistical model, this model may not extrapolate well to populations not included in its derivation. For example, patients having cardiac, ophthalmologic, obstetric, or transplantation procedures, and patients with traumatic injuries are excluded from the NSQIP-Peds program, and thus the derived models in this study would not apply to these patients.[26]
Given the large number and variety of data mining algorithms that have been developed for classification and prediction in the fields of statistics and computer science [2], it may seem somewhat surprising that logistic regression, which has been used for clinical prediction modeling for decades, would perform as well or better than the more recently developed data mining techniques. In fact, the flexible logistic regression model performed better than or equivalently to the data mining algorithms on all model fit criteria except specificity, though the differences in some criteria were very small. There are several reasons for these findings. Firstly, no statistical or data mining algorithm will perform best in all settings. Secondly, the performance of various algorithms depends not only on the population and outcome under examination, but also on the availability and dimensionality of predictors [46] as well as the criteria chosen to evaluate each method’s performance.[47] Numerous studies have compared logistic regression models to data mining algorithms for the prediction of surgical outcomes, and their findings have been heterogeneous. Several studies have compared logistic regression models to artificial neural networks (ANN), which are nonlinear statistical models that extract linear combinations of the input variables as derived features then model the outcome as a nonlinear function of these features.[11, 13, 14, 16, 48] Most of these studies reported that ANNs had superior performance for predicting surgical outcomes, such as mortality after surgery for heart disease, traumatic brain injury, or ascending aortic dissection.[13, 14, 48] A recent study that examined the performance of logistic regression, classification tree, random forest, and SVM models for predicting sentinel lymph node status in patients with cutaneous melanoma found that all four algorithms had similar predictive accuracy.[18] Another study that compared the accuracy and discrimination of nine different statistical and data mining algorithms, including logistic regression, to that of the TNM staging system for predicting survival in colorectal cancer patients, found that all nine algorithms had similar and slightly better performance than the TNM staging system, but that differences among all algorithms were small.[20] More often than not, studies comparing “new” computational algorithms to older techniques claim that the new method performs better than the older method.[49] Many of these claims have come from small studies of fewer than 1,000 patients, a sample size far too small to both develop and validate a model in which dozens of predictor variables are evaluated.[48] Thus, random variation certainly explains some of the heterogeneity in findings across studies. In addition, many comparative studies provide insufficient detail on the method used for choosing parameters to train the algorithm, and many compare models’ performance using only classification accuracy or the area under the receiver operator characteristic curve. There are in fact a number of other characteristics that should be considered when comparing methods, such as the method’s handling of missing data, noise, and highly correlated predictors, variable selection, computational cost, and the generalizability and interpretability of the model. For example, in the present study, the amount of missing data was small and missing values occurred in categorical variables only; thus, a category for patients with unknown values of these variables was simply created and could be easily accommodated by all algorithms. However, in general, logistic regression and SVM models cannot accommodate missing values unless imputation is first performed, whereas the tree-based methods can accommodate missingness through the process of surrogate splitting. [4] The present analysis did not contend with highly correlated predictors or perform variable selection, but regarding computational cost, the data mining methods were more computationally costly to fit than the logistic regression models. This cost would limit the utility of the data mining algorithms in a clinical setting.
Importantly, in predictive modeling, there is always a tradeoff between achieving high accuracy, which is accomplished by constructing a model that is as flexible as necessary without overfitting, and interpretability, which is achieved by constructing a model with parameters that describe the relationships between predictors and the outcome in an understandable way.[4] In the present study, we focused on achieving optimal prediction of the outcome of 30-day surgical morbidity rather than on describing the nature of the relationships between patient and procedure characteristics and surgical morbidity. While the latter task is clearly important in surgical outcomes research, accurate prediction is also critical. By incorporating many characteristics into a global risk prediction score, some of the subjectivity that results from physician overreliance on one or a few patient characteristics can be eliminated. In addition, risk prediction that takes into account all available, relevant preoperative information can assist both surgeons and patients in deciding between different types of procedures and in determining what precautionary measures might be important to take for a patient at high risk of a poor outcome. On the other hand, when interpretability is a primary goal, a single classification tree or a logistic regression model with only linear terms might be the best option, provided that its predictive accuracy and discrimination are sufficiently high. It should be pointed out, however, that although a simple logistic regression model or classification tree may be most easily interpretable, the importance of individual predictors can be evaluated in SVM, random forest, and boosted classification tree models as well. These measures can be derived via recursive feature elimination for SVM [46] and via the sum of the improvements in the split-criterion over all trees for random forests and boosted classification trees [42] The former technique is also useful for feature selection in SVM; however, we chose not to perform feature selection for any models in the present study because of the large sample size available for analyses and also because all preoperative variables were chosen for inclusion in the NSQIP-Peds database by surgeon experts due to their clinical importance.
This study had several limitations. First, we evaluated only a small sample of existing data mining algorithms, focusing on algorithms that have been infrequently used in the clinical research literature and that could easily be implemented in freely available software. Many other predictive algorithms that have been more frequently explored by clinical researchers or that involve more parameters and thus greater complexity than the algorithms chosen for this study are available, such as individual classification trees, bagging of classification trees, artificial neural networks, Bayesian networks, and the recently developed “superlearner” ensemble machine learning algorithm.[4, 50] It is possible that one of these algorithms would have performed better than the flexible logistic regression model derived in the present study. Second, we cannot guarantee that globally optimal parameter values were found for all of the data mining algorithms explored. For example, in the boosting model, we explored only trees of depth 4 since previous studies indicate that interaction depths between 3 and 7 typically yield similar results. For all parameters used to train the other data mining algorithms, we used a grid search method, but we did not perform an exhaustive search of all values within the grids. Third, because only one year of NSQIP-Peds data was available for this study, many surgical procedures were performed in few cases; this prevented us from including every procedure as an indicator variable in the models. Once a larger, multi-year dataset is available, it will be possible to more effectively model the heterogeneity in the risk of surgical morbidity across all types of surgical procedures. However, despite the limited size of the NSQIP-Peds dataset for the number of procedures included, one of its strengths is the variety of standardized and validated preoperative, operative, and postoperative variables it contains. This allowed for higher accuracy and refinement of the statistical models examined compared to those that would be possible using administrative data. Despite the high accuracy of all models explored in this study, all models also unfortunately showed poor sensitivity. This is not an uncommon problem when outcome data are highly imbalanced, and in such cases overall classification accuracy may not be the ideal metric by which to evaluate algorithm performance.[47, 51] Finally, in contrast to the ACS NSQIP surgical risk calculator developed to predict surgical morbidity in adult surgery patients [21], the flexible logistic regression model derived in the present study could not account for the clustering of patients within hospitals due to the absence of a site indicator in the available dataset. However, our model included flexible effects, namely splines and interaction effects, which were not reported to have been evaluated in deriving the adult NSQIP surgical risk calculator. In addition, the area under the curve of our model was slightly larger than that reported for the adult NSQIP surgical risk calculator (0.877 vs. 0.816) [21], indicating that model discrimination was likely not substantively worsened by the nonuse of hierarchical logistic regression modeling in this study.
In conclusion, support vector machine, random forest, and boosted classification tree models do not provide superior prediction of 30-day surgical morbidity in pediatric patients compared to logistic regression. A flexible logistic regression model that includes regression splines for continuous variables and statistically significant and clinically meaningful interactions offers improved accuracy, sensitivity, specificity, negative and positive predictive value, and discrimination for predicting surgical morbidity in children compared to a simpler logistic regression model that assumes linearity and additivity. After further validation, the flexible logistic regression model derived in this study could be used to assist with clinical decision-making based on patient-specific surgical risks in pediatric patients.
Table 5.
Model discrimination
| Model | AUROC | P value for comparison with simple logistic regression model | P value for comparison with flexible logistic regression model |
|---|---|---|---|
| Simple logistic regression model | 0.871 | ------------ | ------------ |
| Flexible logistic regression model | 0.877 | 0.002 | ------------ |
| Support vector machine | 0.818 | <0.0001 | <0.0001 |
| Random forest | 0.864 | 0.04 | 0.0004 |
| Boosted trees | 0.880 | 0.0005 | 0.30 |
Highlights.
We aimed to predict pediatric surgical morbidity using preoperative characteristics
We compared logistic regression models to data mining algorithms
The data mining algorithms performed as well as a simple logistic regression model
A flexible logistic regression model performed best on most model fit criteria
Acknowledgments
This study was supported by intramural funding from the Research Institute at Nationwide Children’s Hospital. However, the study design, analysis and interpretation of data, writing of the manuscript, and decision to publish the manuscript belonged entirely to the authors.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Lai Wei, Email: lai.wei@osumc.edu.
Soledad A. Fernandez, Email: soledad.fernandez@osumc.edu.
Peter C. Minneci, Email: peter.minneci@nationwidechildrens.org.
Katherine J. Deans, Email: katherine.deans@nationwidechildrens.org.
References
- 1.Giudici P. Applied data mining : statistical methods for business and industry. New York: J. Wiley; 2003. [Google Scholar]
- 2.Bellazzi R, Zupan B. Predictive data mining in clinical medicine: current issues and guidelines. Int J Med Inform. 2008;77:81–97. doi: 10.1016/j.ijmedinf.2006.11.006. [DOI] [PubMed] [Google Scholar]
- 3.Hosmer DW, Lemeshow S. Applied logistic regression. 2. New York: Wiley; 2000. [Google Scholar]
- 4.Hastie T, Tibshirani R, Friedman JH. The elements of statistical learning : data mining, inference, and prediction. 2. New York, NY: Springer; 2009. [Google Scholar]
- 5.Szaleniec J, Wiatr M, Szaleniec M, Skladzien J, Tomik J, Oles K, et al. Artificial neural network modelling of the results of tympanoplasty in chronic suppurative otitis media patients. Comput Biol Med. 2013;43:16–22. doi: 10.1016/j.compbiomed.2012.10.003. [DOI] [PubMed] [Google Scholar]
- 6.Schwartz MH, Rozumalski A, Truong W, Novacheck TF. Predicting the outcome of intramuscular psoas lengthening in children with cerebral palsy using preoperative gait data and the random forest algorithm. Gait Posture. 2013;37:473–9. doi: 10.1016/j.gaitpost.2012.08.016. [DOI] [PubMed] [Google Scholar]
- 7.Bouarfa L, Schneider A, Feussner H, Navab N, Lemke HU, Jonker PP, et al. Prediction of intraoperative complexity from preoperative patient data for laparoscopic cholecystectomy. Artificial Intelligence in Medicine. 2011;52:169–76. doi: 10.1016/j.artmed.2011.04.012. [DOI] [PubMed] [Google Scholar]
- 8.Kim SY, Moon SK, Jung DC, Hwang SI, Sung CK, Cho JY, et al. Pre-Operative Prediction of Advanced Prostatic Cancer Using Clinical Decision Support Systems: Accuracy Comparison between Support Vector Machine and Artificial Neural Network. Korean Journal of Radiology. 2011;12:588–94. doi: 10.3348/kjr.2011.12.5.588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Armananzas R, Alonso-Nanclares L, Defelipe-Oroquieta J, Kastanauskaite A, de Sola RG, Defelipe J, et al. Machine learning approach for the outcome prediction of temporal lobe epilepsy surgery. PLoS One. 2013;8:e62819. doi: 10.1371/journal.pone.0062819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Spelt L, Nilsson J, Andersson R, Andersson B. Artificial neural networks--a method for prediction of survival following liver resection for colorectal cancer metastases. Eur J Surg Oncol. 2013;39:648–54. doi: 10.1016/j.ejso.2013.02.024. [DOI] [PubMed] [Google Scholar]
- 11.DiRusso SM, Chahine AA, Sullivan T, Risucci D, Nealon P, Cuff S, et al. Development of a model for prediction of survival in pediatric trauma patients: comparison of artificial neural networks and logistic regression. J Pediatr Surg. 2002;37:1098–104. doi: 10.1053/jpsu.2002.33885. discussion -104. [DOI] [PubMed] [Google Scholar]
- 12.Gurm HS, Seth M, Kooiman J, Share D. A novel tool for reliable and accurate prediction of renal complications in patients undergoing percutaneous coronary intervention. J Am Coll Cardiol. 2013;61:2242–8. doi: 10.1016/j.jacc.2013.03.026. [DOI] [PubMed] [Google Scholar]
- 13.Nilsson J, Ohlsson M, Thulin L, Hoglund P, Nashef SAM, Brandt J. Risk factor identification and mortality prediction in cardiac surgery using artificial neural networks. Journal of Thoracic and Cardiovascular Surgery. 2006;132:12–U31. doi: 10.1016/j.jtcvs.2005.12.055. [DOI] [PubMed] [Google Scholar]
- 14.Shi HY, Hwang SL, Lee KT, Lin CL. In-hospital mortality after traumatic brain injury surgery: a nationwide population-based comparison of mortality predictors used in artificial neural network and logistic regression models. J Neurosurg. 2013;118:746–52. doi: 10.3171/2013.1.JNS121130. [DOI] [PubMed] [Google Scholar]
- 15.Halabi WJ, Nguyen VQ, Carmichael JC, Pigazzi A, Stamos MJ, Mills S. Clostridium difficile colitis in the United States: a decade of trends, outcomes, risk factors for colectomy, and mortality after colectomy. J Am Coll Surg. 2013;217:802–12. doi: 10.1016/j.jamcollsurg.2013.05.028. [DOI] [PubMed] [Google Scholar]
- 16.Shi HY, Lee KT, Wang JJ, Sun DP, Lee HH, Chiu CC. Artificial neural network model for predicting 5-year mortality after surgery for hepatocellular carcinoma: a nationwide study. J Gastrointest Surg. 2012;16:2126–31. doi: 10.1007/s11605-012-1986-3. [DOI] [PubMed] [Google Scholar]
- 17.Chia CC, Rubinfeld I, Scirica BM, McMillan S, Gurm HS, Syed Z. Looking beyond historical patient outcomes to improve clinical models. Sci Transl Med. 2012;4:131ra49. doi: 10.1126/scitranslmed.3003561. [DOI] [PubMed] [Google Scholar]
- 18.Mocellin S, Thompson JF, Pasquali S, Montesco MC, Pilati P, Nitti D, et al. Sentinel node status prediction by four statistical models: results from a large bi-institutional series (n = 1132) Ann Surg. 2009;250:964–9. doi: 10.1097/sla.0b013e3181b07ffd. [DOI] [PubMed] [Google Scholar]
- 19.Chong CF, Li YC, Wang TL, Chang H. Stratification of adverse outcomes by preoperative risk factors in coronary artery bypass graft patients: an artificial neural network prediction model. AMIA Annu Symp Proc; 2003; pp. 160–4. [PMC free article] [PubMed] [Google Scholar]
- 20.Gao P, Zhou X, Wang ZN, Song YX, Tong LL, Xu YY, et al. Which is a more accurate predictor in colorectal survival analysis? Nine data mining algorithms vs. the TNM staging system. PLoS One. 2012;7:e42015. doi: 10.1371/journal.pone.0042015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bilimoria KY, Liu Y, Paruch JL, Zhou L, Kmiecik TE, Ko CY, et al. Development and Evaluation of the Universal ACS NSQIP Surgical Risk Calculator: A Decision Aid and Informed Consent Tool for Patients and Surgeons. J Am Coll Surg. 2013;217:833–42e3. doi: 10.1016/j.jamcollsurg.2013.07.385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gupta H, Gupta PK, Fang X, Miller WJ, Cemaj S, Forse RA, et al. Development and validation of a risk calculator predicting postoperative respiratory failure. Chest. 2011;140:1207–15. doi: 10.1378/chest.11-0466. [DOI] [PubMed] [Google Scholar]
- 23.Gupta PK, Franck C, Miller WJ, Gupta H, Forse RA. Development and validation of a bariatric surgery morbidity risk calculator using the prospective, multicenter NSQIP dataset. J Am Coll Surg. 2011;212:301–9. doi: 10.1016/j.jamcollsurg.2010.11.003. [DOI] [PubMed] [Google Scholar]
- 24.Gupta PK, Ramanan B, Lynch TG, Sundaram A, MacTaggart JN, Gupta H, et al. Development and validation of a risk calculator for prediction of mortality after infrainguinal bypass surgery. J Vasc Surg. 2012;56:372–9. doi: 10.1016/j.jvs.2012.01.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Cohen ME, Bilimoria KY, Ko CY, Hall BL. Development of an American College of Surgeons National Surgery Quality Improvement Program: morbidity and mortality risk calculator for colorectal surgery. J Am Coll Surg. 2009;208:1009–16. doi: 10.1016/j.jamcollsurg.2009.01.043. [DOI] [PubMed] [Google Scholar]
- 26.Dillon P, Hammermeister K, Morrato E, Kempe A, Oldham K, Moss L, et al. Developing a NSQIP module to measure outcomes in children’s surgical care: opportunity and challenge. Semin Pediatr Surg. 2008;17:131–40. doi: 10.1053/j.sempedsurg.2008.02.009. [DOI] [PubMed] [Google Scholar]
- 27.Raval MV, Dillon PW, Bruny JL, Ko CY, Hall BL, Moss RL, et al. Pediatric American College of Surgeons National Surgical Quality Improvement Program: feasibility of a novel, prospective assessment of surgical outcomes. J Pediatr Surg. 2011;46:115–21. doi: 10.1016/j.jpedsurg.2010.09.073. [DOI] [PubMed] [Google Scholar]
- 28.Raval MV, Dillon PW, Bruny JL, Ko CY, Hall BL, Moss RL, et al. American College of Surgeons National Surgical Quality Improvement Program Pediatric: a phase 1 report. J Am Coll Surg. 2011;212:1–11. doi: 10.1016/j.jamcollsurg.2010.08.013. [DOI] [PubMed] [Google Scholar]
- 29.Bruny JL, Hall BL, Barnhart DC, Billmire DF, Dias MS, Dillon PW, et al. American College of Surgeons National Surgical Quality Improvement Program Pediatric: a beta phase report. J Pediatr Surg. 2013;48:74–80. doi: 10.1016/j.jpedsurg.2012.10.019. [DOI] [PubMed] [Google Scholar]
- 30.James G, Witten D, Hastie T, Tibshirani R. An introduction to statistical learning : with applications in R [Google Scholar]
- 31.Leisenring W, Alonzo T, Pepe MS. Comparisons of predictive values of binary medical diagnostic tests for paired designs. Biometrics. 2000;56:345–51. doi: 10.1111/j.0006-341x.2000.00345.x. [DOI] [PubMed] [Google Scholar]
- 32.DeLong ER, DeLong DM, Clarke-Pearson DL. Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics. 1988;44:837–45. [PubMed] [Google Scholar]
- 33.Steyerberg EW. Clinical prediction models : a practical approach to development, validation, and updating. New York, NY: Springer; 2009. [Google Scholar]
- 34.Meyer D. Support Vector Machines: The Interface to libsvm in package e1071. R News. 2001;1:23–6. [Google Scholar]
- 35.Liaw A, Wiener M. Classification and Regression by randomForest. R News. 2002;2:18–22. [Google Scholar]
- 36.Ridgeway G. gbm: Generalized Boosted Regression Models. R package version 2.1. 2013
- 37.Robin X, Turck N, Hainard A, Tiberti N, Lisacek F, Sanchez JC, et al. pROC: an open-source package for R and S+ to analyze and compare ROC curves. BMC Bioinformatics. 2011;12:77. doi: 10.1186/1471-2105-12-77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Harrell F. rms: Regression Modeling Strategies. R package version 4.1-0. 2013 [Google Scholar]
- 39.Vapnik VN. Statistical learning theory. New York: Wiley; 1998. [Google Scholar]
- 40.Noble WS. What is a support vector machine? Nat Biotechnol. 2006;24:1565–7. doi: 10.1038/nbt1206-1565. [DOI] [PubMed] [Google Scholar]
- 41.Lin HT, Lin CJ, Weng RC. A note on Platt’s probabilistic outputs for support vector machines. Machine Learning. 2007;68:267–76. [Google Scholar]
- 42.Breiman L. Classification and regression trees. Belmont, Calif: Wadsworth International Group; 1984. [Google Scholar]
- 43.Breiman L. Random forests. Machine Learning. 2001;45:5–32. [Google Scholar]
- 44.Austin PC, Lee DS, Steyerberg EW, Tu JV. Regression trees for predicting mortality in patients with cardiovascular disease: what improvement is achieved by using ensemble-based methods? Biom J. 2012;54:657–73. doi: 10.1002/bimj.201100251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Friedman JH. Greedy function approximation: A gradient boosting machine. Annals of Statistics. 2001;29:1189–232. [Google Scholar]
- 46.Guyon I, Weston J, Barnhill S, Vapnik V. Gene selection for cancer classification using support vector machines. Machine Learning. 2002;46:389–422. [Google Scholar]
- 47.Roumani YF, May JH, Strum DP, Vargas LG. Classifying highly imbalanced ICU data. Health Care Manag Sci. 2013;16:119–28. doi: 10.1007/s10729-012-9216-9. [DOI] [PubMed] [Google Scholar]
- 48.Sullivan LM, Massaro JM, D’Agostmo RB. Presentation of multivariate data for clinical use: The Framingham Study risk score functions. Stat Med. 2004;23:1631–60. doi: 10.1002/sim.1742. [DOI] [PubMed] [Google Scholar]
- 49.Boulesteix AL, Lauer S, Eugster MJ. A plea for neutral comparison studies in computational sciences. PLoS One. 2013;8:e61562. doi: 10.1371/journal.pone.0061562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.van der Laan MJ, Rose S. Targeted Learning: Causal Inference for Observational and Experimental Data. New York: Springer; 2011. [Google Scholar]
- 51.Maimon OZ, Rokach L. Data mining and knowledge discovery handbook. New York: Springer; 2005. [Google Scholar]