Abstract
A proper internal validation is necessary for the development of a reliable and reproducible prognostic model for external validation. Variable selection is an important step for building prognostic models. However, not many existing approaches couple the ability to specify the number of covariates in the model with a cross-validation algorithm. We describe a user-friendly SAS macro that implements a score selection method and a leave-one-out cross validation approach. We discuss the method and applications behind this algorithm, as well as details of the SAS macro.
Keywords: clinical trials, cross validation, prognostic markers, SAS macro, score selection, survival analysis
1. Introduction
Survival data is commonly found in clinical trials. Survival analysis involves any of time to event, recurrence, death information, along with a censoring indicator. Censoring indicator is needed to specify if the patient has been lost to follow up, or has yet to experience the event of interest. It has quickly become a staple of many areas of clinical research, especially in biomarker analysis, in the era of personalized medicine. Identifying variables associated with better or worse survival prognosis is useful in guiding exploration of the underlying mechanisms in natural disease progression as well as treatment options in clinical trials. However, the variability between labs, and often within the same lab, has made apparent the need for validation of such models. These validation methods typically focus on external validation using independent datasets and derived statistics or internal validation using resampling methods [1].
Each method has its own disadvantages, including sample size constraints, external validation resources, feasibility of usage given data dimensions, and censoring. Suggested or otherwise published methods generally refer to studies with a relatively large sample size and a comparatively small amount of variables of interest (less than 10). Some studies suggest validation approaches such as the split sample method and 2-fold cross-validation (CV) that have been shown to perform very poorly in model selection for smaller samples [4]. Regular incorporation of plasma samples and tools such as multiplex arrays in biomedical research often results in data that is not quite high-dimensional, but does not have the structure of the aforementioned studies, rendering the methods restricted or difficult to implement. These methods along with the 5-fold and 10-fold CV approaches also have the disadvantage of requiring a reduction of the dataset into subsets that may not be conducive to variable selection for a relatively high number of variables without using high-dimensional techniques or penalized methods. Other suggested solutions to the validation question include the use of statistics that may require special consideration of censored observations [2–4]. The Leave One Out Cross-Validation (LOOCV) approach has the advantages of producing model estimates with less bias and more ease in smaller samples [5].
Over the course of our collaboration with medical oncologists and laboratory biomarker scientists across phase II clinical trials exploring 35+ biomarkers, we have developed and implemented a SAS software macro. This macro allows us to identify an internally-validated prognostic signature that can possibly distinguish high and low-risk patients. The method has proven effective in identifying user-specified size of multivariable signatures that are capable of highlighting low risk groups with median survival time that is twice as long as high risk group in both smaller [6] and larger [7] samples. To our knowledge there is no such functionality readily available in SAS software to build these parsimonious models.
We present this macro in the following paper. Sections 2.1–2.4 provide a brief review of statistical concepts related to the macro. Section 2.5 describes the macro and in Section 3 we detail an example of its use. And finally we present a discussion in Section 4.
The SAS Survival LOOCV Macro is available to download from our website http://web.hku.hk/~herbpang/SASsurvLOOCV.html
2. Methods
2.1 Survival Analysis
When looking to model the relationship between a variable xj or set of p variables (x1j, x2j, …, xpj), and the time t between some predetermined start point and the outcome, or event. We employ survival methods that analyze the time t but account for those in the sample who did not have an event before the study ended or who dropped out before one could be recorded. Using SAS software, there are several procedures dedicated to doing these types of analyses with varying functions dependent on what exactly is to be modeled by your data.
It is often of interest to identify a set of variables that can serve as predictors for lower survival times, or increased hazard. These prognostic variables are identified in survival analysis using one of a couple of regression methods. These methods differ from linear regression in that there is no normality assumption, and the variable being modeled is the time to an event as opposed to an average value or response. The Cox Proportional Hazard (Cox PH) (2.1.1) method is most commonly used because it uses a semi-parametric model which makes no strong assumption about the distribution of the survival times [8]. Other methods may require an assumption of some other non-normal but parametric distribution, such as Weibull or Exponential t. In order to perform this regression, the PHREG procedure in SAS software is utilized.
| (2.1.1) |
In this model, hj(t) is the hazard for an individual j with predictor values of x1j, x2j, …, xpj, where the predictors can be continuous or binary, and the βs are the corresponding coefficients determined in regression. h0(t) is the baseline hazard. The macro we describe identifies a subset of predictor variables that potentially explain survival times using this model, while addressing some of the disadvantages of a single-fit approach.
Some of the risks of fitting a model with a large number of covariates are overfitting to the dataset, co-linearity between variables, and usefulness of the model in real application [10]. When a variable selection is performed, it is often at the mercy of the particular data set in use and the conditions under which it is run. By controlling the number of variables selected for the model and employing internal validation, we keep the model manageable and are able to provide a signature that could be clinically useful while decreasing the potential for overfitting. We will take the following steps to identify a set of variables that are key to predicting the survival time.
Create Leave One Out (LOO) training datasets
Variable Selection on training sets
Cross Validation
Survival Prediction
2.2 Creating the Training Sets for Leave One Out Method of Cross-Validation
To create the leave-one-out training sets, we will employ the SAS software Surveyselect procedure to create n independent replicates of the original data set where n is the number of patients for whom you have survival information. Each set (replicate) is identified by a value i where i = 1, …, n. Individual observations are systematically removed from each of the sets, creating a training set itr and testing set ite We accomplished this by creating a second id for each patient based on observation number in the original dataset, then deleting if the second id equals i. These steps simply create the indicator variable for whether the data for a certain individual will be used in that particular training set or as the testing set. For more information about LOOCV see section 2.4 and how it compares to other resampling methods, refer to Molinaro et al [5].
2.3 Variable Selection
We perform the variable selection on training sets 1 through n, using a Cox PH model and the best subset selection method in SAS software’s PHReg procedure [9]. This selection method allows us to control the number of variables we wish to include in the model. In our previous applications, typically 3–5 variables are sufficient for developing a prognostic signature. However, you have the power to control that number should you wish to include more or less variables. The macro is written to select one model for each training set with the highest likelihood score (chi-square) statistic, based on the number of variables requested. This method uses the Furnival-Wilson algorithm (1974) which is limited to continuous or binary numerical variables for model selection; CLASS (categorical) variables are not allowed [9].
2.4 LOOCV
LOOCV consists of splitting the data set randomly into n partitions. At each of the n-th iteration, n − 1 partitions will be used as the training set and the left out sample will be used as the test set. At each of the n iterations, the whole data set is used as the training except one sample which is left out as test set.
2.5 Survival Prediction
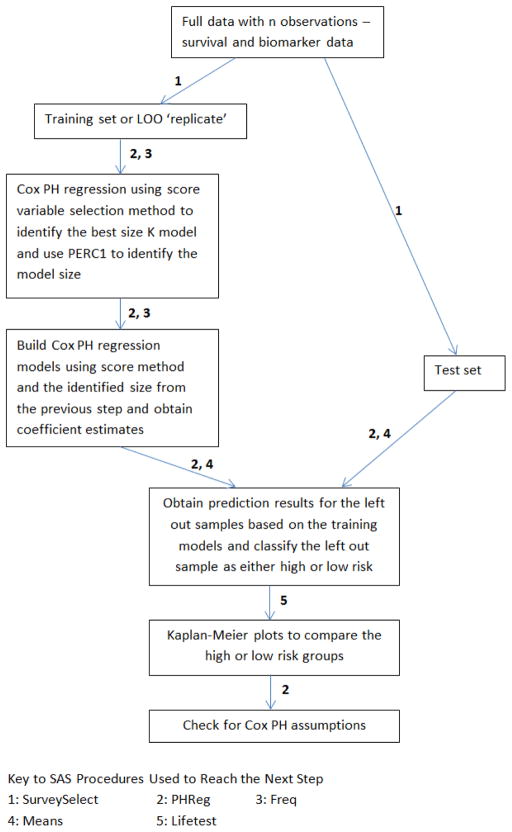
The purpose of this macro is to identify a set of variables, a prognostic signature for survival differences. Similar to Pang [10], we fit a multivariable Cox PH model from the training set itr using the selected variables to perform prediction on the test set ite. We call the linear predictor X′β a risk score, a larger value corresponds to shorter survival. Using the prediction model built from the training set, we can label the subjects in the test set as high risk or low risk coinciding with a linear predictor that is higher or lower than the median, respectively. A Kaplan-Meier plot is generated comparing the high risk and low risk groups [11]. Log-Rank and Wilcoxon tests are performed to test for difference in survival curves between the groups [12,13]. A schematic flowchart can be found in Figure 1.
Figure 1.
Schematic flowchart of our algorithm
2.6 SAS Macro
2.6.1 Required Parameters
The datasets must have one record per patient. The macro explicitly assumes the presence of the separate data sets for the survival information (SURVDS) and the potential predictors (FACTORDS) with the same variable name used to identify observations (PAT) in both. It is also assumed that the datasets are in the same location. Along with the observation id variable (PAT), SURVDS is expected to contain the failure or censoring time (TIMEVR) and the censoring indicator (CENSVR). FACTORDS should contain PAT and only the potential predictor variables the investigator desires to include in modeling. The macro automates the listing of variables such that all variables with the exception of PAT are included in the list of predictors for the model. See table 1 for full listing of macro variables, their uses, and any restrictions.
Table 1.
Parameters required by the SAS macro.
| Parameter | Description |
|---|---|
| ANALYSIS | Location of the data to be analyzed |
| CV | Destination for the permanent datasets created during this process |
| DIR | Destination for the output |
| CENSVR | Name of censoring variable |
| CNS | The value of the censoring variable that indicates censoring |
| PAT | Patient or observation id variable |
| TIMEVR | Survival time variable |
| K | Number of variables to include in the model (score selection). Positive integer |
| PERC1 | First threshold percentage for # of variables included in final model (whole number) |
| PERC2 | Second (and final) threshold percentage for output |
| STUDYNM | Single word name for the study (max 5 letters) – used in naming output and datasets |
| SURVDS | Name of the survival dataset |
| FACTORDS | Name of the dataset containing only PAT (see above) and predictor variables for model selection |
| OSPFS | Overall survival or progression-free survival analysis (values are OS or PFS) – also used in naming output and datasets |
| TIMEPOINT | Typically “base” for baseline readings. Used extensively in naming output and datasets |
2.6.2 Details and output
Once the training sets itr are created the macro performs Cox PH model selection on each itr, specifying the one best model of size K (where K is a positive integer most appropriate for your data, but 3–5 is typically sufficient). The variable subset selected in this step is printed to a permanent dataset, using the ods output function and BestSubsets table, options available in SAS. For the subsequent model selections for each of the remaining n − 1 training sets, the dataset is appended to include the best subset from the most recent run. Once all of the model selections have been completed, the frequency of selection of each variable is calculated. The macro variable PERC1 is utilized to choose only those variables that meet a threshold of selection percentage as set by the user; this step serves to avoid including those variables that were not sufficiently commonly chosen. The value of K, as well as the consistency of the models chosen, impacts the frequency of selection. Thus, the value of PERC1 should be selected with that in mind and with an idea of how stringent you would like the model to be. In our published and ongoing work, a value between 60 and 70 has worked best; this corresponds to a variable being selected in 60% – 70% of the models [6,7]. The list of the variables and their respective percentages will be output to the directory (DIR) identified by the user under the file name “*STUDYNM * TIMEPOINT *OSPFS analytesover*PERC1 date” as an rtf file. The number of variables that meet the threshold set by PERC1 will then be calculated. If it differs from the value previously set by K, that number of variables will be the used as the size of the new models to be generated for each itr in a final round of model selection. It is this round of model selection we refer to in section 2.6.3. As with the previous steps of model building, the frequency of each variable will be obtained, providing a list of the variables and their respective percentages. Those that reach the threshold for PERC2 will be output to the file name “*STUDYNM *TIMEPOINT *OSPFS analytesover*perc2 date” as an rtf file. That is the extent of the use of PERC2, as essentially a housekeeping measure for the frequency of the selection of the variables if the model size differs from K. It should mentioned that if your model is larger than the value you set for K, then your PERC1 may be set too low or your model may be unstable and changing quite often, making the prognostic signature unreliable. If the model is size K, then this particular output should be relatively repetitive. All models from this selection round will be output to the folder DIR under the file name “*STUDYNM training_*TIMEPOINT *OSPFS models”. The asterisks identify variables determined by user input at the top of the macro.
2.6.3 Creating Risk Groups and Testing Prediction
Following each model selection, the macro utilizes the linear predictor X′β to determine high risk and low risk groups. The subset of variables chosen in the final model selection are fitted to the training set itr. The baseline statement in SAS software’s PHReg procedure enables prediction of survival for the subjects previously not included in the modeling [3], i.e. the testing set ite. The model determines X′β using the values for the subset of variables (x1j, x2j, …, xpj) and the βs from the regression. The median X′β is determined for each replicate i. If the X′β for ite is higher than the median then the subject is labeled as high risk, if not then the subject is labeled as low risk. The logic for this is in model 2.1.1. A higher value for the linear predictor corresponds to a higher hazard hj(t) which corresponds to a shorter predicted survival time. Conversely, a lower linear predictor corresponds to a lower hazard and longer predicted survival time. A Kaplan Meier (Product Limit) table and plot, grouped by high or low risk, and a Cox PH model with group as the single predictor variable are generated. These are output to the directory destination given by the user in the DIR variable, as an rtf file under the name “*STUDYNM cvloo_*OSPFS_*TIMEPOINT date”.
3. Example study
To demonstrate the use of the macro, we analyze data described in a previous study [14]. There are 48 patients with survival information measured in months and 38 biological factors associated with tumor angiogenesis. Some of these angiogenic factors can be found in Table 1 of Nixon et al. (2013) [7]. For this example, we will limit our focus to overall survival (OS). We wish to restrict our model to 3 variables. Table 2 provides the values for the macro parameters pertinent to the description of the output.
Table 2.
Selected Macro Parameter Values for the Example Study.
| Parameter | value |
|---|---|
| K | 3 |
| PERC1 | 65 |
| PERC2 | 50 |
| STUDYNM | bevev |
| OSPFS | OS |
| TIMEPOINT | base |
To further demonstrate the ability of our program to handle large number of factors, we analyzed data from ovarian cancer patients of The Cancer Genome Atlas (TCGA) project [15]. There are 578 patients with survival information, 302 of which have survival events, and 98 gene expression measures from Toll-like receptor and TNFR1 signaling pathways [16]. The median survival was 3.7 years with 47.7% of the data being censored. The results of this analysis are presented as supplementary files.
3.1 Results
3.1.1 Tracking Table
Table 3 (tracking table) gives a summary of variable prevalence. The ‘Obs’ column enumerates all variables selected into any of the 48 models. The ‘Factor’ column displays the name of the factors included. For ease of discussion we have included the labels for those variables that are not self-explanatory, but the output will only include the name. In some cases, names will be slightly truncated in the output. ‘Count’ and ‘Percent’ display the relative presence of each factor as a frequency and percent, respectively. C-Reactive Protein (CRP) was present in 100% (48) of the 48 models generated. Chemokine ligand 1 (GROα) and Tissue Factor were each present in 93.75% (45) of the 48 models. ‘Ind’ is the indicator variable for a factor being selected into the model 65% of the time, as determined by PERC1. “Sum” tracks the number of variables that reach that threshold. Since there are 3 ones in the ‘ind’ column, the largest value in the ‘sum’ column should be 3. The maximum value of ‘sum’ is used to generate models of that size if that value does not equal the original K set by the user.
Table 3.
Tracking Table.
| Obs | Factor | COUNT | PERCENT | sum | ind |
|---|---|---|---|---|---|
| 1 | Angiopoietin 2 (Ang_2) | 1 | 2.08 | 0 | 0 |
| 2 | C-Reactive Protein (CRP) | 48 | 100.00 | 1 | 1 |
| 3 | Chemokine ligand 1 (GROa) | 45 | 93.75 | 2 | 1 |
| 4 | P_Selectin | 3 | 6.25 | 2 | 0 |
| 5 | Thrombospondin 2 (TSP_2) | 1 | 2.08 | 2 | 0 |
| 6 | Tissue_Factor | 45 | 93.75 | 3 | 1 |
| 7 | von Willebrand factor (vWF) | 1 | 2.08 | 3 | 0 |
3.1.2 The effect of PERC1
To illustrate the features of the macro under different circumstances, assume the percentages in table 3 were slightly divergent from this example – CRP 90%, GROα 75%, and Tissue Factor 60% with all other factors having a value less than 60%. PERC1 is set at 65, thus only 2 of the variables, CRP and GROα, would meet the threshold. The subsequent step in the macro is to use the training sets to generate 48 models with 2 factors, using that to create the high risk and low risk groups. In that instance a second table such as Table 3 would have been created. In the second table, however, the indicator and tracking variables would be based on PERC2.
For the sample data, the maximum of ‘sum’ is equal to the original K. Thus, no further modeling is performed on the 48 training sets; the macro continues with grouping the patients into the high risk and low risk groups from the models used to generate table 3. Similarly, if more than K variables meet the threshold, a new set of models will be generated using the larger variable size. However, as previously mentioned, if the model is larger than the original K this may signify instability or the need for a higher PERC1 value to achieve model stability across the n replicates.
3.1.3 Survival Analysis
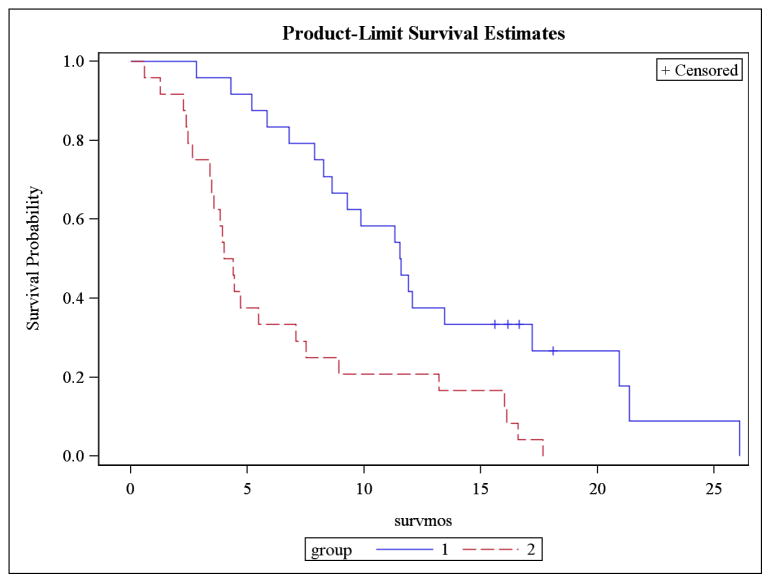
Based on the predicted groups of high and low risk from the test set, as ascertained using the LOOCV, survival analysis is performed on n samples using the observed survival times and the predicted risk groups. We describe the results here. For survival analysis, the standard approach is to report the following: a plot of the survival curve(s), median survival time(s), formal tests, and hazard ratio if comparing groups. Figure 2 is the Kaplan-Meier Plot generated from this macro using the convention of group 1 as low risk and group 2 as high risk. Tables 4a and 4b provide the median survival for group 1 and group2, respectively. Table 5 contains the Log-Rank and Wilcoxon results, testing whether there is a difference in the survival curves of the two groups. There is also a likelihood ratio test available, but it is based on the exponential distribution [9] which is not appropriate for the nonparametric and semiparametric methods outlined here. Table 6 presents the hazard ratio estimate and 95% CI as well as the test of difference in hazard functions for the groups.
Figure 2.
Kaplan Meier Plot of High Risk (2) vs Low Risk (1) groups
Table 4a.
Quartile Estimates (Group 1).
| Percent | Point Estimate | Transform | 95% Confidence Interval |
|---|---|---|---|
| 75 | 20.9256 | LOGLOG | (11.9008,26.0826) |
| 50 | 11.5537 | LOGLOG | (8.2645,17.1901) |
| 25 | 8.0661 | LOGLOG | (2.8099,9.8512) |
Table 4b.
Quartile Estimates (Group 2).
| Percent | Point Estimate | Transform | 95% Confidence Interval |
|---|---|---|---|
| 75 | 8.2149 | LOGLOG | (4.4298,16.0992) |
| 50 | 4.1983 | LOGLOG | (3.4050,7.0744) |
| 25 | 3.0248 | LOGLOG | (0.5950,3.8347) |
Table 5.
Test of Equality over Strata.
| Test | Chi-Square | DF | Pr > Chi-Square |
|---|---|---|---|
| Log-Rank | 12.0967 | 1 | 0.0005 |
| Wilcoxon | 13.5306 | 1 | 0.0002 |
| −2Log(LR) | 7.1855 | 1 | 0.0073 |
Table 6.
Analysis of Maximum Likelihood Estimates (Cox PH).
| Parameter | DF | Parameter Estimate | Standard Error | Chi-Square | Pr > Chi Sq | Hazard Ratio | 95% Hazard Ratio Confidence Limits |
|---|---|---|---|---|---|---|---|
| group | 1 | 1.07363 | 0.32230 | 11.0968 | 0.0009 | 2.926 | (1.556, 5.503) |
3.2 Checking PH Assumption
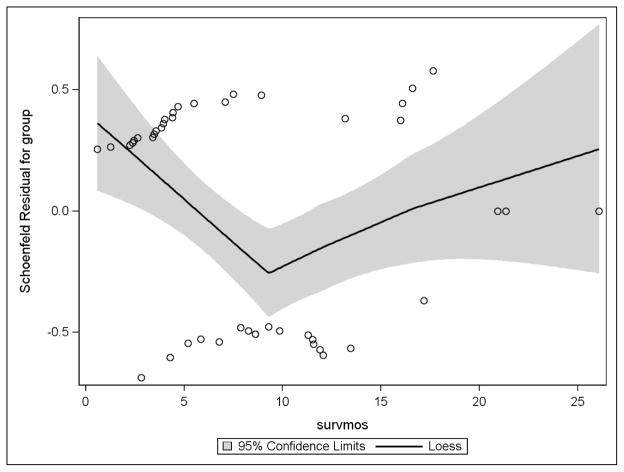
The proportional hazard assumption was checked graphically (Figure 3) as well as through hypothesis testing using a time-dependent covariate (Table 7). The Schoenfeld residuals based on high risk or low risk group were plotted against time with a loess regression line and its confidence bands superimposed. The expected outcome is a horizontal loess line; consistent change from that indicates a possible violation of the assumption. Figure 3 indicated a possible violation, thus a formal test was conducted using a time-dependent group variable, named “group_time” and the PHReg procedure. Table 7 presents the result of said of the test. With a p-value of 0.11 associated with the group_time variable, the assumption was determined to be upheld.
Figure 3.
Testing Proportional Hazards Assumption: Schoenfeld Residuals Plot Over Time
Table 7.
Analysis of Maximum Likelihood Estimates.
| Parameter | DF | Parameter Estimate | Standard Error | Chi-Square | Pr > ChiSq | Hazard Ratio | 95% Hazard Ratio Confidence Limits | |
|---|---|---|---|---|---|---|---|---|
| group | 1 | 2.79364 | 1.16646 | 5.7359 | 0.0166 | 16.340 | 1.661 | 160.753 |
| group_time | 1 | −0.90320 | 0.56890 | 2.5206 | 0.1124 | 0.405 | 0.133 | 1.236 |
3.3 Interpretation
The prevalence of a biological factor in the model selections provides a picture of the relative role of the factor in determining risk group. For this example study, CRP was involved in determining whether a participant was high risk or low risk in every model generated; GROα and Tissue Factor were determinants for risk group placement in approximately 94%. The output “bevev training_base os models.rtf” prints the complete listing of the variables selected for each training set; a sample of that output is provided in table A1.
The KM plot displays a separation of the survival curves for high risk and low risk groups. In reviewing Tables 4, we are interested in the median survival which is found on the 50 ‘percent’ row of the table. The median(95% CI) survival for the low risk group is 11.6 months(8.3, 17.2). The corresponding table for the high risk group displays a median(95% CI) survival of 4.2 months(3.4,7.1). The Log-Rank and Wilcoxon tests in Table 5 return p-values of 0.0005 and 0.0002, respectively, confirming a statistical difference in the survival curves. The methods described here were able to identify a high risk group with a median survival time that is nearly 1/3 of the median survival for the low risk group.
In Table 6, the low risk group is treated as the reference for comparison. The hazard ratio(95%CI) and p-value are clearly labeled as 2.9(1.6,5.5) and 0.0009, respectively. Thus, as the medians located in Tables 4a and 4b suggested using survival times, the hazard rate for the high risk group is nearly 3 times as much as the hazard rate for the low risk group. Note that hazard rate is inversely related to survival time.
Model 3.2.1 is a special case of model 2.1.1 with just one indicator variable which is high risk or low risk for our purposes. Model 3.2.2 includes the estimate for the effect of group as provided by Table 6; h0(t) defaults to the hazard rate for the low risk group.
| (3.2.1) |
| (3.2.2) |
Simple algebraic manipulation leads to the listed hazard ratio:
For this example study, the macro was able to identify a high risk group whose survival statistically differs from the other patients in the dataset labeled as low risk. Using internal validation, it highlighted a small number of variables that could potentially be used as a prognostic signature. Analyzing the hazard ratios associated with the highlighted variables in Cox PH regression models will help the investigator determine how the individual covariates may predict survival.
4. Discussion
With the combination of gaining familiarity with more complex modeling methods in software as well as data available to us and heightened awareness of the pitfalls of modeling while recognizing the need for prognostic models, we are often faced with concerns about the clarity, validity, and relevancy of selection methods when working with more than a few variables.
A variety of means to address these concerns are in practice or currently being developed, each of which has its own disadvantages. Some methods include concordance statistics in developing or performing prognostic analysis on the final model as a validation procedure [2,3]. However, the popular concordance statistic is implemented by ranking survival times, accounting for censoring by limiting the calculation to “useable” (or non-censored) observations. This, of course, lends itself to potential bias based on your specific sample’s censoring distribution [4]. Other methods include validating Cox PH models using a single split sample or external data sets, both of which are less effective than the LOOCV procedure, especially for smaller samples [5].
The macro we describe here utilizes an interval cross-validation and model selection procedure in order to minimize overfitting of the model. In addition to LOOCV, it allows the user to provide a more parsimonious model with as few variables as desired, by using the best subset score method of variable selection, while requiring the variables are consistently selected at some predetermined percentage. The aim of this is to select against potential artifacts of the particular data set. There has not been many simple to apply and control methods with interval validation developed for survival or censored outcomes.
This method is not without its limitations. There are caveats specific to this method, general model selection limitations, and the general impact of biological interactions on model fitting. The PHReg procedure in SAS software displays an incompatibility with high dimensional data where there are more variables than observations; the number of subjects with data for every variable must exceed the number of variables included in the selection process. Since this macro utilizes that procedure, this is a limitation of the macro. Additionally, selecting the one best model may mask models that contain different variables and be potentially better prognostic signatures yet have score statistics slightly below that model. However, that is a general risk of model selection. Finally, for the data sets containing biological information there is the added complexity of how variables are interacting with each other in a healthy or diseased biological system. Interaction terms of variables while computationally challenging can be explored in the future. Changing the number of variables included from 3 to 5, for example, may change the model with some variables’ prevalence diminishing entirely while others that were not present before become the most common because of the way the factors interact biologically. For this reason, using the full set of variables available as a beginning step and then using a significance-based step by step selection method is preferred by some. However, with a large number of factors, this is often neither feasible nor desirable. It also a source of selection bias due to overfitting [17].
Supplementary Material
Highlights.
A cross-validated model selection macro is proposed for prognostic survival data using Cox Proportional Hazards (PH) model
User-friendly with controls included for maximum size of model and prevalence of variable.
Checks Proportional PH assumption graphically and statistically
Acknowledgments
This work was supported by a grant from the National Institutes of Health (R21-AG042894) awarded to Herbert Pang as a co-PI. We thank the editor and two anonymous reviewers for their constructive comments, which helped improve the manuscript.
Footnotes
5. Conflict of Interest Statement
The authors claim no conflicts of interest.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Altman D, McShane L, Sauerbrei W, et al. Reporting recommendations for tumor marker prognostic studies (REMARK): explanation and elaboration. BMC Med. 2012;10:51. doi: 10.1186/1741-7015-10-51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Passamonti F, Thiele J, Girodon F, et al. A prognostic model to predict survival in 867 World Health Organization–defined essential thrombocythemia at diagnosis: a study by the International Working Group on Myelofibrosis Research and Treatment. Blood. 2012;120(6):1197–1201. doi: 10.1182/blood-2012-01-403279. [DOI] [PubMed] [Google Scholar]
- 3.Cheng W, Yang TO, Anastassiou D. Development of a Prognostic Model for Breast Cancer Survival in an Open Challenge Environment. Science Translational Medicine. 2013;5(181):1–10. doi: 10.1126/scitranslmed.3005974. [DOI] [PubMed] [Google Scholar]
- 4.Uno H, Cai T, Pencina M, et al. On the C-statistics for evaluating overall adequacy of risk prediction procedures with censored survival data. Statistics in Medicine. 2011;30(10):1105–1117. doi: 10.1002/sim.4154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Molinaro AM, Simon R, Pfeiffer R. Prediction error estimation: a comparison of resampling methods. Bioinformatics. 2005;21(15):3301–3307. doi: 10.1093/bioinformatics/bti499. [DOI] [PubMed] [Google Scholar]
- 6.Liu Y, Starr M, Bulusu A, et al. Correlation of angiogenic biomarker signatures with clinical outcomes in metastatic colorectal cancer patients receiving capecitabine, oxaliplatin, and bevacizumab. Cancer Medicine. 2013;2(2):234–242. doi: 10.1002/cam4.71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Nixon A, Pang H, Starr M, et al. Prognostic and predictive blood-based biomarkers in patients with advanced pancreatic cancer: Results from CALGB 80303 (Alliance) Clinical Cancer Research. 2013;19(24):6957–6966. doi: 10.1158/1078-0432.CCR-13-0926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cox D. Regression models and life-tables. J R Stat Soc B. 1972;34:187–220. [Google Scholar]
- 9.SAS Institute Inc. SAS 9.3 Help and Documentation. Cary, NC: SAS Institute Inc; 2002–2011. [Google Scholar]
- 10.Pang H, Jung SH. Sample size considerations of prediction-validation methods in high-dimensional data for survival outcomes. Genetic Epidemiology. 2013;37(3):276–82. doi: 10.1002/gepi.21721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kaplan E, Meier P. Nonparametric estimation from incomplete observations. J Am Stat Assoc. 1958;53:457–81. [Google Scholar]
- 12.Mantel N. Evaluation of survival data and two new rank order statistics arising in its consideration. Cancer Chemotherapy Reports. 1966;50(3):163–70. [PubMed] [Google Scholar]
- 13.Gehan E. A generalized two-sample Wilcoxon test for doubly censored data. Biometrika. 1965;52:203–223. [PubMed] [Google Scholar]
- 14.Altomare I, Bendell J, Bullock K, et al. A Phase II Trial of Bevacizumab plus Everolimus for Patients with Refractory Metastatic Colorectal Cancer. The Oncologist. 2011;16(8):1131–1137. doi: 10.1634/theoncologist.2011-0078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.The Cancer Genome Atlas Research Network. Integrated genomic analyses of ovarian carcinoma. Nature. 2011;474:609–615. doi: 10.1038/nature10166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Dellinger A, Nixon A, Pang H. Integrative Pathway Analysis Using Graph-Based Learning with Applications to TCGA Colon and Ovarian Data. Cancer Inform. 2014;13(Suppl 4):1–9. doi: 10.4137/CIN.S13634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Royston P, Moons KGM, Altman DG, et al. Prognosis and prognostic research: Developing a prognostic model. British Medical Journal. 2009;338:1373–1377. doi: 10.1136/bmj.b604. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.