Diagnostic Thresholds with Three Ordinal Groups

Summary

In practice, there exist many disease processes with three ordinal disease classes; for example in the detection of Alzheimer’s disease (AD) a patient can be classified as healthy (disease free stage), mild cognitive impairment (early disease stage) or AD (full disease stage). The treatment interventions and effectiveness of such disease processes will depend on the disease stage. Therefore it is important to develop diagnostic tests with the ability to discriminate between the three disease stages. Measuring the overall ability of diagnostic tests to discriminate between the three classes has been discussed extensively in the literature. However there has been little proposed on how to select clinically meaningful thresholds for such diagnostic tests, except for a method based on the generalized Youden index by Nakas et al. (2010). In this paper, we propose two new criterion for selecting diagnostic thresholds in the three class setting. The numerical study demonstrated that the proposed methods may provide thresholds with less variability and more balance among the correct classification rates for the three stages. The proposed methods are applied to two real examples: the clinical diagnosis of AD from the Washington University Alzheimer’s Disease Research Center and on the detection of liver cancer (LC) using protein segments.

1. Introduction

Traditionally diagnostic tools have been used to discriminate patients between two basic types: healthy (H) and diseased (D). For example, the marker n-acetylasparate over creatine is widely considered as a biomarker of neuronal metabolism in the brain (Nakas et al. 2010). The diagnostic properties of such biomarkers can be described by the receiver operating characteristic (ROC) curve, originally developed in the context of radar technology for differentiating between signal and noise (Leton & Molanes 2009). The ROC curve is a plot of the true-positive rate (portion of times the marker correctly identifies a diseased individual) versus the false-positive rate (portion of time the markers miss-specifies a healthy individual as diseased) over all possible diagnostic thresholds or cut-points (Egan 1975; Greiner et al. 2000; Pepe 2003; Obuchowski 2005). Without loss of generality, an observation above the threshold is classified as diseased while an observation below the threshold is considered healthy.

For reasonable biomarkers, the ROC curve lies above the diagonal chance line from the origin to the point (1, 1), with the point (0, 1) corresponding to perfect discrimination (Greiner et al. 2000; Pepe 2003; Obuchowski 2005). The ROC curve allows researchers to examine the trade-off between the sensitivity (true-positive rate) and the specificity (true-negative rate) for given thresholds (Egan 1975). A variety of approaches are proposed for estimating the ROC curve, with Faraggi & Reiser (2002) providing an extensive discussion on parametric and non-parametric methods. Both Zou et al. (1997) and Lloyd & Yong (1999) suggest the use of kernel smoothed estimates of the ROC curve, which was supported by the empirical studies of Fraggi & Reiser (2002).

The ROC curve is often summarized by a single global measure: the area under the ROC curve (AUC). Suppose we let X₁₁, …, X_1n i.i.d. with continuous distribution F₁ be n observations from the healthy population and let X₂₁, …, X_2m i.i.d. with continuous distribution F₂ be m observations from the disease population. Then Bamber (1975) has shown that the AUC = P(X₁ < X₂), which can be interpreted as the average specificity over all sensitivities or the average sensitivity over all specificities (Obuchowski 2005). The estimate of the AUC is dependent on the estimation of the ROC curve, with values ranging from 0.5 to 1, corresponding to no discrimination and perfect discrimination respectively (Greiner et al. 2000; Faraggi & Reiser 2002; Pepe 2003; Obuchowski 2005). In this regards, the AUC is often used to compare the diagnostic ability of two or more biomarkers. Delong et al. (1988) provided a non-parametric approach for comparing two paired AUC’s, while Molodianvich et al. (2006) presents both parametric and non-parametric methods. In the case where a minimum specificity or sensitivity is required, Zhang et al. (2002) and Li et al. (2008) discuss parametric and non-parametric methods for inferences on the partial AUC (pAUC). Once a biomarker is selected, a threshold needs to be chosen that will “optimally” classify patients between the healthy and diseased populations. Approaches to threshold selection can be based on a variety of clinical constraints (Coffin & Sukhatme 1997; Pepe 2003; Leeflang et al. 2008) or by criteria considered “optimal” within the framework of ROC analysis, which are discussed extensively in Schafer (1989), Greiner et al. (2000) and Pepe (2003). Two commonly applied approaches are the Youden index (Fluss et al. 2005; Perkins & Schisterman 2006; Schisterman et al. 2007; Lai et al. 2012; Nakas et al. 2010) and the northwest corner (i.e. the closest-to-perfection) (Perkins & Schisterman 2006; Leton & Molanes 2009), for which further detail is given in Section 2.

In practice there exist many disease processes, such as Alzheimer’s disease (AD) and liver cancer (LC), in which there is a transitional or intermediate stage (T) between the healthy and diseased states (Xiong et al. 2006; Xiong et al. 2007; Alonzo et al. 2009; Sampat et al. 2009; Nakas et al. 2010; Tian et al. 2010; Zhang & Li 2011). Consider the three class setting where we let X₁₁, …, X_1n i.i.d. with distribution F₁ be n observations from the healthy population; X₂₁, …, X_2m i.i.d. with distribution F₂ be m observations from the transitional-stage population and X₃₁, …, X_3k i.i.d. with distribution F₃ be k observations from the disease population. In this setting, we must now consider two thresholds c₁ and c₂ (c₁ < c₂), with a third dimension added to the ROC graph; the transitional stage probability: t(c₁, c₂) = P(c₁ < X₂ < c₂) (Mossman 1999; Xiong et al. 2006; Xiong et al. 2007; Alonzo et al. 2009; Sampat et al. 2009; Dong et al. 2011). Instead of an ROC curve, we now have an ROC surface that is the plot of the three probabilities: (specificity, sensitivity, transitional probability) = (P(X₁ < c₁), P(X₃ > c₂), P(c₁ < X₂ < c₂)) over all possible values of c₁ and c₂ (Xiong et al. 2006; Nakas et al. 2010). Dong et al. (2011) discusses parametric and non-parametric estimates of the transitional stage coverage given specified levels of specificity and sensitivity. In the case of monotone ordering, the volume under the surface (VUS) has been suggested as an overall measure of a biomarker’s ability to discriminate between the three classes (Mossman 1999; Xiong et al. 2006; Xiong et al. 2007; Alonzo et al. 2009; Nakas et al. 2010). The VUS can be thought of as the percent of patients that would be correctly classified for a given biomarker (He & Frey 2008) and corresponds to the probability that observations are correctly ordered: VUS = P(X₁ < X₂ < X₃) (Xiong et al. 2006; Alonzo et al. 2009). The estimation and comparison of a biomarker’s VUS and partial VUS (PVUS) with ordinal ordering are discussed by Xiong et al. (2007) and Tian et al. (2010). While Alonzo et al. (2009) provides a summary of global measures and tests for a variety of restricted orderings.

While the overall ability of a biomarker to discriminate between three classes can be assessed, a pair of thresholds still needs to be selected with respect to some selection criteria. In the three-class setting, there is limited discussion on threshold selection, with He & Frey (2006) providing a discussion on “optimal” decision making criteria using likelihoods. Among those criteria is the maximum correctness criterion, which maximizes the expected probability of a correct decision given a set of class prevalence (He & Frey 2006). An approach recently proposed by Nakas et al. (2010), the generalized Youden index, maximizes the sum of the correct classification rates and satisfies this maximum correctness criterion. Skaltsa et al. (2012) proposed a method that optimized a cost function based on the classification rates and error rates, while Bayesian classifying procedures have also been suggested for the multi-class setting (Sampat et al. 2009). Unfortunately these methods are reliant on correctly assigning class prevalence or cost coefficients, which may be difficult to obtain in practice (Sampat et al. 2009; Skaltsa et al. 2012). In our study, we suggest two other approaches for three-class threshold selection: the closest to perfection (an extension of the two-class northwest corner) and the max volume (an approach based on the concept of VUS that maximizes another function of the correct classification rates). A numerical study demonstrates that the proposed approaches might be able to overcome some of the limitations of the generalized Youden index proposed by Nakas et al. (2010).

Section 2 provides a review of the existing methods for the two-class settings and the generalized Youden index approach proposed by Nakas et al. (2010) for three-class setting. Section 3 presents two proposed three-class threshold selection methods. Through a simulation study in Section 4, comparisons of the existing and proposed methods are made with respect to their classification rates as well the accuracy and variability of the threshold estimates. Finally these approaches are presented in two examples, the first from a published Alzheimer’s disease (AD) dataset from the neuropsychological database at the Washington University Alzheimer’s Disease Research Center. The second is a study on liver cancer (LC), using the Disialoganglioside GD1a protein segment to discriminate healthy, chronic liver disease and hepatocellular carcinoma subjects.

2. Preliminaries

In this section, we briefly describe the existing selection methods for the two-class setting: the Youden index and the northwest corner, and review the current extension of the Youden index to the three-class setting proposed by Nakas et al. (2010).

2.1 The Youden index Method

The Youden index (J) is a commonly used measure of diagnostic effectiveness first introduced into the medical literature by Youden in 1950 (Youden 1950). The statistic J is defined as the maximum, over all thresholds (c), of the sum of the sensitivity and specificity:

$$J=\underset{c}{max}[p(c)+q(c)-1]$$

where q(c) and p(c) are the sensitivity and specificity respectively for a fixed point c (Fluss et al. 2005; Perkins & Schisterman 2006; Schisterman et al. 2007; Lai et al. 2012). The Youden index can be thought of as the maximum differentiability of the biomarker when equal weight is given to sensitivity and specificity (Gail & Green 1976), with values ranging from 0 to 1 indicating a complete lack of and perfect discrimination, respectively (Fluss et al. 2005; Schisterman et al. 2007). Graphically J is the greatest vertical distance exists between the ROC curve and the diagonal line from the origin to the point of perfection (1, 1) (Perkins & Schisterman 2006).

In this framework, the “optimal” threshold, c_J, is the value that maximizes q(c_J)+p(c_J)−1 and achieves the maximum discrimination between the two-classes (Fluss et al. 2005; Schisterman et al. 2007). Alternatively, this criteria can be considered as minimizing the total misclassification rates (Gail & Green 1976; Perkins & Schisterman 2006) as follow:

$${min}_{\mathrm{c}}[(1-p(c))+(1-q(c))].$$

The Youden index can also be adjusted for cost and prevalence; if so, the corresponding cut-point minimizes the total cost of misclassification (Perkins & Schisterman 2006; Schisterman et al. 2007). A variety of methods for estimating c_J and J have been proposed, with Fluss et al. (2005) providing a discussion on two parametric and non-parametric approaches. Schisterman et al. (2007) provided a closed form solution for both J and c_J in the normal case with asymptotic and bootstrap confidence intervals. Small sample confidence intervals were proposed by Lai et al. (2012) under normality using generalized pivotal quantities and simulation study showed that they outperformed the asymptotic estimates. Other work by Schisterman et al. (2007) and Leton & Molanes (2009) have considered a more realistic scenario and provided interval estimates for the bi-gamma model.

2.2 The Northwest Corner Method

The northwest corner (or closest to perfection) approach is another popular method for threshold selection in the two-class setting (Fawcett 2006; Perkins & Schisterman 2006; Leton & Molanes 2009). It has received little attention in the statistical literature, but is popular in practice because of its intuitive and geometric appeal. This approach selects the threshold c that corresponds to the point on the ROC curve closest to (0, 1), i.e., the point closest to perfection: p(c) = 1 and q(c) = 1. The “optimal” threshold, c_D, is the value that minimizes the distance (D) from (0, 1) to (1-p(c_D), q(c_D)) (Perkins & Schisterman 2006) and is considered more accurate than those thresholds whose point on the ROC curve is further from (0, 1) (Fawcett 2006). Specifically, D is defined as:

$$D=\underset{c}{min}\left[\sqrt{{(1-p(c))}^2+{(1-q(c))}^2}\right].$$

The values of D range from 0 to $\sqrt{0.5}$, indicating perfection and complete lack discrimination respectively. This criterion minimizes the total misclassification rates and a third term, the average of the squared correct classification rates (Perkins & Schisterman 2006), as follows:

$${min}_{\mathrm{c}}[(1-p(c))+(1-q(c))+0.5(p{(c)}^2+q{(c)}^2)].$$

There is no practical justification for this third term. The results differ from the Youden index criteria (Perkins & Schisterman 2006) and generally have higher specificity, producing fewer false positives (Fawcett 2006). The northwest corner can also be adjusted for cost and prevalence by minimizing the total cost of misclassification plus an additional cost term as discussed by Perkins and Schisterman (2006).

2.3 The Generalized Youden Index for the Three-class Setting

The generalized Youden index (J₃) proposed by Nakas et al. (2010) is an extension of the Youden index to the three-class setting. The statistic J₃ is defined as the maximum, over all values c₁ and c₂ (c₁ < c₂), of the sum of the correct classification rates:

$$J_3=\underset{c_1<c_2}{max}[p(c_1)+q(c_2)+t(c_1,c_2)],$$ (2.1)

where p(c₁), q(c₂) and t(c₁, c₂) are the specificity, sensitivity and transitional stage probability, respectively. The transitional stage probability is a function of both thresholds, while the specificity and sensitivity rely only on c₁ or c₂. The J₃ statistic ranges from 1 to 3, with 1 indicating no discrimination and 3 indicating perfect discrimination between the three classes. In this sense, the statistic J₃ can be used to measure and compare biomarkers discriminatory ability, as was proposed by Nakas et al. (2010). The authors found that the generalized Youden index was reasonable for identifying location-scale differences between populations, but not when differences in distributional shapes existed (Nakas et al. 2010).

The “optimal” thresholds are those that produce the J₃ statistic and can be found numerically using constrained maximization (Nakas et al. 2010). The pair of thresholds is considered to be “optimal” by the maximum correctness criteria, as described by He & Frey (2006). It is worth noting that this criterion is equivalent to minimizing the total misclassification rate as follows:

$${min}_{{\mathrm{c}}_1<{\mathrm{c}}_2}[(1-p(c_1))+(1-q(c_2))+(1-t(c_1,c_2))].$$ (2.2)

The generalized Youden index can be adjusted for class prevalence or misclassifications costs by introducing the cost-coefficients. Then the adjusted generalized Youden index (J₃^*) is given by:

$${J_3}^{\ast }=\underset{c_1<c_2}{max}[r_{1}p(c_1)+r_{3}q(c_2)+r_{2}t(c_1,c_2)],$$

where r₁, r,₂ and r₃ are the class prevalence associated with the healthy, intermediate and disease populations.

While the generalized Youden index can be adjusted for prevalence and cost, a potential limitation of such a method, as suggested by the authors, is that there may not be a unique pair of cut-points that produce the J₃ statistic (Nakas et al. 2010). In applications, researchers would have to select the pair of cut-points from the “optimal pool” of pairs that satisfy their specific clinical criteria (e.g. a particular specificity must be achieved) (Nakas et al. 2010).

2.3.1 Under-utilization and Imbalance of the Generalized Youden Index

There are two potential limitations of the generalized Youden index method that are of particular interest: the underutilization of the samples in threshold selection and the imbalance of the resulting classification rates.

The potential underutilization of the samples is actually related to the fact that, for the two-sample Youden index, the optimal threshold occurs at the intersection of the healthy and disease density functions. In the three class setting, if the intersection of the distribution functions of the healthy and transitional populations occurs before that of the transitional and diseased populations, then c₁ can be found using only the healthy and transitional samples and c₂ using only the transitional and disease samples (more details are presented in the Appendix). As an illustrative example, consider tumor size as a biomarker for classifying a patient’s tumor as benign, low risk and high risk. Assume the tumor sizes for these three classes follow a normal distribution with means of 2cm, 4cm and 6cm respectively, and a common standard deviation of 1cm.

In Figure 1, the intersection of the benign and low risk distributions occurs before that of the low risk and high risk distributions. If we view this example as a three class problem and apply the generalized Youden index method, the thresholds c₁ and c₂ are found to be 3cm and 5cm, respectively. From another perspective, treating this example as two two-class problems (one between the benign and low risk distributions and another between the low risk and high risk distributions) also leads to the same thresholds (i.e., the threshold between the healthy and low risk groups is 3cm and the threshold between the low risk and high risk groups is 5cm). Note that under normality with homogeneous variance, the diagnostic threshold in the two-class setting occurs at the mid-point between the means of the two populations (Fluss et al. 2005). It is clear that for this example, the generalized Youden index method uses only a portion of all the samples for calculating c₁ and c₂ (the benign and low risk samples for c₁ and low risk and high risk samples for c₂) and hence there exist an under-utilization of the available information when selecting the diagnostic thresholds.

Figure 1.

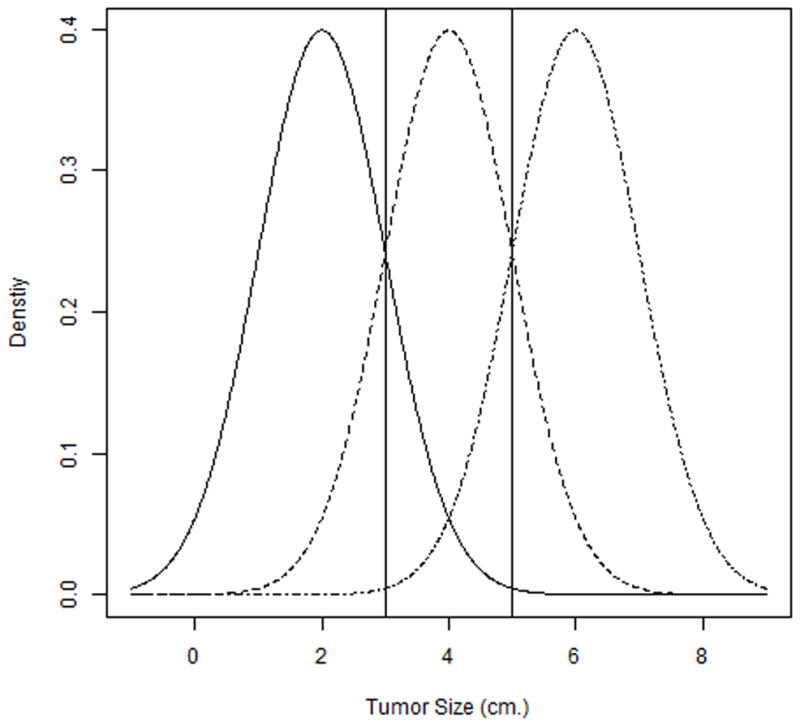
The imbalance among the classifications rates can occur as a result of this sample under-utilization and this can be especially of concern for identifying individuals in the intermediate stage. In the three class setting, such as Alzheimer’s disease or certain cancers, it often important to identify patients in the intermediate stage where treatment is most effective. Unfortunately the generalized Youden index tends to produce an imbalance in classification rates where there is good specificity and sensitivity, but poor intermediate coverage. Consider again the tumor size example where the thresholds by the generalized Youden index are 3cm and 5cm. These thresholds produce a specificity, sensitivity and intermediate coverage of 0.841, 0.841 and 0.683, respectively. Hence, in this example, there exists a clear imbalance among classification rates for three classes where low risk patients have relatively poor identification as compared to the healthy and high risk patients. That is, the intermediate coverage is relatively low as compared to the sensitivity and specificity. In general, the generalized Youden index favors identification of healthy and disease patients at the expense of identification of the intermediate class patients. While not presented here, similar results are observed under varying conditions.

These potential limitations will be further demonstrated and addressed via the results from a numerical study in Section 4.

3. Proposed Selection Methods

This section describes two new proposals for threshold selection in the three-class setting. The first is called the closest to perfection, which is an extension of the northwest corner method for the two class setting. The second method, max volume, is based on the concept of volume under the surface (VUS), the common statistical measure for diagnostic accuracy in the three-class setting.

3.1 The Closest to Perfection Method

The closest to perfection method is a generalization of the two-class northwest corner in which the selected thresholds are those which generate the point on the ROC surface closest to the point of perfection. In the three-class setting described in Section 1, the point (1, 1, 1) corresponds to perfect discrimination. The “optimal” pair of thresholds are those which minimizes the distance D₃, and can be found numerically using constrained minimization with the following definition:

$$D_3=\underset{c_1<c_2}{min}\left[\sqrt{{(1-p(c_1))}^2+{(1-q(c_2))}^2+{(1-t(c_1,c_2))}^2}\right].$$ (3.1)

As in the two-class setting, a distance of 0 would indicate perfect discrimination while increasing distances indicate weaker ability of discrimination among three stages. Similar to the generalized Youden index’s optimality statistic J₃, the statistic D₃ could also be interpreted as a global measure of a biomarker’s discriminatory ability. This method produces thresholds that are “optimal” in the sense that they correspond to the point on the ROC surface closest to perfection. Similar to the two-class case, this method actually minimizes the misclassification rates plus some squared terms involving the correct classification rates as follows:

$$min[(1-p(c_1))+(1-q(c_2))+(1-t(c_1,c_2))+0.5(p{(c_1)}^2+q{(c_2)}^2+t{(c_1,c_2)}^2)].$$

This method generally produces a pair of cut-points that differ from those by the generalized Youden index. The motivation for such a method is the geometric appeal and the fact that under most conditions the “optimal” thresholds obtained using this method will be unique. An additional advantage of this approach, compared to the generalized Youden index, is that information from all three classes is used to obtain both threshold values. Therefore the problem of under-utilization of samples is avoided, and furthermore c₁ and c₂ can be estimated with smaller variances and a higher correlation between them. Hence we can expect that such defined thresholds will provide higher transitional stage coverage t(c₁, c₂) than that by the generalized Youden index method.

Similar to the generalized Youden index, the closest to perfection approach can be adjusted for class prevalence or misclassification costs:

$${D_3}^{\ast }=\underset{c_1<c_2}{min}\left[\sqrt{r_1{(1-p(c_1))}^2+r_3{(1-q(c_2))}^2+r_2{(1-t(c_1,c_2))}^2}\right],$$

where r₁, r,₂ and r₃ are the class prevalence associated with the healthy, intermediate and disease populations.

3.2 The Max Volume Method

This new proposal for threshold selection builds on the concept of volume under surface (VUS), the most widely used diagnostic accuracy index for a biomarker’s ability to correctly order the observations in the three-class setting (Xiong et al. 2006; Xiong et al. 2007; Alonzo et al. 2009). Similar to the generalized Youden index, the max volume approach also selects the thresholds (c₁ < c₂) that maximize a function of the correct classification rates. As reviewed in Section 2.3, the generalized Youden index has a limitation of under-utilization of the available information for threshold selection. To overcome such a shortcoming, the max volume approach uses a target function defined as the product of the true classification rates for three stages. Geometrically, this approach seeks c₁ and c₂ that build the largest box within the ROC surface of which the volume is:

$$V_3=\underset{c_1<c_2}{max}[p(c_1)\times q(c_2)\times t(c_1,c_2)].$$ (3.2)

This approach attempts to utilize more information in threshold selection, and thus provides more balance between the true classification rates than the generalized Youden index, as shown in the following. Note that maximizing [p(c₁) × q(c₂) × t(c₁, c₂)] is equivalent to minimizing

$$min[-log(\mathrm{p}({\mathrm{c}}_1))-log(\mathrm{q}({\mathrm{c}}_2))-log(\mathrm{t}({\mathrm{c}}_1,{\mathrm{c}}_2))].$$

In this form, we can see that small changes in any classification rate may have a larger impact on the objective function than on the one in (2.2). Furthermore, it is easy to see that the determination of c₁ and c₂ involves samples from all three disease categories. Therefore, the max volume method can provide more balance between the three true classification rates than the generalized Youden index approach does since it promotes simultaneous maximization the specificity, transitional probability and sensitivity. Furthermore, the estimated c₁ and c₂ should have smaller variances than those determined by the generalized Youden index approach. Similar to the closest to perfection method, this approach is expected to have higher transitional stage coverage t(c₁, c₂) than the generalized Youden index method. All the above-stated properties of this proposed approach are observed from the numerical study in Section 4.

In addition to the aforementioned advantages of the max volume method, the justification for the use of the proposed target function, i.e. the volume p(c₁) × q(c₂) × t(c₁, c₂), can also be viewed from another perspective. The volume p(c₁) × q(c₂) × t(c₁, c₂) equals to the probability of an event in which a randomly selected subject from each diagnostic group is simultaneously classified correctly. Thus maximizing V₃ = p(c₁) × q(c₂) × t(c₁, c₂) is equivalent to maximizing the probability of such an event. Although the max Volume method does not maximize the total correct classification rates directly as the generalized Youden index approach does, the total loss in overall correct classification rate is very small, as demonstrated by simulation study in Section 4.

The V₃ statistic has a maximum of 1 when all three classification rates are perfect and a minimum of one twenty-seventh, corresponding to the completely uninformative case when all classification rates are one-third. Similar to the previously mentioned optimality statistics J₃ and D₃, V₃ could be considered as a global measure of discriminatory ability of a given biomarker. It would be of interest to compare the three optimality statistics (J₃, D₃ and V₃) with respect to their ability to indentify significant biomarkers, but this is beyond the scope of this paper and will be considered in further study.

The thresholds corresponding to V₃ can be found numerically, as with the previously discussed statistics, using constrained maximization. Similar to the generalized Youden index and closest to perfection methods, the max volume method can also be generalized to account for differing prevalence rates or costs associated with each diagnostic group. For the generalized Youden index and closest to perfection methods, coefficients associated with the cost or prevalence are added to the coverage probabilities (Nakas et al. 2010). While for the max volume approach, the cost or rates can be incorporated in the exponents of the coverage probabilities. Suppose the prevalence for each diagnostic group is known and given by r₁, r₂ and r₃ for the healthy, transitional and disease groups respectively. Then the max volume criterion can be re-written as:

$$V_3=\underset{c_1<c_2}{max}[p{(c_1)}^{r_1}\times q{(c_2)}^{r_3}\times t{(c_1,c_2)}^{r_2}].$$

While further discussion on incorporation of prevalence and misclassification costs in both the overall assessment of the discriminatory ability and the diagnostic thresholds of a biomarker is of interest, it is beyond the current scope of this paper and should be considered for further study.

A potential limitation of the max volume approach, similar to the generalized Youden index approach, the corresponding estimated thresholds may not be unique. In practice a unique solution can often be obtained by simply restricting the domain of possible thresholds to a set of reasonable values (e.g. a consideration such as it does not make practical sense to have a c₁ to produces an extremely small specificity).

4. Simulation Study

A simulation study was conducted using six distributional scenarios similar to those in Nakas et al. (2010), which are shown in Table I. Scenarios 1 and 2 refer to differences resulting from location shifts, while scenarios 3 and 4 refer to differences resulting from location-scale differences under normality. In scenarios 5 and 6, there are location, scale and shape differences. The thresholds (c₁ and c₂) and the optimality statistics (V₃, J₃ and D₃) associated with each method were estimated numerically using equations 2.1, 3.1, 3.2 and the smoothed empirical distribution functions proposed by Lloyd et al. (1999). In each iteration, the distribution functions of the healthy, transitional and diseased populations were estimated empirically and then used to numerically find the “optimal” thresholds associated with each method. A caveat to this step is that for a given iteration the “optimal” thresholds may not be uniquely estimated and when this occurs, a pair of thresholds is selected at random from the pool of “optimal” pairs. This is the same approach used to by Nakas et al. (2010) to handle the issue of non-unique empirical optimum. We also included an unbalanced sample design, with more weight (larger sample) from the healthy population. For each scenario and sample size combination, a total of 2000 iterations (N = 2000) were conducted.

Table I.

Simulation Scenarios

Scenario	Healthy	Transitional	Disease
1	N(0, 1)	N(1, 1)	N(2, 1)
2	N(0, 1)	N(0.5, 1)	N(1, 1)
3	N(0, 1.2)	N(0.5, 0.8)	N(1, 1.4)
4	N(0, 0.8)	N(1.2, 1)	N(2.5, 1.1)
5	Gamma(2, 1)	Gamma(3, 1)	Gamma(5, 2)
6	t(2)	Beta(2, 2)	Chi Square(1)

4.1 Bias and Variability

In each simulation, the relative bias, standard deviation (SD) and root mean square error (RMSE) defined as $\mathit{RMSE}=\sqrt{\mathit{bia}{s}^2+\mathit{var}}$ were calculated for each selection approach based on the estimates from the iterations; for example, the variance and relative bias for estimated c₁ can be obtained as follows:

$$\begin{array}{c}\mathit{Realtive}\mathit{Bias}({\widehat{c}}_1)=\frac{\frac{1}{N}{\sum }_{j=1}^N({\widehat{c}}_{1,j}-c_1)}{c_1}\\ \mathit{Variance}({\widehat{c}}_1)=\frac{{\mathrm{\sum }}_{j=1}^N{({\widehat{c}}_{1,j}-{\overline{c}}_1)}^2}{N-1},\end{array}$$

where ĉ_1,j is the estimate for c₁ in the j^th simulation run, and c̄₁ is the average of simulation estimate of c_1. The relative bias and variance are obtained for c₂ in a similar manner.

Regarding the relative bias, there is no clear winner among these three methods. The generalized Youden index approach tends to have smaller relative bias in the normal cases (scenarios 1, 3, 4 for c₁; and 1 and 4 for c₂), but does not perform as well as in the gamma, mixed distribution cases (scenarios 5 & 6 for c₁, scenario 5 for c₂) or when the sample sizes of the diagnostic groups are imbalanced. The closest to perfection and max volume approaches performed similarly for both thresholds in a few scenarios (1 and 4), while the max volume approach performed better in other scenarios (scenarios 2, 3, and 6 for c₁; and scenarios 2 and 3 for c₂). Both proposed methods did however outperform the generalized Youden index approach in some of the scenarios (scenarios 2, 5 and 6 for c₁, and scenarios 2, 3 and 5 for c₂).

The standard deviation of the estimated thresholds c₁ and c₂ associated with the max volume and the closest to perfection methods are generally smaller than those by the generalized Youden index approach for all normal scenarios. The generalized Youden index outperformed the proposed methods in the mixed distribution scenario for c₁, and the gamma and mixed scenarios for c₂. For the purpose of assessing overall performance in terms of providing accurate threshold estimates, a comparison of the RMSE’s associated with c₁ and c₂ estimates indicates that both the proposed max volume and closest to perfection approaches generally perform better than the existing generalized Youden index method. Again an exception is made with the mixed distribution scenario for c₁ and c₂. This observation is due to the fact that the two newly proposed methods use all three samples in the estimation of both thresholds, while the generalized Youden index method may underutilize the samples as demonstrated in the Appendix. There was no clear pattern for comparing the proposed approaches, as the max volume outperformed in about half the scenarios (scenarios 2, 3, and 6 for c₁; and scenarios 2 and 3 for c₂) and the closest to perfection performed better in the other scenarios.

The three optimality statistics (J_3, D₃ and V₃) associated with the generalized Youden index, the closest to perfection and the max volume approaches respectively, can serve as indices of diagnostic accuracy. That is they reach their corresponding maximums when the test perfectly distinguishes between the healthy, transitional, and diseased stages. While not a primary purpose of this article, it would be of interest to compare the overall performance of the estimates of J_3, D₃ and V₃. This idea has already been proposed for the J₃ statistic by Nakas et al. (2010). In Table IV, we see that the J₃ statistic was, in general, more accurately estimated over all simulation scenarios in terms of relative bias, but it also had largest variability as compared to the D₃ and V₃ statistics. It seems to be a common theme that the closest to perfection and max volume approaches sacrifice some bias for an overall reduction in RMSE as compared to the generalized Youden index approach. With respect to the statistics J_3, D₃ and V₃, the RMSE is a measure of their precision and inferential quality. That is, for a given sample size, the statistic with the lowest RMSE should provide improved inferences as compared to the other statistics. Thus, the reduction in RMSE observed for the closest to perfect and maximum volume approaches provides further support to their use in this diagnostic setting.

Table IV.

Relative bias, standard deviation and root mean squared error (RMSE) for the optimality statistics (V₃, J₃ and D₃) associated with each selection approach

Scenario	True Optimality Statistic	Relative Bias				Standard Deviation				RMSE
		n=m=k=20	n=m=k=40	n=m=k=80	n=50, m=35, k=25	n=m=k=20	n=m=k=40	n=m=k=80	n=50, m=35, k=25	n=m=k=20	n=m=k=40	n=m=k=80	n=50, m=35, k=25
1	Youden: 1.766	0.0104	−0.0023	−0.0036	0.0013	0.1357	0.1016	0.0737	0.1081	0.1369	0.1017	0.0740	0.1082
	CP: 0.725	0.0121	0.0206	0.0153	0.0159	0.0870	0.0643	0.0465	0.0688	0.0874	0.0661	0.0479	0.0697
	Volume: 0.197	0.0029	−0.0260	−0.0229	−0.0137	0.0536	0.0379	0.0274	0.0406	0.0537	0.0383	0.0278	0.0407
2	Youden: 1.395	0.0365	0.0159	0.0064	0.0220	0.1435	0.1033	0.0761	0.1079	0.1523	0.1057	0.0766	0.1121
	CP: 0.938	−0.0033	0.0015	0.0040	−0.0009	0.0880	0.0627	0.0461	0.0669	0.0881	0.0627	0.0462	0.0669
	Volume: 0.096	0.0460	0.0107	−0.0046	0.0234	0.0347	0.0239	0.0170	0.0256	0.0350	0.0240	0.0170	0.0257
3	Youden: 1.501	0.0199	0.0126	0.0044	0.0106	0.1512	0.1100	0.0818	0.1174	0.1541	0.1116	0.0820	0.1184
	CP: 0.876	0.0017	0.0000	0.0033	0.0031	0.0910	0.0657	0.0490	0.0707	0.0910	0.0657	0.0491	0.0707
	Volume: 0.121	0.0254	0.0147	−0.0033	0.0076	0.0404	0.0288	0.0215	0.0308	0.0405	0.0289	0.0215	0.0308
4	Youden: 1.966	−0.0015	−0.0055	−0.0075	−0.0039	0.1384	0.0997	0.0732	0.1099	0.1384	0.1003	0.0746	0.1102
	CP: 0.615	0.0297	0.0252	0.0220	0.0241	0.0882	0.0636	0.0467	0.0693	0.0901	0.0655	0.0486	0.0709
	Volume: 0.271	−0.0182	−0.0262	−0.0288	−0.0215	0.0637	0.0459	0.0344	0.0506	0.0639	0.0464	0.0353	0.0510
5	Youden: 2.039	0.0032	−0.0045	−0.0047	−0.0060	0.1334	0.0975	0.0709	0.0998	0.1336	0.0979	0.0716	0.1005
	CP = 0.589	0.0103	0.0174	0.0126	0.0171	0.0871	0.0631	0.0452	0.0622	0.0873	0.0639	0.0458	0.0630
	Volume: 0.299	0.0029	−0.0182	−0.0163	−0.0191	0.0682	0.0483	0.0347	0.0481	0.0682	0.0486	0.0351	0.0485
6	Youden: 1.833	0.0037	0.0030	0.0021	0.0041	0.1452	0.0992	0.0710	0.1105	0.1453	0.0994	0.0711	0.1108
	CP: 0.789	−0.0229	−0.0221	−0.0199	−0.0247	0.1000	0.0702	0.0504	0.0809	0.1016	0.0723	0.0528	0.0832
	Volume: 0.174	0.0761	0.0601	0.0491	0.0693	0.0618	0.0426	0.0305	0.0496	0.0632	0.0439	0.0317	0.0510

The samples sizes for the healthy, transitional and diseased populations are given by n, m, and k respectively.

Youden = generalized Youden index, CP = closest to perfection, and Volume = max volume

The RMSE, relative bias and standard deviation estimates are as described in section 4.1.

4.2 Correlation

The correlation between c₁ and c₂ was calculated for each selection method based on the threshold estimates from each iteration, and is defined as follows:

$$\mathit{Corr}({\widehat{c}}_1,{\widehat{c}}_2)=\frac{{\mathrm{\sum }}_{j=1}^N({\widehat{c}}_{1,j}-{\overline{c}}_1)({\widehat{c}}_{2,j}-{\overline{c}}_2)}{\sqrt{{\mathrm{\sum }}_{j=1}^N{({\widehat{c}}_{1,j}-{\overline{c}}_1)}^2{\mathrm{\sum }}_{j=1}^N{({\widehat{c}}_{2,j}-{\overline{c}}_2)}^2}}.$$

This is a measure of interest because a natural dependency exists between c₁ and c₂, a result of their respective impacts on the transitional probability: P(c₁ < X₂ < c₂). The correlation between c₁ and c₂ is a measure of how strong this dependency is and can be considered as a surrogate for the amount of information being shared when estimating both c₁ and c₂. Therefore we expect that the generalized Youden index will have a relatively low correlation as there may be an underutilization of the generated samples for some iterations, and then c₁ and c₂ will be computed similarly as two two-class problems. We expect that the proposed methods will have higher correlations since they will utilize all samples and obtain c₁ and c₂ jointly.

As shown in Table V, the correlation is generally higher for the max volume and the closest to perfection approaches as compared to the generalized Youden index method. This is an indication that there is more “sharing” of the three diagnostic samples involved in the estimation of the thresholds associated with the max volume and the closest to perfection approaches, which may be a contributing factor to the decreased variability their estimates. The correlation associated with the max volume approach is higher than that of the closest to perfection approach in scenarios 1, 2, 4 and 5. While it is difficult to view a pattern with the threshold estimates in these scenarios, the optimality statistic of the max volume method tends to be more accurately estimated and has a lower RMSE as compared to the closest to perfection method.

Table V.

Correlation between estimates c₁ and c₂, and % Loss of Total Correct Classification

Scenario	Method	Correlation				% Loss of Total Correct Classification
		n=m=k=20	n=m=k=40	n=m=kl=80	n=50, m=35, k=25	n=m=k=20	n=m=k=40	n=m=k=80	n=50, m=35, k=25
1	Youden	0.147	0.147	0.129	0.124	-	-	-	-
	CP	0.539	0.550	0.527	0.524	1.81%	1.55%	1.28%	1.54%
	Volume	0.573	0.621	0.570	0.592	1.50%	1.28%	1.06%	1.25%
2	Youden	0.254	0.206	0.175	0.205	-	-	-	-
	CP	0.589	0.711	0.706	0.594	2.71%	2.15%	1.83%	2.26%
	Volume	0.766	0.748	0.757	0.767	2.29%	1.85%	1.62%	1.98%
3	Youden	0.229	0.218	0.232	0.235	-	-	-	-
	CP	0.652	0.656	0.670	0.695	1.70%	1.36%	1.16%	1.34%
	Volume	0.611	0.599	0.591	0.652	1.80%	1.39%	1.18%	1.42%
4	Youden	0.166	0.194	0.197	0.223	-	-	-	-
	CP	0.415	0.447	0.425	0.417	1.73%	1.46%	1.28%	1.50%
	Volume	0.520	0.517	0.454	0.495	1.05%	0.92%	0.81%	0.93%
5	Youden	0.294	0.208	0.162	0.259	-	-	-	-
	CP	0.393	0.342	0.312	0.356	1.33%	1.22%	1.09%	1.15%
	Volume	0.462	0.421	0.391	0.444	0.70%	0.58%	0.45%	0.54%
6	Youden	0.057	−0.024	0.044	0.026	-	-	-	-
	CP	0.520	0.569	0.592	0.566	4.30%	4.45%	4.59%	4.40%
	Volume	0.269	0.268	0.217	0.266	1.96%	1.79%	1.72%	1.92%

Youden = generalized Youden index, CP = closest to perfection, and Volume = max volume

The correlation and % loss of total classification estimates are described in sections 4.2 and 4.3 respectively.

4.3 The Loss of Total Correct Classification

Although the max volume method maximizes the volume p(c₁) × q(c₂) × t(c₁, c₂), not the total correct classification rate p(c₁) + q(c₂) + t(c₁, c₂) as the generalized Youden index approach does, the total loss in correct classification is very small. The percent loss of total classification is simply the difference in the sum of the correct classification rates for the max volume (or closest to perfection) and the generalized Youden index approaches divided by the sum of the correct classification rates for the generalized Youden index approach. The percent loss of total classification for the maximum volume is given by:

$$\%\mathit{Classification}\mathit{Loss}=\frac{[p(c_{1J})+q(c_{2J})+t(c_{1J},c_{2J})]-[p(c_{1V})+q(c_{2V})+t(c_{1V},c_{2V})]}{p(c_{1J})+q(c_{2J})+t(c_{1J},c_{2J})},$$

where p(c_1J), q(c_2J) and t(c_1J, c_2J) are the estimated classification rates by the generalized Youden index method, while p(c_1V), q(c_2V) and t(c_1V, c_2V) are the classification rates by the max volume method. A similar formula is applied to obtain the percent loss of total classification rate for the closest to perfection approach.

The simulation results found in Table V indicate that, for the scenarios considered, the percent loss in total correct classification rate for the max volume method is no more than 3%. A similar observation applies to the closest to perfection method. We see that these more accurate estimates for c₁ and c₂ by the proposed max volume and closest to perfection methods, compared to those by the generalized Youden index approach, come with little sacrifice to the overall correct classification rate.

Overall speaking, in comparison with the generalized Youden index, the two proposed approaches generally have smaller variances and RMSE for the threshold estimates, and higher correlation between estimated c₁ and c₂. Despite the fact that these two new methods do not maximize the overall correct classification rate directly, the percent loss is reasonably small. The performance of the proposed max volume and closest to perfection approaches are comparable except that the RSME for the max volume approach is consistently the smallest among all three methods, indicating that V₃ can be estimated most precisely.

5. Examples

5.1 Alzheimer’s Disease

Alzheimer’s Disease (AD) is the most common form of degenerative dementia in the US, affecting up to 47 percent of the population over the age of 85 (Evans et al. 1995; Xiong et al. 2006). The increasing prevalence of AD poses a major health crisis and a great deal of effort has been made to develop non-invasive tests for AD, with cognitive and behavioral deficits being the earliest and most reliable evidence. However, by the time these deficits are clinically detected, it is likely that the disease process has been present for many years (Crystal et al. 1988; Morris et al. 1991; Xiong et al. 2006). With new medicines under development to slow the disease progression, the challenge is to identify those affected, but not yet demented (intermediate stage). For those in the earliest stages of the disease progression, treatment can have a more profound effect on functional status and the rate of cognitive decline (Xiong et al. 2006).

The sample of patients presented are from a longitudinal cohort of Washington University (WU) Alzheimer’s Disease Research Center (ADRC), including only those with dementia of Alzheimer type (DAT) in the demented sample (Xiong et al. 2006). The participants were assessed annually by trained clinicians with diagnosis and severity of the dementia staged by the Clinical Dementia Rating (CDR) (Morris 1993). As in Xiong et al. (2006), our methodology will be applied towards discriminating patients between non-demented (CDR 0, 50 subjects), very mildly demented (CDR 0.5, 29 individuals) and mildly demented (CDR 1, 24 individuals). As part of the clinical evaluation, the participants also completed a battery of standard psychometric tests which generate factor scores (overall, mental control/frontal factor, memory-verbal/temporal factor, and visuospatial/parietal factor) proposed by Kanne et al. (1998) and Rubin et al. (1998). These scores are believed to describe factors that play significant roles during the stages of the AD disease process and were found to be significant by Xiong et al. (2006). We used four factor scores (overall, temporal, frontal and parietal) to apply the threshold selection methodologies previously described, as they are significant factors with potential application in clinical practice.

Histograms of the factor scores are presented in Figures 2a, 2b, 2c and 2d, and indicate that scores need to be multiplied by negative one such that CDR 0 < CDR 0.5 < CDR 1. The optimality statistics and thresholds for each method were estimated as in the simulation study, with the results presented in Table VI. The three methods produce similar thresholds, with the confidence interval widths for the max volume and the closest to perfection approaches being smaller than those by the generalized Youden index approach. This is especially true for the threshold between the CDR 0.5 and CDR 1 patients (c₂) and is an indication that increased variability is associated with the estimates by the generalized Youden index approach. The maximum volume approach has the narrowest intervals for the overall factor, while the closest to perfection approach produced the smallest intervals for all other factors. We have previously attributed this result to the possible under-utilization of the entire sample when estimating the diagnostic thresholds. This is further supported by the estimated correlations, which are generally higher for the max volume approach. In general, the estimated c₁ and c₂ thresholds generated by the max volume approach fall between those estimated using the other two methods, providing balance between the three classification rates.

Figure 2.

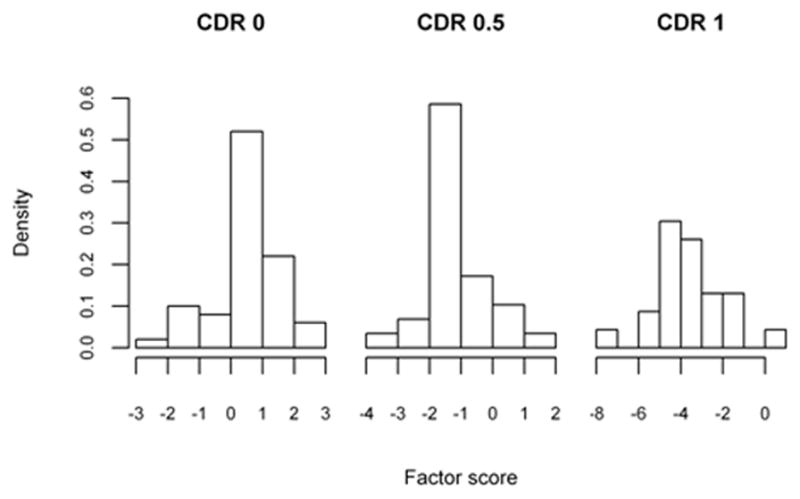
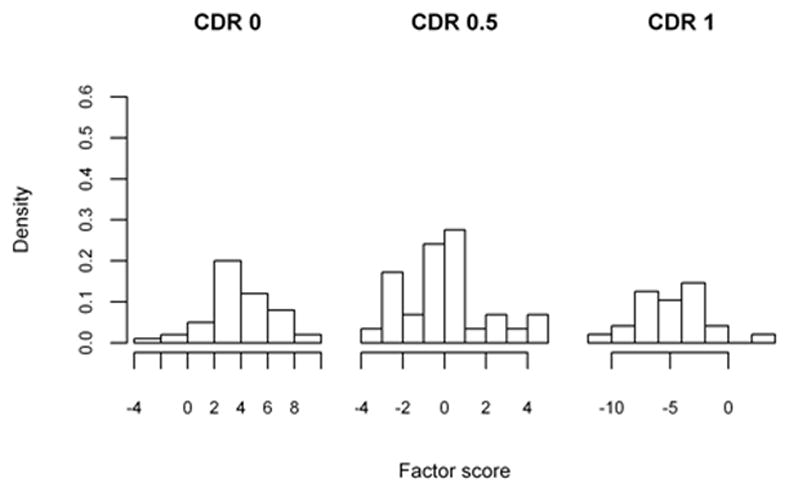
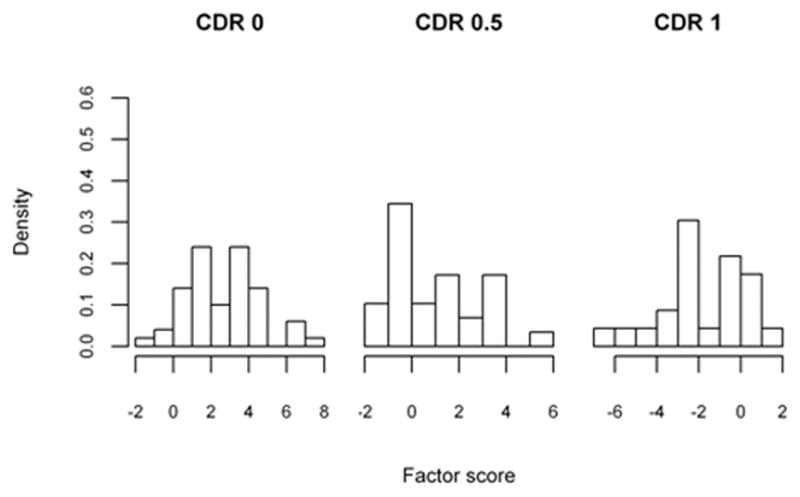
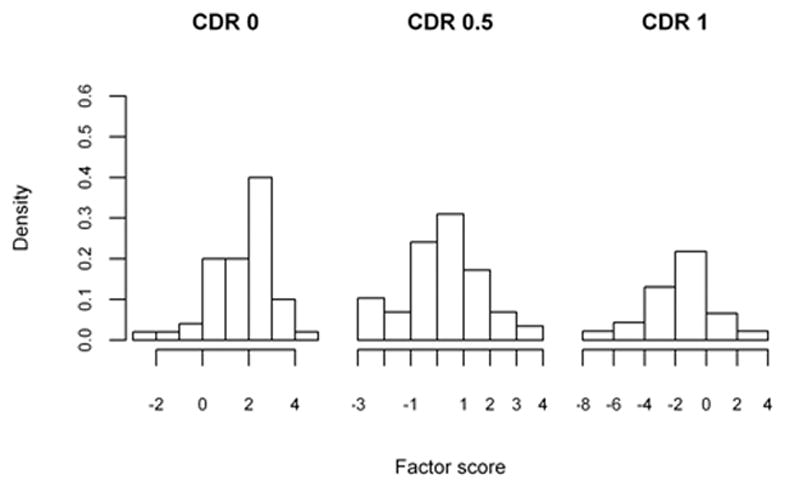
Table VI.

Alzheimer’s disease: Threshold estimates

Factor	Method	Optimality Statistic	Estimated C1	C1 CI Width	Estimated C2	C2 CI Width	BS Correlation	p(c1)	t(c1, c2)	q(c2)
Overall	Youden	2.332 (2.102, 2.561)	0.26 (−0.17, 0.69)	0.86	2.09 (1.61, 2.57)	0.96	0.048	0.817	0.687	0.827
	CP	0.394 (0.257, 0.532)	0.15 (−0.23, 0.53)	0.76	2.22 (1.73, 2.71)	0.98	0.032	0.794	0.728	0.804
	Volume	0.466 (0.320, 0.611)	0.21 (−0.21, 0.63)	0.84	2.15 (1.68, 2.62)	0.94	0.075	0.807	0.707	0.817
Temporal	Youden	2.325 (2.111, 2.539)	−1.66 (−2.29, −1.03)	1.26	2.64 (1.66, 3.62)	1.96	0.114	0.828	0.698	0.799
	CP	0.394 (0.269, 0.522)	−1.88 (−2.54, −1.22)	1.32	2.83 (2.11, 3.55)	1.44	0.116	0.807	0.736	0.777
	Volume	0.462 (0.330, 0.595)	−1.75 (−2.38, −1.08)	1.30	2.75 (1.91, 3.59)	1.68	0.156	0.820	0.718	0.787
Parietal	Youden	1.820 (1.617, 2.025)	−1.18 (−2.07, −0.29)	1.78	0.46 (−0.77, 1.64)	2.41	0.182	0.690	0.403	0.727
	CP	0.690 (0.555, 0.825)	−1.46 (−1.91, −1.01)	0.90	0.91 (0.20, 1.62)	1.42	0.533	0.621	0.559	0.628
	Volume	0.218 (0.129, 0.307)	−1.44 (−1.97, −0.91)	1.06	0.87 (0.07, 1.67)	1.60	0.600	0.626	0.547	0.637
Frontal	Youden	1.816 (1.588, 2.043)	−0.78 (−1.03, 0.47)	1.50	1.46 (−0.20, 3.12)	3.32	0.166	0.819	0.451	0.545
	CP	0.704 (0.549, 0.859)	−1.60 (−2.47, −0.74)	1.73	1.43 (0.72, 2.13)	1.41	0.514	0.677	0.567	0.549
	Volume	0.211 (0.112, 0.310)	−1.44 (−2.45, −0.43)	2.02	1.46 (0.72, 2.21)	1.49	0.554	0.707	0.548	0.545

Youden = generalized Youden index, CP = closest to perfection, and Volume = max volume

The optimality statistics and cut-point estimates are calculated using equations 2.5, 3.1 and 3.2.

The confidence intervals and correlation estimates are calculated using bootstrap normal approximations

The classification rates [p(c₁) = specificity, t(c₁, c₂) = transitional probability and q(c₂) = sensitivity] are estimated using the kernel smoothed empirical CDFs

5.2 Liver Cancer

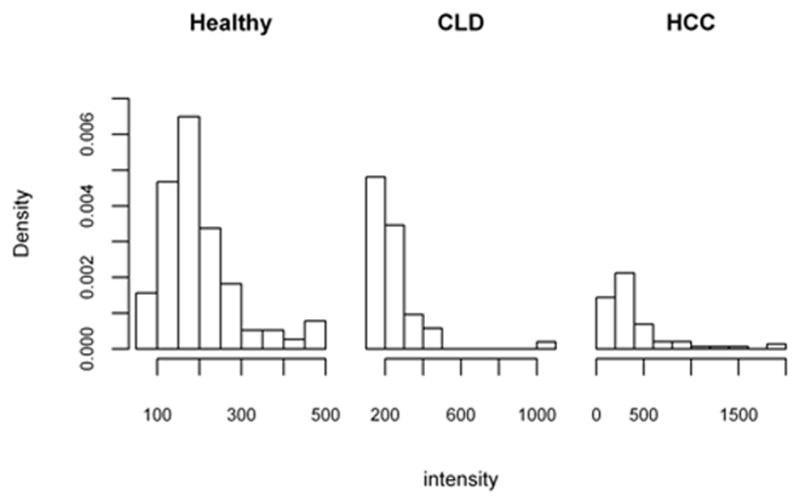
The current diagnosis of hepatocellular carcinoma (HCC) relies on clinical information, liver imaging and serum R-fetoprotein (AFP) (Ressom et al. 2008). The reported classification rates of AFP are insufficient for early diagnosis and treatment; therefore additional markers need to be examined (Gupta et al. 2003; Ressom et al. 2008). This example includes data from 203 individuals in a cohort study for the detection of Glycan biomarkers for liver cancer (Ressom et al. 2008). The biomarker discovery study involved participants from Cairo, Egypt; of which 73 were HCC cases (diseased), 52 patients were with chronic liver disease (CLD, intermediate stage) and 78 were healthy (H). For each patient, a total of 484 protein segments with intensity were obtained after extensive pre-processing. The data can be downloaded in text format². Zhang & Li (2011) and Kang et al. (2012) have discussed this data in the multi-category diagnostic setting, considering each of the protein segments as a diagnostic biomarker. As in Kang et al. (2012), we consider a special protein segment called Disialoganglioside GD1a (m/z value of 1527:6427), which has been shown to be highly correlated with hepatoma in mouse liver (Shaposhnikova et al. 1981). The Disialoganglioside GD1a scores for each diagnostic group are presented as histograms in Figure 3.

Figure 3.

The threshold selection methods are applied to the Disialoganglioside GD1a protein segment in the manner described in the simulation and AD example. The resulting optimality statistics, thresholds and corresponding confidence intervals are found in Table VII. The thresholds for the three approaches are similar, though the confidence intervals for the max volume and closest to perfection approaches are narrower for both c₁ and c₂. Indicating their estimate thresholds have less variability as compared to the thresholds of the generalized Youden index approach. The optimality statistics are 0.125, 0.865 and 1.502 for the max volume, closest to perfection and generalized Youden index respectively. These values indicate that Disialoganglioside GD1a may not be promising in discriminating between healthy individuals, chronic liver disease and liver cancer patients, as was observed by Kang et al. (2012).

Table VII.

Liver cancer: Threshold estimates

Factor	Method	Optimality Statistic	Estimated C1	C1 CI Width	Estimated C2	C2 CI Width	BS Correlation	p(c1)	t(c1, c2)	q(c2)
Disialoganglioside GD1a	Youden	1.502 (1.340, 1.664)	185.5 (123.4, 247.7)	−124.3	311.9 (227.9, 395.9)	−168.0	0.221	0.548	0.490	0.463
	CP	0.865 (0.768, 0.962)	179.1 (159.1, 199.1)	−40.0	306.1 (268.9, 343.3)	−74.4	0.644	0.512	0.514	0.474
	Volume	0.125 (0.081, 0.168)	179.1 (158.6, 199.6)	−41.0	306.1 (269.3, 342.9)	−73.6	0.629	0.512	0.514	0.474

Youden = generalized Youden index, CP = closest to perfection, and Volume = max volume

The optimality statistics and cut-point estimates are calculated using equations 2.5, 3.1 and 3.2.

The confidence intervals and correlation estimates are calculated using bootstrap normal approximations

The classification rates [p(c₁) = specificity, t(c₁, c₂) = transitional probability and q(c₂) = sensitivity] are estimated using the kernel smoothed empirical CDFs

6. Discussion

This paper presents two new methods for selecting thresholds in the three-class setting; namely, the closest to perfection and max volume methods. Via simulations studies, the two proposed methods are compared to the generalized Youden index method. The three methods are applied to examples using published data on Alzheimer’s disease (AD) and Liver cancer (LC).

The newly proposed closest to perfection and the existing generalized Youden index methods are extensions of methods commonly used in the two-class setting, while the max Volume method is a new method based on the concept of VUS. Similar to the generalized Youden index, the max volume method involves maximizing a function of the correct classification rates. The generalized Youden index method has clean and interpretable “optimality” by minimizing the total misclassification rates and achieving the maximum correctness criteria as proposed by He & Frey (2006). The closest to perfection and max volume approaches have nice geometric appeals and the corresponding thresholds provide more reasonable coverage of the transitional or intermediate stage, that is, c₁ and c₂ tend to be wider apart. Despite that the generalized Youden index method having more footing with its motivation and “optimality”, it lacks in the sharing of information from all three samples that potentially leads to increased variability in c₁ and c₂ estimates. The simulation studies demonstrated that the correlations between the estimated thresholds c₁ and c₂ by the max volume and the closest to perfection methods are significantly higher than those by the generalized Youden index. This may then directly contribute to the larger variability associated with the threshold estimates for the generalized Youden index approach and the larger confidence intervals observed in the examples. It is important to note that the increased precision associated with estimates of the max volume and closest to perfection thresholds did not sacrifice much in terms of overall correct classification. The max volume performed better in this respect, it never had a percent of total classification loss greater than 3% as compared to the 5% limit for the closest to perfection approach.

As demonstrated by the simulation study, the uniqueness and selection of “optimal” thresholds is an issue that may require further investigation for all three methods. The unique solution issue for the generalized Youden index was discussed briefly by Nakas et al. (2010) and we adopt their approach for selecting thresholds in our simulations. However, in practice, researchers should not just randomly select a pair of thresholds from an optimal pool, but select a pair based on some additional clinical criteria such as a minimum coverage probability (set a lower bound for specificity, transitional probability or sensitivity) or cost function. Future work should focus on, when multiple thresholds exist, how different coverage restrictions or clinical selection criteria may impact the methodologies described in this paper. Specifically whether the same general results we observed will hold, or if significant improvements can be made to any of the presented threshold selection methods.

We observed some interesting results when the newly proposed methods and the generalized Youden index are applied to a relatively small datasets on clinical diagnosis of Alzheimer’s disease and liver cancer. For example, in the AD data application, the frontal factor was demonstrated to be a reasonable marker for discriminating between the three disease stages based on the VUS by Xiong et al. (2006). However, the confidence intervals for the cut-points c₁ and c₂ associated with the generalized Youden index method overlap, indicating that either this marker may be poor for distinguishing between the three disease stages or that there is too much variability in the threshold estimates. On the other hand, the confidence intervals for c₁ and c₂ by the closest to perfection and the max Volume approaches do not overlap, indicating that the frontal factor may be a reasonable discriminating measure. At the very least this indicates that the estimated thresholds for the proposed methods are less variable than those of the generalized Youden index. This result demonstrates the negative impact resulting from the underutilization of the sample in the generalized Youden index approach, for which larger samples within each of the diagnostic groups would be necessary to accurately estimate the thresholds as compared to the newly proposed methods.

In practice, a researcher may apply all three of these methods and find that, as in our example, the thresholds are practically and statistically indistinguishable. In that instance it would be beneficial for the researcher to select the thresholds that maximize the coverage probabilities that are clinically relevant to their research. In regards to the AD and LC research, it may be beneficial to select the thresholds that maximize the transitional stage probability as this is a critical stage in the treatment of the diseases. Regardless of a researcher’s choice in threshold, as there are now several proposed approaches available, one should be aware of both the strengths and weaknesses of their choice.

Table II.

Relative bias, standard deviation and root mean squared error (RMSE) for the c₁ estimates

Scenario	True c1	Relative Bias				Standard Deviation				RMSE
		n=m=k=20	n=m=k=40	n=m=k=80	n=50, m=35, k=25	n=m=k=20	n=m=k=40	n=m=k=80	n=50, m=35, k=25	n=m=k=20	n=m=k=40	n=m=k=80	n=50, m=35, k=25
1	Youden: 0.500	−0.0280	−0.0345	−0.0105	−0.0501	0.3930	0.3314	0.2392	0.3126	0.3932	0.3319	0.2393	0.3136
	CP: 0.289	−0.0831	−0.0448	−0.0225	−0.0415	0.2317	0.1705	0.1256	0.1676	0.2329	0.1710	0.1257	0.1680
	Volume: 0.307	−0.0746	−0.0454	−0.0203	−0.0463	0.2519	0.1860	0.1402	0.1852	0.2529	0.1865	0.1403	0.1857
2	Youden: 0.250	−1.4777	−0.9731	−0.6279	−0.8623	0.8137	0.6001	0.4618	0.6114	0.8936	0.6476	0.4878	0.6483
	CP: −0.035	1.9036	0.5840	0.3592	0.8170	0.4181	0.2273	0.1744	0.2894	0.4234	0.2282	0.1748	0.2908
	Volume: −0.046	0.4897	0.2426	0.2066	0.3779	0.2879	0.2079	0.1589	0.2133	0.2888	0.2081	0.1592	0.2140
3	Youden: −0.238	0.1216	0.0859	0.0885	0.0381	0.4711	0.3381	0.2630	0.3454	0.4720	0.3387	0.2639	0.3455
	CP: −0.060	0.2522	0.2466	0.1823	0.1490	0.2683	0.1959	0.1496	0.2074	0.2687	0.1965	0.1500	0.2076
	Volume: −0.066	0.1998	0.1854	0.1270	0.1437	0.2581	0.1903	0.1465	0.2001	0.2584	0.1907	0.1468	0.2004
4	Youden: 0.678	0.0022	0.0012	0.0082	0.0164	0.3255	0.2311	0.1690	0.2139	0.3255	0.2311	0.1691	0.2142
	CP: 0.439	0.0086	−0.0237	−0.0098	−0.0008	0.2015	0.1379	0.1045	0.1356	0.2015	0.1383	0.1046	0.1356
	Volume: 0.499	0.0085	−0.0233	−0.0099	−0.0039	0.2146	0.1619	0.1247	0.1591	0.2146	0.1623	0.1248	0.1592
5	Youden: 2.000	0.1137	0.1088	0.0903	0.1138	0.7204	0.5538	0.4216	0.5490	0.7554	0.5950	0.4587	0.5943
	CP: 2.034	0.0464	0.0359	0.0271	0.0338	0.3083	0.2156	0.1593	0.2154	0.3224	0.2276	0.1686	0.2262
	Volume: 2.004	0.0649	0.0478	0.0359	0.0460	0.3520	0.2447	0.1827	0.2467	0.3752	0.2628	0.1963	0.2633
6	Youden: 0.063	−0.1161	−0.1278	−0.1145	−0.0892	0.0711	0.0490	0.0346	0.0517	0.0715	0.0496	0.0354	0.0520
	CP: 0.162	−0.0895	−0.1042	−0.1155	−0.0852	0.0857	0.0636	0.0474	0.0654	0.0869	0.0658	0.0510	0.0668
	Volume: 0.111	−0.0381	−0.0595	−0.0690	−0.0413	0.0763	0.0544	0.0391	0.0568	0.0764	0.0548	0.0398	0.0570

The samples sizes for the healthy, transitional and diseased populations are given by n, m, and k respectively.

Youden = generalized Youden index, CP = closest to perfection, and Volume = max volume

The RMSE, relative bias and standard deviation estimates are as described in section 4.1.

Table III.

Relative bias, standard deviation and root mean squared error (RMSE) for the c₂ estimates

Scenario	True c2	Relative Bias				Standard Deviation				RMSE
		n=m=k=20	n=m=k=40	n=m=k=80	n=50, m=35, k=25	n=m=k=20	n=m=k=40	n=m=k=80	n=50, m=35, k=25	n=m=k=20	n=m=k=40	n=m=k=80	n=50, m=35, k=25
1	Youden: 1.500	0.0138	−0.0021	−0.0006	0.0080	0.3782	0.3103	0.2399	0.3502	0.3788	0.3104	0.2400	0.3504
	CP: 1.711	0.0105	0.0072	0.0065	0.0099	0.2320	0.1713	0.1292	0.1870	0.2327	0.1718	0.1297	0.1878
	Volume: 1.693	0.0094	0.0072	0.0070	0.0100	0.2534	0.1882	0.1440	0.2018	0.2539	0.1886	0.1445	0.2025
2	Youden: 0.750	0.2409	0.2345	0.1527	0.3035	0.6461	0.5193	0.4136	0.5797	0.6709	0.5482	0.4292	0.6228
	CP: 1.035	0.0138	0.0191	0.0212	0.0266	0.3215	0.2211	0.1702	0.2631	0.3218	0.2220	0.1716	0.2645
	Volume: 1.047	0.0083	0.0160	0.0182	0.0152	0.2783	0.2072	0.1575	0.2408	0.2785	0.2079	0.1587	0.2413
3	Youden: 1.373	0.0386	0.0318	0.0289	0.0531	0.4334	0.3086	0.2377	0.3562	0.4367	0.3117	0.2410	0.3636
	CP: 1.171	0.0272	0.0241	0.0192	0.0310	0.3032	0.2076	0.1582	0.2426	0.3048	0.2096	0.1598	0.2453
	Volume: 1.171	0.0137	0.0225	0.0164	0.0221	0.2750	0.1983	0.1507	0.2320	0.2755	0.2000	0.1519	0.2335
4	Youden: 1.899	−0.0149	−0.0062	0.0019	−0.0012	0.3787	0.2817	0.2109	0.3180	0.3798	0.2819	0.2110	0.3180
	CP: 2.060	0.0089	0.0084	0.0086	0.0120	0.2275	0.1698	0.1219	0.1896	0.2283	0.1707	0.1232	0.1911
	Volume: 2.041	0.0096	0.0082	0.0087	0.0115	0.2490	0.1901	0.1407	0.2093	0.2498	0.1908	0.1418	0.2106
5	Youden: 5.260	0.0291	0.0236	0.0221	0.0334	0.7324	0.5510	0.4195	0.6146	0.7481	0.5649	0.4353	0.6393
	CP: 6.090	0.0030	0.0074	0.0108	0.0117	0.7691	0.5572	0.4126	0.6364	0.7693	0.5590	0.4178	0.6403
	Volume: 5.659	0.0227	0.0215	0.0213	0.0284	0.7726	0.5708	0.4373	0.6328	0.7832	0.5837	0.4537	0.6530
6	Youden: 0.956	−0.0071	−0.0082	−0.0061	−0.0072	0.0789	0.0537	0.0386	0.0603	0.0792	0.0542	0.0390	0.0607
	CP: 0.786	−0.0300	−0.0311	−0.0313	−0.0282	0.1065	0.0745	0.0575	0.0833	0.1091	0.0784	0.0625	0.0861
	Volume: 0.860	−0.0448	−0.0375	−0.0305	−0.0404	0.1118	0.0764	0.0584	0.0890	0.1183	0.0829	0.0640	0.0955

The samples sizes for the healthy, transitional and diseased populations are given by n, m, and k respectively.

Youden = generalized Youden index, CP = closest to perfection, and Volume = max volume

The RMSE, relative bias and standard deviation estimates are as described in section 4.1.

Appendix A

Suppose that F, H, and G are the distribution functions and f, h, and g are the density functions of the healthy, transitional-stage, and diseased populations. The J₃ statistic can be written as:

$${\mathrm{J}}_3=max[F(c_1)+H(c_2)-H(c_1)-G(c_2)].$$ (A.1)

The generalized Youden index approach considers the constraint free maximization approach for the threshold section using equation A.2 as follows:

$$max[F(c_1)+H(c_2)-H(c_1)-G(c_2)]=max[F(c_1)-H(c_1)]+max[H(c_2)-G(c_2)].$$ (A.2)

The maximization problem now can be written as the sum of two maximizations, one dependent on c₁ and the other dependent on c₂. These two sub-maximizations are equivalent to that in the two-class Youden index and the optimal thresholds are the intersections of the density functions (Fluss et al. 2005; Schisterman et al. 2007). Hence, the optimal thresholds are found by solving A.3 and A.4.

$$f(c_1)=h(c_1)$$ (A.3)

$$h(c_2)=g(c_2)$$ (A.4)

It is clear that the point c₁ only depends on the healthy and transitional-stage samples while the point c₂ only depends on the transitional-stage and diseased samples. Therefore not all the available information is used in the selection of either threshold.

Now if the intersection of the healthy and transitional-stage populations occurs before the intersection of the transitional-stage and diseased populations, the thresholds for the restricted maximum would be the same as for the unrestricted case.