Abstract
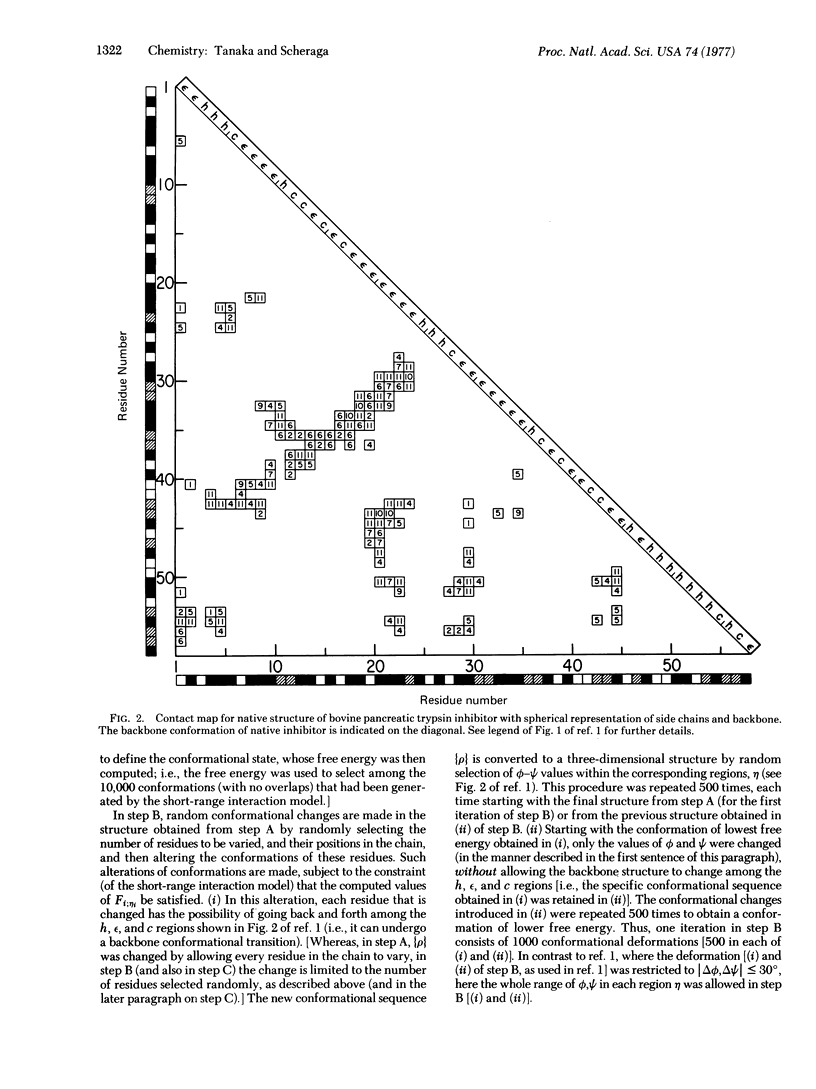
In this paper, we have incorporated a one-dimensional short-range model into a three-dimensional model for protein folding. It has been applied, by extending the concept of the three-step mechanism for protein folding proposed in our previous paper, to simulate the folding of bovine pancreatic trypsin inhibitor, using a Monte Carlo procedure in all three steps, A, B, and C. The statistical mechanical ensemble treatment of the short-range model serves as a constraint on the Monte Carlo procedure, in which conformational transitions are introduced. The preliminary results of 10 independent Monte Carlo trials indicate that, while folding is achieved, improvements are required in order to account for the correct three-dimensional structure of a globular protein.
Full text
PDF


Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Burgess A. W., Scheraga H. A. Assessment of some problems associated with prediction of the three-dimensional structure of a protein from its amino-acid sequence. Proc Natl Acad Sci U S A. 1975 Apr;72(4):1221–1225. doi: 10.1073/pnas.72.4.1221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levitt M., Warshel A. Computer simulation of protein folding. Nature. 1975 Feb 27;253(5494):694–698. doi: 10.1038/253694a0. [DOI] [PubMed] [Google Scholar]
- Ptitsyn O. B., Rashin A. A. A model of myoglobin self-organization. Biophys Chem. 1975 Feb;3(1):1–20. doi: 10.1016/0301-4622(75)80033-0. [DOI] [PubMed] [Google Scholar]
- Tanaka S., Scheraga H. A. Medium- and long-range interaction parameters between amino acids for predicting three-dimensional structures of proteins. Macromolecules. 1976 Nov-Dec;9(6):945–950. doi: 10.1021/ma60054a013. [DOI] [PubMed] [Google Scholar]
- Tanaka S., Scheraga H. A. Model of protein folding: inclusion of short-, medium-, and long-range interactions. Proc Natl Acad Sci U S A. 1975 Oct;72(10):3802–3806. doi: 10.1073/pnas.72.10.3802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanaka S., Scheraga H. A. Statistical mechanical treatment of protein conformation. 4. A four-state model for specific-sequence copolymers of amino acids. Macromolecules. 1976 Sep-Oct;9(5):812–833. doi: 10.1021/ma60053a024. [DOI] [PubMed] [Google Scholar]
- Tanaka S., Scheraga H. A. Statistical mechanical treatment of protein conformation. 5. A multistate model for specific-sequence copolymers of amino acids. Macromolecules. 1977 Jan-Feb;10(1):9–20. doi: 10.1021/ma60055a002. [DOI] [PubMed] [Google Scholar]
- Tanaka S., Scheraga H. A. Statistical mechanical treatment of protein conformation. II. A three-state model for specific-sequence copolymers of amino acids. Macromolecules. 1976 Jan-Feb;9(1):159–167. doi: 10.1021/ma60049a027. [DOI] [PubMed] [Google Scholar]


