A Novel Bioreactor for Mechanobiological Studies of Engineered Heart Valve Tissue Formation Under Pulmonary Arterial Physiological Flow Conditions

Short abstract

The ability to replicate physiological hemodynamic conditions during in vitro tissue development has been recognized as an important aspect in the development and in vitro assessment of engineered heart valve tissues. Moreover, we have demonstrated that studies aiming to understand mechanical conditioning require separation of the major heart valve deformation loading modes: flow, stretch, and flexure (FSF) (Sacks et al., 2009, "Bioengineering Challenges for Heart Valve Tissue Engineering," Annu. Rev. Biomed. Eng., 11(1), pp. 289–313). To achieve these goals in a novel bioreactor design, we utilized a cylindrical conduit configuration for the conditioning chamber to allow for higher fluid velocities, translating to higher shear stresses on the in situ tissue specimens while retaining laminar flow conditions. Moving boundary computational fluid dynamic (CFD) simulations were performed to predict the flow field under combined cyclic flexure and steady flow (cyclic-flex-flow) states using various combinations of flow rate, and media viscosity. The device was successfully constructed and tested for incubator housing, gas exchange, and sterility. In addition, we performed a pilot experiment using biodegradable polymer scaffolds seeded with bone marrow derived stem cells (BMSCs) at a seeding density of 5 × 10⁶ cells/cm². The constructs were subjected to combined cyclic flexure (1 Hz frequency) and steady flow (Re = 1376; flow rate of 1.06 l/min (LPM); shear stress in the range of 0–9 dynes/cm²) for 2 weeks to permit physiological shear stress conditions. Assays revealed significantly (P < 0.05) higher amounts of collagen (2051 ± 256 μg/g) at the end of 2 weeks in comparison to similar experiments previously conducted in our laboratory but performed at subphysiological levels of shear stress (<2 dynes/cm²; Engelmayr et al., 2006, "Cyclic Flexure and Laminar Flow Synergistically Accelerate Mesenchymal Stem Cell-Mediated Engineered Tissue Formation: Implications for Engineered Heart Valve Tissues," Biomaterials, 27(36), pp. 6083–6095). The implications of this novel design are that fully coupled or decoupled physiological flow, flexure, and stretch modes of engineered tissue conditioning investigations can be readily accomplished with the inclusion of this device in experimental protocols on engineered heart valve tissue formation.

1. Introduction

Engineered tissue approaches for the development of tissue engineered heart valves (TEHVs) offer the possibility of accommodating somatic growth, which in principle present a significant advance over current prosthetic valve replacements for the treatment of congenital heart valve disease [1]. The need for bioreactors designed for improving the physical integrity of engineered heart valve tissues prior to implantation has been well established [2–5]. Several studies have shown enhanced cell activity and tissue formation that can occur when simulated physiological culture environments are created in vitro [6–8]. At the organ level, several bioreactors that can provide TEHV leaflets with a dynamic conditioning environment that replicates hemodynamic parameters such as arterial pressure and flow conditions have been developed [9–11]. Early results using these pulsatile flow loop-based devices showed increased cell viability [4] and graded cell/tissue layering with cells orientated with the flow direction in comparison to unconditioned controls [9].

Previously, we subjected TEHV trileaflet constructs seeded with BMSCs, to simulated pulmonary artery pressure hemodynamic conditions for three weeks [12]. Under these conditions, we found quadrupled collagen mass and enhanced presence of deoxyribonucleic acid (DNA). Moreover, evidence from trileaflet valve flow patterns, along with similar patterns evident in our earlier bioreactor studies [13,14], led us to speculate that fluid-induced oscillatory shear stresses are a potential mechanism responsible for substantial enhancement in BMSC-derived de novo collagen formation. More recently, additional investigations have demonstrated the utility of other progenitor cell sources such as adipose derived stem cells [15] and periodontal ligament cells [16] for heart valve tissue engineering. Therefore, heart valve tissue engineering requires an as yet to be determined combination of heart valve-relevant mechanical conditions, cell stimulation, and scaffold for the systematic optimization of engineered heart valve tissues.

However, use of intact trileaflet heart valve constructs in mechanical conditioning studies remain confounded by the complex, simultaneous flow and leaflet deformations that occur during normal function. Moreover, for optimization purposes, the cell type(s), scaffold materials, biochemical constituents of the culturing media, and the specific stress modalities (valves are subject to coupled fluid, tensile, and flexural stresses [1,12,13,17]) are of primary importance. To this end, the effects of individual and combined stress states together with different scaffold materials and cell sources can be systematically evaluated in terms of outcomes such as bulk protein content, cell differentiation capacity, engineered tissue mechanical properties and cellular signaling events, all of which may serve to elucidate how external mechanical factors modulate cell to extracellular matrix interactions. These studies can then subsequently lead to the development of optimal in vitro conditioning protocols with the specific intent of mechanically stimulating engineered tissue formation [1].

We previously developed a bioreactor that permitted coupled or decoupled FSF as applied to rectangular scaffold specimens [13,14,18,19]. The rationale for this bioreactor was to investigate the effects of internal and external stress states found in native heart valves to engineered tissue development. Using this system with BMSCs seeded onto scaffolds, we determined that combined cyclic flexure and fluid-induced shear stresses during conditioning were found to synergistically accelerate tissue production [13]. This study also underscored the need for rational, mechanistic approaches in understanding the role of mechanical conditioning on growing tissues under well-controlled conditions.

However, a limitation of these studies was the inability to produce physiological to supraphysiological hemodynamic flow conditions. Previous investigations have experimentally determined the dynamic range of fluid-induced shear stresses on trileaflet valve geometries, with an upper limit leaflet shear stress of ∼79 dynes/cm², when a flow rate of 22.5 l/min was prescribed [20–22]. Subsequent studies have used this limit in computational models of heart valve dynamics [23] and in the design of shear stress bioreactors [24]. In an in vivo environment, however, native aortic valve leaflet surfaces on the ventricular side are typically exposed to shear stresses in the order of ∼6 dynes/cm² during end systole [25]; the stresses are an order of magnitude lower on the arterial side. In addition, dynamic flexure and stretch states need to be coupled to shear stresses in a bioreactor to make it physiologically relevant for heart valves.

In the present study, we developed a new bioreactor system capable of developing physiologically relevant fluid-induced shear stresses and regionally specific flow patterns to scaffold specimens, and couple these stresses to cyclic flexure and/or stretch states if desired. We utilized a cylindrical conduit configuration for the conditioning chamber to allow for higher fluid velocities, translating to higher shear stresses on the in situ tissue specimens while retaining laminar flow conditions. Moving boundary CFD simulations were performed to predict the flow field under combined cyclic flexure and steady flow (cyclic-flex-flow) states using various combinations of flow rate, and media viscosity. The device was successfully constructed and tested for incubator housing, gas exchange, and sterility. In addition, we performed a pilot experiment using biodegradable polymer scaffolds seeded with BMSCs to demonstrate initial efficacy.

2. Methods

2.1. Design Concept.

Three fundamental requirements for the bioreactor design include: a sterile culture environment, physiologically realistic flow conditions that replicate local heart valve functional patterns, and relative ease of use to facilitate the handling of sterile specimens [26]. In particular, the ability to provide a biomimetic stress environment is considered critical to determine at the very least, the ability of the formed tissues to withstand the physiological environment. Moreover, this feature may be important for basic tissue conditioning, as physiological fluid pressure levels (mean pressure 20 mm Hg) used to mechanically condition dynamic trileaflet engineered heart valves resulted in a 35% increase in the rate of collagen production per scaffold-seeded cell, versus experiments performed under nonphysiologic conditions [12].

The physiologic range of fluid-induced shear stresses was previously identified experimentally in polyurethane valve leaflets resembling native trileaflet heart valve structures [20]. The maximum leaflet shear stress magnitude was found to be ∼79 dynes/cm² [20] and has subsequently been utilized as the upper limit of a shear stress waveform for comparisons with leaflet shear stress profiles, resulting from CFD simulations [24]. However, this magnitude of stress was imparted onto the leaflet surface only when an abnormally high steady flow rate (22.5 l/min) was imposed [20] (noting that normal, cardiac output at rest is 5 l/min). On the other hand, precise, computational prediction of physiologically relevant shear stresses on aortic valve leaflets [25] in its native environment was found to be in the order of 5–6 dynes/cm² on the ventricular side and < 1 dynes/cm² on the aortic side. Thus, from this finding, while the ideal shear stress environment in the context of an optimum tissue formation are still uncertain, it would thus seem that there would be a rational physiological basis to generate mean shear stress magnitudes with an upper limit of ∼6 dynes/cm². Regional shear stress variations would subsequently be dictated by the specimen geometry and configuration. Our complete design criteria allowing for the incorporation of a wide array of mechanical conditioning studies related to TEHV development is summarized in Table 1.

Table 1.

Our proposed design criteria for the development of a novel, physiologically relevant FSF bioreactor device for heart valve tissue engineering studies

Design criteria	Justification
Sterile environment	Maintain healthy cell and engineered tissues
Adequate gas exchange	Promote robust cell and de novo tissue growth
Fit within a standard cell culture incubator	Incubators are typically used to facilitate cell and tissue culture studies
Multiple specimens can be conditions in a single run. In this case, n = 12 specimens, i.e., four conditioning chambers, with three specimens/chamber was possible based on the size of a standard cell culture incubator	Bioreactor experiments are time-consuming and expensive. Meaningful conclusions based on statistical analyses and a reasonable sample size should be attainable from a limited set of well-planned experiments
Provide FSF stress conditioning separately or in any combination	FSF studies, coupled or decoupled are pertinent for heart valve tissue engineering studies as previously established [12,18]
Physiologically relevant scales for flow and flexure/stretch	Previously established to be up to 6 dynes/cm2 for fluid shear stress [25] and ∼ 1.2 Hz (72 beats/min) for flexure and stretch
MRI compatible	Longitudinal noninvasive tracking of cells will provide insights on cell migratory activity within scaffold environment [57]
Flow source or pump should facilitate steady or pulsatile flow regimes. No direct contact between pump and fluid. Fluid flow through tubing connected to pump in addition, should be gas permeable within the incubator but impermeable outside	Physiological pulsatile flow waveforms may be most biomimetic but prescribing more straightforward flow conditions, including square oscillatory waveforms and time-averaged steady flow should be possible since from a mechanobiology viewpoint, the specific roles of individual or combined stress states, as well as relatively simpler versus more complex flow environments (e.g., fully forward flow versus a combination of forward and oscillatory flow) can be identified in a systematic manner. The tubing requirement will maintain a sterile environment

As mentioned (Table 1), the overall system can be accommodated in a standard size cell culture incubator and consists of four conditioning chambers, each permitting the housing of three specimens, thus with a maximum allowable capacity of twelve specimens (Fig. 1). Details of its design, analysis, and validation are provided below:

Fig. 1.

Photo of the overall FSF bioreactor device, showing the four separate chambers, associated pump, tubing and culture media changing system. Key components are labeled as shown.

In developing the overall design, we first note that the chamber geometry is critical in inducing physiological levels of fluid-induced shear stresses. Thus, the main chamber geometry of the bioreactor was a narrow cylindrical tube (Fig. 2), where the Reynolds number (Re) is given by

Fig. 2.

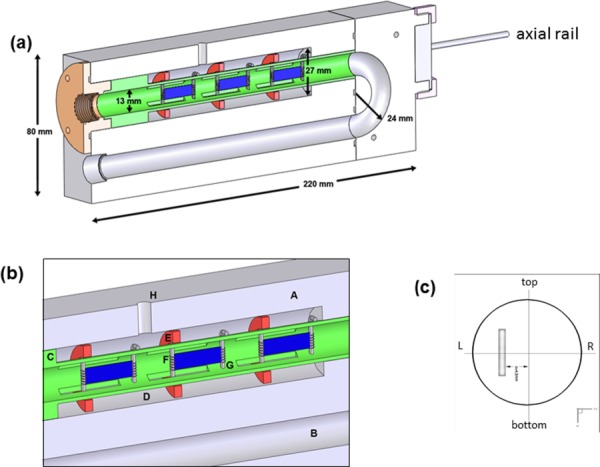
(a) Cut-out longitudinal section of the FSF bioreactor showing several key dimensions, (b) close-up view of key components in one of the bioreactor's conditioning chamber. In (c) is a cross section showing orientation and the placement of a specimen when flat in the flow tube, which were placed off-center by a distance of 4.3 mm. When flexed, the specimen will protrude into the center of the tube, moving in the left to right direction. Legend is as follows: A. ULTEM chamber, B. U-shaped fluid enclosure, C. Sliding sample holder, D. Outer tube, E. Ring, F. Moving post, G. Fixed post, and H. Injection port.

$$\mathrm{Re}=\frac{\mathit{uD}}{\mu }$$ (1)

where ρ is the fluid density, μ the dynamic viscosity, u is the mean fluid velocity, and D is the cross-sectional diameter of the chamber. For a Newtonian fluid, the relation between the fluid shear stress (τ) to the velocity is simply

$$\tau =-\mu \frac{{\mathit{du}}_x}{\mathit{dy}}$$ (2)

where u_x is the fluid velocity in the horizontal direction and y is the vertical direction in a conventional Cartesian coordinate system. Note that laminar flow generally holds for Re < 2300 [27], so that a small cross-sectional diameter would facilitate higher fluid velocities (and hence fluid-induced shear stresses) at a given Re number. Larger diameters, while facilitating the insertion of specimens into the device would reduce control over the flow within the laminar limit, which is important if physiological levels of shear stresses were desired. We note that the maximum velocities (u _max) in a cylindrical tube versus a chamber with a rectangular cross section are $u_{max}=2u$ and $u_{max}=1.5u$, so that a circular cross section allows enhanced flow development capabilities (ultimately, ∼33% higher) over rectangular cross sections. A diameter, D, of 13.0 mm was determined based on the smallest diameter possible that would concomitantly not interfere with specimen insertion and was practical for fabrication (Fig. 2(b)). Finally, a U-shaped flow chamber design was chosen over a straight tube section to allow the device to fit within a standard cell culture incubator. Detailed flow characteristics in the chamber such as the velocity field and fluid-induced shear stresses on the housed specimens were evaluated through moving boundary CFD simulations (see Sec. 2.7).

Adequate dynamic range of the flow rate was necessary for the pump component of the bioreactor. In addition, the flow source would have to be capable of driving more viscous liquids (at or above blood viscosity) in an efficient manner so as to achieve further increases in fluid-induced shear stress levels on the surface of the housed specimens, e.g., from 0.89 cP (water) ≤ $\mu$ ≤ 4.0 cP (viscosity-augmented cell culture media closer to blood viscosity of ∼3.3 cP). To accomplish this task, we chose to use a peristaltic (i.e., roller) pump (Masterflex, Cole-Palmer, Vernon Hill, IL) capable of flow rates of up to 2.3 LPM and which was verified to be efficient in driving fluids up to this limit for fluids whose viscosities fell within the aforementioned range.

2.2. Viscosity and Flow Rate Studies.

Apart from the geometry of the conditioning chamber of the bioreactor, the media viscosity and pump flow rate parameters play a central role in the magnitude of fluid-induced surface shear stresses that can be generated on housed specimens. Our intention here was to simply evaluate the magnitude of viscosity of regular cell culture media, confirm that its viscosity was a constant and finally, to demonstrate that media mimicking blood properties could also be prepared for heart valve tissue engineering experiments, if necessary. Viscosity measurements were thus conducted on two possible scenarios of tissue culture media (i.e., working fluid): (1) Control (standardized) media used in our previous TEHV protocols [12] and (2) increased-viscosity media. Control Media (Dulbecco's modified Eagle's medium (DMEM)) supplemented with 10% fetal bovine serum, 1% antibiotic–antimycotic plus HEPES buffer (all purchased from Invitrogen, Carlsbad, CA), 82 μg/ml ascorbic acid-2 phosphate (Sigma, St. Louis, MO) and 2 ng/ml basic fibroblast growth factor (Peprotech, Inc., Rocky Hill, NJ) was prepared and filter sterilized (Nalgene, Inc., Rochester, NY).

For studies focusing on the effects of fluid shear stress on live cells and tissue, standard culture media has been previously augmented with Dextran [28] or Xanthan Gum [29] to mimic blood viscosity. As previously utilized [29], 0.69 g/L of Xanthan Gum (Sigma) was added to the control media to create blood-analog fluid viscosity. A Brookfield cone and plate rotational rheometer (Middleboro, MA) operating at 25 °C was used to measure the viscosity of the media samples (three samples/group) over the range of shear rates from 50 to 700 s⁻¹. The fluid behavior for control media and Xanthan Gum-augmented media was determined (Fig. 3). The control media was found to be Newtonian with a constant (r ²= 0.974), average viscosity of 1.27 cP. On the other hand, the Xanthan Gum-augmented media exhibited non-Newtonian behavior, similar to blood. Blood viscosity has previously been reported in FSF bioreactor CFD studies [14] to be 3.7 cP. Thus, the viscosity value that we determined here for the commonly implemented media-based experiment (μ = 1.27 cP) as well as the viscosity previously reported (μ = 3.7 cP) [14] for the more hypothetical blood or blood-analog fluid-based experiment were subsequently applied in our CFD models.

Fig. 3.

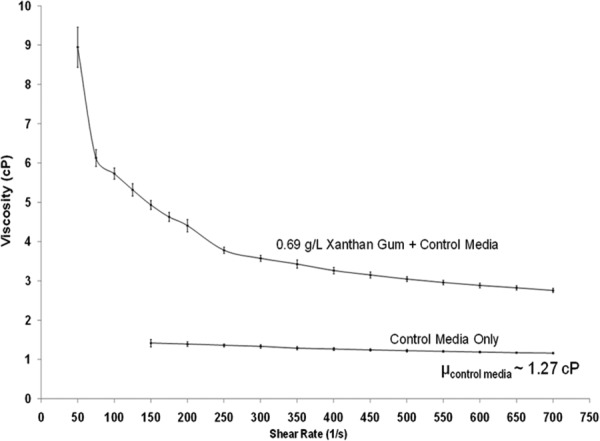
(a) Viscosity versus shear rate measurements for control (regular) cell culture media and increased-viscosity media, augmented with Xanthan Gum

2.3. Device Fabrication.

Several unique design features in the bioreactor were developed in order to enable assembly during use (Fig. 2(a)). A key criterion that allowed for a small (D = 13 mm) cross section for the U-shaped fluid enclosure was the ability to incorporate a separate, sliding sample holder (Fig. 2(b)). This attribute of the device design permitted access of surrounding pins and rings (contained in the outer tube) to the housed specimens, without any possible intrusion to the flow path. In addition, the holder could be separated from the rest of the device and facilitated ease of specimen insertion/removal. Following our previous design [14], we utilized a spiral bound grip for tissue attachment held in place by a pin (McMaster-Carr Elmhurst, IL) (Fig. 2(c)). One pin/specimen was fixed while the other pin was allowed to move. This movement was made possible through rings (McMaster-Carr) that are able to slide axially along the outer tube (Fig. 2(c)). In addition, the rings are coupled (via set screws) to a pair of axial rails (McMaster-Carr) (Fig. 2(a)), which are subsequently connected to a linear actuator (UltraMotion, Mattitick, NY) and can be programmed to prescribe a uniaxial displacement rate. Leakage was prevented at the exit location of the rails with the aid of silicon o-ring seals. The grips, pins, rings, and axial rails of the bioreactor were all made with 316 grade stainless steel, all mounted in the detachable sample holder (Fig. 2(d)).

Polyetherimide (ULTEM^™, General Electric, Pittsfield, MA) plastic was used as the material for device fabrication primarily due to its excellent resilience to withstand sterilization (autoclave and ethylene oxide gas) procedures. An added benefit of ULTEM is its ability to provide outstanding magnetic susceptibility matching to water [30], permitting the bioreactor to be imaged using magnetic resonance imaging (MRI). An effort to facilitate complete MRI-compatibility and image the housed specimens in a noninvasive and nondestructive manner by MRI were demonstrated previously [31]. Connectivity of the bioreactor chambers to the peristaltic pump is performed via gas permeable and impermeable silicone tubing (Cole-Parmer, Vernon Hills, IL) whose combined length is roughly 2.5 ft from one end of the bioreactor chamber to one end of the pump; the gas permeable tubing is used inside the incubator to facilitate gas exchange while the impermeable tubing provides connectivity on the outside to the pump which is also kept outside, thereby minimizing the risk of contamination.

A glass bottle (media volume ∼500 ml VWR, Bridgeport, NJ) is connected to each chamber (Fig. 1) to allow for media exchange. The peristaltic pump is first used to clear all the spent media from the tubing and the conditioning chambers into the bottles. Next the pump is used to evacuate the media from the bottles into a waste container that is housed within a sterile culturing hood. The process of media removal is then reversed to allow entry of fresh media into the system. Prior to each use, the device is gas sterilized with ethylene oxide for 16 h.

2.4. Gas Exchange and pH Measurements.

In order to determine the efficiency of gas exchange between the bioreactor and the ambient air inside a standard cell culture incubator, oxygen partial pressure (pO₂), carbon dioxide partial pressure (pCO₂) and pH measurements were performed using a blood-gas analyzer (Radiometer medical, Westlake, OH). Measurements were conducted under three different experimental settings:

• (1)No flow in the bioreactor. The bioreactor chambers were filled with culture media with the pump switched off.
• (2)Perfusion of flow through the bioreactor (flow rate = 1.06 LPM).
• (3)No flow (no bioreactor used). Media was poured into centrifuge tubes (Fisher Scientific, Pittsburgh, PA) and were sealed with a filtered, vented cap (BD biosciences, San Jose, Ca) that served as a positive control.

Cell culture media (DMEM supplemented with 10% fetal bovine serum, 1% antibiotic–antimycotic plus HEPES buffer, Invitrogen) was prepared and filter sterilized (Nalgene Inc, Rochester, NY). The media was introduced to the three groups. The no flow group utilizing the vented centrifuge tubes (group 3) is routine containment of media in incubators, for example, during scaffold cell seeding processes which can take several hours [12,32], and for which effective gas exchange (pO₂ and pCO₂) and pH preservation is a must. Therefore, groups 1 and 2 were compared in a relative context to group 3 which was regarded as a “best case scenario” for effectuating gas exchange. An initial measurement was taken immediately after the groups were placed into the incubator (Fisher Scientific, Pittsburgh, PA). Measurements from the two bioreactor chamber groups were taken with a syringe through an injection port (see item H in Fig. 2(c)) located at the top of the flow chambers. Thus, media was extracted directly at the site where specimens would normally be housed in an experiment. Measurements of pO₂, pCO₂, and pH were also determined for media from the plastic tube. Media extracts (1 ml volume) were taken for each measurement at half-hour intervals over a 5 h period. In addition, aliquots (n = 3 per group) were assessed from each group after three days. An assessment of the means among the three groups for gas exchange (pO₂ and pCO₂) and pH was performed using a one-way analyses of variance (1-way ANOVA) test, followed by posthoc testing to determine if there were any statistically significant differences (p < 0.05) between the groups.

2.5. Sterility Assessment.

As a means to evaluate contamination risk in the device, histological stains comprising, positive/negative Gram staining for common bacteria and periodic acid Schiff (PAS) light green staining for common fungal organism detection were performed on samples of media that was circulated through the bioreactor. In brief, spent media (after five days of operation) from the bioreactor was smeared onto clean slides with a cotton tipped swab. Slides were then fixed in absolute alcohol for 30 s after which the stains were applied. Once all histological stains had dried, a neutral, yellow background stain was used to permit enhanced visibility. The slides were subsequently photographed under view of an optical microscope.

2.6. Pilot Experiment.

As a proof-of-concept, we conducted a mechanical conditioning experiment with our bioreactor under combined cyclic flexure (1 Hz frequency) and steady flow (Re = 1376 flow rate of 1.06 LPM) conditions. BMSCs were isolated from ovine bone marrow as described previously [33]. In brief, cells were (initiated from passage 4) expanded in DMEM (Invitrogen) and supplemented with 10% fetal bovine serum, 1% antibiotic–antimycotic plus HEPES buffer (all Invitrogen). Upon achieving sufficient cell numbers, BMSCs (passage 9) were seeded onto nonwoven scaffolds consisting of a 50:50 blend of polyglycolic acid (PGA) and poly-L-lactic acid (PLLA) fibers (Concordia Fibers, Coventry, RI). Three separate rectangular (∼22 × 6 × 1.5 mm) scaffolds were seeded for approximately 24 h with a seeding density of 5 × 10⁶ cells/cm². The seeding solution was supplemented with 82 μg/ml of ascorbic acid (Sigma, St. Louis, MO) and 2 ng/ml of basic fibroblast growth factor (Peprotech, Carlsbad, CA) in addition to the regular cell culture ingredients used for expansion. After seeding, three tissue samples were loaded into the bioreactor prototype and were conditioned for a period of two weeks in an incubator (37 °C and 5% CO₂). Media changes were performed once weekly. The core region of each specimen (n = 3), i.e., neglecting the ends of the sample, were assayed for collagen content (Sircol kit, Biocolor, Ltd., Newtownabbey, N. Ireland) as previously described [12,13].

2.7. CFDs

2.7.1. Parabolic Specimen Motion.

The purpose of the CFD simulations performed herein was to delineate: (1) the detailed velocity field surrounding the specimens housed in the bioreactor and (2) the spatial distribution of the specimen surface fluid-induced shear stresses when subjected to combined cyclic flexure and steady flow (cyclic-flex-flow) environments. In developing the CFD simulations we modeled the main components as follows. The bioreactor had a shape of a 180 deg curved pipe with dimensions shown in Fig. 4(a). Three leaflets were 37 mm apart, while the last specimen was located 73 mm from the bioreactor outlet. The specimens were placed 4.3 mm off-center of the pipe. Each of the bioreactor specimens had a rectangular shape with a length of 25 mm, width of 7.5 mm and a thickness of 1 mm. In our CFD model, the surface of the leaflet was meshed using 124 triangular elements (Fig. 4(b)). For the entire bioreactor geometry, a body-fitted, structured computational grid (141 × 141 × 857) was employed following grid independence tests which demonstrated that reasonable shear stress convergence was being achieved (data not shown). As in the previous design [13,14], specimen flexure was induced utilizing an actuator connected to a moving post that is in turn connected to one end of each sample, with the other end connected to a fixed post. Additionally, the shape of each sample along its length (y-direction) conformed to the equation of an arc length with the constraint of a fixed length (L ₀) at any time point of 25 mm

Fig. 4.

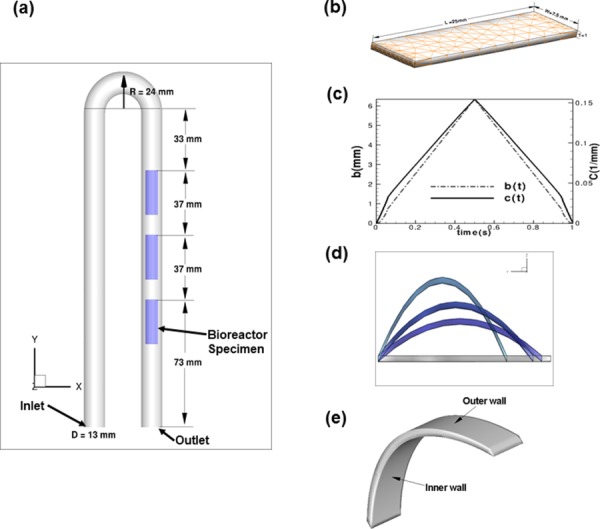
(a) The bioreactor geometry used for CFD modeling. (b) Triangular elements used to mesh the rectangular specimens. (c) Position of the moving post (“b” in Eq. (3)) for the leaflet deformation over one cycle T = 1 s; for completeness, the variation of the quadratic coefficient (“C” in Eq. (3)) with time is also shown. (d) Deformation of the specimens over one cycle, noting that the deforming shape was assumed to take on parabolic profile according to Eq. (3). (e) Location of the specimen inner and outer surfaces.

$$z=-C\left(t\right)y^2+C(t){\left[\frac{L_0-b}{2}\right]}^2$$ (3)

where b is the evolving position of the moving post (determined from the prescribed actuator motion; Fig. 4(c)) that moves toward the stationary post, t is the time and C is the quadratic coefficient that changes according to the new position b with each time step. The value of y denotes the axial distance from the fixed post to the moving post, and the value z denotes the displacement along the Z direction. Since the upstream ends of the specimens are fixed, it deforms as a curved body (Fig. 4(d)). Note that the specimens attained their maximum vertical displacement at t = 0.5 s (mid cycle). The motion resulting from Eq. (3) was prescribed directly into the CFD simulations. Specific flow physics were investigated in regions proximal to the specimen inner and outer walls (Fig. 4(e)).

2.7.2. Moving Boundary Simulations.

We assumed incompressible, Newtonian fluid whose motion is governed by the unsteady, three-dimensional Navier–Stokes equations. The cardiovascular flow solver C²FD-UMN utilized has been previously validated in numerous cases for flow over complex geometries and moving boundaries [34,35] and nonlinear fluid–structure interaction problems [35]. The governing equations were solved in a background mesh that contains the complex geometry using the sharp-interface curvilinear immersed boundary method of Ref. [36]. The algorithm has been shown to be C²-order accurate in space and time [34,36]. The discrete equations were integrated in time using a fractional step method [36]. A Newton–Krylov solver was used to solve the momentum equations in the momentum step and a GMRES solver with multigrid preconditioner was employed for the Poisson equation. A time step of 0.5 ms was used in the simulation. Five CFD simulation cases were conducted (Table 2). Note that the fluid density in the computation of Re (Eq. (2)) was assumed to be 1000 ${\mathrm{kg}/\mathrm{m}}^3$ in all cases.

Table 2.

Summary of the five CFD simulations that were conducted for flow physics evaluation of the bioreactor. Note that the density in the computation of Re (Eq. (2)) was assumed to be unity in all cases.

Case	Q (ml/min)	Viscosity (cP)	U 0 (m/s)	Re
A	1060	1.27	0.1333	1376
B	1060	3.7	0.1333	486
C	850	1.27	0.1067	1100
D	850	3.7	0.1067	375
E	557	3.7	0.0700	246

3. Results

3.1. Gas Exchange.

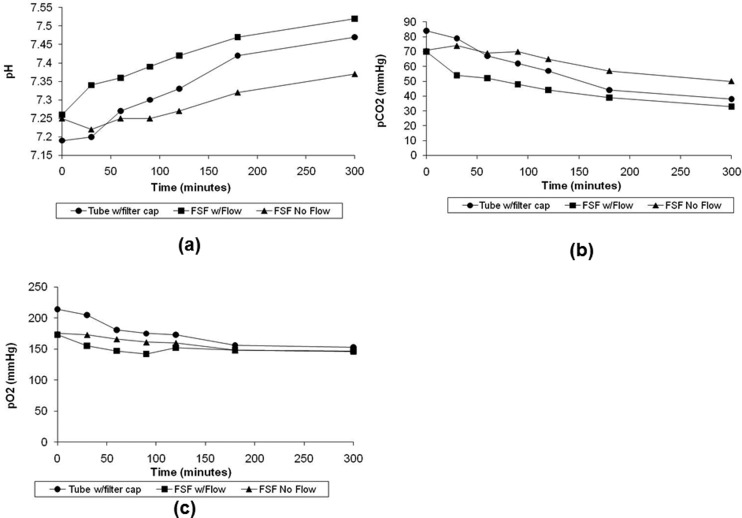
Over a 5-h period, the pH of the media marginally increased (Fig. 5(a)) while slight decreases in the partial pressure of incubator ambient gases were observed (Figs. 5(b) and 5(c)). At the end of 3 days, no statistical significance (p > 0.05) was found in any of the measurements between media contained in the plastic tube with a filtered cap (group 3) and in the bioreactor when the pump was operational (group 2; Table 3). However, without the benefit of flow in the bioreactor (group 1), only the pO₂ levels were found to be insignificant (p > 0.05) in comparison to the positive control group (group 3); on the other hand, differences in the mean pH and pCO₂ were significant (P < 0.05), indicating that flow in the conditioning chamber is essential to ensuring adequate gas exchange.

Fig. 5.

5-h variation of (a) pH, (b) pCO₂,  and (c) pO₂ levels after placement in incubator

Table 3.

Gas and pH measurements (n = 3 samples/group) taken from the bioreactor after 3 days of incubation. p > 0.05, i.e., no significance was found between media contained in vented centrifuge tubes with a filtered cap and in the bioreactor when the pump was operational. However, without flow only the pO₂ levels was insignificant (p > 0.05) in comparison to the control group but differences in the mean pH and pCO₂ were found to be significant (p < 0.05).

Group name	pH	pCO2 (mmHg)	pO2 (mmHg)
Centrifuge tubes with vented filter cap	7.67 ± 0.04	23.3 ± 2.52	148 + 3.61
Bioreactor with flow	7.63 ± 0.01	25.3 ± 0.58	147 ± 1.73
Bioreactor, no flow	7.57 ± 0.02	29.0 ± 1.73	144 ± 2.31

3.2. Sterility Tests.

Absence of common bacterial and fungal contamination was verified by histology in media that circulated in the bioreactor for a 5-day period (data not shown). Positive and negative Gram staining as well as the PAS light green [37] all stained absent for microbial activity. This result provided some confidence that this FSF bioreactor system could be kept sterile when used for live cell and tissue culture experiments.

3.3. Engineered Tissue Formation Study.

Exposure of BMSC-seeded nonwoven scaffolds to two weeks of cyclic flexure combined with flow mechanical conditioning produced an average ± SEM (n = 3) collagen/wet weight of 2051 ± 256 μg/g (cell seeding density of 5 × 10⁶ cells/cm²). This amount was significantly higher (P < 0.05) than equivalent prior experiments in our laboratory (844 ± 278 μg/g; cell seeding density of 17 × 10⁶ cells/cm²) [13], where the time-averaged mean specimen surface shear stresses were lower (<2 dynes/cm²) [14] compared to the range of stresses applied in this study (>5.1 dynes/cm²).

3.4. CFDs.

Flow in the bioreactor created a classical secondary flow pattern for 180 deg bend flow owing to its U-shape construction. These secondary flow patterns occurred and directed the low velocity region at the inner curvature while the higher velocity was pushed toward the outer curvature. Bioreactor specimens were hence strategically placed past the curved bend to leverage the highly 3D flow in this region. The reduction in Re number (either by decreasing the flow rate or using higher viscosity) in the simulations verified that the relative flow features were similar for all Re number cases. Specifically, there were no observable differences (direction, secondary flow structures, separation, vortex shedding, etc.) in the large scale structure of the flow, which was quite similar for all Re number cases (Fig. 6).

Fig. 6.

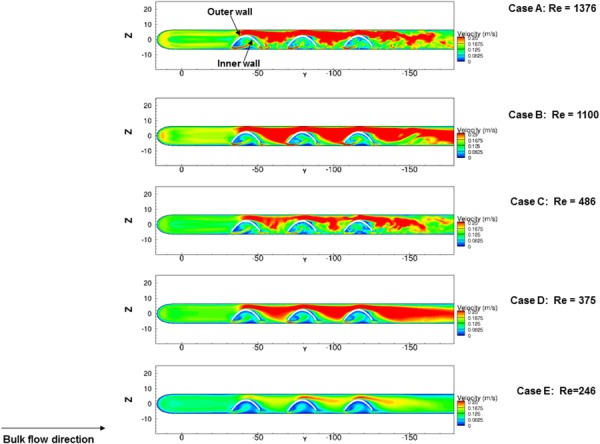
Contour of velocity magnitudes in the plane (x = 17.5 mm) at the centerline of the specimens with different Re numbers at t = 0.5 s. Note that because we carried out the numerical simulations over a relatively wide range of Reynolds number from Re = 246 to Re = 1376, there will be a significant difference in velocity magnitude among the bulk flow of the cases, u = 0.07 m/s to u = 0.1333 m/s. and in turn, the magnitude of velocities in the vicinity of the samples will be substantially different. On the other hand, our reason for choosing u = 0.25 m/s as the “cut-off” level was purely for visualization (color scale) purposes so that the flow structure could be compared between cases.

Since our interest was primarily on physiological flow levels, the following focused on case A (Re = 1376). For the first 0.5 s, the specimen flexure was mainly in a path opposing the main flow direction, whereas from 0.5 to 1 s straightening of the specimens occurred in the same direction as the flow. As expected, an increasing level of narrowing between the flexing samples and the bioreactor tube right wall translated to higher velocities occurring with increasing level of flexure (Fig. 7). Conversely, regional velocities proximal to the flexed surface decreased as the specimens began to straighten out.

Fig. 7.

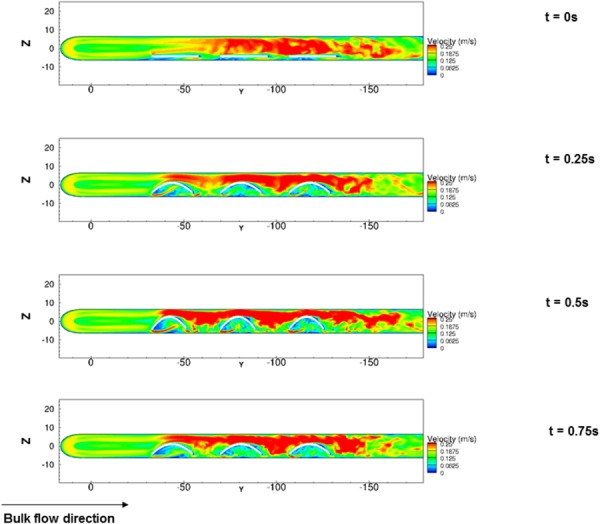
Contour of velocity magnitudes in the plane (X = 17.5 mm) at the center line of the leaflet at different time instants during one cycle t = 0, 0.25, 0.5, and 0.75 s of case A (Re = 1376) depicting increasing degrees of specimen flexure. High velocity streaks were augmented with an increase in specimen flexure. Note that because we carried out the numerical simulations over a relatively wide range of Reynolds number from Re = 246 to Re = 1376, there will be a significant difference in velocity magnitude among the bulk flow of the cases, u = 0.07 m/s to u = 0.1333 m/s and in turn, the magnitude of velocities in the vicinity of the samples will be substantially different. On the other hand, our reason for choosing u = 0.25 m/s as the cut-off level was purely for visualization (color scale) purposes so that the flow structure could be compared between cases.

As the Re number increased, the interaction between the sample motion and the bulk flow became more intense creating heightened disturbances at the downstream of each sample. Recalling that the Re number is the combination of the bulk flow velocity and the viscosity of the fluid, the bulk flow rate (and hence velocity) at the inlet varied in a substantially wide range (Table 2). Therefore, the absolute velocity magnitude that the samples would experience will be considerably different between Re number cases simulated. However, the extent of similarity among the fluid dynamic conditions of three samples within one experimental setup could be adjudicated using the magnitude and directionality of the shear stress, since it is the shear stress that is the fluid-induced mechanical conditioning parameter. As the results show (Fig. 7), the flow structure is quite similar at different time instants. The reasons for this similarity are due to the identical motions of the three samples as well as the unidirectionality of the bulk flow within the flow-conditioning chamber. In order to directly quantify the similarity in shear stresses between three samples housed within the flow-conditioning chamber, we plotted the time-averaged shear stresses and streamlines on the specimen surfaces over a cycle (Fig. 8). The average shear stress was calculated from the instantaneous shear stress magnitude $\left|\overrightarrow{\tau }\right|$ over the cycle T

Fig. 8.

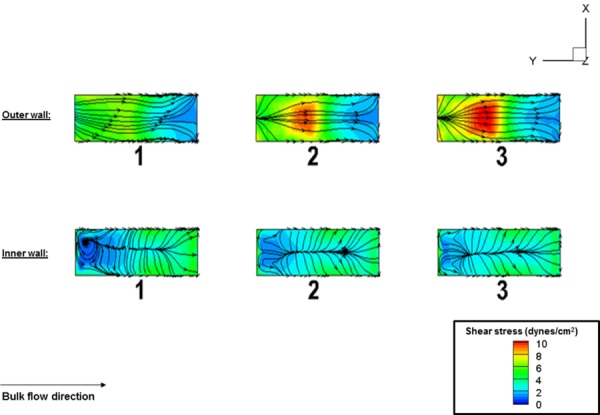
Time-averaged specimen shear stress magnitudes and streamlines over one cycle. The following axial locations (Y/D): − 3.5 (specimen 1), −6.34 (specimen 2), −9.2 (specimen 3), corresponding to the center of each specimen, was where the largest magnitude and variation in shear stress magnitude occurred. The outer wall mean shear stress (dynes/cm²) for specimens 1, 2, 3 were 5.5, 7.6, and 7.4, whereas the corresponding inner wall mean shear stress (dynes/cm²) for specimens 1, 2, and 3 were: 2.7, 2.5, and 2.4. These results showed that the average shear stress magnitude was lower for specimen 1 in comparison to specimens 2 and 3 on the outer surface; nonetheless, the difference was comparably small (less than 10%). For the inner wall, the three specimens were subjected to nearly the same value of average shear stress magnitude.

$$\overline{\tau }={\int }_0^T\frac{\left|\overrightarrow{\tau }\right|}{T}\mathit{dt}$$ (4)

We found that there were magnitude differences in shear stress between samples (Fig. 8). On the outer surface, the shear stress distribution had the largest value at the center of the surface, which also displayed the largest variability between the samples. The lowest value was found at the downstream location of the specimens. The mean, average shear stress on the center location of the outer wall was found to be (n = 3 specimens; mean ± SEM): 6.83 ± 0.6; on the inner wall it was found to be 2.53 ± 0.09 (dynes/cm²). This represents ∼9.8% and 3.5% error in mean, average specimen shear stress on the outer and inner walls, respectively. We deemed this an acceptable amount of variability in consideration that the differences were small, i.e., less than 10% between specimens at any given spatial location and secondarily, that differences would inevitably be caused primarily by the flow development, with the downstream samples (sample 3) possessing slightly higher shear stress magnitudes than the upstream sample (sample 1). Moreover, a trend in the shear stress patterns (streamlines) could also be found on both the specimen inner and outer walls. On the outer wall, the nature of the shear stress patterns was such that it aligned very well with the bulk flow for all three specimens. On the contrary, the shear stress pattern had a “convergence–divergence” structure on the inner wall. This convergence–divergence pattern was found to be consistent for all three specimens, which again confirmed than the fluid dynamic conditions for all three samples were indeed similar throughout the cycle. Thus, in consideration of the aforementioned similarities in shear stress magnitudes (less than 10%) and very similar shear stress patterns, we concluded that the uniformity in flow-conditioning was maintained across all three specimens within one chamber of the bioreactor.

On the specimen outer surface near position “A,” flexure during steady flow created a local stagnation point and a small separation area right toward position “B” (Fig. 9). However, the dynamics was found to be much more complex along the sample inner wall. The onset of flexure of the samples created a suction, which drew fluid particles toward the inner wall resulting in flow entrainment in this region. Such entrainment induced a complex pattern to form. A high-speed leakage jet was observed, which in turn induced a small vortex separation near position A (Fig. 9). It was further observed that the leakage jet was regulated by the flexure event, which also dictated the overall flow patterns along the sample inner wall.

Fig. 9.

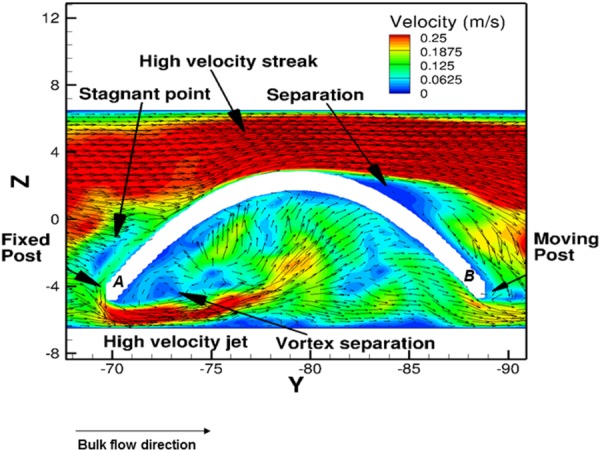
Flow patterns around the center specimen for case A (Re = 1376) during one cycle, at the peak flexure state (t = 0.5 s). The velocity vectors were projected on the plane at X = 17.5 mm (i.e., on the centerline of the leaflets). The high velocity streaks were found to be surrounding the sample outer wall, whereas flow vortex formation and reversal occurred proximal to the inner wall, near to the fixed postlocation. The velocity field was considerably lower in the region surrounding the inner wall of the samples. Note that reference positions proximal to the fixed and moving posts have been labeled as A and B in the figure, respectively.

The shear stress patterns on the surface outer wall of the samples remained aligned with the main flow direction throughout the cycle (Fig. 10). In addition, the shear stress patterns were nearly symmetric across the centerline of the specimens. The magnitude of the shear stress varied largely during the flow cycle. As the leaflet deformed from a straight (t = 0 s) to a curved position (t = 0.25 s) the shear stress magnitude increased at the apex of the samples. It reached its maximum at t = 0.5 s and started to decrease as the specimens began flattening out (t = 0.75 s).

Fig. 10.

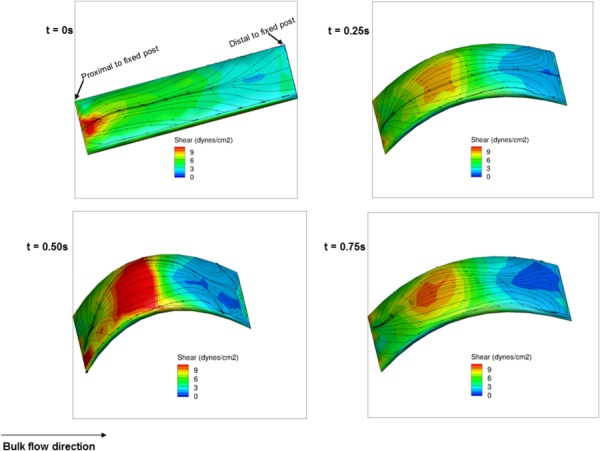
Fluid-induced shear stress distribution on the outer wall surface of the intermediate specimen for case A (Re = 1376) during one cycle at t = 0, 0.25, 0.5, and 0.75 s

The more complex flow physics on the side proximal to the specimen inner wall directly translated to more complex shear stress distribution in that location (Fig. 11). Relatively higher shear stresses occurred in the downstream region along the inner wall because the flow exited at this location. Note that there were two distinct regions of shear stress on the specimen inner walls: (1) the reverse shear pattern region (opposite to main flow direction) and (2) forward shear pattern region. The shear pattern tended to converge into a single line at the center of the sample inner wall. On the other hand, due to the effect of the high-speed jet (Fig. 8), the shear patterns near position A changed considerably from one time instant to the other resulting in an oscillatory effect. The oscillatory shear index (OSI), as defined by He and Ku [38], was used to quantify the extent of oscillatory shear. In brief, OSI was calculated using the following equation:

Fig. 11.

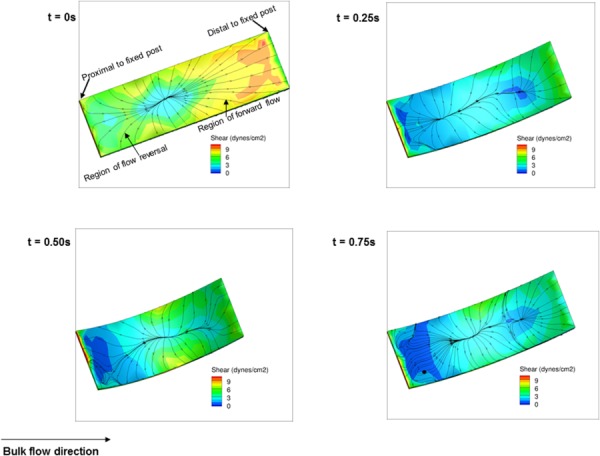
Fluid-induced shear stress distribution on the inner wall surface of the intermediate specimen for case A (Re = 1376) during one cycle at t = 0, 0.25, 0.5, and 0.75 s

$$\mathrm{OSI}=\left(\frac{1}{2}\right)(1-\frac{\left|\left({\int }_0^T\tau \mathit{dt}\right)\right|}{{\int }_0^T\left|\left(\tau \right)\right|\mathit{dt}})$$ (5)

where “T” is the duration of the cycle, “τ” is the instantaneous specimen shear stress vector and “dt” is the time derivative. From the above definition, OSI ranges from 0 to 0.5 where 0 represents completely unidirectional flow and 0.5 describes flow that is purely oscillatory with no net flow in the forward direction. As expected, the OSI was very low on the outer wall of the specimen (maximum OSI = 0.12), except for the distal portion due to exit effects (Fig. 12 ). However, the OSI was considerably higher on the sample inner wall (maximum OSI = 0.35).

Fig. 12.

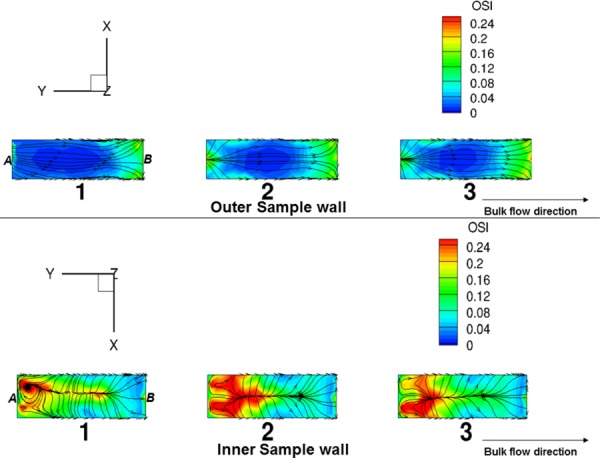
OSI distribution on the outer (top) and inner (bottom) wall of the three bioreactor specimens for case A (Re = 1376). The streamlines represent the mean shear stress pattern on the sample surface. As seen, OSI values were clearly much higher on the sample inner wall suggestive of utilization of the bioreactor device for cell mechanobiology studies involving oscillatory shear stress. Note that reference positions proximal to the fixed and moving post have been labeled as A and B in the figure, respectively.

4. Discussion

4.1. Need for Physiologic Flow Conditions.

Studies on the development of engineered heart valve tissues are relatively more recent than other applications such as skin, blood vessels, and cartilage [2,33,39–46]. A common theme is the notion of promoting tissue formation in a physiological environment. Recent engineered heart valve tissue studies involving simulated pulmonary pressure waveforms (20 mmHg mean value) demonstrated enhanced collagen production per DNA mass by ∼35% over cyclically flexed specimens subjected to concomitant subphysiologic shear stresses [12]. Indeed, it has been shown that in the context of TEHVs, appropriate mechanical stimulation of the constructs is advantageous to its development, specifically, that exposure to mechanical stress states in vitro improves tissue production, organization, and function [47]. However, since optimal mechanical conditioning regimens essential to the overall success of the implant are still largely unknown and likely application specific, there is still an unmet need to develop bioreactors that can provide an avenue to delineate the effects of different stress states on engineered tissue formation.

Although due consideration to the importance of physiological levels of fluid-induced shear stress magnitudes has been considered [48], this was done without flexural and/or stretch components. In fact, few bioreactors [49–52] have to date focused on individual mechanical conditioning effects of external stimuli on engineered cardiovascular tissue formation. Cyclic flexure, stretch and flow stresses are present during native valve leaflet deformation and may produce individual as well as coupled stimulatory effects [13,14], and are thus important for systemic evaluation on different scaffold materials and cell sources.

Previously, we developed a bioreactor permitting coupled or decoupled FSF on rectangular specimens [14]. Subsequent studies demonstrated enhanced tissue formation under combined cyclic flexure and flow stress states [13], but the achievable, maximum fluid-induced stresses were relatively low (less than 2 dynes/cm²) [14]. Our recent findings [12] for BMSC seeded scaffolds suggest that fluid-induced stresses play a major role in collagen formation rates, so that scaling the conditioning to accommodate these effects (i.e., physiologically relevant scales) may have added benefits in forming robust valvular tissues. In addition, specific flow distributions that induce regionally unique flow patterns such as oscillatory flow may also play a critical role depending on the cell sources that are used (e.g., BMSCs) [12,53–55].

Given the clear complexities of cellular response to biophysical stimuli and subsequent engineered tissue formation, these results underscore the significant need for specialized systems that combine the major heart valve deformation/loading modes (FSF) at physiological levels. This sentiment is further emphasized through our current efforts in which we were able to demonstrate the ability of our bioreactor system to support robust engineered tissue growth with modest BMSC seeding densities (5 × 10⁶/cm²) compared to previously reported amounts and seeding densities used in our laboratories [13]. However, further experimentation with the bioreactor will undoubtedly be required to conclusively delineate the effects of physiological shear stress as a mechanical stimulus on BMSC extracellular matrix secretion rates.

4.2. Bioreactor Design Features.

The primary innovative design feature of this novel FSF bioreactor was the use of a narrow cylindrical flow chamber that facilitated proper development of the flow field from its initial generation by the peristaltic pump. Usage of the peristaltic pump in conjunction with tissue experiments is beneficial in several ways, namely, that (i) the pump requires minimal contact with the fluid thereby minimizing contamination risk, (ii) all tubing in contact with the fluid is disposable and can be sterilized, (iii) the pump is efficient at displacing higher viscosity liquids, (iv) the pump design inherently prevents backflow without the need for valves and thus requires minimal maintenance, and (v) the pump can be set to operate in either steady or pulsatile modes.

Importantly, our design of the device's conditioning chamber geometry permits the application of physiological levels of surface, time-averaged, fluid-induced shear stresses (e.g., 5–6 dynes/cm² [25]) on tissue specimens (Figs. 9 and 10). However, a concern is that some fluid particles may experience weak transitional flows (e.g., Re ∼ 2500). This can occur for example at time instances when the specimens are fully flexed (t = 0.5), at spatial locations surrounding the outer wall, and when the inlet Re number exceeds 400. However, this concern was offset by the fact that all three specimens housed within the flow chamber experienced very similar shear stresses (Fig. 8). Nonetheless, if the laminar flow condition needs to absolutely be preserved throughout the entire duration of the tissue culture experiment, the flow rate can be decreased and/or the media viscosity augmented (i.e., Eq. (2)) with additives (e.g., Xanthan Gum [29]), such that the shear stresses still remain physiologically relevant for valves.

Shear stress magnitudes and distribution were very consistent between specimens housed within the bioreactor (Fig. 12). It is also worthwhile noting that the shear stress patterns on the inner and outer walls of the specimens were analogous to the aortic and ventricular sides of the aortic valve [25], given that much lower magnitudes of shear stresses and larger degrees of flow reversal were present on the surface of the inner wall compared to the outer wall (Fig. 12). Such variations that mimic the native valve shear stress spatial distributions may serve useful in detailed evaluation of specific fluid-induced mechanical conditioning effects on regional tissue development. In particular, the combined cyclic-flex-flow studies are likely to also serve useful for investigations probing the effect of oscillatory shear stresses on cell regulatory events and de novo tissue growth; oscillatory shear stress has been shown to affect BMSC differentiation [53–55].

Another aspect of specimen movement relates to its uniformity in flexion. Here, we assumed uniform flexure in our CFD simulations based on the actuator motion and assumptions regarding the sample shape (Eq. (3)). These approaches are valid for relatively stiffer scaffold materials such as the 50:50 PLLA/PGA nonwoven scaffold material that was used in this study. Other scaffolds, however, may be more compliant resulting in nonuniform flexion under the influence of cyclic flexure and/or flow. To circumvent this problem, we can easily modify our current bioreactor design's specimen mounting system by inserting a secondary polymer substrate to guide the flexural shape of the primary scaffold. Such usage has been reported by our group recently using polyvinyl chloride strips to maintain specimen shape during cyclic flexural fatigue testing [56].

The bioreactor was built out of an amorphous thermoplastic ULTEM material mainly because it is nontoxic and resilient to ethylene oxide and autoclave sterilization procedures. This was confirmed by exposure of the device to several cycles in an ethylene oxide gas sterilizer, which did not cause any material deterioration or loss of functionality. Flow could be diverted using stopcocks in the system to pump media out of and into the bioreactor and these media changes were possible without the removal of the device from the incubator, thereby minimizing exposure to nonsterile environments. Sterility studies examining media circulating through the bioreactor for five days revealed no signs of microbial contamination. When the pump is in operation, gas exchange and pH within the main bioreactor chamber was verified to be insignificantly different (P > 0.05) from vented centrifuge tubes that are used for housing of cells and tissues (for at least 24 h) within an incubator. This finding demonstrated that at minimum, the bioreactor when subjected to flow environments provides gas exchange and preservation of pH comparable to containment systems used routinely in the laboratory. In addition, the MRI susceptibility matching properties of ULTEM to water combined with the ability to easily replace specific components (screws, actuator rods, etc.) of the device with plastic equivalents made this novel FSF bioreactor adaptable for use in an MRI instrument. We were able to previously demonstrate that specimens inside the chamber could be successfully imaged by MRI [57].

Although the results herein focus on steady pump flow conditions, we note that the pump could be programmed to generate pulsatile flow waveforms if necessary. Other innovative design features, such as the removable sample holder (Fig. 1, item C) and the ring coupling system (Fig. 1, item E) allowed for the workable implementation of sample insertion, placement, securement (which was particularly important given the small diameter of the flow chambers), and subsequent linkage to an actuator for cyclic flexure/stretch application within the bioreactor. An adequate dynamic range of flow rates was made possible by integrating this novel FSF bioreactor with a peristaltic pump where, either steady or pulsatile flow is possible. In addition, the design will enable more viscous liquids to be efficiently driven through the system.

4.3. Limitations.

A limitation of our current CFD approach is that the flow field near the end of the specimens is likely to have small errors since the specimen holders were not accounted for in our model geometry. However, owing to their small size, the specimen holders would only cause variability to the proximal, local flow field and furthermore, as a general rule, only the belly region of engineered heart valve tissue specimens are typically analyzed, whereas the ends are cut away and discarded. Finally, the fact that we simulated specimen movement during the flow conditions is likely to have contributed toward a high level of accuracy to the prediction of the flow physics thereby rendering the aforementioned errors negligible.

4.4. Conclusions.

We presented a novel bioreactor design that was built for standard incubator housing and successfully tested for gas exchange and sterility for the study of engineered heart valve leaflet tissue formation. An actuator can flex and/or stretch up to 12 specimens (three specimens/chamber with total of four chambers all in parallel) with or without flow and thus, provides a system that can be used to conduct mechanical conditioning-based tissue engineering optimization studies prior to scaling up to more complex trileaflet TEHV experiments. The device focuses on the fluid mechanic advantages inherent to narrow, cylindrical, curved tube geometries that permits physiologically representative magnitudes of shear stress conditioning of relevance to heart valves.

Evidence of collagen production by MSCs was demonstrated in the device. The shear stress range predicted exceeds what we believe to be a plausible limit to the maximum value of physiologically relevant shear stress magnitudes necessary for TEHV studies. The pump and actuator both represent critical elements of the system effectuating flow and cyclic flexure/stretch, respectively, and can be used over long periods with the proviso that they have access to an uninterrupted ac power supply. The pump can operate at much higher flow rates used in this study (up to 2.3 LPM) while the actuator can also be programmed to run up to 6.6 times (i.e., 6.6 Hz or a heart rate of 396 beats/min) higher frequency than that utilized here. Interest in these studies may arise if observing flow, cyclic flexure and/or stretch mechanical conditioning effects of cells and engineered tissues in environments other than adult normalcy, such as in fetal development, in diseased states (e.g., hypertension) and in tachycardia. In addition, investigations on the effect of oscillatory shear stresses on heart valve tissue formation are also possible owing to the large OSI that was observed on the specimen inner wall during cyclic flexure. Overall, the design of the tissue deformation modes (cyclic flexure and/or stretch) in combination with physiological levels of fluid-induced shear stresses make this novel FSF bioreactor a useful tool for mechanical conditioning studies on evolving engineered heart valve tissue constructs.