Inversion of membrane surface charge by trivalent cations probed with a cation-selective channel

Abstract

We demonstrate that the cation-selective channel formed by gramicidin A can be used as a reliable sensor for studying the multivalent ion accumulation at the surfaces of charged lipid membranes and the “charge inversion” phenomenon. In asymmetrically charged membranes with the individual leaflets formed from pure negative and positive lipids bathed by 0.1 M CsCl solutions the channel exhibits current rectification which is comparable to that of a typical n/p semiconductor diode. We show that even at these highly asymmetrical conditions the channel conductance can be satisfactorily described by the electrodiffusion equation in the constant field approximation but, due to predictable limitations, only when the applied voltages do not exceed 50 mV. Analysis of the changes in the voltage-dependent channel conductance upon addition of trivalent cations allows us to gauge their interactions with the membrane surface. The inversion of the sign of the effective surface charge takes place at the concentrations which correlate with the cation size. Specifically, these concentrations are close to 0.05 mM for lanthanum, 0.25 mM for hexaamminecobalt, and 4 mM for spermidine.

1. INTRODUCTION

Long-range electrostatic forces are crucially involved in many interactions within and between biomolecules. Charged groups play the well-recognized roles in functioning of proteins, nucleic acids, phospholipids and their supra-molecular assemblies. Phospholipid molecules, building blocks of cellular membranes, mostly contain zwitterionic or negatively charged headgroups exposed on the membrane/water interface. Membrane surface potential is crucially involved in regulation of membrane transport, cell-cell recognition, and membrane-bound enzymes¹. In the presence of multivalent cations the surface charge screening may be accompanied by its overcompensation, or the so-called “charge inversion” at the membrane surface. This phenomenon has been observed experimentally ^2–12, and discussed in a number of theoretical studies, e.g. ^13–18. Charge inversion by polyvalent ions is thought to be highly relevant for the number of biological processes, including action of drugs ¹⁹, gene delivery ²⁰, DNA condensation⁷, and viral packing ^{21, 22}. However, despite the extensive experimental and theoretical work, problems regarding electrostatics at the charged membrane interfaces, counter-ion screening, and charge inversion phenomenon remain a subject of intense discussions, e.g. ^{11, 23}.

The motivation for this study is two-fold. First, in addition to the biological processes mentioned above, charge inversion could also be involved in regulation of channel function during membrane fusion, which is shown to require the presence of highly charged polypeptide chains ²⁴. Second, most of the approaches for studying charge inversion published so far deal with different modifications of electrokinetic measurements, which involve the notion of a sliding plane. The present study is different in this respect as there is no need to postulate the position of the sliding plane, though we have to use other adjustable parameters as described below. We study the accumulation of multivalent ions at the charged surfaces by using the conductance of an ion channel as a sensor of the potential at the surface of the membrane hosting the channel. With the planar lipid bilayer membranes as established models of cell membranes, the technique of lipid monolayer opposition ²⁵ allows obtaining artificial bilayers with asymmetrical distribution of lipids between the two monolayers. The charge state of the bilayer surface may be probed by measuring ion currents in the presence of lipophilic ions ²⁶, ion transporters ^{27, 28}, or ion pores induced by short peptides ^29–34 and channel-forming proteins ^35–39.

The conductive pore of a benchmark channel formed by pentadecapeptide gramicidin A is composed of two β-helical 15 amino acid monomers and is exclusively permeable for monovalent cations ⁴⁰. As shown in a number of publications, the ion conductance of the gramicidin pore reports well on the charged state of surface bilayer groups. Indeed, charges on the membrane surface attract counter-ions and reduce the concentration of co-ions near the entrance of the pore, thus increasing or decreasing the number of cations, depending on the sign of the surface charge. The effects of the surface charge are particularly strong in electrolytes of low ionic strength.

In the present work we measure the ion conductance of the gramicidin A channel to assess changes in the charge state of phospholipid bilayers as a function of concentration of trivalent ions in the bulk. With 0.1 M cesium as the current-mediating ion we first study the channel conductance in asymmetric bilayers where one monolayer is formed from negatively charged phosphatidylserine (PS) and the other from either neutral phosphatidylcholine (PC) or positively charged trimethylammonium propane (TAP). We demonstrate that at small voltages the gramicidin A channel in asymmetrically charged membranes displays current rectification which is close to that of a typical solid-state diode. We also show that even at these highly asymmetrical conditions, our measurements are reasonably well described by a simple theoretical model of biased diffusion with only two adjustable parameters.

We then investigate the effects of three cations: lanthanum chloride, hexaamminecobalt chloride, and spermidine chloride on negatively charged bilayers. At asymmetrical, one side addition of these trivalent cations the channel conductance becomes asymmetric in applied voltage. Most pronounced reduction of the channel conductance is observed at the voltages that are positive from the side of trivalent cation addition. To estimate the bilayer surface charge in the presence of trivalent cations, we compare the corresponding conductance-voltage relationships with those obtained in control experiments with asymmetrical bilayers formed from lipid monolayers of different charge. All these cations are able to overcompensate the effective surface charge of the PS monolayer at the concentrations that correlate with their size. The most potent is lanthanum, which neutralizes the surface charge felt by the channel at 0.05 mM concentration, followed by hexaamminecobalt with about five-fold higher concentration and then by spermidine with about hundred-fold higher concentration of charge inversion.

2. EXPERIMENTAL METHODS

Bilayer lipid membranes were prepared from diphytanoylphosphoserine (PS), diphytanoylphosphocholine (PC), and dioleoyl trimethylammonium propane (TAP), Avanti Polar Lipids, Alabaster, AL, using monolayer-opposition technique by Montal and Mueller ²⁵. The Teflon chamber, with two (cis and trans) compartments of 1.7 ml, was divided by a 15-μm-thick Teflon partition with a 60–70-μm diameter aperture. PS, PC and TAP monolayers were made from 2 mg/ml aliquots of lipids in pentane. After bilayer formation gramicidin A (a generous gift from O. S. Andersen, Weill Cornell University Medical College) was added from 1–10 nM ethanol stock solutions to both aqueous compartments at the amount sufficient to produce a single channel activity. Buffer solutions contained 100 mM CsCl, 5 mM HEPES at pH 7. Lanthanum chloride (Sigma), hexaamminecobalt chloride (Fluka), and spermidine chloride (Fluka) were admixed from the aliquots to the cis compartment of the membranes, made from PS monolayers. The choice of CsCl over KCl or NaCl was dictated by the fact that the gramicidin channel conductance in CsCl is about 1.8 higher than in KCl and 2.9 higher than in NaCl of the same molarity⁴¹.

The membrane potential was maintained using Ag/AgCl electrodes with 2 M KCl and 15 % (w/v) agarose bridges. The membrane chamber and headstage were isolated from external noise sources with a double metal screen (Amuneal Manufacturing Corp., Philadelphia, PA). Conductance measurements were performed using an Axopatch 200B amplifier (Molecular Devices, Foster City, CA) in the voltage clamp mode. Data were filtered by a low-pass 8-pole Butterworth filter (Model 9002, Frequency Devices, Inc., Haverhill, MA) at 5 kHz, directly saved into the computer memory with a sampling frequency of 10 kHz, and analyzed using pClamp 10 software. All measurements were made at room temperature, T = (23 ± 1) °C. Gramicidin A amplitudes at a given transmembrane voltage were collected from individual single-channel events and calculated by Gaussian fitting of a histogram of ~50 single events.

Liposomes were prepared by sonication according to the Morrissey Laboratory protocol (Morrissey, J. H. 2001. Morrissey laboratory protocol for preparing phospholipid vesicles (SUV) by sonication. http://tf7.org/suv.pdf). Liposome buffer was the same as for bilayer measurements. Liposomes diameter (75–120 nm) was checked with light scattering. Measurement of the liposome ζ-potential and sizing of the liposomes were performed with Zeta-Plus ζ-potential analyzer (Brookhaven Instruments Corporation, Holtsville, NY). Diluted (1:10) PS or TAP liposome solutions in 1.5 ml cuvettes were injected with appropriate amounts of trivalent cations and transferred into the analyzer. PC liposomes were used as a standard of neutrality of the liposome surface in ζ-potential measurements. The measurements were performed at room temperature, T = (23 ± 1) °C.

3. RESULTS AND DISCUSSION

The results of a control experiment with gramicidin A channels incorporated into asymmetric planar lipid bilayers made of the negatively charged lipid (PS, the cis monolayer) and the positively charged lipid (TAP, the trans monolayer) are shown in Figure 1. Raw data in panels A and B and the corresponding current-voltage curves in panel C demonstrate that in asymmetric membranes the channel exhibits a highly non-linear behavior with a significant asymmetry resembling that of a solid-state diode rectifier. The current at +150 mV applied from the side of the negative monolayer is more than an order of magnitude higher than the current at the opposite polarity. Non-linear current-voltage dependencies were first reported for gramicidin A channel in membranes with only one lipid leaflet charged in a classical study by Frohlich ²⁹. Here, in Fig. 1B, C we present experiments with the membranes where the leaflets are oppositely charged.

Figure 1.

A: Currents through single cationic channels formed by gramicidin A in a symmetrically charged membrane do not show rectification. The magnitude of the current steps is independent of the applied voltage polarity. (B) In an asymmetrically charged membrane the current becomes highly sensitive to voltage polarity. At 150 mV, positive from the side of the positive leaflet, the currents are much smaller than those at the opposite polarity. C: The current-voltage characteristic of the channel in an asymmetrically charged membrane (filled diamonds) shows strong rectification, which, within the voltage range of −50 mV to +50 mV, is very close to that of a typical n/p diode. Symmetric membranes were formed from the negatively charged PS; asymmetric membranes were from the positively charged TAP (the cis leaflet) and negatively charged PS (the trans leaflet) in 0.1 M CsCl.

It is instructive to compare the current-voltage characteristic of the gramicidin channel presented in Fig. 1C (filled diamonds) with the typical characteristics of semiconductor n/p diodes. The expression for the diode current I_d as a function of applied voltage V can be written in the form:

$$I_d\propto exp\left(\frac{-eV}{n{k}_{B}T}\right)-1,$$ (1)

where e is the elementary (proton) charge, k_B and T have their standard meaning of the Boltzmann constant and absolute temperature, and n is the so-called “ideality factor” which reflects recombination enhancement by defects. Typically, for semiconductor diodes the value of n is between 1.0 and 2.0 ⁴². Fitting Eq. (1) to the data for small voltages, |V|< 50 mV, in Fig. 1C, we obtain n ⊔ 1.8. Thus, the ionic diode represented by the symmetric gramicidin A channel incorporated into asymmetrically charged bilayer is close by this parameter to its solid state counterparts. However, as both experiment and analytical considerations (see below) demonstrate, at larger voltages the rectification of this “ionic diode” starts to saturate. At voltages higher than ±100 mV the ratio of the currents tends to a constant value.

Rectification in protein channels and synthetic nanopores has been reported in a number of earlier studies. The asymmetry was either an inherent property of the channel ^43–49 or was introduced by a gradient of acidity across the membrane ^{50, 51}. The rectification factor calculated as the ratio of the current in the higher conductance branch of the I/V characteristic to the current at the opposite polarity at ±100 mV reaches about 5.0 or smaller values ^{50, 51}. For example, the rectification factor for the gramicidin channel in the membrane with only one leaflet negatively charged was found to increase with the decreasing salt concentration, but did not exceed 3.0 even when the concentration was reduced to 10 mM (see Fig. 5 of Ref. ²⁹). The rectification factor calculated for ±100 mV from the data in Fig. 1 is close to 7.0, thus representing the so far most efficient ionic diode.

The physics of rectification in a cation-selective channel incorporated in asymmetrically charged membrane is similar to that of a semiconductor diode. In both cases the origin of rectification is the asymmetry in concentration of available charge carriers. However, analytical description as well as the final expressions and their limiting behavior are quite different.

The profile of electric potential across an asymmetrically charged lipid bilayer is schematically shown in Figure 2. In this particular example the cis side monolayer is positively charged, and the trans monolayer is negatively charged. If the potential of the trans side of the membrane-bathing solution at x → ∞ is considered to be zero, the potential at distance z from the trans surface can be calculated using the Gouy-Chapman expression¹

Figure 2.

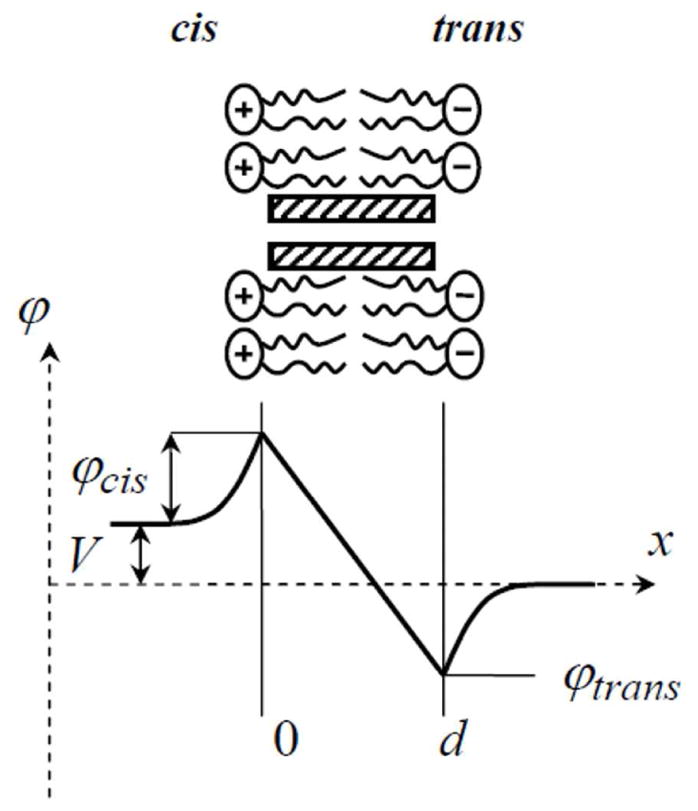
A schematic illustration of potential distribution along the channel axis shows that the total potential difference includes contributions from the surface charge on both sides of the membrane, thus imposing a pronounced asymmetry in the case of oppositely charged leaflets.

$$\phi (z)=\frac{2k_{B}T}{e}ln\left[\frac{1-\gamma exp\left(-z/{\lambda }_D\right)}{1+\gamma exp\left(-z/{\lambda }_D\right)}\right].$$ (2)

Here γ is defined through the Debye length, λ_D = (εε₀k_BT/8πe²c^(b))^1/2, and the Gouy-Chapman length, λ_GC = εε₀k_BT / 2πσe, as $\gamma =\sqrt{{({\lambda }_{GC}/{\lambda }_D)}^2+1}-{\lambda }_{GC}/{\lambda }_D$, where ε is the dielectric constant of the aqueous phase, ε₀ is the permittivity of free space, c^(b) is electrolyte number concentration in the bulk, and σ is the surface charge density. The potential at the cis surface of the membrane is a combination of the applied voltage V and the potential given by Eq. (2) taken with the minus sign to account for the positively charged lipids of the cis side.

Approximation given by Eqs. (2) and (3) for monovalent strong electrolytes after a self-consistent correction ⁵² to relate intrinsic binding constants for protons and ions with their apparent binding constants gives a surprisingly accurate description of the surface potential. This was confirmed in numerous experiments ¹. One of the most recent ones is a surface-sensitive synchrotron X-ray scattering study ⁵³ of Cs distribution in the vicinity of the surface with charge density as high as one elementary charge per 41 Ų. It was shown that for 0.1 M solutions of CsI at neutral pH the corrections to Eq. (3) due to the protonation of lipid headgroup charges are negligible. The protonation turned out to be significant only at much smaller salt concentration.

Another correction described by Ninham and Parsegian ⁵² is due to Cs⁺ binding to the lipid headgroups. This correction seems to be out of reach of the synchrotron X-ray scattering because of the finite resolution function on these experiments ⁵³. Though small, it is readily measurable by other, more traditional methods. For example, it was shown ⁵⁴ that in 0.1 M cesium chloride the ζ-potential of phosphatidylserine vesicles is changed from the “ideal” value of about −90 mV to the experimentally obtained −80 mV, thus giving the intrinsic association constant of cesium cation with this lipid of about 0.05 M⁻¹.

Yet the most significant correction for the potential at the entrance of the channel comes from the finite size of the channel-forming molecule. As a result, the channel entrance feels only a fraction of the potential at the surface given by Eq. (2) for z = 0. This is a well-known fact. To account for this correction researchers introduce the so-called effective distance between the nearest charge and channel entrance ^{30, 34–38, 55}. However, as it was discussed elsewhere ³³ there is no straightforward analytical procedure to calculate the drop in potential because of the generally complex geometry of the system. We will follow one of the ad hoc approaches discussed in a previous study of gramicidin channel in a symmetrically charged lipid bilayer ³³. Specifically, we assume that potentials at the channel entrance can be described by Eq. (2) at some value of z > 0 treated as an adjustable parameter.

The cationic current through a cylindrical channel can be calculated using the following one-dimensional diffusion equation

$$I_c={eA}_{\mathit{eff}}D\left(\frac{dc(x)}{dx}+\frac{e}{k_{B}T}c(x)\frac{d\phi (x)}{dx}\right),$$ (3)

where c(x) and φ(x) are position-dependent cation concentration and potential, correspondingly, A_eff is the effective cross section of the channel and D is the diffusion coefficient of cations in the channel. Potential along the channel axis is distributed as shown in Fig. 2. At x = 0 it is φ_cis + V, at x = d it is φ_trans. In this approach we assume that the flux through the channel is small enough not to disturb equilibrium counter-ion concentrations at the channel entrances. This assumption was repeatedly used to describe conductance properties of lipid bilayers in the presence of charged surface active agents, e.g. ^{56, 57} and synthetic nanopores with fixed charges ⁵⁸. Integrating Eq. (3) between x = 0 and x = d in the constant field approximation, and taking into account the following relations between the bulk concentrations, $c_{\mathit{cis}}^{(b)}$ and $c_{\mathit{trans}}^{(b)}$, and cation concentrations at the channel entrances $c(0)=c_{\mathit{cis}}^{(b)}exp(-e{\phi }_{\mathit{cis}}/k_{B}T)$ and $c(d)=c_{\mathit{trans}}^{(b)}exp(-e{\phi }_{\mathit{trans}}/k_{B}T)$, we have

$$I(V)=\frac{e^2{A}_{\mathit{eff}}D(V+{\phi }_{\mathit{cis}}-{\phi }_{\mathit{trans}})}{k_{B}Td}\frac{c_{\mathit{trans}}^{(b)}-c_{\mathit{cis}}^{(b)}exp\left(\frac{eV}{k_{B}T}\right)}{exp\left(\frac{e{\phi }_{\mathit{trans}}}{k_{B}T}\right)-exp\left(\frac{e(V+{\phi }_{\mathit{cis}})}{k_{B}T}\right)}.$$ (4)

This result can also be obtained from the classical analysis of Neumcke ⁵⁶ in the limit of small surface potentials ³².

Eq. (4) contains only two adjustable parameters. One is the effective cross section of the channel multiplied by the diffusion coefficient of cations in the channel, A_effD. The other one is the effective distance z in Eq. (2). The rest of the parameters in Eqs. (2) – (4) are given by structural data (the length of the gramicidin channel ⁵⁹, d = 2.2 nm) and by the surface charge density σ, which, in principle, can be measured independently. However, different studies give significantly different estimates for its value. Depending on the study, σ varies from as high as 0.32 C/m^{2 37} to as low as 0.2 C/m^{2 60}, assuming one elementary charge per lipid headgroup). Even for the structurally close lipids estimates for the surface charge can differ significantly, with the carrier conductance method ²⁷ giving higher charge densities ³³ than it may follow from the lipid packing densities obtained with X-ray methods ^{61, 62}. The reasons for these discrepancies are not clear, but could be tentatively attributed to the membrane dipole potential influencing carrier conductance. Because of this uncertainty we assume that σ = 0.25 C/m², keeping in mind that the error in the surface charge density could be compensated by the adjustable parameter z in Eq. (2) used to calculate the potentials φ_cis and φ_trans at the channel entrances. Indeed, if the actual σ is smaller than the assumed, it could be corrected by the choice of a smaller z, and vice versa.

It is seen that Eq. (4) differs significantly from Eq. (1) for the current-voltage relationship for a n/p semiconductor diode. In particular, analysis of Eq. (4) at the high applied voltages predicts linear, Ohmic behavior with the current rectification ratio at |V| →∞ tending to a constant value of

$${\left|\frac{I(-V)}{I(V)}\right||}_{V\to \infty }=\frac{c_{\mathit{trans}}^{(b)}}{c_{\mathit{cis}}^{(b)}}exp\left[\frac{e\left({\phi }_{\mathit{cis}}-{\phi }_{\mathit{trans}}\right)}{k_{B}T}\right].$$ (5)

Figure 3 illustrates the best fit of Eq. (4) to the data for PS/TAP and PS/PC bilayers. The fitting parameters are A_effD = 7.3×10⁻²⁹ m⁴/s and z = 0.55 nm. The agreement between the experiment and the model is good for the applied voltages in the range |V| ≤ 50 mV. The systematic deviations at higher voltages are expected consequences of the model limitations. At large negative biases the conductance tends to saturate because the channel approaches the states of the maximum ion occupancy ⁴⁰; at high positive biases the diffusion-limited access starts to dominate ⁶³. Nevertheless, the correspondence bonetween the model and experiment at small voltages suggests that the origin of the rectification is in enrichment of penetrating charge carriers at the surface of the negatively charged lipid leaflet and their depletion at the surface of the positively charged one.

Figure 3.

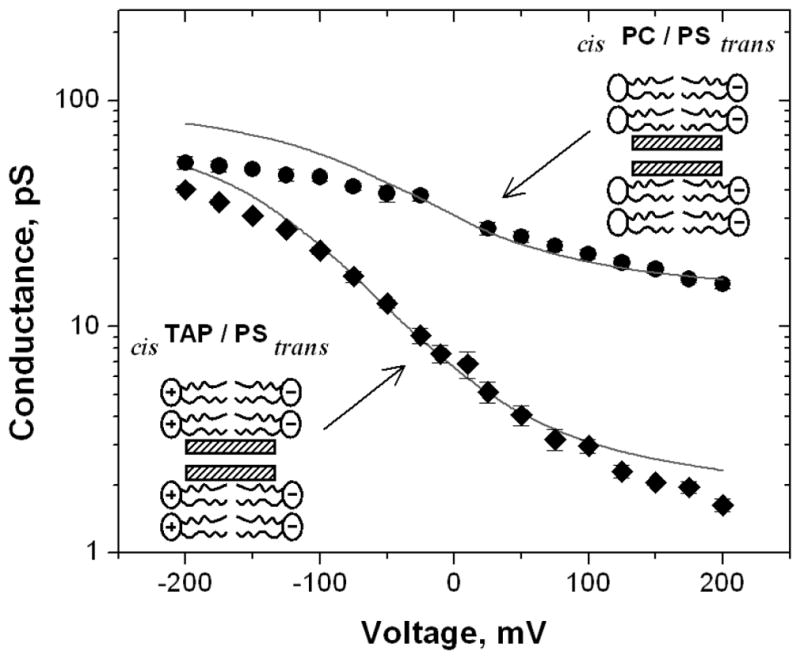
The dependence of the channel conductance on voltage in asymmetrically charged bilayers can be attributed to the different density of cations at the two surfaces of the membrane. The solid lines through the data are for both positive/negative and neutral/negative membranes are drawn according to Eqs. (2) and (4) with two adjustable parameters. They are the effective distance z from the nearest lipid charge to the channel entrance, Eq. (2), and the product of the channel cross section by diffusion coefficient, Eq. (4). The deviations at high voltage are expected due to the saturation effects mentioned in the text.

Addition of trivalent cations to the negatively charged membranes (PS/PS) decreases the channel conductance at both polarities of the applied voltage, but much more profoundly at voltages that are positive at the side of trivalent cation addition. Figure 4 gives raw data in the form of channel current records (represented as conductance for the convenience of comparison) at plus and minus 100 mV at increasing La⁺³ concentrations. While in symmetrically charged membranes in the absence of La⁺³ the amplitudes of the currents at negative and positive voltages are indeed equal, the one-sided La⁺³ addition introduces asymmetry: the conductance at positive voltages is larger than its counterpart at negative ones. The effect is hardly discernible at 1 μM of lanthanum chloride, but is quite obvious for the higher concentrations.

Figure 4.

The effect of trivalent cation addition is seen as a reduction of the currents through the single channels initially reconstituted into PS/PS (negative/negative) membrane. Increased lanthanum chloride concentrations, added from cis side only, progressively decrease the cationic current through the channel for both polarities; however, the effect is larger at potentials positive from the side of trivalent cation addition.

The trivalent cation accumulation at the membrane surface can be analyzed and quantified with the help of Eqs. (2) and (4) with the membrane surface charge used as an adjustable parameter. As we are interested only in the trivalent cation concentration that inverses the charge of the membrane surface, the straightforward way is to compare the channel conductance in the presence of trivalent cations with that of the channel in an asymmetric charged/neutral membrane. Figure 5 shows such a comparison for the channel conductances interpolated to zero voltage for PS/PS membranes in the presence of trivalent cations in the cis side of the cell and the channels in PS/PC membranes. It is seen that at their increasing concentrations, all three cations first decrease the effective surface charge of the cis leaflet of the membrane and then inverse its sign when the channel conductance becomes decreases below its value in PS/PC membranes. Specifically, charge inversion takes place at the concentrations exceeding (0.048±0.004) mM for lanthanum, (0.25±0.03) mM for hexaamminecobalt, and (4.3±0.8) mM for spermidine. The charge inverting concentration for lanthanum is close to that reported in recent experiments with PS liposomes ⁶⁴.

Figure 5.

Addition of trivalent cations to the membrane-bathing solution not only compensates the negative charge of the cis leaflet of the initially negative/negative membrane, but, at a certain concentration, overcompensates it. Trivalent cations were added to the cis side of the reconstitution cell. The data-points are interpolations of single-channel conductance, which was measured in a range of applied voltages similarly to the data in Figs. 1 and 3, to zero voltage. The inversion of the effective surface charge happens when the channel conductance, as a function of trivalent cation concentration, crosses the level corresponding to its value in the neutral/negative membrane.

To verify our finding with the cation-selective channel conductance, we also performed more traditional measurements of liposome ζ-potential, which were repeatedly used to study the charge inversion phenomenon (e.g., ^{11, 12} and references therein). The data obtained by the two methods are compared in Table 1 that shows reasonable agreement.

Table 1.

Trivalent cation	Cation concentration producing the effective surface charge inversion of membrane surface, mM
	GrA channel conductance	ζ-potential of liposomes
Lanthanum	0.048±0.004	0.058±0.014
Hexaamminecobalt	0.25±0.03	0.42±0.14
Spermidine	4.3±0.8	3.4±0.9

Though there is still no consensus on the adequate theoretical description of the charge inversion phenomenon, our data suggest that the charge reversing concentrations correlate with the cation size. The smaller the cation size, the smaller is the concentration. This observation may support one of the available approaches that explains the phenomenon by the gain of entropy upon release of counter-ions ¹⁵ (see also ref. ¹⁸). The impact of the ion size on short-range correlations and on the charge inversion in electrolyte mixtures was recently investigated using Monte Carlo simulations ^{65, 66}.

4. CONCLUSIONS

We use the effects of the surface charge on the conductance of an ion channel embedded inside the object under study – a lipid bilayer. We show that analysis of the current-voltage dependences of the cation-selective channel, gramicidin A, is a reliable method for studies of multivalent ion adsorption to the membrane surface. Control experiments with the asymmetrically charged membranes serve as a consistent calibration of the membrane surface potential and its modification by multivalent ions and permit characterization of the surface charge state. In particular, we find that:

In asymmetric membranes formed by opposing monolayers of pure PS and TAP at the salt concentrations close to physiological, the current-voltage relationship of the channel at small voltages displays rectification characterized by the parameters that are typical for semiconductor n/p diodes.

Accumulation of multivalent ions at the membrane surface and the corresponding changes of the effective surface charge can be seen through the changes in the channel conductance. For the negatively charged PS membrane in 0.1 M CsCl its surface charge can be compensated and overcompensated by trivalent cations with the surface charge inversion observed at the concentrations in a series lanthanum < hexaamminecobalt ≪ spermidine, which correlates with the cation size.